Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps
Abstract
:1. Introduction
2. Mathematical Models
2.1. Non-Newtonian Fluid Models
2.2. Turbulent Models
3. Model Description
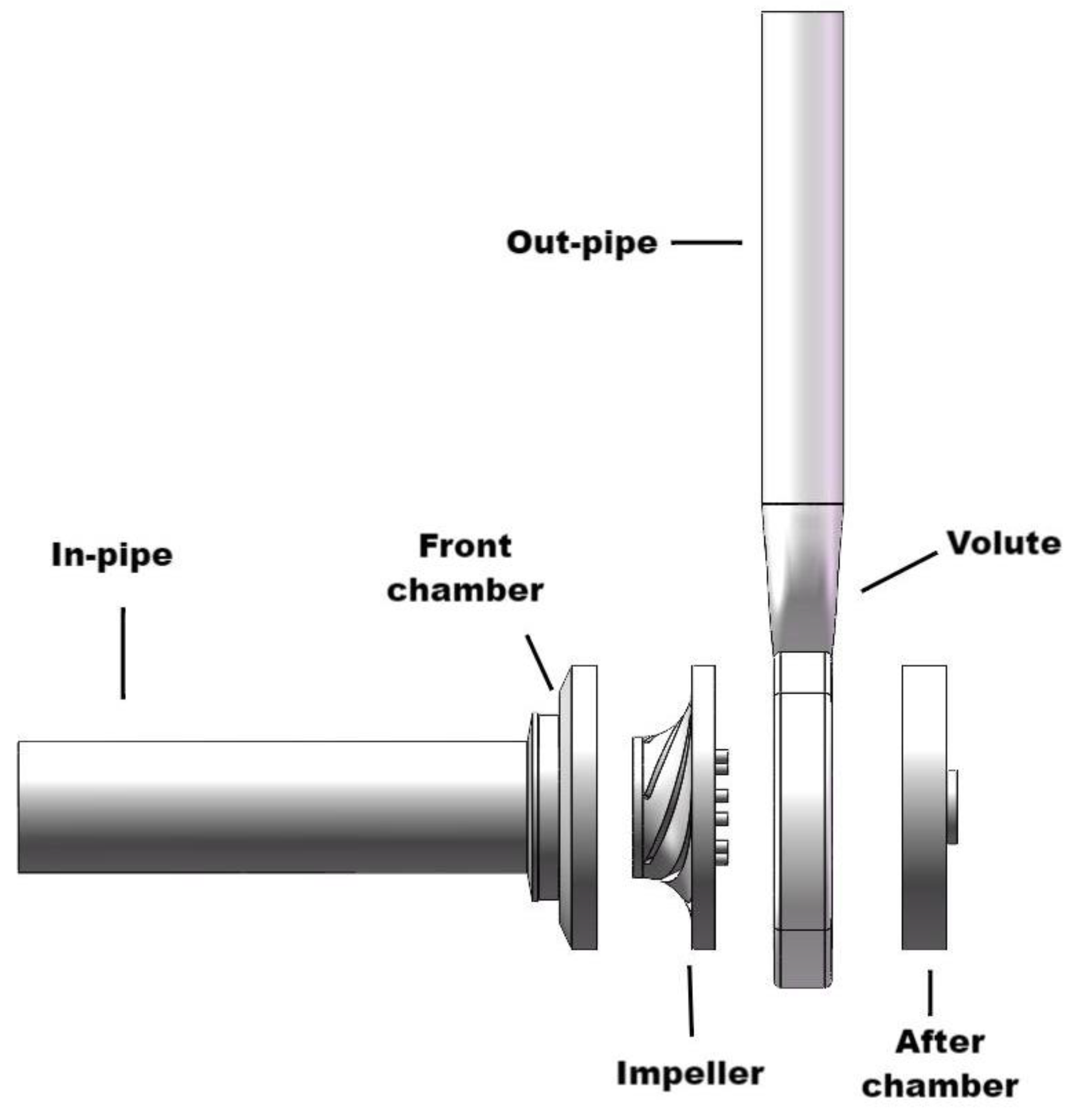
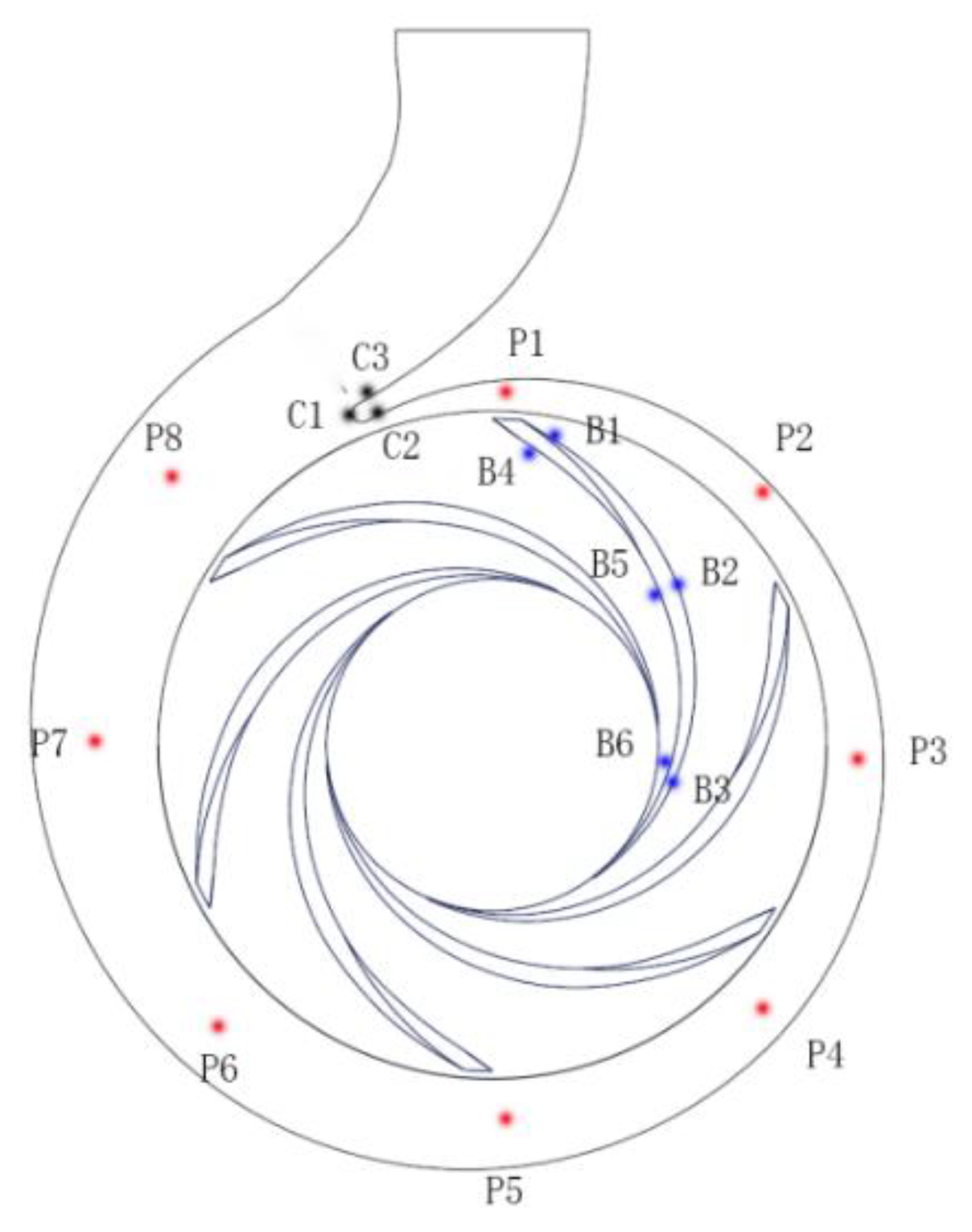
3.1. Computational Domain and Meshing
3.2. Grid Independence Tests and Model Validation
4. Results and Discussion
4.1. Pump Performance
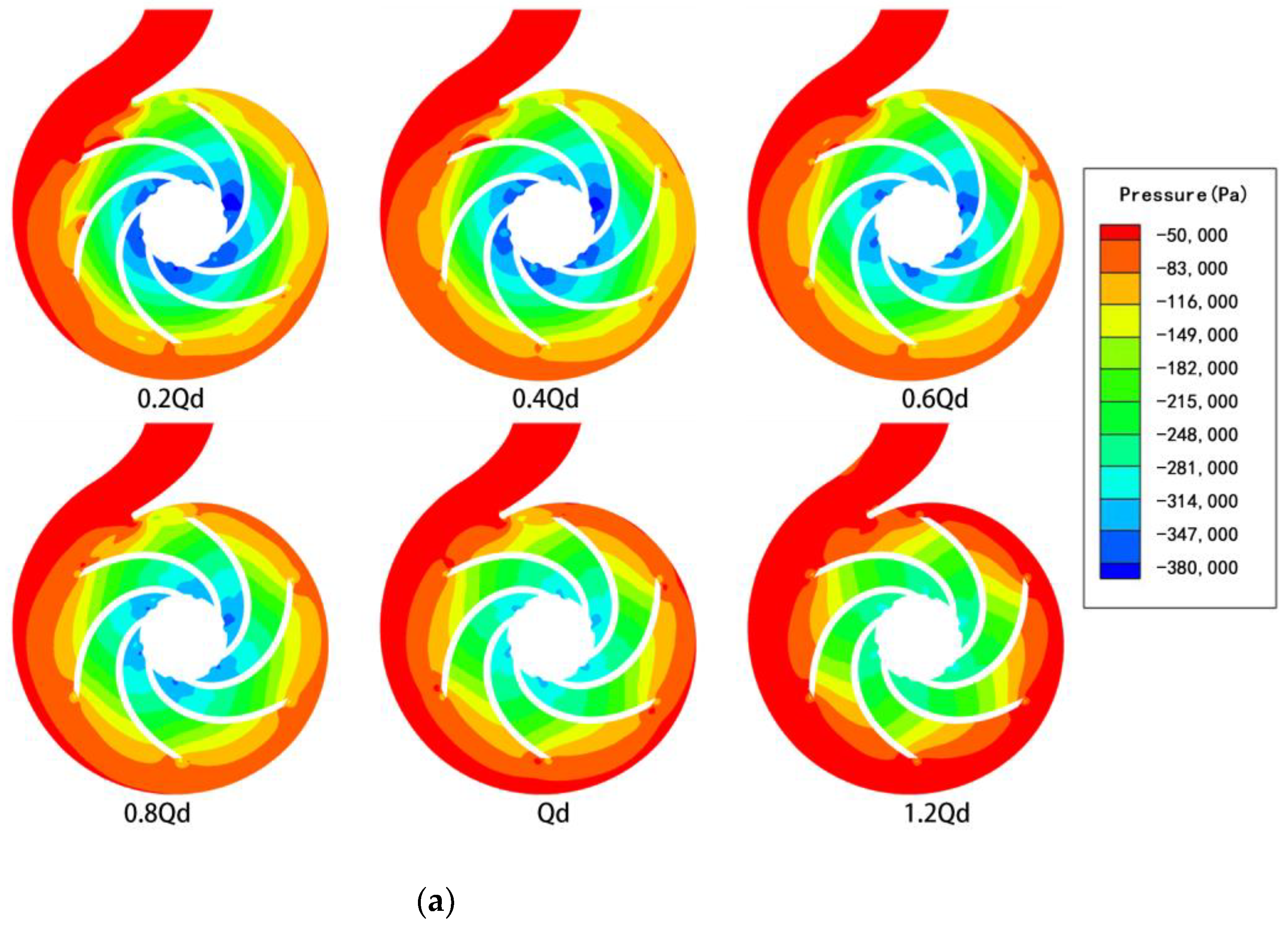
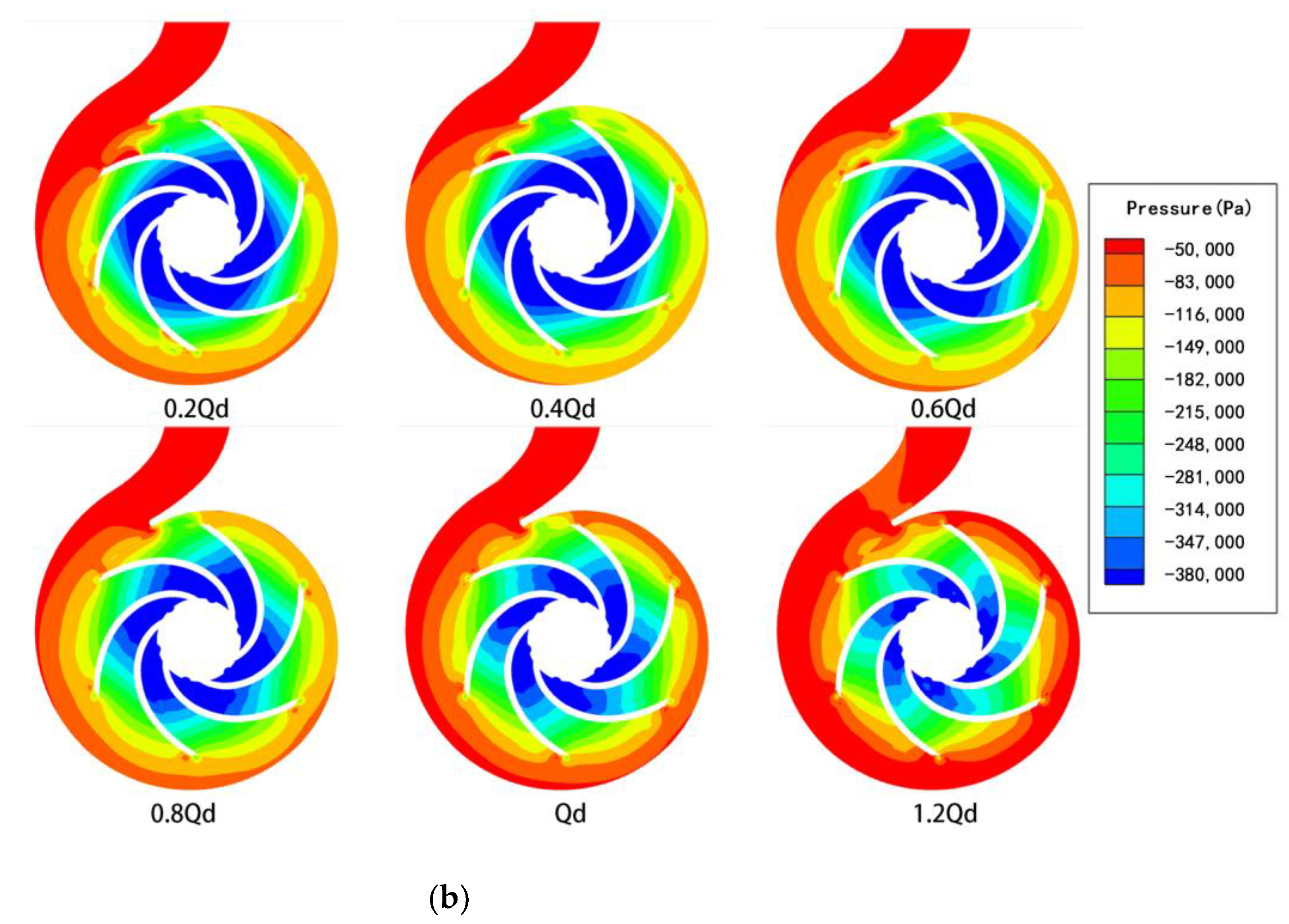
4.2. Pressure Distributions
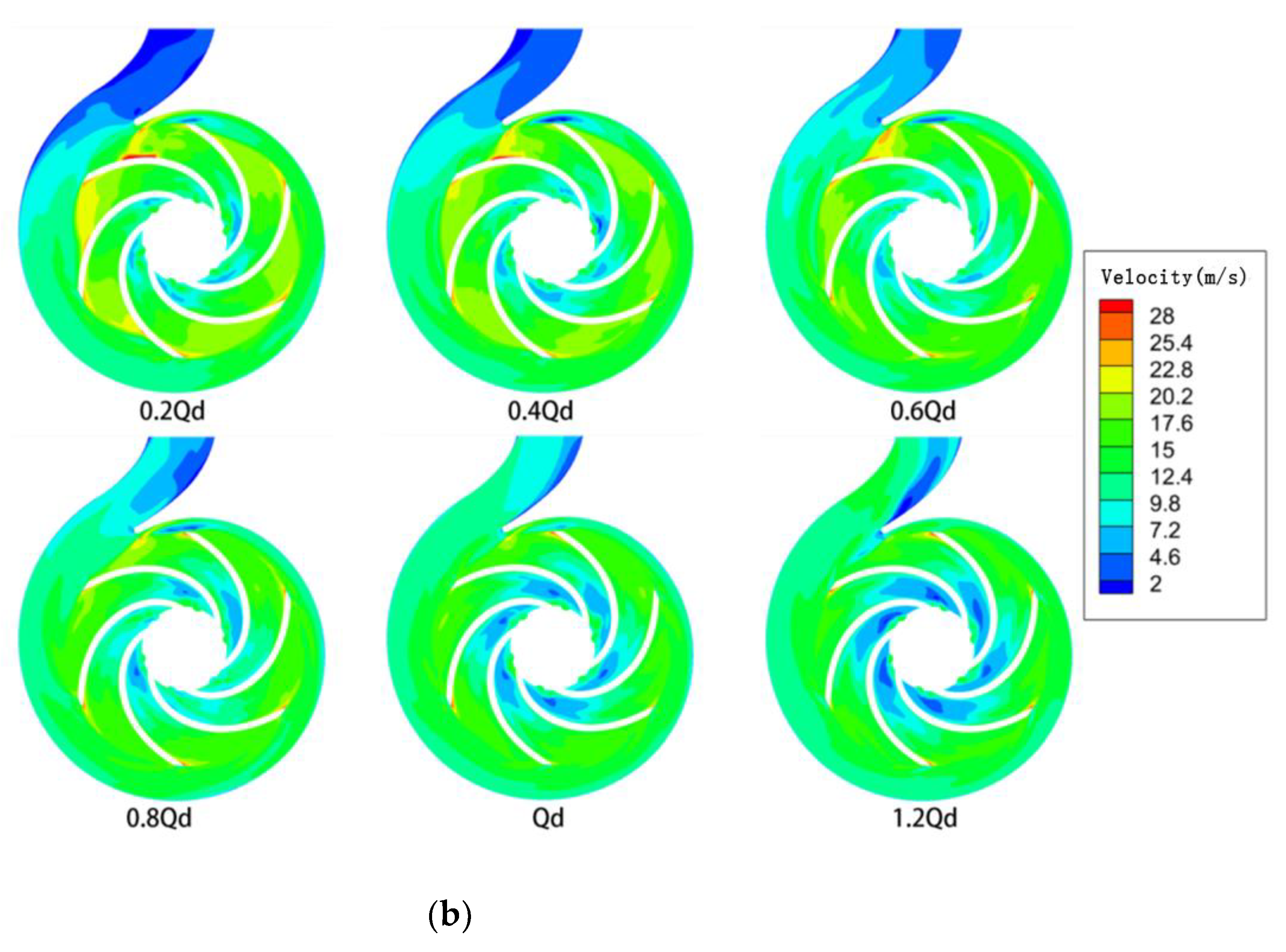
4.3. Turbulent Kinetic Energy and Velocity Distributions
5. Conclusions
- The blades consumed mechanical energy through friction with the fluid contact during the operation of the centrifugal pump. The viscosity of the drilling fluid was higher than that of the water. Therefore, the head and efficiency of the drilling fluid were lesser than those of the water at the same flow rate. However, stronger torque and lager power were generated for the drilling-fluid cases. In practice, when transporting high-viscosity non-Newtonian fluids, attention should be paid to the reasonable use of larger rotating speeds in centrifugal pumps as a means of achieving greater efficiency.
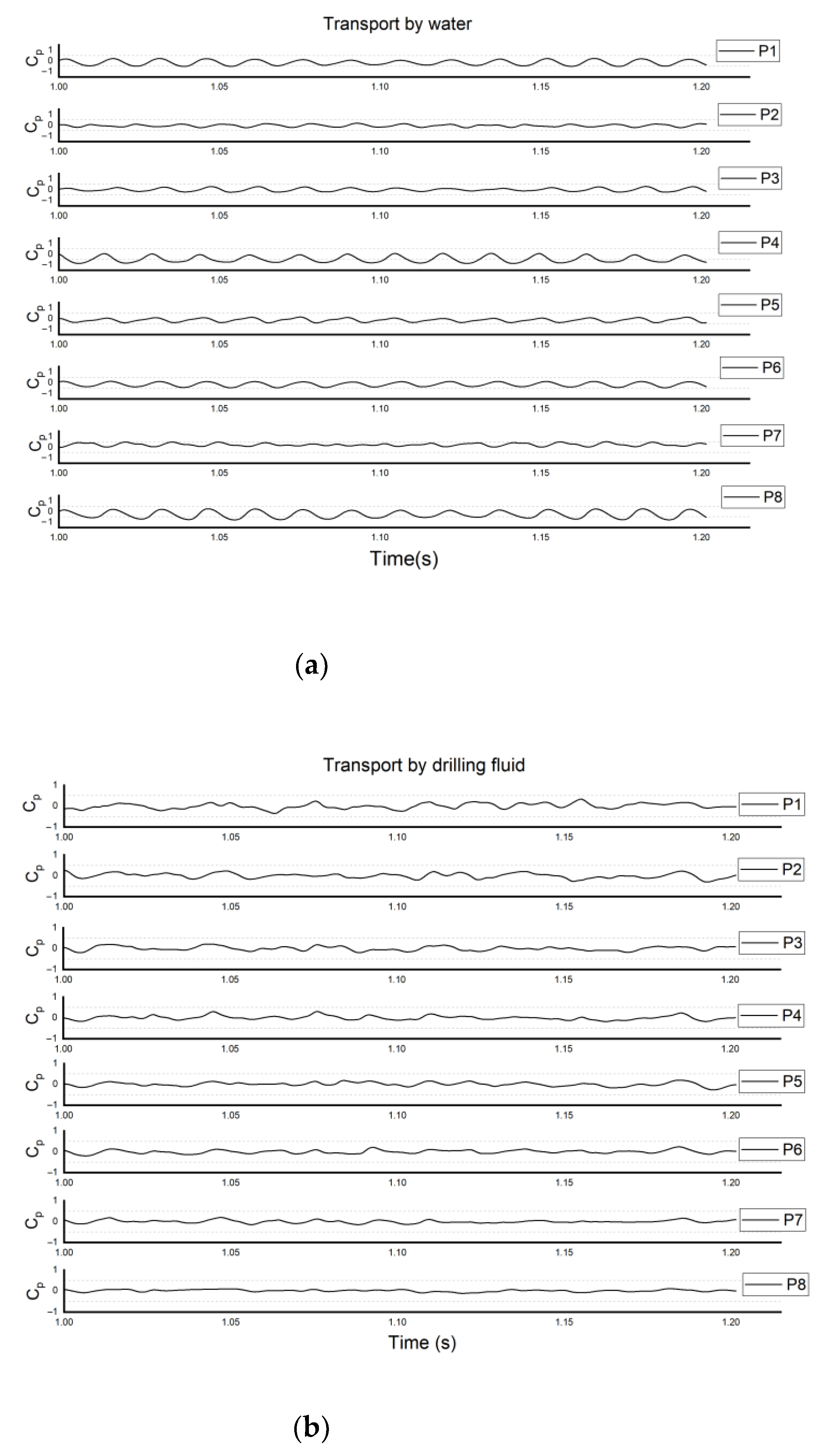
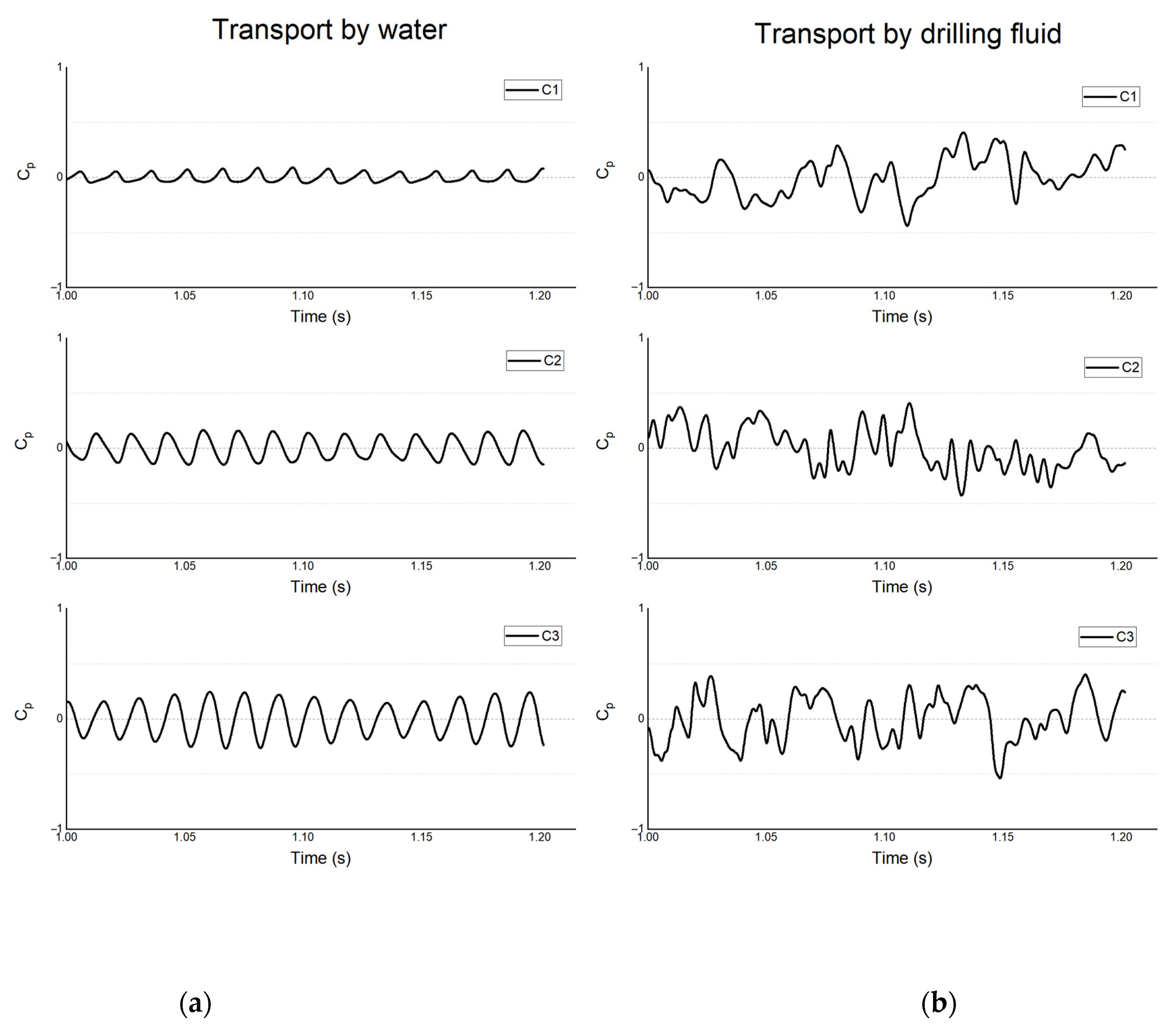
- For the drilling-fluid cases, irregular variations in pressure distribution were observed, which could be attributed to the effects of viscous forces causing the fluid to cling to the volute wall. The pressure did not change with changes in the mode of impeller rotation. This could be attributed to the blocking effect of the volute. This affected the flow conditions under different viscosity conditions and potentially contributed to the differences in the radial or axial velocity at the different cross-sections. It was also observed that the nature of the fluid flow in the small cross-sections of the volute was highly sensitive to the rotation of the rotor.
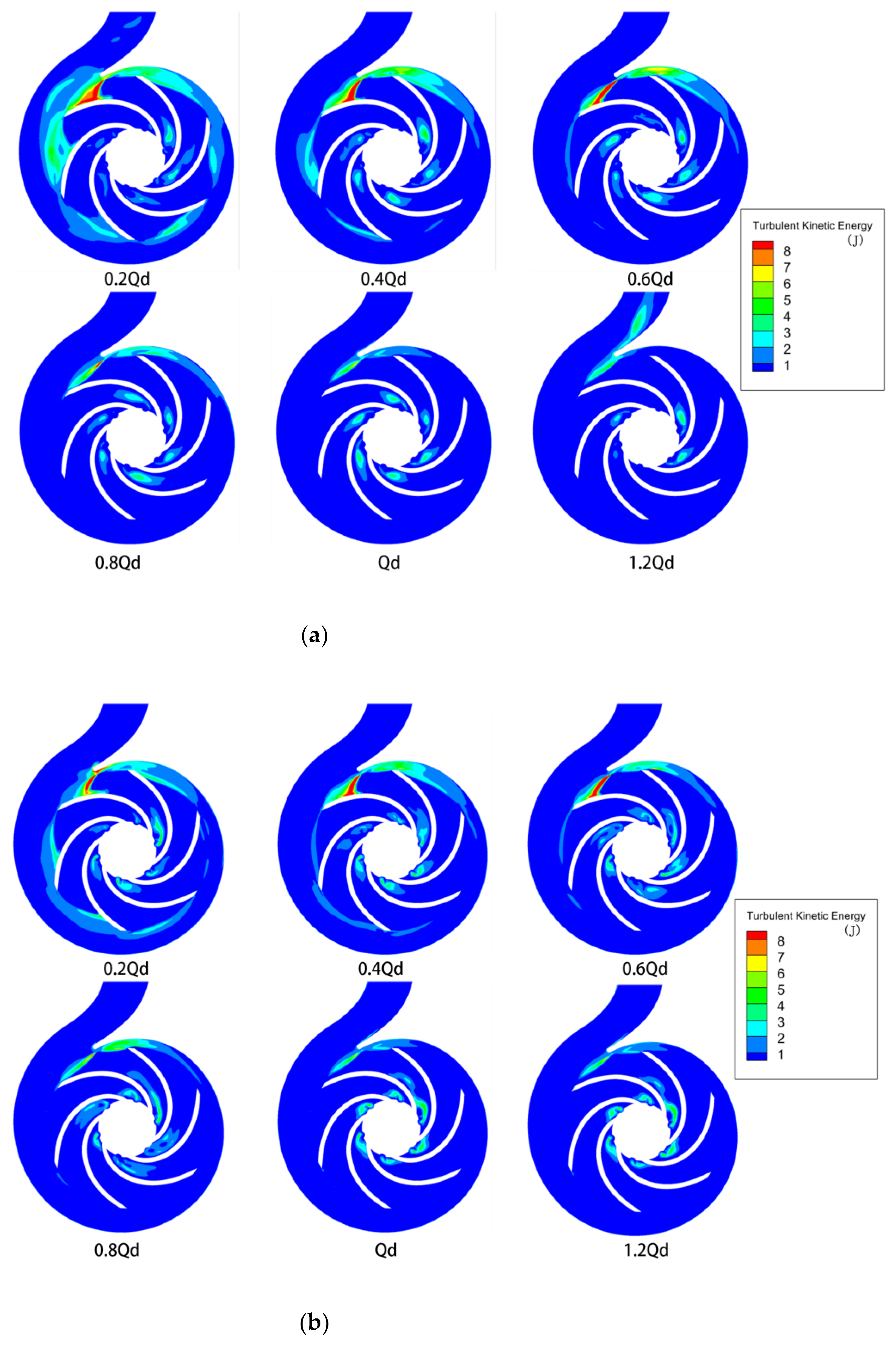
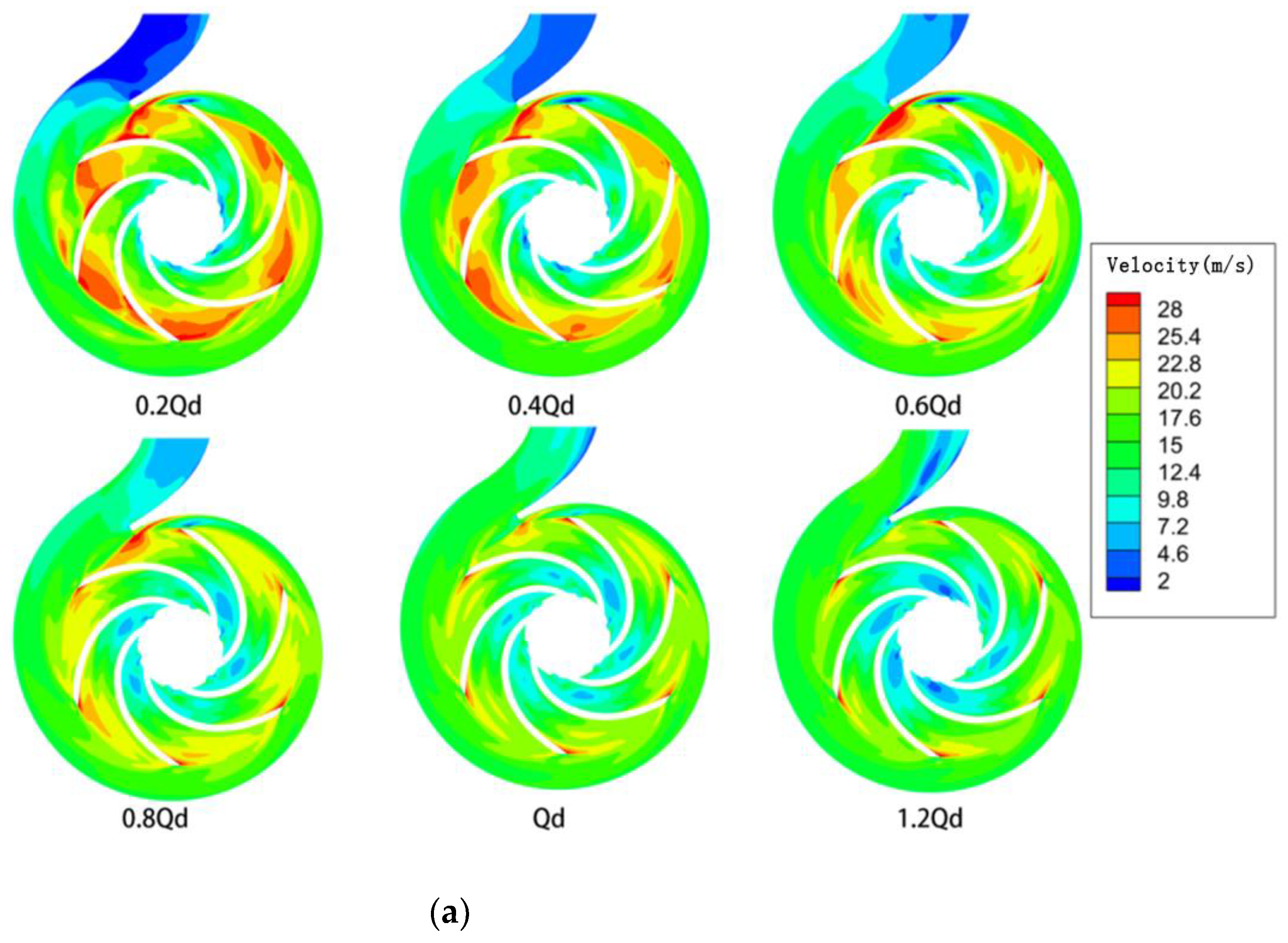
- When the pump drew the power-law fluid, as the flow rate increased and after it flowed into the stationary front chamber, its velocity gradually decreased. This resulted in flow detachment at the back of the blades. At the same time, the non-Newtonian fluid became less detached from the flow at the blade, and swirls were generated at the impeller inlet. The effects of shear collision exerted on the outlet fluid of the impeller and the fluid in the snail casing area, as well as the dynamic and static interferences, made the non-Newtonian power-law fluid consume more mechanical energy than the water.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guan, X.F. Modern Pump Theory and Design; China Astronautic Publishing House: Beijing, China, 2011. [Google Scholar]
- Lee, T.H. Centrifugal Pumps. In Drilling Fluids Processing Handbook; Elsevier Inc.: Newyork, NY, USA, 2005; pp. 465–520. [Google Scholar]
- Pumps, S. Centrifugal Pump Handbook, 3rd ed.; Sulzer Pumps Ltd.: Winterthur, Switzerland, 2010. [Google Scholar]
- Wu, Y.; Li, S.; Liu, S.; Dou, H.S.; Qian, Z. Vibration of Hydraulic Machinery; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Brennen, C.E. Hydrodynamics of Pumps: Preface; Cambridge University Press: Oxford, UK, 2011; pp. 105–132. [Google Scholar] [CrossRef] [Green Version]
- Kang, C.; Zhang, G.; Li, B.; Feng, Y.; Zhang, Z. Virtual reconstruction and performance assessment of an eroded centrifugal pump impeller. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2340–2348. [Google Scholar] [CrossRef]
- Kalombo, J.; Haldenwang, R.; Chhabra, R.P.; Fester, V.G. Centrifugal Pump Derating for Non-Newtonian Slurries. J. Fluids Eng. 2014, 136, 031302. [Google Scholar] [CrossRef]
- Leuprecht, A.; Perktold, K. Computer Simulation of Non-Newtonian Effects on Blood Flow in Large Arteries. Comput. Meth. Biomech. Biomed. Eng. 2001, 4, 149–163. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Yuan, S.; Liu, H.; Tan, M. Three-Dimensional Coupled Impeller-Volute Simulation of Flow in Centrifugal Pump and Performance Prediction. Chin. J. Mech. Eng. 2006, 19, 59–62. [Google Scholar] [CrossRef]
- Pullum, L.; Graham, L.J.W.; Rudman, M. Centrifugal pump performance calculation for homogeneous and complex heterogeneous suspensions. J. South. Afr. Inst. Min. Metall. 2007, 107, 373–379. [Google Scholar] [CrossRef] [Green Version]
- Graham, L.; Pullum, L.; Slatter, P.; Sery, G.; Rudman, M. Centrifugal Pump Performance Calculation for Homogeneous Suspensions; Wiley: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Crawford, J.; Sittert, F.V.; Walt, M.V.D. The performance of centrifugal pumps when pumping ultra-viscous paste slurries. J. S. Afr. Inst. Min. Metall. 2011, 112, 959–964. [Google Scholar] [CrossRef]
- Ma, X.D.; Li, Z.F.; Yu, H.; Wu, D.Z.; Wang, L.Q. Experimental Study on a Medium Consistency Pump. J. Fluids Eng. 2013, 135, 104503. [Google Scholar] [CrossRef]
- Zhou, W.Y.; Yu, D.; Wang, Y.; Shi, J.; Gan, B. Research on the Fluid-induced Excitation Characteristics of the Centrifugal Pump Considering the Compound Whirl Effect. Facta Univ. Ser. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Xuan, L.N.; Huan, X.L. The Simulation of Non-Newtonian Power-Law Fluid Flow in a Centrifugal Pump Impeller. J. Appl. Mech. Eng. 2016, 5, 381–390. [Google Scholar] [CrossRef]
- Aldi, N.; Buratto, C.; Casari, N.; Dainese, D.; Mazzanti, V.; Mollica, F.; Munari, E.; Occari, M.; Pinelli, M.; Randi, S. Experimental and Numerical Analysis of a Non-Newtonian Fluids Processing Pump. Energy Procedia 2017, 126, 762–769. [Google Scholar] [CrossRef]
- Aldi, N.; Buratto, C.; Pinelli, M.; Spina, P.R.; Suman, A.; Casari, N. CFD Analysis of a Non-newtonian Fluids Processing Pump. Energy Procedia 2016, 101, 742–749. [Google Scholar] [CrossRef]
- Buratto, C.; Occari, M.; Aldi, N.; Casari, N.; Suman, A. Centrifugal pumps performance estimation with non-Newtonian fluids: Review and critical analysis. In Proceedings of the European Conference on Turbomachinery Fluid Dynamics & Hermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Mrinal, K.R.; Siddique, M.H.; Samad, A. Performance prediction of a centrifugal pump delivering non-Newtonian slurry. Part. Sci. Technol. 2018, 36, 38–45. [Google Scholar] [CrossRef]
- Valdés, J.; Becerra, D.; Rozo, D.; Cediel, A.; Ratkovich, N. Comparative analysis of an electrical submersible Pump’s performance handling viscous Newtonian and non-Newtonian fluids through experimental and CFD approaches. J. Pet. Sci. Eng. 2019, 187, 106749. [Google Scholar] [CrossRef]
- Donmez, M.; Yemenici, O. A Numerical Study on Centrifugal Pump Performance with the Influence of Non-Newtonian Fluids. Int. J. Sci. 2019, 8, 39–45. [Google Scholar] [CrossRef]
- Abdolahnejad, E.; Moghimi, M.; Derakhshan, S. Experimental and numerical investigation of slip factor reduction in centrifugal slurry pump. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 179. [Google Scholar] [CrossRef]
- Achour, L.; Specklin, M.; Belaidi, I.; Kouidri, S. Numerical Assessment of the Hydrodynamic Behavior of a Volute Centrifugal Pump Handling Emulsion. Entropy 2022, 24, 221. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Fan, H.; Ji, R.; Li, C.; Wang, Y. Four-Parameter Rheological Model and Its Application in Cementing Slurry. Pet. Drill. Tech. 2013, 41, 76–81. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Turbulence, Heat and Mass Transfer 4; Begell House, Inc.: Newyork, NY, USA, 2003; pp. 625–632. [Google Scholar]
- Zheng, L. Unsteady Flow Mechanism of Centrifugal Pump Port Ring Clearance. Ph.D. Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2019. [Google Scholar]







| Parameters | Value | |
|---|---|---|
| Design flow rate | 45 m3/h | |
| Design head | 31.8 m | |
| Design efficiency | 66.85% | |
| Rated speed | 2900 rpm | |
| Specific speed | 90 | |
| Number of blades | Z | 6 |
| Volute inlet diameter | 86 mm | |
| Volute outlet diameter | 161 mm | |
| Volute base circle diameter | 173 mm | |
| Pump inlet diameter | 80 mm | |
| Pump outlet diameter | 50 mm | |
| Mesh | Impeller | Volute | Front Chamber | After Chamber | In-Pipe | Out-Pipe | Total |
|---|---|---|---|---|---|---|---|
| 1 | 449,862 | 53,480 | 145,495 | 307,532 | 147,355 | 412,901 | 1,516,625 |
| 2 | 872,733 | 600,705 | 297,415 | 307,532 | 83,289 | 108,078 | 2,267,952 |
| 3 | 1,333,972 | 1,251,006 | 297,415 | 307,532 | 83,289 | 108,078 | 3,381,292 |
| 4 | 1,333,972 | 1,251,006 | 500,475 | 500,873 | 195,580 | 235,695 | 4,017,601 |
| 5 | 1,676,438 | 1,965,268 | 500,475 | 500,873 | 195,580 | 235,695 | 5,074,329 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Li, K.; Su, W.; Zhao, X. Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps. Water 2023, 15, 992. https://doi.org/10.3390/w15050992
Hu J, Li K, Su W, Zhao X. Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps. Water. 2023; 15(5):992. https://doi.org/10.3390/w15050992
Chicago/Turabian StyleHu, Jianxin, Ke Li, Wenfeng Su, and Xinyi Zhao. 2023. "Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps" Water 15, no. 5: 992. https://doi.org/10.3390/w15050992





