The Copula Application for Analysis of the Flood Threat at the River Confluences in the Danube River Basin in Slovakia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Method
3. Results
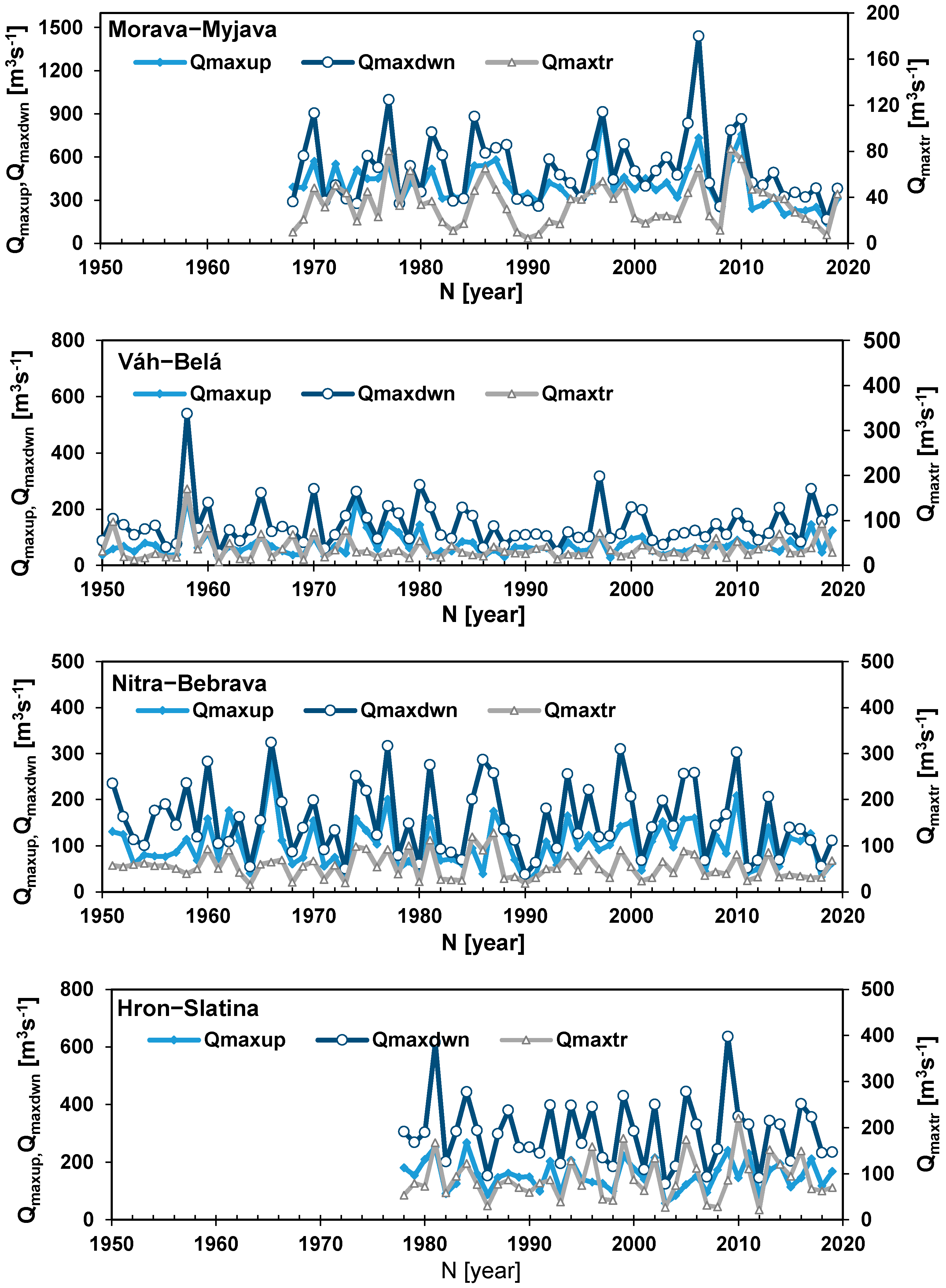
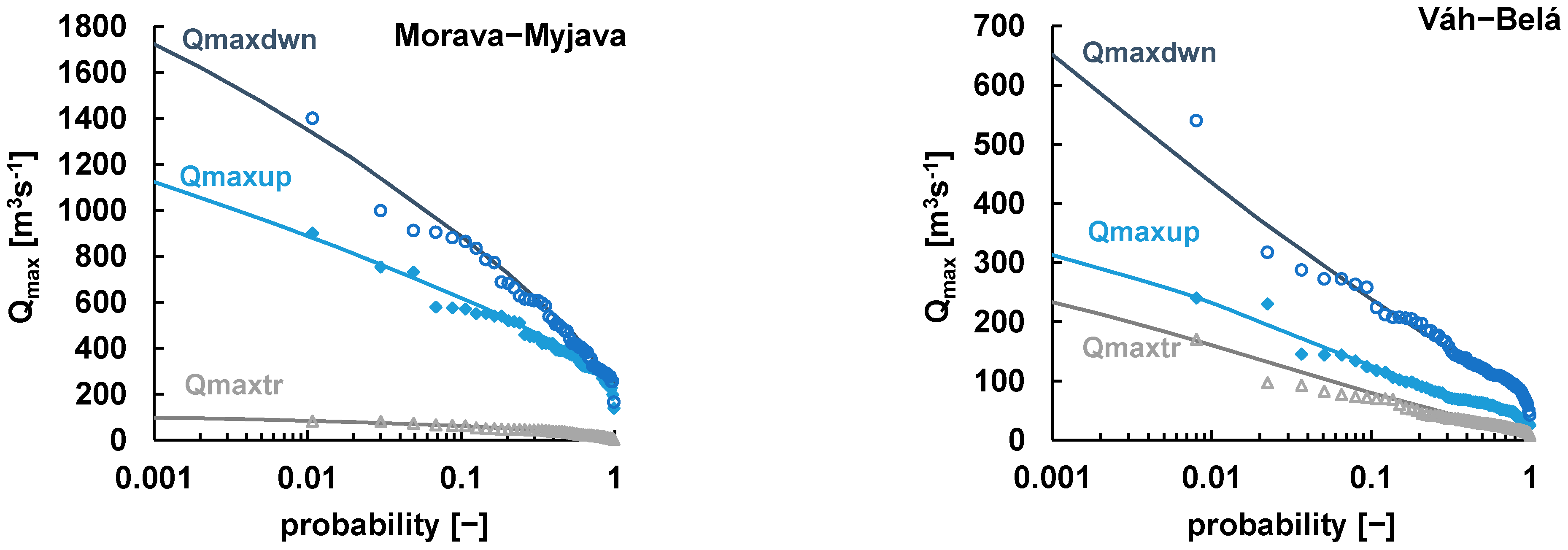
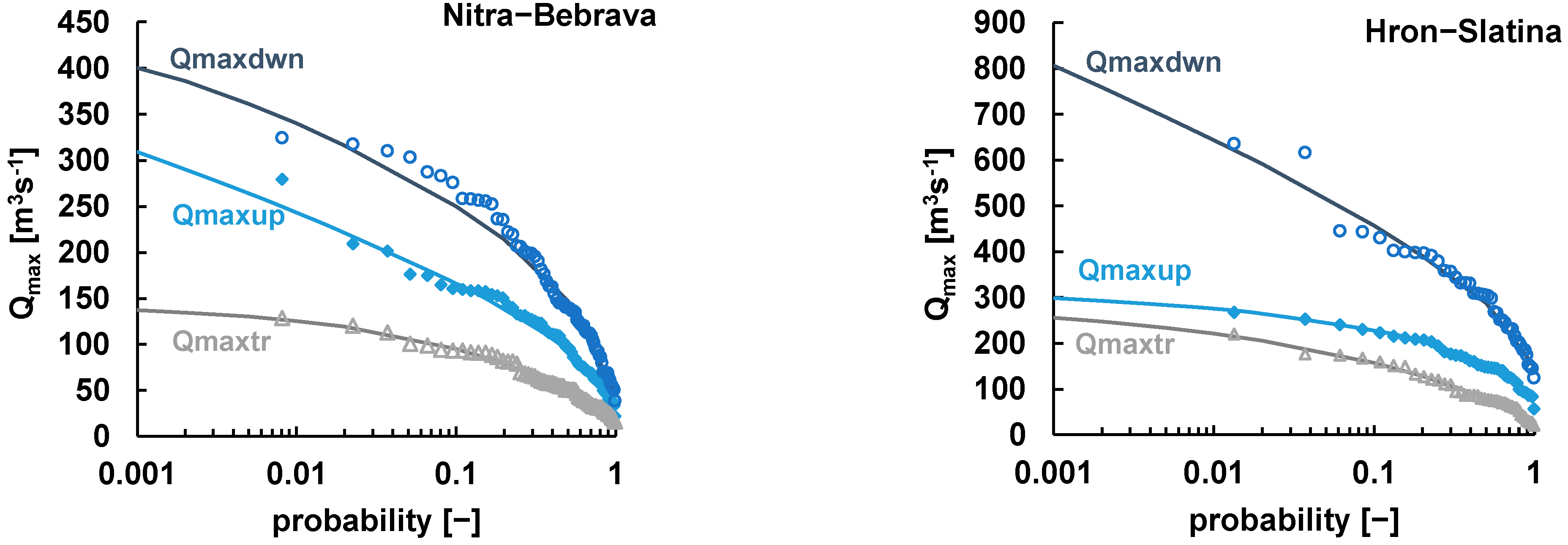
3.1. Univariate Statistical Analysis of Flood Hazards
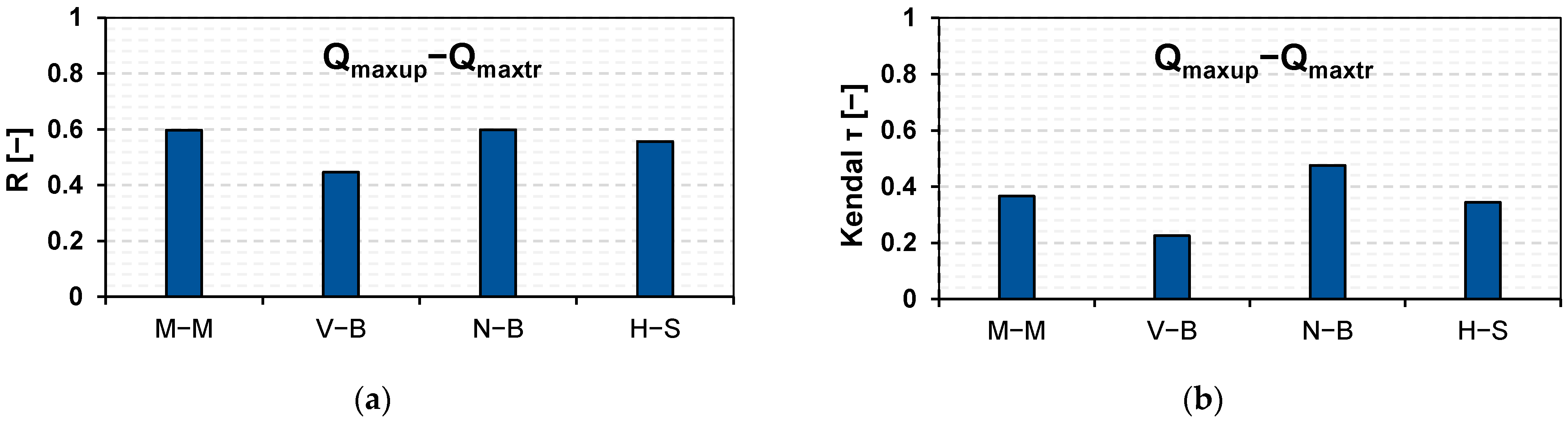
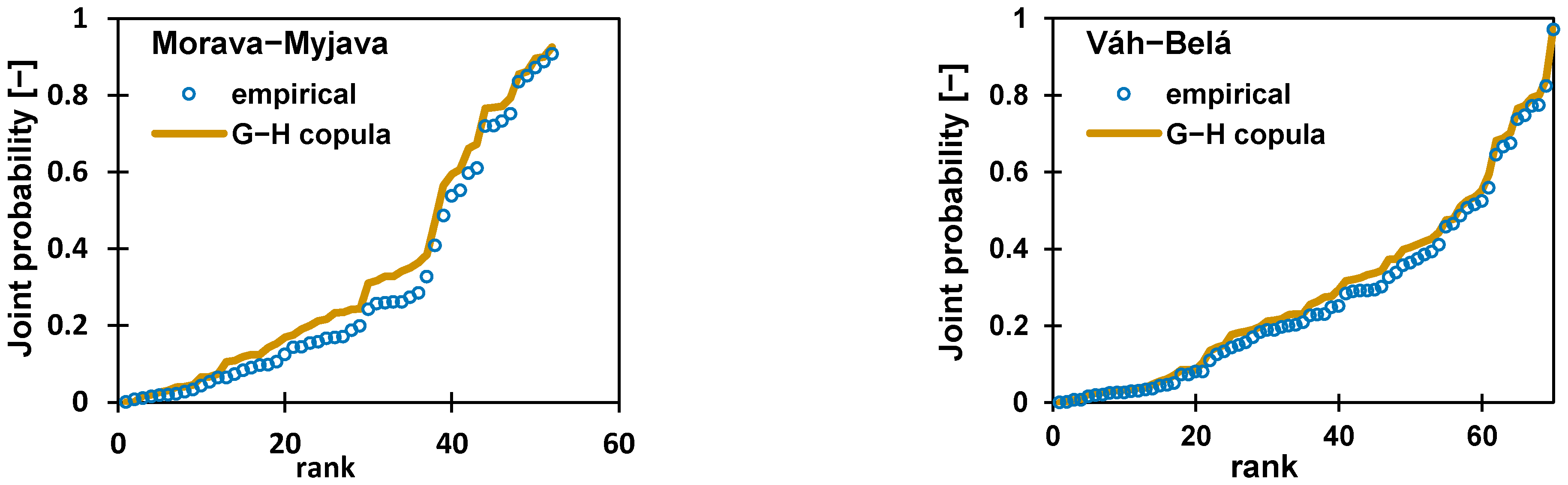
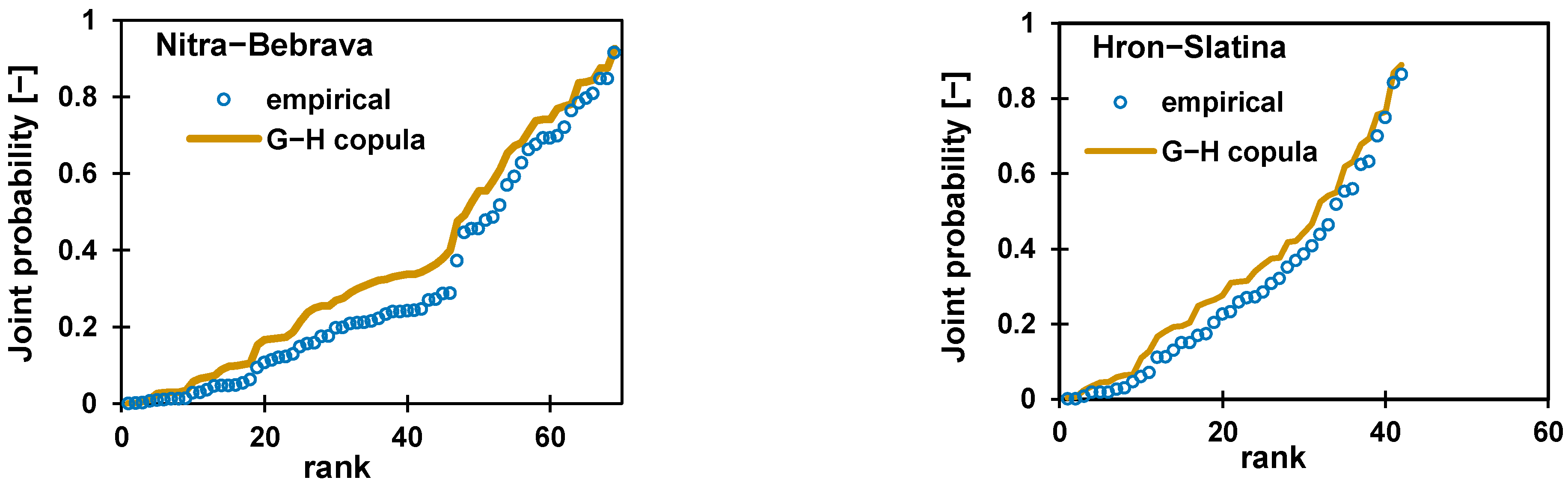
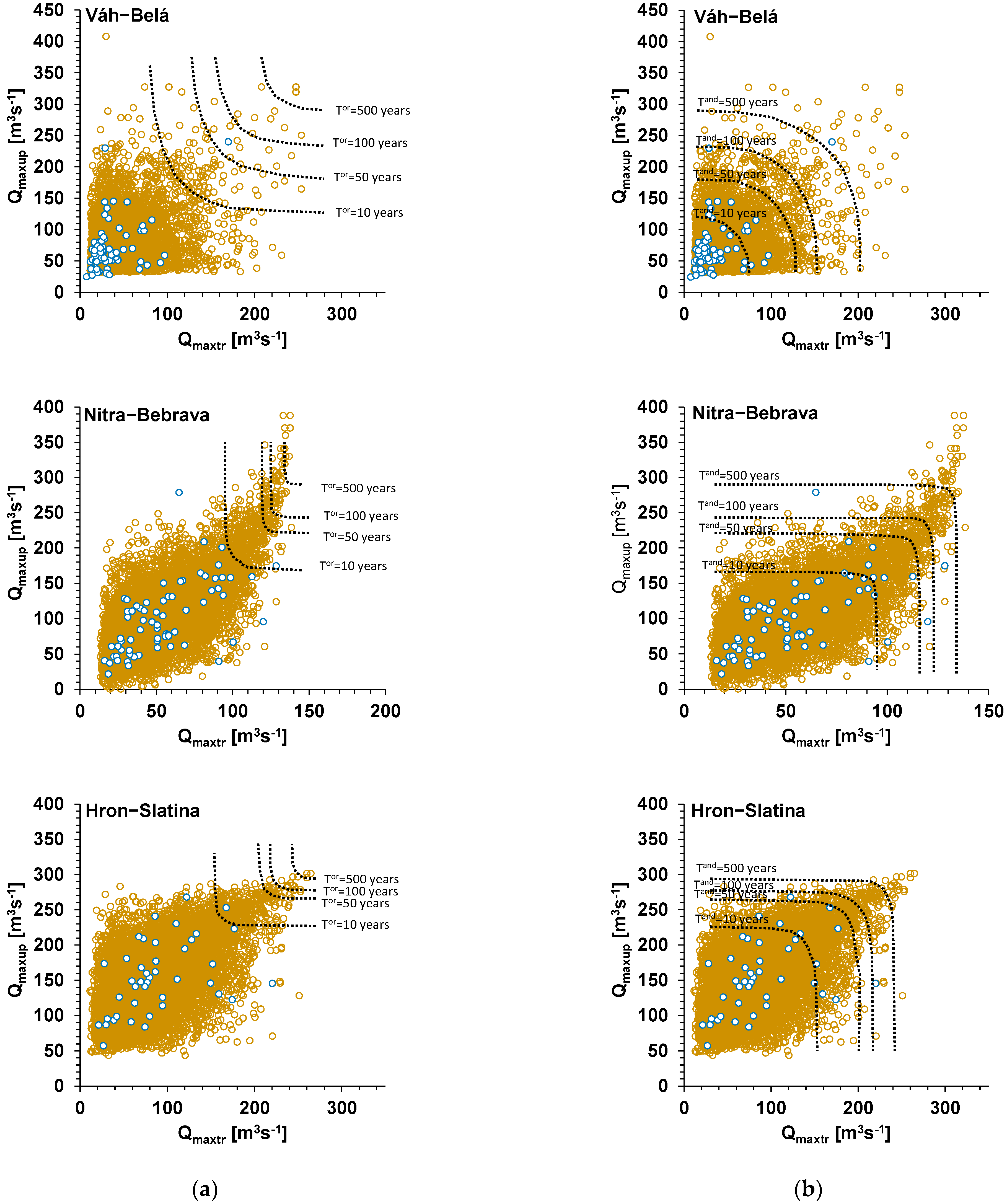
3.2. Bivariate Statistical Analysis of Flood Hazards at River Confluences Using Gumbel–Hougaard Copula
4. Discussion
5. Conclusions
- -
- The copula-based joint probability approach for the confluence flood estimation performed well for the selected river basins;
- -
- The copula-based joint probability approach provides a way to estimate the confluence flood without the discharge records needed for the mainstream below the confluence and without difficult computations such as flow routing;
- -
- The copula functions for the multivariate analyses enable the use of various types of marginal distributions and thus release the limitation of the others in the case of multivariate approaches where the margins follow the same type of distributions. In our study, based on the selected criterions and the tests, the same type of probability distribution fit the analyzed data, except for Nitrianska Streda Station, situated below the Nitra–Bebrava confluence;
- -
- The joint return periods calculated using copulas could be used to determine the severity of floods based on the desired relations between the mainstreams and their tributaries, looking for the exceedance of both variables.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bačová Mitková, V.; Halmová, D. Analysis of the Joint Impact of Synchronous Discharges in Estimating the Flood Risk: Case Study on Hron River. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 012034. [Google Scholar] [CrossRef]
- Hasino, M. Formulation of the joint return period of two hydrologic variates associated with a Poisson process. J. Hydrosci. Hydraul. Engng 1985, 3, 73–84. [Google Scholar]
- Correia, F.N. Multivariate partial duration series in flood risk analysis. In Hydrologic Frequency Modelling; Reidel: Dordrecht, The Netherlands, 1987; pp. 541–554. [Google Scholar] [CrossRef]
- Bačová Mitková, V. Bivariate joint probability analysis of flood hazard at river confluence. Acta Hydrol. Slovaca 2020, 21, 129–138. [Google Scholar] [CrossRef]
- Prohaska, S. Coincidence of flood flow of the Danube River and its tributaries. In A Hydrological Monograph Follow-up Volume 4, 1st ed.; Research Institute of Water Management: Bratislava, Slovakia, 2000; p. 187. ISBN 8096828231. [Google Scholar]
- Report of T. G. Assessment of the Catastrophic Floods in August 2002 and Proposal for Adaptation of the Flood Prevention System; Final report on the 2002 project; Masaryk Water Research Institute: Prague, Czech Republic, 2002; p. 174. (In Czech) [Google Scholar]
- Espinoza, J.C.; Ronchail, J.; Frappart, F. The Major Floods in the Amazonas River and Tributaries (Western Amazon Basin) during the 1970–2012 Period: A Focus on the 2012 Flood. J. Meteorol. 2013, 14, 1000–1008. [Google Scholar] [CrossRef] [Green Version]
- Li, C.H.; Li, N.; Wu, L.C.; Hu, A.J. A relative vulnerability estimation of flood disaster using data envelopment analysis in the Dongting Lake region of Hunan. Nat. Hazards Earth Syst. Sci. 2013, 13, 1723–1734. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A. and Rosso, R. Bivariate statistical approach to check adequacy of dam spillway. J. Hydrol. Eng. 2005, 10, 50–57. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate flood frequency analysis using the Gumbel-Hougaard copula. J. Hydrol. Eng. Special Issue Copulas Hydrol. 2007, 12, 431–439. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Bivariate flood frequency analysis of upper Godavari River flows using archimedean copulas. Water Resour. Manag. 2012, 26, 3995–4018. [Google Scholar] [CrossRef]
- Bačová Mitková, V.; Halmová, D. Joint modeling of flood peak discharges, volume and duration: A case study of the Danube River in Bratislava. J. Hydrol. Hydromech. 2014, 62, 186–196. [Google Scholar] [CrossRef] [Green Version]
- Šraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the Litija station on the Sava River. Hydrol. Process. 2014, 225–238. [Google Scholar] [CrossRef]
- Szolgay, J.; Gaál, L.; Bacigal, T.; Kohnová, S.; Hlavcova, K.; Výleta, R.; Blöschl, G. A regional comparative analysis of empirical and theoretical flood peak-volume relationships. J. Hydrol. Hydromech. 2016, 64, 367–381. [Google Scholar] [CrossRef] [Green Version]
- Papaioannou, G.; Kohnova, S.; Bacigal, T.; Szolgay, J.; Hlavcova, K.; Loukas, A. Joint modelling of flood peaks and volumes: A copula application for the Danube River. J. Hydrol. Hydromech. 2016, 64, 382–392. [Google Scholar] [CrossRef] [Green Version]
- Matúš, R. The modeling of hydrological joint events on the Morava river using aggregation operators. Slovak J. Civ. Eng. 2009, 3, 9–15. [Google Scholar]
- Lee, T.; Modarres, R.; Ouarda, T. Data-based analysis of bivariate copula tail dependence for drought duration and severity. Hydrol. Process. 2013, 27, 1454–1463. [Google Scholar] [CrossRef]
- Bezak, N.; Šraj, M.; Mikoš, M. Copula-based IDF curves and empirical rainfall thresholds for flash floods and rainfall-induced landslides. J. Hydrol. 2016, 541, 272–284. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S. Flood Coincidence Risk Analysis Using Multivariate Copula Functions. J. Hydrol. Eng. 2012, 17, 742–755. [Google Scholar] [CrossRef]
- Bender, J.; Wahl, T.; Müller, A.; Jensen, J. A multivariate design framework for river confluences. Hydrol. Sci. J. 2016, 61, 471–481. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Shi, Y.; Yan, H.; Chen, K.; Zhang, J. Coincidence risk analysis of floods using multivariate copulas: Case study of Jinsha River and Min River, China. J. Hydrol. Eng. 2019, 24, 05018030. [Google Scholar] [CrossRef]
- Fischer, S.; Schumann, A.H. Multivariate Flood Frequency Analysis in Large River Basins Considering Tributary Impacts and Flood Types. Water Res. Res. 2021, 57, e2020WR029029. [Google Scholar] [CrossRef]
- Gilja, G.; Ocvirk, E.; Kuspilić, N. Joint probability analysis of flood hazard at river confluences using bivariate copulas. J. Croat. Assoc. Civ. Eng. 2018, 70, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Tadić, L.; Bonacci, O.; Dadić, T. Analysis of the Drava and Danube rivers floods in Osijek (Croatia) and possibility of their coincidence. Environ. Earth Sci. 2016, 75, 12. [Google Scholar] [CrossRef]
- Pekárová, P.; Szolgay, J. Scenarios of Changes in Selected Hydrosphere and Biosphere Components in the Hron and Váh Catchment Areas due to Climate Change, 1st ed.; Press Bratislava: Veda, Slovakia, 2005; p. 496. ISBN 80-224-0884-0. (In Slovak) [Google Scholar]
- Karmakar, S.; Simonovic, S.P. Flood Frequency Analysis Using Copula with Mixed Distributions; Project Report No. 055; Department of Civil and Environmental Engeenering, The University of Western Ontario: London, ON, Canada, 2007; p. 58. [Google Scholar]
- Bender, J.; Wahl, T.; Mudersbach, C.; Jensen, J. Flood Frequency Analysis at River Confluences—Univariate vs. Multivariate Extreme Value Statistics. In Proceedings of the Water & Environmental Dynamics—6th International Conference on Water Resources and Environment Research, Koblenz, Germany, 3–7 June 2013; pp. 316–328. [Google Scholar]
- Xu, C.; Yin, J.; Guo, S.; Liu, Z.; Hong, X. Deriving Design Flood Based on Conditional Distribution: A Case Study of Danjiangkou Reservoir in Hanjiang Basin. Math. Probl. Eng. 2016, 11, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Guo, S.; Liu, Z.; Xiong, L.; Yin, J. Bivariate design flood quantile selection using copulas. Hydrol. Res. 2017, 48, 997–1103. [Google Scholar] [CrossRef]
- Han, C.H.; Liu, S.; Guo, Y.; Lin, H.; Liang, Y.; Zhang, H. Copula-Based Analysis of Flood Peak Level and Duration: Two Case Studies in Taihu Basin, China. J. Hydrol. Eng. 2018, 23. [Google Scholar] [CrossRef]
- Lacko, M.; Potočki, K.; Škreb, K.A.; Bezak, N. Joint Modelling of Flood Hydrograph Peak, Volume and Duration Using Copulas—Case Study of Sava and Drava River in Croatia, Europe. Water 2022, 14, 2481. [Google Scholar] [CrossRef]
- Nelsen, R.B. An introduction to Copula, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Yan, J. A Goodness-of-Fit Test for Multivariate Multiparameter Copulas Based on Multiplier Central Limit Theorems. Stat. Comput. 2011, 21, 17–30. [Google Scholar] [CrossRef]
- Karmakar, S.; Simonovic, S.P. Bivariate flood frequency analysis. Part 1: Determination of marginals by parametric and nonparametric techniques. J. Flood Risk Manag. 2009, 1, 190–200. [Google Scholar] [CrossRef]
- Shiau, J.T.; Wang, H.Y. and Tsai, Ch. T. Copula-based depth-duration-frequency analysis of thyphoons in Taiwan. Hydrol. Res. 2010, 41, 414–422. [Google Scholar] [CrossRef]
- Chowdhary, H.; Escobar, L.A.; Singh, P. Identification of suitable copulas for bivariate frequency analysis of flood peak and flood volume data. Hydrol. Res. 2011, 42, 193–215. [Google Scholar] [CrossRef]
- Meylan, P.; Favre, A.C.; Musy, A. Predictive Hydrology: A Frequency Analysis Approach; CRC Press: Boca Raton, FL, USA, 2012; p. 212. [Google Scholar]
- Gringorten, I.I. A plotting rule for extreme probability paper. J. Geophys. Res. 1963, 68, 813–814. [Google Scholar] [CrossRef]
- Cunnane, C. Methods and merits of regional flood frequency analysis. J. Hydrol. 1988, 100, 269–290. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.M.J.; Bobée, B.; Legendre, P.; Bruneau, P. The Gumbel mixed model for flood frequency analysis. J. Hydrol. 1999, 226, 88–100. [Google Scholar] [CrossRef]
- Shiau, J.T. Return period of bivariate distributed extreme hydrological events. Stoch. Envir. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Salvadori, G. Bivariate return periods via 2-Copulas. Stat. Methodol. 2004, 1, 129–144. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour Res. 2004, 40, W12511. [Google Scholar] [CrossRef]
- Svanidze, G.G.; Grigolia, G.L. The use of Johnson distribution in the stream-flow calculations. Vodn. Resur. 1974, 6, 45–59. [Google Scholar]
- Markovic, R.D. Probability Functions of Best Fit to Distributions of Annual Precipitation and Runoff. Doctoral Dissertation, Colorado State University, Fort Collins, CO, USA, 1965; p. 30. Available online: https://mountainscholar.org/bitstream/handle/10217/61285/HydrologyPapers_n8.pdf (accessed on 1 August 1965).
- Fidalgo Fonseca, T.; Pacheco Marques, C.R.; Parreso, B. Describing Maritime Pine Diameter Distributions with Johnson’s SB Distribution Using a New All-Parameter Recovery Approach. Forest SC 2009, 55, 367–373. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, P.; Qu, S.; Mou, S.; Chen, C.; Dong, F. Nonstationary flood coincidence risk analysis using time-varying copula functions. Sci. Rep. 2020, 10, 10. [Google Scholar] [CrossRef] [Green Version]
- Lam, D.; Thompson, C.; Croke, J.; Sharma, A.; Macklin, M. Reducing uncertainty with flood frequency analysis: The contribution of paleoflood and historical flood information. Water Resour. Res. 2017, 53, 2312–2327. [Google Scholar] [CrossRef] [Green Version]
- Coxon, G.; Freer, J.; Westerberg, I.K.; Wagener, T.; Woods, R.; Smith, P.J. A novel framework for discharge uncertainty quantification applied to 500 UK gauging stations. Water Resour. Res. 2015, 51, 5531–5546. [Google Scholar] [CrossRef] [Green Version]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Frequency Analysis of Extreme Events, Handbook of Hydrology; Maidment, D.R., Ed.; chap. 18; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Millington, N.; Das, S.; Simonovic, S.P. The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models; Water Resources Research Report; Department of Civil and Environmental Engineering, The University of Western Ontario London: London, ON, Canada, 2011; pp. 1–54. [Google Scholar]
- Wang, C. A Joint Probability Approach for the Confluence Flood Frequency Analysis; Iowa State University ProQuest Dissertations Publishing: Ames, IO, USA, 2007; p. 24. [Google Scholar]
- Jianping, B.; Pengxin, D.; Xiang, Z.; Sunyun, L.; Marani, M.; Yi, X. Flood coincidence analysis of Poyang Lake and Yangtze River: Risk and influencing factors. Stoch. Environ. Res. Risk Assess. 2018, 32, 879–891. [Google Scholar] [CrossRef]
- Le Clerc, S.; Lang, M. Flood frequency analysis downstream confluences. Comparison between bivariate densities and experimental data. In Proceedings of the International Conference on Flood Estimation, Berne, Switzerland, 6–8 March 2002; pp. 295–304. [Google Scholar]
- Favre, A.C.; El Adlouni, S.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40, 12. [Google Scholar] [CrossRef] [Green Version]
- Huang, K.; Chen, L.; Zhou, J.; Zhang, J.; Singh, V.P. Flood hydrograph coincidence analysis for mainstream and its tributaries. J. Hydrol. 2018, 65, 341–353. [Google Scholar] [CrossRef]


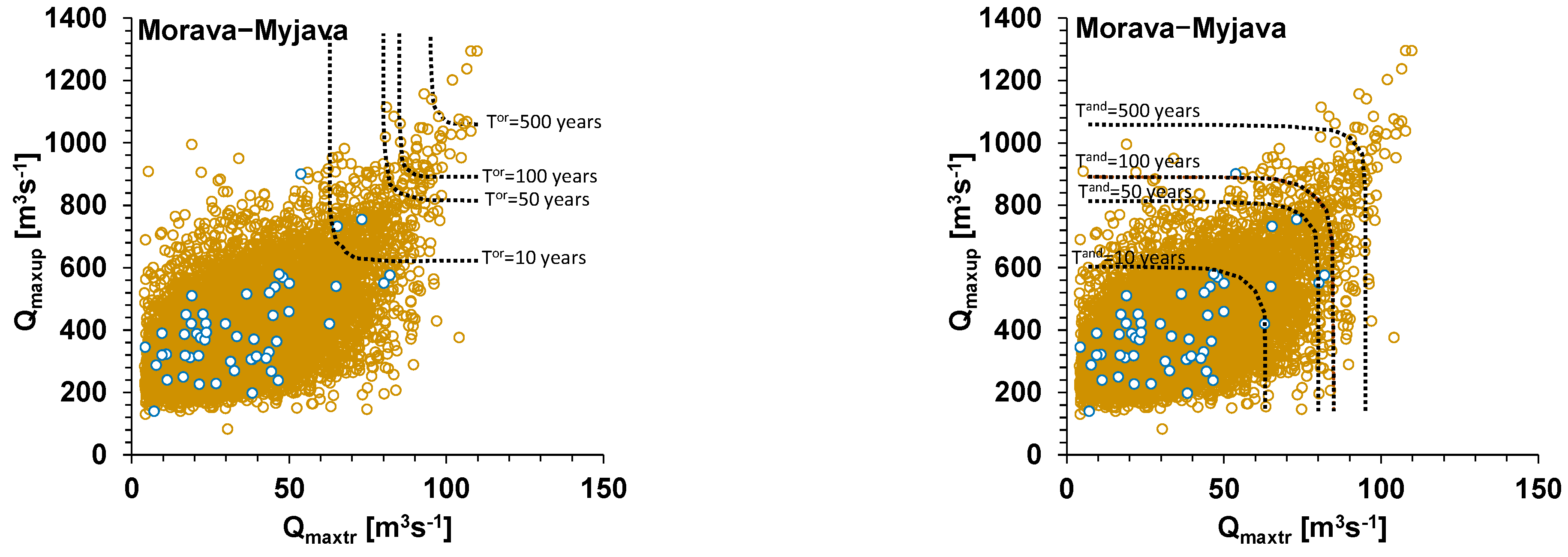
| River | Gauging Station | Period [Year] | Qmax [m3 s−1] | River Kilometer [rkm] | Area [km2] |
|---|---|---|---|---|---|
| Morava | Strážnica (up) | 1968–2019 | 901 | 134.3 | 9146.92 |
| Moravský Svätý Ján (dwn) | 1968–2019 | 1400 | 67.15 | 24,129.30 | |
| Myjava | Šaštín Stráže (tr) | 1968–2019 | 82 | 15.15 | 644.89 |
| Váh | Liptovský Hrádok (up) | 1950–2019 | 240 | 359.3 | 638.38 |
| Liptovský Mikuláš (dwn) | 1950–2019 | 540 | 343.6 | 1107.21 | |
| Belá | Podbanské (tr) | 1950–2019 | 170 | 21.35 | 93.49 |
| Nitra | Chynorany (up) | 1951–2019 | 279 | 106 | 1134.28 |
| Nitrianska Streda (dwn) | 1951–2019 | 324 | 91.1 | 2093.71 | |
| Bebrava | Nadlice (tr) | 1951–2019 | 128 | 6.2 | 598.8 |
| Hron | Banská Bystrica (up) | 1972–2019 | 260 | 175.2 | 1766.48 |
| Žiar nad Hronom (dwn) | 1972–2019 | 636 | 131.5 | 3310.69 | |
| Slatina | Zvolen (tr) | 1972–2019 | 220 | 12.1 | 790.16 |
| Copula Function | C (u, v, θ) | Parameter θ | Kendall’s τ | Generator φ(t) |
|---|---|---|---|---|
| Gumbel–Hougaard | [1, ) |
| Confluence | Q [m3 s−1] | Distr. | p Value | Estimated QT [m3 s−1] | Monitored Qmax [m3 s−1] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q50 | Q100 | Q200 | Q500 | Q1000 | Qmax | T [year] | ||||
| Morava–Myjava | Qmaxup | JSB | 0.932 | 815 | 892 | 966 | 1059 | 1127 | 901 | 145 |
| Qmaxtr | JSB | 0.812 | 80 | 85 | 90 | 95 | 98 | 82 | 70 | |
| Qmaxdwn | JSB | 0.911 | 1221 | 1351 | 1473 | 1621 | 1723 | 1400 | 160 | |
| Váh–Belá | Qmaxup | JSB | 0.24 | 200 | 232 | 259 | 290 | 313 | 240 | 160 |
| Qmaxtr | JSB | 0.95 | 136 | 160 | 185 | 213 | 234 | 170 | 160 | |
| Qmaxdwn | JSB | 0.87 | 372 | 435 | 499 | 587 | 652 | 540 | 310 | |
| Nitra–Bebrava | Qmaxup | JSB | 0.92 | 225 | 247 | 268 | 295 | 314 | 279 | 220 |
| Qmaxtr | JSB | 0.91 | 119 | 125 | 130 | 134 | 137 | 128 | 140 | |
| Qmaxdwn | Weib. | 0.76 | 322 | 346 | 368 | 386 | 400 | 324 | 60 | |
| Hron–Slatina | Qmaxup | JSB | 0.97 | 266 | 277 | 285 | 294 | 299 | 268 | 50 |
| Qmaxtr | JSB | 0.83 | 206 | 221 | 234 | 247 | 256 | 220 | 100 | |
| Qmaxdwn | JSB | 0.86 | 590 | 643 | 692 | 756 | 806 | 636 | 90 | |
| Confluence | Pair | Kendall’s τ | Parameter Copula | MAE [%] | p-Value |
|---|---|---|---|---|---|
| Morava–Myjava | Qmaxup–Qmaxtr | 0.366 | 1.577 | 4.02 | 0.73 |
| Váh–Belá | Qmaxup−Qmaxtr | 0.225 | 1.290 | 2.27 | 0.96 |
| Nitra–Bebrava | Qmaxup−Qmaxtr | 0.476 | 1.908 | 5.94 | 0.052 |
| Hron–Slatina | Qmaxup−Qmaxtr | 0.366 | 1.567 | 4.94 | 0.78 |
| Confluence (Station on Mainstream below the Confluence) | Method/Differences | Estimated QT [m3 s−1] | ||||
|---|---|---|---|---|---|---|
| Q50 | Q100 | Q200 | Q500 | Q1000 | ||
| Morava–Myjava (Morava: Moravský Sv. Ján) | Uni−SB distr. | 1221 | 1351 | 1473 | 1621 | 1723 |
| copula G–H | 1369 | 1500 | 1623 | 1722 | 1878 | |
| Difference [%] | 12 | 11 | 10 | 6 | 9 | |
| Váh–Belá (Váh: Liptovský Mikuláš) | Uni−JSB distr. | 372 | 435 | 499 | 587 | 652 |
| copula G–H | 446 | 508 | 570 | 651 | 712 | |
| Difference [%] | 20 | 17 | 14 | 11 | 9 | |
| Nitra–Bebrava (Nitra: Nitrianska Streda) | Uni−weib. distr. | 322 | 346 | 368 | 386 | 400 |
| copula G–H | 336 | 354 | 369 | 388 | 401 | |
| Difference [%] | 4 | 2 | 0 | 1 | 0 | |
| Hron–Slatina (Hron: Žiar nad Hronom) | Uni−JSB distr. | 590 | 643 | 692 | 756 | 806 |
| copula G–H | 649 | 699 | 747 | 808 | 853 | |
| Difference [%] | 10 | 9 | 8 | 7 | 6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bačová Mitková, V.; Halmová, D.; Pekárová, P.; Miklánek, P. The Copula Application for Analysis of the Flood Threat at the River Confluences in the Danube River Basin in Slovakia. Water 2023, 15, 984. https://doi.org/10.3390/w15050984
Bačová Mitková V, Halmová D, Pekárová P, Miklánek P. The Copula Application for Analysis of the Flood Threat at the River Confluences in the Danube River Basin in Slovakia. Water. 2023; 15(5):984. https://doi.org/10.3390/w15050984
Chicago/Turabian StyleBačová Mitková, Veronika, Dana Halmová, Pavla Pekárová, and Pavol Miklánek. 2023. "The Copula Application for Analysis of the Flood Threat at the River Confluences in the Danube River Basin in Slovakia" Water 15, no. 5: 984. https://doi.org/10.3390/w15050984






