A Review of Advances in Groundwater Evapotranspiration Research
Abstract
:1. Introduction
2. Methodology
2.1. Advances in Research on Groundwater Evapotranspiration
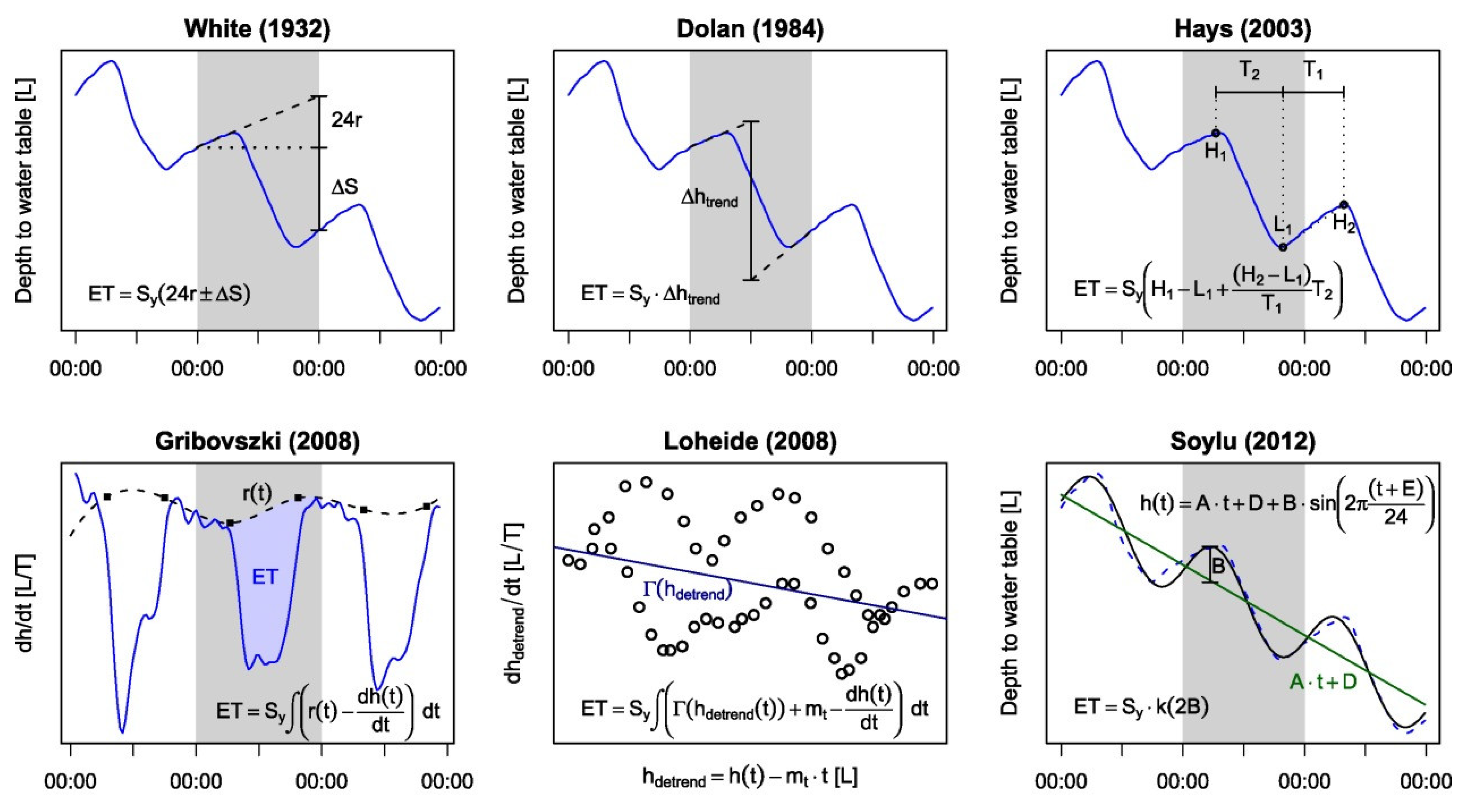
2.2. Using the WTF Method to Calculate the ETg
2.2.1. White Method
2.2.2. Dolan Method
2.2.3. Hays Method
2.2.4. Loheide Method
2.2.5. Yin Method
2.2.6. Gribovszki Method
2.2.7. Soylu Method
2.2.8. Wang Method
2.2.9. Other Improvements and Applications
2.3. Using the Numerical Model to Calculate the Groundwater Evapotranspiration
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xue, J.Y.; Guan, H.D.; Huo, Z.L.; Wang, F.X.; Huang, G.H.; Boll, J. Water saving practices enhance regional efficiency of water consumption and water productivity in an arid agricultural area with shallow groundwater. Agric. Water Manag. 2017, 194, 78–89. [Google Scholar] [CrossRef]
- Rijsberman, F.R. Water scarcity: Fact or fiction? Agric. Water Manag. 2006, 80, 5–22. [Google Scholar] [CrossRef] [Green Version]
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R. Global water resources:vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [Green Version]
- Yeh, P.J.F.; Famiglietti, J.S. Regional groundwater evapotranspiration inillinois. J. Hydrometeorol. 2009, 10, 464–478. [Google Scholar] [CrossRef] [Green Version]
- Babajimopoulos, C.; Panoras, A.; Georgoussis, H.; Arampatzis, G.; Hatzigiannakis, E.; Papamichail, D. Contribution to irrigation from shallow water table under field conditions. Agric. Water Manag. 2007, 92, 205–210. [Google Scholar] [CrossRef]
- Dregne, H.E. Global status of desertification Ann. Arid Zone 1991, 30, 179–185. [Google Scholar]
- NOAA, JetStream: Online School for Weather. Available online: http://www.srh.noaa.gov/jetstream/global/climate_max.htm (accessed on 26 February 2023).
- Bulter, J.J., Jr.; Kluitenberg, G.J.; Whittemore, D.O.; Loheide, S.P., II; Jin, W.; Billinger, M.A.; Zhan, X.Y. A field investigation of phreatophyte-induced fluctuations in the water–table. Water Resoureces Res. 2007, 43, W02404. [Google Scholar]
- Gribovszki, Z.; Szilágyi, J.; Kalicz, P. Diurnal fluctuations in shallow groundwater levels and streamflow rates and their interpretation-A review. J. Hydrol. 2010, 385, 371–383. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Qi, S.Z.; Luo, F. Hydrological indicators of desertification in the Heihe River Basin of arid northwest China. AMBIO A J. Hum. Environ. 2006, 35, 319–321. [Google Scholar]
- Yin, L.H.; Zhou, Y.X.; Ge, S.M.; Wen, D.G.; Zhang, E.Y.; Dong, J.Q. Comparison and modification of methods for estimating evapotranspiration using diurnal groundwater level fluctuations in arid and semiarid regions. J. Hydrol. 2013, 496, 9–16. [Google Scholar] [CrossRef]
- Wang, P.; Grinevsky, S.O.; Pozdniakov, S.P. Application of the water table fluctuation method for estimating evapotranspiration at two phreatophyte-dominated sites under hyper-arid environments. J. Hydrol. 2014, 519, 2289–2300. [Google Scholar] [CrossRef]
- Goodrich, D.C.; Scott, R.; Qi, J.; Goff, B.; Unkrich, C.L.; Moran, M.S.; Williams, D.; Schaeffer, S.; Snyder, R.K.; MacNish, R.; et al. Seasonal estimates of riparian evapotranspiration using remote and in situ measurements. Agric. For. Meteorol. 2000, 105, 281–309. [Google Scholar] [CrossRef]
- Wang, X.W.; Huo, Z.L.; Feng, S.Y.; Guo, P.; Guan, H.D. Estimating groundwater evapotranspiration from irrigated cropland incorporating root zone soil texture and moisture dynamics. J. Hydrol. 2016, 543, 501–509. [Google Scholar] [CrossRef]
- Drexler, J.Z.; Snyder, R.L.; Spano, D.; Tha Paw, U.K. A review of models and micrometeorological methods used to estimate wetland evapotranspiration. Hydrol. Process. 2004, 18, 2071–2101. [Google Scholar] [CrossRef]
- Cooper, D.J.; Sanderson, J.S.; Stannard, D.I.; Groeneveldd, D.P. Effects of long-term water table drawdown on evapotranspiration and vegetation in an arid region phreatophyte community. J. Hydrol. 2006, 325, 21–34. [Google Scholar] [CrossRef]
- Naumburg, E.; Mata-Gonzalez, R.; Hunter, R.G.; Mclendon, T.; Martin, D.W. Phreatophytic vegetation and groundwater fluctuations: A review of current research and application of ecosystem response modeling with an emphasis on great basin vegetation. Environ. Manag. 2005, 35, 726–740. [Google Scholar] [CrossRef]
- Orellana, F.; Verma, P.; Loheide, S.P., II; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater-dependent ecosystems. Rev. Geophys. 2012, 50, 3. [Google Scholar] [CrossRef]
- Yuan, G.F.; Zhang, P.; Shao, M.A.; Luo, Y.; Zhu, X.C. Energy and water exchanges over a riparian Tamarix spp. stand in the lower Tarim River basin under a hyper-arid climate. Agric. For. Meteorol. 2014, 194, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Salama, R.B.; Fitzpatrick, O. Contributions of groundwater conditions to soil and water salinization. Hydrogeol. J. 1999, 7, 46–64. [Google Scholar] [CrossRef]
- Northey, J.E.; Christen, E.W.; Ayars, J.E.; Jankowski, J. Occurrence and measurement of salinity stratification in shallow groundwater in the Murrumbidgee Irrigation Area, south-eastern Australia. Agric. Water Manag. 2006, 81, 23–40. [Google Scholar] [CrossRef]
- Zipper, S.C.; Soylu, M.E.; Booth, E.G.; Loheide, S.P., II. Untangling the effects of shallow groundwater and soil texture as drivers of subfield-scale yield variability. Water Resour. Res. 2015, 51, 6338–6358. [Google Scholar] [CrossRef] [Green Version]
- Ayars, J.E.; Schoneman, R.A. Use of saline water from a shallow water table by cotton. Trans ASAE 1986, 29, 1674–1678. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, G.; Yin, X.; Liu, Z.; Huang, Z. Study on capillary rise from shallow groundwater and critical water table depth of a saline-sodic soil in western Songnen plain of China. Environ. Earth Sci. 2011, 64, 2119–2126. [Google Scholar] [CrossRef]
- Pratharpar, S.A.; Qureshi, A.S. Modelling the effects of deficit irrigation on soil salinity, depth to water table and transpiration in semi-arid zones with monsoonal rains. Int. J. Water Resour. Dev. 1999, 15, 141–159. [Google Scholar] [CrossRef]
- Yang, J.F.; Li, B.Q.; Liu, S.P. A large weighing lysimeter for evapotranspiration and soil-water-groundwater exchange studies. Hydrol. Process. 2000, 14, 1887–1897. [Google Scholar] [CrossRef]
- Kahlown, M.A.; Ashraf, M. Zia-ul-Haq, Effect of shallow groundwater table on crop water requirements and crop yields. Agric. Water Manag. 2005, 76, 24–35. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, T.; Paredes, P.; Duan, L.; Pereira, L.S. Water use by a groundwater dependent maize in a semi-arid region of Inner Mongolia: Evapotranspiration partitioning and capillary rise. Agric. Water Manag. 2015, 152, 222–232. [Google Scholar] [CrossRef] [Green Version]
- Gou, S.; Miller, G. A groundwater-soil-plant-atmosphere continuum approach for modelling water stress, uptake, and hydraulic redistribution in phreatophytic vegetation. Ecohydrology 2014, 7, 1029–1041. [Google Scholar] [CrossRef]
- Newman, B.D.; Wilcox, B.P.; Archer, S.R.; Breshears, D.D.; Dahm, C.N.; Duffy, C.J.; McDowell, N.G.; Phillips, F.M.; Scanlon, B.R.; Vivoni, E.R. Ecohydrology of water-limited environments: A scientific vision. Water Resour. Res. 2006, 42, W06302. [Google Scholar] [CrossRef]
- Allen, R.G. Assessing integrity of weather data for reference evapotranspiration estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Balugani, E.; Lubczynski, M.W.; Reyes-Acosta, L.; Van Der, T.C.; Francés, A.P.; Metselaar, K. Groundwater and unsaturated zone evaporation and transpiration in a semi-arid open wood land. J. Hydrol. 2017, 547, 54–66. [Google Scholar] [CrossRef]
- Lubczynski, M.W.; Gurwin, J. Integration of various data sources for transient groundwater modeling with spatio-temporally variable fluxes—Sardon study case, Spain. J. Hydrol. 2005, 306, 71–96. [Google Scholar] [CrossRef]
- Gavilán, P.; Berengena, J.; Allen, R.G. Measuring versus estimating net radiation and soil heat flux: Impact on penman–monteith reference et estimates in semiarid regions. Agric. Water Manag. 2007, 89, 275–286. [Google Scholar] [CrossRef]
- Gazal, R.M.; Scott, R.L.; Goodrich, D.C.; Williams, D.G. Controls on transpiration in a semiarid riparian cottonwood forest. Agric. For. Meteorol. 2006, 137, 56–67. [Google Scholar] [CrossRef]
- Hultine, K.R.; Bush, S.E.; West, A.G.; Ehleringer, J.R. Effect of gender on sap-flux-scaled transpiration in a dominant riparian tree species: Box elder (acer negundo). J. Geophys. Res. Biogeosci. 2015, 112, 87–101. [Google Scholar] [CrossRef]
- Moore, D.J.P.; Hu, J.; Sacks, W.J.; Schimel, D.S.; Monson, R.K. Estimating transpiration and the sensitivity of carbon uptake to water availability in a subalpine forest using a simple ecosystem process model informed by measured net CO2 and H2O fluxes. Agric. For. Meteorol. 2008, 148, 1467–1477. [Google Scholar] [CrossRef]
- Lenka, S.; Singh, A.K.; Lenka, N.K. Water and nitrogen interaction on soil profile water extraction and ET in maize-wheat cropping system. Agric. Water Manag. 2009, 96, 195–207. [Google Scholar] [CrossRef]
- Richard, G.; Benyon, S.; Theiveyanathan Doody, T.M. Impacts of tree plantations on groundwater in south-eastern Australia. Aust. J. Bot. 2006, 54, 181–192. [Google Scholar]
- Doody, T.; Benyon, R. Quantifying water savings from willow removal in Australian streams. J. Environ. Manag. 2011, 92, 926–935. [Google Scholar] [CrossRef]
- Nachabe, M.; Shah, N.; Ross, M.; Vomacka, J. Evapotranspiration of two vegetation covers in a shallow water table environment. Soil Sci. Soc. Am. J. 2005, 69, 492–499. [Google Scholar] [CrossRef]
- Devitt, D.A.; Fenstermaker, L.F.; Young, M.H.; Conrad, B.; Baghzouz, M.; Bird, B.M. Evapotranspiration of mixed shrub communities in phreatophytic zones of the Great Basin region of Nevada (USA). Ecohydrology 2011, 4, 807–822. [Google Scholar] [CrossRef]
- Moore, G.W.; Cleverly, J.R.; Owens, M.K. Nocturnal transpiration in riparian Tamarix thickets authenticated by sap flux, eddy covariance and leaf gas exchange measurements. Tree Physiol. 2008, 28, 521–528. [Google Scholar] [CrossRef] [Green Version]
- Scott, R.L.; Edwards, E.A.; Shuttleworth, W.J.; Huxman, T.E.; Watts, C.; Goodrich, D.C. Interannual and seasonal variation in fluxes of water and carbon dioxide from a riparian woodland ecosystem. Agric. For. Meteorol. 2004, 122, 65–84. [Google Scholar] [CrossRef]
- Scott, R.L.; Huxman, T.E.; Williams, D.G.; Goodrich, D.C. Ecohydrological impacts of woody-plant encroachment: Seasonal patterns of water and carbon dioxide exchange within a semiarid riparian environment. Glob. Change Biol. 2006, 12, 311–324. [Google Scholar] [CrossRef]
- Scott, R.L.; Shuttleworth, W.J.; Goodrich, D.C. The water use of two dominant vegetation communities in a semiarid riparian ecosystem. Agric. For. Meteorol. 2000, 105, 241–256. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL).: Part 2: Valiation. J. Hydrol. 1998, 212, 213–229. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Gellens-Meulenberghs, F.; Arboleda, A.; Ghilain, N. Towards a continuous monitoring of evapotranspiration based on MSG data. Environ. Sci. 2007, 316, 228–234. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-model. J. Irrigat. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M.C. Modelling surface energy fluxes over maize using a two-source patch model and radiometric soil and canopy temperature observations. Remote Sens. Environ. 2008, 112, 1130–1143. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; DeJeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. Discuss. 2011, 7, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Wu, B.F.; Yan, N.N.; Xiong, J.; Bastiaanssen, W.G.M.; Zhu, W.W.; Stein, A. Validation of ETWatch using field measurements at diverse landscapes: A case study in Hai basin of China. J. Hydrol. 2012, 436, 67–80. [Google Scholar] [CrossRef]
- Mazur, M.C.; Wiley, M.J.; Wilcox, D.A. Estimating evapotranspiration and groundwater flow from water-table fluctuations for a general wetland scenario. Ecohydrology 2014, 7, 378–390. [Google Scholar] [CrossRef] [Green Version]
- Ridolfi, L.; Odorico, P.D.; Laio, F. Vegetation dynamics induced by phreatophyte--aquifer interactions. J. Theor. Biol. 2007, 248, 301–310. [Google Scholar] [CrossRef]
- Sanderson, J.S.; Cooper, D.J. Ground water discharge by evapotranspiration in wetlands of an arid intermountain basin. J. Hydrol. 2008, 351, 344–359. [Google Scholar] [CrossRef]
- Healy, R.W.; Scanlon, B.R. Estimating Groundwater Recharge: Groundwater Recharge; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Loheide II, S.P. A method for estimating subdaily evapotranspiration of shallow groundwater using diurnal water table fluctuations. Ecohydrology 2008, 1, 59–66. [Google Scholar] [CrossRef]
- Simmers, I.; Hendrickx, J.; Kruseman, G.P.; Rushton, K.R. Recharge of Phreatic Aquifers in (Semi-) Arid Areas; Balkema: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Yu, L.Y.; Zeng, Y.J.; Su, Z.B.; Cai, H.J.; Zheng, Z. The effect of different evapotranspiration methods on portraying soil water dynamics and ET partitioning in a semi-arid environment in Northwest China. Hydrol. Earth Syst. Sci. 2016, 20, 975–990. [Google Scholar] [CrossRef] [Green Version]
- Remson, I.; Fox, G.S. Capillary losses from ground water. Trans. Am. Geophys. Union 1955, 36, 304–310. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Willis, W.O. Evaporation from layered soils in the presence of a water table. Soil Sci. Soc. Am. J. 1960, 24, 239–242. [Google Scholar] [CrossRef]
- Schoeller, H. Les Eaux Souterraines; Mason and Cie: Paris, France, 1962; Volume 642. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. FAO Guidelines for Predicting Crop Water Requirements; FAO Irrigation & Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1975. [Google Scholar]
- Steinwand, A.L.; Harrington, R.F.; Or, D. Water balance for great basin phreatophytes derived from eddy covariance, soil water, and water table measurements. J. Hydrol. 2006, 329, 595–605. [Google Scholar] [CrossRef]
- Stuff, R.G.; Dale, R.F. A soil moisture budget model accounting for shallow water table influences. Soil Sci. Soc. Am. J. 1978, 42, 637–643. [Google Scholar] [CrossRef]
- Wallender, W.W.; Grimes, D.W.; Henderson, D.W.; Stromberg, L.K. Estimating the contribution of a perched water table to the seasonal evapotranspiration of cotton. Agron. J. 1979, 71, 1056–1060. [Google Scholar] [CrossRef]
- Loheide, S.P., II; Butler, J.J.; Gorelick, S.M. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations: A saturated-unsaturated flow assessment. Water Resour. Res. 2005, 41, W07030. [Google Scholar] [CrossRef]
- Wang, X.W.; Huo, Z.L.; Shukla, M.K.; Wang, X.H.; Guo, P.; Xu, X.; Huang, G.H. Energy fluxes and evapotranspiration over irrigated maize field in an arid area with shallow groundwater. Agric. Water Manag. 2020, 228, 105922. [Google Scholar] [CrossRef]
- Ren, D.Y.; Xu, X.; Hao, Y.Y.; Huang, G.H. Modeling and assessing field irrigation water use in a canal system of Hetao, upper Yellow River basin: Application to maize, sunflower and watermelon. J. Hydrol. 2016, 532, 122–139. [Google Scholar] [CrossRef]
- Lai, J.; Liu, T.; Luo, Y. Evapotranspiration Partitioning for Winter Wheat with Shallow Groundwater in the Lower Reach of the Yellow River Basin. Agric. Water Manag. 2022, 266, 107561. [Google Scholar] [CrossRef]
- Karimov, A.K.; Šimůnek, J.; Hanjra, M.A.; Avliyakulov, M.; Forkutsa, I. Effects of the shallow water table on water use of winter wheat and ecosystem health: Implications for unlocking the potential of groundwater in the Fergana Valley (Central Asia). Agric. Water Manag. 2014, 131, 57–69. [Google Scholar] [CrossRef]
- Nirjhar, S.; Mahmood, N.; Mark, R. Extinction depth and evapotranspiration from ground water under selected land covers. Ground Water 2007, 45, 329–338. [Google Scholar]
- Lautz, L.K. Estimating groundwater evapotranspiration rates using diurnal water-table fluctuations in a semi-arid riparian zone. Hydrogeol. J. 2008, 16, 483–497. [Google Scholar] [CrossRef]
- Mould, D.J.; Frahm, E.; Salzmann Th Miegel, K.; Acreman, M.C. Evaluating the use of diurnal groundwater fluctuations for estimating evapotranspiration in wetland environments: Case studies in southeast England and northeast Germany. Ecohydrology 2010, 3, 294–305. [Google Scholar] [CrossRef]
- White, W.N. Method of Estimating Ground-Water Supplies Based on Discharge by Plants and Evaporation from Soil: Results of Investigation in Escalante Valley, Utah (R); Geological Survey Water Supply Paper, 659-A; United States Department of the Interior, Government Printing Office: Washington, DC, USA, 1932; Volume 115. [Google Scholar]
- Meyboom, P. Three observations on streamflow depletion by phreatophytes. J. Hydrol. 1965, 2, 248–261. [Google Scholar] [CrossRef]
- Gerla, P.J. The Relationship of Water-Table Changes to the Capillary Fringe, Evapotranspiration, and Precipitation in Intermittent Wetlands. Wetlands 1992, 12, 91–98. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Kalicz, P.; Szilagyi, J.; Kucsara, M. Riparian zone evapotranspiration estimation from diurnal groundwater level fluctuations. J. Hydrol. 2008, 349, 6–17. [Google Scholar] [CrossRef]
- Soylu, M.E.; Lenters, J.D.; Istanbulluoglu, E.; Loheide, S.P., II. On evapotranspiration and shallow groundwater fluctuations:\na fourier-based improvement to the white method. Water Resources Res. 2012, 48, W06506. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Yu, J.J.; Pozdniakov, S.P.; Grinevsky, S.O.; Liu, C.M. Shallow groundwater dynamics and its driving forces in extremely arid areas: A case study of the lower Heihe river in northwestern China. Hydrol. Process. 2014, 28, 1539–1553. [Google Scholar] [CrossRef]
- Troxell, H.C. The diurnal fluctuation in the ground-water and flow of the santa ana river and its meaning. Trans. Am. Geophys. Union 1936, 17, 496–504. [Google Scholar] [CrossRef]
- Gatewood, J.S. Use of water by bottom-land vegetation in lower safford valley, Arizona. US Geol. Surv. Water Supply Pap. 1950, 1103, 210. [Google Scholar]
- Laczniak, R.J.; Demeo, G.A.; Reiner, S.R.; Smith, J.L.; Nylund, W.E. Estimates of Ground-Water Discharge as Determined from Measurements of Evapotranspiration, Ash Meadows area, Nye County, Nevada; USGS US Geological Survey Water Resources Investigations Report 99-4079; Geological Survey: Las Vegas, NV, USA, 1999. [Google Scholar]
- Mclaughlin, D.L.; Cohen, M.J. Ecosystem specific yield for estimating evapotranspiration and groundwater exchange from diel surface water variation. Hydrol. Process. 2013, 28, 1495–1506. [Google Scholar] [CrossRef]
- Schilling, K.E. Water table fluctuations under three riparian land covers, Iowa (USA). Hydrol. Process. 2010, 21, 2415–2424. [Google Scholar] [CrossRef]
- Martinet, M.C.; Vivoni, E.R.; Cleverly, J.R.; Thibault, J.R.; Dahm, C.N. On groundwater fluctuations, evapotranspiration, and understory removal in riparian corridors. Water Resour. Res. 2009, 45, 207–213. [Google Scholar] [CrossRef] [Green Version]
- Miller, G.R.; Chen, X.; Rubin, Y.; Ma, S.; Baldocchi, D.D. Groundwater uptake by woody vegetation in a semiarid oak savanna. Water Resour. Res. 2010, 46, 2290–2296. [Google Scholar] [CrossRef] [Green Version]
- Vincke, C.; Thiry, Y. Water table is a relevant source for water uptake by a Scots pine (Pinus sylvestris L.) stand: Evidences from continuous evapotranspiration and water table monitoring. Agric. For. Meteorol. 2008, 148, 1419–1432. [Google Scholar] [CrossRef]
- Dolan, T.J.; Hermann, A.J.; Bayley, S.E.; Zoltek, J.J. Evapotranspiration of a Florida, U.S.A. freshwater wetland. J. Hydrol. 1984, 74, 355–371. [Google Scholar] [CrossRef]
- Hays, K.B. Water Use by Saltcedar (Tamarix sp.) and Associated Vegetation on the Canadian, Colorado and Pecos Rivers in Texas. Master’s Thesis, Texas A & M University, Texas, TX, USA, 2003. [Google Scholar]
- Czikowsky, M.J.; Fitzjarrald, D.R. Evidence of seasonal changes in evapotranspiration in eastern u.s. hydrological records. J. Hydrometeorol. 2009, 5, 974–988. [Google Scholar] [CrossRef]
- Wang, T.Y.; Wang, P.; Yu, J.J.; Pozdniakov, S.P.; Zhang, Y. Revisiting the white method for estimating groundwater evapotranspiration: A consideration of sunset and sunrise timings. Environ. Earth Sci. 2019, 78, 412.1–412.7. [Google Scholar] [CrossRef]
- Su, Y.H.; Feng, Q.; Zhu, G.F.; Zhang, Q. Evaluating the different methods for estimating groundwater evapotranspiration using diurnal water table fluctuations. J. Hydrol. 2022, 607, 127508. [Google Scholar]
- Fahle, M.; Dietrich, O. Estimation of evapotranspiration using diurnal groundwater level fluctuations: Comparison of different approaches with groundwater lysimeter data. Water Resour. Res. 2014, 50, 273–286. [Google Scholar] [CrossRef]
- Acharya, S.; Jawitz, J.W.; Mylavarapu, R.S. Analytical expressions for drainable and fillable porosity of phreatic aquifers under vertical fluxes from evapotranspiration and recharge. Water Resour. Res. 2012, 48, W11526. [Google Scholar] [CrossRef]
- Sophocleous, M. The role of specific yield in ground-water recharge estimations: A numerical study. Groundwater 1985, 23, 52–58. [Google Scholar] [CrossRef]
- Cheng, D.H.; Li, Y.; Chen, X.; Wang, W.K.; Hou, G.C.; Wang, C.L. Estimation of groundwater evaportranspiration using diurnal water table fluctuations in the mu us desert, northern China. J. Hydrol. 2013, 490, 106–113. [Google Scholar] [CrossRef]
- Duke, H.R. Capillary properties of soils–influence upon specific yield. Amer Soc Agr Eng Trans Asae 1972, 15, 688–691. [Google Scholar] [CrossRef]
- Alley, W.M.; Healy, R.W.; Labaugh, J.W.; Reilly, T.E. Flow and storage in groundwater systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Mcmahon, P.B. Groundwater depletion and sustainability of irrigation in the us high plains and central valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [Green Version]
- Rushton, B. Hydrologic budget for a freshwater marsh in Florida. Water Resour. Bull. 1996, 32, 13–21. [Google Scholar] [CrossRef]
- Bethenod, O.; Katerji, N.; Goujet, R.; Bertolini, J.M.; Rana, G. Determination and validation of corn crop transpirationby sap flow measurement under field conditions. Theor. Appl. Climatol. 2000, 67, 153–160. [Google Scholar] [CrossRef]
- Hsiao, B.T.; Xu, L. Evapotranspiration and Relative Contribution by the Soil and the Plant. Calif. Water Plan Update 2005, 4, 129–160. [Google Scholar]
- Wilson, K.B.; Hanson, P.J.; Baldocchi, D.D. Factors controlling evaporation and energy partitioning beneath a deciduous forest over an annual cycle. Agric. For. Meteorol. 2000, 102, 83–103. [Google Scholar] [CrossRef]
- Coenders-Gerrits, A.M.J.; van der Ent, R.J.; Bogaard, T.A.; Wang, E.L.; Harchowitz, M.; Savenijie, H.H.G. Uncertainties in transpiration estimates. Nature 2014, 506, E1–E2. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Good, S.P.; Noone, D.; Bowen, G. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes. Science 2015, 349, 175–177. [Google Scholar] [CrossRef] [Green Version]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189, 115–117. [Google Scholar] [CrossRef]
- Cavanaugh, M.L.; Kurc, S.A.; Scott, R.L. Evapotranspiration partitioning in semiarid shrubland ecosystems: A two-site evaluation of soil moisture control on transpiration. Ecohydrology 2011, 4, 671–681. [Google Scholar] [CrossRef]
- Schlaepfer, D.R.; Ewers, B.E.; Shuman, B.N.; Williams, D.G.; Frank, J.M.; Massman, W.J.J.; Lauenroth, W.K. Terrestrial water fluxes dominated by transpiration: Comment. Ecosphere 2016, 5, 1–9. [Google Scholar] [CrossRef]
- Nichols, W.D. Estimating discharge of shallow groundwater by transpiration from greasewood in the northern great basin. Water Resour. Res. 1993, 29, 2771–2778. [Google Scholar] [CrossRef]
- Nichols, W.D. Groundwater discharge by phreatophyte shrubs in the great basin as related to depth to groundwater. Water Resour. Res. 1994, 30, 3265–3274. [Google Scholar] [CrossRef]
- Oliveira, R.S.; Dawson, T.E.; Burgess, S. Hydraulic redistribution in three Amazonian trees. Oecologia 2005, 145, 354–363. [Google Scholar] [CrossRef]
- Amenu, G.G.; Kumar, P. A model for hydraulic redistribution incorporating coupled soil-root moisture transport. Hydrol. Earth Syst. Sci. 2008, 12, 55–74. [Google Scholar] [CrossRef] [Green Version]
- Nepstad, D.C.; Carvalho, C.D.; Davidson, E.A.; Jipp, P.H.; Lefebvre, P.A.; Negreiros, G.H.; Silva, E.D.D.; Stone, T.A.; Trumbore, S.E.; Vieira, S. The role of deep roots in the hydrological and carbon cycles of Amazonian forests and pastures. Nature 1994, 372, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Maraux, F.; Lafolie, F. Modeling Soil Water Balance of a Maize-Sorghum Sequence. Soil Sci. Soc. Am. J. 2011, 62, 75–82. [Google Scholar] [CrossRef]
- Kleidon, A.; Heimann, M. Assessing the role of deep rooted vegetation in the climate system with model simulations: Mechanism, comparison to observations and implications for Amazonian deforestation. Clim. Dyn. 2000, 16, 183–199. [Google Scholar] [CrossRef] [Green Version]
- Saleska, S.R.; Didan, K.; Huete, A.R.; da Rocha, H.R. Amazon forests green-up during 2005 drought. Science 2007, 318, 612. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Luo, Y. An empirical approach simulating evapotranspiration from groundwater under different soil water conditions. Environ. Earth Sci. 2012, 67, 1345–1355. [Google Scholar] [CrossRef]
- Schmid, W.; Hanson, R.T.; Iii, T.M.; Leake, S. User guide for the Farm Process (FMP1) for the U.S. Geological Survey’s modular three-dimensional finite-difference ground-water flow model, MODFLOW-2000. In Book 6: Modeling Techniques, Section A. Ground-Water; The U.S. Geological Survey Office of Ground Water, Ground-Water Resources Program: Reston, VA, USA, 2006; Chapter 17. [Google Scholar]
- Mermoud, A.; Morelseytoux, H.J. Modélisation et observation du flux hydriquevers la surface du sol depuisune nappe peu profonde. J. Cardiovasc. Pharmacol. 1989, 4, 11–23. [Google Scholar]
- Yuan, G.F.; Luo, Y.; Shao, M.A.; Zhang, P.; Zhu, X.C. Evapotranspiration and its main controlling mechanism over the desert riparian forests in the lower Tarim river basin. Sci. China Earth Sci. 2015, 58, 1032–1042. [Google Scholar] [CrossRef]
- Yue, W.; Wang, T.; Franz, T.E. Spatiotemporal patterns of water table fluctuations andevapotranspiration induced by riparian vegetation in a semiarid area. Water Resour. Res. 2016, 52, 1948–1960. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.J. Study on the Evapotranspiration and Water Balance of Lake Basin in the Hinterland of Badain Jaran Desert. Master’s Thesis, Lanzhou University, Lanzhou, China, 2020. (In Chinese with English abstract). [Google Scholar]
- Wondzell, S.M.; Gooseff, M.N.; Mcglynn, B.L. An analysis of alternative conceptual models relating hyporheic exchange flow to diel fluctuations in discharge during baseflow recession. Hydrol. Process. 2010, 24, 686–694. [Google Scholar] [CrossRef]
- Jia, W.H.; Yin, L.H.; Zhang, M.S.; Zhang, J.; Zhang, X.X.; Gu, X.F.; Dong, J.Q. Modified method for the estimation of groundwater evapotranspiration under very shallow water table conditions based on diurnal water table fluctuations. J. Hydrol. 2021, 597, 126193. [Google Scholar] [CrossRef]
- Diouf, O.A.; Weihermüller, L.; Diedhiou, M.; Vereecken, H.; CisséFaye, S.C.; Faye, S.; Sylla, S.N. Modelling groundwater evapotranspiration in a shallow aquifer in a semi-arid environment. J. Hydrol. 2020, 587, 124967. [Google Scholar] [CrossRef]
- Zhao, K.Y.; Jiang, X.W.; Wang, X.S.; Wan, L. Restriction of groundwater recharge and evapotranspiration due to a fluctuating water table: A study in the Ordos Plateau, China. Hydrogeol. J. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Zhu, Y.; Ren, L.; Skaggs, T.H.; Lue, H.; Yu, Z.; Wu, Y.; Fang, X. Simulation of Populus euphratica root uptake of groundwater in an arid woodland of the Ejina Basin, China. Hydrol. Process. 2010, 23, 2460–2469. [Google Scholar] [CrossRef]
- Mcdonald, M.G. A Modular Three-Dimensional Finite-Difference Groundwater Flow Model; Techniques of Water-Resources; U. S. Geological Survey: Reston, VA, USA, 1988. [Google Scholar]
- Banta, E.R. MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water Model-Documentation of Packages for Simulating Evapotranspiration with a Segmented Function (EST1) and Drains with Return Flow (DRT1); The U.S. Geological Survey in cooperation with the Colorado Water Conservation Board and the Colorado Division of Water Resources: Reston, VA, USA, 2000. [Google Scholar]
- Warrick, W.A. Additional solutions for steady-state evaporation from a shallow water table. Soil Sci. 1988, 146, 63–66. [Google Scholar] [CrossRef]
- Pozdniakov, S.P.; Vasilevsky, P.Y.; Wang, P. Analysis of a steady-state model of groundwater discharge in a river valley without and with evapotranspiration Adv. Water Resour. Res. 2022, 168, 104306. [Google Scholar] [CrossRef]
- Baird, K.J.; Maddock, T. III. Simulating riparian evapotranspiration: A new methodology and application for groundwater models. J. Hydrol. 2015, 312, 176–190. [Google Scholar] [CrossRef]
- Ajami, H. Maddock III, T. Meixner, T. Hogan, J.F. Guertin, D.P. RIPGIS-NET: A GIS tool for riparian groundwater evapotranspiration in MODFLOW. Groundwater 2012, 50, 154–158. [Google Scholar] [CrossRef]
- El-Zehairy, A.A.; Lubczynski, M.W.; Gurwin, J. Interactions of artificial lakes with groundwater applying an integrated MODFLOW solution. Hydrogeol. J. 2017, 26, 109–132. [Google Scholar] [CrossRef] [Green Version]
- Sergey, G. Elena, F. Victor, S. Vsevolod, S. Sergey, P. Evapotranspiration capture and stream depletion due to groundwater pumping under variable boreal climate conditions: Sudogda River basin, Russia. Hydrogeol. J. 2018, 26, 2753–2767. [Google Scholar]
- Hou, X.L.; Wang, S.Q.; Jin, X.R.; Li, M.L.; Lv, M.Y.; Feng, W.Z. Using an ETWatch (RS)-UZF-MODFLOW coupled model to optimize joint use of transferred water and local water sources in a saline water area of the North China Plain. Water 2020, 12, 3361. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Wood, E.F. Multiscale modeling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef] [Green Version]
- Stieglitz, M.; Rind, D.; Famiglietti, J. An efficient approach to modeling the topographic control of surface hydrology for regional and global climate modeling. J. Clim. 1997, 10, 118–137. [Google Scholar] [CrossRef]
- Koster, R.D.; Ducharne, A.; Stieglitz, M.; Kumar, P.; Suare, M.J. A catchment-based approach to modeling land surface processes in a general circulation model 1. Model structure. Journal of Geophysical Research. Biogeosciences 2000, 105, 24809–24822. [Google Scholar]
- Gutowski, W.J., Jr.; Vorosmarty, C.J.; Person, M.; Otles, Z.; Fekete, B.; York, J. A coupled land-atmosphere simulation program (CLASP): Calibration and validation. J. Geophys. Res. Atmos. 2002, 107, 1–17. [Google Scholar] [CrossRef] [Green Version]
- York, J.P.; Person, M.; Gutowski, W.J.; Winter, T.C. Putting aquifers into atmospheric simulation models: An example from the mill creek watershed, northeastern Kansas. Adv. Water Resour. 2002, 25, 221–238. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Xie, Z.H.; Huang, M.Y. A new parameterization for groundwater and surface water interactions and its impact on water budgets with the variable infiltration capacity (VIC) land surface model. J. Geophys. Res. Atmos. 2003, 108, 1–17. [Google Scholar] [CrossRef]
- Miller, N.L.; Maxwell, R.M. Development of a coupled land surface and groundwater model. J. Hydrometeorol. 2005, 6, 233–247. [Google Scholar]
- Yeh, P.J.F.; Eltahir, E.A.B. Representation of water table dynamics in a land surface scheme. Part I: Model development. J. Clim. 2005, 18, 1861–1880. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Eltahir, E.A.B. Representation of water table dynamics in a land surface scheme: Observations, models, and analyses. Representation of Water Table Dynamics in a Land Surface Scheme. Part II Subgrid Variability. J. Clim. 2005, 18, 1881–1901. [Google Scholar]
- Cohen, D.; Person, M.; Daannen, R.; Locke, S.; Dahlstrom, D.; Zabielski, V.; Winter, T.C.; Rosenbery, D.O.; Wright, H.; Ito, E.; et al. Groundwater-supported evapotranspiration within glaciated watersheds under conditions of climate change. J. Hydrol. 2006, 320, 484–500. [Google Scholar] [CrossRef] [Green Version]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E.; Su, H. Development of a simple groundwater model for use in climate models and evaluation with gravity recovery and climate experiment data. J. Geophys. Res. 2007, 112, D07103. [Google Scholar] [CrossRef]
- Fan, Y.; Miguez-Macho, G.; Weaver, C.P.; Walko, R.; Robock, A. Incorporating water table dynamics in climate modeling: 1. Water table observations and equilibrium water table simulations. J. Geophys. Res. Atmos. 2007, 112, D10125. [Google Scholar] [CrossRef]
- Jorenush, M.H.; Sepaskhah, A.R. Modelling capillary rise and soil salinity for shallow saline water table under irrigated and non-irrigated conditions. Agric. Water Manag. 2003, 61, 125–141. [Google Scholar] [CrossRef]
- Blin, N.; Suárez, F. Evaluating the contribution of satellite-derived evapotranspiration in the calibration of numerical groundwater models in remote zones using the EEFlux tool. Sci. Total Environ. 2023, 858, 15. [Google Scholar] [CrossRef]
- Liu, Y.; Pereira, L.S.; Fernando, R.M. Fluxes through the bottom boundary of the root zone in silty soils: Parametric approaches to estimate groundwater contribution and percolation. Agric. Water Manag. 2006, 84, 27–40. [Google Scholar] [CrossRef]
- Askri, B.; Bouhlila, R.; Job, J.O. Development and application of a conceptual hydrologic model to predict soil salinity within modern Tunisian oases. J. Hydrol. 2010, 380, 45–61. [Google Scholar] [CrossRef]
| Method | Experimental Period |
|---|---|
| White [81] | 0:00~4:00 |
| Dolan et al. [96] | 0:00~4:00 |
| Hays [97] | 0:00~4:00 |
| Loheide [62] | 0:00~6:00 |
| Yin et al. [12] | the previous day 21:00~5:00 |
| Rushton [108] | the previous day 18:00~6:00 |
| Miller et al. [94] | the previous day 22:00~7:00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Yang, H.; Cao, J.; Feng, W.; Zhang, Y. A Review of Advances in Groundwater Evapotranspiration Research. Water 2023, 15, 969. https://doi.org/10.3390/w15050969
Hou X, Yang H, Cao J, Feng W, Zhang Y. A Review of Advances in Groundwater Evapotranspiration Research. Water. 2023; 15(5):969. https://doi.org/10.3390/w15050969
Chicago/Turabian StyleHou, Xianglong, Hui Yang, Jiansheng Cao, Wenzhao Feng, and Yuan Zhang. 2023. "A Review of Advances in Groundwater Evapotranspiration Research" Water 15, no. 5: 969. https://doi.org/10.3390/w15050969






