Mechanism Study of Differential Permeability Evolution and Microscopic Pore Characteristics of Soft Clay under Saturated Seepage: A Case Study in Chongming East Shoal
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Investigation
2.2. Basic Properties
2.3. Variable Head Permeability Test
2.4. Microscopic Tests
2.4.1. MIP Test
2.4.2. SEM Test
2.5. Grey Relation Entropy
3. Results
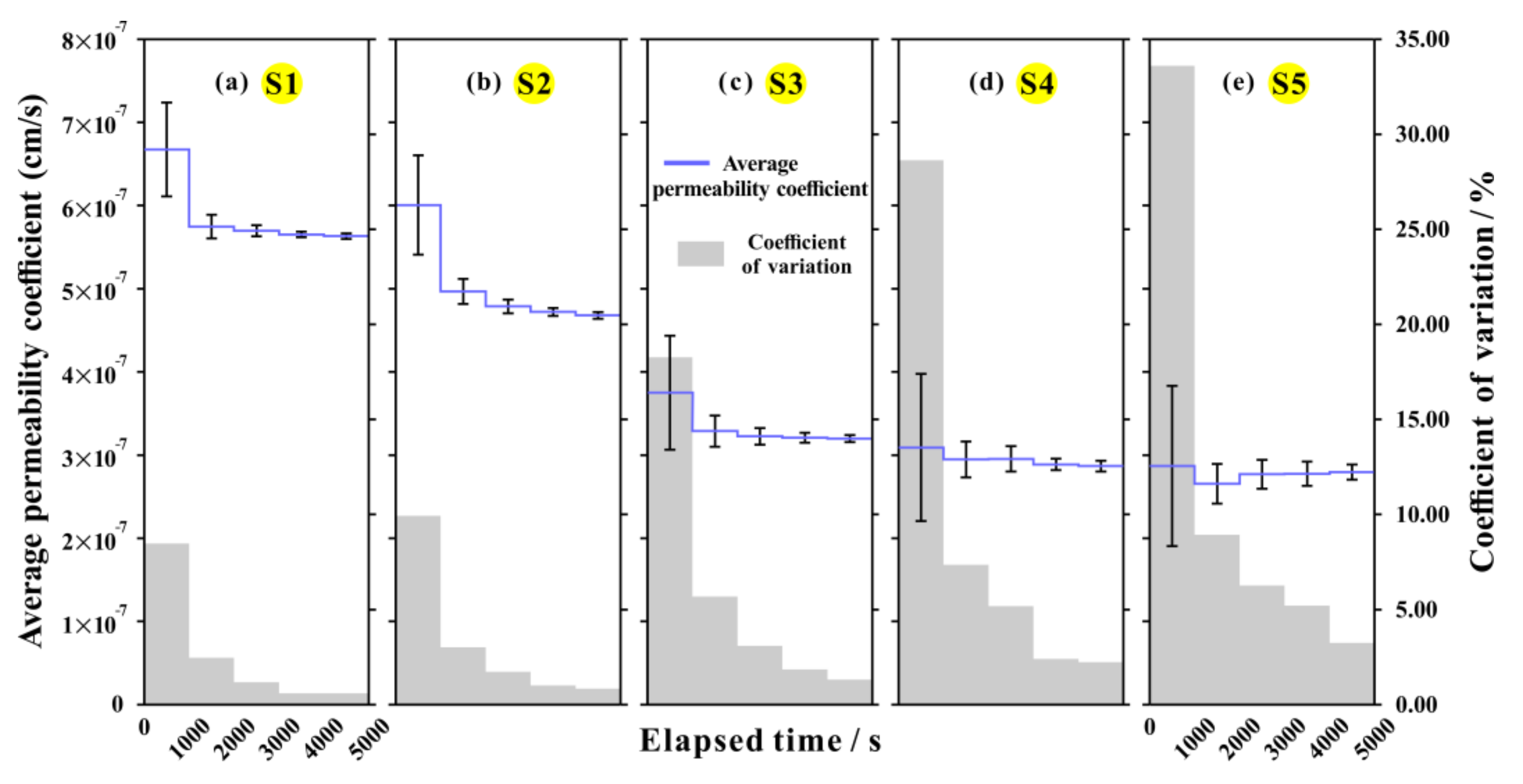
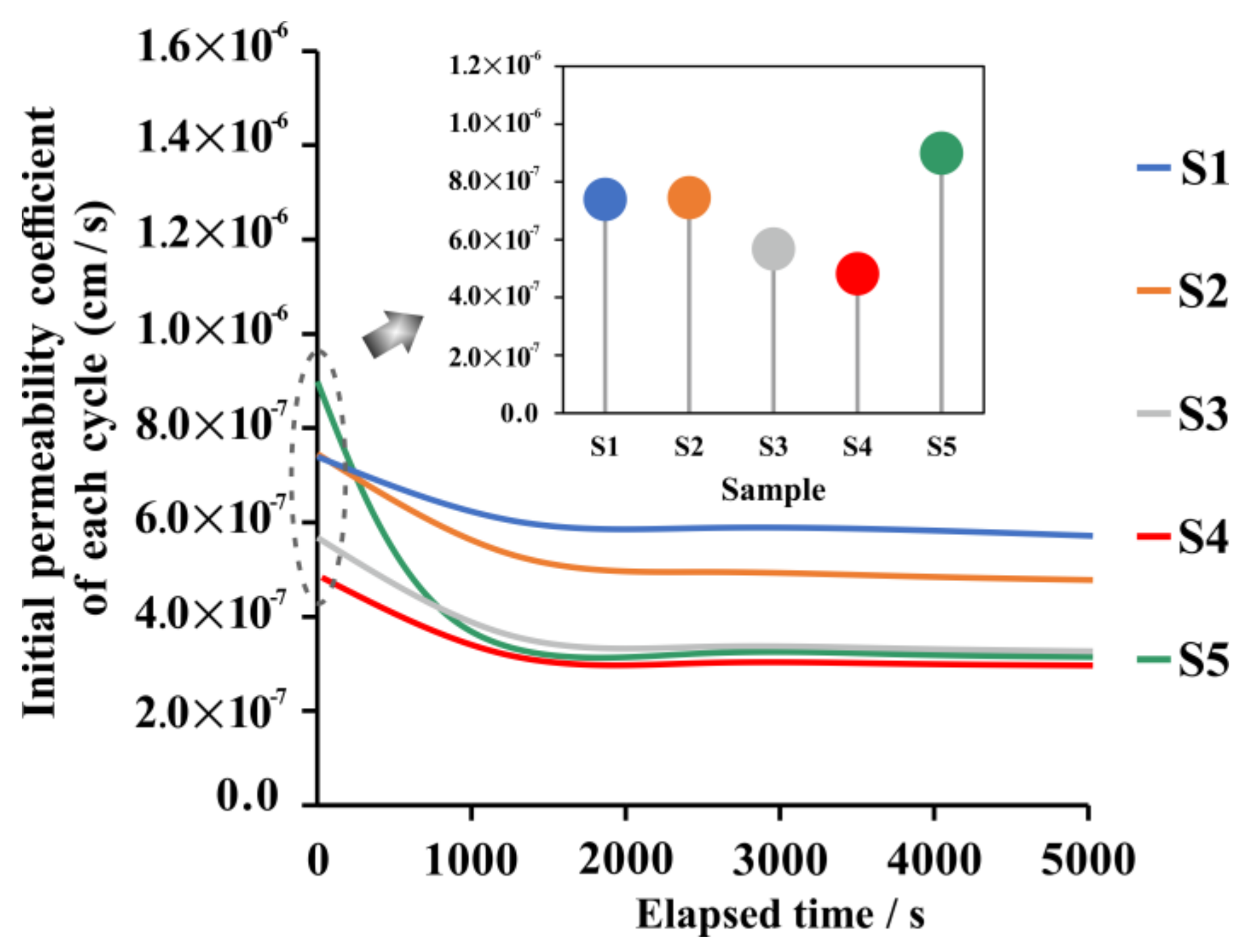
3.1. Permeability Characteristics
3.1.1. Dynamic evolution
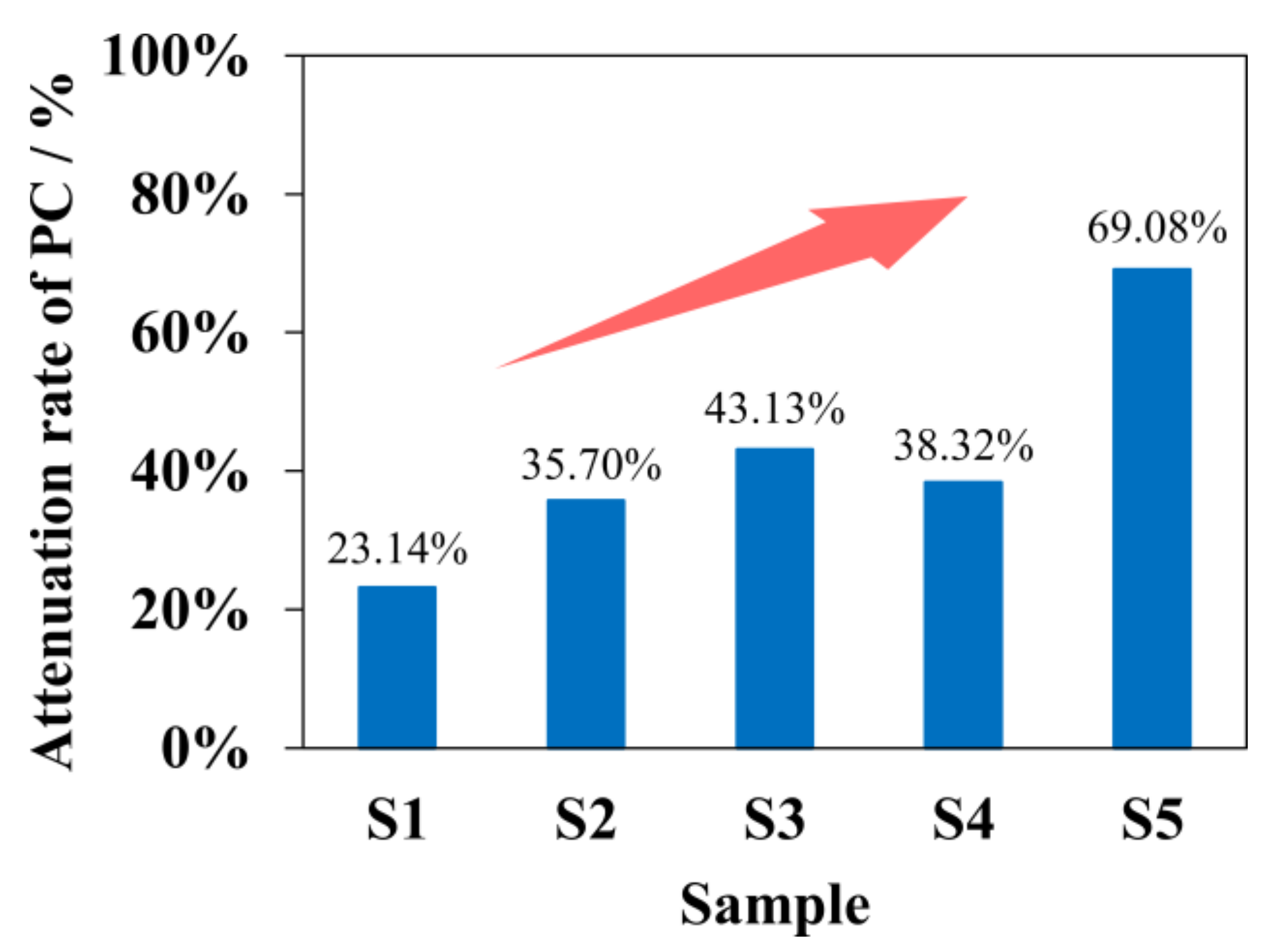
3.1.2. Differential Permeability Patterns among Reclamation Areas
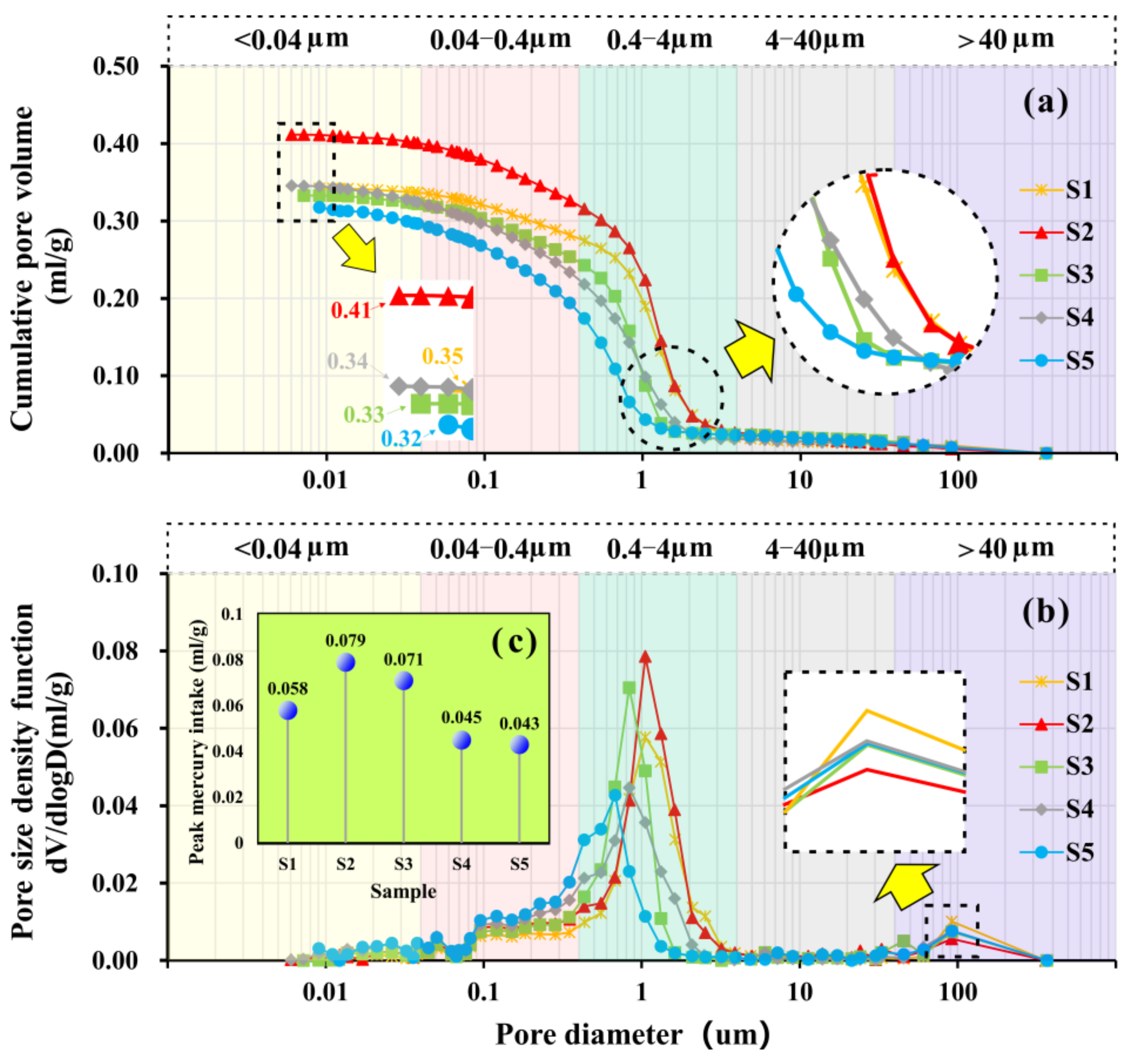
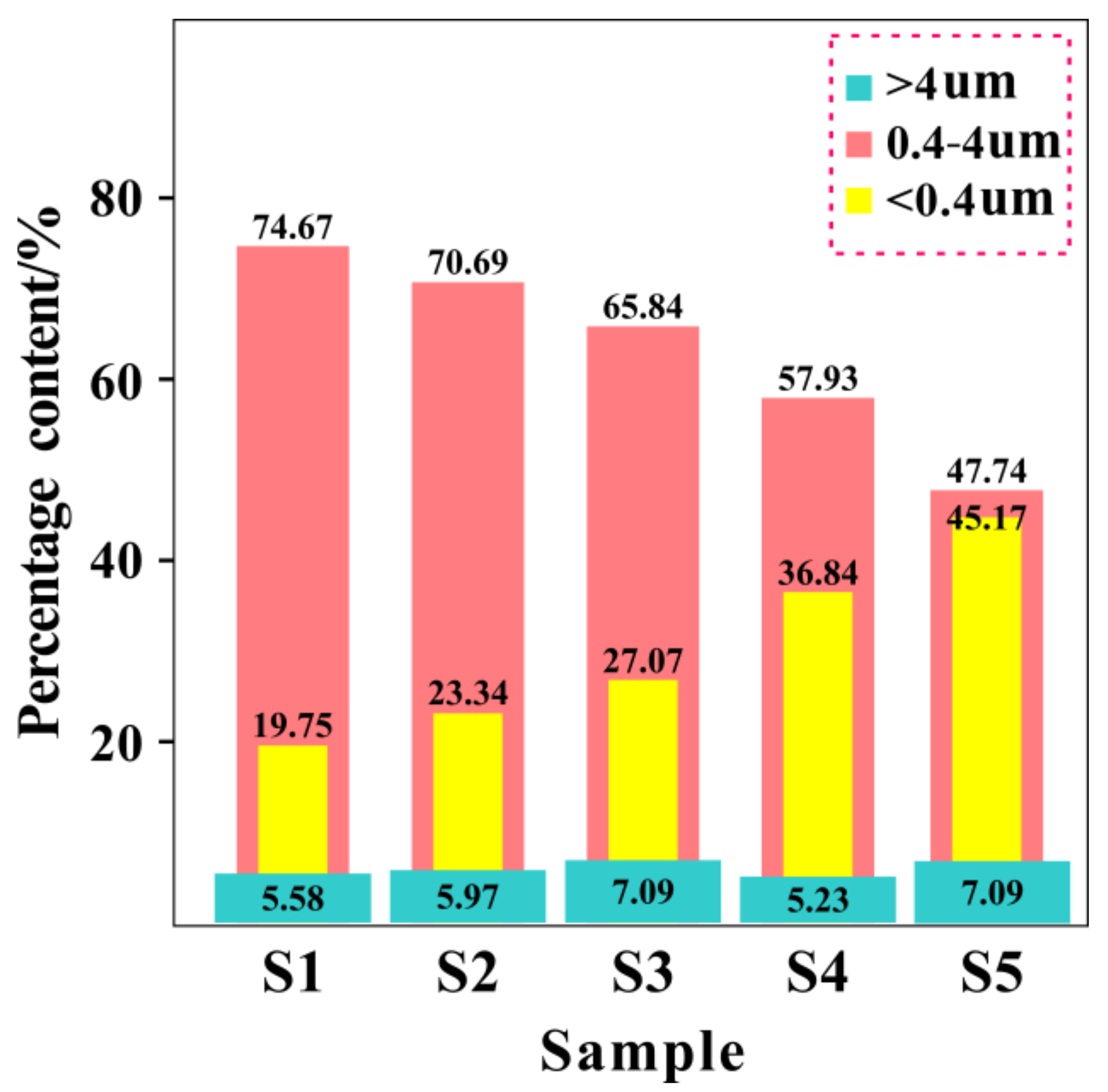
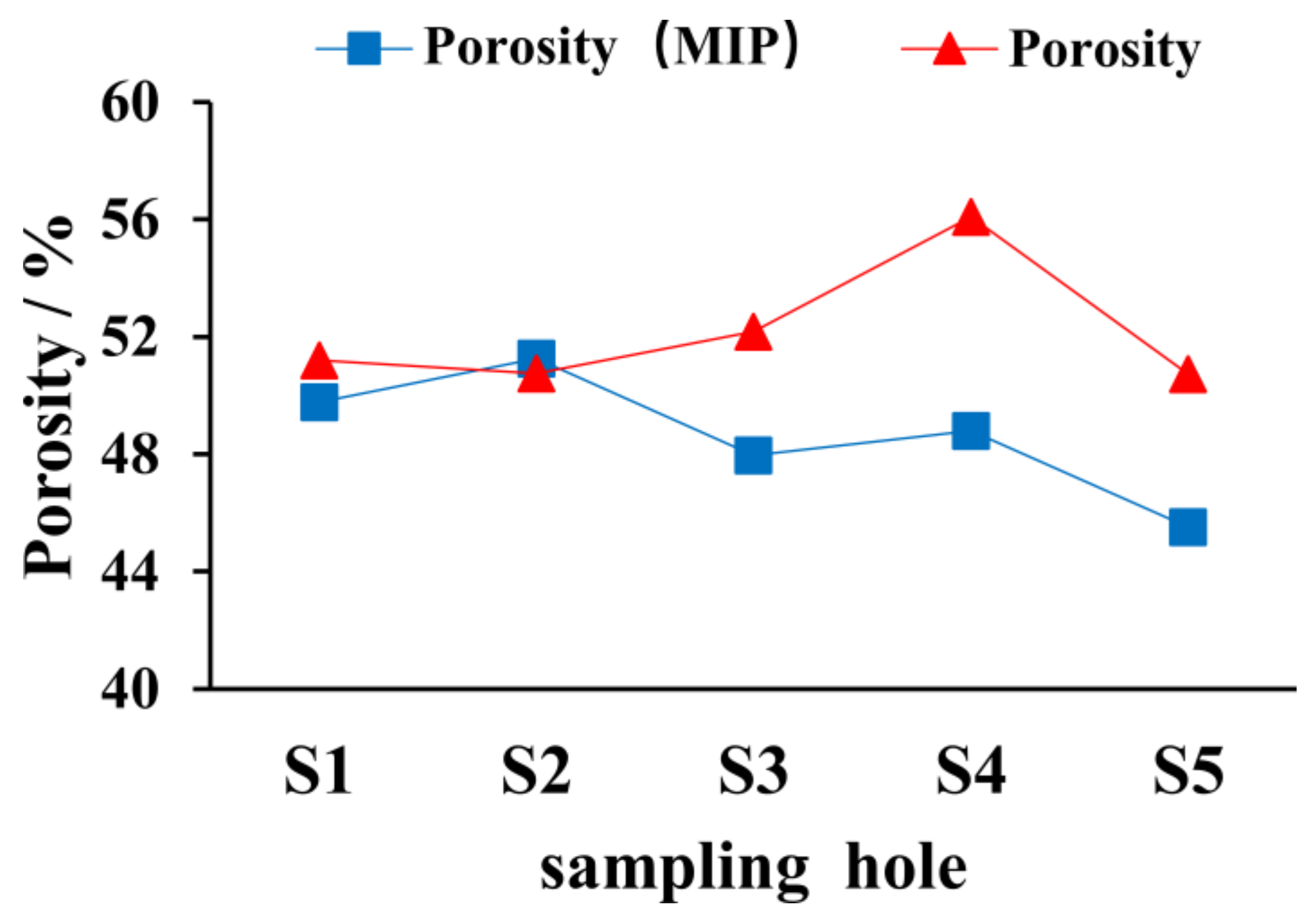
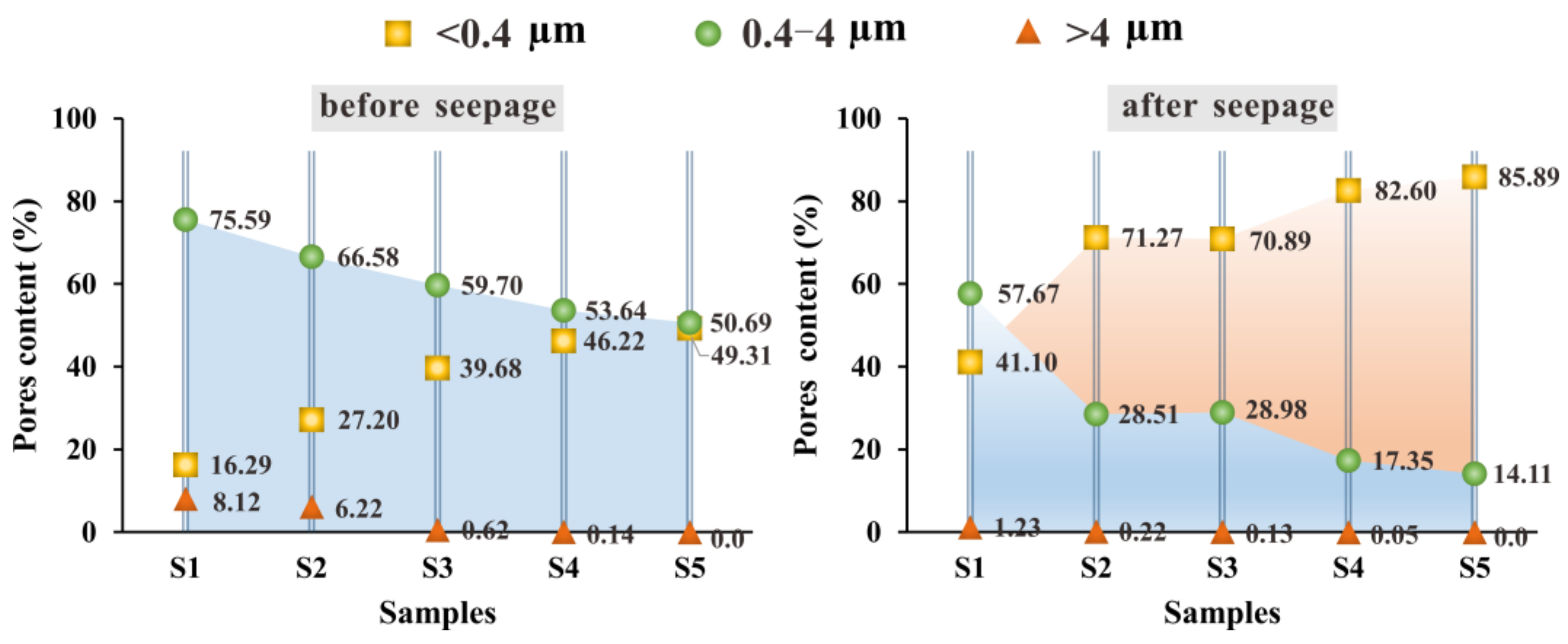
3.2. Pore Characteristics
3.2.1. Pore Distribution
3.2.2. Pore Size
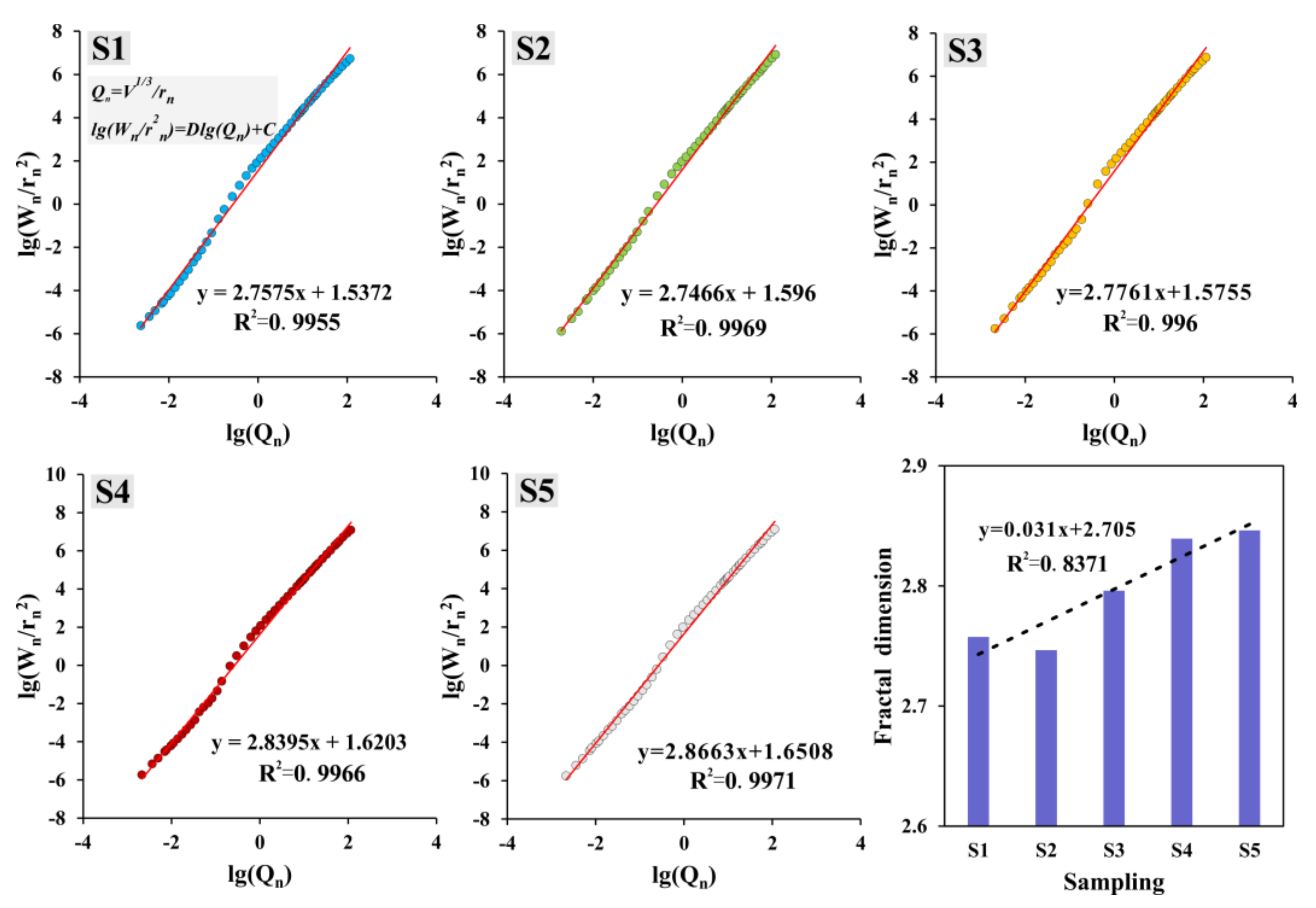
3.2.3. Pore Complexity
3.3. Microstructure Characteristics
4. Discussion
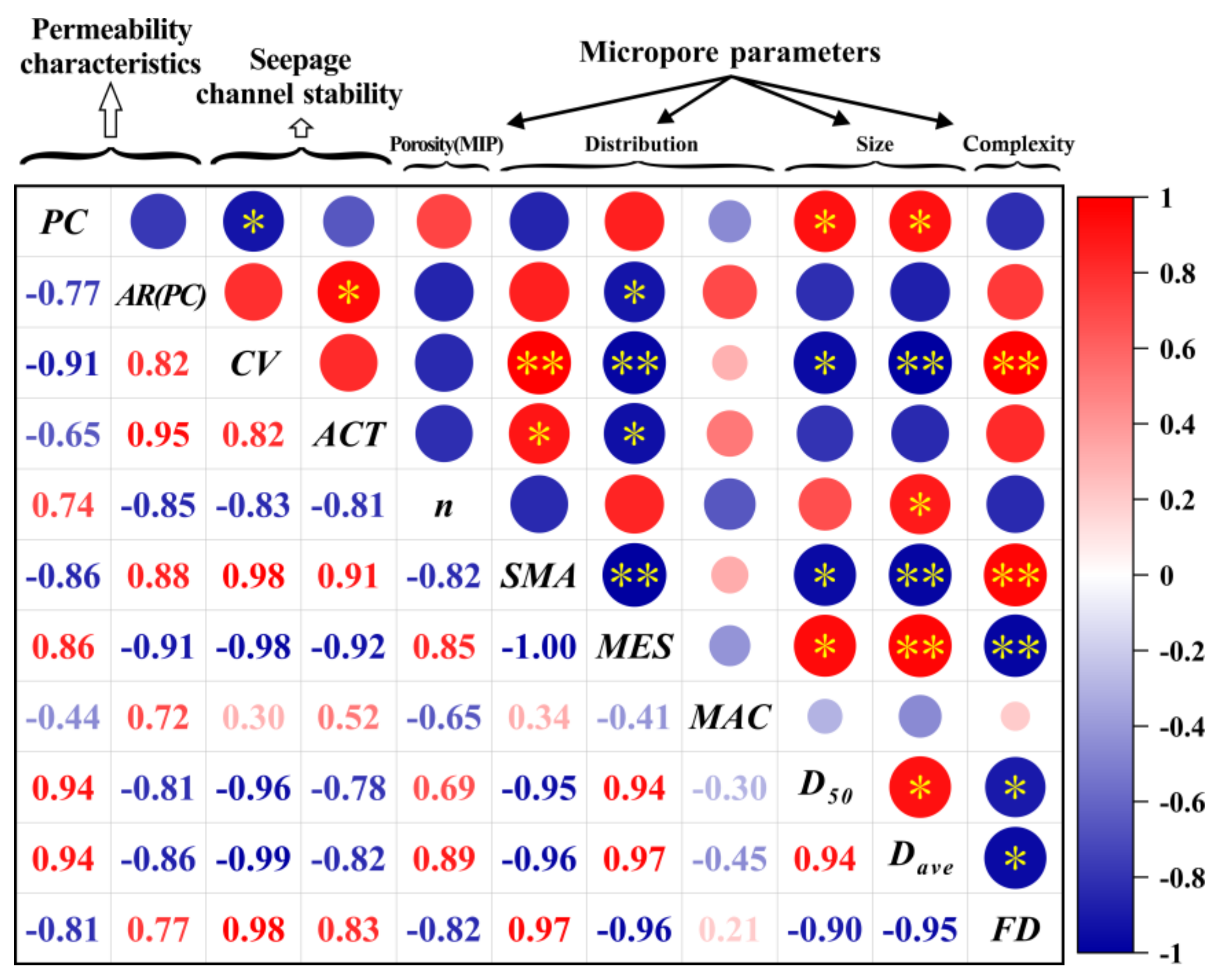
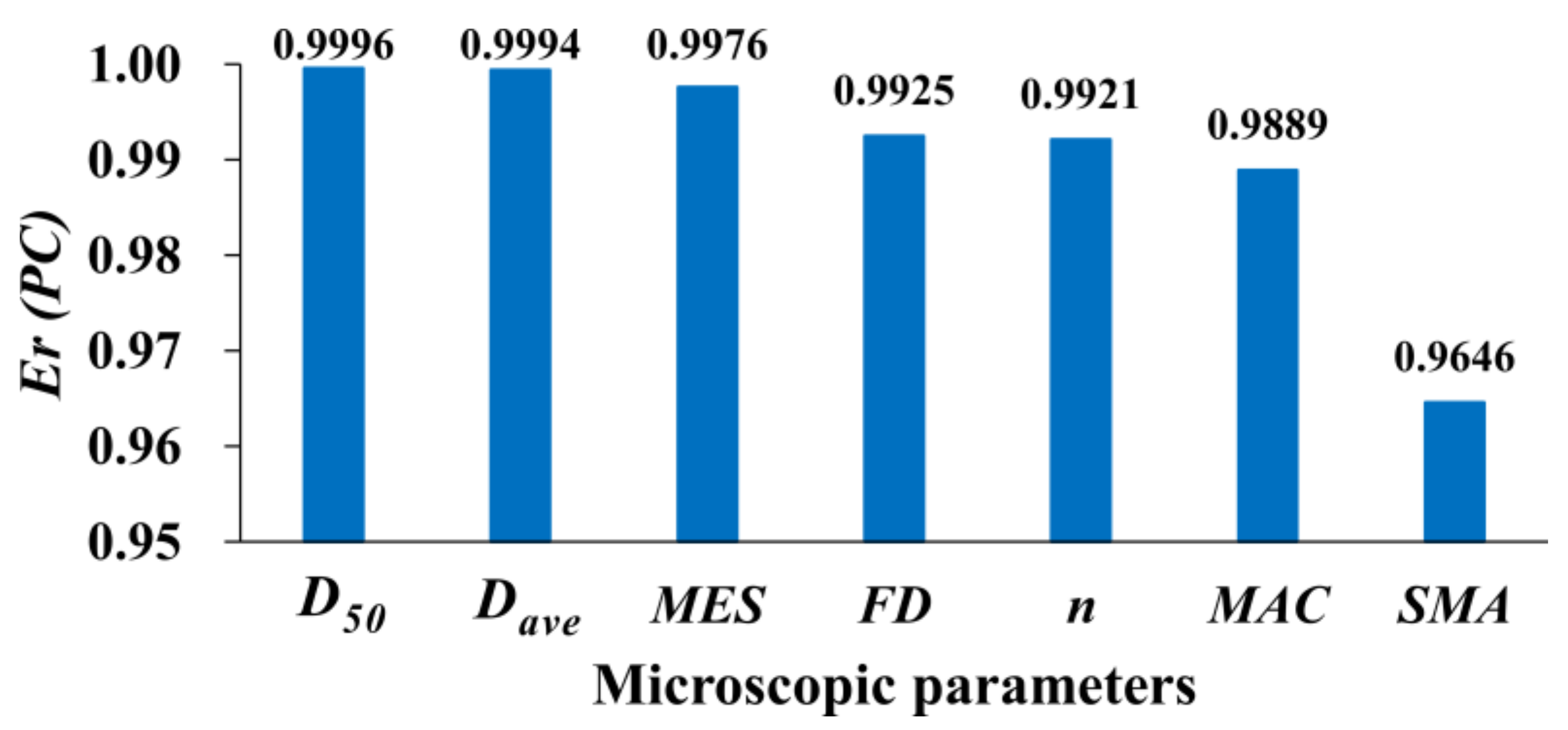
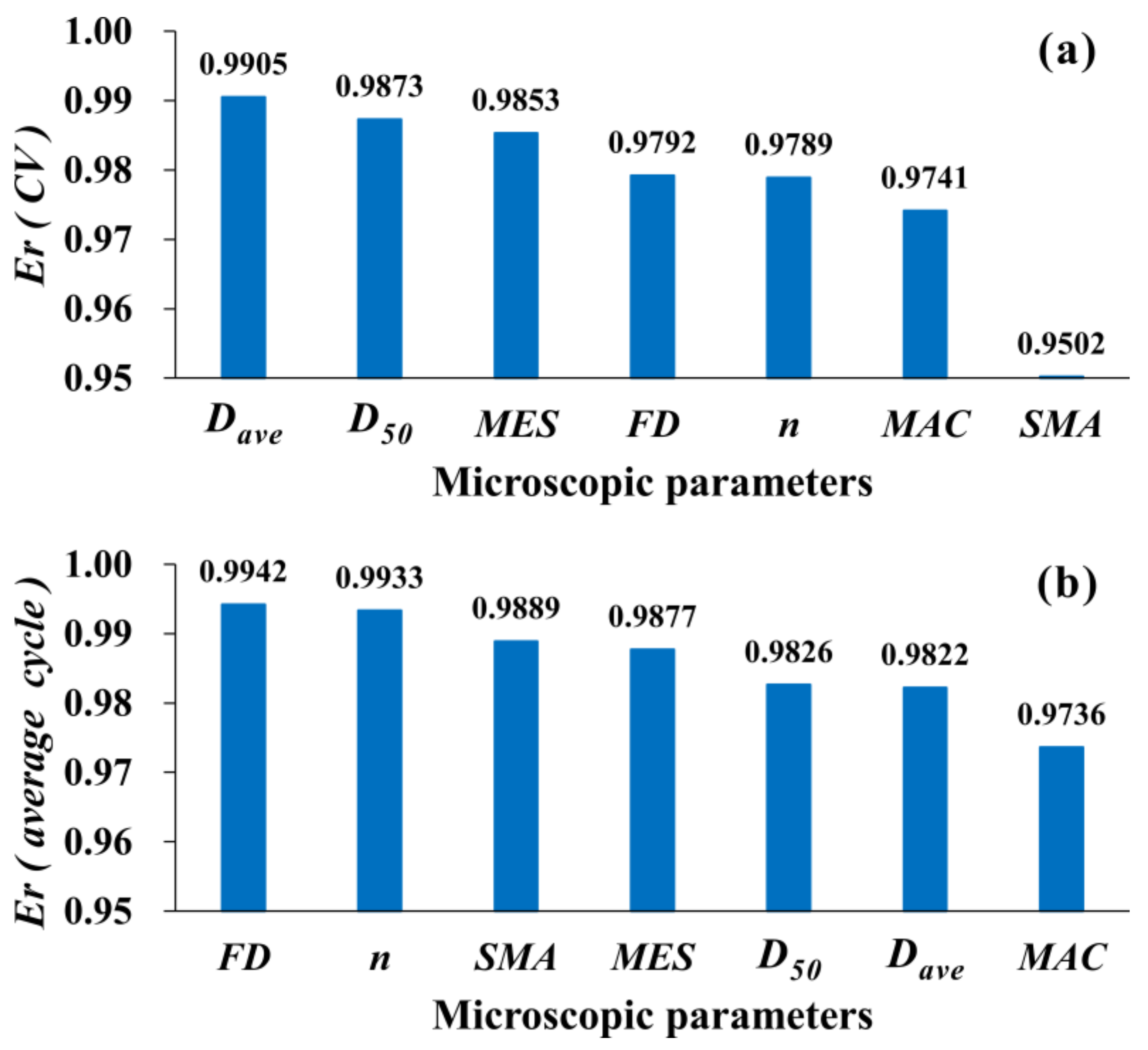
4.1. Correlation between Micropore Parameters and Stable Permeability Coefficient
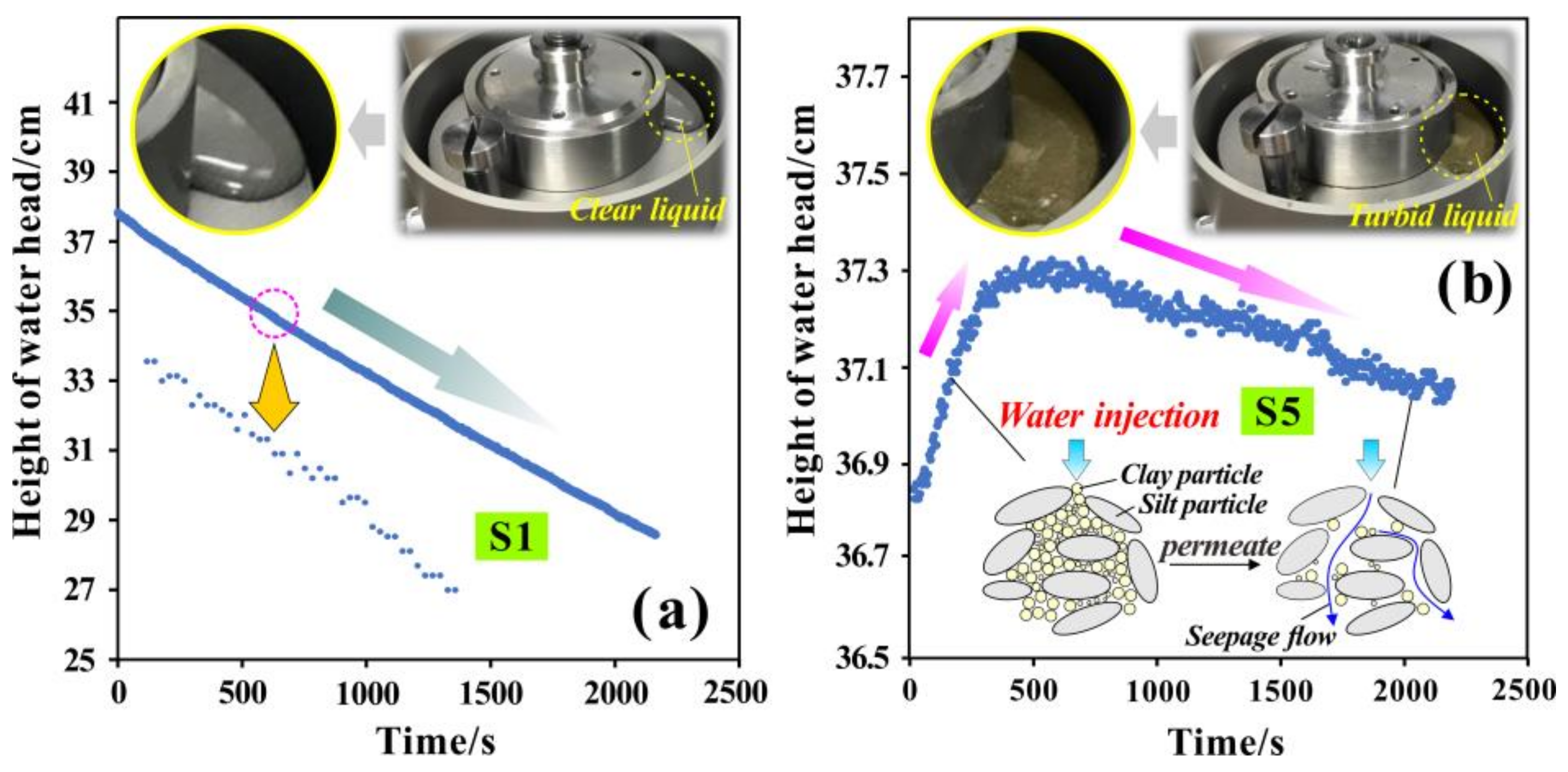
4.2. Analysis of Seepage Channel Stability and Pore Clogging
4.3. Microscopic Verification and Mechanism Analysis of Clogging Effect
5. Conclusions
- (1)
- During clay seepage, the PC was not constant, but gradually decayed and tended to become stable with time, which indicated the transition from the unstable seepage stage to the relatively stable seepage stage. Compared with inland clay, the PC of offshore clay not only deteriorated more seriously with time but also took longer to reach a relatively stable seepage state, indicating the unstable seepage channel.
- (2)
- The attenuation of PC with time was not monotonic but cyclic, resulting from the alternating action of closing and opening seepage channels. During seepage, the clay particles may have migrated with the water flow and changed the original pore structure; these clay particles could be intercepted by pores, thereby clogging the seepage channels. With the advancement of seepage, some weakly-connected particles, derived from the increased pore water pressure caused by the clogging effect, could migrate again. Then, the pores could be gradually expanded and new seepage channels could be generated. If repeated, the unstable seepage channel could lead to the cyclic dynamic change of the PC.
- (3)
- The PC of the USC in the early reclamation area in the stable stage was abnormally higher than that of the USC in the late reclamation area. Although the overall porosity of the early reclamation area USC was lower, its higher mesopores content, lower FD, and skeleton aggregation structure promoted the water flow effectively. It could be seen that, although the USC in the late-reclamation area suffered from the dredged load for a shorter time, it did not necessarily present high permeability and consolidation efficiency. The effects of pore structure, distribution, and complexity on permeability cannot be ignored, which is characterized by long-term and gradual change.
- (4)
- Even though particle migration is common in the clay seepage process, the USC in the early reclamation area had a stronger anti-clogging ability controlled by the different pore characteristics. When soil particles are intercepted by the pores, they may cover part of the pores or fill in the pores, both of which results in changing the pore distribution, so that the mesopores will be converted to small pores. Compared with offshore clay, this pore conversion rate was lower in inland clay, and the pore channels were relatively stable, allowing for more effective seepage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| USC | underlying soft clay |
| CES | Chongming East Shoal |
| MIP | mercury intrusion porosimetry |
| SEM | scanning electron microscope |
| PC | permeability coefficient |
| Dave | average pore diameter |
| D50 | medium entrance pore diameter |
| FD | fractal dimension |
| CV | coefficient of variation |
| AR(PC) | attenuation rate of permeability coefficient |
| ACT | average cycle time |
| SMA | small pores content |
| MES | mesopores content |
| MAC | macropores content |
References
- Breber, P.; Povilanskas, R.; Armaitienė, A. Recent evolution of fishery and land reclamation in Curonian and Lesina lagoons. Hydrobiologia 2008, 611, 105. [Google Scholar] [CrossRef]
- Mcleod, E.; Poulter, B.; Hinkel, J.; Reyes, E.; Salm, R. Sea-level rise impact models and environmental conservation: A review of models and their applications. Ocean Coast. Manag. 2010, 53, 507–517. [Google Scholar] [CrossRef]
- Wang, W.; Liu, H.; Li, Y.Q.; Su, J.L. Development and management of land reclamation in China. Ocean Coast. Manag. 2014, 102, 415–425. [Google Scholar] [CrossRef]
- Yu, Q.B.; Yan, X.X.; Wang, Q.; Yang, T.L.; Kong, Y.Y.; Huang, X.L.; Mehmood, Q. X-ray computed tomography-based evaluation of the physical properties and compressibility of soil in a reclamation area. Geoderma 2020, 375, 114524. [Google Scholar] [CrossRef]
- Yuan, X.Q.; Wang, Q.; Lu, W.X.; Zhang, W.; Chen, H.E.; Zhang, Y. Indoor simulation test of step vacuum preloading for high-clay content dredger fill. Mar. Geores. Geotechnol 2018, 36, 83–90. [Google Scholar] [CrossRef]
- Yu, Q.B.; Wang, Q.; Yan, X.X.; Yang, T.L.; Song, S.Y.; Yao, M.; Zhou, K.; Huang, X.L. Ground Deformation of the Chongming East Shoal Reclamation Area in Shanghai Based on SBAS-InSAR and Laboratory Tests. Remote Sens. 2020, 12, 1016. [Google Scholar] [CrossRef]
- Hu, H.J.; Jiang, M.J.; Peng, J.B.; Shen, Z.F. Pore fractal features of different kinds of loesses before and after stress path tests. Rock Soil Mech. 2014, 35, 2479–2485. [Google Scholar]
- Nguyen, B.P.; Kim, Y.T. An analytical solution for consolidation of PVD-installed deposit considering nonlinear distribution of hydraulic conductivity and compressibility. Eng. Comput. 2019, 36, 707–730. [Google Scholar] [CrossRef]
- Geng, X.Y.; Yu, H.S. A large-strain radial consolidation theory for soft clays improved by vertical drains. Geotechnique 2017, 67, 1020–1028. [Google Scholar] [CrossRef]
- Lee, D.; Anm, Y.; Kwak, T.; Lee, T.; Choi, H. Nonlinear finite-strain self-weight consolidation of dredged material with radial drainage using Carrillo’s formula. J. Waterw. Port Coast. Ocean Eng. 2016, 142, 06016002. [Google Scholar] [CrossRef]
- Romero, E. A microstructural insight into compacted clayey soils and their hydraulic properties. Eng. Geol. 2013, 165, 3–19. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Q.; Xia, W.T.; Liu, J.; Wang, J.Q.; Chen, Y.T.; Shen, J.J. Experimental study on the hydraulic conductivity of un-saturated dispersive soil with different salinities subjected to freeze-thaw. J. Hydrol. 2020, 583, 124297. [Google Scholar] [CrossRef]
- Zhang, X.D.; Wu, Y.J.; Zhai, E.C.; Ye, P. Coupling analysis of the heat-water dynamics and frozen depth in a seasonally frozen zone. J. Hydrol. 2021, 593, 125603. [Google Scholar] [CrossRef]
- Kong, L.W.; Li, X.M.; Tian, H.N. Effect of fines content on permeability coefficient of sand and its correlation with state pa-rameters. Rock Soil Mech. 2011, 32, 21–26. [Google Scholar]
- Zhang, M.X.; Zhu, X.W.; Yu, G.L.; Yan, J.M.; Wang, X.B.; Chen, M.L.; Wang, W.M. Permeability of muddy clay and settlement simulation. Ocean Eng. 2015, 104, 521–529. [Google Scholar] [CrossRef]
- Levy, G.J.; Eisenberg, H.; Shainberg, I. Clay dispersion as related to soil properties and water permea-bility. Soil Sci. 1993, 155, 15–22. [Google Scholar] [CrossRef]
- Xu, P.P.; Zhang, Q.Y.; Qian, H.; Qu, W.G.; Li, M.N. Microstructure and permeability evolution of remolded loess with different dry densities under saturated seepage. Eng. Geol. 2021, 282, 105875. [Google Scholar] [CrossRef]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Zhang, X.D.; Zhai, E.C.; Wu, Y.J.; Sun, D.A.; Lu, Y.T. Theoretical and Numerical Analyses on Hydro–Thermal–Salt–Mechanical Interaction of Unsaturated Salinized Soil Subjected to Typical Unidirectional Freezing Process. Int. J. Geomech. 2021, 21, 04021104. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.W.; Xiao, H.B.; Wang, B.; Nie, X.D.; Liu, C.; Ni, L.S.; Wang, D.Y. The transport of aggregates associated with soil organic carbon under the rain-induced overland flow on the Chinese Loess Plateau. Earth Surf. Process. Landf. 2019, 44, 1895–1909. [Google Scholar] [CrossRef]
- Shan, X.Z.; Wei, Y.Q.; Yan, H.J.; Liu, J.F.; Zhang, Y. Influence of organic matter content on soil hydrodynamic parameters. Acta Pedol. Sin. 1998, 3, 1–9. [Google Scholar]
- Dong, Z.L.; Chen, P.S.; Mo, H.H.; Zhang, G.X. Effects of permeability coefficients on consolidation of soft clay under by vacuum preloading. Rock Soil Mech. 2010, 31, 1452–1456. [Google Scholar]
- Tang, Y.Q.; Yan, J.J. Effect of freeze–thaw on hydraulic conductivity and microstructure of soft soil in Shanghai area. Environ. Earth Sci. 2015, 73, 7679–7690. [Google Scholar] [CrossRef]
- Ren, X.W.; Santamarina, J.C. The hydraulic conductivity of sediments: A pore size perspective. Eng. Geol. 2018, 233, 48–54. [Google Scholar] [CrossRef]
- Chen, J.; Fang, Y.; Gu, R.; Shu, H.; Ba, L.; Li, W. Study on pore size effect of low permeability clay seepage. Arab. J. Geosci. 2019, 12, 238. [Google Scholar] [CrossRef]
- Zhou, J.; Luo, L.H.; Yu, L.G.; Nangulama, H. Experimental study about the influence of cyclic load on the hydraulic conduc-tivity of clay. Acta Geotech. 2020, 15, 3357–3370. [Google Scholar] [CrossRef]
- Wang, H.L.; Sun, H.; Huang, Z.X.; Ge, X.R. A microstructural investigation on hydraulic conductivity of soft clay. Bull. Eng. Geol. Environ. 2021, 80, 4067–4078. [Google Scholar] [CrossRef]
- Zhao, J.L.; Sun, M.D.; Pan, Z.J.; Liu, B.; Ostadhassan, M.; Hu, Q.H. Effects of pore connectivity and water saturation on matrix permeability of deep gas shale. Adv. Geo-Energy Res. 2022, 6, 54–68. [Google Scholar] [CrossRef]
- Lu, H.J.; Wang, C.F.; Li, D.G.; Li, J.X.; Wan, Y. Permeability, Pore, and Structural Parameters of Undisturbed Silty Clay Presented in Landfill Leachate. Water Air Soil Pollut. 2020, 231, 190. [Google Scholar] [CrossRef]
- Zha, F.S.; Liu, C.M.; Kang, B.; Yang, X.H.; Zhou, Y.; Yang, C.B. Acid rain leaching behavior of Zn-contaminated soils solidi-fied/stabilized using cement–soda residue. Chemosphere 2021, 281, 130916. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Siqueira, F.D.; Furtado, C.A.; Souza, A.L.S. Modified Particle Detachment Model for Colloidal Transport in Porous Media. Transp. Transp. Porous Media 2011, 86, 353–383. [Google Scholar] [CrossRef]
- Touch, N.; Hibino, T.; Nakashita, S. Permeability Reduction by Sediment Retention in Saturated Sand Columns. Transp. Transp. Porous Media 2013, 98, 615–630. [Google Scholar] [CrossRef]
- Khilar, K.C.; Fogler, H.S. Migration of Fines in Porous Media; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Civan, F. Non-isothermal Permeability Impairment by Fines Migration and Deposition in Porous Media including Dispersive Transport. Transp. Porous Media 2010, 85, 233–258. [Google Scholar] [CrossRef]
- Horikoshi, K.; Takahashi, A. Suffusion-induced change in spatial distribution of fine fractions in embankment subjected to seepage flow. Soils Found. 2015, 55, 1293–1304. [Google Scholar] [CrossRef]
- Chang, F.F.; Civan, F. Predictability of Formation Damage by Modeling Chemical and Mechanical Processes. In Proceedings of the SPE Formation Damage Control Symposium, Lafayette, LA, USA, 26–27 February 1992. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, L.X.; Lin, G.Q.; Yan, X.J.; Chen, X.L.; Pang, H.L. Chemical mechanism of flocculation and deposition of clay colloids in coastal aquifers. J. Ocean Univ. 2016, 15, 847–852. [Google Scholar] [CrossRef]
- Yang, M.S.; Yang, T.L.; Zhang, L.; Lin, J.X.; Qin, X.Q.; Liao, M.S. Spatio-Temporal Characterization of a Reclamation Settlement in the Shanghai Coastal Area with Time Series Analyses of X-, C-, and L-Band SAR Datasets. Remote Sens. 2018, 10, 329. [Google Scholar] [CrossRef]
- Xu, Y.S.; Wu, H.N.; Wang, B.Z.F.; Yang, T.L. Dewatering induced subsidence during excavation in a Shanghai soft deposit. Environ. Earth Sci. 2017, 76, 351. [Google Scholar] [CrossRef]
- Ye, G.L.; Lin, N.; Bao, X.H.; Gu, L.L.; Yadav, S.K. Effect of Quaternary transgression and regression on the engineering properties of Shanghai soft clays. Eng. Geol. 2018, 239, 321–329. [Google Scholar] [CrossRef]
- Dong, J.Q.; Wang, B.X.; Yan, X.X.; Xu, X.C.; Xiao, G.P.; Yu, Q.B.; Yao, M.; Wang, Q. Prediction of Undisturbed Clay Rebound Index Based on Soil Microstructure Parameters and PSO-SVM Model. KSCE J. Civ. Eng. 2022, 26, 2097–2111. [Google Scholar] [CrossRef]
- Yu, Q.B.; Yan, X.X.; Wang, Q.; Yang, T.L.; Lu, W.X.; Yao, M.; Dong, J.Q.; Zhan, J.W.; Huang, X.L.; Niu, C.C.; et al. A Spatial-Scale Evaluation of Soil Consolidation Concerning Land Subsidence and Integrated Mechanism Analysis at Macro-, and Micro-Scale: A Case Study in Chongming East Shoal Reclamation Area, Shanghai, China. Remote Sens. 2021, 13, 2418. [Google Scholar] [CrossRef]
- Tanaka, H.; Shiwakoti, D.R.; Omukai, N.; Rito, F.; Locat, J.; Tanaka, M. Pore Size Distribution of Clayey Soils Measured by Mercury Intrusion Porosimetry and its Relation to Hydraulic Conductivity. Soils Found. 2003, 43, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.F.; Yue, X.B.; Liu, S.Y.; Chen, Y.G.; Zhang, D.W. Hydraulic conductivity of cement-stabilized marine clay with metakaolin and its correlation with pore size distribution. Eng. Geol. 2015, 193, 146–152. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, Q.; Kong, Y.Y.; Han, Y.; Cheng, S.K. Analysis of the pore structure characteristics of freeze-thawed saline soil with different salinities based on mercury intrusion porosimetry. Environ. Earth Sci. 2020, 79, 161. [Google Scholar] [CrossRef]
- Chen, H.E.; Li, H.; Jiang, Y.L.; Yu, Q.B.; Yao, M.; Shan, W.C. Feasibility study on artificial preparation of structured loess. Geosci. Lett. 2022, 9, 21. [Google Scholar] [CrossRef]
- Lv, F.; Liu, X.; Liu, Q. A Comparative Study on the Correlation Degrees of Seven Grey Systems. J. Wuhan Univ. Tech. 2000, 2, 41–43. [Google Scholar]
- Liu, Q.; Zhao, B.D.; Santamarina, J.C. Particle migration and clogging in porous media: A convergent flow microfluidics study. J. Geophys. Res. Solid Earth 2019, 124, 9495–9504. [Google Scholar] [CrossRef]
- Liu, Y.W.; Zheng, W.L.; Wang, Q.; Cao, C.J.; Chang, M.S.; Rocchi, I. Evaluating sulfur-free lignin as a sustainable additive for soil improvement against frost resistance. J. Clean Prod. 2020, 251, 119504. [Google Scholar] [CrossRef]
- Romero, E.; Simms, P.H. Microstructure Investigation in Unsaturated Soils: A Review with Special Attention to Contribu-tion of Mercury Intrusion Porosimetry and Environmental Scanning Electron Microscopy. Geotech. Geol. Eng. 2008, 26, 705–727. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Zhou, W.H.; Cai, Y.Q. Large-strain elastic viscoplastic consolidation analysis of very soft clay layers with vertical drains under preloading. Can. Geotech. J. 2014, 51, 144–157. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Li, S.F. Determination of the Surface Fractal Dimension for Porous Media by Mercury Porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
- Zhou, J.; Tang, Y.Q. Experimental inference on dual-porosity aggravation of soft clay after freeze-thaw by fractal and probability analysis. Cold Reg. Sci. Technol. 2018, 153, 181–196. [Google Scholar] [CrossRef]
- Jiao, W.C.; Zhou, D.; Wang, Y.T. Effects of Clay Content on Pore Structure Characteristics of Marine Soft Soil. Water 2021, 13, 1160. [Google Scholar] [CrossRef]
- Feng, S.X.; Xu, Z.G.; Chai, J.R.; Li, Y.L. Using pore size distribution and porosity to estimate particle size distribution by nuclear magnetic resonance. Soils Found. 2020, 60, 1011–1019. [Google Scholar] [CrossRef]
- Zhang, X.D.; Shu, C.J.; Wu, Y.J.; Ye, P.; Du, D.W. Advances of coupled water-heat-salt theory and test techniques for soils in cold and arid regions: A review. Geoderma 2023, 432, 116378. [Google Scholar] [CrossRef]
- Zhang, Y.T. Study on the Influence of Temperature on the Permeability of Remolded Malan Loess. Master’s Thesis, Chang’an University, Xi’an, China, 2019. [Google Scholar]
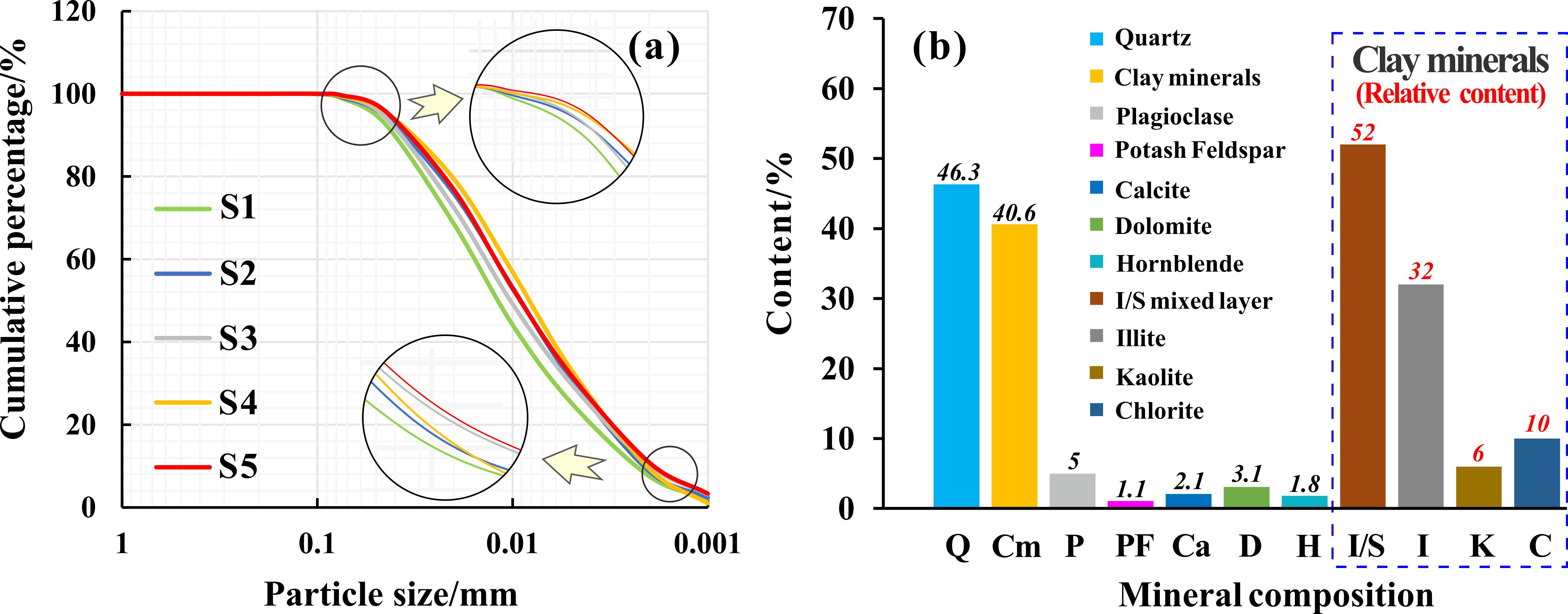




| Sampling Hole | A | B | C | D | E |
|---|---|---|---|---|---|
| Sample | S1 | S2 | S3 | S4 | S5 |
| Natural density (g/cm3) | 1.82 | 1.84 | 1.77 | 1.76 | 1.78 |
| Natural water content ω (%) | 38.1 | 38.4 | 37.1 | 48.41 | 49.14 |
| Porosity (%) | 51.19 | 50.76 | 52.18 | 56.08 | 55.80 |
| Sand (%) | 1.06 | 0.86 | 0.52 | 0.64 | 0.38 |
| Silt (%) | 73.7 | 68.22 | 69.67 | 66.09 | 65.71 |
| Clay (%) | 25.24 | 30.92 | 29.81 | 33.27 | 33.91 |
| Liquid limit (%) | 47.69 | 43.04 | 45.32 | 52.4 | 58.87 |
| Plasticity limit (%) | 18.51 | 24.46 | 28.02 | 30.33 | 25.8 |
| Plasticity index | 29.18 | 18.58 | 17.3 | 22.07 | 33.07 |
| Organic matter (%) | 0.23 | 0.44 | 0.67 | 0.18 | 0.26 |
| Sample | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| Average cycle amplitude (cm/s) | 6.64 × 10−8 | 6.93 × 10−8 | 7.43 × 10−8 | 7.48 × 10−8 | 1.97 × 10−7 |
| Average cycle time (s) | 226 | 253 | 247 | 268 | 371 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, M.; Wang, Q.; Yu, Q.; Wu, J.; Li, H.; Dong, J.; Xia, W.; Han, Y.; Huang, X. Mechanism Study of Differential Permeability Evolution and Microscopic Pore Characteristics of Soft Clay under Saturated Seepage: A Case Study in Chongming East Shoal. Water 2023, 15, 968. https://doi.org/10.3390/w15050968
Yao M, Wang Q, Yu Q, Wu J, Li H, Dong J, Xia W, Han Y, Huang X. Mechanism Study of Differential Permeability Evolution and Microscopic Pore Characteristics of Soft Clay under Saturated Seepage: A Case Study in Chongming East Shoal. Water. 2023; 15(5):968. https://doi.org/10.3390/w15050968
Chicago/Turabian StyleYao, Meng, Qing Wang, Qingbo Yu, Jianzhong Wu, Hui Li, Jiaqi Dong, Weitong Xia, Yan Han, and Xinlei Huang. 2023. "Mechanism Study of Differential Permeability Evolution and Microscopic Pore Characteristics of Soft Clay under Saturated Seepage: A Case Study in Chongming East Shoal" Water 15, no. 5: 968. https://doi.org/10.3390/w15050968
APA StyleYao, M., Wang, Q., Yu, Q., Wu, J., Li, H., Dong, J., Xia, W., Han, Y., & Huang, X. (2023). Mechanism Study of Differential Permeability Evolution and Microscopic Pore Characteristics of Soft Clay under Saturated Seepage: A Case Study in Chongming East Shoal. Water, 15(5), 968. https://doi.org/10.3390/w15050968







