Robust Optimal Operation of Water Distribution Systems
Abstract
:1. Introduction
1.1. WDS Operation under Uncertainty
1.2. Robust Optimization
- Implementing the RO theory on optimal operation problems with a better approximation of the system’s hydraulics.
- Illustrate the robust optimal operation methodology on a large real-life network.
- Address multiple uncertainties in the same problem including both objective and right-hand side (RHS) uncertainties simultaneously.
- Model multi-dimensional correlated uncertainties to capture the temporal–spatial correlations between the elements of the system.
2. Methodology
2.1. Uncertainty Sets
2.2. Robust Counterpart
2.3. Case Studies
2.3.1. Case Study 1: Illustrative Network
2.3.2. Case Study 2: Sopron Network
3. Results
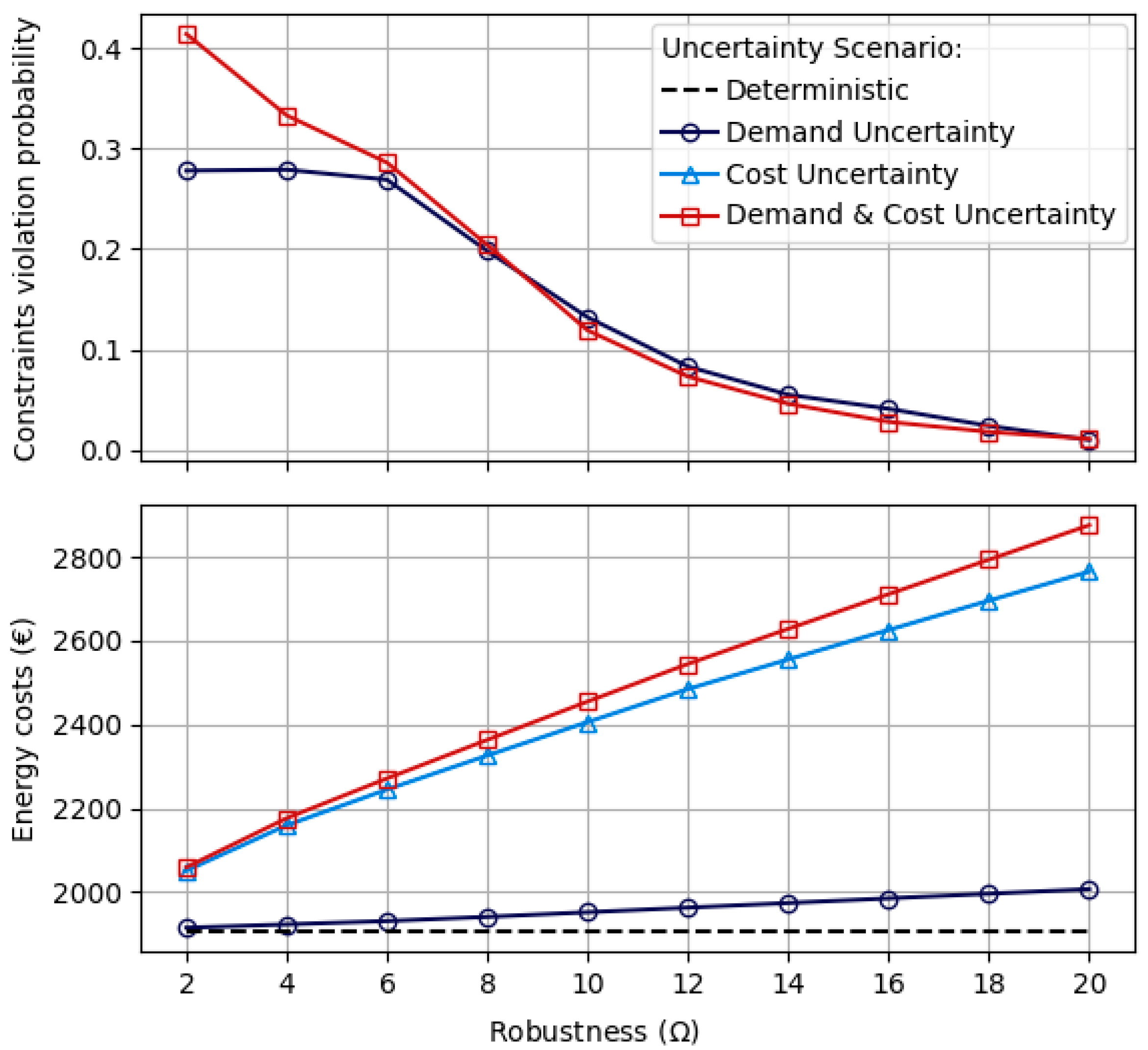
3.1. Case Study 1: Illustrative Network Results
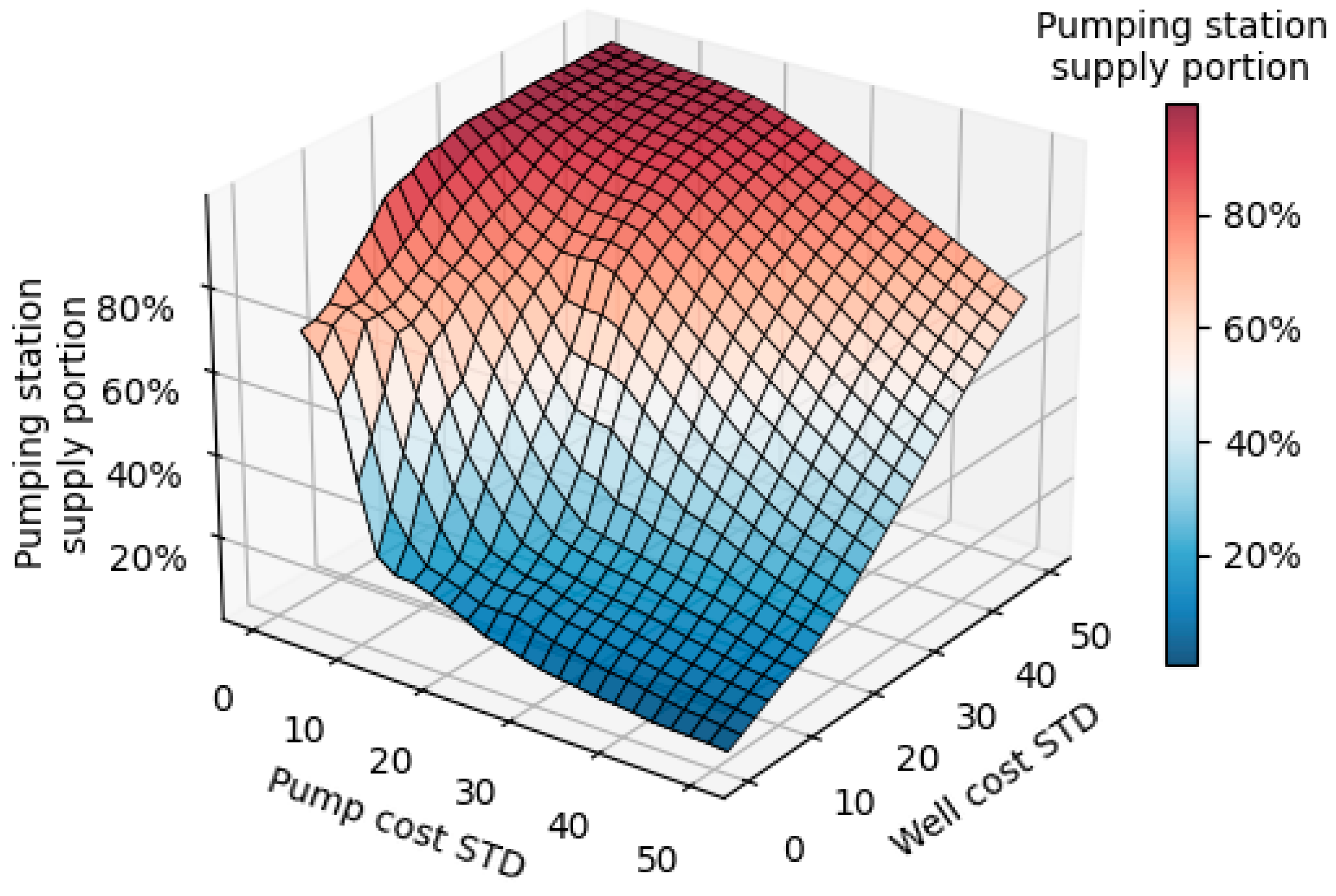
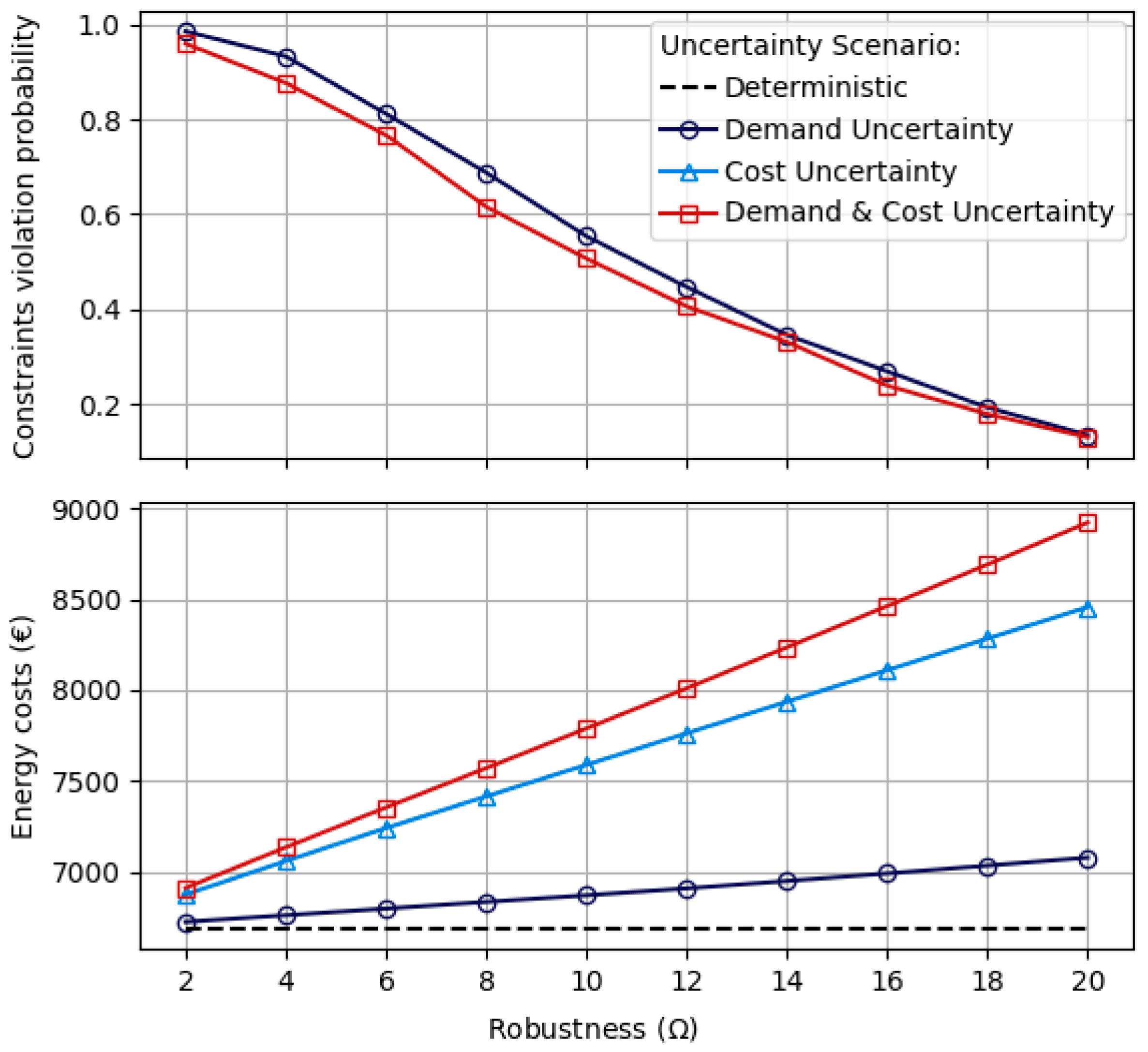
3.2. Case Study 2: Sopron Network Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in Optimisation of Water Distribution Systems? A Literature Review of System Operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef] [Green Version]
- Avni, N.; Fishbain, B.; Shamir, U. Water Consumption Patterns as a Basis for Water Demand Modeling. Water Resour. Res. 2015, 51, 8165–8181. [Google Scholar] [CrossRef] [Green Version]
- Meniconi, S.; Maietta, F.; Alvisi, S.; Capponi, C.; Marsili, V.; Franchini, M.; Brunone, B. A Quick Survey of the Most Vulnerable Areas of a Water Distribution Network Due to Transients Generated in a Service Line: A Lagrangian Model Based on Laboratory Tests. Water 2022, 14, 2741. [Google Scholar] [CrossRef]
- Marsili, V.; Meniconi, S.; Alvisi, S.; Brunone, B.; Franchini, M. Stochastic Approach for the Analysis of Demand Induced Transients in Real Water Distribution Systems. J. Water Resour. Plan. Manag. 2022, 148, 04021093. [Google Scholar] [CrossRef]
- Maiolo, M.; Mendicino, G.; Pantusa, D.; Senatore, A. Optimization of Drinking Water Distribution Systems in Relation to the Effects of Climate Change. Water 2017, 9, 803. [Google Scholar] [CrossRef]
- Aghapoor Khameneh, P.; Miri Lavasani, S.M.; Nabizadeh Nodehi, R.; Arjmandi, R. Water Distribution Network Failure Analysis under Uncertainty. Int. J. Environ. Sci. Technol. 2020, 17, 421–432. [Google Scholar] [CrossRef]
- Housh, M.; Salomons, E.; Sela, L.; Simpson, A.R. Water Distribution Systems on the Spot: Energy Market Opportunities for Water Utilities. J. Water Resour. Plan. Manag. 2022, 148, 02522002. [Google Scholar] [CrossRef]
- McPhail, C.; Maier, H.R.; Westra, S.; van der Linden, L.; Kwakkel, J.H. Guidance Framework and Software for Understanding and Achieving System Robustness. Environ. Model. Softw. 2021, 142, 105059. [Google Scholar] [CrossRef]
- Maier, H.R.; Guillaume, J.H.A.; van Delden, H.; Riddell, G.A.; Haasnoot, M.; Kwakkel, J.H. An Uncertain Future, Deep Uncertainty, Scenarios, Robustness and Adaptation: How Do They Fit Together? Environ. Model. Softw. 2016, 81, 154–164. [Google Scholar] [CrossRef]
- Walker, W.E.; Lempert, R.J.; Kwakkel, J.H. Deep uncertainty. In Encyclopedia of Operations Research and Management Science, 3rd ed.; Grass, S.I., FU, M.C., Eds.; Springer: New York, NY, USA, 2013; Volume 1, pp. 395–402. [Google Scholar]
- Pallottino, S.; Sechi, G.M.; Zuddas, P. A DSS for Water Resources Management under Uncertainty by Scenario Analysis. Environ. Model. Softw. 2005, 20, 1031–1042. [Google Scholar] [CrossRef]
- Napolitano, J.; Sechi, G.M.; Zuddas, P. Scenario Optimisation of Pumping Schedules in a Complex Water Supply System Considering a Cost–Risk Balancing Approach. Water Resour. Manag. 2016, 30, 5231–5246. [Google Scholar] [CrossRef]
- Schwartz, R.; Housh, M.; Ostfeld, A.; Asce, F. Limited Multistage Stochastic Programming for Water Distribution Systems Optimal Operation. J. Water Resour. Plan. Manag. 2016, 142, 06016003. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Chance-Constrained Programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Ahmed, S.; Shapiro, A. Solving Chance-Constrained Stochastic Programs via Sampling and Integer Programming. INFORMS Tutor. Oper. Res. 2008, 261–269. [Google Scholar] [CrossRef] [Green Version]
- Khatavkar, P.; Mays, L.W. Model for Optimal Operation of Water Distribution Pumps with Uncertain Demand Patterns. Water Resour. Manag. 2017, 31, 3867–3880. [Google Scholar] [CrossRef]
- Grosso, J.M.; Ocampo-Martínez, C.; Puig, V.; Joseph, B. Chance-Constrained Model Predictive Control for Drinking Water Networks. J. Process Control 2014, 24, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-O.; Eum, H.-I.; Lee, E.-G.; Ko, I.H. Optimizing Operational Policies of a Korean Multireservoir System Using Sampling Stochastic Dynamic Programming with Ensemble Streamflow Prediction. J. Water Resour. Plan. Manag. 2007, 133, 4–14. [Google Scholar] [CrossRef]
- Ben-Tal, A.; el Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; ISBN 1400831059. [Google Scholar]
- Chung, G.; Lansey, K.; Bayraksan, G. Reliable Water Supply System Design under Uncertainty. Environ. Model. Softw. 2009, 24, 449–462. [Google Scholar] [CrossRef]
- Perelman, L.; Housh, M.; Ostfeld, A. Robust Optimization for Water Distribution Systems Least Cost Design. Water Resour. Res. 2013, 49, 6795–6809. [Google Scholar] [CrossRef]
- Boindala, S.P.; Ostfeld, A. Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty. Water 2022, 14, 2199. [Google Scholar] [CrossRef]
- Housh, M.; Ostfeld, A.; Shamir, U. Optimal Multiyear Management of a Water Supply System under Uncertainty: Robust Counterpart Approach. Water Resour. Res. 2011, 47, 1–15. [Google Scholar] [CrossRef]
- Pan, L.; Housh, M.; Liu, P.; Cai, X.; Chen, X. Robust Stochastic Optimization for Reservoir Operation. Water Resour. Res. 2015, 51, 409–429. [Google Scholar] [CrossRef] [Green Version]
- Housh, M. Non-Probabilistic Robust Optimization Approach for Flood Control System Design. Environ. Model. Softw. 2017, 95, 48–60. [Google Scholar] [CrossRef]
- Goryashko, A.P.; Nemirovski, A.S. Robust Energy Cost Optimization of Water Distribution System with Uncertain Demand. Autom. Remote Control 2014, 75, 1754–1769. [Google Scholar] [CrossRef] [Green Version]
- Jowitt, P.W.; Germanopoulos, G. Optimal Pump Scheduling in Water-Supply Networks. J. Water Resour. Plan. Manag. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust Solutions of Uncertain Linear Programs. Oper. Res. Lett. 1999, 25, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Li, Z.; Huang, B. Robust Optimization under Correlated Uncertainty: Formulations and Computational Study. Comput. Chem. Eng. 2016, 85, 58–71. [Google Scholar] [CrossRef]
- Gomes, S.C.; Vinga, S.; Henriques, R. Spatiotemporal Correlation Feature Spaces to Support Anomaly Detection in Water Distribution Networks. Water 2021, 13, 2551. [Google Scholar] [CrossRef]
- Eck, B.; McKenna, S.; Akrhiev, A.; Kishimoto, A.; Palmes, P.; Taheri, N.; van den Heever, S. Pump Scheduling for Uncertain Electricity Prices. In Proceedings of the World Environmental and Water Resources Congress 2014: Water Without Borders, Portland, OR, USA, 1–5 June 2014; pp. 426–434. [Google Scholar] [CrossRef]
- Perelman, G.; Fishbain, B. Critical Elements Analysis of Water Supply Systems to Improve Energy Efficiency in Failure Scenarios. Water Resour. Manag. 2022, 36, 3797–3811. [Google Scholar] [CrossRef]
- Selek, I.; Bene, J.G.; Hs, C. Optimal (Short-Term) Pump Schedule Detection for Water Distribution Systems by Neutral Evolutionary Search. Appl. Soft. Comput. 2012, 12, 2336–2351. [Google Scholar] [CrossRef]
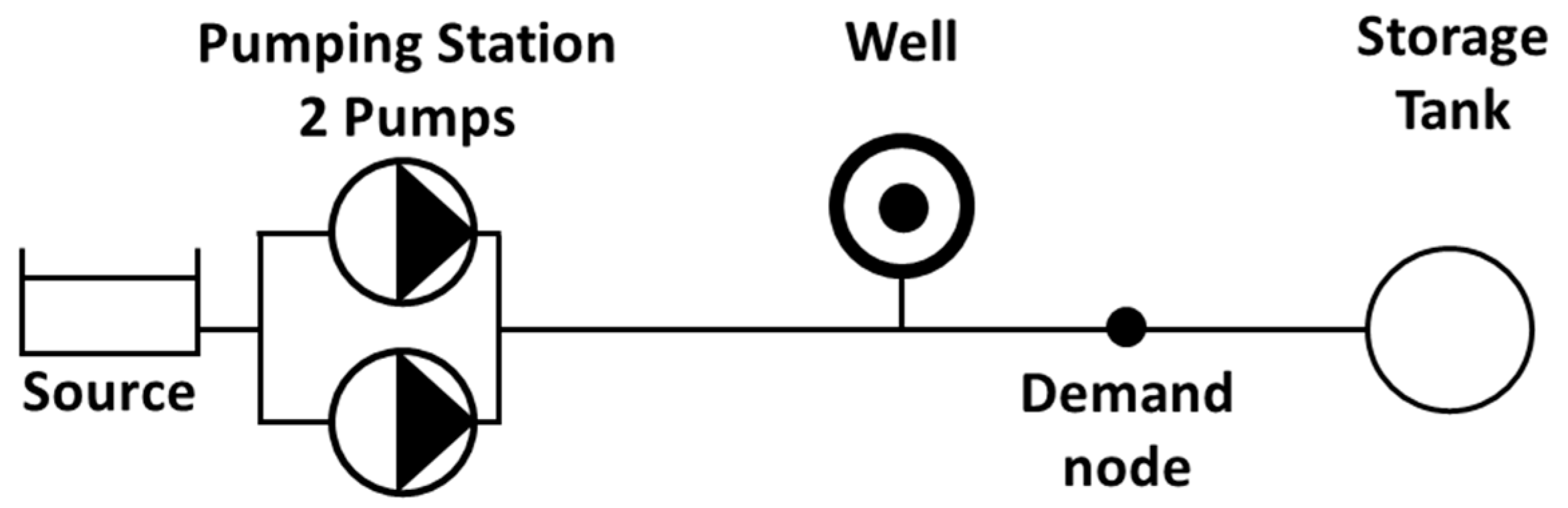


| Flow (m3/h) | Mean Power (kWatt) | STD Power (kWatt) | S. Energy (kWatt-h/m3) | Unit 1 | Unit 2 |
|---|---|---|---|---|---|
| 250 | 100 | 10 | 0.4 | 1 | 0 |
| 250 | 95 | 10 | 0.38 | 0 | 1 |
| 400 | 172 | 10 | 0.43 | 1 | 1 |
| Flow (m3/h) | Mean Power (kWatt) | STD Power (kWatt) | S. Energy (kWatt-h/m3) | Well |
|---|---|---|---|---|
| 300 | 126 | 5 | 0.42 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perelman, G.; Ostfeld, A.; Fishbain, B. Robust Optimal Operation of Water Distribution Systems. Water 2023, 15, 963. https://doi.org/10.3390/w15050963
Perelman G, Ostfeld A, Fishbain B. Robust Optimal Operation of Water Distribution Systems. Water. 2023; 15(5):963. https://doi.org/10.3390/w15050963
Chicago/Turabian StylePerelman, Gal, Avi Ostfeld, and Barak Fishbain. 2023. "Robust Optimal Operation of Water Distribution Systems" Water 15, no. 5: 963. https://doi.org/10.3390/w15050963






