Predictive Modelling of Reference Evapotranspiration Using Machine Learning Models Coupled with Grey Wolf Optimizer
Abstract
:1. Introduction
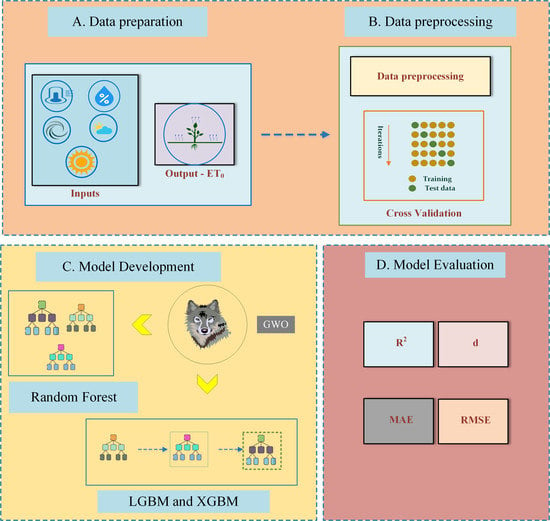
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. ET0 Estimaton Using FAO-56 Penman-Monteith and Empirical Equations
2.3. Description of Machine Learning Models and Optimizer
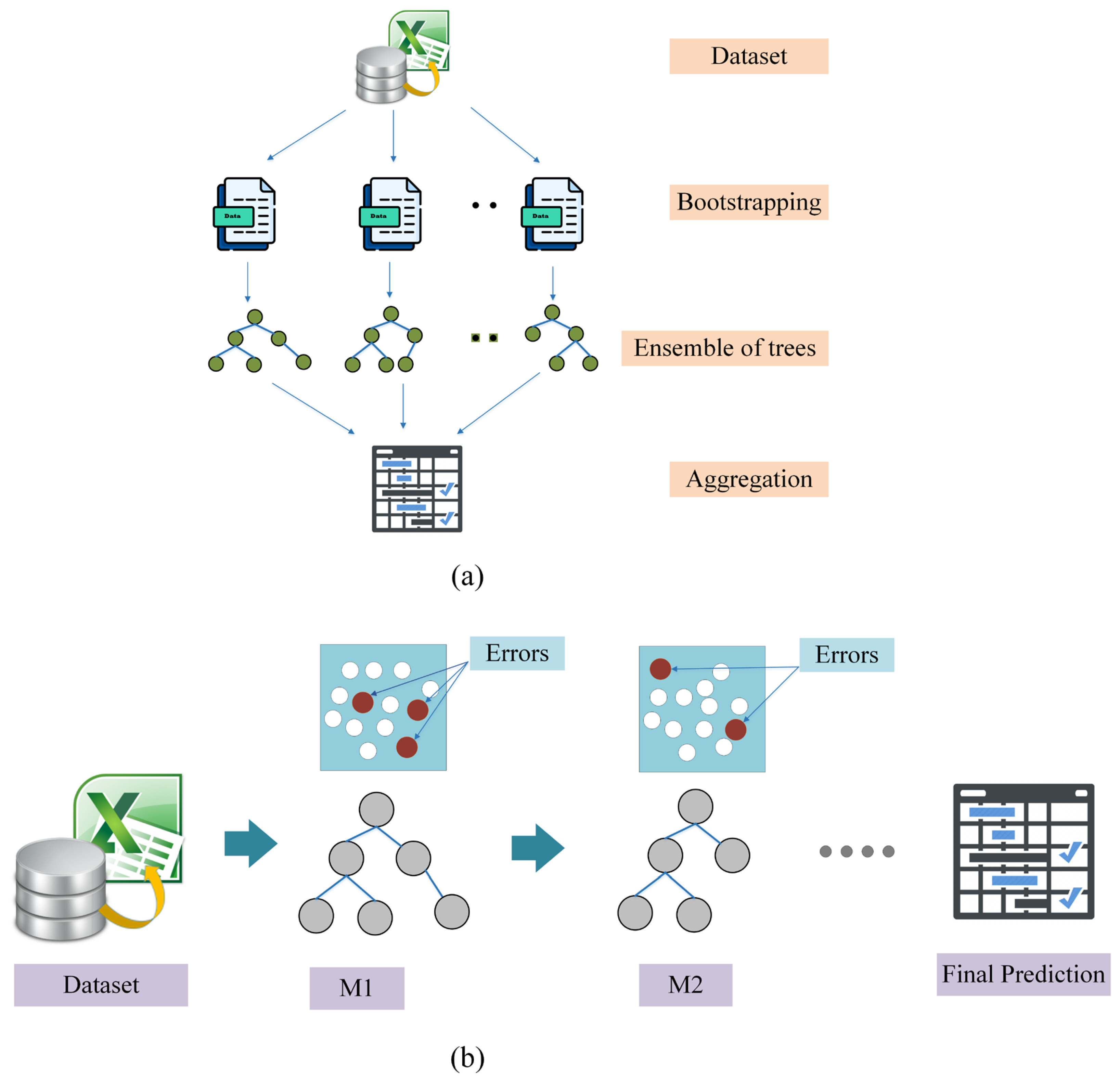
2.3.1. Random Forest (RF)
2.3.2. Extreme Gradient Boosting Model (XGB)
2.3.3. Light Gradient Boosting Model (LGB)
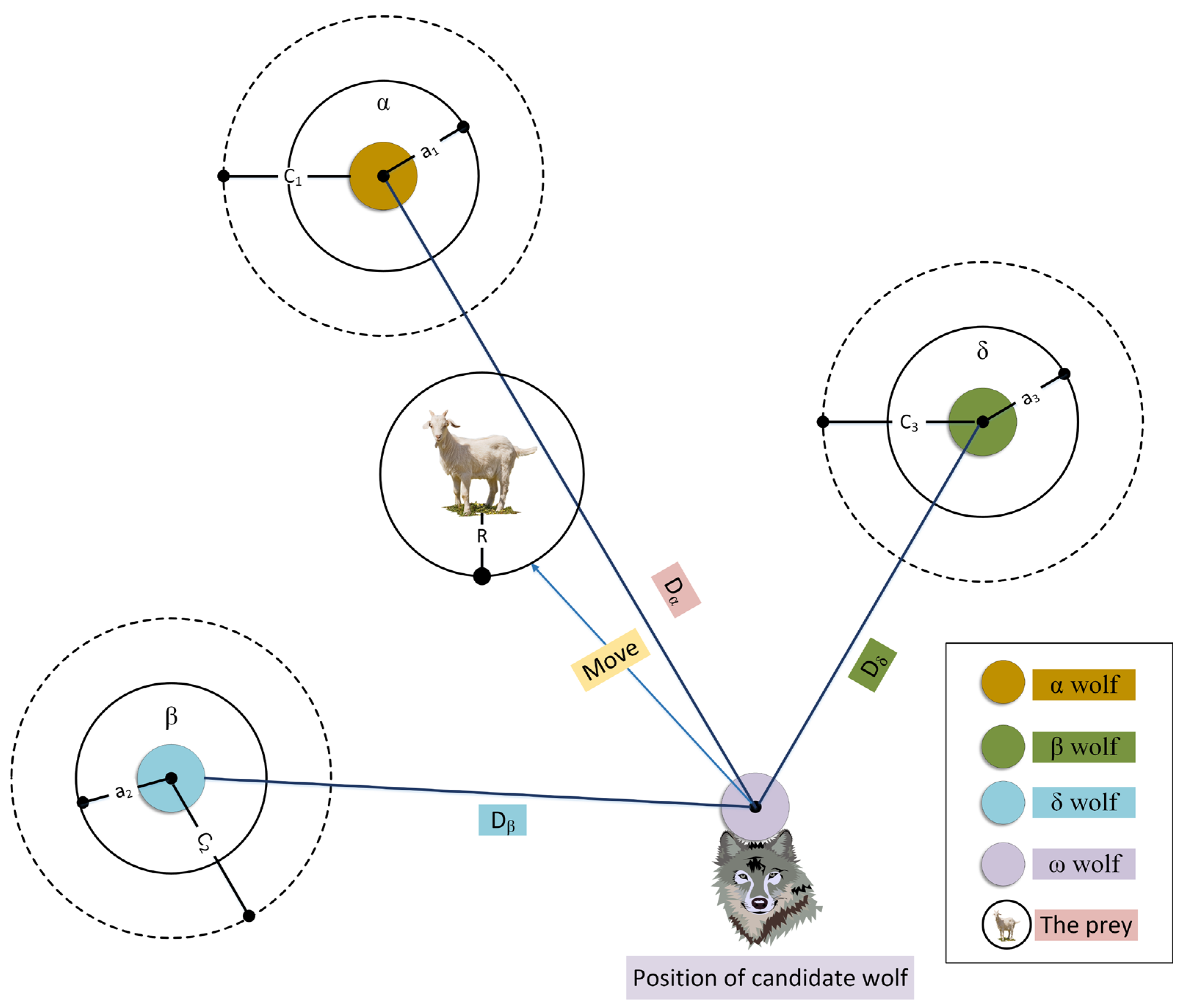
2.3.4. Grey Wolf Optimizer (GWO)
2.4. ET0 Estimaton Using ML and Hybrid ML
2.4.1. Input Scenarios
2.4.2. Model Development
2.4.3. Hyper Parameter Tuning in Hybrid ML
2.5. Model Performance Indicators
Global Performance Indicator (GPI)
3. Results
3.1. Comparison of the Empirical Models in Estimating ET0
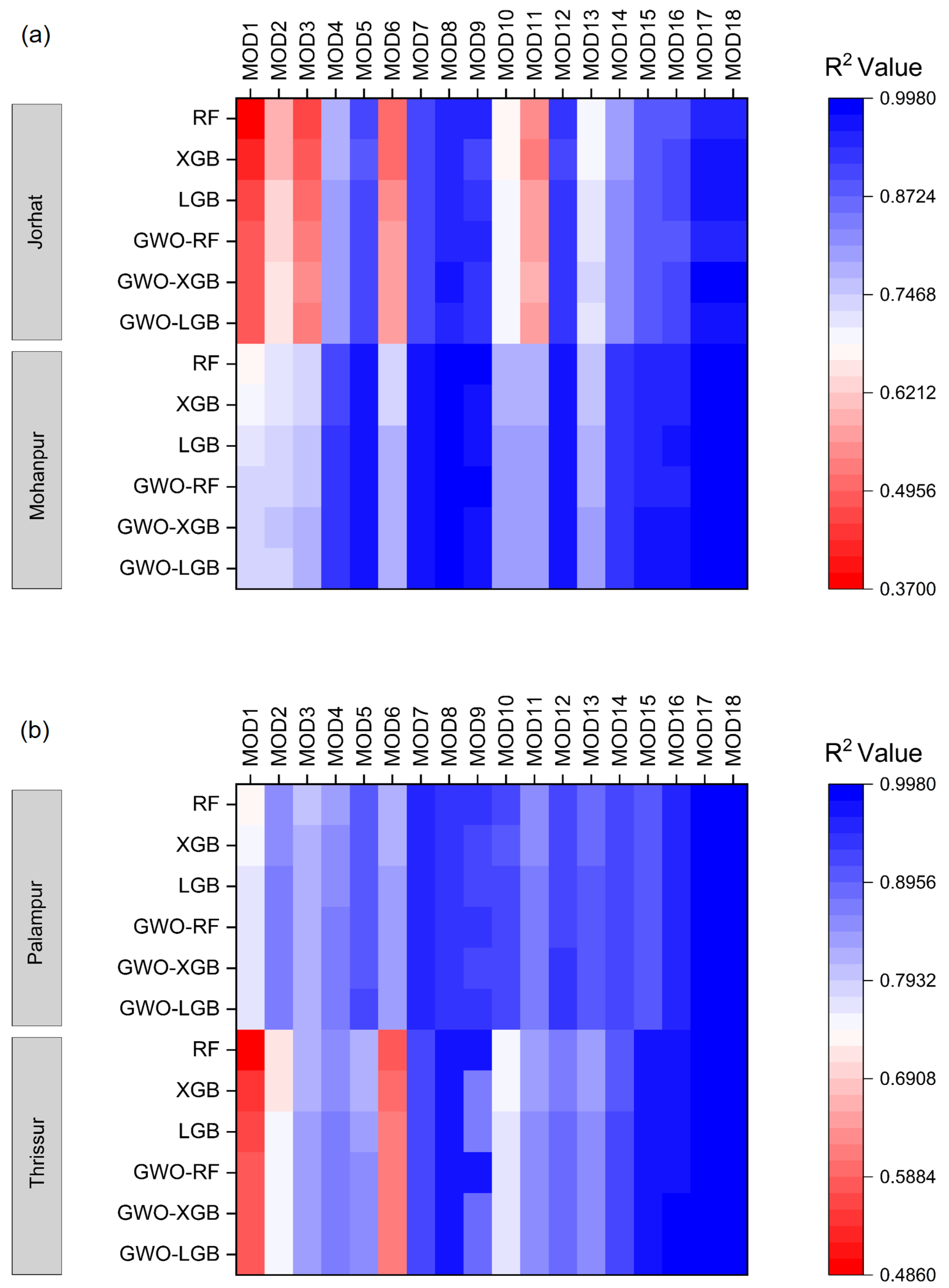
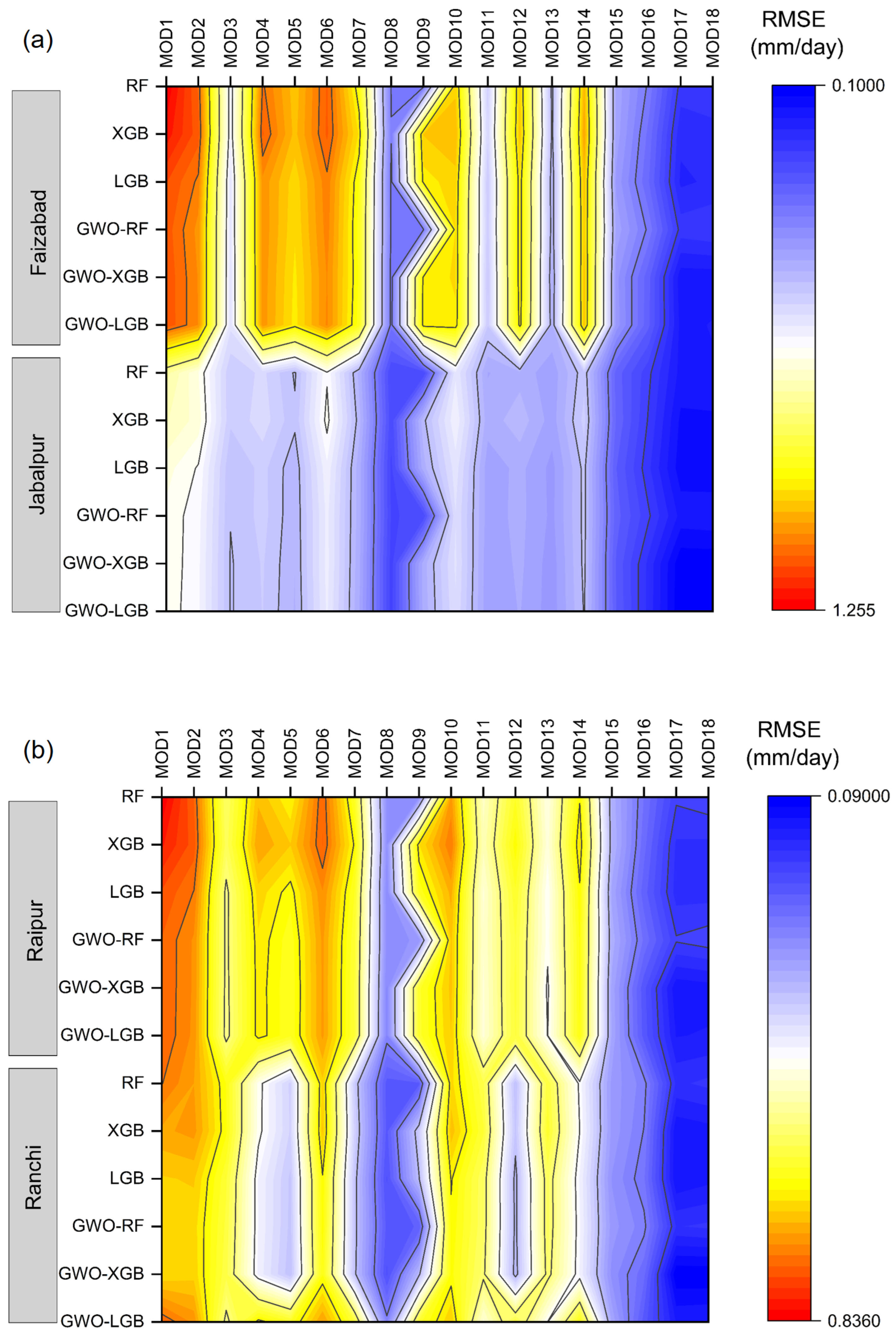
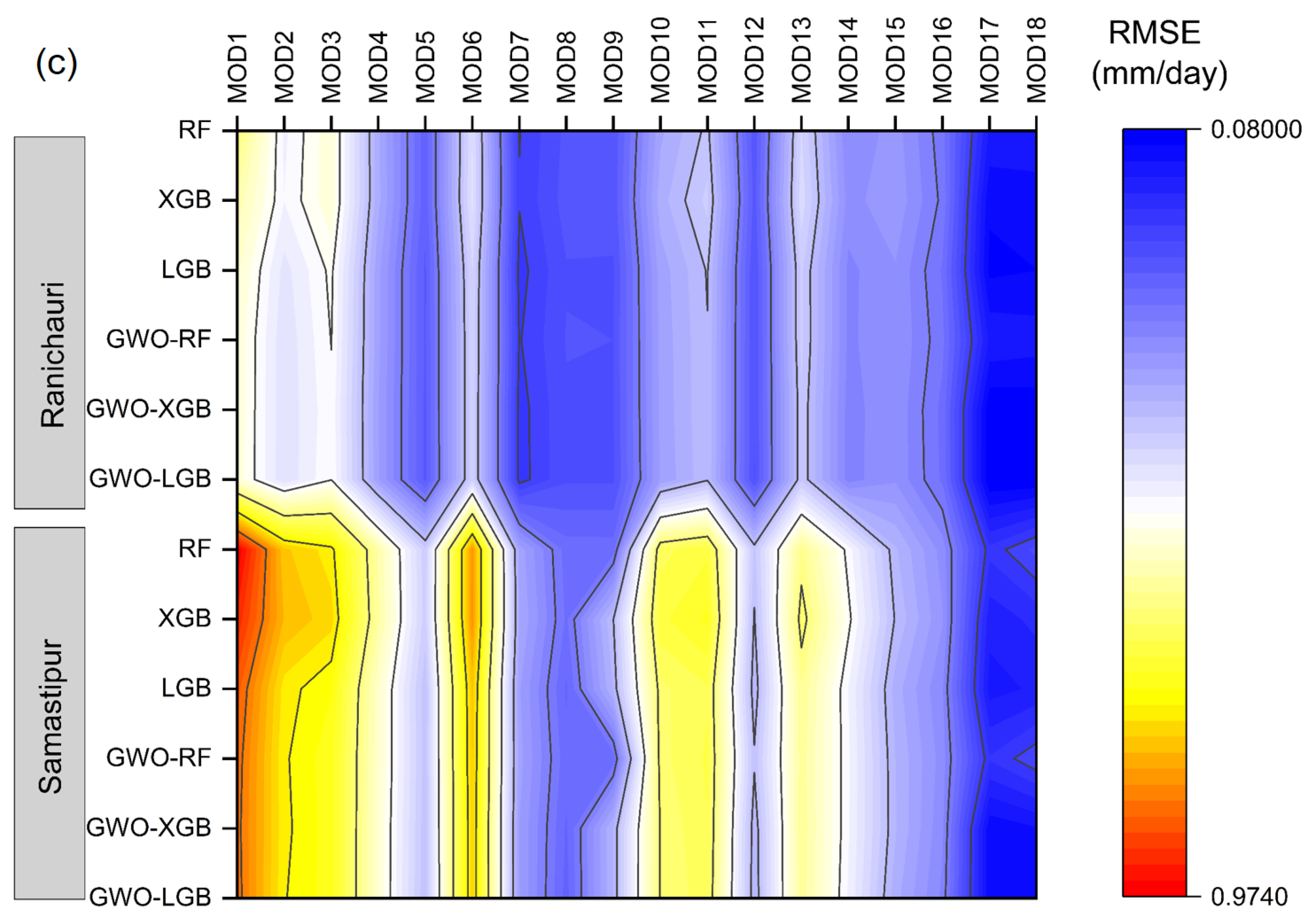
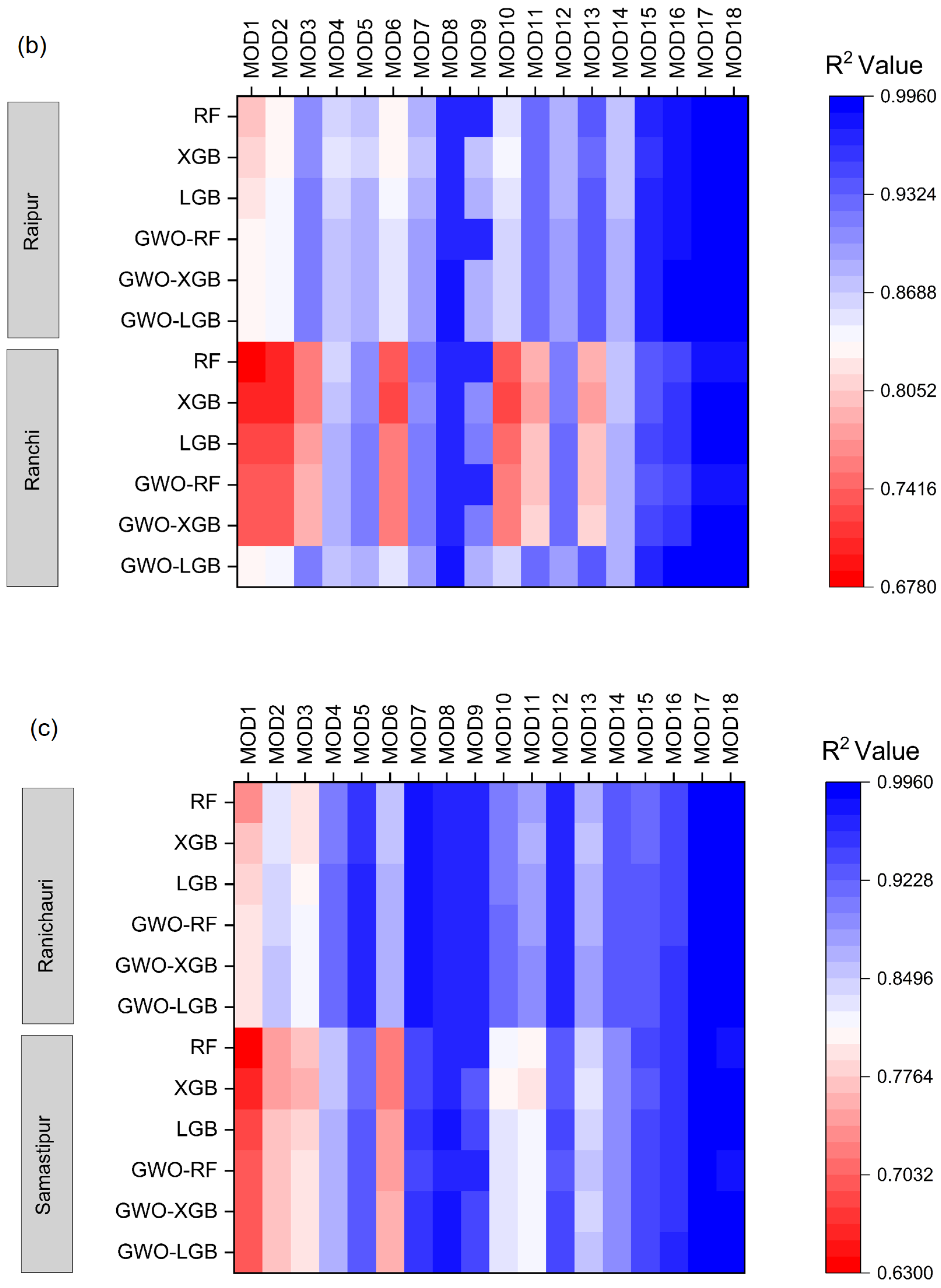
3.2. Comparison of Various Input Combinations in Conventional ML Models
3.2.1. Best-Performing Models in ML
3.2.2. Least-Performing Models in ML
3.3. Empirical Models v/s Conventional ML Models
3.4. Comparison of Various Input Combinations in GWO Hybrid ML Models
3.4.1. Best-Performing Models in Hybrid ML
3.4.2. Least Performing Models in Hybrid ML
3.5. Best-Performing Models across Conventional and Hybrid MLs
3.6. Least-Performing Models across Conventional and Hybrid MLs
4. Discussion
5. Conclusions
- The LGB and XGB models outperformed the RF models, while all the ML models were found to be more accurate than empirical models.
- Among the empirical methods investigated in the study, the Turc model was determined to have the greatest performance with higher GPI values.
- Solar radiation was adjudged to be an important parameter that could improve the prediction capability.
- The GWO hybrid ML models had the highest prediction efficiencies at all the locations, with RF models improving considerably well.
- The study consolidated the fact that the use of optimizers would substantially reduce the modelling error.
- Further studies could be done using cross-station data and other optimizers to improve the accuracy.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Department of Economic and Social Affairs, Population Division. World Population Prospects 2022: Summary of Results; UN DESA/POP/2022/TR/NO. 3; United Nations: New York, NY, USA, 2022. [Google Scholar]
- Lybbert, T.J.; Sumner, D.A. Agricultural Technologies for Climate Change in Developing Countries: Policy Options for Innovation and Technology Diffusion. Food Policy 2012, 37, 114–123. [Google Scholar] [CrossRef]
- Srilakshmi, M.; Jhajharia, D.; Gupta, S.; Yurembam, G.S.; Patle, G.T. Analysis of Spatio-Temporal Variations and Change Point Detection in Pan Coefficients in the Northeastern Region of India. Theor. Appl. Climatol. 2022, 147, 1545–1559. [Google Scholar] [CrossRef]
- George, B.A.; Reddy, B.; Raghuwanshi, N.; Wallender, W. Decision Support System for Estimating Reference Evapotranspiration. J. Irrig. Drain. Eng. 2002, 128, 1–10. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N. Evaluation of Variable Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, F. Die Methoden zur Bestimmung der Verdunstung der natürlichen Erdoberfläche. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1950, 2, 1–38. [Google Scholar] [CrossRef]
- Mahringer, W. Verdunstungsstudien am Neusiedler See. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1970, 18, 1–20. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Abtew, W. Evapotranspiration Measurements and Modeling for Three Wetland Systems in South Florida1. JAWRA J. Am. Water Resour. Assoc. 1996, 32, 465–473. [Google Scholar] [CrossRef]
- Hansen, S. Estimation of Potential and Actual Evapotranspiration: Paper Presented at the Nordic Hydrological Conference (Nyborg, Denmark, August—1984). Hydrol. Res. 1984, 15, 205–212. [Google Scholar] [CrossRef]
- Rosenberg, N.J.; Blad, B.L.; Verma, S.B. Microclimate: The Biological Environment; John Wiley & Sons: Hoboken, NJ, USA, 1983; ISBN 0-471-06066-6. [Google Scholar]
- McGuinness, J.L.; Bordne, E.F. A Comparison of Lysimeter-Derived Potential Evapotranspiration with Computed Values; US Department of Agriculture: Washington, DC, USA, 1972. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Turc, L. Estimation of Irrigation Water Requirements, Potential Evapotranspiration: A Simple Climatic Formula Evolved up to Date. Ann. Agron. 1961, 12, 13–49. [Google Scholar]
- Hargreaves, G.H. Moisture Availability and Crop Production. Trans. ASAE 1975, 18, 980–0984. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating Reference Evapotranspiration under Inaccurate Data Conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Alexandris, S.; Kerkides, P.; Liakatas, A. Daily Reference Evapotranspiration Estimates by the “Copais” Approach. Agric. Water Manag. 2006, 82, 371–386. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simple ET0 Forms of Penman’s Equation without Wind and/or Humidity Data. II: Comparisons with Reduced Set-FAO and Other Methodologies. J. Irrig. Drain. Eng. 2013, 139, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Yaseen, Z.M.; Shahid, S.; Saggi, M.K.; Tao, H.; Kisi, O.; Salih, S.Q.; Al-Ansari, N.; Chau, K.-W. Implementation of Evolutionary Computing Models for Reference Evapotranspiration Modeling: Short Review, Assessment and Possible Future Research Directions. Eng. Appl. Comput. Fluid Mech. 2019, 13, 811–823. [Google Scholar] [CrossRef] [Green Version]
- Ayodele, T.O. Machine Learning Overview. New Adv. Mach. Learn. 2010, 2, 9–18. [Google Scholar]
- Shiri, J.; Zounemat-Kermani, M.; Kisi, O.; Mohsenzadeh Karimi, S. Comprehensive Assessment of 12 Soft Computing Approaches for Modelling Reference Evapotranspiration in Humid Locations. Meteorol. Appl. 2020, 27, e1841. [Google Scholar] [CrossRef] [Green Version]
- Bellido-Jiménez, J.A.; Estévez, J.; Vanschoren, J.; García-Marín, A.P. AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models. Agronomy 2022, 12, 656. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and Four Tree-Based Ensemble Models for Predicting Daily Reference Evapotranspiration Using Limited Meteorological Data in Different Climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Liu, X.; Wu, L.; Zhang, F.; Huang, G.; Yan, F.; Bai, W. Splitting and Length of Years for Improving Tree-Based Models to Predict Reference Crop Evapotranspiration in the Humid Regions of China. Water 2021, 13, 3478. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, N.; Gong, D.; Zhu, F.; Xing, L.; Zhu, B.; Chen, X.; Wen, S.; Liu, Q. Simulation of Daily Maize Evapotranspiration at Different Growth Stages Using Four Machine Learning Models in Semi-Humid Regions of Northwest China. J. Hydrol. 2022, 617, 128947. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, L.; Lin, A.; Qin, W.; Lu, Y.; Li, J.; Zhong, Y.; He, L. Exploring the Potential of Deep Factorization Machine and Various Gradient Boosting Models in Modeling Daily Reference Evapotranspiration in China. Arab. J. Geosci. 2021, 13, 1287. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y. Machine Learning Models for the Estimation of Monthly Mean Daily Reference Evapotranspiration Based on Cross-Station and Synthetic Data. Hydrol. Res. 2019, 50, 1730–1750. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Ma, X.; Wu, L.; Zhang, F.; Yu, X.; Zeng, W. Light Gradient Boosting Machine: An Efficient Soft Computing Model for Estimating Daily Reference Evapotranspiration with Local and External Meteorological Data. Agric. Water Manag. 2019, 225, 105758. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, W.; Jiao, X.; Guo, W.; Hamoud, Y.A. Comparison of Five Boosting-Based Models for Estimating Daily Reference Evapotranspiration with Limited Meteorological Variables. PLoS ONE 2020, 15, e0235324. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Meng, F.; Xu, J.; Liu, Z.; Meng, J. Evaluation of Machine Learning Models for Daily Reference Evapotranspiration Modeling Using Limited Meteorological Data in Eastern Inner Mongolia, North China. Water 2022, 14, 2890. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. New Approach to Estimate Daily Reference Evapotranspiration Based on Hourly Temperature and Relative Humidity Using Machine Learning and Deep Learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Mokari, E.; DuBois, D.; Samani, Z.; Mohebzadeh, H.; Djaman, K. Estimation of Daily Reference Evapotranspiration with Limited Climatic Data Using Machine Learning Approaches across Different Climate Zones in New Mexico. Theor. Appl. Climatol. 2022, 147, 575–587. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, W.; Jiao, X.; Guo, W.; Alhaj Hamoud, Y. Evaluation of Stacking and Blending Ensemble Learning Methods for Estimating Daily Reference Evapotranspiration. Comput. Electron. Agric. 2021, 184, 106039. [Google Scholar] [CrossRef]
- Yan, S.; Wu, L.; Fan, J.; Zhang, F.; Zou, Y.; Wu, Y. A Novel Hybrid WOA-XGB Model for Estimating Daily Reference Evapotranspiration Using Local and External Meteorological Data: Applications in Arid and Humid Regions of China. Agric. Water Manag. 2021, 244, 106594. [Google Scholar] [CrossRef]
- Maroufpoor, S.; Bozorg-Haddad, O.; Maroufpoor, E. Reference Evapotranspiration Estimating Based on Optimal Input Combination and Hybrid Artificial Intelligent Model: Hybridization of Artificial Neural Network with Grey Wolf Optimizer Algorithm. J. Hydrol. 2020, 588, 125060. [Google Scholar] [CrossRef]
- Dong, J.; Liu, X.; Huang, G.; Fan, J.; Wu, L.; Wu, J. Comparison of Four Bio-Inspired Algorithms to Optimize KNEA for Predicting Monthly Reference Evapotranspiration in Different Climate Zones of China. Comput. Electron. Agric. 2021, 186, 106211. [Google Scholar] [CrossRef]
- Devendra, C.; Thomas, D. Crop–Animal Systems in Asia: Importance of Livestock and Characterisation of Agro-Ecological Zones. Agric. Syst. 2002, 71, 5–15. [Google Scholar] [CrossRef]
- Mandal, D.; Mandal, C.; Singh, S. Delineating Agro-Ecological Regions. ICAR-NBSSLUP Technol. 2016, 1–8. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative Analysis of 31 Reference Evapotranspiration Methods under Humid Conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Xystrakis, F.; Matzarakis, A. Evaluation of 13 Empirical Reference Potential Evapotranspiration Equations on the Island of Crete in Southern Greece. J. Irrig. Drain. Eng. 2011, 137, 211–222. [Google Scholar] [CrossRef] [Green Version]
- Rosenberry, D.O.; Stannard, D.I.; Winter, T.C.; Martinez, M.L. Comparison of 13 Equations for Determining Evapotranspiration from a Prairie Wetland, Cottonwood Lake Area, North Dakota, USA. Wetlands 2004, 24, 483–497. [Google Scholar] [CrossRef]
- Bourletsikas, A.; Argyrokastritis, I.; Proutsos, N. Comparative Evaluation of 24 Reference Evapotranspiration Equations Applied on an Evergreen-Broadleaved Forest. Hydrol. Res. 2017, 49, 1028–1041. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.F.; Ganesh, S.; Liu, P. A Comparison of Random Forest Regression and Multiple Linear Regression for Prediction in Neuroscience. J. Neurosci. Methods 2013, 220, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.; Li, H. Chapter 9—Noninvasive Fracture Characterization Based on the Classification of Sonic Wave Travel Times. In Machine Learning for Subsurface Characterization; Misra, S., Li, H., He, J., Eds.; Gulf Professional Publishing: Houston, TX, USA, 2020; pp. 243–287. ISBN 978-0-12-817736-5. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting. In R Package; Version 04-2; R Foundation for Statistical Computing: Vienna, Austria, 2015; Volume 1, pp. 1–4. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Al Daoud, E. Comparison between XGBoost, LightGBM and CatBoost Using a Home Credit Dataset. Int. J. Comput. Inf. Eng. 2019, 13, 6–10. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Sweidan, A.H.; El-Bendary, N.; Hassanien, A.E.; Hegazy, O.M.; Mohamed, A.E. Water Quality Classification Approach Based on Bio-Inspired Gray Wolf Optimization. In Proceedings of the 2015 7th International Conference of Soft Computing and Pattern Recognition (SoCPaR), Fukuoka, Japan, 13–15 November 2015; pp. 1–6. [Google Scholar]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey Wolf Optimizer: A Review of Recent Variants and Applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Mohammadi, B.; Guan, Y.; Aghelpour, P.; Emamgholizadeh, S.; Pillco Zolá, R.; Zhang, D. Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm. Water 2020, 12, 3015. [Google Scholar] [CrossRef]
- Sharma, I.; Kumar, V.; Sharma, S. A Comprehensive Survey on Grey Wolf Optimization. Recent Adv. Comput. Sci. Commun. Former. Recent Pat. Comput. Sci. 2022, 15, 323–333. [Google Scholar]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and Empirical Models for Estimating Reference Evapotranspiration in Humid Region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- He, H.; Liu, L.; Zhu, X. Optimization of Extreme Learning Machine Model with Biological Heuristic Algorithms to Estimate Daily Reference Evapotranspiration in Hetao Irrigation District of China. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1939–1956. [Google Scholar] [CrossRef]
- Heramb, P.; Kumar Singh, P.; Ramana Rao, K.V.; Subeesh, A. Modelling Reference Evapotranspiration Using Gene Expression Programming and Artificial Neural Network at Pantnagar, India. Inf. Process. Agric. 2022; in press. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Review and Statistical Analysis of Different Global Solar Radiation Sunshine Models. Renew. Sustain. Energy Rev. 2015, 52, 1869–1880. [Google Scholar] [CrossRef]
- Zhu, B.; Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. Hybrid Particle Swarm Optimization with Extreme Learning Machine for Daily Reference Evapotranspiration Prediction from Limited Climatic Data. Comput. Electron. Agric. 2020, 173, 105430. [Google Scholar] [CrossRef]
- Pandey, P.K.; Dabral, P.P.; Pandey, V. Evaluation of Reference Evapotranspiration Methods for the Northeastern Region of India. Int. Soil Water Conserv. Res. 2016, 4, 52–63. [Google Scholar] [CrossRef] [Green Version]
- Üneş, F.; Kaya, Y.Z.; Mamak, M. Daily Reference Evapotranspiration Prediction Based on Climatic Conditions Applying Different Data Mining Techniques and Empirical Equations. Theor. Appl. Climatol. 2020, 141, 763–773. [Google Scholar] [CrossRef]
- Salam, R.; Islam, A.R.M.T. Potential of RT, Bagging and RS Ensemble Learning Algorithms for Reference Evapotranspiration Prediction Using Climatic Data-Limited Humid Region in Bangladesh. J. Hydrol. 2020, 590, 125241. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost Method for Prediction of Reference Evapotranspiration in Humid Regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
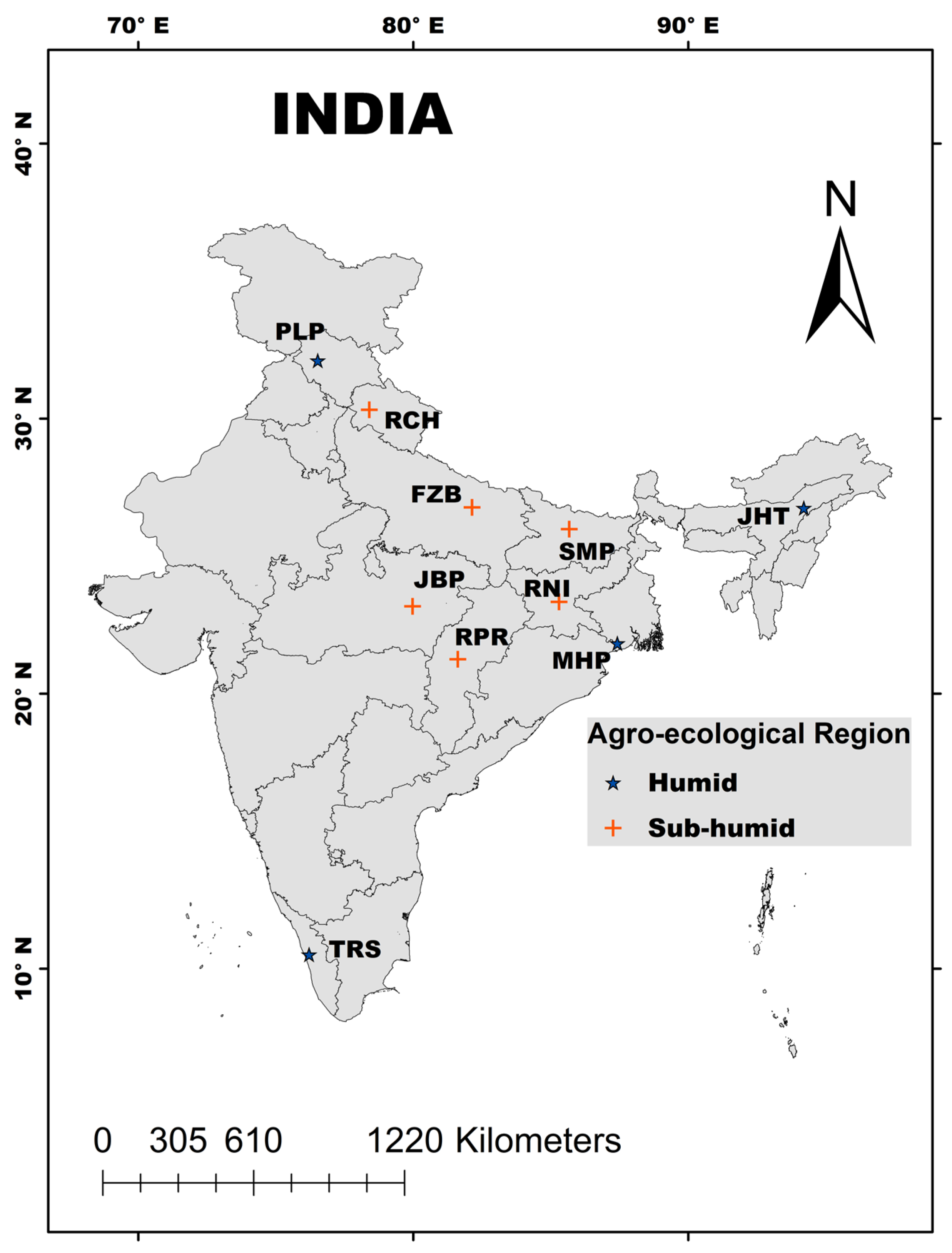


| S. No. | State | Station | Code | AER | Latitude (N) | Longitude (E) | Altitude (m) |
|---|---|---|---|---|---|---|---|
| 1 | Assam | Jorhat | JHT | Humid | 26°45′ | 94°12′ | 116 |
| 2 | West Bengal | Mohanpur | MHP | Humid | 21°50′ | 87°15′ | 17 |
| 3 | Himachal Pradesh | Palampur | PLP | Humid | 32°07′ | 76°32′ | 1220 |
| 4 | Kerala | Thrissur | TRS | Humid | 10°31′ | 76°13′ | 28 |
| 5 | Uttar Pradesh | Faizabad | FZB | Sub-humid | 26°46′ | 82°08′ | 97 |
| 6 | Madhya Pradesh | Jabalpur | JBP | Sub-humid | 23°11′ | 79°59′ | 412 |
| 7 | Chattisgarh | Raipur | RPR | Sub-humid | 21°15′ | 81°37′ | 290 |
| 8 | Jharkhand | Ranchi | RNI | Sub-humid | 23°20′ | 85°18′ | 651 |
| 9 | Uttarakhand | Ranichauri | RCH | Sub-humid | 30°19′ | 78°24′ | 1800 |
| 10 | Bihar | Samastipur | SMP | Sub-humid | 25°59′ | 85°40′ | 51 |
| Method | Symbol and Equations | Reference | |
|---|---|---|---|
| Target for the Models | |||
| FAO-56 Penman-Monteith | (1) | [40] | |
| Mass Transfer based | |||
| Albrecht (ALB) | ETALB = where | (2) | [6] |
| Mahringer (MAH) | where | (3) | [7] |
| Penman (PEN) | where | (4) | [8,41] |
| Radiation based | |||
| Jensen-Haise (JH) | (5) | [11,42] | |
| Makkink (MAK) | (6) | [43] | |
| McGuinness-Bordne (MGB) | (7) | [12] | |
| Priestly-Taylor (PT) | (8) | [13] | |
| Turc (TUR) | (9) | [14] | |
| Temperature based | |||
| Hargreaves-Samani (HS) | (10) | [16] | |
| Hargreaves-Samani 1 (HS1) | (11) | [17] | |
| Hargreaves-Samani 2 (HS2) | (12) | [17] | |
| Thorththwaite (Modified) (THO) | (13) | [44] | |
| Combination based | |||
| Copais (COP) | (14) | [18] | |
| Valiantzas 1 (VA1) | ETVA1 = | (15) | [19] |
| Valiantzas 2 (VA2) | ETVA2 = | (16) | [19] |
| Model Index | Input Combinations | Model Index | Input Combinations |
|---|---|---|---|
| 1 | Tmax, Tmin | 10 | Tmax, Tmin, RH, Ra |
| 2 | Tmax, Tmin, RH | 11 | Tmax, Tmin, U2, Ra |
| 3 | Tmax, Tmin, U2 | 12 | Tmax, Tmin, n, Ra |
| 4 | Tmax, Tmin, n | 13 | Tmax, Tmin, RH, U2 |
| 5 | Tmax, Tmin, Rs | 14 | Tmax, Tmin, RH, n |
| 6 | Tmax, Tmin, Ra | 15 | Tmax, Tmin, U2, n |
| 7 | Tmax, Tmin, RH, Rs | 16 | Tmax, Tmin, RH, U2, n |
| 8 | Tmax, Tmin, U2, Rs | 17 | Tmax, Tmin, RH, U2, n, Rs |
| 9 | Tmax, Tmin, n, Rs | 18 | Tmax, Tmin, RH, U2, n, Ra |
| Cross-Validation | Training | Testing |
|---|---|---|
| V1 | 2005–2020 | 2001–2004 |
| V2 | 2001–2004 and 2009–2020 | 2005–2008 |
| V3 | 2001–2008 and 2013–2020 | 2009–2012 |
| V4 | 2001–2012 and 2017–2020 | 2013–2016 |
| V5 | 2001–2016 | 2017–2020 |
| Model | Parameter | Default Value | Hyperparameter Range for Tuning |
|---|---|---|---|
| RF | n_estimators | 100 | Range of 10 to 500, increment by 10 |
| min_samples_leaf | 1 | Range of 1 to 6, increment by 2 | |
| max_depth | None | Range of 2 to 20, increment by 2 and None | |
| XGB | n_estimators | 100 | Range of 10 to 500, increment by 10 |
| learning_rate | 0.3 | [0.05, 0.1, 0.15, 0.3] | |
| max_depth | 6 | Range of 2 to 20, increment by 2 and None | |
| LGB | n_estimators | 100 | Range of 10 to 500, increment by 10 |
| learning_rate | 0.3 | [0.05, 0.1, 0.15, 0.3] | |
| max_depth | 6 | Range of 2 to 20, increment by 2 and None |
| Indicator | Code | Formula | |
|---|---|---|---|
| Root mean square error | RMSE | (18) | |
| Coefficient of determination | R2 | (19) | |
| Mean absolute error | MAE | (20) | |
| Agreement index | d | (21) | |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | TUR | 1.467 | MAK | 1.521 | TUR | 1.423 | TUR | 1.439 |
| 2 | PT | 1.390 | TUR | 1.508 | VA2 | 1.292 | VA2 | 1.305 |
| 3 | MAK | 1.276 | PT | 1.330 | JH | 0.863 | PT | 0.818 |
| 4 | VA2 | 1.216 | VA2 | 1.027 | HS | 0.783 | MAK | 0.769 |
| 5 | JH | 0.550 | VA1 | 0.813 | PT | 0.721 | PEN | 0.372 |
| 6 | VA1 | 0.484 | HS | 0.361 | HS2 | 0.663 | JH | 0.154 |
| 7 | HS | −0.265 | HS2 | 0.082 | MAK | 0.613 | ALB | 0.034 |
| 8 | ALB | −0.302 | HS1 | 0.052 | HS1 | 0.467 | HS | 0.028 |
| 9 | COP | −0.370 | THO | 0.032 | THO | −0.233 | MAH | −0.084 |
| 10 | HS2 | −0.488 | JH | −0.092 | MAH | −0.516 | HS2 | −0.111 |
| 11 | HS1 | −0.552 | COP | −0.812 | PEN | −0.517 | COP | −0.171 |
| 12 | THO | −0.579 | ALB | −1.033 | ALB | −0.586 | HS1 | −0.351 |
| 13 | PEN | −0.782 | PEN | −1.173 | COP | −1.071 | VA1 | −0.727 |
| 14 | MAH | −0.807 | MAH | −1.687 | MGB | −1.323 | THO | −0.917 |
| 15 | MGB | −2.238 | MGB | −1.927 | VA1 | −2.577 | MGB | −2.559 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | TUR | 1.037 | TUR | 1.234 | TUR | 1.117 | TUR | 1.587 | VA2 | 1.487 | TUR | 1.037 |
| 2 | JH | 0.882 | VA2 | 1.014 | VA2 | 0.969 | PT | 1.510 | TUR | 1.468 | JH | 0.882 |
| 3 | VA2 | 0.840 | PT | 0.887 | HS | 0.894 | VA2 | 1.294 | MAK | 1.258 | VA2 | 0.840 |
| 4 | HS | 0.642 | HS | 0.686 | PT | 0.784 | MAK | 1.122 | JH | 1.048 | HS | 0.642 |
| 5 | HS1 | 0.520 | JH | 0.646 | HS1 | 0.722 | JH | 0.347 | PT | 0.932 | HS1 | 0.520 |
| 6 | PT | 0.517 | HS1 | 0.487 | HS2 | 0.705 | HS | 0.311 | HS | 0.875 | PT | 0.517 |
| 7 | HS2 | 0.500 | THO | 0.444 | JH | 0.556 | THO | 0.262 | HS2 | 0.762 | HS2 | 0.500 |
| 8 | THO | 0.390 | HS2 | 0.440 | THO | 0.414 | HS1 | −0.059 | HS1 | 0.544 | THO | 0.390 |
| 9 | COP | 0.119 | MAK | 0.377 | MAK | 0.171 | HS2 | −0.065 | THO | −0.279 | COP | 0.119 |
| 10 | PEN | 0.050 | PEN | −0.150 | PEN | −0.131 | ALB | −0.643 | ALB | −1.032 | PEN | 0.050 |
| 11 | MAK | −0.007 | COP | −0.554 | COP | −0.386 | PEN | −0.661 | MGB | −1.038 | MAK | −0.007 |
| 12 | MGB | −0.737 | MAH | −0.883 | MAH | −1.053 | MAH | −0.729 | MAH | −1.230 | MGB | −0.737 |
| 13 | MAH | −1.148 | MGB | −1.016 | MGB | −1.106 | VA1 | −0.744 | VA1 | −1.552 | MAH | −1.148 |
| 14 | ALB | −1.212 | ALB | −1.501 | ALB | −1.523 | COP | −1.493 | COP | −1.567 | ALB | −1.212 |
| 15 | VA1 | −2.392 | VA1 | −2.110 | VA1 | −2.131 | MGB | −2.041 | PEN | −1.675 | VA1 | −2.392 |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | XGB17 | 1.889 | XGB17 | 1.941 | LGB18 | 1.952 | LGB18 | 1.199 |
| 2 | XGB18 | 1.753 | LGB17 | 1.939 | LGB17 | 1.893 | LGB17 | 1.187 |
| 3 | LGB17 | 1.717 | LGB18 | 1.721 | XGB18 | 1.777 | XGB17 | 1.159 |
| 4 | LGB18 | 1.716 | XGB18 | 1.691 | XGB17 | 1.755 | XGB18 | 1.118 |
| 5 | RF17 | 0.795 | RF17 | 1.424 | RF18 | 1.658 | RF17 | 0.911 |
| 6 | XGB8 | 0.748 | RF18 | 1.286 | RF17 | 1.501 | RF18 | 0.769 |
| 7 | LGB8 | 0.721 | LGB8 | 0.853 | LGB7 | −0.063 | LGB16 | 0.224 |
| 8 | RF18 | 0.582 | XGB8 | 0.702 | RF7 | −0.146 | LGB8 | 0.130 |
| 9 | RF8 | 0.309 | RF9 | 0.607 | XGB7 | −0.258 | XGB16 | 0.077 |
| 10 | RF9 | 0.304 | RF8 | 0.598 | LGB16 | −0.337 | XGB8 | 0.067 |
| 11 | LGB12 | −0.699 | LGB9 | −1.208 | RF16 | −0.527 | RF16 | −0.008 |
| 12 | LGB9 | −0.726 | LGB12 | −1.369 | XGB16 | −0.628 | RF8 | −0.010 |
| 13 | RF12 | −1.040 | RF12 | −1.439 | LGB8 | −1.070 | RF9 | −0.017 |
| 14 | XGB9 | −1.231 | LGB7 | −1.546 | RF8 | −1.191 | LGB15 | −0.413 |
| 15 | XGB12 | −1.321 | XGB9 | −1.619 | RF9 | −1.212 | RF15 | −0.536 |
| 16 | LGB7 | −1.633 | RF7 | −1.712 | XGB8 | −1.373 | XGB15 | −0.558 |
| 17 | RF7 | −1.806 | XGB12 | −1.815 | LGB12 | −1.684 | LGB7 | −2.499 |
| 18 | XGB7 | −2.079 | XGB7 | −2.053 | XGB12 | −2.048 | XGB7 | −2.801 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | LGB17 | 1.752 | LGB18 | 1.265 | LGB18 | 1.265 | LGB17 | 1.637 | LGB17 | 2.374 | LGB17 | 1.908 |
| 2 | LGB18 | 1.682 | LGB17 | 1.222 | LGB17 | 1.248 | XGB17 | 1.593 | LGB18 | 2.303 | LGB18 | 1.821 |
| 3 | XGB17 | 1.630 | XGB18 | 1.138 | XGB18 | 1.197 | LGB18 | 1.566 | XGB17 | 2.207 | XGB17 | 1.761 |
| 4 | XGB18 | 1.561 | XGB17 | 1.137 | XGB17 | 1.191 | XGB18 | 1.546 | XGB18 | 2.034 | XGB18 | 1.583 |
| 5 | RF17 | 1.373 | RF17 | 0.993 | RF17 | 1.036 | RF17 | 1.147 | RF18 | 1.693 | RF17 | 1.397 |
| 6 | RF18 | 1.321 | RF18 | 0.965 | RF18 | 0.973 | RF18 | 1.065 | RF17 | 1.531 | RF18 | 1.041 |
| 7 | LGB16 | 0.162 | LGB16 | 0.347 | LGB16 | 0.473 | LGB8 | 0.463 | LGB7 | 0.216 | LGB8 | 0.282 |
| 8 | XGB16 | −0.027 | XGB16 | 0.195 | XGB16 | 0.323 | RF8 | 0.321 | RF7 | −0.005 | RF9 | 0.135 |
| 9 | LGB8 | −0.125 | RF16 | 0.112 | RF16 | 0.247 | RF9 | 0.304 | XGB7 | −0.071 | RF8 | 0.128 |
| 10 | RF9 | −0.156 | LGB8 | 0.079 | LGB8 | −0.070 | XGB8 | 0.281 | LGB9 | −1.159 | XGB8 | 0.037 |
| 11 | RF8 | −0.195 | RF8 | 0.016 | RF9 | −0.131 | LGB16 | −0.394 | LGB8 | −1.164 | LGB16 | −0.586 |
| 12 | RF16 | −0.289 | RF9 | 0.015 | RF8 | −0.140 | XGB16 | −0.601 | LGB12 | −1.237 | RF16 | −0.746 |
| 13 | XGB8 | −0.298 | XGB8 | −0.076 | XGB8 | −0.193 | RF16 | −0.749 | RF9 | −1.358 | XGB16 | −0.888 |
| 14 | LGB15 | −1.194 | LGB15 | −0.608 | LGB15 | −0.607 | LGB15 | −1.136 | RF8 | −1.388 | LGB7 | −1.211 |
| 15 | XGB15 | −1.460 | RF15 | −0.769 | RF15 | −0.771 | RF15 | −1.357 | RF12 | −1.416 | RF7 | −1.354 |
| 16 | RF15 | −1.520 | XGB15 | −0.845 | XGB15 | −0.851 | XGB15 | −1.361 | XGB9 | −1.459 | XGB7 | −1.502 |
| 17 | LGB13 | −1.970 | LGB13 | −2.450 | LGB13 | −2.455 | LGB12 | −1.962 | XGB8 | −1.474 | LGB15 | −1.713 |
| 18 | XGB13 | −2.248 | XGB13 | −2.735 | XGB13 | −2.735 | XGB12 | −2.363 | XGB12 | −1.626 | XGB12 | −2.092 |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 54 | RF1 | −2.139 | RF1 | −2.503 | RF1 | −2.748 | RF1 | −2.429 |
| 53 | XGB1 | −1.541 | XGB1 | −1.401 | XGB1 | −2.185 | XGB1 | −1.862 |
| 52 | LGB1 | −1.099 | RF2 | −1.098 | LGB1 | −1.766 | LGB1 | −1.542 |
| 51 | RF3 | −0.885 | XGB2 | −0.907 | RF3 | −0.781 | RF6 | −1.450 |
| 50 | XGB3 | −0.743 | LGB1 | −0.789 | XGB3 | −0.390 | XGB6 | −1.296 |
| 49 | XGB6 | −0.458 | RF3 | −0.404 | RF6 | −0.249 | LGB6 | −1.054 |
| 48 | LGB3 | −0.405 | LGB2 | −0.208 | XGB6 | −0.071 | RF2 | −0.006 |
| 47 | RF6 | −0.403 | XGB3 | −0.142 | LGB3 | −0.042 | XGB2 | 0.111 |
| 46 | XGB11 | −0.036 | RF6 | 0.032 | LGB6 | 0.410 | XGB10 | 0.332 |
| 45 | RF11 | −0.028 | XGB6 | 0.117 | RF4 | 0.497 | LGB2 | 0.334 |
| 44 | LGB6 | 0.029 | XGB13 | 0.513 | RF2 | 0.607 | RF10 | 0.362 |
| 43 | LGB11 | 0.198 | LGB3 | 0.533 | XGB4 | 0.704 | LGB10 | 0.569 |
| 42 | RF2 | 0.649 | RF13 | 0.728 | XGB11 | 0.733 | RF3 | 1.111 |
| 41 | XGB2 | 0.682 | LGB6 | 0.813 | XGB2 | 0.807 | XGB3 | 1.130 |
| 40 | LGB2 | 1.076 | XGB10 | 0.884 | RF11 | 0.976 | LGB3 | 1.335 |
| 39 | XGB10 | 1.532 | RF10 | 1.141 | LGB4 | 1.110 | XGB13 | 1.372 |
| 38 | RF10 | 1.709 | LGB13 | 1.192 | LGB11 | 1.190 | RF5 | 1.413 |
| 37 | LGB10 | 1.861 | LGB10 | 1.497 | LGB2 | 1.197 | LGB5 | 1.571 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 54 | RF1 | −2.377 | RF1 | −2.344 | RF1 | −2.271 | RF1 | −2.028 | RF1 | −2.560 | RF1 | −2.505 |
| 53 | XGB1 | −1.815 | XGB1 | −1.787 | XGB1 | −1.686 | XGB2 | −1.328 | XGB1 | −1.774 | XGB1 | −1.999 |
| 52 | LGB1 | −0.991 | LGB1 | −1.128 | LGB1 | −0.998 | RF2 | −1.215 | LGB1 | −1.307 | LGB1 | −1.514 |
| 51 | XGB2 | −0.618 | XGB2 | −1.103 | XGB2 | −0.758 | XGB1 | −1.164 | RF3 | −1.065 | RF6 | −0.654 |
| 50 | RF2 | −0.471 | RF2 | −0.919 | RF2 | −0.629 | LGB2 | −0.549 | XGB3 | −1.047 | XGB6 | −0.624 |
| 49 | RF6 | −0.439 | XGB6 | −0.504 | XGB6 | −0.544 | LGB1 | −0.509 | LGB3 | −0.596 | XGB2 | −0.315 |
| 48 | XGB4 | −0.407 | LGB2 | −0.475 | RF6 | −0.524 | XGB10 | −0.480 | XGB2 | −0.131 | RF2 | −0.202 |
| 47 | XGB6 | −0.388 | RF6 | −0.283 | LGB2 | −0.302 | XGB6 | −0.419 | RF2 | −0.075 | LGB6 | −0.161 |
| 46 | RF4 | −0.171 | LGB6 | 0.106 | XGB10 | −0.096 | RF6 | −0.268 | LGB2 | 0.287 | XGB3 | 0.053 |
| 45 | LGB2 | −0.021 | XGB10 | 0.132 | LGB6 | 0.072 | RF10 | −0.097 | XGB6 | 0.497 | LGB2 | 0.172 |
| 44 | LGB6 | 0.068 | RF10 | 0.479 | RF10 | 0.333 | LGB10 | 0.354 | RF6 | 0.560 | RF3 | 0.224 |
| 43 | LGB4 | 0.357 | LGB10 | 0.601 | XGB4 | 0.449 | LGB6 | 0.419 | XGB13 | 0.641 | LGB3 | 0.523 |
| 42 | XGB14 | 0.792 | XGB4 | 0.842 | LGB10 | 0.615 | XGB3 | 0.629 | RF13 | 0.790 | XGB11 | 0.790 |
| 41 | RF14 | 1.069 | RF4 | 0.912 | RF4 | 0.713 | RF3 | 0.677 | LGB6 | 0.843 | RF11 | 1.055 |
| 40 | XGB10 | 1.185 | LGB4 | 1.255 | LGB4 | 1.088 | XGB13 | 1.228 | LGB13 | 1.026 | XGB10 | 1.115 |
| 39 | LGB14 | 1.263 | XGB3 | 1.277 | XGB5 | 1.178 | LGB3 | 1.306 | XGB11 | 1.104 | LGB11 | 1.232 |
| 38 | RF5 | 1.339 | RF3 | 1.285 | RF5 | 1.632 | RF13 | 1.473 | RF11 | 1.366 | RF10 | 1.316 |
| 37 | LGB10 | 1.623 | LGB14 | 1.656 | LGB14 | 1.729 | LGB13 | 1.972 | LGB11 | 1.440 | LGB10 | 1.495 |
| Jorhat | Mohanpur | Palampur | Thrissur | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Inputs used | RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| Tmax, Tmin, RH, U2 | 1 | LGB13 | 1.708 | LGB13 | 1.696 | LGB13 | 1.908 | LGB13 | 1.802 |
| 2 | RF13 | 1.576 | RF13 | 1.639 | RF13 | 1.844 | RF13 | 1.690 | |
| 3 | XGB13 | 1.561 | XGB13 | 1.612 | XGB13 | 1.808 | XGB13 | 1.639 | |
| 4 | ALB | −0.988 | ALB | −1.315 | MAH | −1.786 | PEN | −1.195 | |
| 5 | PEN | −1.823 | PEN | −1.501 | PEN | −1.849 | ALB | −1.842 | |
| 6 | MAH | −2.034 | MAH | −2.132 | ALB | −1.925 | MAH | −2.093 | |
| Tmax, Tmin, Rs | 1 | LGB5 | 0.824 | LGB5 | 0.982 | LGB5 | 1.037 | LGB5 | 0.942 |
| 2 | RF5 | 0.792 | RF5 | 0.974 | XGB5 | 0.990 | RF5 | 0.907 | |
| 3 | XGB5 | 0.786 | XGB5 | 0.966 | RF5 | 0.975 | XGB5 | 0.902 | |
| 4 | PT | 0.560 | MAK | 0.501 | JH | 0.178 | PT | 0.337 | |
| 5 | MAK | 0.410 | PT | 0.435 | PT | −0.001 | MAK | 0.293 | |
| 6 | JH | −0.246 | JH | −0.870 | MAK | −0.216 | JH | −0.323 | |
| 7 | MGB | −3.126 | MGB | −2.988 | MGB | −2.963 | MGB | −3.058 | |
| Tmax, Tmin, Ra | 1 | LGB6 | 2.110 | LGB6 | 1.864 | LGB6 | 1.306 | LGB6 | 1.678 |
| 2 | RF6 | 1.483 | XGB6 | 1.660 | XGB6 | 1.071 | XGB6 | 1.525 | |
| 3 | XGB6 | 1.369 | RF6 | 1.635 | RF6 | 0.984 | RF6 | 1.436 | |
| 4 | HS | −0.676 | HS | −0.685 | HS | 0.352 | HS | −0.212 | |
| 5 | HS1 | −1.245 | HS2 | −1.400 | HS2 | −0.163 | HS2 | −0.746 | |
| 6 | HS2 | −1.328 | HS1 | −1.416 | HS1 | −0.856 | HS1 | −1.398 | |
| 7 | THO | −1.713 | THO | −1.657 | THO | −2.694 | THO | −2.282 | |
| Tmax, Tmin, RH, Rs | 1 | LGB7 | 1.272 | LGB7 | 1.219 | LGB7 | 1.177 | LGB7 | 1.235 |
| 2 | RF7 | 1.230 | RF7 | 1.206 | RF7 | 1.168 | RF7 | 1.227 | |
| 3 | XGB7 | 1.162 | XGB7 | 1.180 | XGB7 | 1.156 | XGB7 | 1.199 | |
| 4 | TUR | 0.731 | TUR | 0.361 | TUR | 0.880 | TUR | 0.854 | |
| 5 | VA2 | 0.177 | VA2 | −0.368 | VA2 | 0.760 | VA2 | 0.638 | |
| 6 | VA1 | −1.113 | VA1 | −0.455 | COP | −1.439 | COP | −1.656 | |
| 7 | COP | −2.728 | COP | −2.781 | VA1 | −2.823 | VA1 | −2.643 | |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Inputs used | RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| Tmax, Tmin, RH, U2 | 1 | LGB13 | 1.535 | LGB13 | 1.502 | LGB13 | 1.523 | LGB13 | 1.860 | LGB13 | 1.763 | LGB13 | 1.425 |
| 2 | RF13 | 1.517 | RF13 | 1.465 | RF13 | 1.498 | RF13 | 1.746 | RF13 | 1.705 | RF13 | 1.404 | |
| 3 | XGB13 | 1.507 | XGB13 | 1.458 | XGB13 | 1.487 | XGB13 | 1.690 | XGB13 | 1.668 | XGB13 | 1.317 | |
| 4 | PEN | −0.909 | PEN | −0.982 | PEN | −0.970 | PEN | −1.665 | ALB | −1.308 | PEN | −0.827 | |
| 5 | MAH | −1.687 | MAH | −1.336 | MAH | −1.433 | ALB | −1.720 | MAH | −1.590 | MAH | −1.464 | |
| 6 | ALB | −1.962 | ALB | −2.107 | ALB | −2.104 | MAH | −1.910 | PEN | −2.237 | ALB | −1.854 | |
| Tmax, Tmin, Rs | 1 | LGB5 | 1.303 | LGB5 | 1.210 | LGB5 | 1.280 | LGB5 | 0.960 | LGB5 | 0.913 | LGB5 | 1.536 |
| 2 | RF5 | 1.211 | RF5 | 1.175 | RF5 | 1.253 | RF5 | 0.924 | RF5 | 0.882 | RF5 | 1.496 | |
| 3 | XGB5 | 1.196 | XGB5 | 1.156 | XGB5 | 1.189 | XGB5 | 0.918 | XGB5 | 0.881 | XGB5 | 1.490 | |
| 4 | JH | 0.465 | PT | 0.064 | PT | 0.002 | PT | 0.582 | MAK | 0.424 | JH | −0.090 | |
| 5 | PT | −0.483 | JH | −0.131 | JH | −0.141 | MAK | 0.159 | JH | 0.058 | PT | −0.749 | |
| 6 | MAK | −1.162 | MAK | −0.684 | MAK | −0.862 | JH | −0.503 | PT | −0.071 | MAK | −1.365 | |
| 7 | MGB | −2.530 | MGB | −2.790 | MGB | −2.720 | MGB | −3.040 | MGB | −3.087 | MGB | −2.318 | |
| Tmax, Tmin, Ra | 1 | LGB6 | 1.866 | LGB6 | 1.741 | LGB6 | 1.716 | LGB6 | 1.517 | LGB6 | 1.138 | LGB6 | 1.917 |
| 2 | XGB6 | 1.615 | RF6 | 1.613 | RF6 | 1.531 | RF6 | 1.280 | RF6 | 0.992 | XGB6 | 1.559 | |
| 3 | RF6 | 1.593 | XGB6 | 1.539 | XGB6 | 1.523 | XGB6 | 1.226 | XGB6 | 0.960 | RF6 | 1.535 | |
| 4 | HS | −0.667 | HS | −0.636 | HS | −0.367 | HS | −0.514 | HS | 0.522 | HS | −0.772 | |
| 5 | HS1 | −1.265 | THO | −1.342 | HS1 | −1.161 | THO | −0.632 | HS2 | 0.036 | HS1 | −1.147 | |
| 6 | HS2 | −1.365 | HS1 | −1.386 | HS2 | −1.201 | HS1 | −1.429 | HS1 | −0.785 | HS2 | −1.246 | |
| 7 | THO | −1.777 | HS2 | −1.530 | THO | −2.040 | HS2 | −1.448 | THO | −2.862 | THO | −1.845 | |
| Tmax, Tmin, RH, Rs | 1 | LGB7 | 0.946 | LGB7 | 1.071 | RF7 | 1.063 | LGB7 | 1.156 | LGB7 | 0.979 | LGB7 | 1.141 |
| 2 | RF7 | 0.938 | RF7 | 1.063 | LGB7 | 1.061 | RF7 | 1.132 | RF7 | 0.966 | RF7 | 1.131 | |
| 3 | XGB7 | 0.875 | XGB7 | 1.039 | XGB7 | 1.021 | XGB7 | 1.103 | XGB7 | 0.962 | XGB7 | 1.120 | |
| 4 | TUR | 0.477 | TUR | 0.675 | TUR | 0.544 | TUR | 0.724 | VA2 | 0.794 | TUR | 0.143 | |
| 5 | VA2 | 0.275 | VA2 | 0.436 | VA2 | 0.387 | VA2 | 0.441 | TUR | 0.776 | VA2 | −0.028 | |
| 6 | COP | −0.457 | COP | −1.354 | COP | −1.139 | VA1 | −1.982 | COP | −2.163 | COP | −0.648 | |
| 7 | VA1 | −3.054 | VA1 | −2.929 | VA1 | −2.937 | COP | −2.574 | VA1 | −2.312 | VA1 | −2.859 | |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | GWOXGB17 | 2.175 | GWOXGB17 | 2.176 | GWOXGB18 | 2.078 | GWOXGB18 | 1.376 |
| 2 | GWOXGB18 | 2.134 | GWOXGB18 | 2.072 | GWOLGB18 | 2.078 | GWOLGB18 | 1.360 |
| 3 | GWOLGB18 | 1.843 | GWOLGB17 | 2.052 | GWOXGB17 | 2.038 | GWOXGB17 | 1.287 |
| 4 | GWOLGB17 | 1.747 | GWOLGB18 | 1.798 | GWOLGB17 | 2.030 | GWOLGB17 | 1.271 |
| 5 | GWOXGB8 | 0.854 | GWORF17 | 1.209 | GWORF18 | 1.621 | GWORF17 | 0.820 |
| 6 | GWORF17 | 0.530 | GWORF18 | 1.079 | GWORF17 | 1.466 | GWORF18 | 0.687 |
| 7 | GWOLGB8 | 0.469 | GWOXGB8 | 0.812 | GWOXGB7 | −0.197 | GWOLGB16 | 0.220 |
| 8 | GWORF18 | 0.313 | GWOLGB8 | 0.731 | GWOLGB7 | −0.207 | GWOXGB16 | 0.183 |
| 9 | GWORF8 | 0.041 | GWORF8 | 0.421 | GWORF7 | −0.252 | GWOLGB8 | 0.101 |
| 10 | GWORF9 | −0.167 | GWORF9 | 0.357 | GWOLGB16 | −0.457 | GWOXGB8 | 0.059 |
| 11 | GWOLGB12 | −0.835 | GWOLGB9 | −1.312 | GWOXGB16 | −0.468 | GWORF16 | −0.103 |
| 12 | GWOLGB9 | −0.886 | GWOXGB9 | −1.368 | GWORF16 | −0.705 | GWORF8 | −0.123 |
| 13 | GWOXGB9 | −0.912 | GWOLGB12 | −1.496 | GWOLGB8 | −1.258 | GWORF9 | −0.203 |
| 14 | GWORF12 | −0.971 | GWORF12 | −1.599 | GWORF8 | −1.295 | GWOXGB15 | −0.513 |
| 15 | GWOXGB12 | −0.983 | GWOLGB7 | −1.673 | GWORF9 | −1.318 | GWOLGB15 | −0.538 |
| 16 | GWOLGB7 | −1.765 | GWOXGB12 | −1.726 | GWOXGB8 | −1.372 | GWORF15 | −0.650 |
| 17 | GWOXGB7 | −1.782 | GWOXGB7 | −1.749 | GWOLGB12 | −1.861 | GWOLGB7 | −2.610 |
| 18 | GWORF7 | −1.807 | GWORF7 | −1.786 | GWOXGB12 | −1.922 | GWOXGB7 | −2.624 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | GWOXGB17 | 1.865 | GWOLGB18 | 1.366 | GWOXGB17 | 1.412 | GWOXGB18 | 1.856 | GWOLGB17 | 2.504 | GWOXGB17 | 1.985 |
| 2 | GWOXGB18 | 1.855 | GWOXGB18 | 1.361 | GWOXGB18 | 1.384 | GWOXGB17 | 1.847 | GWOXGB17 | 2.486 | GWOLGB17 | 1.982 |
| 3 | GWOLGB17 | 1.826 | GWOLGB17 | 1.360 | GWOLGB17 | 1.332 | GWOLGB17 | 1.747 | GWOLGB18 | 2.476 | GWOXGB18 | 1.883 |
| 4 | GWOLGB18 | 1.759 | GWOXGB17 | 1.350 | GWOLGB18 | 1.310 | GWOLGB18 | 1.696 | GWOXGB18 | 2.439 | GWOLGB18 | 1.868 |
| 5 | GWORF17 | 1.207 | GWORF17 | 0.900 | GWORF17 | 0.929 | GWORF17 | 0.996 | GWORF18 | 1.547 | GWORF17 | 1.286 |
| 6 | GWORF18 | 1.160 | GWORF18 | 0.877 | GWORF18 | 0.866 | GWORF18 | 0.947 | GWORF17 | 1.393 | GWORF18 | 0.985 |
| 7 | GWOLGB16 | 0.215 | GWOLGB16 | 0.378 | GWOXGB16 | 0.519 | GWOXGB8 | 0.348 | GWOLGB7 | 0.060 | GWOLGB8 | 0.186 |
| 8 | GWOXGB16 | 0.176 | GWOXGB16 | 0.358 | GWOLGB16 | 0.483 | GWOLGB8 | 0.321 | GWOXGB7 | 0.054 | GWOXGB8 | 0.122 |
| 9 | GWOXGB8 | −0.214 | GWORF16 | 0.007 | GWORF16 | 0.149 | GWORF8 | 0.166 | GWORF7 | −0.176 | GWORF8 | 0.011 |
| 10 | GWOLGB8 | −0.255 | GWOXGB8 | −0.009 | GWOLGB8 | −0.113 | GWORF9 | 0.063 | GWOLGB8 | −1.359 | GWORF9 | 0.004 |
| 11 | GWORF8 | −0.359 | GWOLGB8 | −0.013 | GWOXGB8 | −0.142 | GWOXGB16 | −0.338 | GWOXGB8 | −1.365 | GWOLGB16 | −0.653 |
| 12 | GWORF9 | −0.376 | GWORF8 | −0.092 | GWORF8 | −0.259 | GWOLGB16 | −0.423 | GWOLGB9 | −1.369 | GWOXGB16 | −0.762 |
| 13 | GWORF16 | −0.447 | GWORF9 | −0.201 | GWORF9 | −0.363 | GWORF16 | −0.904 | GWOLGB12 | −1.399 | GWORF16 | −0.894 |
| 14 | GWOXGB15 | −1.269 | GWOXGB15 | −0.724 | GWOXGB15 | −0.730 | GWOXGB15 | −1.253 | GWOXGB9 | −1.422 | GWOXGB7 | −1.330 |
| 15 | GWOLGB15 | −1.325 | GWOLGB15 | −0.764 | GWOLGB15 | −0.762 | GWOLGB15 | −1.304 | GWOXGB12 | −1.455 | GWOLGB7 | −1.357 |
| 16 | GWORF15 | −1.679 | GWORF15 | −0.898 | GWORF15 | −0.903 | GWORF15 | −1.488 | GWORF9 | −1.457 | GWORF7 | −1.475 |
| 17 | GWOXGB13 | −2.011 | GWOLGB13 | −2.625 | GWOXGB13 | −2.522 | GWOLGB12 | −2.131 | GWORF12 | −1.464 | GWOLGB15 | −1.837 |
| 18 | GWOLGB13 | −2.128 | GWOXGB13 | −2.630 | GWOLGB13 | −2.588 | GWOXGB12 | −2.144 | GWORF8 | −1.496 | GWOXGB9 | −2.001 |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 54 | GWORF1 | −1.832 | GWOXGB1 | −2.195 | GWOXGB1 | −2.715 | GWOXGB1 | −2.220 |
| 53 | GWOLGB1 | −1.798 | GWOLGB1 | −2.163 | GWOLGB1 | −2.690 | GWORF1 | −2.217 |
| 52 | GWOXGB1 | −1.789 | GWORF1 | −2.158 | GWORF1 | −2.666 | GWOLGB1 | −2.183 |
| 51 | GWOLGB3 | −0.965 | GWORF2 | −1.330 | GWOXGB3 | −0.542 | GWORF6 | −1.687 |
| 50 | GWORF3 | −0.944 | GWOLGB2 | −1.314 | GWOLGB3 | −0.523 | GWOLGB6 | −1.648 |
| 49 | GWOXGB3 | −0.802 | GWOXGB2 | −1.142 | GWORF3 | −0.513 | GWOXGB6 | −1.584 |
| 48 | GWORF6 | −0.413 | GWORF3 | −0.257 | GWORF6 | −0.002 | GWORF2 | 0.139 |
| 47 | GWOXGB6 | −0.361 | GWOXGB3 | 0.095 | GWOXGB6 | 0.044 | GWOLGB2 | 0.172 |
| 46 | GWOLGB6 | −0.339 | GWOLGB3 | 0.159 | GWOLGB6 | 0.131 | GWOXGB2 | 0.180 |
| 45 | GWORF11 | −0.271 | GWORF6 | 0.487 | GWORF4 | 0.922 | GWORF10 | 0.422 |
| 44 | GWOLGB11 | −0.189 | GWOLGB6 | 0.576 | GWOXGB4 | 0.924 | GWOLGB10 | 0.475 |
| 43 | GWOXGB11 | 0.065 | GWOXGB6 | 0.600 | GWOXGB11 | 0.953 | GWOXGB10 | 0.490 |
| 42 | GWORF2 | 1.016 | GWORF13 | 0.955 | GWOLGB4 | 0.957 | GWORF3 | 1.447 |
| 41 | GWOLGB2 | 1.072 | GWOLGB13 | 1.301 | GWORF11 | 1.066 | GWOLGB3 | 1.495 |
| 40 | GWOXGB2 | 1.139 | GWOXGB13 | 1.362 | GWOLGB11 | 1.070 | GWOXGB3 | 1.503 |
| 39 | GWORF10 | 2.119 | GWORF10 | 1.560 | GWORF2 | 1.108 | GWORF11 | 1.711 |
| 38 | GWOLGB10 | 2.134 | GWOLGB10 | 1.679 | GWOXGB2 | 1.234 | GWOXGB13 | 1.727 |
| 37 | GWOXGB10 | 2.157 | GWOXGB11 | 1.786 | GWOLGB2 | 1.241 | GWOLGB13 | 1.777 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 54 | GWOXGB1 | −2.067 | GWOXGB1 | −2.069 | GWOXGB1 | −2.052 | GWOXGB2 | −1.696 | GWOLGB1 | −2.296 | GWOLGB1 | −2.328 |
| 53 | GWOLGB1 | −2.059 | GWORF1 | −2.025 | GWOLGB1 | −2.029 | GWOLGB2 | −1.618 | GWORF1 | −2.272 | GWORF1 | −2.322 |
| 52 | GWORF1 | −1.942 | GWOLGB1 | −2.018 | GWORF1 | −1.977 | GWORF2 | −1.599 | GWOXGB1 | −2.257 | GWOXGB1 | −2.276 |
| 51 | GWORF6 | −0.563 | GWORF2 | −1.151 | GWOXGB2 | −0.901 | GWOXGB1 | −1.542 | GWORF3 | −1.348 | GWORF6 | −0.666 |
| 50 | GWOLGB2 | −0.460 | GWOXGB2 | −1.084 | GWORF2 | −0.900 | GWORF1 | −1.535 | GWOLGB3 | −1.296 | GWOLGB6 | −0.583 |
| 49 | GWOLGB6 | −0.404 | GWOLGB2 | −1.063 | GWOLGB2 | −0.853 | GWOLGB1 | −1.535 | GWOXGB3 | −1.218 | GWOXGB6 | −0.552 |
| 48 | GWOXGB2 | −0.402 | GWOXGB6 | −0.375 | GWOLGB6 | −0.579 | GWORF10 | −0.354 | GWORF2 | 0.031 | GWOXGB2 | −0.230 |
| 47 | GWOXGB6 | −0.373 | GWORF6 | −0.300 | GWOXGB6 | −0.548 | GWORF6 | −0.304 | GWOXGB2 | 0.032 | GWORF2 | −0.195 |
| 46 | GWORF2 | −0.252 | GWOLGB6 | −0.273 | GWORF6 | −0.514 | GWOXGB10 | −0.148 | GWOLGB2 | 0.046 | GWOLGB2 | −0.165 |
| 45 | GWORF4 | −0.238 | GWOXGB10 | 0.356 | GWOXGB10 | 0.422 | GWOLGB10 | −0.106 | GWORF6 | 0.776 | GWOXGB3 | 0.321 |
| 44 | GWOXGB4 | −0.143 | GWORF10 | 0.462 | GWORF10 | 0.429 | GWOXGB6 | −0.023 | GWOLGB6 | 0.790 | GWOLGB3 | 0.337 |
| 43 | GWOLGB4 | −0.139 | GWOLGB10 | 0.503 | GWOLGB10 | 0.534 | GWOLGB6 | 0.035 | GWOXGB6 | 0.799 | GWORF3 | 0.368 |
| 42 | GWOXGB14 | 1.105 | GWORF4 | 1.126 | GWORF4 | 1.036 | GWORF3 | 1.161 | GWORF13 | 0.956 | GWORF11 | 1.073 |
| 41 | GWOLGB14 | 1.180 | GWOXGB4 | 1.265 | GWOLGB4 | 1.083 | GWOXGB3 | 1.365 | GWOLGB13 | 1.136 | GWOXGB11 | 1.127 |
| 40 | GWORF14 | 1.239 | GWOLGB4 | 1.286 | GWOXGB4 | 1.108 | GWOLGB3 | 1.404 | GWOXGB13 | 1.143 | GWOLGB11 | 1.240 |
| 39 | GWOXGB10 | 1.791 | GWORF14 | 1.757 | GWOXGB14 | 1.904 | GWORF13 | 1.959 | GWORF11 | 1.640 | GWORF10 | 1.534 |
| 38 | GWORF5 | 1.817 | GWOXGB14 | 1.782 | GWORF14 | 1.915 | GWOXGB13 | 2.237 | GWOXGB11 | 1.645 | GWOLGB10 | 1.651 |
| 37 | GWOLGB10 | 1.909 | GWOLGB3 | 1.823 | GWOLGB14 | 1.922 | GWOLGB13 | 2.299 | GWOLGB11 | 1.692 | GWOXGB10 | 1.665 |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | GWOXGB17 | 2.031 | GWOXGB17 | 2.077 | GWOXGB18 | 1.953 | GWOXGB18 | 1.302 |
| 2 | GWOXGB18 | 1.995 | GWOXGB18 | 1.982 | GWOLGB18 | 1.953 | GWOLGB18 | 1.288 |
| 3 | GWOLGB18 | 1.740 | GWOLGB17 | 1.964 | GWOXGB17 | 1.916 | GWOXGB17 | 1.222 |
| 4 | GWOLGB17 | 1.656 | GWOLGB18 | 1.732 | GWOLGB17 | 1.909 | GWOLGB17 | 1.207 |
| 5 | XGB17 | 1.538 | XGB17 | 1.635 | LGB18 | 1.810 | LGB18 | 1.062 |
| 6 | XGB18 | 1.419 | LGB17 | 1.633 | LGB17 | 1.754 | LGB17 | 1.051 |
| 7 | LGB17 | 1.388 | LGB18 | 1.439 | XGB18 | 1.642 | XGB17 | 1.025 |
| 8 | LGB18 | 1.388 | XGB18 | 1.413 | XGB17 | 1.621 | XGB18 | 0.987 |
| 9 | GWOXGB8 | 0.869 | GWORF17 | 1.193 | GWORF18 | 1.537 | GWORF17 | 0.799 |
| 10 | GWORF17 | 0.589 | RF17 | 1.176 | RF18 | 1.528 | RF17 | 0.793 |
| 11 | RF17 | 0.579 | GWORF18 | 1.075 | GWORF17 | 1.395 | GWORF18 | 0.679 |
| 12 | GWOLGB8 | 0.533 | RF18 | 1.054 | RF17 | 1.376 | RF18 | 0.661 |
| 13 | XGB8 | 0.533 | GWOXGB8 | 0.829 | GWOXGB7 | −0.110 | GWOLGB16 | 0.252 |
| 14 | LGB8 | 0.510 | GWOLGB8 | 0.755 | GWOLGB7 | −0.119 | GWOXGB16 | 0.220 |
| 15 | GWORF18 | 0.399 | LGB8 | 0.673 | LGB7 | −0.129 | LGB16 | 0.152 |
| 16 | RF18 | 0.392 | XGB8 | 0.540 | GWORF7 | −0.159 | GWOLGB8 | 0.150 |
| 17 | GWORF8 | 0.159 | GWORF8 | 0.473 | RF7 | −0.210 | GWOXGB8 | 0.112 |
| 18 | RF8 | 0.148 | RF9 | 0.454 | XGB7 | −0.318 | LGB8 | 0.063 |
| 19 | RF9 | 0.144 | RF8 | 0.445 | GWOLGB16 | −0.348 | XGB16 | 0.015 |
| 20 | GWORF9 | −0.023 | GWORF9 | 0.414 | GWOXGB16 | −0.358 | XGB8 | 0.005 |
| 21 | GWOLGB12 | −0.607 | GWOLGB9 | −1.103 | LGB16 | −0.393 | GWORF16 | −0.037 |
| 22 | GWOLGB9 | −0.652 | GWOXGB9 | −1.154 | GWORF16 | −0.571 | GWORF8 | −0.050 |
| 23 | GWOXGB9 | −0.675 | LGB9 | −1.169 | RF16 | −0.577 | RF16 | −0.065 |
| 24 | GWORF12 | −0.726 | GWOLGB12 | −1.270 | XGB16 | −0.673 | RF8 | −0.069 |
| 25 | GWOXGB12 | −0.736 | LGB12 | −1.313 | GWOLGB8 | −1.068 | RF9 | −0.075 |
| 26 | LGB12 | −0.739 | GWORF12 | −1.363 | GWORF8 | −1.101 | GWORF9 | −0.123 |
| 27 | LGB9 | −0.762 | RF12 | −1.376 | LGB8 | −1.102 | GWOXGB15 | −0.407 |
| 28 | RF12 | −1.040 | GWOLGB7 | −1.433 | GWORF9 | −1.122 | GWOLGB15 | −0.430 |
| 29 | XGB9 | −1.208 | LGB7 | −1.469 | GWOXGB8 | −1.171 | LGB15 | −0.445 |
| 30 | XGB12 | −1.288 | GWOXGB12 | −1.478 | RF8 | −1.218 | GWORF15 | −0.529 |
| 31 | GWOLGB7 | −1.422 | GWOXGB7 | −1.501 | RF9 | −1.238 | RF15 | −0.561 |
| 32 | GWOXGB7 | −1.436 | GWORF7 | −1.535 | XGB8 | −1.394 | XGB15 | −0.581 |
| 33 | GWORF7 | −1.458 | XGB9 | −1.537 | GWOLGB12 | −1.611 | GWOLGB7 | −2.275 |
| 34 | LGB7 | −1.564 | RF7 | −1.617 | GWOXGB12 | −1.665 | GWOXGB7 | −2.288 |
| 35 | RF7 | −1.717 | XGB12 | −1.712 | LGB12 | −1.694 | LGB7 | −2.413 |
| 36 | XGB7 | −1.958 | XGB7 | −1.923 | XGB12 | −2.047 | XGB7 | −2.698 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 1 | GWOXGB17 | 1.810 | GWOLGB18 | 1.315 | GWOXGB17 | 1.368 | GWOXGB18 | 1.739 | GWOLGB17 | 2.383 | GWOXGB17 | 1.944 |
| 2 | GWOXGB18 | 1.801 | GWOXGB18 | 1.311 | GWOXGB18 | 1.343 | GWOXGB17 | 1.731 | GWOXGB17 | 2.366 | GWOLGB17 | 1.941 |
| 3 | GWOLGB17 | 1.774 | GWOLGB17 | 1.310 | GWOLGB17 | 1.295 | GWOLGB17 | 1.642 | GWOLGB18 | 2.357 | GWOXGB18 | 1.847 |
| 4 | GWOLGB18 | 1.711 | GWOXGB17 | 1.301 | GWOLGB18 | 1.273 | GWOLGB18 | 1.595 | GWOXGB18 | 2.323 | GWOLGB18 | 1.834 |
| 5 | LGB17 | 1.556 | LGB18 | 1.146 | LGB18 | 1.120 | LGB17 | 1.434 | LGB17 | 2.136 | LGB17 | 1.726 |
| 6 | LGB18 | 1.491 | LGB17 | 1.104 | LGB17 | 1.105 | XGB17 | 1.394 | LGB18 | 2.069 | LGB18 | 1.644 |
| 7 | XGB17 | 1.443 | XGB18 | 1.025 | XGB18 | 1.056 | LGB18 | 1.369 | XGB17 | 1.980 | XGB17 | 1.588 |
| 8 | XGB18 | 1.378 | XGB17 | 1.023 | XGB17 | 1.052 | XGB18 | 1.352 | XGB18 | 1.818 | XGB18 | 1.421 |
| 9 | RF17 | 1.203 | GWORF17 | 0.887 | GWORF17 | 0.921 | RF17 | 0.985 | GWORF18 | 1.505 | GWORF17 | 1.284 |
| 10 | GWORF17 | 1.199 | RF17 | 0.887 | RF17 | 0.907 | GWORF17 | 0.964 | RF18 | 1.499 | RF17 | 1.245 |
| 11 | GWORF18 | 1.155 | GWORF18 | 0.866 | GWORF18 | 0.863 | GWORF18 | 0.921 | GWORF17 | 1.364 | GWORF18 | 1.002 |
| 12 | RF18 | 1.155 | RF18 | 0.860 | RF18 | 0.849 | RF18 | 0.910 | RF17 | 1.347 | RF18 | 0.909 |
| 13 | GWOLGB16 | 0.278 | GWOLGB16 | 0.406 | GWOXGB16 | 0.540 | GWOXGB8 | 0.382 | GWOLGB7 | 0.144 | GWOLGB8 | 0.247 |
| 14 | GWOXGB16 | 0.241 | GWOXGB16 | 0.388 | GWOLGB16 | 0.507 | GWOLGB8 | 0.358 | GWOXGB7 | 0.139 | LGB8 | 0.194 |
| 15 | LGB16 | 0.073 | LGB16 | 0.270 | LGB16 | 0.381 | LGB8 | 0.357 | LGB7 | 0.114 | GWOXGB8 | 0.187 |
| 16 | XGB16 | −0.103 | XGB16 | 0.125 | XGB16 | 0.241 | RF8 | 0.226 | GWORF7 | −0.071 | GWORF8 | 0.083 |
| 17 | GWOXGB8 | −0.119 | GWORF16 | 0.066 | GWORF16 | 0.199 | GWORF8 | 0.219 | RF7 | −0.094 | GWORF9 | 0.077 |
| 18 | GWOLGB8 | −0.157 | GWOXGB8 | 0.053 | RF16 | 0.169 | RF9 | 0.210 | XGB7 | −0.156 | RF9 | 0.055 |
| 19 | LGB8 | −0.196 | GWOLGB8 | 0.050 | GWOLGB8 | −0.042 | XGB8 | 0.189 | GWOLGB8 | −1.152 | RF8 | 0.048 |
| 20 | RF9 | −0.225 | RF16 | 0.045 | GWOXGB8 | −0.069 | GWORF9 | 0.127 | GWOXGB8 | −1.158 | XGB8 | −0.038 |
| 21 | GWORF8 | −0.253 | LGB8 | 0.014 | LGB8 | −0.128 | GWOXGB16 | −0.234 | GWOLGB9 | −1.161 | GWOLGB16 | −0.541 |
| 22 | RF8 | −0.262 | GWORF8 | −0.022 | GWORF8 | −0.175 | GWOLGB16 | −0.310 | LGB9 | −1.178 | LGB16 | −0.627 |
| 23 | GWORF9 | −0.269 | RF8 | −0.047 | RF9 | −0.185 | LGB16 | −0.432 | LGB8 | −1.183 | GWOXGB16 | −0.642 |
| 24 | GWORF16 | −0.335 | RF9 | −0.047 | RF8 | −0.193 | XGB16 | −0.624 | GWOLGB12 | −1.189 | GWORF16 | −0.767 |
| 25 | RF16 | −0.348 | GWORF9 | −0.121 | XGB8 | −0.243 | GWORF16 | −0.741 | GWOXGB9 | −1.210 | RF16 | −0.779 |
| 26 | XGB8 | −0.358 | XGB8 | −0.135 | GWORF9 | −0.272 | RF16 | −0.760 | GWOXGB12 | −1.240 | XGB16 | −0.913 |
| 27 | GWOXGB15 | −1.096 | GWOXGB15 | −0.602 | GWOXGB15 | −0.612 | GWOXGB15 | −1.053 | GWORF9 | −1.242 | GWOXGB7 | −1.176 |
| 28 | GWOLGB15 | −1.148 | GWOLGB15 | −0.638 | LGB15 | −0.631 | GWOLGB15 | −1.098 | GWORF12 | −1.248 | GWOLGB7 | −1.201 |
| 29 | LGB15 | −1.196 | LGB15 | −0.644 | GWOLGB15 | −0.642 | LGB15 | −1.118 | LGB12 | −1.252 | LGB7 | −1.219 |
| 30 | XGB15 | −1.445 | GWORF15 | −0.760 | GWORF15 | −0.771 | GWORF15 | −1.263 | GWORF8 | −1.277 | GWORF7 | −1.312 |
| 31 | GWORF15 | −1.476 | RF15 | −0.798 | RF15 | −0.785 | RF15 | −1.323 | RF9 | −1.366 | RF7 | −1.355 |
| 32 | RF15 | −1.501 | XGB15 | −0.871 | XGB15 | −0.860 | XGB15 | −1.326 | RF8 | −1.393 | XGB7 | −1.495 |
| 33 | GWOXGB13 | −1.783 | GWOLGB13 | −2.335 | GWOXGB13 | −2.261 | GWOLGB12 | −1.831 | RF12 | −1.420 | GWOLGB15 | −1.653 |
| 34 | GWOLGB13 | −1.891 | GWOXGB13 | −2.340 | GWOLGB13 | −2.322 | GWOXGB12 | −1.843 | XGB9 | −1.461 | LGB15 | −1.695 |
| 35 | LGB13 | −1.923 | LGB13 | −2.411 | LGB13 | −2.368 | LGB12 | −1.888 | XGB8 | −1.475 | GWOXGB9 | −1.805 |
| 36 | XGB13 | −2.183 | XGB13 | −2.684 | XGB13 | −2.632 | XGB12 | −2.261 | XGB12 | −1.617 | XGB12 | −2.054 |
| Jorhat | Mohanpur | Palampur | Thrissur | |||||
|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 108 | RF1 | −2.443 | RF1 | −2.685 | RF1 | −2.858 | RF1 | −2.488 |
| 107 | XGB1 | −1.829 | XGB1 | −1.645 | XGB1 | −2.313 | XGB1 | −1.934 |
| 106 | LGB1 | −1.374 | RF2 | −1.357 | LGB1 | −1.909 | LGB1 | −1.620 |
| 105 | GWORF1 | −1.158 | XGB2 | −1.176 | GWOXGB1 | −1.811 | GWOXGB1 | −1.543 |
| 104 | RF3 | −1.150 | LGB1 | −1.066 | GWOLGB1 | −1.793 | GWORF1 | −1.541 |
| 103 | GWOLGB1 | −1.134 | GWOXGB1 | −0.891 | GWORF1 | −1.774 | RF6 | −1.530 |
| 102 | GWOXGB1 | −1.128 | GWOLGB1 | −0.875 | RF3 | −0.956 | GWOLGB1 | −1.515 |
| 101 | XGB3 | −1.001 | GWORF1 | −0.871 | XGB3 | −0.578 | XGB6 | −1.380 |
| 100 | XGB6 | −0.703 | RF3 | −0.703 | RF6 | −0.439 | LGB6 | −1.144 |
| 99 | LGB3 | −0.655 | LGB2 | −0.517 | XGB6 | −0.266 | GWORF6 | −1.143 |
| 98 | RF6 | −0.644 | XGB3 | −0.455 | LGB3 | −0.242 | GWOLGB6 | −1.114 |
| 97 | GWOLGB3 | −0.504 | GWORF2 | −0.413 | GWOXGB3 | −0.202 | GWOXGB6 | −1.066 |
| 96 | GWORF3 | −0.488 | GWOLGB2 | −0.405 | GWOLGB3 | −0.188 | RF2 | −0.120 |
| 95 | GWOXGB3 | −0.379 | GWOXGB2 | −0.310 | GWORF3 | −0.180 | XGB2 | −0.006 |
| 94 | XGB11 | −0.264 | RF6 | −0.292 | LGB6 | 0.198 | XGB10 | 0.210 |
| 93 | RF11 | −0.259 | XGB6 | −0.212 | GWORF6 | 0.201 | LGB2 | 0.211 |
| 92 | LGB6 | −0.200 | XGB13 | 0.163 | GWOXGB6 | 0.235 | GWORF2 | 0.221 |
| 91 | GWORF6 | −0.078 | GWORF3 | 0.180 | RF4 | 0.281 | RF10 | 0.239 |
| 90 | GWOXGB6 | −0.040 | LGB3 | 0.182 | GWOLGB6 | 0.299 | GWOLGB2 | 0.246 |
| 89 | LGB11 | −0.025 | RF13 | 0.367 | RF2 | 0.386 | GWOXGB2 | 0.252 |
| 88 | GWOLGB6 | −0.024 | GWOXGB3 | 0.374 | XGB4 | 0.481 | GWORF10 | 0.431 |
| 87 | GWORF11 | 0.028 | GWOLGB3 | 0.409 | XGB11 | 0.511 | LGB10 | 0.442 |
| 86 | GWOLGB11 | 0.090 | LGB6 | 0.446 | XGB2 | 0.580 | GWOLGB10 | 0.470 |
| 85 | GWOXGB11 | 0.284 | XGB10 | 0.513 | RF11 | 0.744 | GWOXGB10 | 0.481 |
| 84 | RF2 | 0.450 | GWORF6 | 0.593 | LGB4 | 0.873 | RF3 | 0.971 |
| 83 | XGB2 | 0.484 | GWOLGB6 | 0.640 | GWORF4 | 0.882 | XGB3 | 0.989 |
| 82 | LGB2 | 0.888 | GWOXGB6 | 0.653 | GWOXGB4 | 0.883 | LGB3 | 1.189 |
| 81 | GWORF2 | 1.004 | RF10 | 0.756 | GWOXGB11 | 0.906 | GWORF3 | 1.192 |
| 80 | GWOLGB2 | 1.045 | LGB13 | 0.804 | GWOLGB4 | 0.908 | XGB13 | 1.226 |
| 79 | GWOXGB2 | 1.097 | GWORF13 | 0.848 | LGB11 | 0.952 | GWOLGB3 | 1.228 |
| 78 | XGB10 | 1.359 | GWOLGB13 | 1.038 | LGB2 | 0.957 | GWOXGB3 | 1.234 |
| 77 | RF10 | 1.540 | GWOXGB13 | 1.071 | GWORF11 | 0.990 | RF5 | 1.269 |
| 76 | LGB10 | 1.695 | LGB10 | 1.092 | GWOLGB11 | 0.993 | GWORF11 | 1.387 |
| 75 | GWORF10 | 1.826 | GWORF10 | 1.183 | GWORF2 | 1.019 | GWOXGB13 | 1.398 |
| 74 | GWOLGB10 | 1.837 | GWOLGB10 | 1.250 | GWOXGB2 | 1.113 | LGB5 | 1.423 |
| 73 | GWOXGB10 | 1.854 | GWOXGB11 | 1.312 | GWOLGB2 | 1.118 | GWOLGB13 | 1.435 |
| Faizabad | Jabalpur | Raipur | Ranchi | Ranichauri | Samastipur | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RANK | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI | MODEL | GPI |
| 108 | RF1 | −2.488 | RF1 | −2.511 | RF1 | −2.473 | RF1 | −2.276 | RF1 | −2.703 | RF1 | −2.620 |
| 107 | XGB1 | −1.954 | XGB1 | −1.969 | XGB1 | −1.909 | XGB2 | −1.606 | XGB1 | −1.931 | XGB1 | −2.127 |
| 106 | LGB1 | −1.173 | LGB1 | −1.330 | LGB1 | −1.246 | RF2 | −1.498 | LGB1 | −1.471 | LGB1 | −1.656 |
| 105 | GWOXGB1 | −1.140 | XGB2 | −1.304 | GWOXGB1 | −1.036 | XGB1 | −1.449 | GWOLGB1 | −1.322 | GWOLGB1 | −1.492 |
| 104 | GWOLGB1 | −1.135 | RF2 | −1.126 | GWOLGB1 | −1.020 | LGB2 | −0.861 | GWORF1 | −1.305 | GWORF1 | −1.487 |
| 103 | GWORF1 | −1.058 | GWOXGB1 | −1.119 | XGB2 | −1.013 | LGB1 | −0.823 | GWOXGB1 | −1.295 | GWOXGB1 | −1.454 |
| 102 | XGB2 | −0.819 | GWORF1 | −1.090 | GWORF1 | −0.986 | XGB10 | −0.793 | RF3 | −1.233 | RF6 | −0.818 |
| 101 | RF2 | −0.679 | GWOLGB1 | −1.086 | RF2 | −0.889 | XGB6 | −0.735 | XGB3 | −1.215 | XGB6 | −0.789 |
| 100 | RF6 | −0.648 | XGB6 | −0.719 | XGB6 | −0.806 | GWOXGB2 | −0.690 | LGB3 | −0.772 | XGB2 | −0.488 |
| 99 | XGB4 | −0.618 | LGB2 | −0.695 | RF6 | −0.787 | GWOLGB2 | −0.643 | GWORF3 | −0.698 | RF2 | −0.379 |
| 98 | XGB6 | −0.599 | GWORF2 | −0.520 | LGB2 | −0.574 | GWORF2 | −0.631 | GWOLGB3 | −0.665 | LGB6 | −0.339 |
| 97 | RF4 | −0.394 | RF6 | −0.504 | XGB10 | −0.372 | GWOXGB1 | −0.597 | GWOXGB3 | −0.614 | GWORF6 | −0.293 |
| 96 | LGB2 | −0.253 | GWOXGB2 | −0.477 | GWOXGB2 | −0.297 | GWOLGB1 | −0.593 | XGB2 | −0.313 | GWOLGB6 | −0.234 |
| 95 | LGB6 | −0.167 | GWOLGB2 | −0.463 | GWORF2 | −0.296 | GWORF1 | −0.593 | RF2 | −0.258 | GWOXGB6 | −0.212 |
| 94 | GWORF6 | −0.139 | LGB6 | −0.127 | GWOLGB2 | −0.266 | RF6 | −0.591 | LGB2 | 0.098 | XGB3 | −0.131 |
| 93 | GWOLGB2 | −0.075 | XGB10 | −0.100 | LGB6 | −0.212 | RF10 | −0.427 | GWOXGB2 | 0.203 | LGB2 | −0.016 |
| 92 | GWOXGB2 | −0.036 | GWOXGB6 | −0.009 | GWOLGB6 | −0.088 | LGB10 | 0.005 | GWORF2 | 0.203 | GWOXGB2 | 0.015 |
| 91 | GWOLGB6 | −0.034 | GWORF6 | 0.040 | GWOXGB6 | −0.068 | LGB6 | 0.066 | GWOLGB2 | 0.213 | RF3 | 0.035 |
| 90 | GWOXGB6 | −0.014 | GWOLGB6 | 0.057 | GWORF6 | −0.044 | GWORF10 | 0.121 | XGB6 | 0.304 | GWORF2 | 0.040 |
| 89 | GWORF2 | 0.063 | RF10 | 0.236 | RF10 | 0.040 | GWORF6 | 0.151 | RF6 | 0.366 | GWOLGB2 | 0.062 |
| 88 | GWORF4 | 0.074 | LGB10 | 0.354 | XGB4 | 0.152 | GWOXGB10 | 0.246 | XGB13 | 0.445 | LGB3 | 0.326 |
| 87 | LGB4 | 0.106 | GWOXGB10 | 0.468 | LGB10 | 0.313 | XGB3 | 0.267 | RF13 | 0.592 | GWOXGB3 | 0.412 |
| 86 | GWOXGB4 | 0.137 | GWORF10 | 0.536 | RF4 | 0.405 | GWOLGB10 | 0.271 | LGB6 | 0.645 | GWOLGB3 | 0.423 |
| 85 | GWOLGB4 | 0.139 | GWOLGB10 | 0.563 | GWOXGB10 | 0.556 | RF3 | 0.313 | GWORF6 | 0.696 | GWORF3 | 0.446 |
| 84 | XGB14 | 0.520 | XGB4 | 0.585 | GWORF10 | 0.559 | GWOXGB6 | 0.321 | GWOLGB6 | 0.706 | XGB11 | 0.586 |
| 83 | RF14 | 0.783 | RF4 | 0.652 | GWOLGB10 | 0.626 | GWOLGB6 | 0.356 | GWOXGB6 | 0.711 | RF11 | 0.844 |
| 82 | XGB10 | 0.893 | GWORF4 | 0.964 | LGB4 | 0.767 | XGB13 | 0.840 | GWORF13 | 0.810 | XGB10 | 0.903 |
| 81 | LGB14 | 0.967 | LGB4 | 0.986 | XGB5 | 0.857 | LGB3 | 0.915 | LGB13 | 0.825 | GWORF11 | 0.954 |
| 80 | GWOXGB14 | 0.967 | XGB3 | 1.006 | GWORF4 | 0.942 | GWORF3 | 1.036 | XGB11 | 0.902 | GWOXGB11 | 0.993 |
| 79 | GWOLGB14 | 1.017 | RF3 | 1.014 | GWOLGB4 | 0.972 | RF13 | 1.075 | GWOLGB13 | 0.927 | LGB11 | 1.016 |
| 78 | RF5 | 1.039 | GWOXGB4 | 1.055 | GWOXGB4 | 0.986 | GWOXGB3 | 1.159 | GWOXGB13 | 0.932 | GWOLGB11 | 1.074 |
| 77 | GWORF14 | 1.054 | GWOLGB4 | 1.068 | RF5 | 1.293 | GWOLGB3 | 1.183 | RF11 | 1.159 | RF10 | 1.098 |
| 76 | LGB10 | 1.309 | LGB14 | 1.377 | LGB14 | 1.387 | GWORF13 | 1.519 | LGB11 | 1.232 | LGB10 | 1.271 |
| 75 | GWOXGB10 | 1.420 | GWORF14 | 1.378 | GWOXGB14 | 1.504 | LGB13 | 1.552 | GWORF11 | 1.263 | GWORF10 | 1.287 |
| 74 | GWORF5 | 1.439 | GWOXGB14 | 1.394 | GWORF14 | 1.511 | GWOXGB13 | 1.687 | GWOXGB11 | 1.266 | GWOLGB10 | 1.370 |
| 73 | GWOLGB10 | 1.497 | GWOLGB3 | 1.417 | GWOLGB14 | 1.514 | GWOLGB13 | 1.724 | GWOLGB11 | 1.297 | GWOXGB10 | 1.380 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heramb, P.; Ramana Rao, K.V.; Subeesh, A.; Srivastava, A. Predictive Modelling of Reference Evapotranspiration Using Machine Learning Models Coupled with Grey Wolf Optimizer. Water 2023, 15, 856. https://doi.org/10.3390/w15050856
Heramb P, Ramana Rao KV, Subeesh A, Srivastava A. Predictive Modelling of Reference Evapotranspiration Using Machine Learning Models Coupled with Grey Wolf Optimizer. Water. 2023; 15(5):856. https://doi.org/10.3390/w15050856
Chicago/Turabian StyleHeramb, Pangam, K. V. Ramana Rao, A. Subeesh, and Ankur Srivastava. 2023. "Predictive Modelling of Reference Evapotranspiration Using Machine Learning Models Coupled with Grey Wolf Optimizer" Water 15, no. 5: 856. https://doi.org/10.3390/w15050856
APA StyleHeramb, P., Ramana Rao, K. V., Subeesh, A., & Srivastava, A. (2023). Predictive Modelling of Reference Evapotranspiration Using Machine Learning Models Coupled with Grey Wolf Optimizer. Water, 15(5), 856. https://doi.org/10.3390/w15050856