1. Introduction
Filling events are frequently performed for water utilities companies in order to operate drinking water distribution systems to supply the required water demands [
1,
2,
3,
4]. To analyse the performing of filling operations is crucial for the understanding of the pressurised liquid phase (water) and the compression of the gas phase (entrapped air pocket). Conduits in storm drainage networks can also be pressurised when a return period occurrence is higher compared to the designed one [
5,
6,
7]. The air–water interface exhibits a dynamic behaviour in pressurised installations while the water phase replaces part of the portion occupied by the entrapped air pocket. The phenomenon can generate pressure surges and temperature gradients [
2]. Air valves are used as protection devices to avoid risky conditions with regard to over-pressures [
8,
9,
10,
11,
12], where several studies have been developed using experimental measurements and analytical formulations [
8,
9,
10,
13]. Water filling processes have been analysing using elastic [
14] and rigid [
1,
11,
12,
15] column models, which can provide information regarding the water filling velocity, air pocket pressure, air pocket temperature, air density, and position of the air–water interface.
In addition, filling operations have been modelled using computational fluid dynamics (CFD) in order to represent the hydraulic and thermodynamic evolution of the water and air phases, respectively [
16,
17]. A 3D CFD analysis can provide detailed information in each cell of an entire water installation compared to analytical models [
16]. Besharat et al. [
18] developed a 2D CFD model for studying the dynamic behaviour during the compression of an entrapped air pocket, which showed a good agreement in regards to experimental measurements. Martins et al. [
19] studied the over-pressure peaks in rapid filling events, where the influence of an air pocket size was evaluated. Zhou et al. [
4] studied different hydraulic and thermodynamic phenomena of an entrapped air pocket in a vertical pipeline during rapid filling events. Fang et al. [
20] studied the motion of entrapped air pockets in a storm-water drainage system. Aguirre-Mendoza et al. [
17,
21] developed a 2D CFD model to analyse the effects of orifice sizes in the control of filling processes of water pipelines. Many researches have used the SST k-
model to analyse the dynamic interaction between water and air [
17,
22,
23,
24]. CFD models for simulating a two-phase transient flow in pipelines have rarely been used to analyse their numerical accuracy, to verify the behaviour of the air–water interface, even to verify the pressure patterns of the entrapped air pocket. Air–water mixing accumulates multiple hydraulic–thermodynamic phenomena that have been studied to a limited extent in the literature. The aim of this research is to analyse the thermodynamic behaviour of an entrapped air pocket and the hydraulic transients during a rapid filling event with the upstream end closed in a water pipeline with an irregular profile using a 3D CFD model (OpenFOAM software v8). The experimental tests were performed at the hydraulic lab at the Instituto Superior Técnico (University of Lisbon, Lisbon, Portugal). A 7.6 m long PVC pipe with nominal diameter DN63 was used, considering several initial hydro-pneumatic tank pressures and air pocket sizes. Experimental measurements were used to validate the 3D CFD model.
2. Experimental Facility
The experimental facility corresponds to a water pipeline with a total length of 7.6 m and nominal diameter DN63 (internal diameter of 51.4 mm), which has two branch pipes (left and right).
Figure 1 presents the experimental scheme.
and
correspond to inclined pipe for the left and the right branch pipes, respectively, with lengths of 1.5 m each. Horizontal branch pipes
and
have lengths of 2.05 and 1.85 m, respectively. The left branch is connected to an electro-pneumatic ball valve. A hydro-pneumatic tank is used to supply different initial absolute pressure. The ball valve located at downstream end at the right branch pipe was closed for all experimental tests. A pressure transducer was located at the highest point of the installation to measure the air pocket pressure.
An initial air pocket size was defined with a length
located at the left branch pipe. The filling event starts with the opening of the electro-pneumatic ball valve. After that, the entrapped air pocket is compressed causing the air pocket pressure to increase its tendency. The water column located inside of the branch pipe remains at rest, acting as a boundary condition. A total of six (6) experimental measurements of pressure oscillations of the air pocket trapped in the branched pipe were performed. Their initial characteristics are shown in
Table 1.
3. Three-Dimensional Model
CFD models have been used for analysing the air–water interface during different hydraulic events [
24,
25,
26,
27,
28]. Two-dimensional CFD models have been implemented for studying filling events [
4,
17,
18,
21]. In this research, a 3D CFD model was used to simulate a rapid filling process using the computational software OpenFOAM [
29], developed by OpenFOAM Foundation. It allows to simulate multiphase compressible flows, considering an interface capture of fluid. A geometric domain in multiple blocks with small finite volumes should be defined in the software. The air–water interface is represented under user-defined conditions. Computational fundamentals are described as follows.
3.1. Governing Equations
The CFD model involves the solution of a set of mathematical equations involving different physical principles, such as mass conservation, momentum, transport, turbulence, and thermodynamic principles.
3.1.1. Partial Vof Equations
The volume of fluid equations are partially evaluated using a partial volume of fluid (PVoF) model, where the combination of fluids (air and water) is solved numerically using the phase fraction (
) for the calculation of density and dynamic viscosity (
and
) of each cell of the geometrical domain [
30,
31]. The equations of the density and dynamic viscosity are
where
= air density,
= water density.
and
correspond to dynamic viscosity of air and water, respectively. Transport model associated to PVoF model uses a rate change of volume fraction, convective transport terms, and compressibility of the fluid combination. The equation of the PVoF transport model is
where
= flow velocity vector in a cell, and
= velocity field.
3.1.2. Navier–Stokes Equations
The behaviour of multiphase flows can be analysed by the Navier–Stokes equations for compressible flows using the interface capture of the phase fraction of the PVoF model. The continuity formulation is
where
= density, and
= flow velocity vector. The momentum equation is represented by the following expression:
where
= pressure gradient term,
= gravitational acceleration vector, and
= surface tension forces.
3.1.3. Thermodynamic Equations
The principle of conservation of energy is based on the sum of the rates of change in thermodynamic energy and mechanical energy during fluid motion [
29]. Equation (
6) shows the principle of the conservation of energy.
where
= specific heat at constant pressure,
T = temperature,
= heat flux, and
= thermal energy source. The heat flux is calculated using the Fourier conduction law, which depends on the product of the thermal diffusivity (
) and the temperature gradient (
), as shown in Equation (
7):
The thermodynamic behaviour of air density is evaluated through the equation of state, which relates air pressure (
), the universal gas constant (
R), and air phase temperature (
). Equation (
8) represents the thermodynamic ratio of the above-mentioned parameters of the air phase.
3.1.4. SST k- Turbulence Model
The SST
k-
turbulence model was used to represent the turbulent phenomenon occurring in the analysed pipeline with entrapped air because aerodynamic flows are facing adverse pressure gradients [
32]. This model was implemented for a suitable resolution of the viscous laminar sub-layer and the effects of vorticity in areas far from the walls [
33]. The fundamental equations of the SST
k-
turbulence model are
where
k = turbulent kinetic energy,
= specific turbulence dissipation rate.
and
are diffusive terms for
k and
, respectively.
G = generation of turbulence kinetic energy,
= turbulent kinematic viscosity,
= blending function, and
= closure coefficient of
k and
. Coefficients such as
,
,
,
, and
depend on turbulence model. In addition, wall functions were used to calculate the logarithmic region between viscous sub-layer and far-wall zone.
3.2. Numerical Approach
The Pressure-Implicit with Splitting of Operators (PISO) algorithm was used for the numerical resolution of the governing equations, using the coupling system as a function of pressure and flow velocity in finite volumes. Pressure equation and momentum were corrected twice. On the other hand, non-orthogonal and outer correction were applied to solve the pressure term associated to transient flows. The numerical approach of the time and divergence schemes of the governing equations was performed using first-order and implicit Gaussian approximations to guarantee a stable numerical approximation. Second-order linear schemes were applied for the resolution of Laplacian terms and gradients.
3.3. Mesh Computational and Boundary Conditions
Figure 2 shows the spatial distribution of geometric domain associated to the pipeline of irregular profile for representing the filling processes. Geometric domain was distributed by unstructured cells, which are adequate for complex geometries [
34]. The opening of the electro-pneumatic ball valve was simulated using a dynamic mesh function. The geometric domain was distributed with a total of 151,539 cells, where 150,847 cells are tetrahedral cells and 692 cells are polyhedral cells. The 3D CFD model presents a non-orthogonality of 23.0, maximum skewness of 1.96, maximum aspect ratio of 117.3. Mesh sensitivity analysis was performed through tests with structured and unstructured meshes, which were performed in the contribution of Besharat et al. [
18] for an irregular pipeline of similar dimensions.
Different boundaries were defined in 3D CFD model, which are described as shown in
Table 2.
A no-slip boundary condition was defined in all boundaries with regard to walls. Initial pressure (inlet boundary) corresponds to absolute pressure (), which was supplied by the hydro-pneumatic tank. The system is at rest with an initial air temperature of 293 K. The air pocket is found to atmospheric pressure (p = 101,325 Pa).
4. Results and Discussion
A 3D CFD model was developed to analyse the thermodynamic and hydraulic variables during rapid filling processes in water pipelines. A detailed analysis was performed using Test No. 1 and Test No. 2, which correspond to hydraulic scenarios with
= 0.46 m and initial gauge pressures of 20 and 75 kPa, respectively. The CFD model was validated using the experimental measurements of the air pocket pressure gauge oscillations, which were conducted at the hydraulic lab at the Instituto Superior Técnico of the University of Lisbon, Portugal. The comparison between the numerical results and experimental measurements was performed.
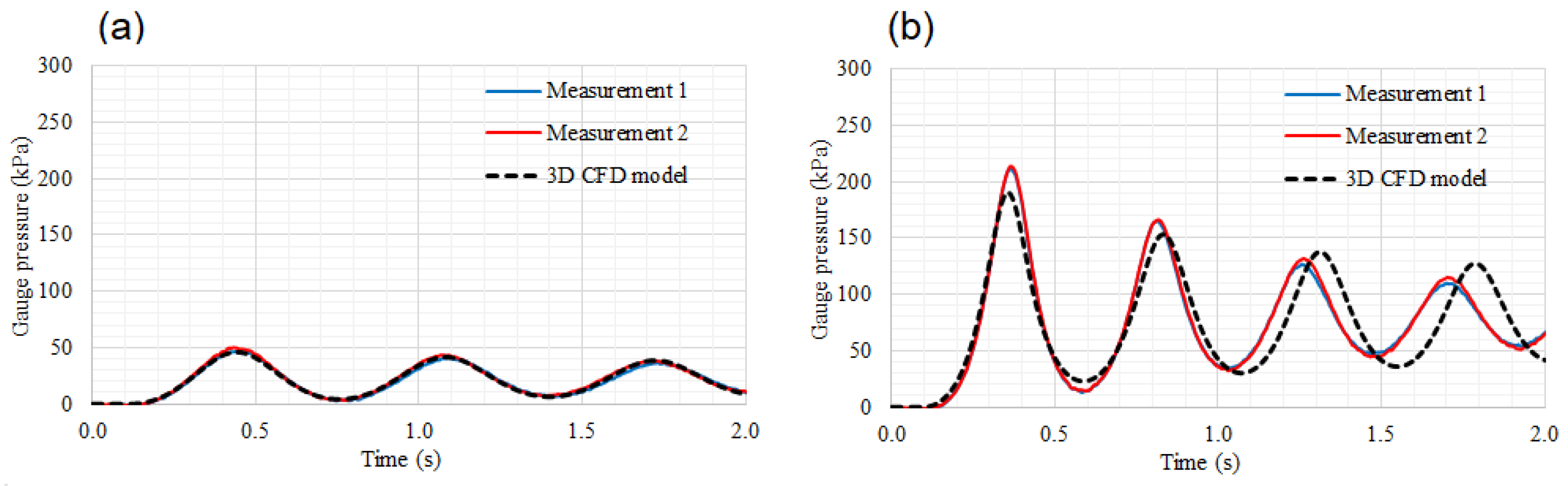
Figure 3a shows the behaviour of the air pocket gauge pressure pulses for Test No. 1, where a maximum value of 46 kPa was reached at
t = 0.44 s. The gauge pressure patterns decreased to a value of 4 kPa (at
t = 0.77 s). The 3D CFD model is capable of representing the air pocket gauge pressure oscillations with regard to the experimental measurements with a good accuracy.
Figure 3b shows the air pocket gauge pressure oscillations for Test No. 2, where a maximum value of 214 kPa was reached, while the CFD model shows a maximum gauge pressure of 190 kPa at
t = 0.37s and
t = 0.38 s, respectively. Subsequently, the minimum pressure gauge of the first oscillation of the CFD model reaches a value of 22 kPa at
t = 0.59 s. The gauge undergoes four oscillations, where the last one has peak maximum and minimum values of 156 kPa and 40 kPa at
t = 1.78 s and
t = 2.0 s, respectively.
4.1. Air–Water Interaction
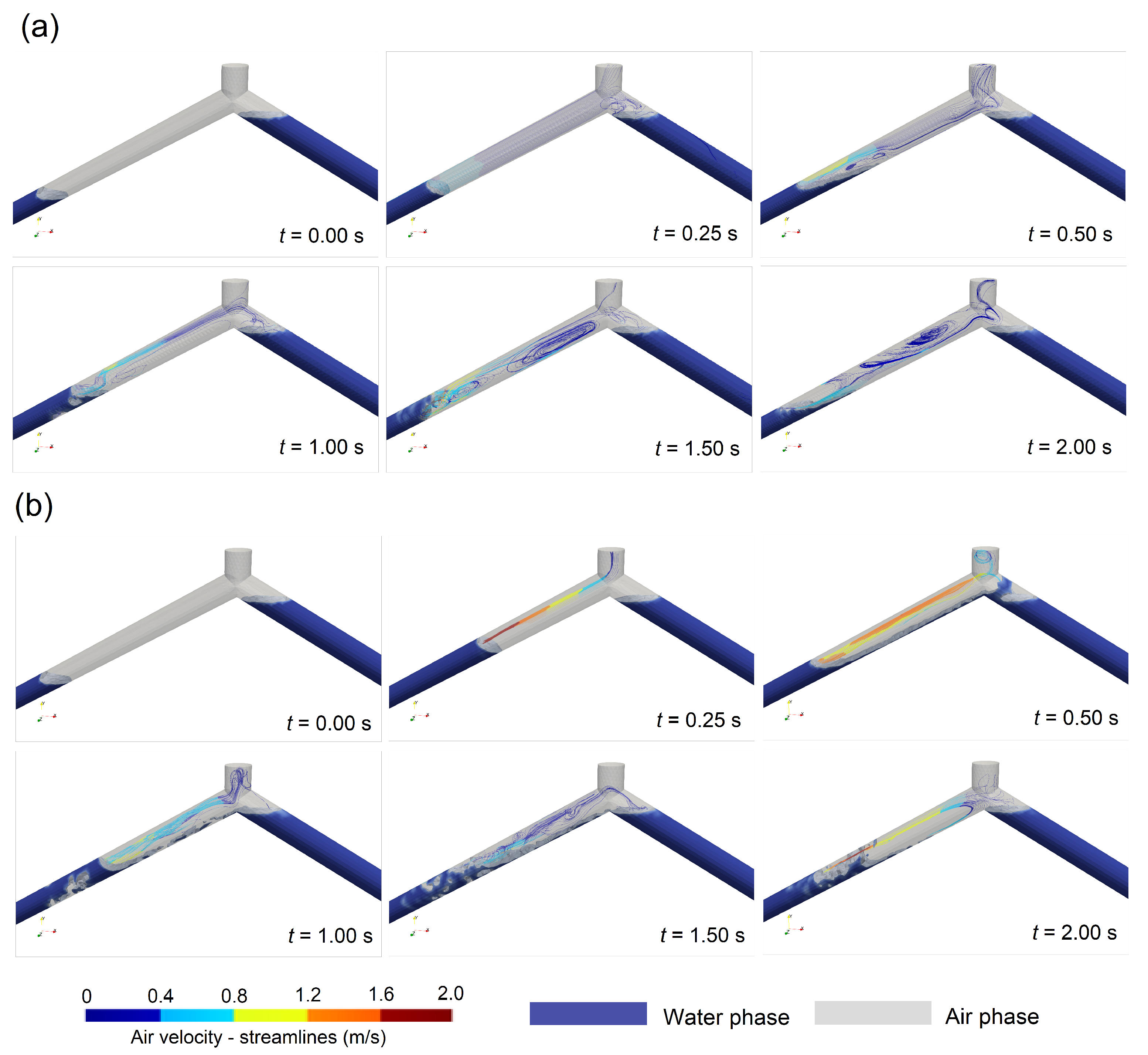
The dynamic behaviour of the air–water interaction was explored using a 3D CFD model. The model shows how the air–water interface is not totally perpendicular to the main direction of the pipe. A complex air–water interface is presented from 1.0 to 2.0 s, which cannot be predicted using 1D models. The air–water interface exhibits a compression process, reaching the peak of the air pocket gauge pressure.
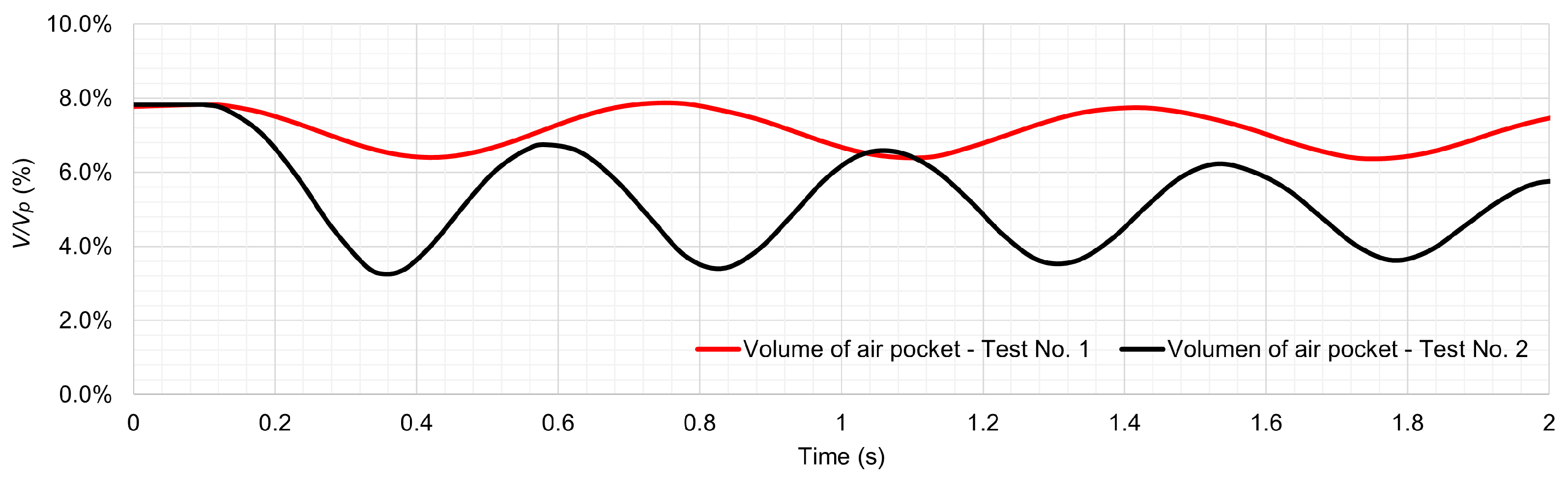
Figure 4 shows the behaviour of the air–water interface for Tests No. 1 and No. 2. In addition, the streamlines and contours data are presented for the gas phase (entrapped air pocket) in order to observe the variation in the air volume in the geometric domain of the pipeline with an irregular profile (see
Figure 5).
The entrapped air pocket shows dynamic behaviour for Test No. 1, considering an inlet gauge pressure supplied by the hydro-pneumatic tank of 20 kPa (see
Figure 4a), where the air phase is compressing, generating a vorticity on the vertices of the left and right branch pipes (
and
) at
t = 0.25 s. The filling event generates an initial compression of the entrapped air pocket from the initial fraction
= 7.8% to 6.2% (see the first peak of the air pocket pressure in
Figure 5) at
t = 0.44 s. Here,
corresponds to the volume of fluid over the total volume of the analysed pipeline. After that, the entrapped air pocket expands because the effect of the accumulated compression energy generates a rupture of the air–water interface above the water column, as shown at
t = 0.50 s (see
Figure 4a), and at the same time, the streamlines of the air velocity show values varying between 0.4 and 1.2 m/s. The entrapped air pocket reached maximum values between 0.4 and 0.8 m/s over the air–water interface at
t = 1.0 s. The water and air are mixed from
t = 1.5 to 2.0 s (see
Figure 4a). The volume of the entrapped air pocket oscillates between 6.2% and 7.8% for the analysed tests (
Figure 5).
Figure 4b shows the air–water interface for the filling event for Test No. 2. There is an increasing trend in the air velocity, which is occurring for the compression of the gas phase. The entrapped air pocket begins to move with values greater than 1.2 m/s, as shown from
t = 0.25 to 0.50 s. Small bubbles are formed because the transient event is rapidly occurring for the initial gauge pressure of 75 kPa. Test No. 2 shows that the air pocket is compressed, where an initial volume of 7.8%
reaches a value of 3.2%
at
t = 0.37 s (see
Figure 5). Afterwards, the air pocket volume gradually expands from 3.2% to 6.4% (at
t = 0.6 s). The second oscillation of the air pocket volume shows peak values of 3.4%
and 6.3%
. During the last pulse, values of 3.6%
and 5.8%
are reached.
4.2. Water Velocity
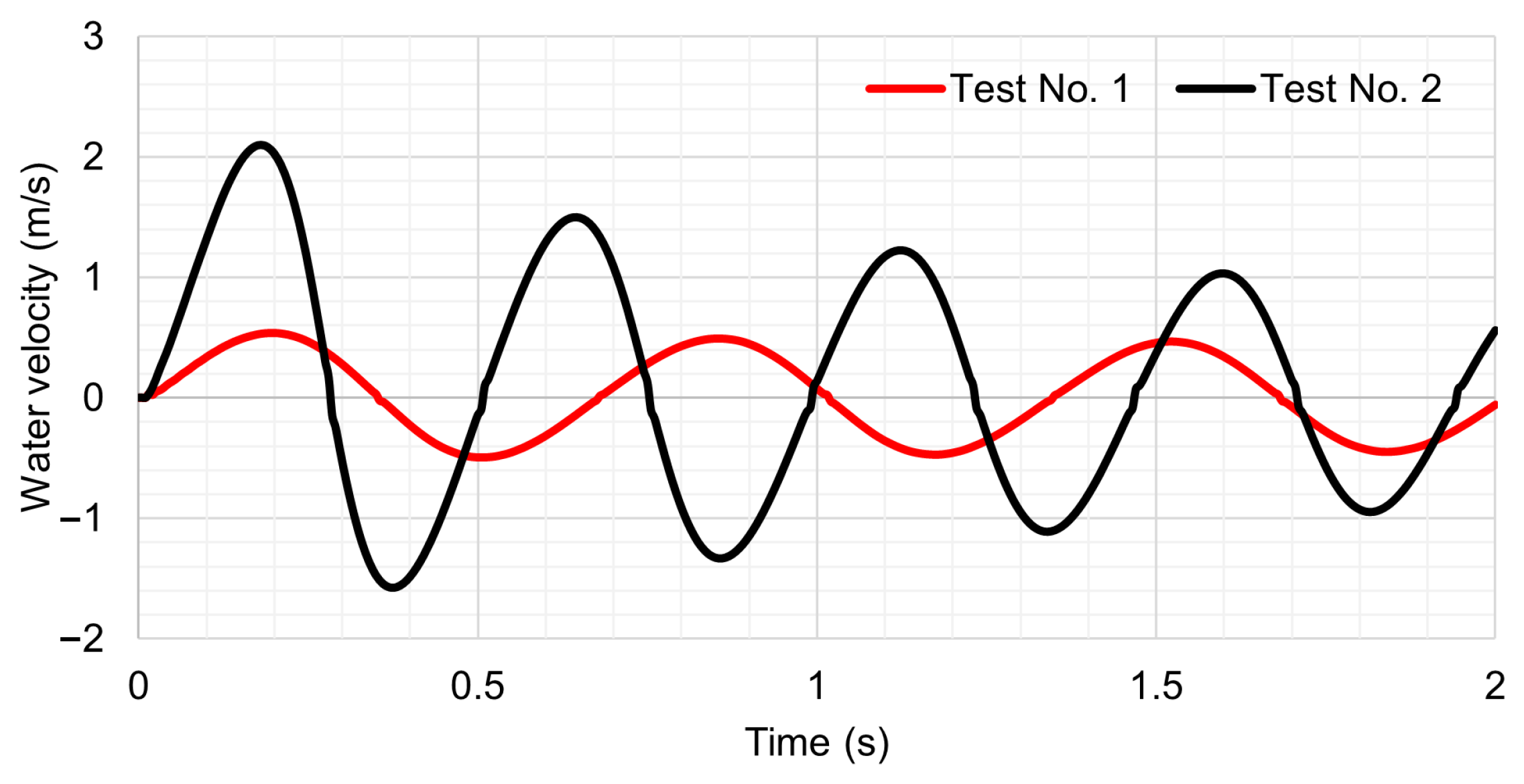
The analysed transient event produces permanent changes in the water velocity patterns. The 3D CFD model provides the numerical information on these variations.
Figure 6 shows the water velocity oscillations for Tests No. 1 and No. 2 along the entire pipeline.
The water column is capable of generating a rapid compression of the entrapped air pocket, where a maximum water velocity of 0.56 m/s (at
t = 0.20 s) is reached for Test No. 1 (see
Figure 6). After that, a decreasing trend is detected, reaching a null value at
t = 0.36 s. Negative water velocities are found in the left pipe branch. For the analysed time periods, there are three peaks and drops of the water flow pulses. The lowest value was −0.5 m/s at
t = 0.5 s.
Figure 7a presents the vector field of the water velocities for time values of 0.1 s, 0.2 s, 0.8 s, and 1.6 s for both tests. Negative water velocities are occurring at
t = 0.4 and 0.6 s. The results of Test No. 2 are more more critical compared to Test No. 1, because a maximum value of 2.1 m/s (at
t = 0.18 s) is attained, and a minimum value of −1.6 m/s is found at
t = 0.37 s. The water velocity shows a similar trend compared to Test No. 1 (see
Figure 7b).
4.3. Air Pocket Behaviour
The rapid changes produced by the filling event rapidly cause a compression of the entrapped air pocket.
Figure 8 shows how the temperature changes are occurring in the entrapped air pocket, where polytropic behaviour is presented.
Figure 8a shows the temperature behaviour of the entrapped air pocket for Test No. 1. It shows a maximum value of 42 °C (at
t = 0.40 s). After that, the temperature pattern decreases to a value of 32 °C at
t = 0.5 s. When the air pocket is being compressed for the second oscillation, the temperature pattern rises up to 40 °C at
t = 1.0 s, where a heterogeneous temperature gradient is shown.
Figure 8b shows the thermodynamic evolution for Test No. 2. A maximum temperature of 120 °C was reached at
t = 0.35 s according to the 3D CFD model. The temperature pulse tends to decrease to a value varying from 40 °C to 60 °C. Finally, the air pocket temperature reaches values lower than 30 °C after
t = 1.0 s. The air temperature changes are strongly included by the initial gauge pressure supplied by the hydro-pneumatic tank. In all the tests, the temperature gradients are non-uniform over the air phase, due to the heat transfer between the fluids, showing that the temperature in the air–water interface zone is not higher than 30 °C.
The analysis of the permissible overheating in water pipelines should be conducted for design purposes using mathematical models that involve the analysis of the air–water interface, because thermoplastic materials (e.g., PVC) should not be exposed to values higher than 60 °C to avoid undesirable deformations.
5. Conclusions
The study of transient flows during different filling events through 3D CFD models allowed to analyse the different behaviours presented that are related to the gauge pressure oscillations, collapse of the air–water interface, water flow velocities, and thermodynamic phenomena in the air phase. This study highlights the good numerical accuracy presented by the 3D CFD model in predicting the gauge pressure oscillations of the air pocket measured in the experimental facility. The pressure damping of the entrapped air pocket leads to the generation of water flow velocity transitions by changing the displacement of the water flow at different time instants over the hydraulic pipeline and mixing level of the air and water, which becomes more intense when the inlet gauge pressure is higher. The main focus of this research was to obtain the relevant information related to the hydraulic phenomena associated with water and the thermodynamic phenomena associated with air, which help the user to identify the magnitude of these phenomena and relate them to transient events that may occur in hydraulic installations of different scales. From the hydraulic–thermodynamic phenomena analysed, the following statements can be defined:
The entrapped air pocket exhibits constant volume changes over time. The water column compresses the air pocket to a limit state and then it tends to expand to release the compression energy that was accumulated during the filling event. This compression–expansion phenomenon of the air pocket is cyclic over time. The dynamic behaviour of the trapped air during the volume changes can be visualised in detail through streamlines and velocity contours, where such events manifest their volume reduction and expansion through vortices located at the air–water interface zones that can physically reach maximum velocities of 1.2 m/s (in Test No. 2).
Transient flows can result in backflows towards the pumping source, which can lead to a loss of the hydraulic efficiency during filling events. During the first few seconds, the velocity transitions are abrupt, and then they gradually dissipate over time due to the damping pressure of the entrapped air pocket. These backflows are more critical in scenarios with higher inlet gauge pressures. In addition, the CFD model predicts in detail the vector field of the water flow by showing the changes in the water trajectory at different time instants.
Temperature changes are inevitable during filling processes, considering that the compression of the trapped air causes a change in the thermodynamic conditions of the air phase. In such phenomena, the trapped air pocket undergoes adiabatic behaviour, which has been reproduced in previous research on filling processes. The 3D CFD model in the analysed tests shows a non-uniform temperature distribution, showing that away from the air–water interface the highest temperatures occur (up to 120 °C in Test No. 2), whereas in the air pocket near the air–water interface, temperatures between 20 °C and 30 °C occur.
The development of the three-dimensional model allowed for representing an integral behaviour of the hydraulic–thermodynamic phenomena from a physical approach. The application of an unstructured mesh with the number of cells defined in this research favoured the convergence of the numerical solution and an adequate simulation with a Courant number less than 1.0. Moreover, the unstructured mesh favoured the detailed visualisation of the contours of the different variables analysed. The application of 3D CFD models to simulate hydraulic and thermodynamic phenomena in pipes with entrapped air represents a high computational cost considering the rapidity of the hydraulic event; however, it guarantees a more detailed and complete level of information compared to other computational models.
It is important to evaluate the selection of the pipe class in large-scale water installations because the compression of entrapped air pockets can produce absolute pressure values higher than those values reached when considering a monophasic fluid (water). The current regulations around the world do not consider a complete model of a two-phase flow when designing these systems. In this sense, the utilisation of a 3D CFD can be used to compute the extreme values of the air pocket oscillations to increase the reliability during the filling operation.
For future research, the three-dimensional behaviour of hydraulic events with air expulsion orifices, which has not been studied in detail in the literature using 3D CFD models, should be studied. Additionally, it is important to test the simulation of large-scale hydraulic scenarios, considering the presence and absence of air expulsion orifices.
Author Contributions
Conceptualisation, D.A.P.-V. and O.E.C.-H.; methodology, D.A.P.-V. and H.G.E.-R.; software, D.A.P.-V. and H.G.E.-R.; validation, O.E.C.-H. and D.A.P.-V.; formal analysis, D.A.P.-V.; investigation, D.A.P.-V. and O.E.C.-H.; resources, H.M.R. and O.E.C.-H.; writing—original draft preparation, D.A.P.-V.; writing—review and editing, D.A.P.-V. and O.E.C.-H.; visualisation, H.M.R. and V.S.F.-M.; supervision, H.M.R. and V.S.F.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research project was funded through Grant No. INV03CI2214 of the Universidad Tecnológica de Bolívar.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Dirección de Investigación, Innovación y Emprendimiento of the Universidad Tecnológica de Bolívar for funding this research project through Grant No. INV03CI2214.
Conflicts of Interest
The authors declare no conflict of interest.
Notation
The following notations are used in this manuscript:
| thermal conductivity (W/(m·K)) |
| specific heat (J/(kg K)) |
| diffusion term for k (m/s) |
| diffusion term for (m/s) |
| blending function (–) |
| surface tension (kg m/s) |
| gravitational acceleration vector (m/s) |
| G | turbulent kinetic energy generation (m/s) |
| k | turbulent kinetic energy (m/s) |
| initial air pocket (m) |
| p | static pressure (N/m) |
| initial absolute pressure (N/m) |
| heat flux vector (W/m) |
| R | universal gas constant (J/(K·mol)) |
| T | temperature (°C) |
| t | time (s) |
| velocity vector (m/s) |
| velocity field (m/s) |
| distance function (–) |
| phase of fraction (water) (–) |
| dynamic viscosity (Ns/m) |
| turbulent kinematic viscosity (m/s) |
| density (kg/m) |
| dissipation frequency (1/s) |
| Subscripts | |
| a | refers to air (e.g., air density) |
| w | refers to water (e.g., water density) |
| m | refers to the mixture between air and water (e.g., mixed density) |
| t | refers to a turbulent condition (e.g., turbulent dynamic viscosity) |
References
- Fuertes, V. Hydraulic Transients with Entrapped Air Pockets. Ph.D. Thesis, Department of Hydraulic Engineering, Polytechnic University of Valencia, Editorial Universitat Politècnica de València, Valencia, Spain, 2001. [Google Scholar]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Mora-Meliá, D.; Iglesias-Rey, P.L. Hydraulic modeling during filling and emptying processes in pressurized pipelines: A literature review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Karney, B. Investigation of hydraulic transients of two entrapped air pockets in a water pipeline. J. Hydraul. Eng. 2013, 139, 949–959. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Karney, B.; Liu, D.; Wang, P.; Guo, S. Dynamic behavior of entrapped air pocket in a water filling pipeline. J. Hydraul. Eng. 2018, 144, 04018045. [Google Scholar] [CrossRef]
- Vasconcelos, J.G. Dynamic Approach to the Description of Flow Regime Transition in Stormwater Systems. Ph.D. Thesis, University of Michigan Library, Ann Arbor, MI, USA, 2005. [Google Scholar]
- Vasconcelos, J.G.; Wright, S.J. Experimental investigation of surges in a stormwater storage tunnel. J. Hydraul. Eng. 2005, 131, 853–861. [Google Scholar] [CrossRef] [Green Version]
- Chosie, C.D.; Hatcher, T.M.; Vasconcelos, J.G. Experimental and numerical investigation on the motion of discrete air pockets in pressurized water flows. J. Hydraul. Eng. 2014, 140, 04014038. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.; Steffler, P. Transient flow in a rapidly filling horizontal pipe containing trapped air. J. Hydraul. Eng. 2002, 128, 625–634. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.; Steffler, P. Analysis of effects of air pocket on hydraulic failure of urban drainage infrastructure. Can. J. Civ. Eng. 2004, 31, 86–94. [Google Scholar] [CrossRef]
- De Martino, G.; Fontana, N.; Giugni, M. Transient flow caused by air expulsion through an orifice. J. Hydraul. Eng. 2008, 134, 1395–1399. [Google Scholar] [CrossRef] [Green Version]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical modelling of pipelines with air pockets and air valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Coronado-Hernández, Ó.E.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of a commercial air valve on the rapid filling of a single pipeline: A numerical and experimental analysis. Water 2019, 11, 1814. [Google Scholar] [CrossRef] [Green Version]
- Martin, C.; Lee, N.H. Rapid expulsion of entrapped air through an orifice. In BHR Group Conference Series Publication; St. Edmunds, B., Ed.; Professional Engineering Publishing: London, UK, 1998; Volume 39, pp. 125–132. [Google Scholar]
- Zhou, L.; Pan, T.; Wang, H.; Liu, D.; Wang, P. Rapid air expulsion through an orifice in a vertical water pipe. J. Hydraul. Res. 2019, 57, 307–317. [Google Scholar] [CrossRef]
- Romero, G.; Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Ponz-Carcelén, R.; Biel-Sanchis, F. Transient phenomena generated in emptying operations in large-scale hydraulic pipelines. Water 2020, 12, 2313. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.Y.; Ou, C.Q. Simulation of flow transients in a water filling pipe containing entrapped air pocket with VOF model. Eng. Appl. Comput. Fluid Mech. 2011, 5, 127–140. [Google Scholar] [CrossRef] [Green Version]
- Aguirre-Mendoza, A.M.; Oyuela, S.; Espinoza-Román, H.G.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Paternina-Verona, D.A. 2D CFD Modeling of Rapid Water Filling with Air Valves Using OpenFOAM. Water 2021, 13, 3104. [Google Scholar] [CrossRef]
- Besharat, M.; Tarinejad, R.; Aalami, M.T.; Ramos, H.M. Study of a compressed air vessel for controlling the pressure surge in water networks: CFD and experimental analysis. Water Resour. Manag. 2016, 30, 2687–2702. [Google Scholar] [CrossRef]
- Martins, N.M.; Delgado, J.N.; Ramos, H.M.; Covas, D.I. Maximum transient pressures in a rapidly filling pipeline with entrapped air using a CFD model. J. Hydraul. Res. 2017, 55, 506–519. [Google Scholar] [CrossRef]
- Fang, H.; Zhou, L.; Cao, Y.; Cai, F.; Liu, D. 3D CFD simulations of air-water interaction in T-junction pipes of urban stormwater drainage system. Urban Water J. 2021, 19, 74–86. [Google Scholar] [CrossRef]
- Aguirre-Mendoza, A.M.; Paternina-Verona, D.A.; Oyuela, S.; Coronado-Hernández, O.E.; Besharat, M.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Ramos, H.M. Effects of Orifice Sizes for Uncontrolled Filling Processes in Water Pipelines. Water 2022, 14, 888. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Liu, D.; Karney, B.; Wang, P.; Xia, L.; Ma, J.; Xu, C. CFD approach for column separation in water pipelines. J. Hydraul. Eng. 2016, 142, 04016036. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Duan, X.; Zhu, J.; Li, X.; Tang, X.; Gao, H. Investigations of hydraulic transient flows in pressurized pipeline based on 1D traditional and 3D weakly compressible models. J. Hydroinform. 2021, 23, 231–248. [Google Scholar] [CrossRef]
- Paternina-Verona, D.A.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S. Numerical modelling for analysing drainage in irregular profile pipes using OpenFOAM. Urban Water J. 2022, 19, 569–578. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Backflow air and pressure analysis in emptying a pipeline containing an entrapped air pocket. Urban Water J. 2018, 15, 769–779. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Computational fluid dynamics for sub-atmospheric pressure analysis in pipe drainage. J. Hydraul. Res. 2019, 58, 553–565. [Google Scholar] [CrossRef]
- Hurtado-Misal, A.D.; Hernández-Sanjuan, D.; Coronado-Hernández, O.E.; Espinoza-Román, H.; Fuertes-Miquel, V.S. Analysis of Sub-Atmospheric Pressures during Emptying of an Irregular Pipeline without an Air Valve Using a 2D CFD Model. Water 2021, 13, 2526. [Google Scholar] [CrossRef]
- Paternina-Verona, D.A.; Coronado-Hernández, O.E.; Espinoza-Román, H.G.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Three-Dimensional Analysis of Air-Admission Orifices in Pipelines during Hydraulic Drainage Events. Sustainability 2022, 14, 14600. [Google Scholar] [CrossRef]
- Greenshields, C.; Weller, H. Notes on Computational Fluid Dynamics: General Principles; CFD Direct Ltd.: Reading, UK, 2022. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Hirt, C.; García, M.H.; Matthews, B.; Fletcher, C.; Partridge, A.; Vasquez, S. Computations of curved free surface water flow on spiral concentrators. J. Hydraul. Eng. 2001, 127, 629–631. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).