Abnormal Waves Observation and Analysis of the Mechanism in the Pearl River Estuary, South China
Abstract
1. Introduction
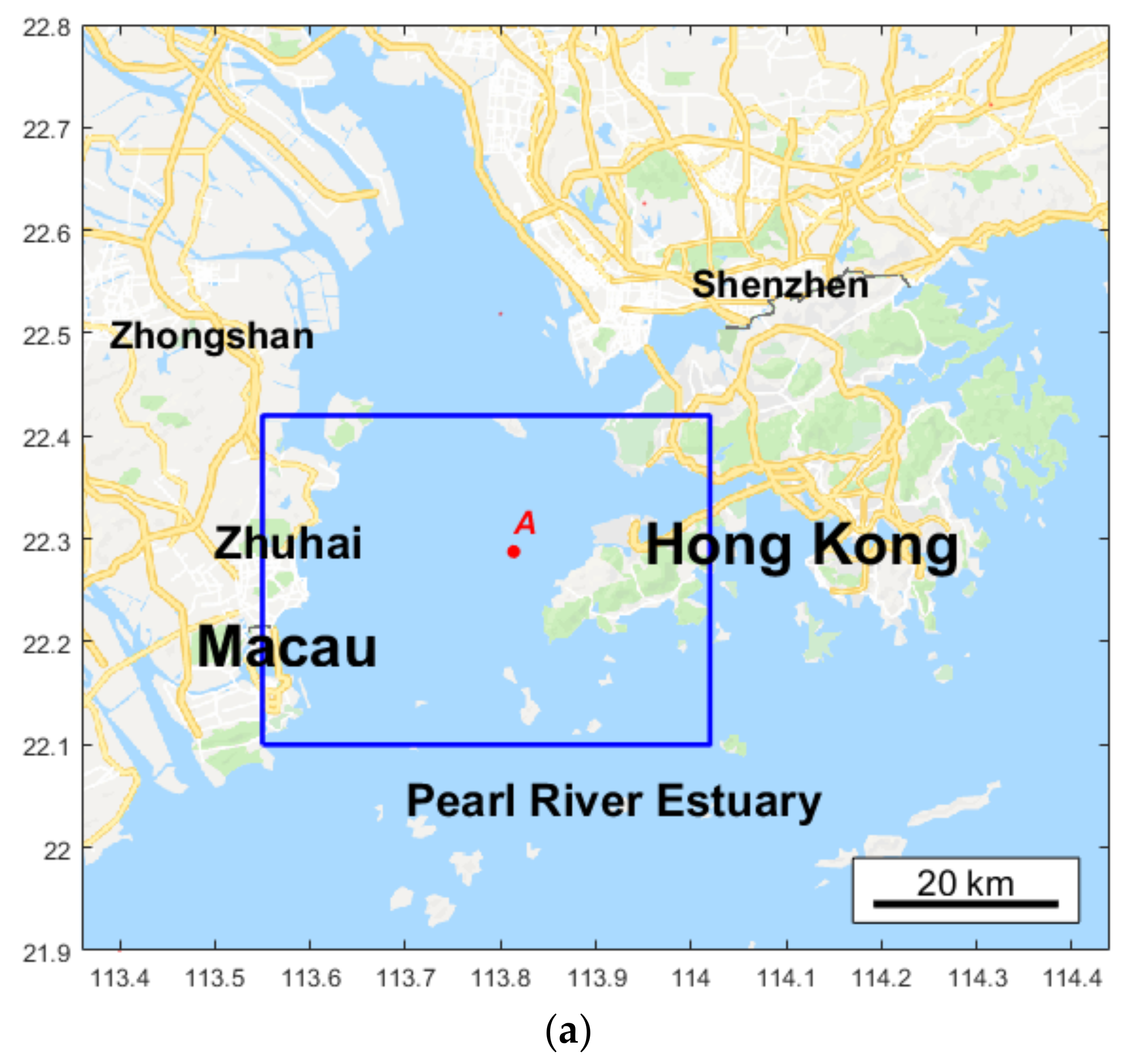
2. Instrument and Methods
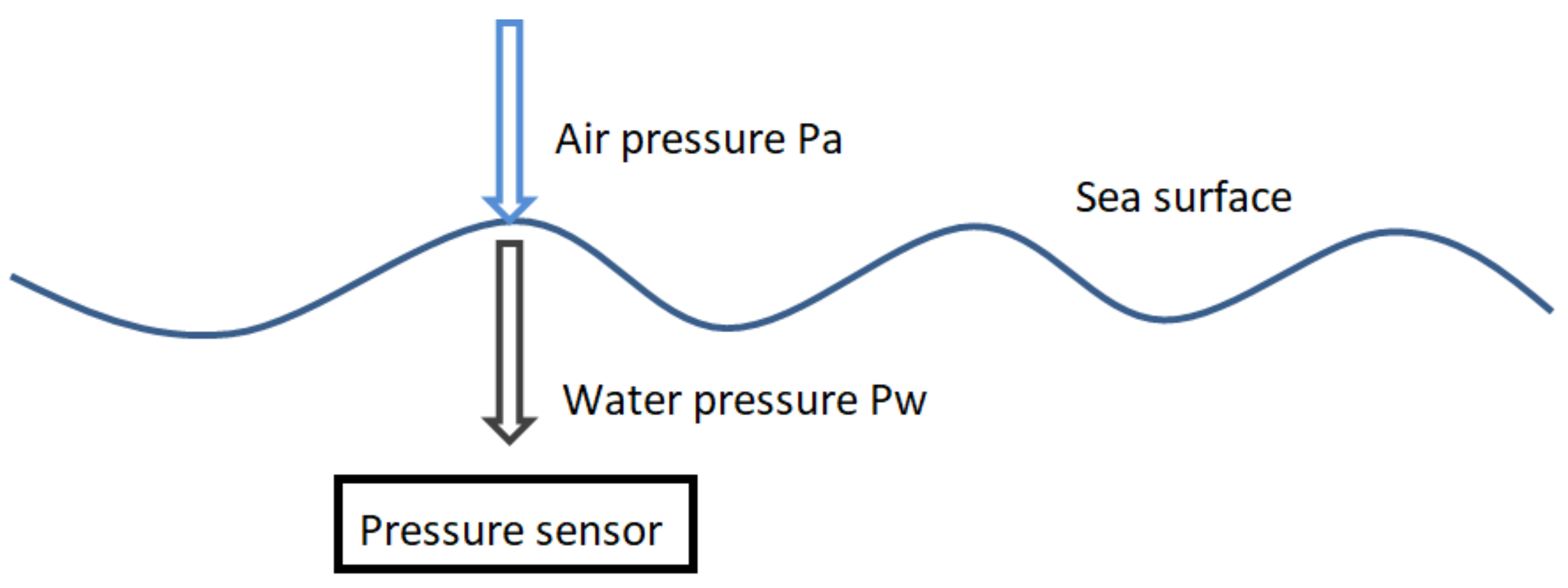
2.1. Principle of the Instrument
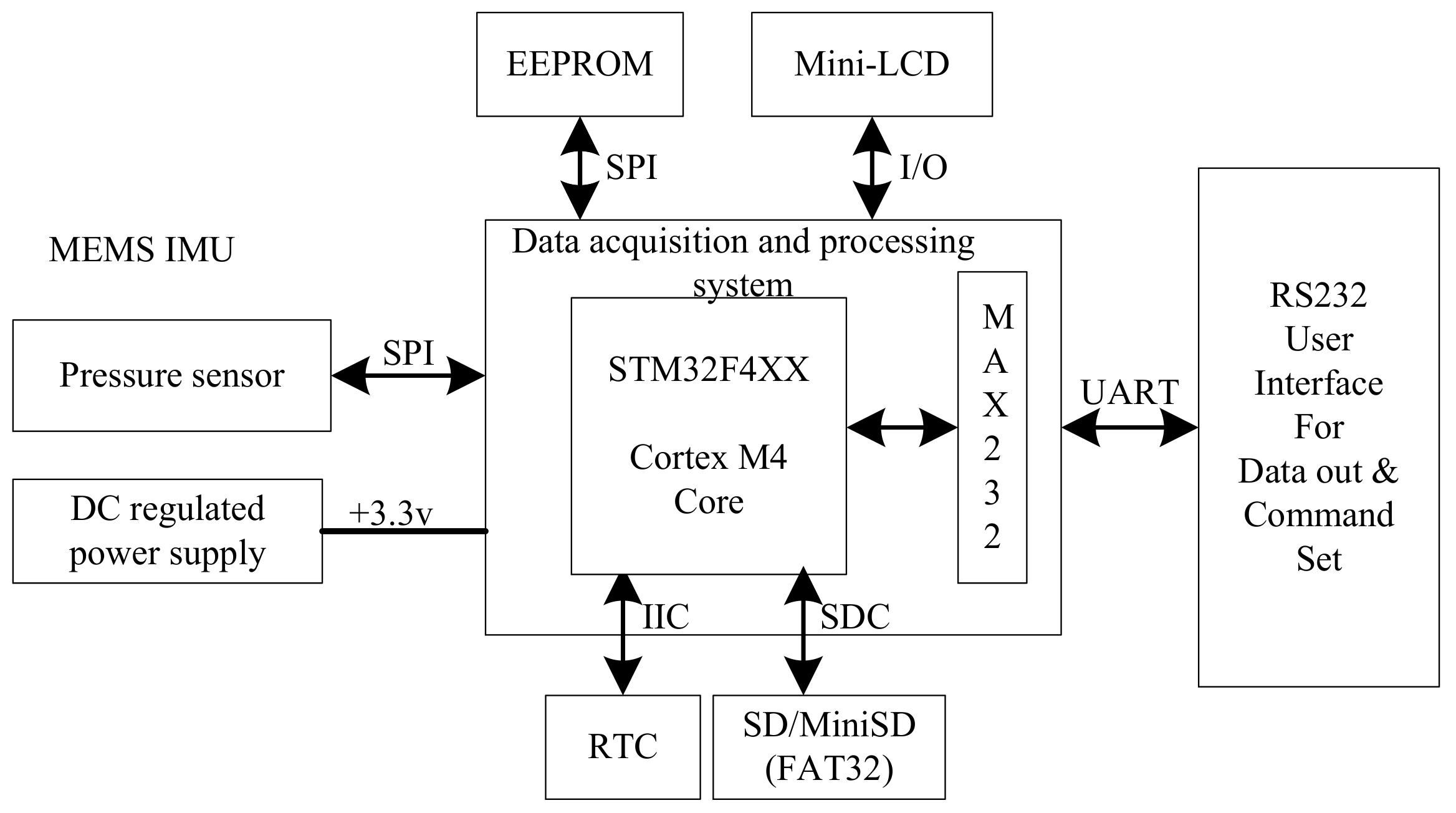
2.2. Wave Instrument Composition
2.3. Data and Wave Parameters
3. Results
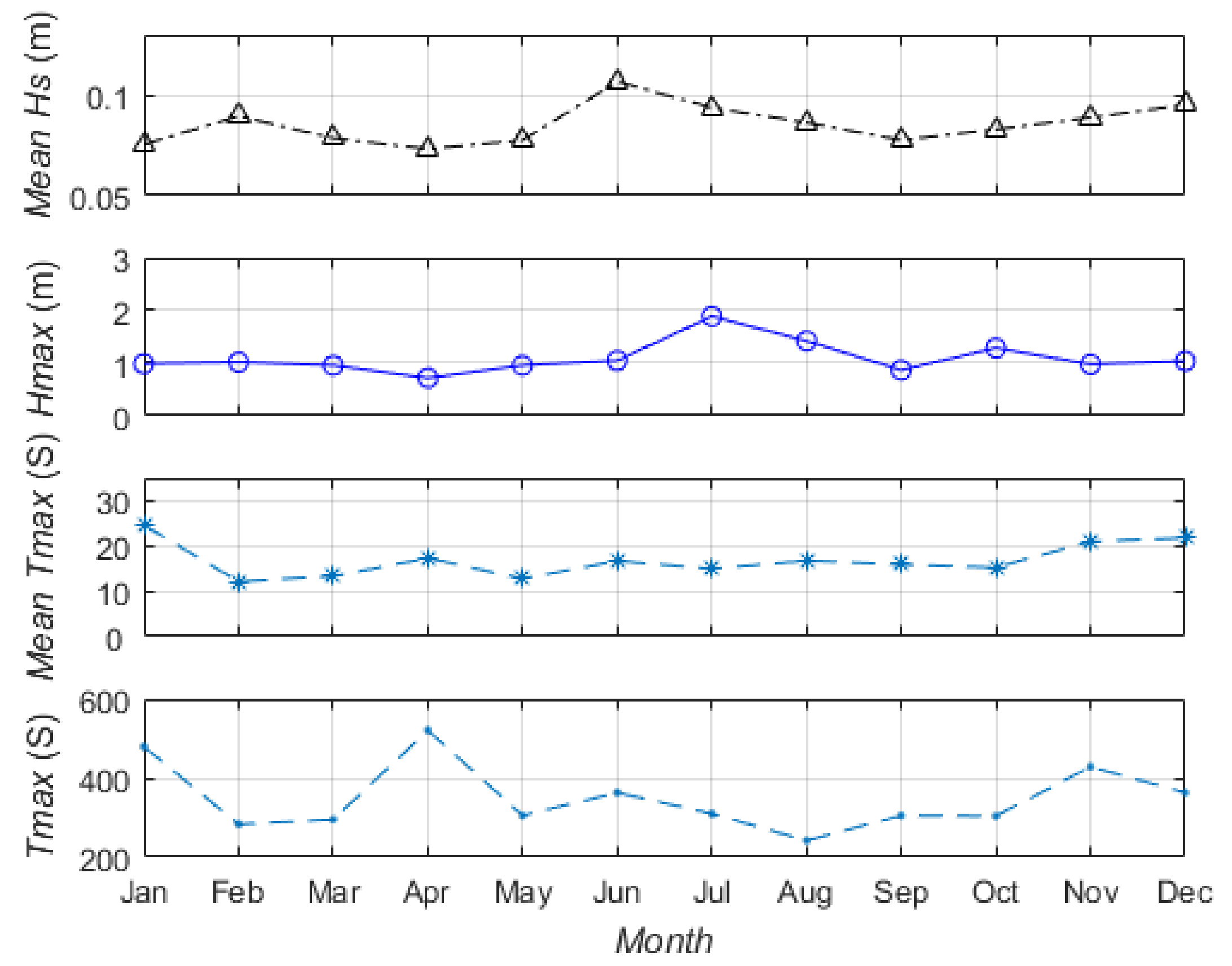
3.1. Wind Wave Parameters Statistics
3.2. Ship Wakes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gill, J.A.; Norris, K.; Potts, P.M.; Gunnarsson, T.G.; Atkinson, P.W.; Sutherland, W.J. The buffer effect and large-scale population regulation in migratory birds. Nature 2001, 412, 436–438. [Google Scholar] [CrossRef] [PubMed]
- Gemmrich, J.; Thomson, J. Observations of the shape and group dynamics of rogue waves. Geophys. Res. Lett. 2017, 44, 1823–1830. [Google Scholar] [CrossRef]
- Gillanders, B.; Able, K.; Brown, J.; Eggleston, D.; Sheridan, P. Evidence of connectivity between juvenile and adult habitats for mobile marine fauna: An important component of nurseries. Mar. Ecol. Prog. Ser. 2003, 247, 281–295. [Google Scholar] [CrossRef]
- Ge, C.; Zhang, W.; Dong, C.; Wang, F.; Feng, H.; Qu, J.; Yu, L. Tracing sediment erosion in the Yangtze River subaqueous delta using magnetic methods. J. Geophys. Res. Earth Surf. 2017, 122, 2064–2078. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Li, G.; Oguchi, T.; He, H.; Shen, H. Discrimination in magnetic properties of different-sized sediments from the Changjiang and Huanghe Estuaries of China and its implication for provenance of sediment on the shelf. Mar. Geol. 2009, 260, 121–129. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; Wang, Z.B.; van Braeckel, A.; van Holland, G.; Kösters, F. Man-induced regime shifts in small estuaries—II: A comparison of rivers. Ocean Dyn. 2013, 63, 1293–1306. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, Y.P.; Ni, W.; Gao, J.; Li, M.; Yang, L.; Gong, X.; Gao, S. Effects of intertidal reclamation on tides and potential environmental risks: A numerical study for the southern Yellow Sea. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Hong, B.; Liu, Z.; Shen, J.; Wu, H.; Gong, W.; Xu, H.; Wang, D. Potential physical impacts of sea-level rise on the Pearl River Estuary. China J. Mar. Syst. 2020, 201, 103245. [Google Scholar] [CrossRef]
- Chu, N.; Yang, Q.; Liu, F.; Luo, X.; Cai, H.; Yuan, L.; Huang, J.; Li, J. Distribution of magnetic properties of surface sediment and its implications on sediment provenance and transport in Pearl River Estuary. Mar. Geol. 2020, 424, 106162. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Y. Monitoring coastline variations in the Pearl River Estuary from 1978 to 2018 by integrating Canny edge detection and Otsu methods using long time series Landsat dataset. CATENA 2022, 209, 105840. [Google Scholar] [CrossRef]
- Wu, Z.; Milliman, J.D.; Zhao, D.; Cao, Z.; Zhou, J.; Zhou, C. Geomorphologic changes in the lower. Pearl River Delta 1850–2015, largely due to human activity. Geomorphology 2018, 314, 42–54. [Google Scholar] [CrossRef]
- Kalantzi, G.D.; Gommenginger, C.; Srokosz, M. Assessing the performance of the dissipation parameterizations in WAVEWATCH III using collocated altimetry data. J. Phys. Oceanogr. 2009, 39, 2800–2819. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yang, J.; Bao, W.; Wu, G.; Ren, Q. An evaluation of input/dissipation terms in wavewatch iii using in situ and satellite significant wave height data in the South China Sea. Acta Oceanol. Sin. 2017, 36, 20–25. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yang, J. The validation of HY-2 altimeter measurements of a significant wave height based on buoy data. Acta Oceanol. Sin. 2013, 32, 87–90. [Google Scholar] [CrossRef]
- Young, I.R. Global ocean wave statistics obtained from satellite observations. Appl. Ocean Res. 1994, 16, 235–248. [Google Scholar] [CrossRef]
- Young, I.R. Seasonal variability of the global ocean wind and wave climate. Int. J. Climatol. 1999, 19, 931–950. [Google Scholar] [CrossRef]
- Reikard, G.; Pinson, P.; Bidlot, J.R. Forecasting ocean wave energy: The ECMWF wave model and time series methods. Ocean Eng. 2011, 38, 1089–1099. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ecmwf reanalysis interim and the ncep climate forecast system reanalysis. Ocean Modell. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Forlini, C.; Qayyum, R.; Malej, M.; Lam, M.; Sheremet, A. On the problem of modeling the boat wake climate: The florida intracoastal waterway. J. Geophys. Res. Ocean. 2020, 126, e2020JC016676. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Zang, J. Investigation on the effects of bragg reflection on harbor oscillations. Coast. Eng. 2021, 9, 103977. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Guedes Soares, C.G. Modelling distributions of significant wave height. Coast. Eng. 2000, 40, 361–374. [Google Scholar] [CrossRef]
- Forristall, G.Z. On the statistical distribution of wave heights in a storm. J. Geophys. Res. 1978, 83, 2353–2358. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. On the joint distribution of the periods and amplitudes sea waves. J. Geophys. Res. 1975, 80, 2688–2694. [Google Scholar] [CrossRef]
- Rapizo, H.; Babanin, A.V.; Schulz, E.; Hemer, M.A.; Durrant, T.H. Observation of wind-waves from a moored buoy in the Southern Ocean. Ocean Dyn. 2015, 65, 1275–1288. [Google Scholar] [CrossRef]
- Hofmann, H.; Lorke, A.; Peeters, F. The relative importance of wind and ship waves in the littoral zone of a large lake. Limnol. Oceanogr. 2008, 53, 368–380. [Google Scholar] [CrossRef]
- Didenkulova, I.; Parnell, K.E.; Soomere, T.; Pelinovsky, E.; Kurrenoy, D. Shoaling and run up of long waves induced by high-speed ferries in Tallinn Bay. J. Coast. Res. 2009, 56, 491–495. [Google Scholar]
- Gelinas, M.; Bokuniewicz, H.; Rapaglia, J.; Lwiza, K.M.M. Sediment resuspension by ship wakes in the Venice Lagoon. J. Coast. Res. 2013, 286, 8–17. [Google Scholar] [CrossRef]
- Gharbi, S.; Valkov, G.; Hamdi, S.; Nistor, I. Numerical and field study of ship-induced waves along the St. Lawrence waterway, Canada. Nat. Hazards 2010, 54, 605–621. [Google Scholar] [CrossRef]
- Göransson, G.; Larson, M.; Althage, J. Ship-generated waves and induced turbidity in the Göta Älv River in Sweden. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 04014004. [Google Scholar] [CrossRef]
- Soomere, T.; Parnell, K.E.; Didenkulova, I. Water transport in wake waves from high-speed vessels. J. Mar. Syst. 2011, 88, 74–81. [Google Scholar] [CrossRef]
- Torsvik, T.; Didenkulova, I.; Soomere, T.; Parnell, K.E. Variability in spatial patterns of long nonlinear waves from fast ferries in Tallinn Bay. Nonlinear Process. Geo-Phys. 2009, 16, 351–363. [Google Scholar] [CrossRef]
- Parnell, K.E.; Soomere, T.; Zaggia, L.; Rodin, A.; Lorenzetti, G.; Rapaglia, J.; Scarpa, G.M. Ship-induced solitary Riemann waves of depression in Venice Lagoon. Phys. Lett. A 2015, 379, 555–559. [Google Scholar] [CrossRef]
- Rapaglia, J.; Zaggia, L.; Ricklefs, K.; Gelinas, M.; Bokuniewicz, H. Characteristics of ships’ depression waves and associated sediment resuspension in Venice lagoon, Italy. J. Mar. Syst. 2011, 85, 45–56. [Google Scholar] [CrossRef]
- Long, X.M.; Wang, S.A.; Cai, S.Q.; Chen, J.C. SZS3-1 Type Wave-Tide Gauge. J. Trop. Oceanogr. 2005, 24, 81–85. (In Chinese) [Google Scholar] [CrossRef]
- Brodtkorb, P.A.; Johannesson, P.; Lindgren, G.; Rychlik, I.; Rydén, J.; Sjö, E. Wafo—A MATLAB toolbox for analysis of random waves and loads. In Proceedings of the 10th International Offshore and Polar Engineering Conference, Seattle, WA, USA, 28 May–2 June 2000; Volume III, pp. 343–350. [Google Scholar]
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic rogue waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. On the joint distribution wave periods and amplitudes in a random wave field. Proc. R. Soc. Lond. A 1983, 389, 24–258. [Google Scholar]
- Torsvik, T.; Soomere, T.; Didenkulova, I.; Sheremet, A. Identification of ship wake structures by a time–frequency method. J. Fluid Mech. 2015, 765, 229–251. [Google Scholar] [CrossRef]
- Grue, J. Mini-Tsunami made by ship moving across a depth change. J. Waterw. Port. Coast. Ocean Eng. 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Grue, J. Ship generated mini-tsunamis. J. Fluid Mech. 2017, 816, 142–166. [Google Scholar] [CrossRef]
- Gourlay, T.P. The supercritical bore produced by a high-speed ship in a channel. J. Fluid Mech. 2001, 434, 399–409. [Google Scholar] [CrossRef]
- Wang, P.; Cheng, J. Mega-Ship-Generated Tsunami: A Field Observation in Tampa Bay, Florida. J. Mar. Sci. Eng. 2021, 9, 437. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, C.; Liu, J.; Xing Huanlin Zhou, F.; Wang, D.; Long, X.; Wang Shengan Wang, W.; Shi, F. Identifying ship-wakes in a shallow estuary using machine learning. Ocean Eng. 2022, 246, 110456. [Google Scholar] [CrossRef]



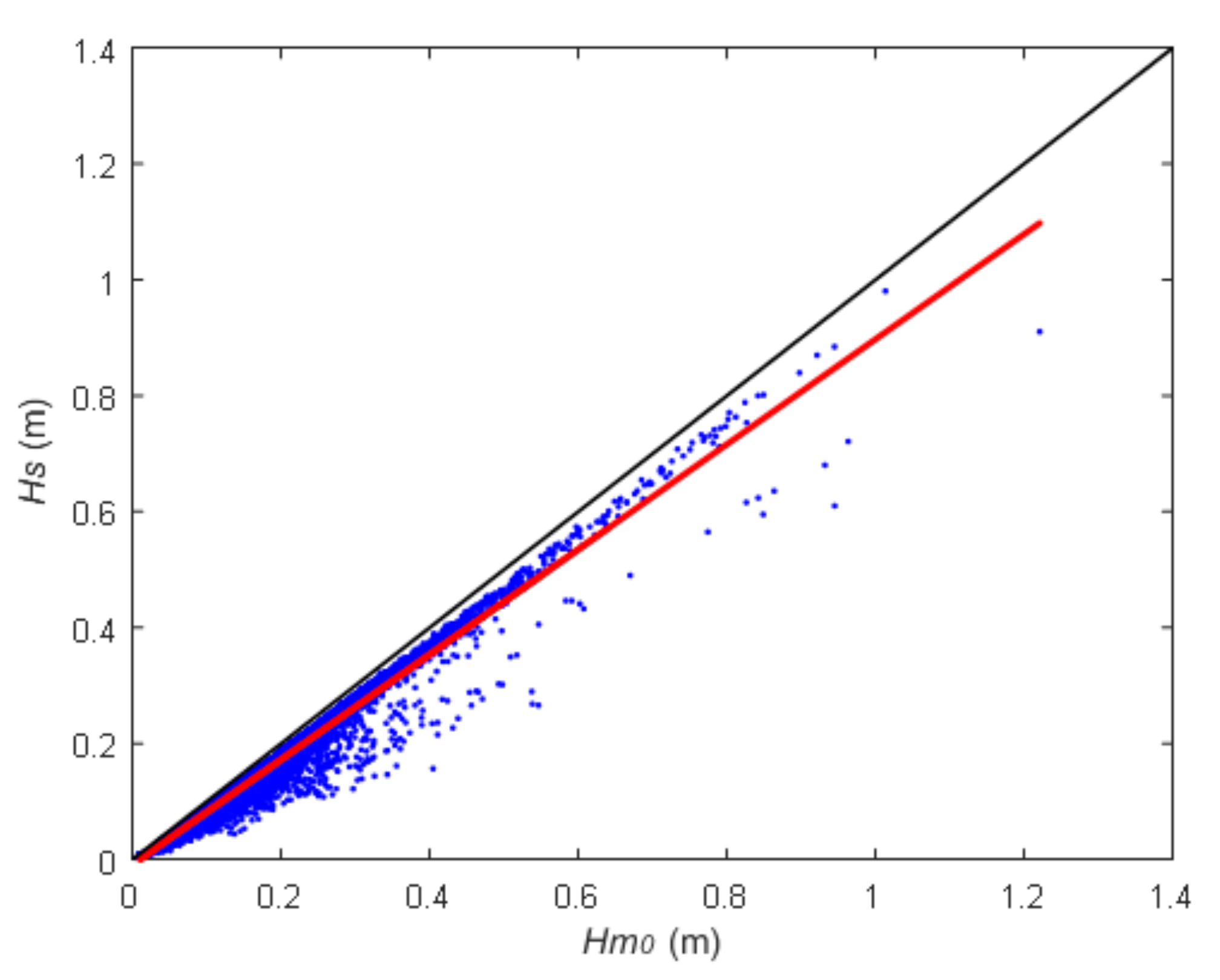
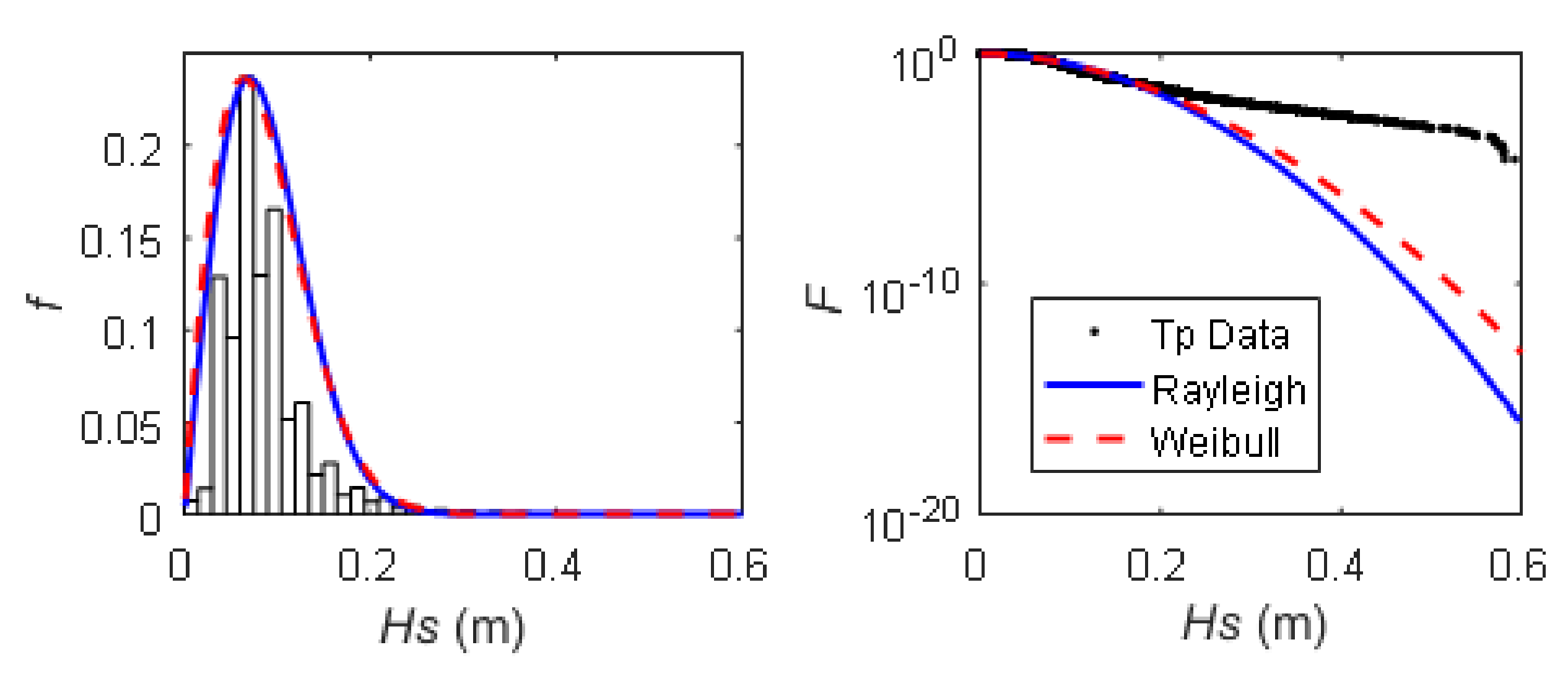


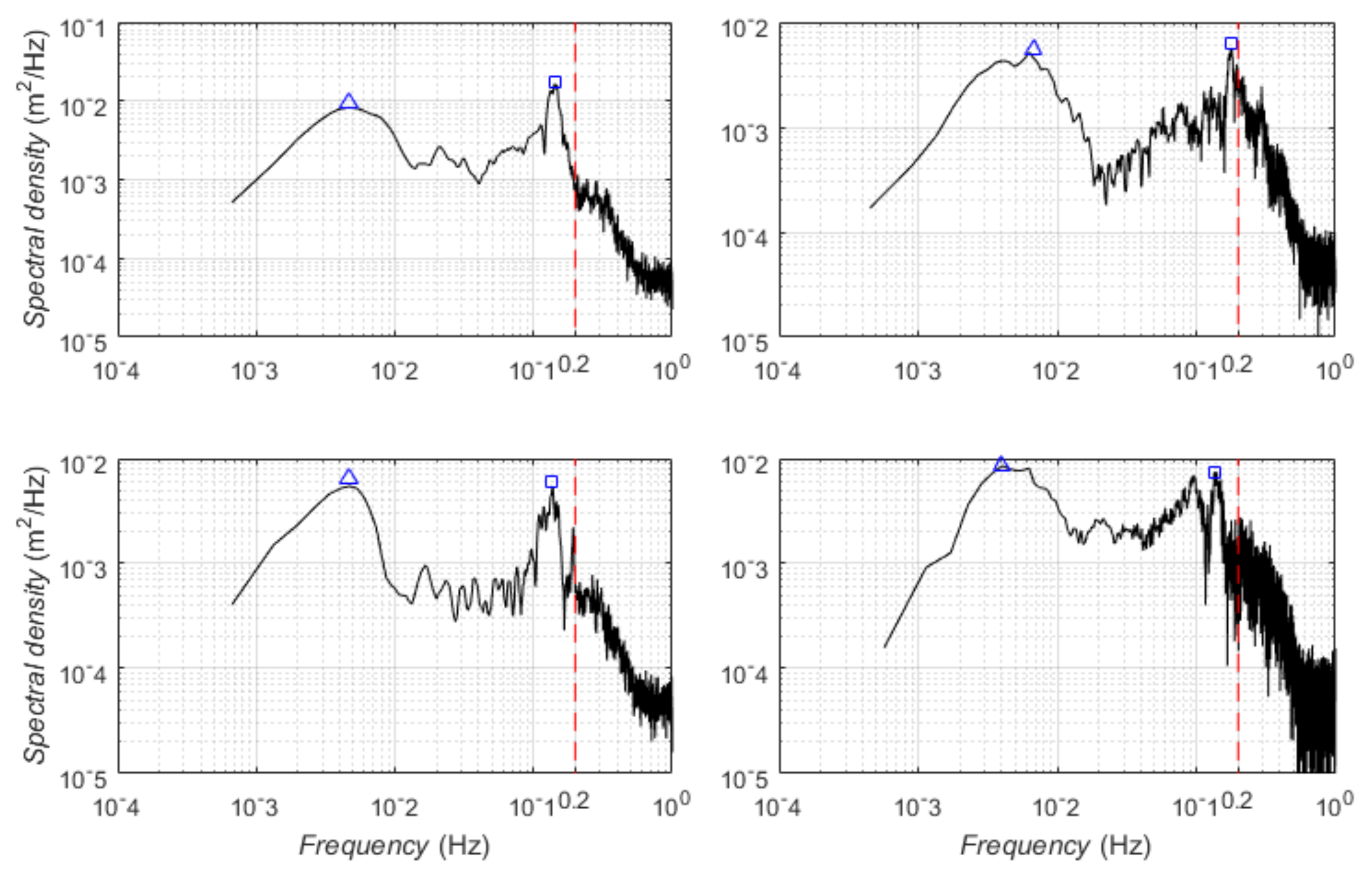
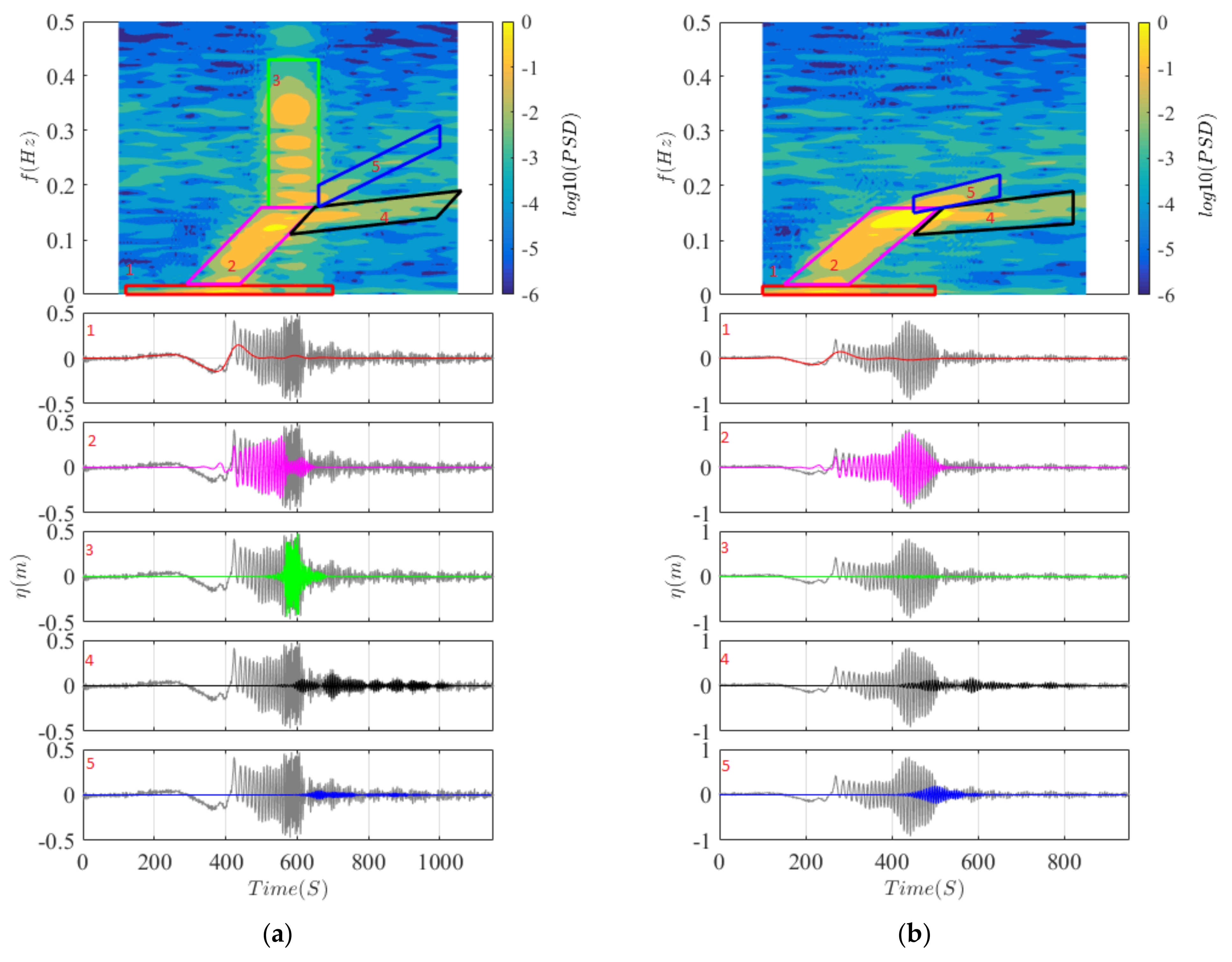
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Luo, Y.; Zhou, F.; Qiu, C.; Wang, D.; Zhang, Z. Abnormal Waves Observation and Analysis of the Mechanism in the Pearl River Estuary, South China. Water 2023, 15, 1001. https://doi.org/10.3390/w15051001
Shi H, Luo Y, Zhou F, Qiu C, Wang D, Zhang Z. Abnormal Waves Observation and Analysis of the Mechanism in the Pearl River Estuary, South China. Water. 2023; 15(5):1001. https://doi.org/10.3390/w15051001
Chicago/Turabian StyleShi, Hui, Yao Luo, Fenghua Zhou, Chunhua Qiu, Dongxiao Wang, and Zhenqiu Zhang. 2023. "Abnormal Waves Observation and Analysis of the Mechanism in the Pearl River Estuary, South China" Water 15, no. 5: 1001. https://doi.org/10.3390/w15051001
APA StyleShi, H., Luo, Y., Zhou, F., Qiu, C., Wang, D., & Zhang, Z. (2023). Abnormal Waves Observation and Analysis of the Mechanism in the Pearl River Estuary, South China. Water, 15(5), 1001. https://doi.org/10.3390/w15051001







