Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fractal Theory
2.2. Fractal Model of the SWCC
2.3. Data Sources
3. Results and Discussion
3.1. Fractal Dimension of Different Textural Soil
3.2. Fractal Modeling of the SWCC
4. Conclusions
- The fractal characteristic of soil with different textures was significantly different, and fractal dimension was strongly dependent on the clay content in the soil. The average fractal dimensions of the 12 different textures ranged from 2.4024 to 2.8928. Clay had the largest fractal dimension, whereas sand had the lowest one. The particle size composition of soil will significantly change the fractal dimension of soil. The fractal dimension of finely textured soil was larger than that of medium and coarse textured soil. Correlation analysis also suggests that the fractal dimension of soil particles is intensively related to the contents of clay, silt, and sand (p < 0.01). A higher ratio of clay content in the soil can produce a greater mass fractal dimension of soil particles. Fractal theory can quantitatively describe the features of soil particle composition.
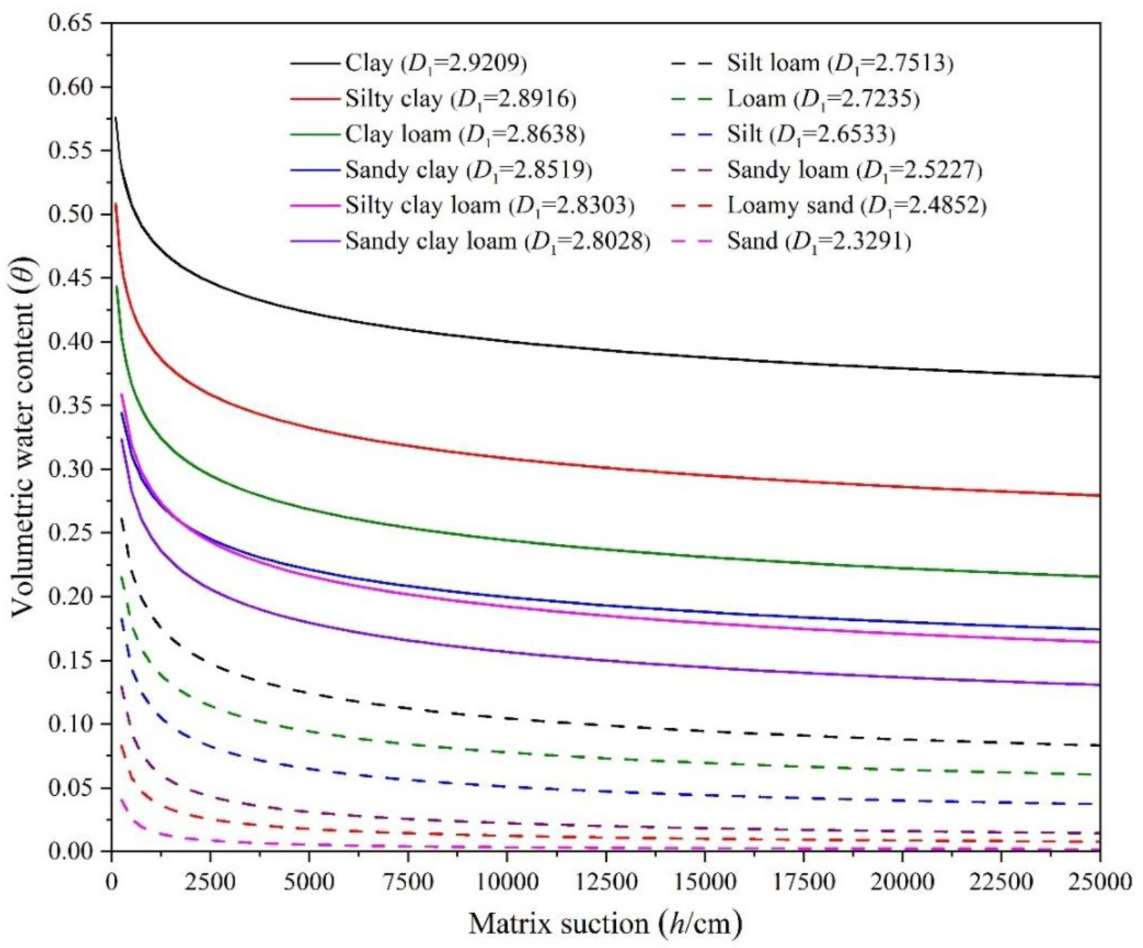
- The SWCC of unsaturated soil was strongly dependent on soil texture. The relationship of soil structure with hydraulic properties can be established using fractal analysis. The fractal model representing SWCC has good fitting results for soils of different textures, and the estimated fractal dimension (D2) in this fractal model can be obtained by particle size distribution. The fitting results of the SWCC fractal model showed that soil with different textures had different changes in SWCC. The soil water retention capacity gradually increased with increasing fractal dimension. In the low suction stage, the changes in the SWCC of coarse textured soil were steeper than those of fine textured soil. Fine textured soil had a larger residual moisture content, while coarse textured soil had a smaller one.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Yang, X. Three-dimensional stability analysis of slope in unsaturated soils considering strength nonlinearity under water drawdown. Eng. Geol. 2018, 237, 102–115. [Google Scholar] [CrossRef]
- Rahardjo, H.; Kim, Y.; Satyanaga, A. Role of unsaturated soil mechanics in geotechnical engineering. Int. J. Geo-Eng. 2019, 10, 8. [Google Scholar] [CrossRef] [Green Version]
- Tian, K.; Yang, A.; Nie, K.Y.; Zhang, H.; Xu, J.; Wang, X. Experimental study of steady seepage in unsaturated loess soil. Acta Geotech. 2020, 15, 2681–2689. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.Y.; He, X.; Chen, Q.; Zhang, H.; Liu, X.Y. Improved prediction of water retention characteristic based on soil gradation and clay fraction. Geoderma 2021, 404, 115293. [Google Scholar] [CrossRef]
- Karakan, E. Comparative Analysis of Atterberg Limits, Liquidity Index, Flow Index and Undrained Shear Strength Behavior in Binary Clay Mixtures. Appl. Sci. 2022, 12, 8616. [Google Scholar] [CrossRef]
- Fiori, A.; Pomarico, I.; Zarlenga, A.; Catani, V.; Leone, G. Extending the Overlay and Index: A Simple Method for Assessing Aquifer Vulnerability in a Combined Vadose Zone—Groundwater Flow System. Water 2023, 15, 364. [Google Scholar] [CrossRef]
- Leong, E.C.; Rahardjo, H. Review of Soil-Water Characteristic Curve Equations. Geotech. Geol. Eng. 1997, 123, 1106–1117. [Google Scholar] [CrossRef] [Green Version]
- Rudiyanto; Sakai, M.; van Genuchten, M.T.; Alazba, A.A.; Setiawan, B.I.; Minasny, B. A complete soil hydraulic model accounting for capillary and adsorptive water retention capillary and film conductivity and hysteresis. Water Resour. Res. 2015, 51, 8757–8772. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Wu, G.; Wang, D.; Shi, Z. Soil-hydrological properties response to grazing exclusion in a steppe grassland of the Loess Plateau. Environ. Earth Sci. 2013, 71, 745–752. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Nie, W.; Ma, X. Inverse Modeling of Soil Hydraulic Parameters Based on a Hybrid of Vector-Evaluated Genetic Algorithm and Particle Swarm Optimization. Water 2018, 10, 84. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Wei, C. Numerical procedure for simulating the two-phase flow in unsaturated soils with hydraulic hysteresis. Int. J. Geomech. 2016, 16, 04015030. [Google Scholar] [CrossRef]
- Zeng, L.; Li, F.; Liu, J.; Gao, Q.; Bian, H. Effect of initial gravimetric water content and cyclic wetting-drying on soil-water characteristic curves of disintegrated carbonaceous mudstone. Trans. Saf. Environ. 2019, 1, 230–240. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Chen, Q.; Zhang, L.; Li, X. A framework to determine soil-water retention relation for mine wastes and its applications in emergency risk assessment. Hydrol. Res. 2021, 52, 389–413. [Google Scholar] [CrossRef]
- Moazeni-Noghondar, S.; Golkarian, A.; Azari, M.; Lajayer, B.A. Study on soil water retention and infiltration rate: A case study in eastern Iran. Environ. Earth Sci. 2021, 80, 474. [Google Scholar] [CrossRef]
- Wen, T.; Shao, L.; Guo, X.; Zhao, Y. Experimental investigations of the soil water retention curve under multiple drying-wetting cycles. Acta Geotech. 2020, 15, 3321–3326. [Google Scholar] [CrossRef]
- Liu, Q.; Yasufuku, N.; Omine, K.; Hazarika, H. Automatic soil water retention test system with volume change measurement for sandy and silty soils. Soils Found. 2012, 52, 369–380. [Google Scholar] [CrossRef] [Green Version]
- Fattah, M.Y.; Salim, N.M.; Irshayyid, E.J. Determination of the soil-water characteristic curve of unsaturated bentonite-sand mixtures. Environ. Earth Sci. 2017, 76, 201. [Google Scholar] [CrossRef]
- Dang, M.; Chai, J.; Xu, Z.; Qin, Y.; Cao, J.; Liu, F. Soil water characteristic curve test and saturated-unsaturated seepage analysis in Jiangcungou municipal solid waste landfill, China. Eng. Geol. 2019, 264, 105374. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, C.; Lourenco, S.D.N.; Dong, S.; Jiang, Y. Factors affecting the soil-water retention curve of Chinese loess. Bull. Eng. Geol. Environ. 2021, 80, 717–729. [Google Scholar] [CrossRef]
- Chen, P.; Liu, J.; Wei, C.; Xue, W.; Tian, H. Approach to Rapidly Determining the Water Retention Curves for Fine-Grained Soils in Capillary Regime Based on the NMR Technique. J. Eng. Mech. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- Lu, P.; He, Y.; Zhang, Z.; Ye, W. Predicting chemical influence on soil water retention curves with models established based on pore structure evolution of compacted clay. Comput. Geotech. 2021, 138, 104360. [Google Scholar] [CrossRef]
- Iyer, K.; Jayanth, S.; Gurnani, S.; Singh, D.N. Influence of Initial Water Content and Specimen Thickness on the SWCC of Fine-Grained Soils. Int. J. Geomech. 2013, 13, 894–899. [Google Scholar] [CrossRef]
- Li, D.; Gao, G.; Shao, M.; Fu, B. Predicting available water of soil from particle-size distribution and bulk density in an oasis-desert transect in northwestern China. J. Hydrol. 2016, 538, 539–550. [Google Scholar] [CrossRef]
- Mahmoodlu, M.G.; Raoof, A.; Sweijen, T.; van Genuchten, M.T. Effects of Sand Compaction and Mixing on Pore Structure and the Unsaturated Soil Hydraulic Properties. Vadose Zone J. 2016, 15, 1–11. [Google Scholar] [CrossRef]
- Shen, J.; Hu, M.; Wang, X.; Zhang, C.; Xu, D. SWCC of Calcareous Silty Sand Under Different Fines Contents and dry Densities. Front. Environ. Sci. 2021, 9, 682907. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, L.; Wei, Y. Influence of Fine Content on the Soil-Water Characteristic Curve of Unsaturated Soils. Geotech. Geol. Eng. 2020, 38, 1371–1378. [Google Scholar] [CrossRef]
- Zhu, J.; Su, Z.; Zhang, H. Soil-water characteristic curves and hydraulic conductivity of Gaomiaozi bentonite pellet-contained materials. Environ. Earth Sci. 2022, 81, 92. [Google Scholar] [CrossRef]
- Bockheim, J.G. Genesis of soils with an abrupt textural contrast in the United States. Catena 2016, 137, 422–431. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous medium and Their Relation to Drainage Design. Trans. ASAE 1964, 7, 26–28. [Google Scholar] [CrossRef]
- Castellini, M.; Prima, S.D.; Iovino, M. An assessment of the BEST procedure to estimate the soil water retention curve. Geoderma 2018, 320, 82–94. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Z.; Sun, D.; Yu, H. A simple method for predicting the hydraulic properties of unsaturated soils with different void ratios. Soil Till. Res. 2021, 209, 104913. [Google Scholar] [CrossRef]
- Matlan, S.J.; Taha, M.R.; Mukhlisin, M. Assessment of Model Consistency for Determination of Soil-Water Characteristic Curves. Arab. J. Sci. Eng. 2016, 41, 1233–1240. [Google Scholar] [CrossRef]
- Soltani, A.; Azimi, M.; Deng, A.; Taheri, A. A simplified method for determination of the soil–water characteristic curve variables. Int. J. Geotech. Eng. 2019, 13, 316–325. [Google Scholar] [CrossRef]
- Tao, G.; Lei, D.; Liu, L.; Li, Y.; Zhu, X. Prediction of Soil Water Characteristic Curve Based on Soil Water Evaporation. Adv. Civ. Eng. 2021, 2021, 6686442. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Yu, B. Analysis of Flow in Fractal Porous Media. Appl. Mech. Rev. 2008, 61, 050801. [Google Scholar] [CrossRef]
- Wang, L.; Yang, R.; Zhang, S.; Zhang, G. Fractal features and infiltration characteristics of the soil from different land uses in a small watershed in a rocky, mountainous area in Shandong Province. J. For. Res. 2019, 31, 1017–1024. [Google Scholar] [CrossRef]
- Zhu, J. Impact of fractal characteristics on evaporation and infiltration in unsaturated heterogeneous soils. Hydrol. Sci. J. 2020, 65, 1872–1878. [Google Scholar] [CrossRef]
- Echogdali, F.Z.; Boutaleb, S.; Abioui, M.; Aadraoui, M.; Bendarma, A.; Kpan, R.B.; Ikirri, M.; El Mekkaoui, M.; Essoussi, S.; El Ayady, H.; et al. Spatial Mapping of Groundwater Potentiality Applying Geometric Average and Fractal Models: A Sustainable Approach. Water 2023, 15, 336. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, R. Evaluation of soil water retention curve with the pore-solid fractal model. Geoderma 2005, 127, 52–61. [Google Scholar] [CrossRef]
- Peng, G.; Xiang, N.; Lv, S.; Zhang, G. Fractal characterization of soil particle-size distribution under different land-use patterns in the Yellow River Delta Wetland in China. J. Soil Sediment. 2014, 14, 1116–1122. [Google Scholar] [CrossRef]
- Zolfaghari, A.A.; Taghizadeh-Mehrjardi, R.; Asadzadeh, F.; Hajabbasi, M.A. Soil structure changes due to different land-use practices in the central Zagruos region, Iran. Arch. Agron. Soil Sci. 2016, 62, 163–175. [Google Scholar] [CrossRef]
- Qi, F.; Zhang, R.; Liu, X.; Niu, Y.; Zhang, H.; Li, H.; Li, J.; Wang, B.; Zhang, G. Soil particle size distribution characteristics of different land-use types in the Funiu mountainous region. Soil Till. Res. 2018, 184, 45–51. [Google Scholar] [CrossRef]
- Qiu, S.; Yang, M.; Xu, P.; Rao, B. A new fractal model for porous media based on low-field nuclear magnetic resonance. J. Hydrol. 2020, 586, 124890. [Google Scholar] [CrossRef]
- Dai, L.; Wang, G.; He, Y. Assessing soil fractal and sorting characteristics based on geostatistics and modeling approaches in a typical basin of North China plain. Earth Sci. Inform. 2021, 14, 819–829. [Google Scholar] [CrossRef]
- Russell, A.R.; Buzzi, O. A fractal basis for soil-water characteristics curves with hydraulic hysteresis. Géotechnique 2012, 62, 269–274. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Gao, P.; Wang, B.; Liu, Y. Fractal Characteristics of Soil Retention Curve and Particle Size Distribution with Different Vegetation Types in Mountain Areas of Northern China. Int. J. Environ. Res. Public Health 2015, 12, 15379–15389. [Google Scholar] [CrossRef] [Green Version]
- Tyler, S.W.; Wheatcraft, S.W. Fractal processes in soil water retention. Water Resour. Res. 1990, 26, 1047–1056. [Google Scholar] [CrossRef]
- Bird, N.R.A.; Perrier, E.; Rieu, M. The water retention function for a model of soil structure with pore and solid fractal distributions. Eur. J. Soil Sci. 2000, 51, 51–63. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, R.; Huang, Q. Modeling Soil Water Retention Curve with a Fractal Method. Pedosphere 2006, 16, 137–146. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Kong, L.; Xiao, H.; Chen, Q.; Xia, Y. A Simple Fractal-Based Model for Soil-Water Characteristic Curves Incorporating Effects of Initial Void Ratios. Energies 2018, 11, 1419. [Google Scholar] [CrossRef] [Green Version]
- Zhou, A.; Fan, Y.; Cheng, W.; Zhang, J. A Fractal Model to Interpret Porosity-Dependent Hydraulic Properties for Unsaturated Soils. Adv. Civ. Eng. 2019, 2019, 3965803. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, W.; Wang, L.; Liu, Y.; Liu, Y.; Feng, Q. Relationship between soil water content and soil particle size on typical slopes of the Loess Plateau during a drought year. Sci. Total Environ. 2019, 648, 943–954. [Google Scholar] [CrossRef] [Green Version]
- Turcotte, D.L. Fractals in geology and geophysics. Pure Appl. Geophys. 1989, 131, 171–196. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle-size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Perrier, E.; Bird, N.R.A.; Rieu, M. Generalizing the fractal model of soil structure: The pore-solid fractal approach. Geoderma 1999, 88, 137–164. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Campbell, G.S. A simple method for determining unsaturated hydraulic conductivity from moisture retention data. Soil Sci. 1974, 177, 311–314. [Google Scholar] [CrossRef]
- Pasha, A.Y.; Khoshghalb, A.; Khalili, N. Pitfalls in Interpretation of Gravimetric Water Content-Based Soil-Water Characteristic Curve for Deformable Porous Media. Int. J. Geomech. 2016, 16, D4015004. [Google Scholar] [CrossRef]
- Soltani, A.; Azimi, M.; Boroomandnia, A.; O’Kelly, B.C. An objective framework for determination of the air-entry value from the soil-water characteristic curve. Results Eng. 2021, 12, 100298. [Google Scholar] [CrossRef]
- Tao, G.; Wu, Z.; Li, W.; Li, Y.; Dong, H. Simplified Relation Model of Soil Saturation Permeability Coefficient and Air-Entry Value and Its Application. Fractal Fract. 2021, 5, 180. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxtonn, K.E. Estimation of Soil Water Properties. Trans. Am. Soc. Agri. Eng. 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Nemes, A.; Schaap, M.G.; Leij, F.J. Description of the unsaturated soil hydraulic database UNSODA version 2.0. J. Hydrol. 2001, 251, 151–162. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA: Washington, DC, USA; National Resources Conservation Service: Washington, DC, USA; National Soil Survey Center: Lincoln, NE, USA, 2014. [Google Scholar]
- Millán, M.; González-Posada, M.; Aguilar, M.; Domínguez, J.; Céspedes, L. On the fractal scaling of soil data. Particle-size distributions. Geoderma 2003, 117, 117–128. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Q.; Yang, H. Soil salinity distribution and its relationship with soil particle size in the lower reaches of Heihe River, Northwestern China. Environ. Earth Sci. 2016, 75, 810. [Google Scholar] [CrossRef]
- Ding, D.; Zhao, Y.; Feng, H.; Si, B.; Hill, R.L. A user-friendly modified pore-solid fractal model. Sci. Rep. 2016, 6, 39029. [Google Scholar] [CrossRef] [Green Version]
- Xia, D.; Deng, Y.; Wang, S.; Ding, S.; Cai, C. Fractal features of soil particle-size distribution of different weathering profiles of the collapsing gullies in the hilly granitic region, south China. Nat. Hazards 2015, 79, 455–478. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shabanpour, M.; Mohammadi, M.H.; Davatgar, N. Characterizing Spatial Variability of Soil Textural Fractions and Fractal Parameters Derived from Particle Size Distributions. Pedosphere 2019, 29, 224–234. [Google Scholar] [CrossRef]
- Huang, G.; Zhan, W. Modeling the soil water retention curve with fractal theory. Adv. Water Sci. 2002, 13, 55–60. (In Chinese) [Google Scholar]
- Peng, Y.; Yin, Z.; Zhou, C.; Ding, X. Micromechanical analysis of capillary suction effect on bearing capacity of unsaturated fine granular foundation soil using coupled CFD-DEM method. Comput. Geotech. 2022, 153, 105092. [Google Scholar] [CrossRef]
- Li, X.; Hu, C.; Li, F.; Gao, H. Determining soil water characteristic curve of lime treated loess using multiscale structure fractal characteristic. Sci. Rep. 2020, 10, 21569. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Xiao, H.; Chen, Q.; Wan, J. Determining Soil-Water Characteristic Curves from Mercury Intrusion Porosimeter Test Data Using Fractal Theory. Energies 2019, 12, 752. [Google Scholar] [CrossRef] [Green Version]
- Rusell, A.R. How water retention in fractal soils depends on particle and pore sizes, shapes, volumes and surface areas. Geotechnique 2014, 64, 379–390. [Google Scholar] [CrossRef]
- Fuentes, C.; Chavez, C.; Brambila, F. Relating Hydraulic Conductivity Curve to Soil-Water Retention Curve Using a Fractal Model. Mathematics 2020, 8, 2201. [Google Scholar] [CrossRef]
- Li, P.; Qian, H.; Wu, J. Accelerate research on land creation. Nature 2014, 510, 29–31. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Qian, H. Water in loess. In Encyclopedia of Sustainability Science and Technology; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2018; pp. 1–17. [Google Scholar] [CrossRef]
- Su, F.; Wu, J.; Wang, D.; Zhao, H.; Wang, Y.; He, X. Moisture movement, soil salt migration, and nitrogen transformation under different irrigation conditions: Field experimental research. Chemosphere 2022, 300, 134569. [Google Scholar] [CrossRef]

| Soil Texture | Clay | Silty Clay | Sandy Clay | Clay Loam | Silty Clay Loam | Sandy Clay Loam | Loam | Silt Loam | Sandy Loam | Silt | Loamy Sand | Sand |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 37.30 | 34.19 | 29.17 | 25.89 | 32.56 | 28.08 | 11.15 | 20.76 | 14.66 | 20.00 | 8.69 | 7.26 |
| Soil Textures | Number | Slope | Fractal Dimension | Clay Content | R2 |
|---|---|---|---|---|---|
| Clay | 15 | 0.1072 | 2.8928 | 51.01 | 0.8509 |
| Silty clay | 12 | 0.1327 | 2.8673 | 40.33 | 0.7425 |
| Sandy clay | 3 | 0.1470 | 2.8530 | 39.13 | 0.9116 |
| Clay loam | 14 | 0.1483 | 2.8517 | 37.32 | 0.8993 |
| Silty clay loam | 20 | 0.1595 | 2.8405 | 36.65 | 0.7565 |
| Sandy clay loam | 24 | 0.2154 | 2.7846 | 24.60 | 0.9120 |
| Loam | 50 | 0.2482 | 2.7519 | 21.49 | 0.8655 |
| Silt loam | 78 | 0.2832 | 2.7168 | 18.59 | 0.7190 |
| Sandy loam | 50 | 0.3439 | 2.6561 | 13.16 | 0.8654 |
| Silt | 3 | 0.3589 | 2.6411 | 9.10 | 0.6503 |
| Loamy sand | 34 | 0.4767 | 2.5233 | 6.72 | 0.8489 |
| Sand | 53 | 0.5976 | 2.4024 | 3.02 | 0.7875 |
| Index | D1 | Clay Content | Silt Content | Sand Content |
|---|---|---|---|---|
| D1 | 1.000 | |||
| Clay content | 0.943 ** | 1.000 | ||
| Silt content | 0.449 ** | 0.474 ** | 1.000 | |
| Sand content | −0.678 ** | −0.726 ** | −0.917 ** | 1.000 |
| Soil Textures | Number | D1 | D2 | Relative Error (%) | R2 |
|---|---|---|---|---|---|
| Clay | 15 | 2.8928 | 2.9497 | 1.92 | 0.8911 |
| Silty clay | 12 | 2.8673 | 2.9152 | 1.64 | 0.9365 |
| Sandy clay | 3 | 2.8530 | 2.9113 | 2.00 | 0.8539 |
| Clay loam | 14 | 2.8517 | 2.9105 | 2.02 | 0.9419 |
| Silty clay loam | 20 | 2.8405 | 2.8865 | 1.59 | 0.9222 |
| Sandy clay loam | 24 | 2.7846 | 2.8854 | 3.49 | 0.9083 |
| Loam | 50 | 2.7519 | 2.8836 | 4.56 | 0.9208 |
| Silt loam | 78 | 2.7168 | 2.8798 | 5.66 | 0.9008 |
| Sandy loam | 50 | 2.6561 | 2.8650 | 7.29 | 0.8786 |
| Silt | 3 | 2.6411 | 2.8504 | 7.34 | 0.8584 |
| Loamy sand | 34 | 2.5233 | 2.6751 | 5.03 | 0.9304 |
| Sand | 53 | 2.4024 | 2.5712 | 6.56 | 0.8625 |
| Soil Textures | Code | Particle Density | Porosity | D1 | Clay Content |
|---|---|---|---|---|---|
| Clay | 2362 | 2.65 | 0.56 | 2.9249 | 63.0% |
| Silty clay | 3030 | 2.66 | 0.50 | 2.8916 | 42.0% |
| Sandy clay | 1135 | — | — | 2.8568 | 41.0% |
| Clay loam | 2701 | 2.61 | 0.34 | 2.8325 | 31.2% |
| Silty clay loam | 3110 | 2.54 | 0.47 | 2.8195 | 31.0% |
| Sandy clay loam | 2630 | 2.72 | 0.53 | 2.8028 | 25.8% |
| Loam | 2591 | 2.65 | 0.43 | 2.7809 | 21.8% |
| Silt loam | 2671 | 2.78 | 0.49 | 2.7513 | 17.3% |
| Sandy loam | 2560 | 2.61 | 0.48 | 2.6567 | 9.4% |
| Silt | 4670 | 2.65 | 0.46 | 2.4931 | 9.0% |
| Loamy sand | 2763 | 2.67 | 0.43 | 2.4852 | 2.8% |
| Sand | 4660 | 2.56 | 0.46 | 2.3291 | 2.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wu, J.; Li, P.; Wang, Y.; Yang, N. Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis. Water 2023, 15, 772. https://doi.org/10.3390/w15040772
Yang C, Wu J, Li P, Wang Y, Yang N. Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis. Water. 2023; 15(4):772. https://doi.org/10.3390/w15040772
Chicago/Turabian StyleYang, Chunliu, Jianhua Wu, Peiyue Li, Yuanhang Wang, and Ningning Yang. 2023. "Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis" Water 15, no. 4: 772. https://doi.org/10.3390/w15040772
APA StyleYang, C., Wu, J., Li, P., Wang, Y., & Yang, N. (2023). Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis. Water, 15(4), 772. https://doi.org/10.3390/w15040772








