Third-Monthly Hydropower Scheduling of Cascaded Reservoirs Using Successive Quadratic Programming in Trust Corridor
Abstract
:1. Introduction
2. Problem Formulation
- (1)
- The water balance,
- (2)
- Upper and lower bounds on storage or release,
- (3)
- Firm hydropower output,
- (4)
- The hydropower output determined by,
3. Solution Techniques
3.1. Formulation of a QP Problem
3.2. Finding a Feasible Solution
4. Case Studies
4.1. Engineering Background
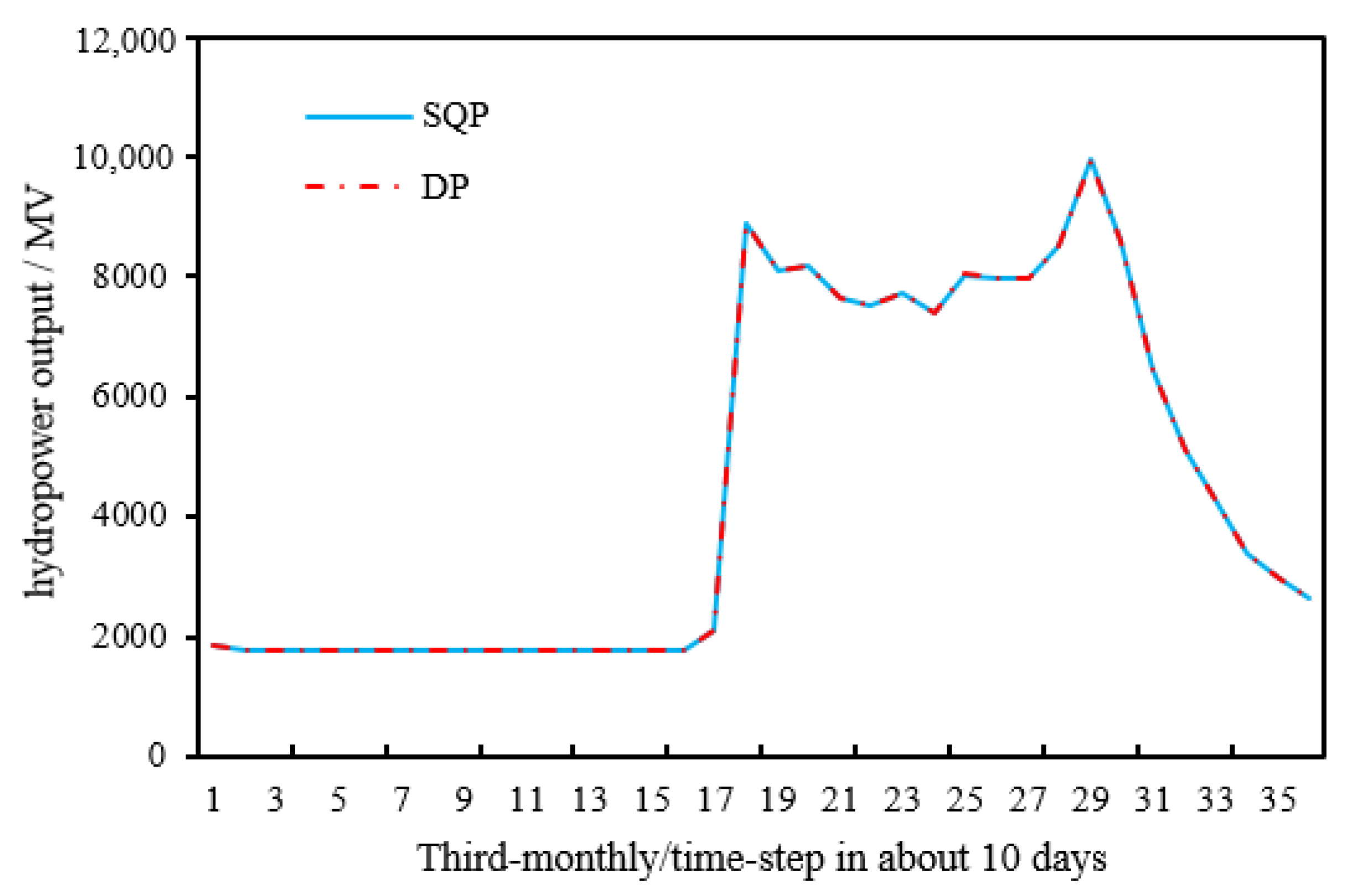
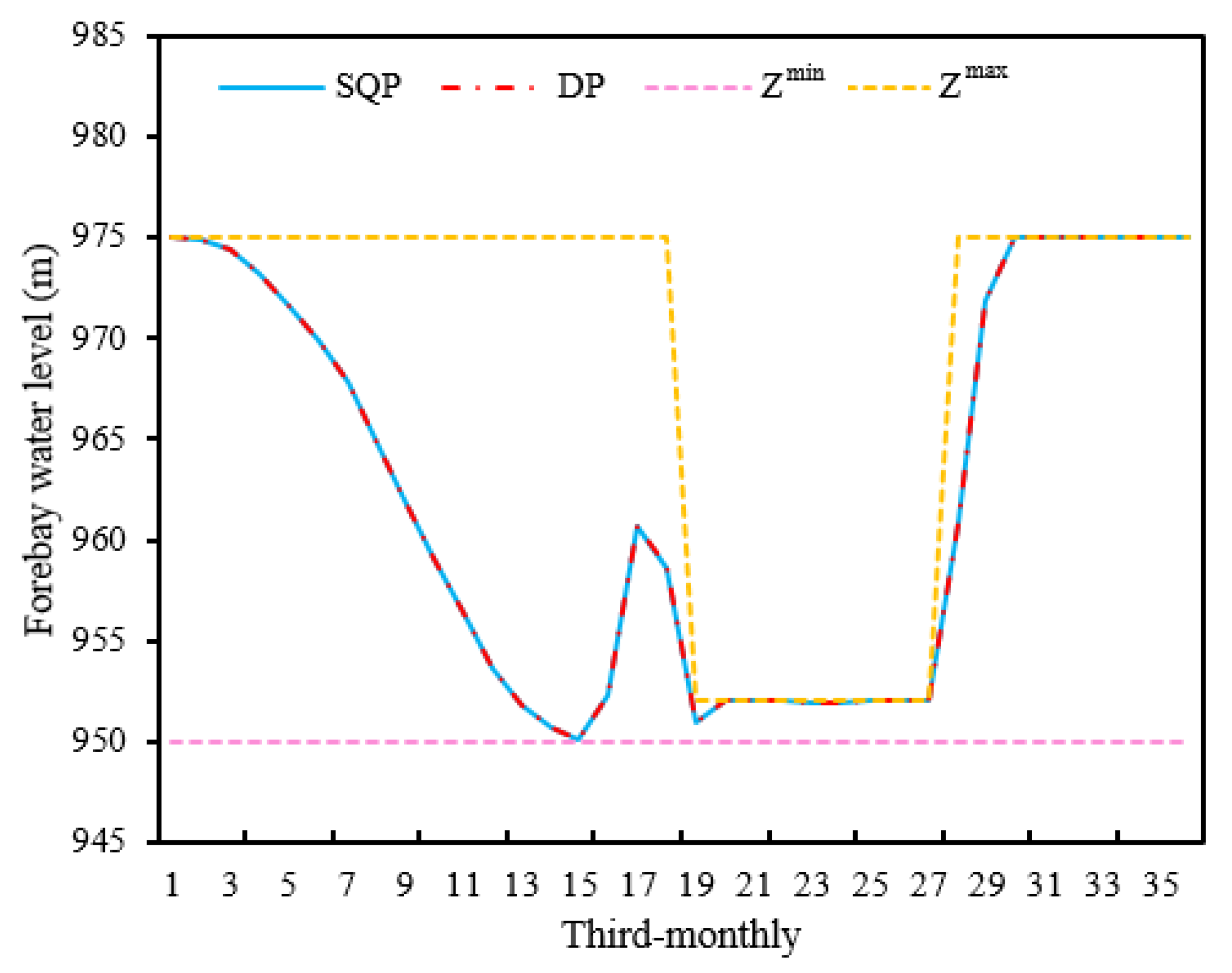
4.2. Comparison with Dynamic Programming (DP)
4.3. Solution Efficiency
4.4. Convergence of the Method
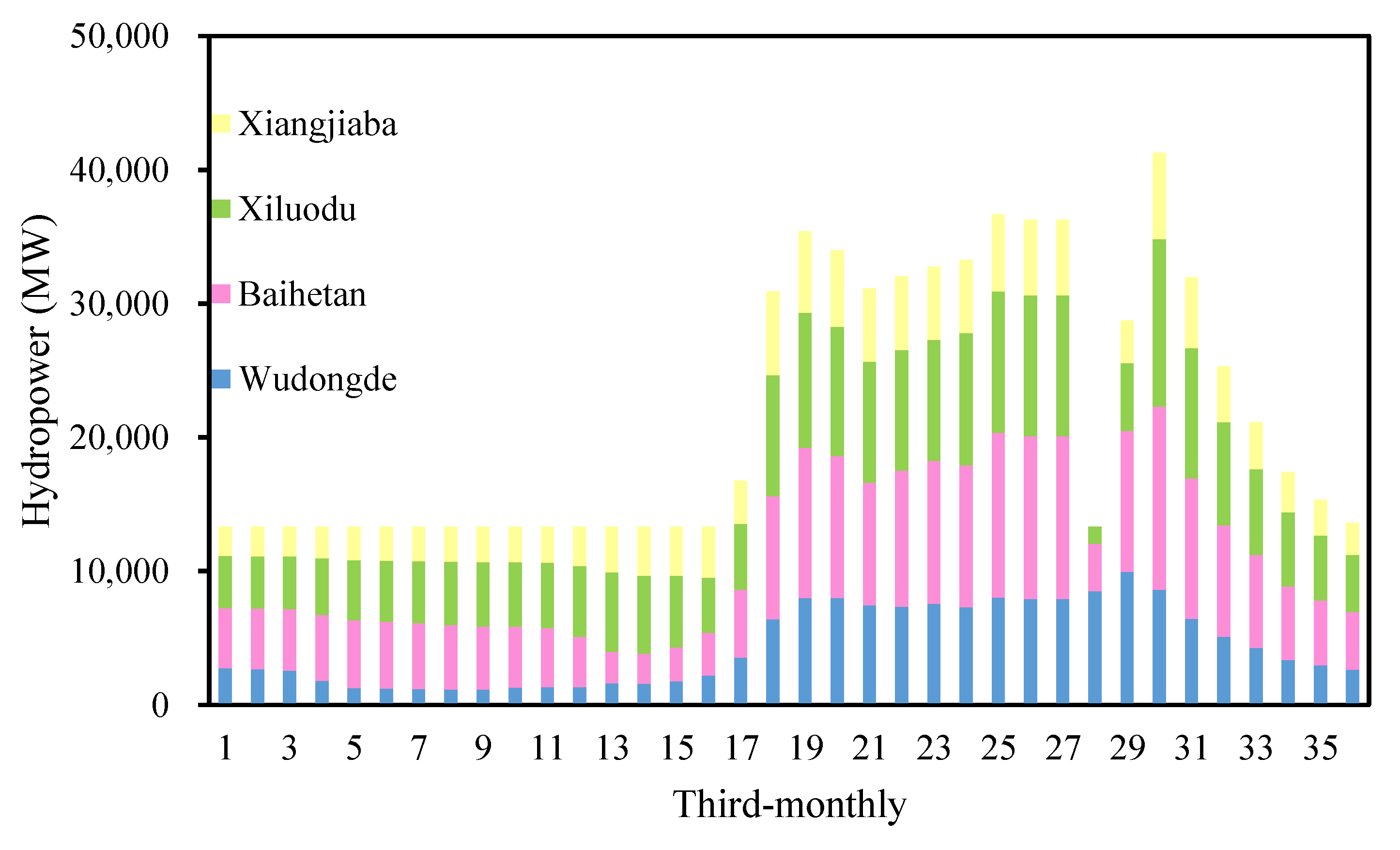
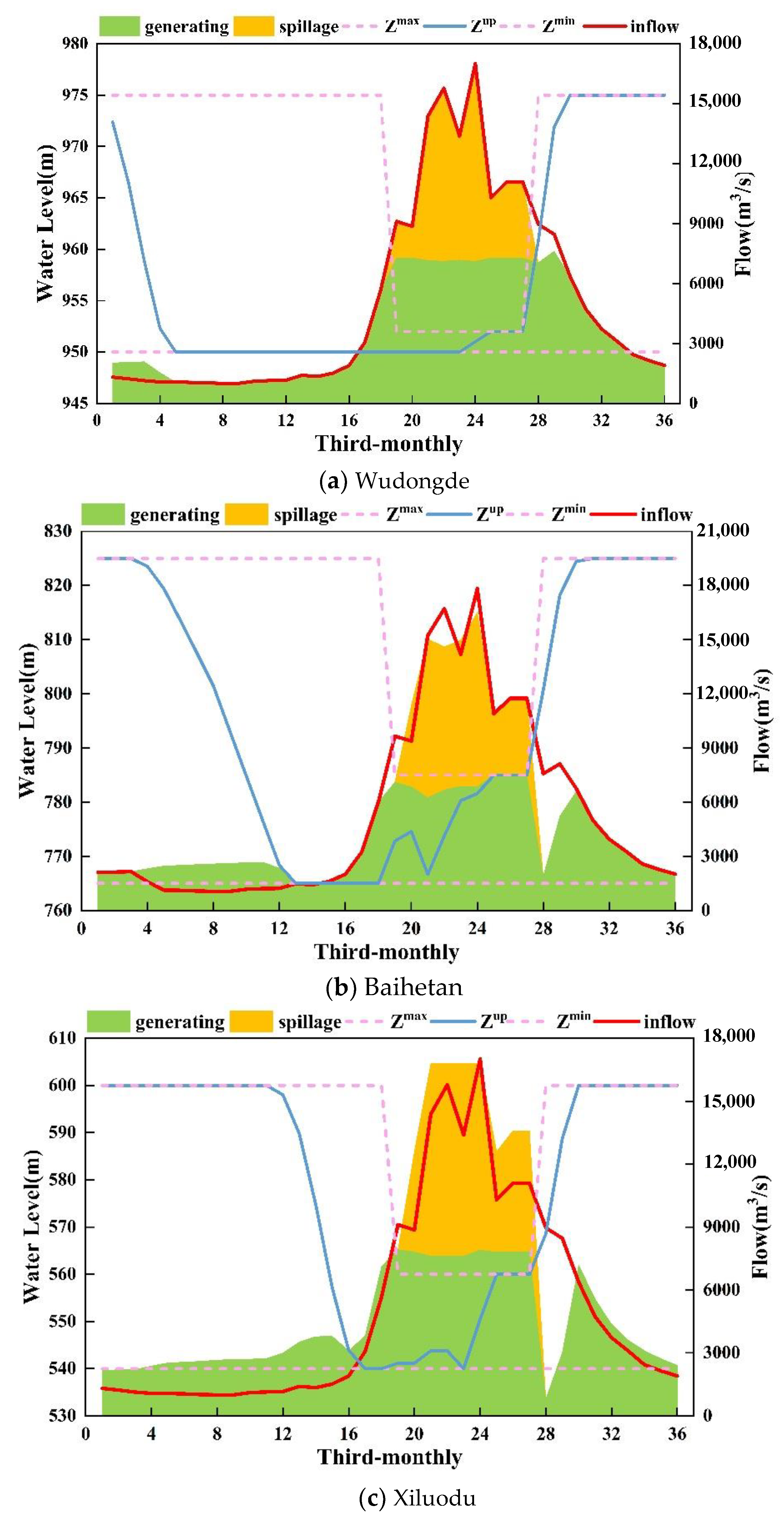
4.5. Results in Detail
5. Conclusions
- (1)
- Successive quadratic programming (SQP) can derive results consistent with dynamic programming (DP), which is well known and capable of securing the global optimal solution to a small-scale problem.
- (2)
- The present procedure has the computational time increasing linearly as the number of reservoirs increases, taking about 1 min to solve the problem involving all four cascaded hydropower reservoirs.
- (3)
- The convergence of the SQP can be achieved at the fifth iteration, with objective functional value monotonically increasing and improving the most significantly in the second iteration by about 20%, while in the following iterations by only about 1%.
- (4)
- The cascaded hydropower reservoirs coordinate very well to maximize the firm hydropower output at the top priority by regulating their storage capacities to give a constant power yield during the dry seasons, and then making full use of their installed capacities to convert the coming inflows into hydropower energy as much as possible during the flood seasons.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allen, R.B.; Bridgeman, S.G. Dynamic Programming in Hydropower Scheduling. J. Water Resour. Plan. Manag. 1986, 112, 339–353. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, J.; Lu, P.; Yuan, L. Long-term scheduling of large cascade hydropower stations in Jinsha River, China. Energy Convers. Manag. 2015, 90, 476–487. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, P.; Cheng, L.; Wang, H.; Ming, B.; Gong, W. Deriving operating rules for a large-scale hydro-photovoltaic power system using implicit stochastic optimization. J. Clean. Prod. 2018, 195, 562–572. [Google Scholar] [CrossRef]
- Zambelli, M.S.; Soares, S.; Silva, D.D. Deterministic versus stochastic dynamic programming for long term hydropower scheduling. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–7. [Google Scholar]
- Martins, L.S.A.; Azevedo, A.T.; Soares, S. Nonlinear Medium-Term Hydro-Thermal Scheduling With Transmission Constraints. IEEE Trans. Power Syst. 2014, 29, 1623–1633. [Google Scholar] [CrossRef]
- Zheng, H.; Feng, S.; Chen, C.; Wang, J. A new three-triangle based method to linearly concave hydropower output in long-term reservoir operation. Energy 2022, 250, 123784. [Google Scholar] [CrossRef]
- Yakowitz, S. Dynamic programming applications in water resources. Water Resour. Res. 1982, 18, 673–696. [Google Scholar] [CrossRef]
- Heidari, M.; Chow, V.T.; Kokotović, P.V.; Meredith, D.D. Discrete Differential Dynamic Programing Approach to Water Resources Systems Optimization. Water Resour. Res. 1971, 7, 273–282. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Ouyang, S.; Ding, X.; Chen, L. Improved decomposition–coordination and discrete differential dynamic programming for optimization of large-scale hydropower system. Energy Convers. Manag. 2014, 84, 363–373. [Google Scholar] [CrossRef]
- Turgeon, A. Optimal short-term hydro scheduling from the principle of progressive optimality. Water Resour. Res. 1981, 17, 481–486. [Google Scholar] [CrossRef]
- Cheng, C.; Shen, J.; Wu, X.; Chau, K.-w. Short-Term Hydroscheduling with Discrepant Objectives Using Multi-Step Progressive Optimality Algorithm1: Short-Term Hydroscheduling with Discrepant Objectives Using Multi-step Progressive Optimality Algorithm. J. Am. Water Resour. Assoc. 2012, 48, 464–479. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.-J.; Xu, C.-Y. Boosting hydropower output of mega cascade reservoirs using an evolutionary algorithm with successive approximation. Appl. Energy 2018, 228, 1726–1739. [Google Scholar] [CrossRef]
- Ahmed, J.A.; Sarma, A.K. Genetic Algorithm for Optimal Operating Policy of a Multipurpose Reservoir. Water Resour. Manag. 2005, 19, 145–161. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Arunkumar, R. Optimization of Hydropower Reservoir Using Evolutionary Algorithms Coupled with Chaos. Water Resour. Manag. 2013, 27, 1963–1979. [Google Scholar] [CrossRef]
- Chang, Y.T.; Chang, L.C.; Chang, F.J. Intelligent control for modeling of real-time reservoir operation, part II: Artificial neural network with operating rule curves. Hydrol. Process. 2005, 19, 1431–1444. [Google Scholar] [CrossRef]
- Chaves, P.; Chang, F.J. Intelligent reservoir operation system based on evolving artificial neural networks. Adv. Water Resour. 2008, 31, 926–936. [Google Scholar] [CrossRef]
- Reddy, M.J.; Nagesh Kumar, D. Multi-objective particle swarm optimization for generating optimal trade-offs in reservoir operation. Hydrol. Process. 2007, 21, 2897–2909. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Qin, H. Optimal operation of multi-reservoir hydropower systems using enhanced comprehensive learning particle swarm optimization. J. Hydro-Environ. Res. 2016, 10, 50–63. [Google Scholar] [CrossRef]
- Bai, T.; Kan, Y.B.; Chang, J.X.; Huang, Q.; Chang, F.J. Fusing feasible search space into PSO for multi-objective cascade reservoir optimization. Appl. Soft. Comput. 2017, 51, 328–340. [Google Scholar] [CrossRef]
- Needham, J.T.; Watkins, D.W.; Lund, J.R.; Nanda, S.K. Linear Programming for Flood Control in the Iowa and Des Moines Rivers. J. Water Resour. Plan. Manag. 2000, 126, 118–127. [Google Scholar] [CrossRef]
- Consoli, S.; Matarazzo, B.; Pappalardo, N. Operating rules of an irrigation purposes reservoir using multi-objective optimization. Water Resour. Manag. 2008, 22, 551–564. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Jiang, Z.-Q.; Qin, H.; Song, Z.-G. Monthly Operation Optimization of Cascade Hydropower Reservoirs with Dynamic Programming and Latin Hypercube Sampling for Dimensionality Reduction. Water Resour. Manag. 2020, 34, 2029–2041. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Z.; Ji, C.; Sun, P. Contrastive analysis of three parallel modes in multi-dimensional dynamic programming and its application in cascade reservoirs operation. J. Hydrol. 2015, 529, 22–34. [Google Scholar] [CrossRef]
- Yoo, J.-H. Maximization of hydropower generation through the application of a linear programming model. J. Hydrol. 2009, 376, 182–187. [Google Scholar] [CrossRef]
- dos Santos Abreu, D.L.; Finardi, E.C. Continuous Piecewise Linear Approximation of Plant-Based Hydro Production Function for Generation Scheduling Problems. Energies 2022, 15, 1699. [Google Scholar] [CrossRef]
- Vielma, J.P. Mixed Integer Linear Programming Formulation Techniques. SIAM Rev. 2015, 57, 3–57. [Google Scholar] [CrossRef]
- Azevedo, A.T.; Oliveira, A.R.L.; Soares, S. Interior point method for long-term generation scheduling of large-scale hydrothermal systems. Ann. Oper. Res. 2008, 169, 55. [Google Scholar] [CrossRef]
- Zhou, B.; Feng, S.; Xu, Z.; Jiang, Y.; Wang, Y.; Chen, K.; Wang, J. A Monthly Hydropower Scheduling Model of Cascaded Reservoirs with the Zoutendijk Method. Water 2022, 14, 3978. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, S.; Gong, J.; Liu, R.; Li, X.; Fan, Q. Improved genetic algorithm for economic load dispatch in hydropower plants and comprehensive performance comparison with dynamic programming method. J. Hydrol. 2017, 554, 306–316. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, K.; Lu, X. Limited adaptive genetic algorithm for inner-plant economical operation of hydropower station. Hydrol. Res. 2013, 44, 583–599. [Google Scholar] [CrossRef]
- Grygier, J.C.; Stedinger, J.R. Algorithms for optimizing hydropower system operation. Water Resour. Res. 1985, 21, 1–10. [Google Scholar] [CrossRef]
- Cheng, X.; Feng, S.; Zheng, H.; Wang, J.; Liu, S. A hierarchical model in short-term hydro scheduling with unit commitment and head-dependency. Energy 2022, 251, 123908. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Scheduling of head-dependent cascaded hydro systems: Mixed-integer quadratic programming approach. Energy Convers. Manag. 2010, 51, 524–530. [Google Scholar] [CrossRef]
- Niu, W.-J.; Feng, Z.-K.; Cheng, C.-T. Optimization of variable-head hydropower system operation considering power shortage aspect with quadratic programming and successive approximation. Energy 2018, 143, 1020–1028. [Google Scholar] [CrossRef]
- Díaz, G.E.; Fontane, D.G. Hydropower Optimization Via Sequential Quadratic Programming. J. Water Resour. Plan. Manag. 1989, 115, 715–734. [Google Scholar] [CrossRef]
- Arnold, E.; Tatjewski, P.; Wołochowicz, P. Two methods for large-scale nonlinear optimization and their comparison on a case study of hydropower optimization. J. Optim. Theory Appl. 1994, 81, 221–248. [Google Scholar] [CrossRef]






| Number | Name | Installed Capacity (MW) | Storage Capacity (GL) | Dam Height (m) | Water Level (m) | Operability | ||
|---|---|---|---|---|---|---|---|---|
| Flood | Normal | Dead | ||||||
| 1 | Wudongde | 10,200 | 7408 | 270 | 952 | 975 | 950 | Seasonal |
| 2 | Baihetan | 16,000 | 20,600 | 289 | 785 | 825 | 760 | Annual |
| 3 | Xiluodu | 12,600 | 12,670 | 285.5 | 560 | 600 | 540 | Annual |
| 4 | Xiangjiaba | 6400 | 5163 | 380 | 370 | 380 | 370 | Seasonal |
| Number of Reservoirs | Computing Time(s) | Number of Variables | Number of Constraints | ||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | ||
| 4 | 61.784 | 725 | 725 | 1348 | 1644 |
| 3 | 46.478 | 544 | 544 | 1020 | 1242 |
| 2 | 17.981 | 363 | 363 | 1242 | 840 |
| 1 | 7.444 | 182 | 182 | 364 | 438 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Luo, J.; Chen, H.; Wang, Y.; Li, X.; Zhang, J.; Wang, J. Third-Monthly Hydropower Scheduling of Cascaded Reservoirs Using Successive Quadratic Programming in Trust Corridor. Water 2023, 15, 716. https://doi.org/10.3390/w15040716
Liu S, Luo J, Chen H, Wang Y, Li X, Zhang J, Wang J. Third-Monthly Hydropower Scheduling of Cascaded Reservoirs Using Successive Quadratic Programming in Trust Corridor. Water. 2023; 15(4):716. https://doi.org/10.3390/w15040716
Chicago/Turabian StyleLiu, Shuangquan, Jingzhen Luo, Hui Chen, Youxiang Wang, Xiangyong Li, Jie Zhang, and Jinwen Wang. 2023. "Third-Monthly Hydropower Scheduling of Cascaded Reservoirs Using Successive Quadratic Programming in Trust Corridor" Water 15, no. 4: 716. https://doi.org/10.3390/w15040716





