Abstract
In accordance with the rapid proliferation of machine learning (ML) and data management, ML applications have evolved to encompass all engineering disciplines. Owing to the importance of the world’s water supply throughout the rest of this century, much research has been concentrated on the application of ML strategies to integrated water resources management (WRM). Thus, a thorough and well-organized review of that research is required. To accommodate the underlying knowledge and interests of both artificial intelligence (AI) and the unresolved issues of ML in WRM, this overview divides the core fundamentals, major applications, and ongoing issues into two sections. First, the basic applications of ML are categorized into three main groups, prediction, clustering, and reinforcement learning. Moreover, the literature is organized in each field according to new perspectives, and research patterns are indicated so attention can be directed toward where the field is headed. In the second part, the less investigated field of WRM is addressed to provide grounds for future studies. The widespread applications of ML tools are projected to accelerate the formation of sustainable WRM plans over the next decade.
1. Introduction
In recent years, machine learning (ML) applications in water resources management (WRM) have garnered significant interest [1]. The advent of big data has substantially enhanced the ability of hydrologists to address existing challenges and encouraged novel applications of ML. The global data sphere is expected to reach 175 zettabytes by 2025 [2]. The availability of this large amount of data is forming a new era in the field of WRM. The next step for hydrological sciences is determining a method to integrate traditional physical-based hydrology into new machine-aided techniques to draw information directly from big data. An extensive range of decisions, from superficial to complicated scientific problems, is now handled by various ML techniques. Only a machine is capable of fully utilizing big data because of its veracity, velocity, volume, and variety. In recent decades, ML has attracted a great deal of attention from hydrologists and has been widely applied to a variety of fields because of its ability to manage complex environments.
In the coming decades, the issues surrounding climate change, increasing constraints on water resources, population growth, and natural hazards will force hydrologists worldwide to adapt and develop strategies to maintain security related to WRM. The Intergovernmental Hydrological Programme (IHP) just started its ninth phase plans (IHP-IX, 2022-2029), which place hydrologists, scholars, and policymakers on the frontlines of action to ensure a water-secure world despite climate change, with the goal of creating a new and sustainable water culture [3]. Moreover, the rapid growth in the availability of hydrologic data repositories, alongside advanced ML models, offers new opportunities for improved assessments in the field of hydrology by simplifying the existing complexity. For instance, it is possible to switch from traditional single-step prediction to multi-step ahead prediction, from short-term to long-term prediction, from deterministic models to their probabilistic counterparts, from univariate to multivariate models, from the application of structured data to volumetric and unstructured data, and from spatial to spatio-temporal and the more advanced geo-spatiotemporal environment. Moreover, ML models have contributed to optimal decision-making in WRM by efficiently modeling the nonlinear, erratic, and stochastic behaviors of natural hydrological phenomena. Furthermore, when solving complicated models, ML techniques can dramatically reduce the computational cost, which allows decision-makers to switch from physical-based models to ML models for cumbersome problems. Therefore, the new emerging hydrological crises, such as droughts and floods, can now be efficiently investigated and mitigated with the assistance of the advancements in ML algorithms.
Recent research has focused on the feasibility of applying ML techniques, specifically the subset of ML known as deep learning (DL), to various subfields of hydrology. In accordance with the research advancements in this field, various review articles have been published. The research domains, and descriptions of the recent review articles are summarized in Table 1. Previous reviews have effectively encouraged the development of well-known WRM subjects, provided in-depth explorations of those subjects, and addressed future research trends to better handle significant problems. However, a thorough review is required for some reasons. Prior to this review, multidisciplinary reviews tended to be objective and disregard the reader’s background knowledge. Moreover, they have rarely considered the instructional components of the subject and provided a comprehensive overview of an advanced problem or illuminated the mathematical structures of algorithms rather than focusing on their applications. Additionally, some cutting-edge engineering applications of ML, such as RL and other novel approaches to adapting ML to traditional prediction issues, have not yet been covered.

Table 1.
Recent review articles on machine learning applications in WRM.
An organized, and comprehensive review of the state-of-the-art literature, with a focus on research frontlines in WRM is the goal of this work. The remainder of the paper is structured as follows. Section 2 presents the systematic literature review. Section 3 provides details of the major application of ML in water resources management, along with subsections on prediction (Section 3.1), clustering (Section 3.2), and reinforcement learning (Section 3.3). Section 4 discusses less studied areas in the field of WRM for ML applications. Finally, the challenges and directions for future research, along with the concluding remarks of this review study are discussed in Section 5 and Section 6, respectively.
2. Systematic Literature Review
This study adopted a comprehensive systematic literature review to provide a deep understanding regarding the application of ML in the field of WRM. Popular academic databases were used, including arXiv by Cornell University, IEEE Xplore, Directory of Open Access Journals, Science Direct, Google Scholar, Taylor & Francis Online, Web of Science, Wiley Online Library, and Scopus. These databases were selected for the literature search based on the thorough coverage of their articles. Figure 1 was generated using the VOS viewer software to show the occurrences of major keywords on the implementation of ML models in the field of WRM. Because the previous review in this field thoroughly covered the articles published until 2020, this review only considered the articles published between 2021 and 2022. The former was used to obtain comprehensive insights, and the latter was used for reports using the tables in this review.
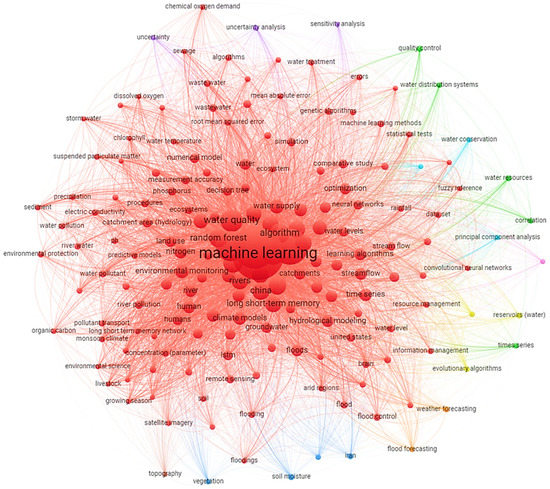
Figure 1.
Reported keyword occurrences in the literature on the implementation of ML models within the research domain of WRM.
3. Major Application of ML in WRM
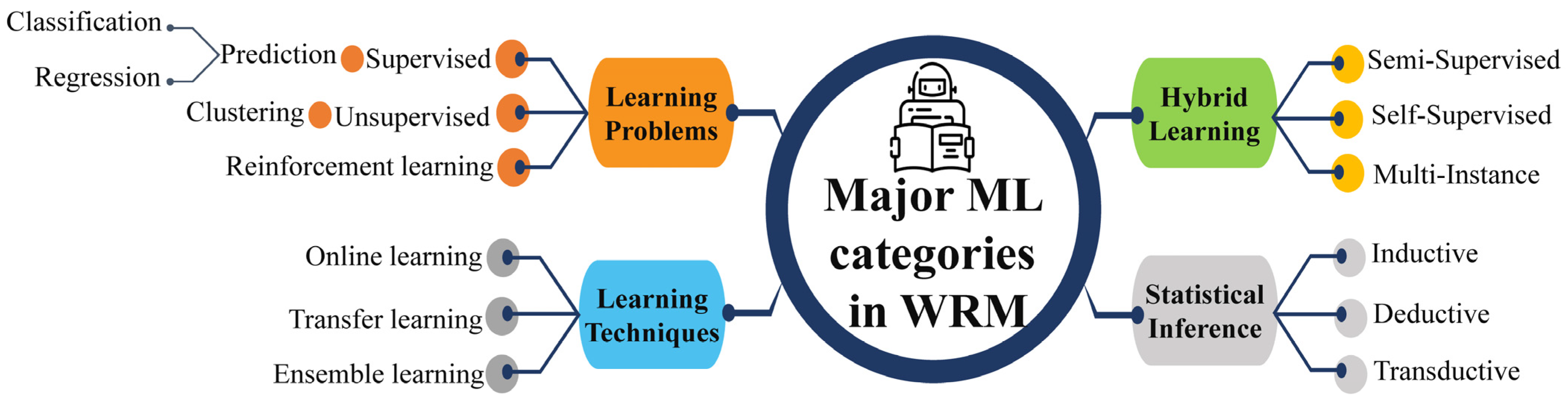
ML algorithms are typically categorized into three main groups: supervised, unsupervised, and RL [5]. A comparison of these is summarized in Table 2. Supervised learning algorithms employ labeled datasets to train the algorithms to classify or predict the output, where both the input and output values are known beforehand. Unsupervised learning algorithms are trained using unlabeled datasets for clustering. These algorithms discover hidden patterns or data groupings without the need for human intervention. RL is an area of ML that concerns how intelligent an agent is to take action in an environment to obtain the maximum reward. In both supervised and RL, inputs and outputs are mapped such that the agent is informed of the best strategy to take in order to complete a task. In RL, positive and negative behaviors are signaled through incentives and penalties, respectively. As a result, in supervised learning, a machine learns the behavior and characteristics of labeled datasets, detects patterns in unsupervised learning, and explores the environment without any prior training in RL algorithms. Thus, an appropriate category of ML is required based on the engineering application. The major ML learning types in WRM are summarized in Figure 2, where the first segment covers the core contents of the research reviewed in the following sections.

Table 2.
Comparison of supervised, unsupervised, and reinforcement learning algorithms.
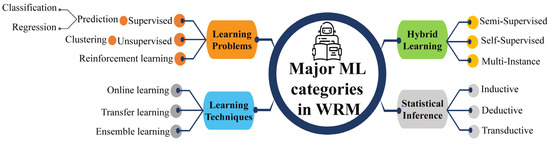
Figure 2.
Four major types of machine learning.
3.1. Prediction
The term “prediction” refers to any technique that uses data processing to get an estimation of an outcome. This is the outcome of an algorithm that was trained on a prior dataset and is now being applied to new data to assess the likelihood of a certain result in order to generate an output model. Forecasting is the probabilistic version of predicting an event in the future. In this review paper, the terms prediction and forecasting are used interchangeably. ML model predictions can be used to create very accurate estimations of the potential outcomes of a situation based on past data, and they can be about anything. For each record in the new data, the algorithm will generate probability values for an unknown variable, allowing the model builder to determine the most likely value. Prediction models can have either a parametric or non-parametric form; however, most WRM models are parametric. The development steps consist of four phases: data processing, feature selection, hyperparameter tuning, and training. Raw historical operation data are translated to a normalized scale in the data transformation step to increase the accuracy of the prediction model. The feature extraction stage extracts the essential variables that influence the output. These retrieved features are then used to train the model. The model’s hyperparameters are optimized to acquire the best model structure. Finally, the model’s weights are automatically modified to produce the final forecast model, which is of paramount importance for optimal control, performance evaluation, and other purposes.
3.1.1. Essential Data Processing in ML
For prediction purposes, ML algorithms can be applied to a wide variety of data types and formats, including time series, big data, univariate, and multivariate datasets. Time series are observations of a particular variable collected at regular intervals and in chronological order across time. A feature dataset is a collection of feature classes that utilize the same coordinate system and are connected. Its major purpose is to collect similar feature classes into a single dataset, which can be used to generate a network dataset. Many real-world datasets are becoming increasingly multi-featured because the ability to acquire information from a variety of sources is continuously expanding. Big data was first defined in 2005 as a large volume of data that cannot be processed by typical database systems or applications because of its size and complexity. Big data are extremely massive, complex, and challenging to process with the current infrastructure. Big data can be classified as structured, unstructured, or semi-structured. Structured data are the most well-known among hydrologist researchers because of their easy accessibility; they are usually stored in spreadsheets. Unstructured data such as images, video, and audio cannot be directly analyzed with a machine, whereas semi-structured data such as user-defined XML files can be read by a machine. Big data have five distinguishing characteristics (namely, the five Vs): volume, variety, velocity, veracity, and value. Recent developments in graphics processing units (GPUs) have paved the way for ML and its subset to get the advantage of big data and learn the complex and high dimensional environment. The establishment of a prediction model begins with the assimilation of data. It includes the phases of data collection, cleansing, and processing.
After adequate components have been gathered, any dataset needs to be structured. Predefined programs allow for the application of a variety of data manipulation, imputation, and cleaning procedures to achieve this goal. Anomalies and missing data are common in datasets and require special attention throughout the preprocessing phase. Depending on the goals of the prediction and the techniques selected, the clean data will require further processing. Depending on the type of prediction model being used, a dataset may employ a single labeled category or multiple categories. In ML, there are four types of data: numerical, categorical, time series, and text. The selected data category affects the techniques available for feature engineering and modeling, as well as the research questions that can be posed. Depending on how many variables need to be predicted, a prediction model will either be univariate, bivariate, or multivariate. In the processing phase, the raw data are remodeled, combined, reorganized, and reconstructed to meet the needs of the model.
3.1.2. Algorithms and Metrics for Evaluation
Because the outcomes of various ML approaches are not always the same, their performances are assessed by considering the outcomes acquired. Numerous statistical assessment measures have been proposed to measure the efficacy of the ML prediction technique. Table 3 summarizes some commonly used ML evaluation metrics, classifying them as either magnitude, absolute, or squared error metrics. The mean normalized bias and mean percentage error, which measures the discrepancies between predicted and observed values, fall under the first group. When only the amount by which the data deviate from the norm is of interest, an absolute function can be used to report an absolute error as a positive value, where , , , and denote the observed, predicted, the mean of the observed, and the mean of the predicted value, respectively.

Table 3.
Performance criteria for prediction model evaluation [19,20].
3.1.3. Applications and Challenges
The metrics used to evaluate the performance of ML models based on the accuracy of the predicted values are presented in Table 3. Choosing the correct metric to evaluate a model is crucial, as some models may only produce favorable results when evaluated using a specific metric. Researchers’ assessments of the significance of various characteristics in the outcomes are influenced by the metrics they use to evaluate and compare the performances of ML algorithms. Each year, a considerable number of papers are published to share the successes and achievements in the vast area of WRM. In the field of hydrology, some studies employ recorded data such as streamflow, precipitation, and temperature data, whereas others employ processed data such as large-scale atmospheric data, which are generated using gauge and satellite data. When it comes to predictions in the field of WRM, data-driven models perform better than statistical models owing to their higher capability in a complex environment. Table 4 provides a brief overview of some of the recent applications of ML for WRM prediction, with the relevant abbreviations defined in the glossary.

Table 4.
Recent applications of ML for prediction in WRM.
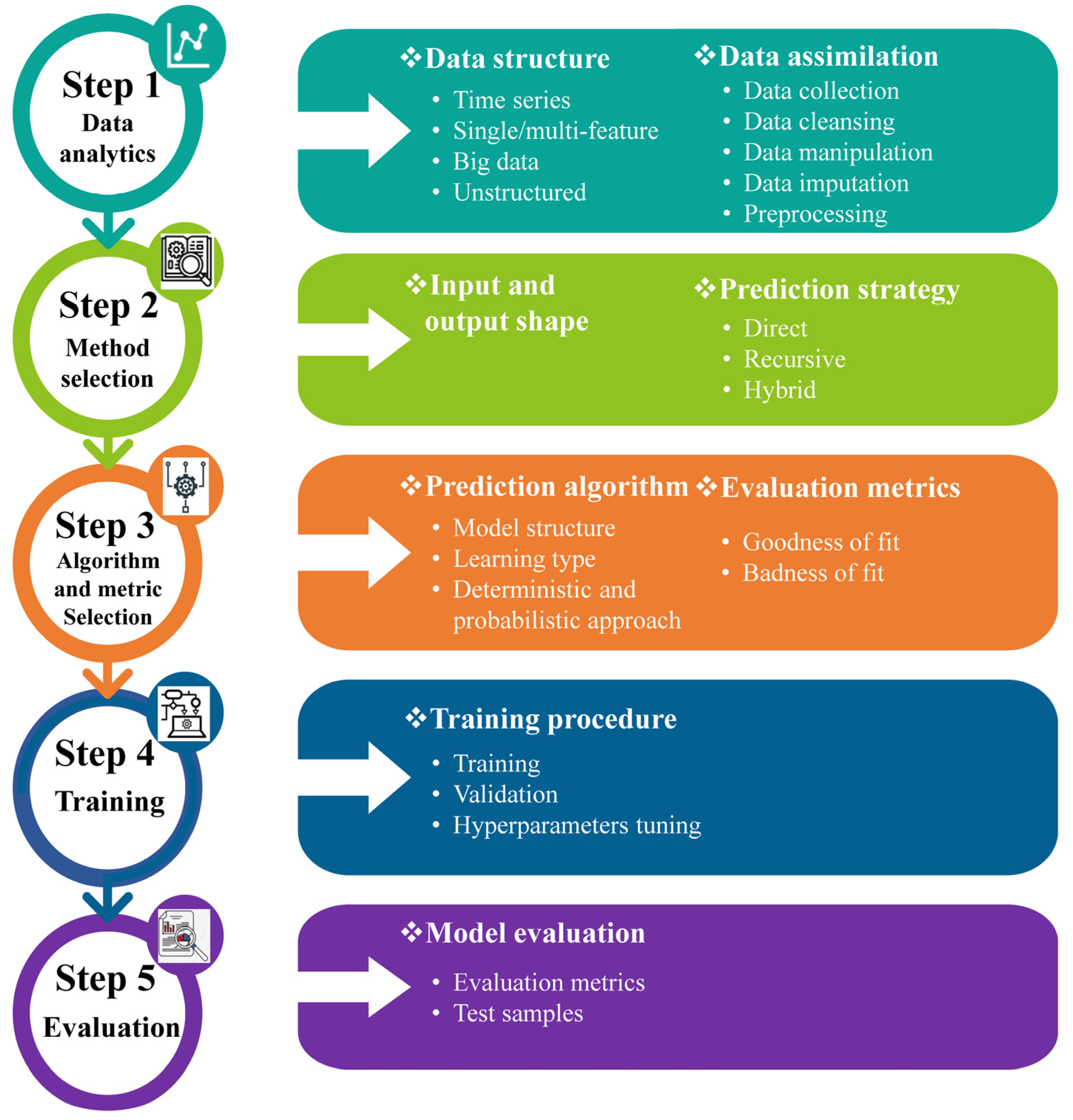
Today, most countries are putting more pressure on their water resources than ever before. The world’s population is growing quickly, and if things stay the same, there will be a 40% gap between how much water is needed and how much is available by 2030. In addition, extreme weather events like floods and droughts are seen as some of the biggest threats to global prosperity and stability. People are becoming more aware of how water shortages and droughts make fragile situations and conflicts worse. Changes in hydrological cycles due to climate change will exacerbate the problem by making water more volatile and increasing the frequency and severity of floods and droughts. Approximately 1 billion people call monsoonal basins home, while another 500 million call deltas home. In this situation, the lives of millions of people are relying on a sustainable integrated WRM plan, which is an essential issue being handled by engineers and hydrologists. To increase water security in the face of increasing demand, water scarcity, growing uncertainty, and severe natural hazards such as floods and droughts, politicians, governments, and all shareholders will be required to invest in institutional strengthening, data management, and hazard control infrastructure facilities. Institutional instruments such as regulatory frameworks, water prices, and incentives are needed for better allocation, governance, and conservation of water resources. Having open access to information is essential for water resources monitoring, decision-making under uncertainty, hydro-meteorological prediction, and early warning. Ensuring the quick spread and appropriate adaptation or use of these breakthroughs is critical for increasing global water resilience and security. However, the absence of appropriate data sets restricts the accuracy of prediction models, especially in complex real-world applications. Moreover, advanced multi-dimensional prediction models are scarce in hydrology and WRM studies. ML algorithms should be able to self-learn and make accurate predictions based on the provided data. It is anticipated that models that integrate various efficient algorithms into elaborate ML architectures will form the groundwork for future research lines. Some of the difficulties currently encountered in hydrological prediction may be overcome by employing newly emerging networks such as graph neural networks. The lack of widespread adaption of cutting-edge algorithms in the water-resource field, such as those used in image and natural language processing, hampers the creation of cutting-edge multidisciplinary models for integrated WRM. Table 4 shows no signs of the implementation of attention-based models, CNNs, or even more compatible models with long sequence time-series forecasting (LSTF), such as informer and conformer. Finding an appropriate prediction model and prediction strategy is the primary difficulty in prediction research. The five initial steps for ML prediction models are shown in Figure 3. If even one of these steps is conducted poorly, it will affect the rest, and as a result, the entire prediction strategy will fail.
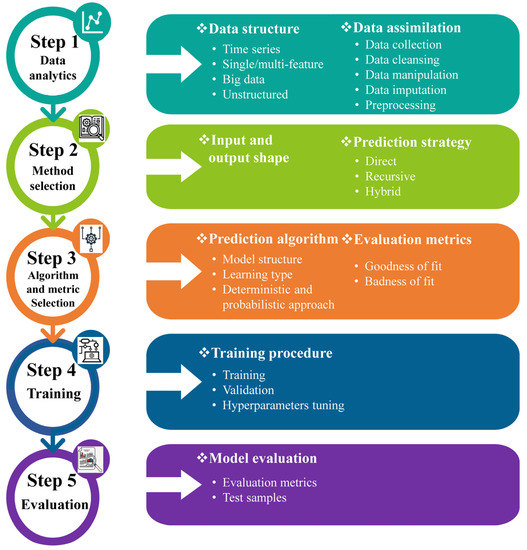
Figure 3.
Steps of machine learning–based prediction strategies.
3.2. Clustering
The importance of clustering in hydrology cannot be overstated. The clustering of hydrological data provides rich insights into diverse concepts and relations that underline the inherent heterogeneity and complexity of hydrological systems. Clustering is a form of unsupervised ML that can identify hidden patterns in data and classify them into sets of items that share the most similarities. Similarities and differences among cluster members are revealed by the clustering procedure. The intra-cluster similarity is just as important as inter-cluster dissimilarity in cluster analysis. Different clustering algorithms vary in how they detect different types of data patterns and distances. Classification is distinct from clustering. In other words, a machine uses a supervised procedure called classification to learn the pattern, structure, and behavior of the data that it is fed. In supervised learning, the machine is fed with labeled historical data in order to learn the relationships between inputs and outputs, whereas in unsupervised learning, the machine is fed only input data and then asked to discover the hidden patterns. In this method, data is clustered to make models more manageable, decrease their dimensionality, or improve the efficiency of the learning process. Each of these applications, along with the pertinent literature, is discussed in this section.
3.2.1. Algorithms and Metrics for Evaluation
There are numerous discussions of clustering algorithms in the literature. Some studies classify clustering algorithms as monothetic or polythetic. Members of a cluster share a common set of characteristics in monothetic approaches, whereas polythetic approaches are based on a broader measure of similarity [48]. Depending on the algorithm’s parameters, a clustering algorithm may produce either hard or soft clusters. Hard clustering requires that an element is either a member of a cluster or not. Soft clustering allows for the possibility of cluster overlap. The structure of the resulting clusters may be flat or hierarchical. While some strategies for clustering produce collections of groups, others benefit from a systematic approach. Algorithms for hierarchical clustering may be agglomerative or divisive [49]. A dataset’s points are clustered by combining them with their neighbors using agglomerative approaches. The desired number of clusters is attained by repeatedly dividing the original unit in divisive approaches.
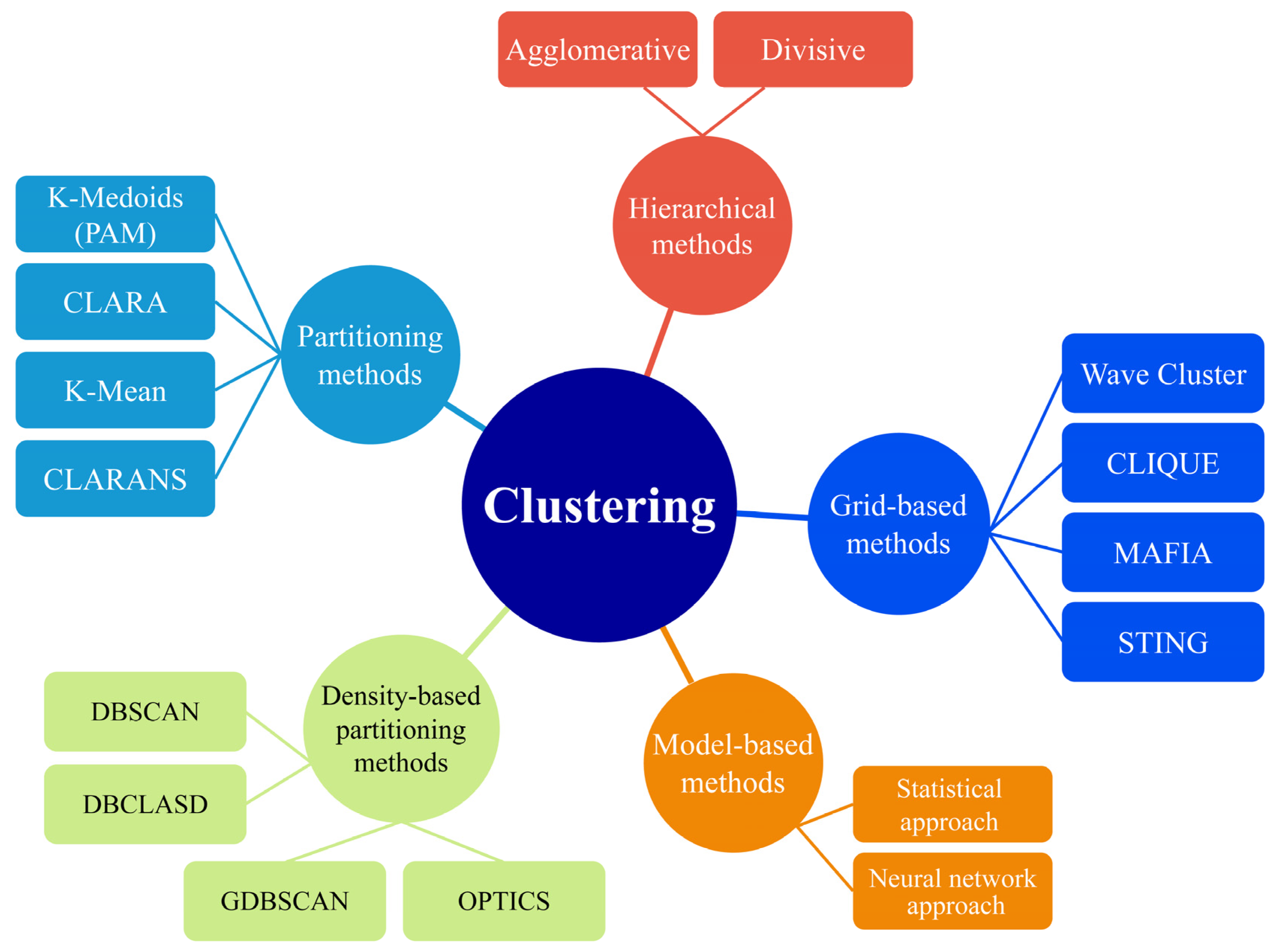
The well-known clustering algorithms in WRM are shown in Figure 4. Many clustering algorithms fall into the individual branches of the figure. Some of the famous partitional methods are K-means, K-medians, and K-modes. These algorithms are centroid-based methods that form clusters around known data centroids. Fuzzy sets and fuzzy C-means are soft clustering techniques applied extensively in control systems and reliability studies. The density-based spatial clustering of applications with noise (DBSCAN) and its updated version, distributed density-based clustering for multi-target regression, deals with probabilities while clustering. Divisive clustering analysis (DIANA) and agglomerative nesting (AGNES) are two hierarchical methods and functions that readily visualize the clustering procedure. The performances of these algorithms significantly depend on the distance functions chosen. Distribution-based clustering of large spatial databases (DBCLASD) and Gaussian mixed models are some of the popular distribution-based functions built upon mature experiments. The statistics of support vectors are used by the support vector clustering algorithms to develop data clusters with some margins. Table 5 lists some of the error functions commonly used to assess the performance of clustering algorithms. These metrics can be used to answer both the question of which clustering method performs better and the question of how many clusters should be used in a given dataset. These issues may be addressed in a variety of ways, such as through the use of graphical inspection and the implementation of an optimization algorithm. Nonetheless, this relies on the clustered dataset, and no comprehensive approaches have yet been proposed.
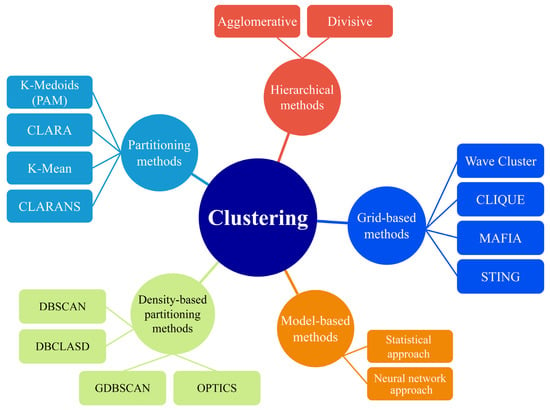
Figure 4.
Clustering algorithms organization.

Table 5.
Common error functions in clustering.
3.2.2. Clustering in the Field of WRM
Clustering techniques are extensively applied in different WRM fields. It is up to the discretion of the decision maker (DM) to choose the best strategy for the growth and use of water resources. When the DM has access to relevant data, better decisions should follow. However, as more data become available, the DM will have a harder time compiling relevant summaries and settling on a single decision option. Clustering analysis has proven to be a useful method of condensing large amounts of data into manageable chunks for easier analysis and management in a decision-making environment [56].
Some of the applications of clustering algorithms in hydrology include time series modeling [57], interpolation and data mining [58], delineation of homogenous hydro-meteorological regions [59], catchment classification [60], regionalization of the catchment for flood frequency analysis and prediction [61], flood risk studies [62], hydrological modeling [63], hydrologic similarity [64], and groundwater assessment [65,66]. Clustering is useful in these situations because it simplifies the creation of effective executive plans and maps by reducing the problem diversity. Furthermore, one of the more traditional uses of clustering analysis is in spotting outliers and other anomalies in the dataset. Any clustering approach can be used for anomaly detection, but the choice will depend on the nature and structure of the data. To sum up, cluster analysis is advantageous for complex projects because it enables accurate dimension reduction for both models and features without compromising accuracy.
3.2.3. Clustering Applications and Challenges in WRM
Some recent applications of clustering algorithms in WRM are summarized in Table 6. Model simplification, ease of learning, and dimensionality reduction are all areas where K-means variants contribute significantly to hydrological research. Moreover, they are easy to change to fit different types, shapes, and distributions of data, and they are easy to apply and available in most commercial data analysis and statistics packages. As shown in Table 6, K-means and hierarchical clustering are the most commonly used methods in WRM. The former can handle big data well, while the later cannot. This is because the time complexity of K-means is linear, whereas that of hierarchical clustering is quadratic [67]. Hierarchical algorithms are predominantly used for dimension reduction [68]. Data imputation and cleaning are two examples of secondary data analytics applications that benefit from density-based algorithms. Furthermore, a recent study by Gao et al. [69] reported the capability of density-based algorithms for clustering a dataset with missing features. Most studies report the number of clusters required for the successful application of a clustering algorithm because conventional clustering algorithms cannot efficiently handle real-world data clustering challenges [70]. As shown in Table 6, the required number of clusters varies considerably based on the nature of the problem. While the optimal method for determining the number of clusters to employ is discussed in the majority of clustering papers, this is still a topic of debate in the ML community.

Table 6.
Applications of clustering algorithms in WRM.
Although unsupervised learning performs well in reducing the dimensions of complicated models, the rate at which new clustering algorithms are created has fallen in recent years. Various neural networks can play a role as clustering algorithms. It is anticipated that new ML algorithms will be required to solve multidisciplinary WRM problems, and data clustering will be an important step in defining a constructive problem. After discovering their hidden patterns, ML algorithms are able to autonomously solve these problems. Clustering ensembles, as opposed to single clustering models, are at the forefront of computer science. The effectiveness of diverse ensemble architectures still needs to be investigated. The reliability of probabilistic clustering algorithms, which are an updated version of classic decision-making tools, have also been investigated in recent research. Unsupervised learning-based predictive models and their accuracy evaluation are a new field of research.
3.3. Reinforcement Learning
This section provides an in-depth introduction to RL, covering all the fundamental concepts and algorithms. After years of being ignored, this subfield of ML has recently gained much attention as a result of the successful application of Google DeepMind to learning to play Atari games in 2013 (and, later, learning to play Go at the highest level) [92]. This modern subfield of ML is a crowning achievement of DL. RL deals with how to learn control strategies to interact with a complex environment. In other words, RL defines how to interact with the environment based on experience (by trial and error) as a framework for learning. Currently, RL is the cutting-edge research topic in the field of modern artificial intelligence (AI), and its popularity is growing in all scientific fields. It is all about taking appropriate action to maximize reward in a particular environment. In contrast to supervised learning, in which the answer key is included in the training data by labeling them, and the model is trained with the correct answer itself, RL does not have an answer; instead, the reinforcement autonomous agent determines what to do in order to accomplish the given task. In other words, unlike supervised learning, where the model is trained on a fixed dataset, RL works in a dynamic environment and tries to explore and interact with that environment in different ways to learn how to best accomplish its tasks in that environment without any form of human supervision [93,94]. The Markov decision process (MDP), which is a framework that can be utilized to model sequential decision-making issues, along with the methodology of dynamic programming (DP) as its solution, serves as the mathematical basis for RL [95]. RL extends mainly to conditions with known and unknown MDP models. The former refers to model-based RL, and the latter refers to model-free RL. Value-based RL, including Monte Carlo (MC) and temporal difference (TD) methods, and policy-search-based RL, including stochastic and deterministic policy gradient methods, fall into the category of model-free RL. State–action–reward–state–action (SARSA) and Q-learning are two well-known TD-based RL algorithms that are widely employed in RL-related research, with the former employing an on-policy method and the latter employing an off-policy method [90,91].
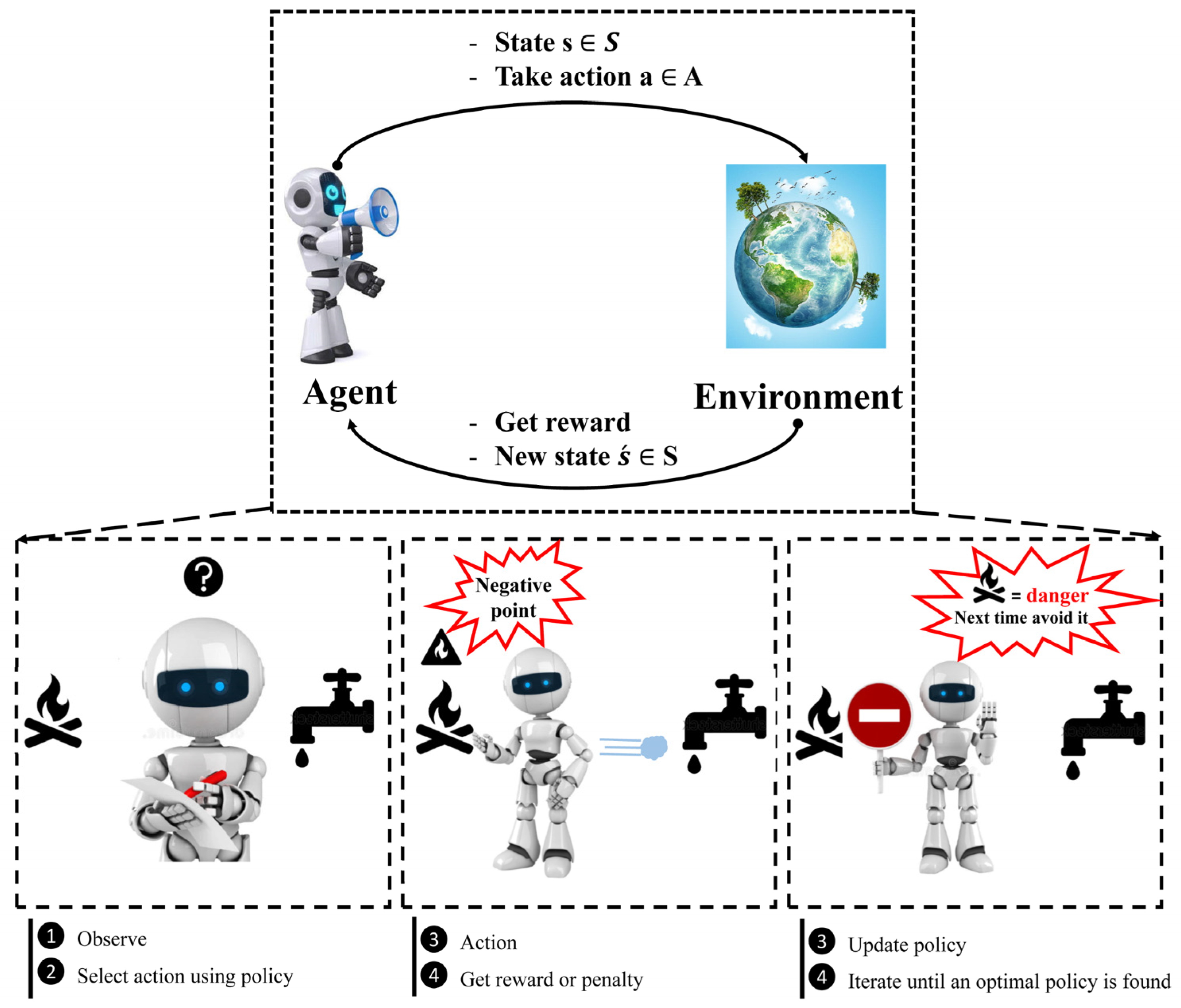
When it comes to training agents for optimal performance in a regulated Markovian domain, Q-learning is one of the most popular RL techniques [96]. It is an off-policy method in which the agent discovers the optimal policy without following the policy. The MDP framework consists of five components, as shown in Figure 5. To comprehend RL, it is required to understand agents, environments, states, actions, and rewards. An autonomous agent takes action, where the action is the set of all possible moves the agent can take [97]. The environment is a world through which the agent moves and responds. The agent’s present state and action are inputs, while the environment returns the agent’s reward and its next state as outputs. A state is the agent’s concrete and immediate situation. An action’s success or failure in a given state can be measured through the provision of feedback in the form of a reward, as shown in Figure 5. Another term in RL is policy, which refers to the agent’s technique for determining the next action based on the current state. The policy could be a neural network that receives observations as inputs and outputs the appropriate action to take. The policy can be any algorithm one can think of and does not have to be deterministic. Owing to inherent dynamic interactions and complex behaviors of the natural phenomena dealt with in WRM, RL could be considered a remedy to solve a wide range of tasks in the field of hydrology. Most real-world WRM challenges can be handled by RL for efficient decision-making, design, and operation, as elucidated in this section.
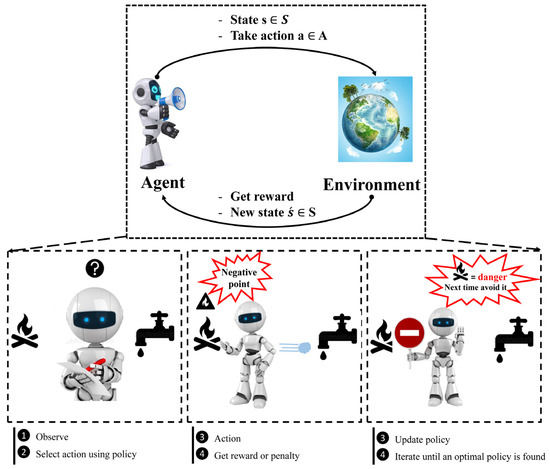
Figure 5.
Concept of reinforcement learning (RL).
Water resources have always been vital to human society as sources of life and prosperity [98]. Owing to social development and uneven precipitation, water resources security has become a global issue, especially in many water-shortage countries where competing demands over water among its users are inevitable [99]. Complex and adaptive approaches are needed to allocate and use water resources properly. Allocating water resources properly is difficult because many different factors, including population, economic, environmental, ecologic, policy, and social factors, must be considered, all of which interact with and adapt to water resources and related socio-economic and environmental aspects.
RL can be utilized to model the behaviors of agents, simplify the process of modeling human behavior, and locate the optimal solution, particularly in an uncertain decision-making environment, to optimize the long-term reward. Simulating the actions of agents and the feedback corresponding to those actions from the environment is the aim of RL-based approaches. In other words, RL involves analyzing the mutually beneficial relationships that exist between the agents and the system, which is an essential requirement in an optimal water resources allocation and management scenario. Another challenging yet less investigated issue in WRM and allocation is shared resource management. Without simultaneously considering the complicated and challenging social, economic, and political aspects, along with the roles of all the beneficiaries and stakeholders, providing an applicable decision-making plan for water demand management is not possible, especially in countries located in arid regions suffering from water crises. Various frameworks have been proposed to analyze and model such a multi-level, complex, and dynamic environment. In the last two decades, complex adaptive systems (CASs) have received much attention because of their efficacy [100].
In the realm of WRM, agent-based modeling (ABM) is a popular simulation method for investigating the non-linear adaptive interactions inherent to a CAS [95]. ABM has been widely used for simulating human decisions when modeling complex natural and socioecological systems. In contrast, the application of ABM in WRM is still relatively new [101], despite the fact that it can be used to define and simulate water resources wherein individual actors are described as unique and autonomous entities that interact regionally with one another and with a shared environment, thus addressing the complexity of integrated WRM [102,103]. In RL water resources-related studies, when addressing water allocation systems, from water infrastructure systems and ecological water consumers to municipal water supply and demand problem management, agents have been conceptualized to represent urban water end-users [104,105].
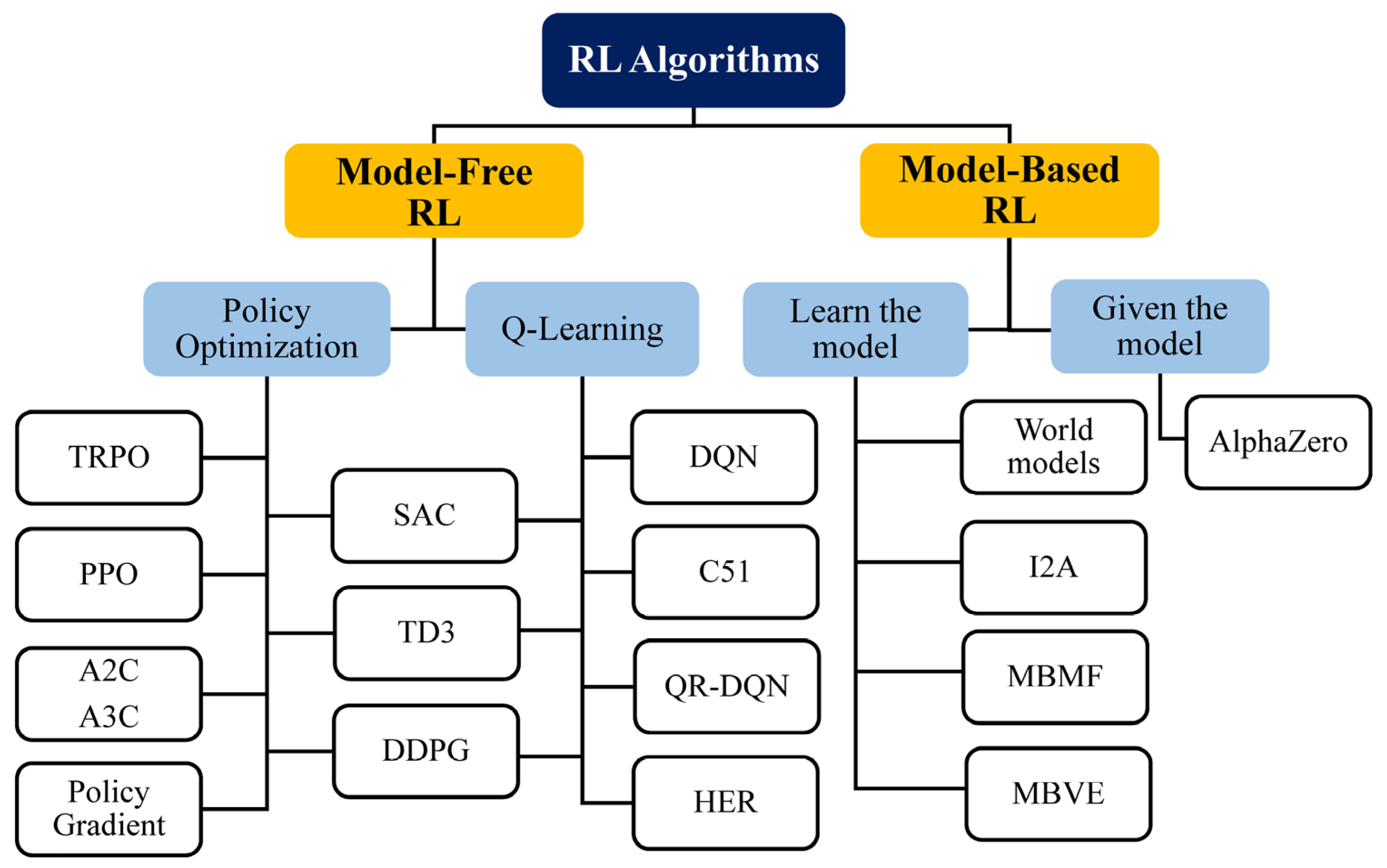
While RL has shown promise in self-driving cars, games, and robot applications, it has not been given widespread attention related to applications in the field of hydrology. However, RL is expected to take over an increasingly wide range of real-world applications in the future, especially to obtain better WRM schemes. Over the past five years, numerous frameworks have emerged, including Tensorforce, which is a useful RL open-source library based on TensorFlow [106], and Keras-RL [107]. In addition to these, it is notable that there are now additional frameworks such as TF-agents [108], RL-coach [109], acme [110], dopamine [111], RLlib [112], and stable baselines3 [113]. RL can be integrated with a DNN as a function approximator to improve its performance. Deep reinforcement learning (DRL) is capable of automatically and directly abstracting and extracting high-level features while avoiding complex feature engineering for a specific task. Some trendy DRL algorithms that are modified from Q-learning include the deep Q-network (DQN) [92], double DQN (DDQN) [114], and dueling DQN [115]. Other packages for the Python programming language are available to facilitate the implementation of RL, including the PyTorch-based RL (PFRL) library [116]. Other fundamental, engineering-focused programming languages such as MATLAB (MathWorks), and Modelica (Modelica Association Project) have also been utilized for the development and instruction of RL agents. The application of RL in WRM and planning will simplify the complexity of all the conflicting interests and their interactions. It will also provide a powerful tool for simulating new management scenarios to understand the consequences of decisions in a more straightforward way [95]. The categorization of RL algorithms by OpenAI using [112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129] was utilized to draw the overall picture in Figure 6.
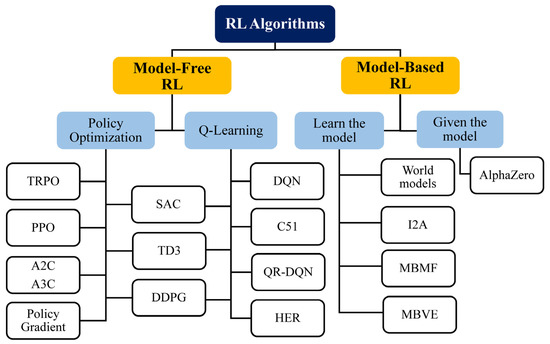
Figure 6.
Reinforcement learning (RL) categorization (all the abbreviations are provided in the nomenclature).
4. Less-Studied Areas for ML Applications in WRM
In this section, less-studied areas for ML application, including spatiotemporal, geo-spatiotemporal, and probabilistic challenges in WRM are reviewed in order of their significance to future research. The following sections review the state-of-the-art applications of ML techniques in the field of WRM, the relevant problems, and a future trend.
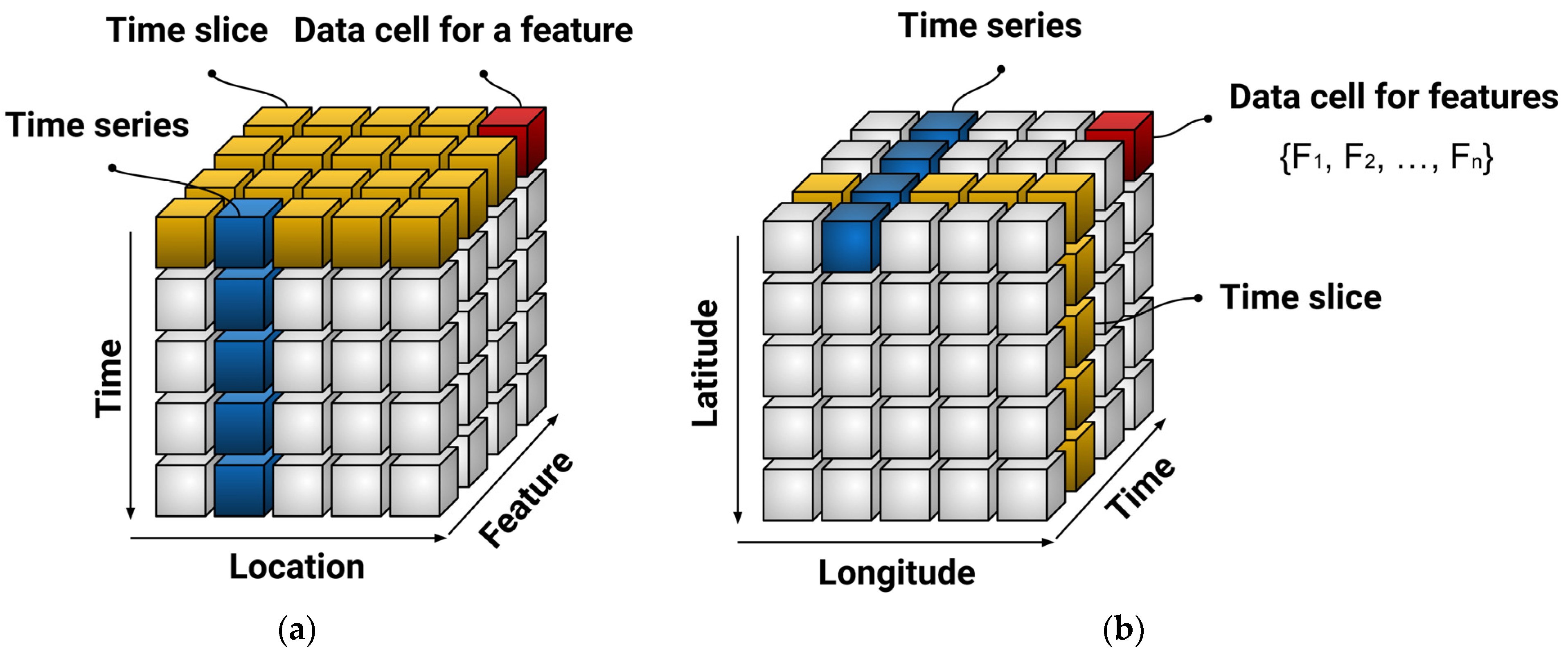
Spatiotemporal studies model and analyze simultaneously how phenomena change over space and time. Due to the fact that they construct a one-dimensional picture of a multifaceted problem, they are of the utmost importance for the development of WRM strategies. In recent years, the emphasis on ML-driven spatiotemporal analysis tools has increased significantly. This is mainly due to the significant technical advancements made in the implementation of new assets, such as sensors and online devices that collect geographical and temporal data. At the beginning of the training process for an ML model, the input data are annotated with geo-spatial and temporal features. This is done in order to model the data’s dynamics while the machine is being trained. Various techniques have already been developed and formulated in order to make progress toward this objective. Depending on the geo-spatiotemporal context, time data can be presented as a continuous sequence, as a collection of sets that form an n-dimensional shape, or as a hidden component within the dynamic model itself. In the first, the machine can be trained with a single or multiple time series or the observation time can be recorded alongside the model’s other variables as an independent variable. The second type of data includes the date, hour, and minute to facilitate the learning process. In the third scenario, the input data are organized according to the timestamps of the occurrences, increasing the monitoring efficiency. Similarly, geographic coordinates can be used to precisely assign the geo-spatiotemporal characteristics of data. In addition, data inputs can be labeled with geo-spatiotemporal information, or model variables can be explored across discrete cells on different grids. Each of these methods can be used to train a variety of algorithms; the most appropriate method typically depends on the available modeling environment and library resources, as well as the individual’s preferences. Overall, the features of spatiotemporal and geo-spatiotemporal frameworks are instructed to consider time and location labels in spatiotemporal and longitude and latitude in geo-spatiotemporal frameworks, as depicted schematically in Figure 7a,b, respectively.
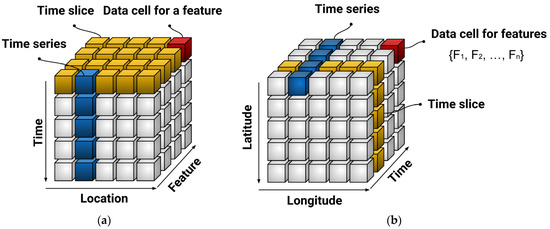
Figure 7.
Schematic representation of ML–driven for (a) spatiotemporal model, and (b) geo-spatiotemporal model.
The field of hydrology is characterized by a high degree of epistemic uncertainty and limited knowledge of the inherent complexity. The limited quality and availability of data have been hindrances in both areas. In the field of hydrology, the development of automatic monitoring and surveillance sensors, as well as high-resolution remote sensing data from a variety of sources, has resulted in an abundance of new, high-quality data known as big data. Utilizing large-scale hydrological datasets necessitates the creation and implementation of new geo-spatiotemporal tools for use in computational analytics and hydrological modeling. In particular, technologies that fall under the concept of geospatial and geo-spatiotemporal AI, such as DL and parallel computing, provide the ways to effectively employ this geo-spatiotemporal dataset and improve integrated hydrological system modeling, especially in poorly gauged or even ungauged basins.
The application of newly emerging ML technologies, along with accessible large-scale hydroclimate data, simplifies the existing challenges in WRM due to the intermittent nature of natural phenomena and complexities of the existing correlations and inter-dependencies among them. Future studies must consider not only the complexity of integrated WRM systems, but also the hydrological uncertainties. Probabilistic method is an alternative to consider the uncertainties in ML applications. A probabilistic approach is a method that considers uncertainty in the data not only to optimize the expected value but also to infer the distribution of such uncertainty. A probabilistic method such as the Bayesian approach can serve as a straightforward illustration of uncertainty investigation. The fitting of stochastic processes and determination of the parameters of distributions are examples of applications of probabilistic methods in WRM. These applications can be utilized for a wide variety of purposes, including streamflow prediction, pollution detection, resource allocation, and groundwater level prediction.
Another less-studied issue in the field of hydrology is considering the complex geo-spatiotemporal interdependencies among the input features in ML-driven models. Some recent spatiotemporal studies are summarized in Table 7. ML tools have been employed in a wide range of WRM fields, from streamflow prediction to pollution detection in a water distribution network. Due to the complexity of hydro-meteorological data’s spatiotemporal patterns, predictive models typically require more complex algorithms to detect as many dependencies as possible. Newly emerged DNN algorithms can effectively capture spatiotemporal patterns in data. The type of geo-spatiotemporal problem, chosen algorithm, and the main objective of the simulation all influence the data resolution. Studies of basins at different scales can be conducted from the national to the local scale. Likewise, the temporal resolution can vary from monthly to just a few seconds in WRM studies. Many developed and developing countries throughout the world have used ML algorithms extensively. Prior to attention-based algorithms, which are more capable in handling the geo-spatiotemporal complexities, CNN, and LSTM were the most widely used algorithms in this field.

Table 7.
State-of-the-art applications of ML to spatiotemporal studies.
5. Challenges and Future Research
There are still significant limitations, despite the fact that all of the aforementioned studies have achieved great success. First, the majority of previous research focused on conventional ML models, whereas the newly emerging DL attention-based models (i.e., long- and short-term time-series networks (LSTNet), transformer, informer, and conformer) are in their infancy, particularly in the field of WRM. In addition, previous studies focused primarily on one or two aspects of prediction improvement, such as spatial or temporal dependencies, whereas the geo-spatiotemporal studies are still in the early stages. Notably, traditional algorithms often ignore spatiotemporal consistency. Nonetheless, a framework that can generate 3D input data (i.e., high resolution, high spatiotemporal continuity, and high precision) is urgently required. Even though autocorrelated patterns are frequently identified in recorded datasets, ML algorithms have not been thoroughly utilized to manage geo-spatiotemporal problems in WRM. In this regard, Ghobadi et al. [20] proposed the application of multimedia tensors as inputs in order to extract the complex relationships in a geo-spatiotemporal environment and increase the accuracy of long-term multi-step ahead streamflow prediction. Moreover, in their research, the application of networks comprising different topping and bottoming models, each focusing on different types of interdependencies, was also proposed. Last but not least, attention-based DL, a new generation of ML technology, has been validated as a promising approach in a variety of domains, outperforming conventional ML models with considerable performance improvements.
It is anticipated that geo-spatiotemporal models will be developed as an extension of the current spatiotemporal models. In the absence of sufficient historical data, ML algorithms struggle to make accurate predictions. Therefore, it is anticipated that transfer learning algorithms will be developed in this area to take advantage of the data availability in some areas for use in a location with a lack of sufficient in-situ data. Moreover, the majority of recent nationwide spatiotemporal studies have employed static models that oversimplify the problem. It is anticipated that future research will develop dynamic models with accelerated data extraction. The remaining obstacles in spatiotemporal and geo-spatiotemporal research include the removal of irrelevant information from spatial data frames, the selection of the optimal temporal horizon and resolution, and the simplification of the interface between data mining tools and ML algorithms.
The advent of global hydroclimate data provides a permanent solution to hydrologic prediction at various geo-spatiotemporal scales for regions without sufficient stations or ungauged basins. Several prior studies evaluated the global applicability of hydroclimate data to improve prediction accuracy through spatiotemporal modeling [136,137]. These models form multivariate time series by concatenating time series across columns for each location. The open literature review indicates that the gradient vanishing issues prevent standalone prediction models like LSTM and GRU from providing an accurate long-term prediction, while integrated models can increase prediction accuracy [138]. Self-attention allows for the re-representation of an input sequence by focusing on different positions and capturing precise, long-term, and long-range dependencies. Recent studies suggest that the transformer network can improve long-term multivariate time series (MTS) prediction [20]. To the best of our knowledge, an open challenge in the field of hydrology is a systematic approach to dealing with complex geo-spatiotemporal dependencies to achieve robust long-term prediction. Moreover, another major bottleneck in DL is automatic feature engineering compatible with 3D data. [139]. To sum up, intelligent and cutting-edge integrated networks are necessary to address the existing complex and dynamic long-term dependencies in order to make accurate predictions and manage LSTF.
6. Conclusions
The first part of this review classified the major ML techniques into prediction, clustering, and reinforcement learning categories. Determining an appropriate prediction strategy as the main challenge of prediction studies has been addressed. Moreover, a prediction model procedure has been divided into five main steps to facilitate future studies, including data analytics, method selection, algorithm and metric selection, training, and evaluation. Data have been clustered in order to simplify models, reduce their dimensions, or facilitate the learning procedure in WRM-related studies. Several metrics have been reported to address major clustering challenges, including figuring out the ideal number of clusters and the clustering algorithm that best fits the data. The clustering algorithms were considered according to their goals, overlap, and structure to pave the way for configuring efficient ensembles of clustering algorithms in future studies. The second part of this review introduced spatiotemporal and geo-spatiotemporal views in existing studies that contribute to the design and operation of long-term WRM and planning. In order to solve complex multiobjective, multiperiod, nonlinear water resources-related problems, this review suggested focusing on the RL method, which could be used to model the decision-making of agents capable of adapting to a dynamic environment by learning from past experiences. The spatiotemporal data resolution varies from miles and monthly values to inches and seconds. Future geo-spatiotemporal studies will develop multidimensional models that go beyond the spatial and temporal dimensions by employing new variants of attention-based networks such as LSTNet, transformer, conformer, and informer. Because integrated WRM and planning gives consideration to stakeholders’ cognitive beliefs and values, the circular economy; water demand management; and natural, political, social, and economic disputes that contribute to water management problems count as essential aspects that must be considered. Moreover, owing to the existence of dynamic interactions and adaptations between water resources and related socio-economic and environmental areas, water crises, and resource allocation, this review suggests using RL in dealing with multidimensional research related to integrated WRM. In the near future, it is anticipated that RL agents will focus on this field in order to comprehend the behaviors of integrated hydrological systems, develop policies by employing an integrated pathway, and reveal the optimal management frameworks. Thanks to advancements in ML techniques, the WRM field is anticipated to witness the growth of intelligent control and monitoring infrastructure in the coming years.
Author Contributions
F.G.: conceptualization, methodology, investigation, software, validation, formal analysis, data curation, writing—original draft, writing—review and editing, visualization. D.K.: supervision, validation, writing—review and editing, resources, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by (1) the Korea Ministry of Environment (MOE) as “Graduate School specialized in Climate Change” and (2) the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (20224000000260).
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| A2c-A3c | Asynchronous Advantage Actor-Critic |
| ABM | Agent-based modeling |
| AGNES | Agglomerative nesting |
| AI | Artificial intelligence |
| AR | Autoregressive |
| ARIMA | AR-integrated moving average |
| BART | Bayesian additive regression tree |
| BNN | Bayesian neural network |
| BP-ANN | Back-propagation artificial neural network |
| C51 | Categorical 51-Atom DQN |
| CAS | Complex adaptive systems |
| CLARA | Clustering Large Applications |
| CLARANS | Clustering Large Applications based on RANdomized Search |
| CNN | Convolutional neural networks |
| DBCLASD | Distribution-based clustering of large spatial databases |
| DBSCAN | Density-based spatial clustering of applications with noise |
| DDPG | Deep Deterministic Policy Gradient |
| DDQN | Double DQN |
| DIANA | Divisive clustering analysis |
| DL | Deep learning |
| DM | Data management |
| DM | Decision maker |
| DNN | Deep neural networks |
| DP | Dynamic programming |
| DQN | Deep Q-Network |
| DRL | Deep reinforcement learning |
| ELM | Extreme learning machine |
| EMD | Empirical mode decomposition |
| GA | Genetic algorithm |
| GNG | Growing neural gas |
| GRU | Gated recurrent unit |
| GWL | Groundwater level |
| HER | Hindsight Experience Replay |
| I2A | Imagination-Augmented Agents |
| IHP | Intergovernmental Hydrological Programme |
| KNN | K-nearest neighbors |
| LSTF | Long sequence time-series forecasting |
| LSTM | Long and short-term memory |
| LSTNet | Long- and Short-term Time-series network |
| MBMF | Model-Based RL with Model-Free Fine-Tuning |
| MBVE | Model-Based Value Expansion |
| MC | Monte Carlo |
| MDP | Markov Decision Process |
| ML | Machine learning |
| MLP | multi-layer perceptron |
| MODWT | Maximal Overlap Discrete Wavelet Transform |
| MTS | Multivariate time series |
| PCSA | parallel cooperation search algorithm |
| PPO | Proximal Policy Optimization |
| QR-DQN | Quantile Regression DQN |
| RF | Random forest |
| RL | Reinforcement learning |
| RNN | Recurrent neural networks |
| SAC | Soft Actor-Critic |
| SARSA | State–action–reward–state–action |
| STDM | Serial triple diagram model |
| SVM | Support vector machine |
| SWOT | Strengths, weaknesses, opportunities, and threats |
| TD | Temporal Difference |
| TD3 | Twin Delayed DDPG |
| TRPO | Trust Region Policy Optimization |
References
- Razavi, S.; Hannah, D.M.; Elshorbagy, A.; Kumar, S.; Marshall, L.; Solomatine, D.P.; Dezfuli, A.; Sadegh, M.; Famiglietti, J. Coevolution of Machine Learning and Process-Based Modelling to Revolutionize Earth and Environmental Sciences A Perspective. Hydrol. Process. 2022, 36, e14596. [Google Scholar] [CrossRef]
- Reinsel, D.; Gantz, J.; Rydning, J. The Digitization of the World From Edge to Core; International Data Corporation: Framingham, MA, USA, 2018; Available online: https://www.seagate.com/files/www-content/our-story/trends/files/idc-seagate-dataage-whitepaper.pdf (accessed on 7 October 2022).
- UNESCO IHP-IX: Strategic Plan of the Intergovernmental Hydrological Programme: Science for a Water Secure World in a Changing Environment, Ninth Phase 2022-2029. 2022. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000381318 (accessed on 7 October 2022).
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A Review of the Hybrid Artificial Intelligence and Optimization Modelling of Hydrological Streamflow Forecasting. Alexandria Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- Mosaffa, H.; Sadeghi, M.; Mallakpour, I.; Naghdyzadegan Jahromi, M.; Pourghasemi, H.R. Application of Machine Learning Algorithms in Hydrology. Comput. Earth Environ. Sci. 2022, 585–591. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Daccache, A.; Fogg, G.E.; Sadegh, M. Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water 2022, 14, 949. [Google Scholar] [CrossRef]
- Bernardes, J.; Santos, M.; Abreu, T.; Prado, L.; Miranda, D.; Julio, R.; Viana, P.; Fonseca, M.; Bortoni, E.; Bastos, G.S. Hydropower Operation Optimization Using Machine Learning: A Systematic Review. AI 2022, 3, 78–99. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Sungwon, K.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater Level Prediction Using Machine Learning Models: A Comprehensive Review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Santosh, M. Artificial Neural Networks in Drought Prediction in the 21st Century–A Scientometric Analysis. Appl. Soft Comput. 2022, 114, 108080. [Google Scholar] [CrossRef]
- Ewuzie, U.; Bolade, O.P.; Egbedina, A.O. Application of Deep Learning and Machine Learning Methods in Water Quality Modeling and Prediction: A Review. Curr. Trends Adv. Comput. Intell. Environ. Data Eng. 2022, 185–218. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A Review of the Application of Machine Learning in Water Quality Evaluation. Eco-Environment Heal. 2022, 1, 107–116. [Google Scholar] [CrossRef]
- Saha, S.; Mallik, S.; Mishra, U. Groundwater Depth Forecasting Using Machine Learning and Artificial Intelligence Techniques: A Survey of the Literature. Lect. Notes Civ. Eng. 2022, 207, 153–167. [Google Scholar] [CrossRef]
- Hamitouche, M.; Molina, J.-L. A Review of AI Methods for the Prediction of High-Flow Extremal Hydrology. Water Resour. Manag. 2022, 36, 3859–3876. [Google Scholar] [CrossRef]
- Nourani, V.; Paknezhad, N.J.; Tanaka, H. Prediction Interval Estimation Methods for Artificial Neural Network (ANN)-Based Modeling of the Hydro-Climatic Processes, a Review. Sustain 2021, 13, 1633. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.; Zhang, L.; Wang, Z. Regionalization of Hydrological Modeling for Predicting Streamflow in Ungauged Catchments: A Comprehensive Review. Wiley Interdiscip. Rev. Water 2021, 8, e1487. [Google Scholar] [CrossRef]
- Gupta, D.; Hazarika, B.B.; Berlin, M.; Sharma, U.M.; Mishra, K. Artificial Intelligence for Suspended Sediment Load Prediction: A Review. Environ. Earth Sci. 2021, 80, 346. [Google Scholar] [CrossRef]
- Ahansal, Y.; Bouziani, M.; Yaagoubi, R.; Sebari, I.; Sebari, K.; Kenny, L. Towards Smart Irrigation: A Literature Review on the Use of Geospatial Technologies and Machine Learning in the Management of Water Resources in Arboriculture. Agronomy 2022, 12, 297. [Google Scholar] [CrossRef]
- Kikon, A.; Deka, P.C. Artificial Intelligence Application in Drought Assessment, Monitoring and Forecasting: A Review. Stoch. Environ. Res. Risk Assess. 2021, 36, 1197–1214. [Google Scholar] [CrossRef]
- Ghobadi, F.; Kang, D. Multi-Step Ahead Probabilistic Forecasting of Daily Streamflow Using Bayesian Deep Learning: A Multiple Case Study. Water 2022, 14, 3672. [Google Scholar] [CrossRef]
- Ghobadi, F.; Kang, D. Improving Long-Term Streamflow Prediction in a Poorly Gauged Basin Using Geo-Spatiotemporal Mesoscale Data and Attention-Based Deep Learning: A Comparative Study. J. Hydrol. 2022, 615, 128608. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Hazarika, B.B.; Gupta, D.; Heddam, S.; Kisi, O. Streamflow Prediction in Mountainous Region Using New Machine Learning and Data Preprocessing Methods: A Case Study. Neural Comput. Appl. 2022, 1–18. Available online: https://link.springer.com/article/10.1007/s00521-022-08163-8 (accessed on 7 October 2022). [CrossRef]
- Granata, F.; Di Nunno, F.; de Marinis, G. Stacked Machine Learning Algorithms and Bidirectional Long Short-Term Memory Networks for Multi-Step Ahead Streamflow Forecasting: A Comparative Study. J. Hydrol. 2022, 613, 128431. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; Najafzadeh, M.; Demir, I. A Stacked Machine Learning Algorithm for Multi-Step Ahead Prediction of Soil Moisture. Hydrology 2022, 10, 1. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Jiang, Y.; Sun, L.; Zhao, R.; Yan, K.; Wang, W. Accurate Prediction of Water Quality in Urban Drainage Network with Integrated EMD-LSTM Model. J. Clean. Prod. 2022, 354, 131724. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, C.; Liu, H.; Zhang, C.; Zhao, M.; Gong, Q.; Fu, G. Developing Stacking Ensemble Models for Multivariate Contamination Detection in Water Distribution Systems. Sci. Total Environ. 2022, 828, 154284. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zou, L.; Xia, J.; Qiao, Y.; Cai, D. Inner Dynamic Detection and Prediction of Water Quality Based on CEEMDAN and GA-SVM Models. Remote Sens. 2022, 14, 1714. [Google Scholar] [CrossRef]
- Lee, S.S.; Lee, H.H.; Lee, Y.J. Prediction of Minimum Night Flow for Enhancing Leakage Detection Capabilities in Water Distribution Networks. Appl. Sci. 2022, 12, 6467. [Google Scholar] [CrossRef]
- Kizilöz, B. Prediction of Daily Failure Rate Using the Serial Triple Diagram Model and Artificial Neural Network. Water Supply 2022, 22, 7040–7058. [Google Scholar] [CrossRef]
- Zanfei, A.; Brentan, B.M.; Menapace, A.; Righetti, M.; Herrera, M. Graph Convolutional Recurrent Neural Networks for Water Demand Forecasting. Water Resour. Res. 2022, 58, e2022WR032299. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H.; Lee, M.; Han, H.; Kim, D.; Kim, H.S. Development of a Deep Learning-Based Prediction Model for Water Consumption at the Household Level. Water 2022, 14, 1512. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, D.; Peng, Q.; Lin, J.; Jin, T.; Yang, T.; Sorooshian, S.; Liu, Y. Prediction of the Outflow Temperature of Large-Scale Hydropower Using Theory-Guided Machine Learning Surrogate Models of a High-Fidelity Hydrodynamics Model. J. Hydrol. 2022, 606, 127427. [Google Scholar] [CrossRef]
- Drakaki, K.K.; Sakki, G.K.; Tsoukalas, I.; Kossieris, P.; Efstratiadis, A. Day-Ahead Energy Production in Small Hydropower Plants: Uncertainty-Aware Forecasts through Effective Coupling of Knowledge and Data. Adv. Geosci. 2022, 56, 155–162. [Google Scholar] [CrossRef]
- Sattar Hanoon, M.; Najah Ahmed, A.; Razzaq, A.; Oudah, A.Y.; Alkhayyat, A.; Feng Huang, Y.; kumar, P.; El-Shafie, A. Prediction of Hydropower Generation via Machine Learning Algorithms at Three Gorges Dam, China. Ain Shams Eng. J. 2022, 14, 101919. [Google Scholar] [CrossRef]
- Park, K.; Jung, Y.; Seong, Y.; Lee, S. Development of Deep Learning Models to Improve the Accuracy of Water Levels Time Series Prediction through Multivariate Hydrological Data. Water 2022, 14, 469. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Tiefenbacher, J.P. Using Optimized Deep Learning to Predict Daily Streamflow: A Comparison to Common Machine Learning Algorithms. Water Resour. Manag. 2022, 36, 699–716. [Google Scholar] [CrossRef]
- Sun, J.; Hu, L.; Li, D.; Sun, K.; Yang, Z. Data-Driven Models for Accurate Groundwater Level Prediction and Their Practical Significance in Groundwater Management. J. Hydrol. 2022, 608, 127630. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Zhang, Y.; Ghaneei, P. Conjunction of Cluster Ensemble-Model Ensemble Techniques for Spatiotemporal Assessment of Groundwater Depletion in Semi-Arid Plains. J. Hydrol. 2022, 610, 127984. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, X.; Zeng, J.; Jiao, Y.; Li, Y.; Zhong, L.; Yao, L. Ensemble Streamflow Forecasting over a Cascade Reservoir Catchment with Integrated Hydrometeorological Modeling and Machine Learning. Hydrol. Earth Syst. Sci. 2022, 26, 265–278. [Google Scholar] [CrossRef]
- Cho, K.; Kim, Y. Improving Streamflow Prediction in the WRF-Hydro Model with LSTM Networks. J. Hydrol. 2022, 605, 127297. [Google Scholar] [CrossRef]
- Apaydin, H.; Taghi Sattari, M.; Falsafian, K.; Prasad, R. Artificial Intelligence Modelling Integrated with Singular Spectral Analysis and Seasonal-Trend Decomposition Using Loess Approaches for Streamflow Predictions. J. Hydrol. 2021, 600, 126506. [Google Scholar] [CrossRef]
- Peng, L.; Wu, H.; Gao, M.; Yi, H.; Xiong, Q.; Yang, L. TLT: Recurrent Fine-Tuning Transfer Learning for Water Quality Long-Term Prediction. Water Res. 2022, 225, 119171. [Google Scholar] [CrossRef]
- Feng, Z.K.; Shi, P.F.; Yang, T.; Niu, W.J.; Zhou, J.Z.; Cheng, C. tian Parallel Cooperation Search Algorithm and Artificial Intelligence Method for Streamflow Time Series Forecasting. J. Hydrol. 2022, 606, 127434. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Le, X.H.; Anh, D.T.; Kim, S.H.; Bae, D.H. Hourly Streamflow Forecasting Using a Bayesian Additive Regression Tree Model Hybridized with a Genetic Algorithm. J. Hydrol. 2022, 606, 127445. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, G.; Huang, F.; Qin, H.; Wang, B.; Yi, L. Directed Graph Deep Neural Network for Multi-Step Daily Streamflow Forecasting. J. Hydrol. 2022, 607, 127515. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Elbeltagi, A.; Yaseen, Z.M.; Shahid, S.; Kisi, O. Development of New Machine Learning Model for Streamflow Prediction: Case Studies in Pakistan. Stoch. Environ. Res. Risk Assess. 2022, 36, 999–1033. [Google Scholar] [CrossRef]
- Adnan, R.M.; R. Mostafa, R.; Kisi, O.; Yaseen, Z.M.; Shahid, S.; Zounemat-Kermani, M. Improving Streamflow Prediction Using a New Hybrid ELM Model Combined with Hybrid Particle Swarm Optimization and Grey Wolf Optimization. Knowledge-Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Ewees, A.A.; Parmar, K.S.; Yaseen, Z.M.; Shahid, S.; Kisi, O. The Viability of Extended Marine Predators Algorithm-Based Artificial Neural Networks for Streamflow Prediction. Appl. Soft Comput. 2022, 131, 109739. [Google Scholar] [CrossRef]
- Chavent, M.; Lechevallier, Y.; Briant, O. DIVCLUS-T: A Monothetic Divisive Hierarchical Clustering Method. Comput. Stat. Data Anal. 2007, 52, 687–701. [Google Scholar] [CrossRef]
- Tokuda, E.K.; Comin, C.H.; Costa, L. da F. Revisiting Agglomerative Clustering. Phys. Stat. Mech. Its Appl. 2022, 585, 126433. [Google Scholar] [CrossRef]
- Caliñski, T.; Harabasz, J. A Dendrite Method Foe Cluster Analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Chou, C.H.; Su, M.C.; Lai, E. A New Cluster Validity Measure and Its Application to Image Compression. Pattern Anal. Appl. 2004, 7, 205–220. [Google Scholar] [CrossRef]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern 2008, 3, 32–57. [Google Scholar] [CrossRef]
- Wang, J.S.; Chiang, J.C. A Cluster Validity Measure with Outlier Detection for Support Vector Clustering. IEEE Trans. Syst. Man, Cybern. Cybern. 2008, 38, 78–89. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Ramakrishna, R.S. New Indices for Cluster Validity Assessment. Pattern Recognit. Lett. 2005, 26, 2353–2363. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Marsili, F.; Bödefeld, J. Integrating Cluster Analysis into Multi-Criteria Decision Making for Maintenance Management of Aging Culverts. Mathematics 2021, 9, 2549. [Google Scholar] [CrossRef]
- Javed, A. Cluster Analysis of Time Series Data with Application to Hydrological Events and Serious Illness Conversations. Graduate College Dissertations and Theses, The University of Vermont and State Agricultural College, Burlington, Vermont, 2021. [Google Scholar]
- Hamed Javadi, S.; Guerrero, A.; Mouazen, A.M. Clustering and Smoothing Pipeline for Management Zone Delineation Using Proximal and Remote Sensing. Sensors 2022, 22, 645. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Zhang, X.; Ma, Q.; Ren, L. Mapping Homogeneous Regions for Flash Floods Using Machine Learning: A Case Study in Jiangxi Province, China. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102717. [Google Scholar] [CrossRef]
- Tshimanga, R.M.; Bola, G.B.; Kabuya, P.M.; Nkaba, L.; Neal, J.; Hawker, L.; Trigg, M.A.; Bates, P.D.; Hughes, D.A.; Laraque, A.; et al. Towards a Framework of Catchment Classification for Hydrologic Predictions and Water Resources Management in the Ungauged Basin of the Congo River: An a priori approach. In Congo Basin Hydrology, Climate, and Biogeochemistry: A Foundation for the Future; Wiley: New York, NY, USA. [CrossRef]
- Kebebew, A.S.; Awass, A.A. Regionalization of Catchments for Flood Frequency Analysis for Data Scarce Rift Valley Lakes Basin, Ethiopia. J. Hydrol. Reg. Stud. 2022, 43, 101187. [Google Scholar] [CrossRef]
- Sikorska-Senoner, A.E. Clustering Model Responses in the Frequency Space for Improved Simulation-Based Flood Risk Studies: The Role of a Cluster Number. J. Flood Risk Manag. 2022, 15, e12772. [Google Scholar] [CrossRef]
- Li, K.; Huang, G.; Wang, S.; Baetz, B.; Xu, W. A Stepwise Clustered Hydrological Model for Addressing the Temporal Autocorrelation of Daily Streamflows in Irrigated Watersheds. Water Resour. Res. 2022, 58, e2021WR031065. [Google Scholar] [CrossRef]
- Bajracharya, P.; Jain, S. Hydrologic Similarity Based on Width Function and Hypsometry: An Unsupervised Learning Approach. Comput. Geosci. 2022, 163, 105097. [Google Scholar] [CrossRef]
- Zhong, C.; Wang, H.; Yang, Q. Hydrochemical Interpretation of Groundwater in Yinchuan Basin Using Self-Organizing Maps and Hierarchical Clustering. Chemosphere 2022, 309, 136787. [Google Scholar] [CrossRef] [PubMed]
- He, B.; He, J.T.; Zeng, Y.; Sun, J.; Peng, C.; Bi, E. Coupling of Multi-Hydrochemical and Statistical Methods for Identifying Apparent Background Levels of Major Components and Anthropogenic Anomalous Activities in Shallow Groundwater of the Liujiang Basin, China. Sci. Total Environ. 2022, 838, 155905. [Google Scholar] [CrossRef] [PubMed]
- Karypis, M.S.G.; Kumar, V.; Steinbach, M. A comparison of document clustering techniques. In TextMining Workshop at KDD2000; Boston, MA, USA, 2000; pp. 428–439. [Google Scholar]
- Eskandarnia, E.; Al-Ammal, H.M.; Ksantini, R. An Embedded Deep-Clustering-Based Load Profiling Framework. Sustain. Cities Soc. 2022, 78, 103618. [Google Scholar] [CrossRef]
- Gao, K.; Khan, H.A.; Qu, W. Clustering with Missing Features: A Density-Based Approach. Symmetry 2022, 14, 60. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Ikotun, A.M.; Oyelade, O.O.; Abualigah, L.; Agushaka, J.O.; Eke, C.I.; Akinyelu, A.A. A Comprehensive Survey of Clustering Algorithms: State-of-the-Art Machine Learning Applications, Taxonomy, Challenges, and Future Research Prospects. Eng. Appl. Artif. Intell. 2022, 110, 104743. [Google Scholar] [CrossRef]
- Arsene, D.; Predescu, A.; Truica, C.-O.; Apostol, E.-S.; Mocanu, M.; Chiru, C. Consumer Profiling Using Clustering Methods for Georeferenced Decision Support in a Water Distribution System. In 2022 14th International Conference on Electronics, Computers and Artificial Intelligence (ECAI); IEEE: Toulouse, France, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Arsene, D.; Predescu, A.; Truica, C.O.; Apostol, E.S.; Mocanu, M.; Chiru, C. Clustering Consumption Activities in a Water Monitoring System. In Proceedings of the 2022 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2022. [Google Scholar] [CrossRef]
- Bodereau, N.; Delaval, A.; Lepage, H.; Eyrolle, F.; Raimbault, P.; Copard, Y. Hydrological Classification by Clustering Approach of Time-Integrated Samples at the Outlet of the Rhône River: Application to Δ14C-POC. Water Res. 2022, 220, 118652. [Google Scholar] [CrossRef] [PubMed]
- Rami, O.; Hasnaoui, M.D.; Ouazar, D.; Bouziane, A. A Mixed Clustering-Based Approach for a Territorial Hydrological Regionalization. Arab J Geosci. 2022, 15, 75. [Google Scholar] [CrossRef]
- Arsene, D.; Predescu, A.; Pahont, B.; Gabriel Chiru, C.; Apostol, E.-S.; Truică, C.-O. Advanced Strategies for Monitoring Water Consumption Patterns in Households Based on IoT and Machine Learning. Water 2022, 14, 2187. [Google Scholar] [CrossRef]
- Morbidelli, R.; Prakaisak, I.; Wongchaisuwat, P. Hydrological Time Series Clustering: A Case Study of Telemetry Stations in Thailand. Water 2022, 14, 2095. [Google Scholar] [CrossRef]
- Nourani, V.; Ghaneei, P.; Kantoush, S.A. Robust Clustering for Assessing the Spatiotemporal Variability of Groundwater Quantity and Quality. J. Hydrol. 2022, 604, 127272. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Uhlemann, S.; Franklin, M.; Falco, N.; Bouskill, N.J.; Newcomer, M.E.; Dafflon, B.; Siirila-Woodburn, E.R.; Minsley, B.J.; Williams, K.H.; et al. Watershed Zonation through Hillslope Clustering for Tractably Quantifying Above-and below-Ground Watershed Heterogeneity and Functions. Hydrol. Earth Syst. Sci. 2022, 26, 429–444. [Google Scholar] [CrossRef]
- Yin, J.; Medellín-Azuara, J.; Escriva-Bou, A. Groundwater Levels Hierarchical Clustering and Regional Groundwater Drought Assessment in Heavily Drafted Aquifers. Hydrol. Res. 2022, 53, 1031–1046. [Google Scholar] [CrossRef]
- Akstinas, V.; Šarauskienė, D.; Kriaučiūnienė, J.; Nazarenko, S.; Jakimavičius, D. Spatial and Temporal Changes in Hydrological Regionalization of Lowland Rivers. Int. J. Environ. Res. 2021, 16, 1–14. [Google Scholar] [CrossRef]
- Eskandari, E.; Mohammadzadeh, H.; Nassery, H.; Vadiati, M.; Zadeh, A.M.; Kisi, O. Delineation of Isotopic and Hydrochemical Evolution of Karstic Aquifers with Different Cluster-Based (HCA, KM, FCM and GKM) Methods. J. Hydrol. 2022, 609, 127706. [Google Scholar] [CrossRef]
- Lee, Y.; Toharudin, T.; Chen, R.-C.; Kuswanto, H.; Noh, M.; Mariana Che Mat Nor, S.; Milleana Shaharudin, S.; Ismail, S.; Aimi Mohd Najib, S.; Leong Tan, M.; et al. Statistical Modeling of RPCA-FCM in Spatiotemporal Rainfall Patterns Recognition. Atmosphere 2022, 13, 145. [Google Scholar] [CrossRef]
- Akbarian, H.; Gheibi, M.; Hajiaghaei-Keshteli, M.; Rahmani, M. A Hybrid Novel Framework for Flood Disaster Risk Control in Developing Countries Based on Smart Prediction Systems and Prioritized Scenarios. J. Environ. Manag. 2022, 312, 114939. [Google Scholar] [CrossRef]
- James, N.; Bondell, H. Temporal and Spectral Governing Dynamics of Australian Hydrological Streamflow Time Series. J. Comput. Sci. 2022, 63, 101767. [Google Scholar] [CrossRef]
- Xu, M.; Wang, G.; Wang, Z.; Hu, H.; Kumar Singh, D.; Tian, S. Temporal and Spatial Hydrological Variations of the Yellow River in the Past 60 Years. J. Hydrol. 2022, 609, 127750. [Google Scholar] [CrossRef]
- Giełczewski, M.; Piniewski, M.; Domański, P.D. Mixed Statistical and Data Mining Analysis of River Flow and Catchment Properties at Regional Scale. Stoch. Environ. Res. Risk Assess. 2022, 36, 2861–2882. [Google Scholar] [CrossRef]
- Tafvizi, A.; James, A.L.; Yao, H.; Stadnyk, T.A.; Ramcharan, C. Investigating Hydrologic Controls on 26 Precambrian Shield Catchments Using Landscape, Isotope Tracer and Flow Metrics. Hydrol. Process. 2022, 36, e14528. [Google Scholar] [CrossRef]
- Hung, F.; Son, K.; Yang, Y.C.E. Investigating Uncertainties in Human Adaptation and Their Impacts on Water Scarcity in the Colorado River Basin, United States. J. Hydrol. 2022, 612, 128015. [Google Scholar] [CrossRef]
- Saber, J.; Hales, R.C.; Sowby, R.B.; Williams, G.P.; James Nelson, E.; Ames, D.P.; Dundas, J.B.; Ogden, J. SABER: A Model-Agnostic Postprocessor for Bias Correcting Discharge from Large Hydrologic Models. Hydrology 2022, 9, 113. [Google Scholar] [CrossRef]
- Tang, T.; Jiao, D.; Chen, T.; Gui, G. Medium- and Long-Term Precipitation Forecasting Method Based on Data Augmentation and Machine Learning Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1000–1011. [Google Scholar] [CrossRef]
- Rahman, A.T.M.S.; Kono, Y.; Hosono, T. Self-Organizing Map Improves Understanding on the Hydrochemical Processes in Aquifer Systems. Sci. Total Environ. 2022, 846, 157281. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow SECOND EDITION Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2022. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT press: Cambridge, MA, USA, 2016; Volume 521, ISBN 978-0262035613. [Google Scholar]
- Agha-Hoseinali-Shirazi, M.; Bozorg-Haddad, O.; Laituri, M.; DeAngelis, D. Application of Agent Base Modeling in Water Resources Management and Planning. Springer Water 2021, 177–216. [Google Scholar] [CrossRef]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Zhu, Z.; Hu, Z.; Chan, K.W.; Bu, S.; Zhou, B.; Xia, S. Reinforcement Learning in Deregulated Energy Market: A Comprehensive Review. Appl. Energy 2023, 329, 120212. [Google Scholar] [CrossRef]
- Nurcahyono, A.; Fadhly Jambak, F.; Rohman, A.; Faisal Karim, M.; Neves-Silva, P.; Cruz Foundation, O.; Horizonte, B. Shifting the Water Paradigm from Social Good to Economic Good and the State’s Role in Fulfilling the Right to Water. F1000Research 2022, 11, 490. [Google Scholar] [CrossRef]
- Damascene123, N.J.; Dithebe, M.; Laryea, A.E.N.; Medina, J.A.M.; Bian, Z.; Gilbert, M.A.S.E.N.G.O. Prospective Review of Mining Effects on Hydrology in a Water-Scarce Eco-Environment; North American Academic Research: San Francisco, CA, USA, 2022; Volume 5, pp. 352–365. [Google Scholar] [CrossRef]
- Yan, B.; Jiang, H.; Zou, Y.; Liu, Y.; Mu, R.; Wang, H. An Integrated Model for Optimal Water Resources Allocation under “3 Redlines” Water Policy of the Upper Hanjiang River Basin. J. Hydrol. Reg. Stud. 2022, 42, 101167. [Google Scholar] [CrossRef]
- Xiao, Y.; Fang, L.; Hipel, K.W.; Wre, H.D.; Asce, F. Agent-Based Modeling Approach to Investigating the Impact of Water Demand Management; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Lin, Z.; Lim, S.H.; Lin, T.; Borders, M. Using Agent-Based Modeling for Water Resources Management in the Bakken Region. J. Water Resour. Plan. Manag. 2020, 146, 05019020. [Google Scholar] [CrossRef]
- Berglund, E.Z.; Asce, M. Using Agent-Based Modeling for Water Resources Planning and Management. J. Water Resour. Plan. Manag. 2015, 141, 04015025. [Google Scholar] [CrossRef]
- Tourigny, A.; Filion, Y. Sensitivity Analysis of an Agent-Based Model Used to Simulate the Spread of Low-Flow Fixtures for Residential Water Conservation and Evaluate Energy Savings in a Canadian Water Distribution System. J. Water Resour. Plan. 2019, 145, 1. [Google Scholar] [CrossRef]
- Giacomoni, M.H.; Berglund, E.Z. Complex Adaptive Modeling Framework for Evaluating Adaptive Demand Management for Urban Water Resources Sustainability. J. Water Resour. Plan. Manag. 2015, 141, 11. [Google Scholar] [CrossRef]
- Tensorforce: A TensorFlow Library for Applied Reinforcement Learning—Tensorforce 0.6.5 Documentation. Available online: https://tensorforce.readthedocs.io/en/latest/ (accessed on 26 October 2022).
- Plappert, M. keras-rl. “GitHub—Keras-rl/Keras-rl: Deep Reinforcement Learning for Keras.” GitHub Repos. 2019. Available online: https://github.com/keras-rl/keras-rl (accessed on 26 October 2022).
- Guadarrama, S.; Korattikara, A.; Ramirez, O.; Castro, P.; Holly, E.; Fishman, S.; Wang, K.; Gonina, E.; Wu, N.; Kokiopoulou, E.; et al. TF-Agents: A Library for Reinforcement Learning in Tensorflow. GitHub Repos. 2018. Available online: https://github.com/tensorflow/agents (accessed on 26 October 2022).
- Caspi, I.; Leibovich, G.; Novik, G.; Endrawis, S. Reinforcement Learning Coach, December 2017. [CrossRef]
- Hoffman, M.W.; Shahriari, B.; Aslanides, J.; Barth-Maron, G.; Nikola Momchev, D.; Sinopalnikov, D.; Stańczyk, P.; Ramos, S.; Raichuk, A.; Vincent, D.; et al. Acme: A Research Framework for Distributed Reinforcement Learning. arXiv 2020, arXiv:2006.00979. [Google Scholar]
- Castro, P.S.; Moitra, S.; Gelada, C.; Kumar, S.; Bellemare, M.G.; Brain, G. Dopamine: A Research Framework for Deep Reinforcement Learning. arXiv 2018, arXiv:1812.06110. [Google Scholar]
- Liang, E.; Liaw, R.; Nishihara, R.; Moritz, P.; Fox, R.; Gonzalez, J.; Goldberg, K. Ray RLlib: A Composable and Scalable Reinforcement Learning Library. arXiv 2017, preprint. arXiv:1712.09381. [Google Scholar]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-Baselines3: Reliable Reinforcement Learning Implementations. J. Mach. Learn. Res. 2021, 22, 12348–12355. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. Proc. AAAI Conf. Artif. Intell. 2016, 30, 2094–2100. [Google Scholar] [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning 2016. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY USA, 19–24 June 2016; pp. 1995–2003. [Google Scholar]
- PFRL, a Deep Reinforcement Learning Library — PFRL 0.3.0 Documentation. Available online: https://pfrl.readthedocs.io/en/latest/ (accessed on 26 October 2022).
- Mnih, V.; Badia, A.P.; Mirza, L.; Graves, A.; Harley, T.; Lillicrap, T.P.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783v2. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Racanière, S.; Weber, T.; Reichert, D.P.; Buesing, L.; Guez, A.; Rezende, D.; Badia, A.P.; Vinyals, O.; Heess, N.; Li, Y.; et al. Imagination-Augmented Agents for Deep Reinforcement Learning. arxiv 2017, preprint. arXiv:1707.06203. [Google Scholar]
- Feinberg, V.; Wan, A.; Stoica, I.; Jordan, M.I.; Gonzalez, J.E.; Levine, S. Model-Based Value Estimation for Efficient Model-Free Reinforcement Learning. arxiv 2018, arXiv:1803.00101. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv 2017, arXiv:1712.01815. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.; Abbeel, P. Trust Region Policy Optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971v6. [Google Scholar]
- Fujimoto, S.; Van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018, arXiv:1801.01290. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, preprint. arXiv:1312.5602. [Google Scholar]
- Bellemare, M.G.; Dabney, W.; Munos, R. A Distributional Perspective on Reinforcement Learning. arXiv 2017, arXiv:1707.06887. [Google Scholar]
- Dabney, W.; Rowland, M.; Bellemare, M.G.; Munos, R. Distributional Reinforcement Learning with Quantile Regression. arXiv 2017, arXiv:1710.10044. [Google Scholar]
- Andrychowicz, M.; Wolski, F.; Ray, A.; Schneider, J.; Fong, R.; Welinder, P.; McGrew, B.; Tobin, J.; Abbeel, P.; Zaremba, W. Hindsight Experience Replay. arXiv 2017, arXiv:1707.01495. [Google Scholar]
- Anshuka, A.; Chandra, R.; Buzacott, A.J.V.; Sanderson, D.; van Ogtrop, F.F. Spatio Temporal Hydrological Extreme Forecasting Framework Using LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess 2022, 36, 3467–3485. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, J.; Liao, Z.; Zhou, Y.; Wang, H.; Pei, Q. A Short-Term Flood Prediction Based on Spatial Deep Learning Network: A Case Study for Xi County, China. J. Hydrol. 2022, 607, 127535. [Google Scholar] [CrossRef]
- Marco, Z.; Elena, A.; Anna, S.; Silvia, T.; Andrea, C. Spatio-Temporal Cross-Validation to Predict Pluvial Flood Events in the Metropolitan City of Venice. J. Hydrol. 2022, 612, 128150. [Google Scholar] [CrossRef]
- Wahla, S.S.; Kazmi, J.H.; Sharifi, A.; Shirazi, S.A.; Tariq, A.; Smith, H.J. Assessing Spatio-Temporal Mapping and Monitoring of Climatic Variability Using SPEI and RF Machine Learning Models. Geocarto Int. 2022, 1–20. [Google Scholar] [CrossRef]
- Roushangar, K.; Ghasempour, R.; Nourani, V. Spatiotemporal Analysis of Droughts Over Different Climate Regions Using Hybrid Clustering Method. Water Resour. Manag. 2021, 36, 473–488. [Google Scholar] [CrossRef]
- Liu, J.; Xu, L.; Chen, N. A Spatiotemporal Deep Learning Model ST-LSTM-SA for Hourly Rainfall Forecasting Using Radar Echo Images. J. Hydrol. 2022, 609, 127748. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling Monthly Streamflow in Mountainous Basin by MARS, GMDH-NN and DENFIS Using Hydroclimatic Data. Neural Comput. Appl. 2020, 33, 2853–2871. [Google Scholar] [CrossRef]
- Senatore, A.; Furnari, L.; Mendicino, G. Impact of High-Resolution Sea Surface Temperature Representation on the Forecast of Small Mediterranean Catchments’ Hydrological Responses to Heavy Precipitation. Hydrol. Earth Syst. Sci. 2020, 24, 269–291. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-Term Water Quality Variable Prediction Using a Hybrid CNN–LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Gu, K.; Vosoughi, S.; Prioleau, T. Feature Selection for Multivariate Time Series via Network Pruning. In 2021 International Conference on Data Mining Workshops (ICDMW); IEEE: Toulouse, France, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).