1. Introduction and Background
It is needless to say that climate changes drastically affect the distribution of water resources on Earth. As an essential part of the hydrological balance, river flow is also exposed to climate changes and anthropogenic impacts, especially in water management, i.e., regulation works and the excessive exploitation of drinking water. This makes it difficult to predict the size and time of individual flows, especially the peaks. The general fact is that flood hazards will increase over half the globe [
1], as well as in the analyzed area of Eastern Europe [
2].
Many tools, models, and methodologies exist for such predictions/forecasting. Many of them are not “user-friendly” and require at least basic knowledge about the input datasets. Additionally, some of the user data are not often available. In general, such models can be broadly classified as conceptually based and empirical models, i.e., the “black-box” approach [
3]. In conceptually based models, the flood propagation process is usually described by the Saint Venant equations, comprising partial differential equations of continuity and momentum. In addition to the Saint Venant equations-based models, there are also routing techniques, usually referred as zero-order models, which were used in the past to track floodwave propagation in a river and also for a quick assessment of flood damage [
4]. Finally, empirical models are based on evidence of relationships manifested in historical input and output records without analyzing the internal structure of the physical process.
A time series is a series of data points, which is a prerequisite to give a conclusion based on analyzing the historical dataset and its patterns, understanding and matching the current situation with patterns derived from the previous stage, and understanding the factors influencing specific variable(s) in different periods [
5]. Time series analysis allows for the preparation of numerous time-based studies and results, i.e., forecasting, segmentation, classification, descriptive analysis, and intervention analysis [
6]. Such research could determine trends, seasonality, cyclicity, or irregularities in series data.
Regarding hydrology, the river Bednja was a subject of research, but only in a small number of publications. The first analysis of the hydrological properties of the river Bednja was presented in [
7], in a review form of the river basin data and figures. The last known reference is [
8], which deals with the length calculation of rivers in Croatia, where the river Bednja is also included. There was a lot of study documentation [
9], elaborated reports [
10], regulation projects [
11], and similar documentation, including student theses [
12,
13]. These were prepared with an accent on flood protection. In addition, this documentation deals with the design and building of small hydropower plants [
14].
Although these results, graphical data, and table data are beneficial in understanding the characteristics of the river Bednja, further research improvements were made in a small number of literature studies. In [
15], the correlation between the precipitation from the Bednja river basin and the flow rates measured from stations located along the river is investigated, which results in a comparison of the values of the flow and the existing values to forecast the flows in the future. Despite the high values of the validation (calibration) parameters used for testing, which imply a high correlation between the modeled and observed values, there were discrepancies regarding the maximum observed values. In other words, the modeled values differed from the observed ones by a range of a minimum of 5 m
3/s to 10 m
3/s [
15]. These facts indicate difficulties in modeling flow from rivers flowing through the alluvial river basin, regarding the observed values.
The analysis provided by [
16] was based on applying the rescaled adjusted partial sums (RAPS) method to the example of three rivers in Croatia, including the river Bednja. The paper aimed to demonstrate the application of the RAPS method for determining the possible irregularities and periodicities which may occur in the original time series and cannot be observed by simple trend analysis. This research aims to define and understand the relations between the flows of the river Bednja, as measured/calculated on the hydrological gauging stations, and determine the possible alterations that impact the hydrological regime. These are essential for predicting the river’s reaction to the basin’s natural and anthropogenic activities. Concerning similar research, such relationships can be used for establishing river management and designing restoration and regulation operations [
5]. Such a method provides a great starting point for better understanding the river flow size and intensity at measurement stations, which is the primary goal of the research.
2. Study Area and Dataset
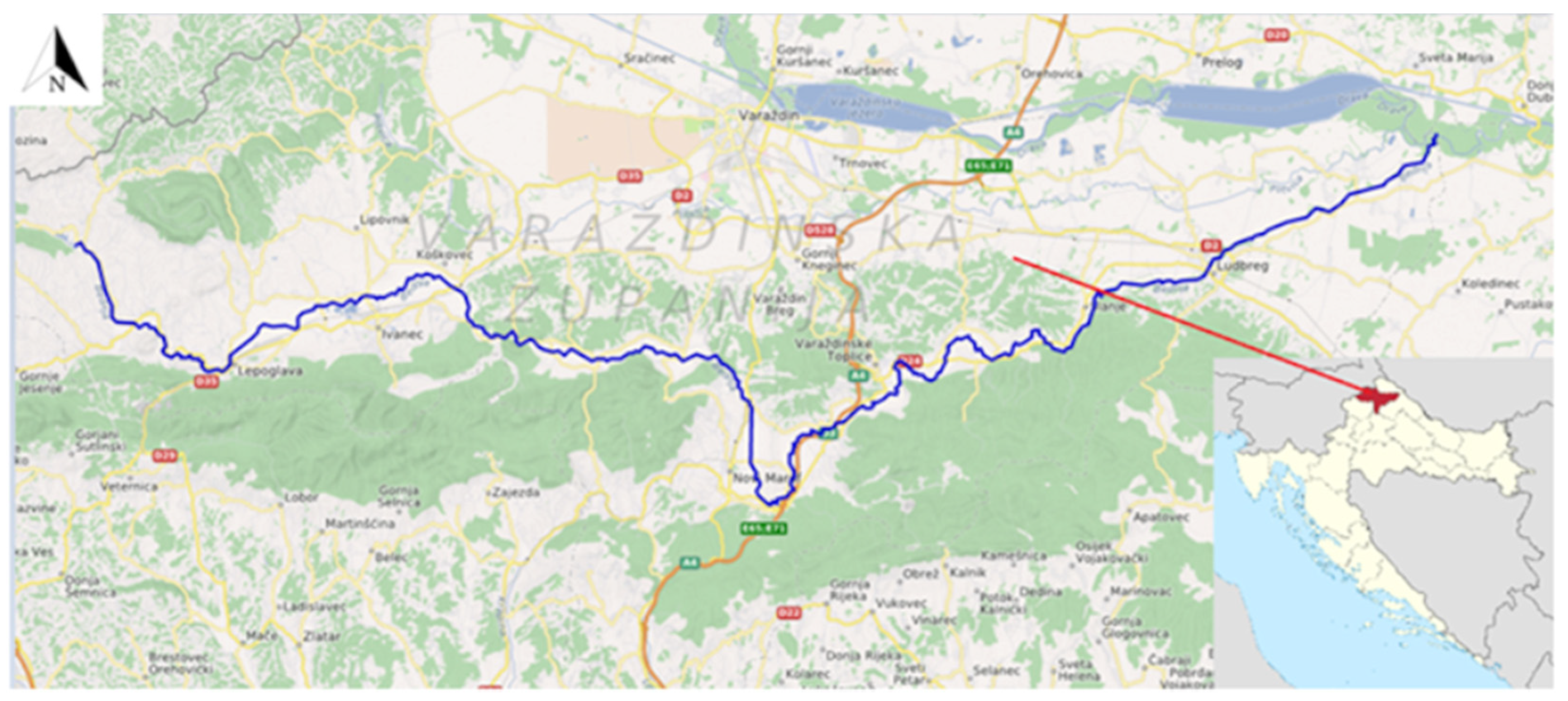
River Bednja is the right tributary of the Drava River, which springs from littler streams at the height of 300 m and creates a constant flow at the foot of Macelj, near Brezova Gora in the northwest part of Croatia (
Figure 1). It should be emphasized that Bednja is the longest river in Croatia with a source and estuary in the same country.
Bednja flows into the Drava River near Mali Bukovec (at a height of 136 m), and is 133 km long, while the area of its basin is 596 km
2 [
18]. In the Bednja basin, three relief units stand out: alluvial plain, tertiary mountains, and Paleozoic mountains. This river is selected for its torrential flow, proximity, and accessibility compared with other rivers provided in available publications [
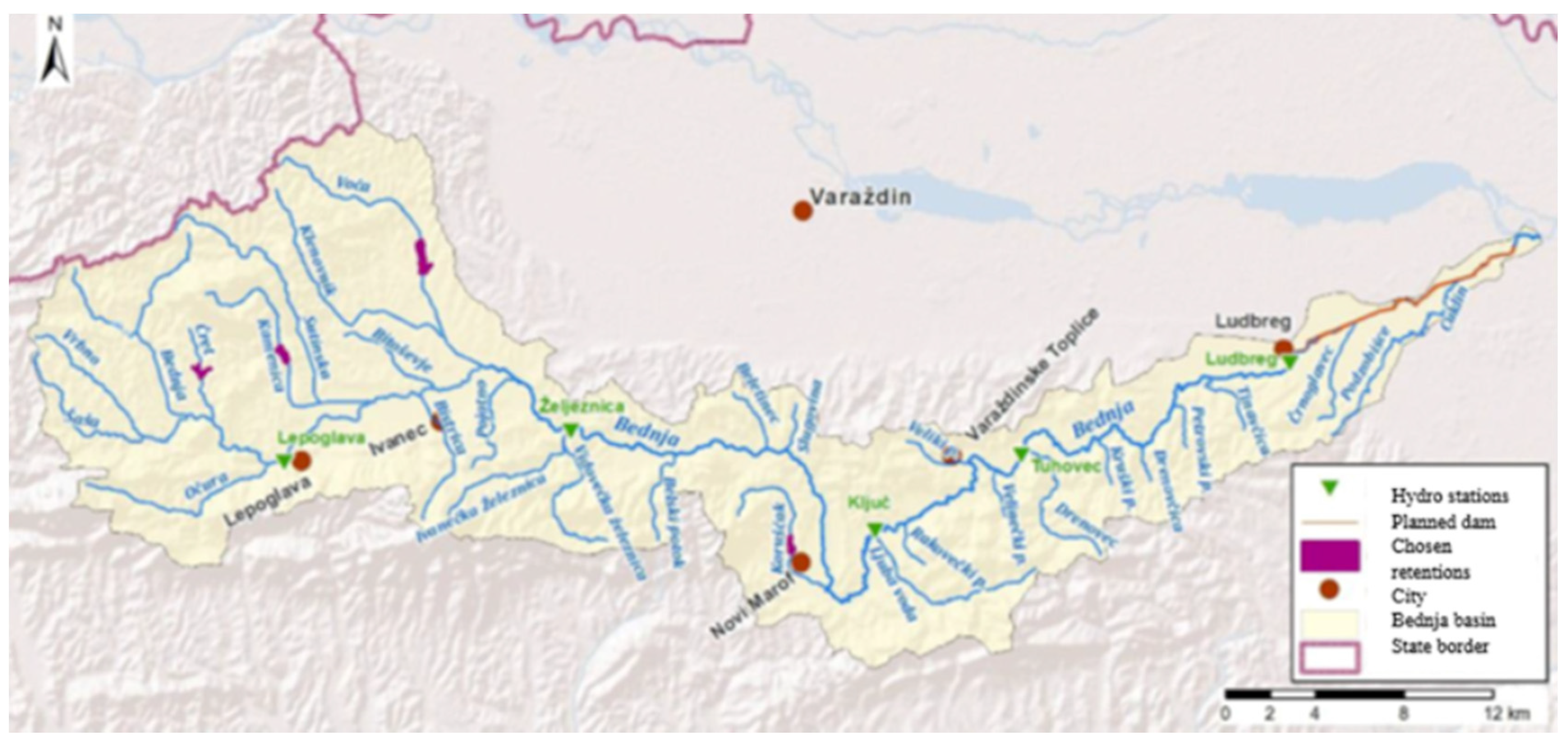
8]. Its flow and depth were measured constantly through five hydrologic measurement stations, Lepoglava, Željeznica, Ključ, Tuhovec, and Ludbreg,
Figure 2.
The data on elevation, geographic coordinates, area, and maximum and minimum flow for all five stations are given in
Table 1 and
Table 2 [
20]. The characteristics of River Bednja are its buoyant (variable) flow, its increased flow during more considerable precipitation periods, and its possibility of a drastic reduction in flow during summers [
21].
Input data for time series analysis consist of data from these five measurement stations on river flow from January 2007 to December 2018.
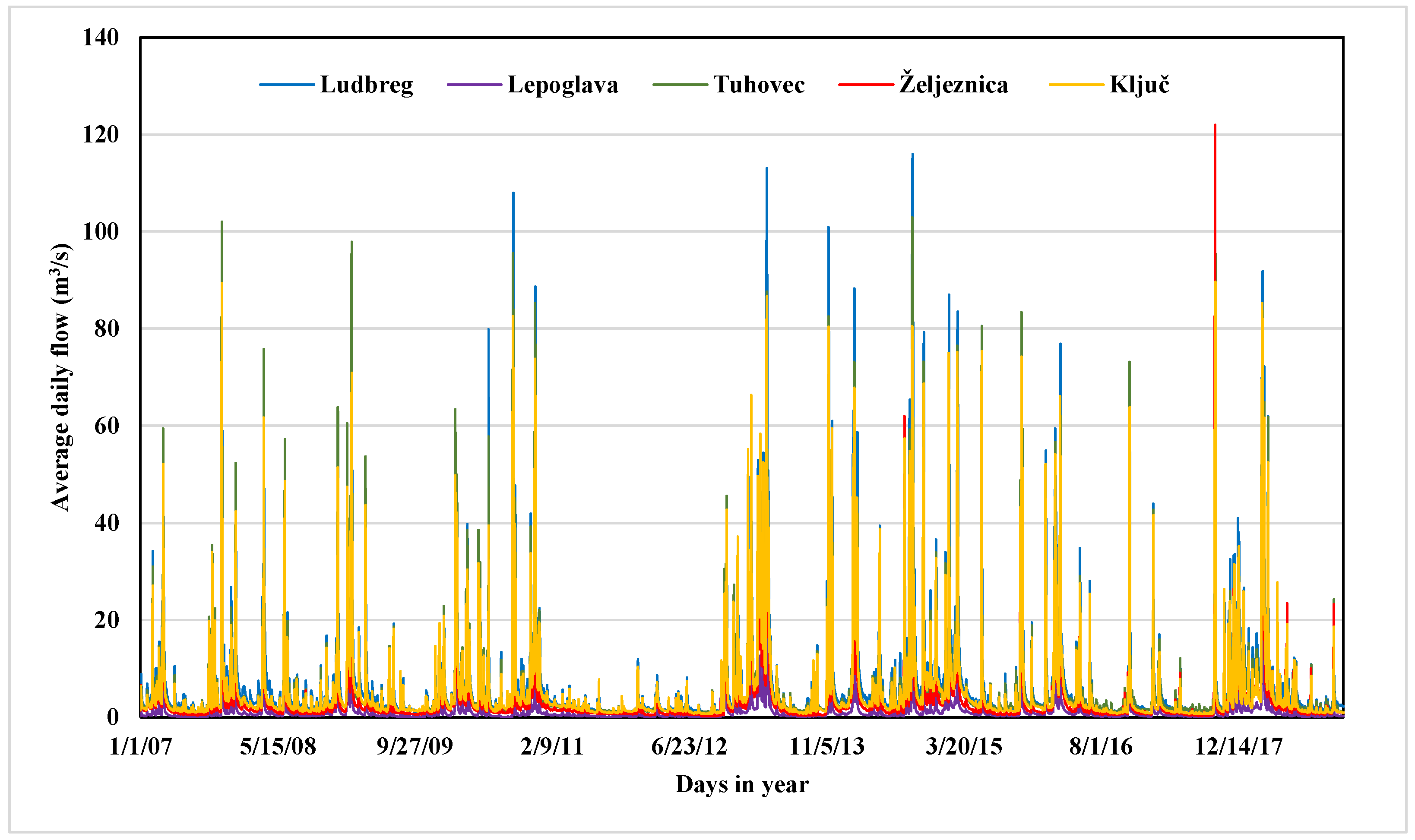
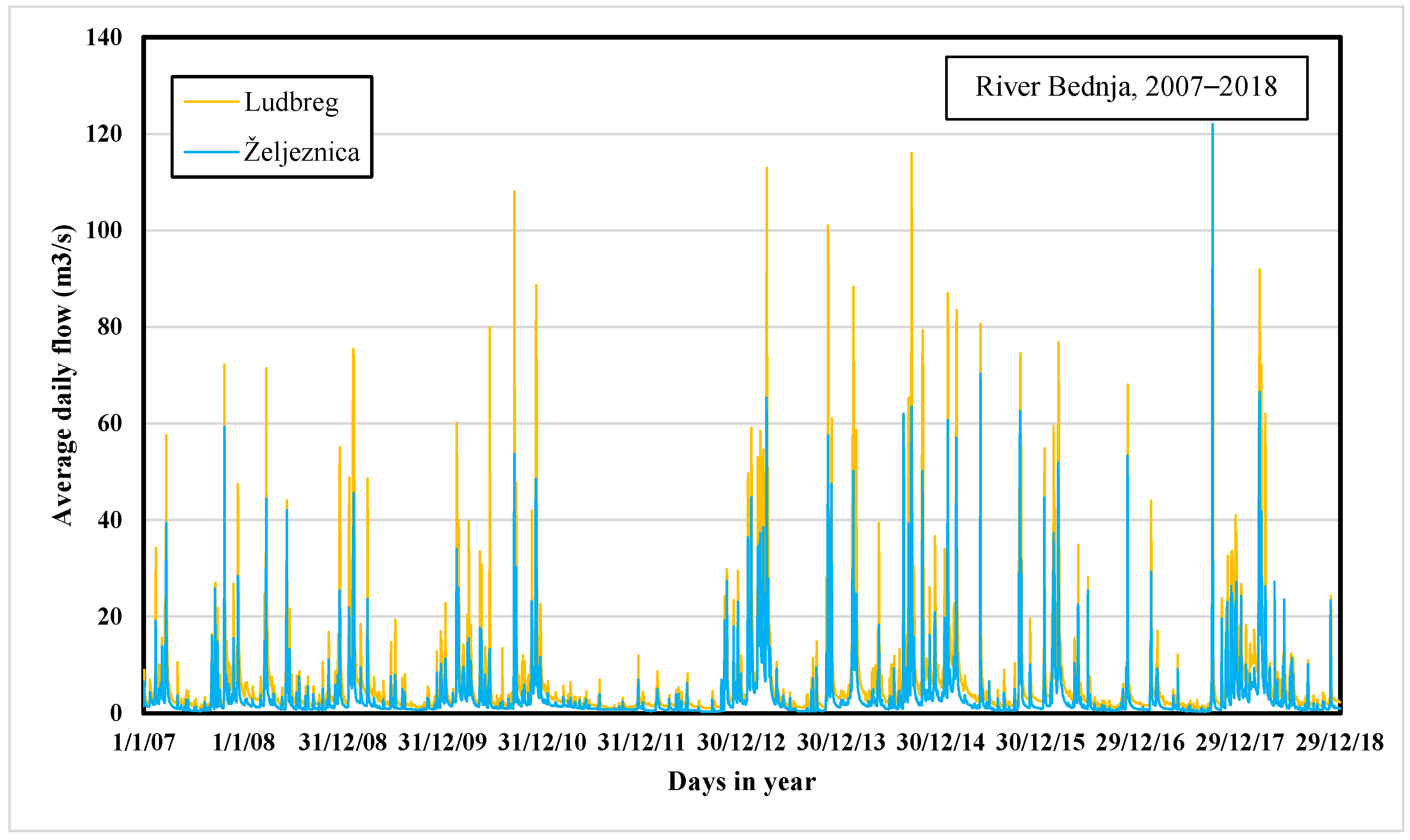
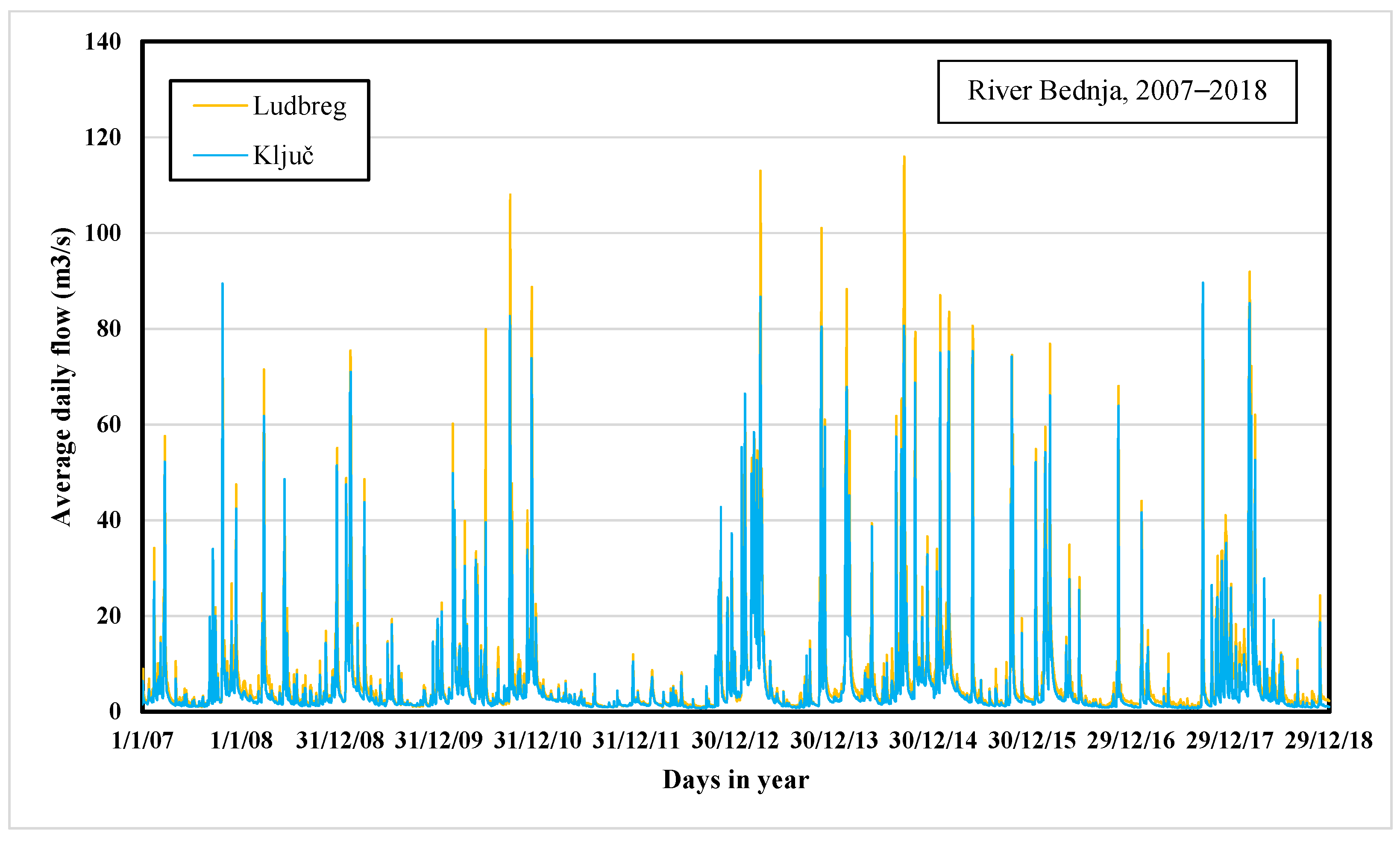
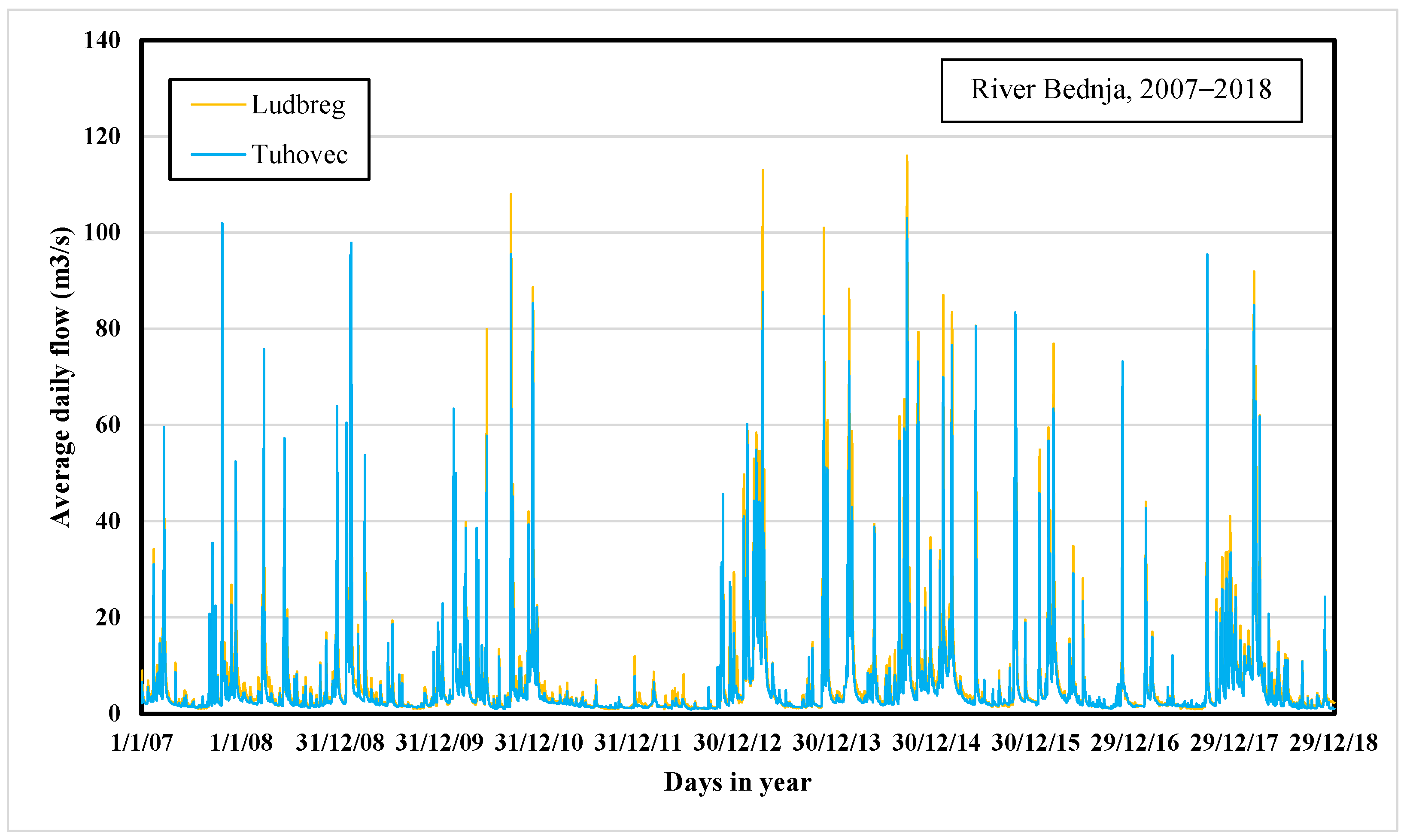
Figure 3 shows the average daily flow of River Bednja at each measurement station. Analyzed periods, i.e., durations, were selected because continuous data were only available from this period, without the days with the unmeasured, i.e., uncalculated values. In addition, statistics related to the streamflow rate for the five measurement stations in the monitoring period are also reported in
Table 3. Proceeding from upstream to downstream, we observe an increase in the minimum, mean, and maximum streamflow rates, with the lower values for the station in Lepoglava and the higher for the Ludbreg one. An exception was observed for the maximum flow recorded in Željeznica and equal to 122 m
3/s. However, this peak is not reflected in the downstream stations, indicating possible flooding along the river. Furthermore, the skewness ranges from 0.80 to 0.95, indicating a positive asymmetry between the mean and median, becoming increasingly marked from upstream to downstream.
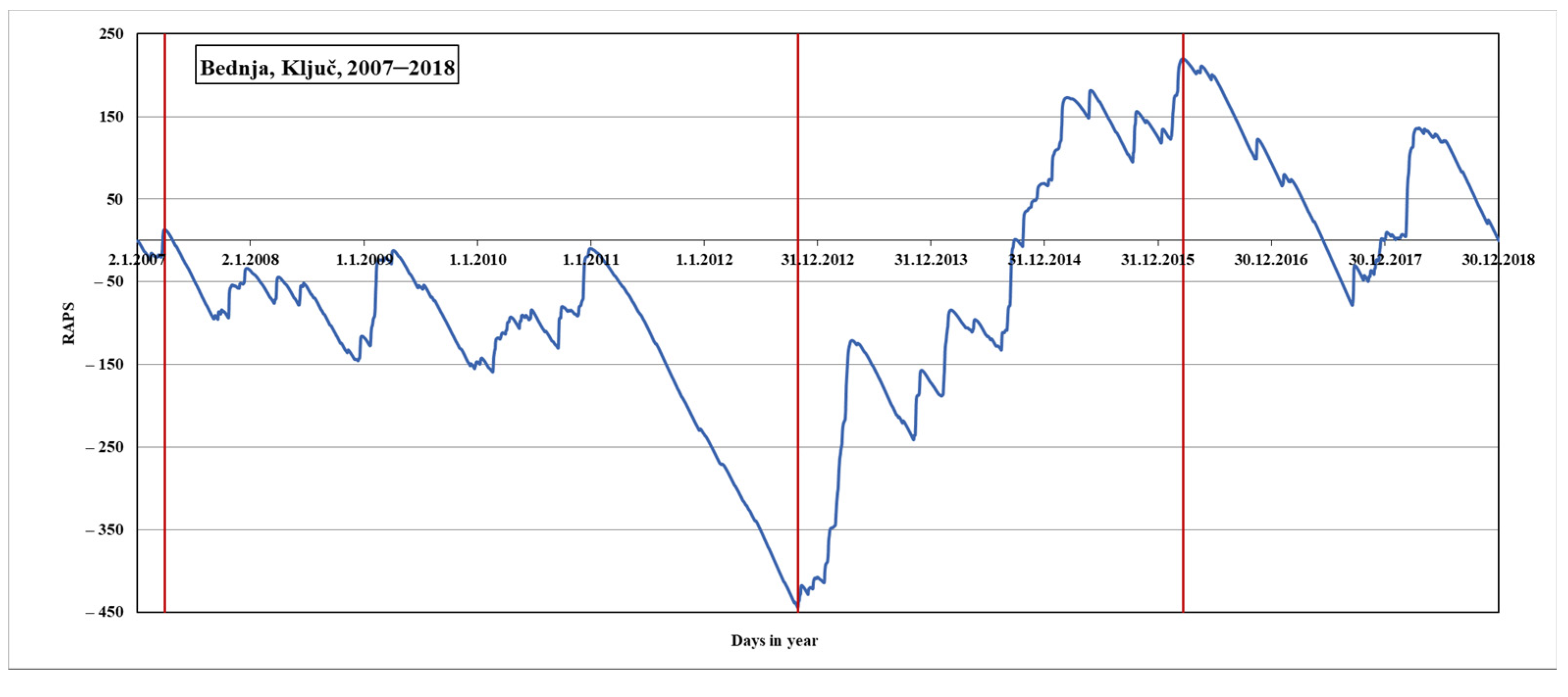
There is a similarity for all measuring stations regarding the drought period between 2011 and 2012. Furthermore, the common feature of all analyzed time series is that flows are smaller during the summer than in spring, autumn, and winter. The precipitation and melting of the snow explain as such.
Figure 3 shows that the biggest river flow oscillations occur at the Lepoglava and Ludbreg stations, which is a starting point for further and more extensive flow analysis.
3. Methodology
The proposed methodology will consist of three steps.
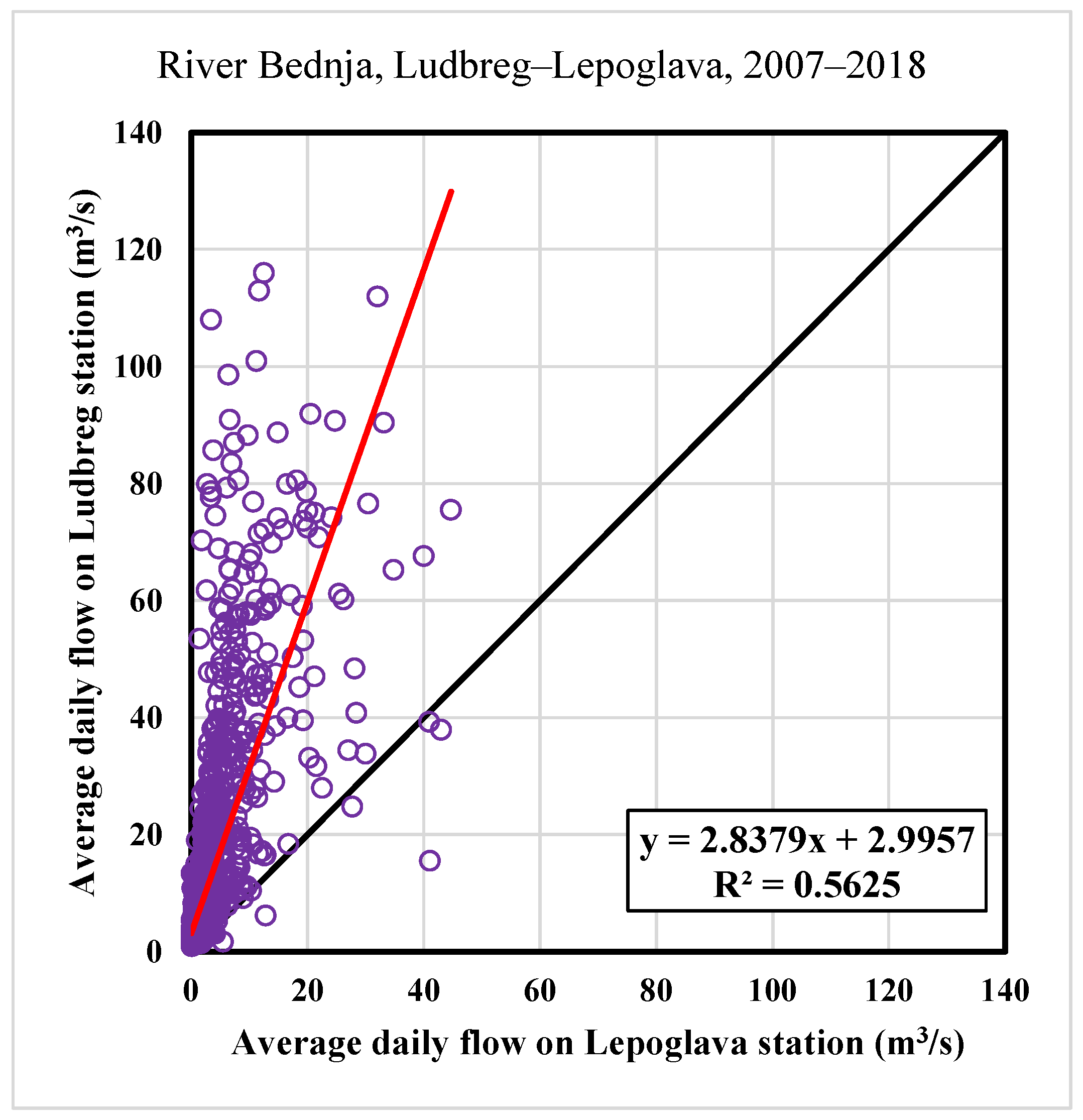
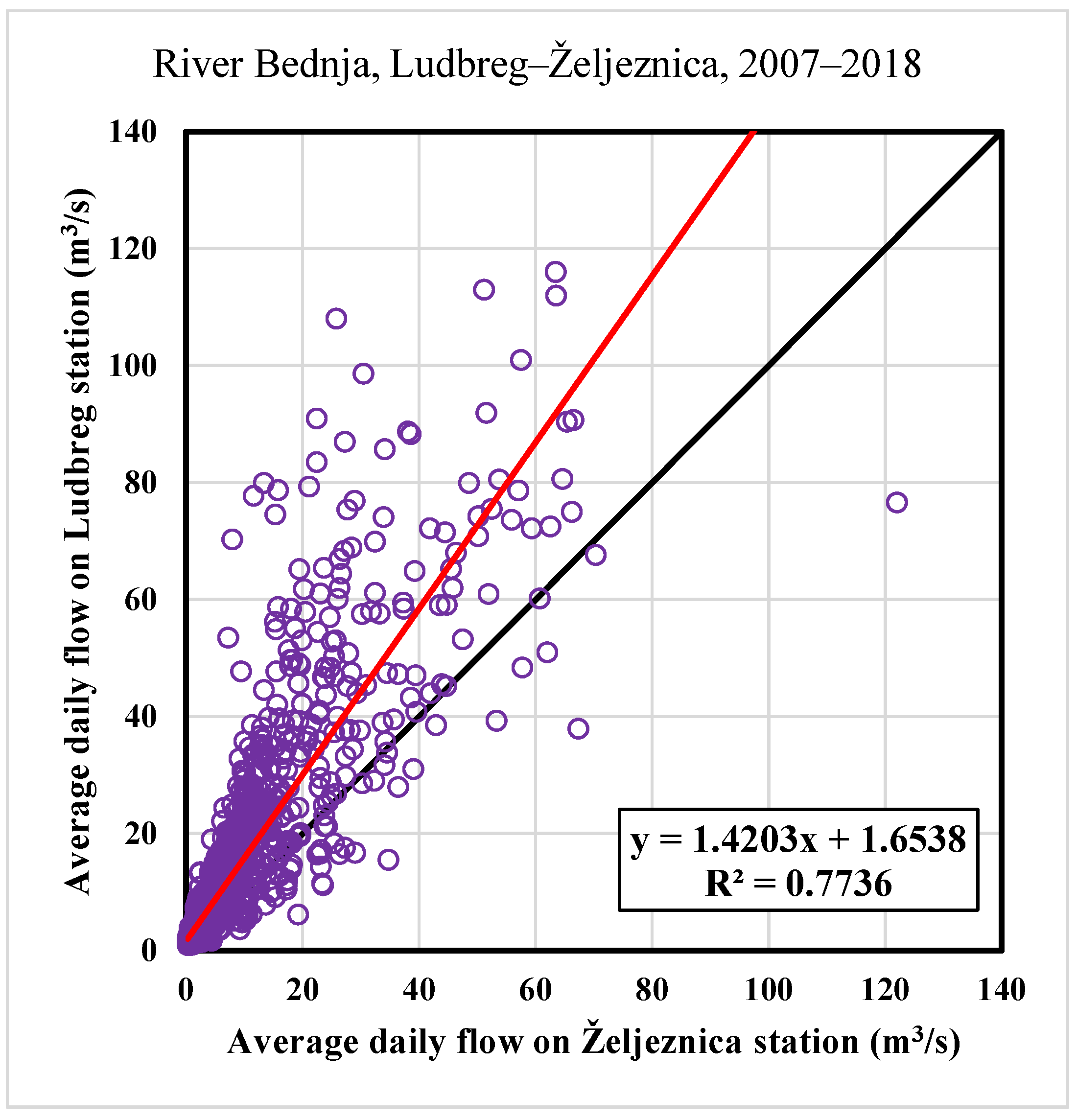
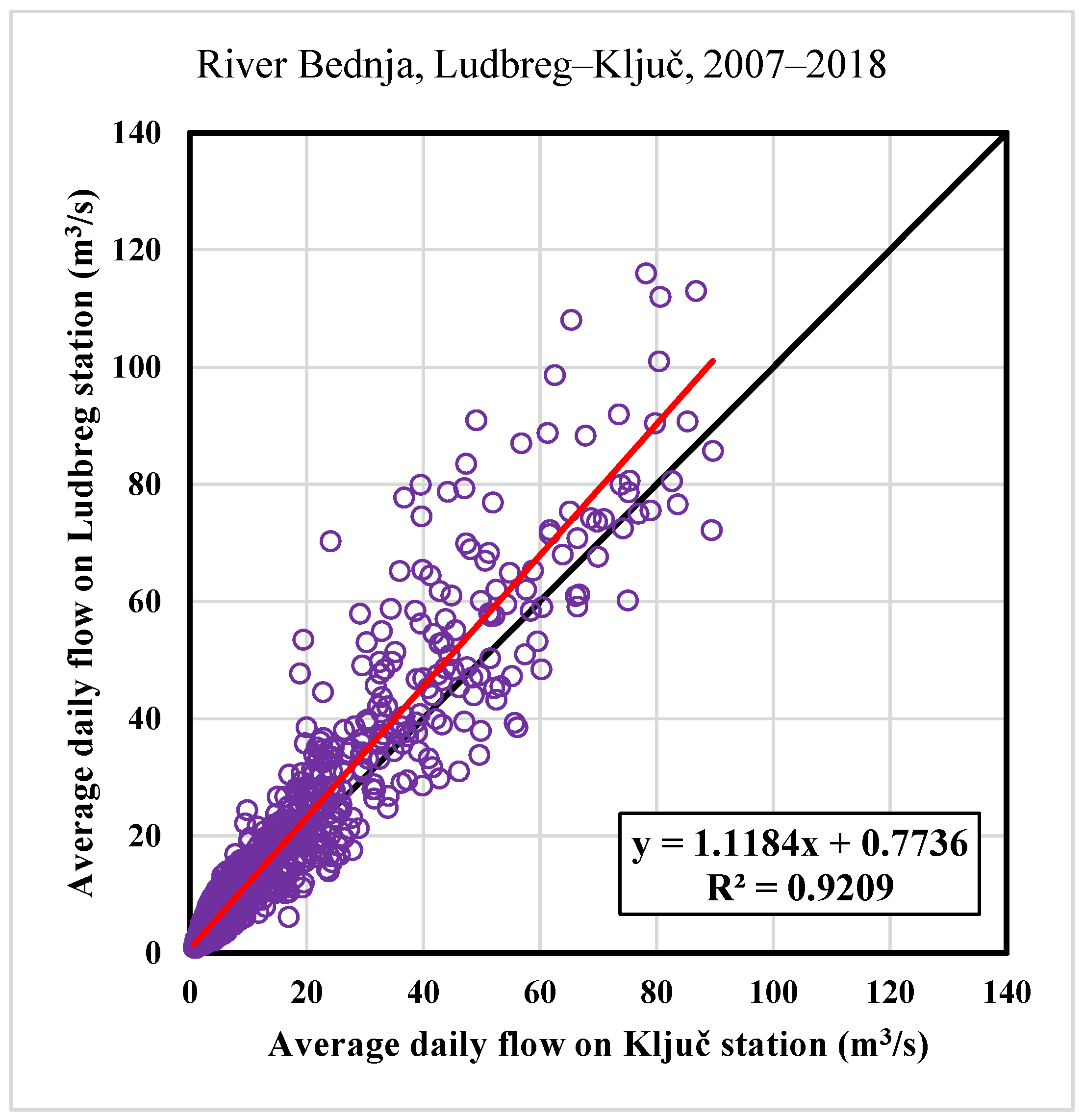
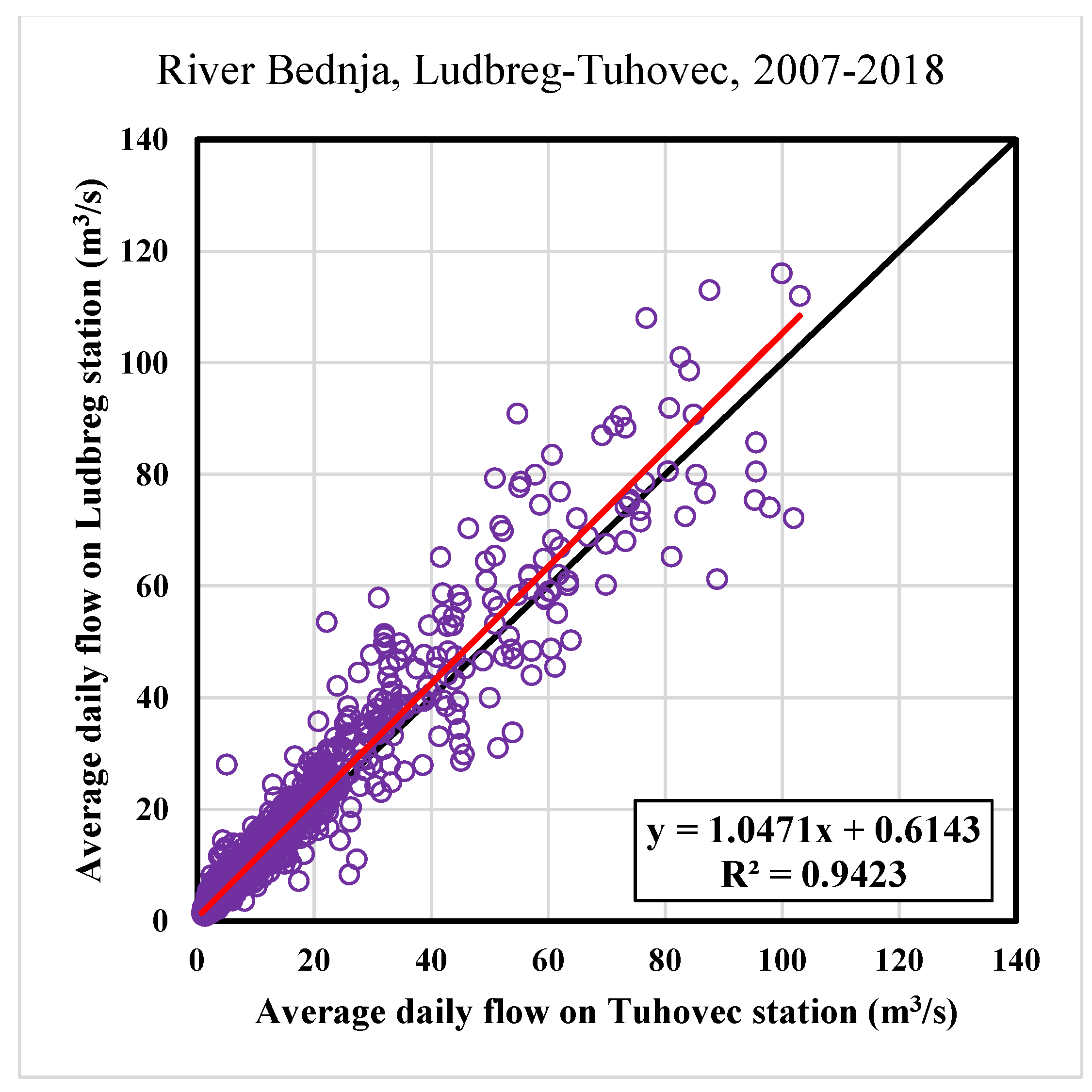
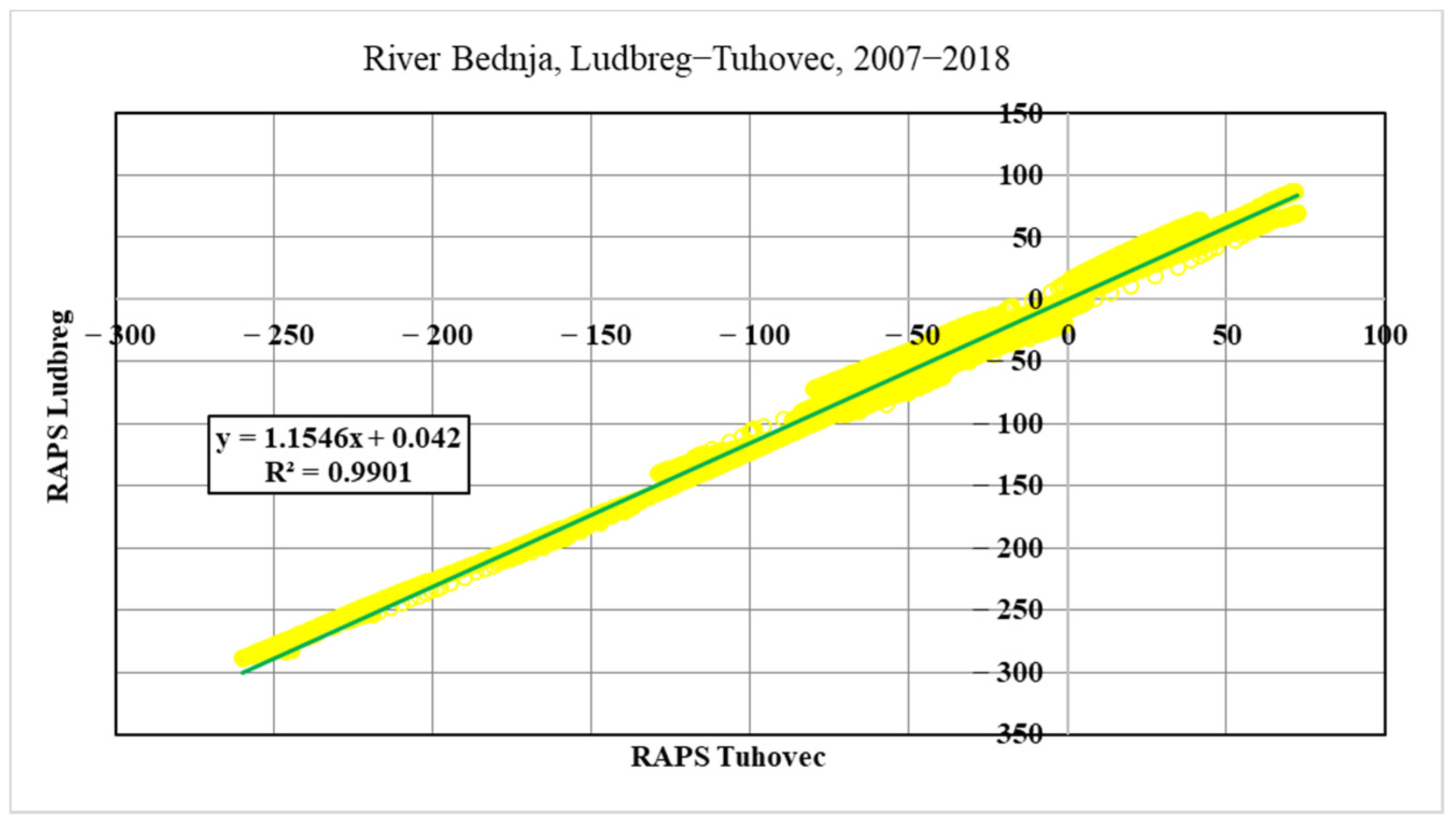
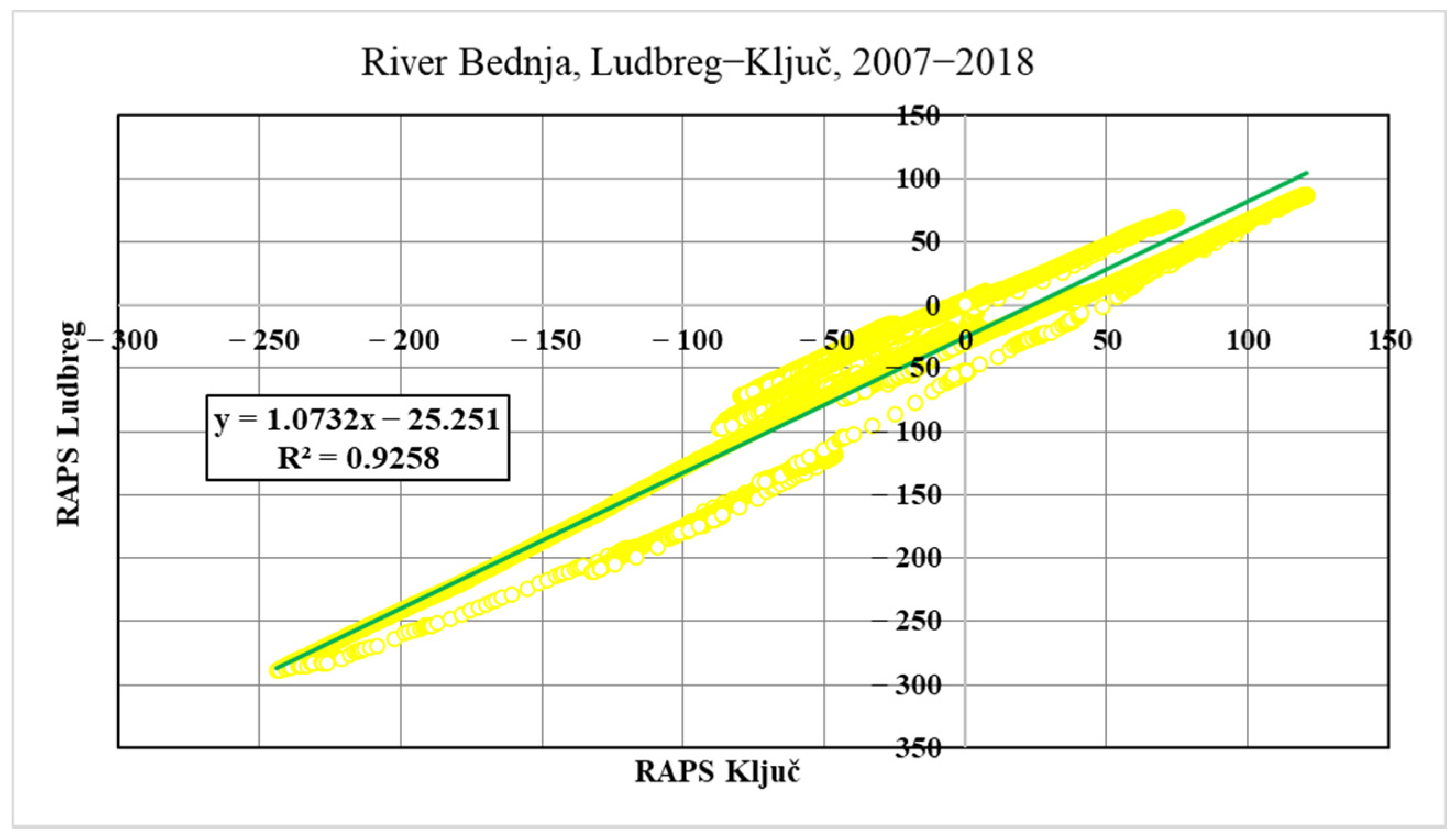
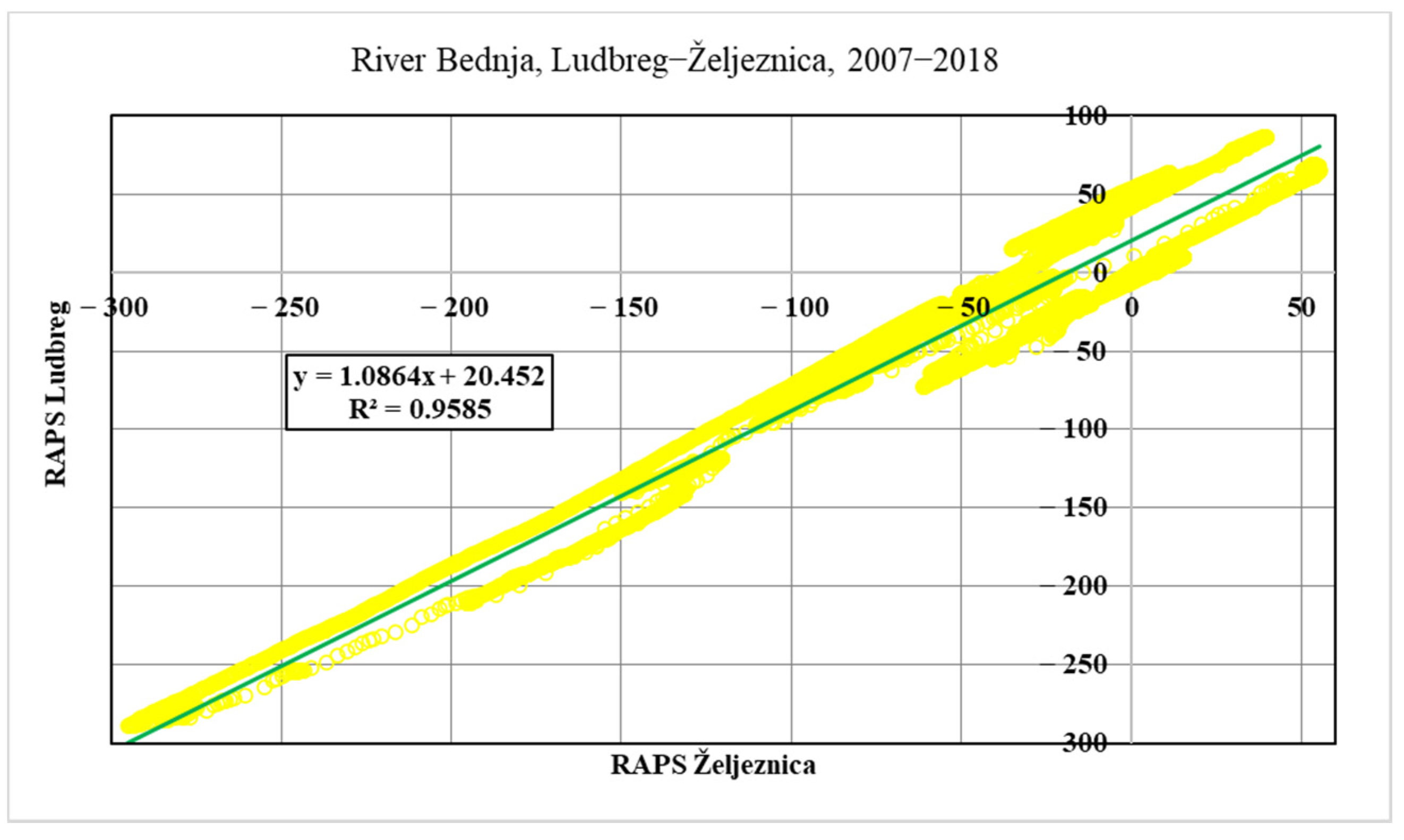
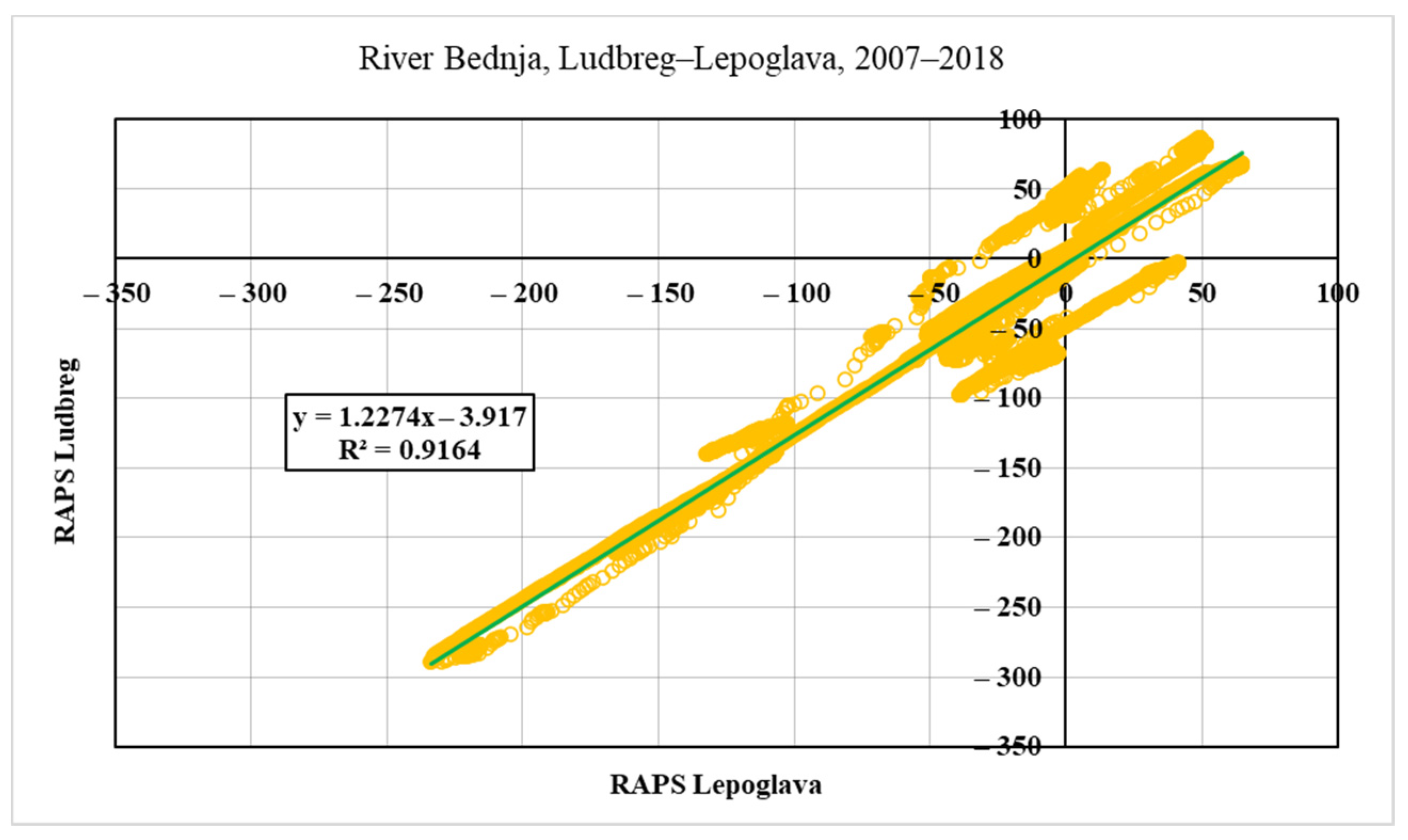
The first step is a definition of the correlation between average daily flows for all analyzed stations. This will be provided so that the most downstream measuring station in Ludbreg will be analyzed concerning all other downstream stations. The measuring station in Ludbreg has the most significant values of the average daily flows, so this is the reason to determine Ludbreg a “dependent” measuring station. The correlation coefficient is expected to be the smallest regarding the upstream station Lepoglava, while the correlation with the closest measuring station in Tuhovec will be the biggest compared with all other stations.
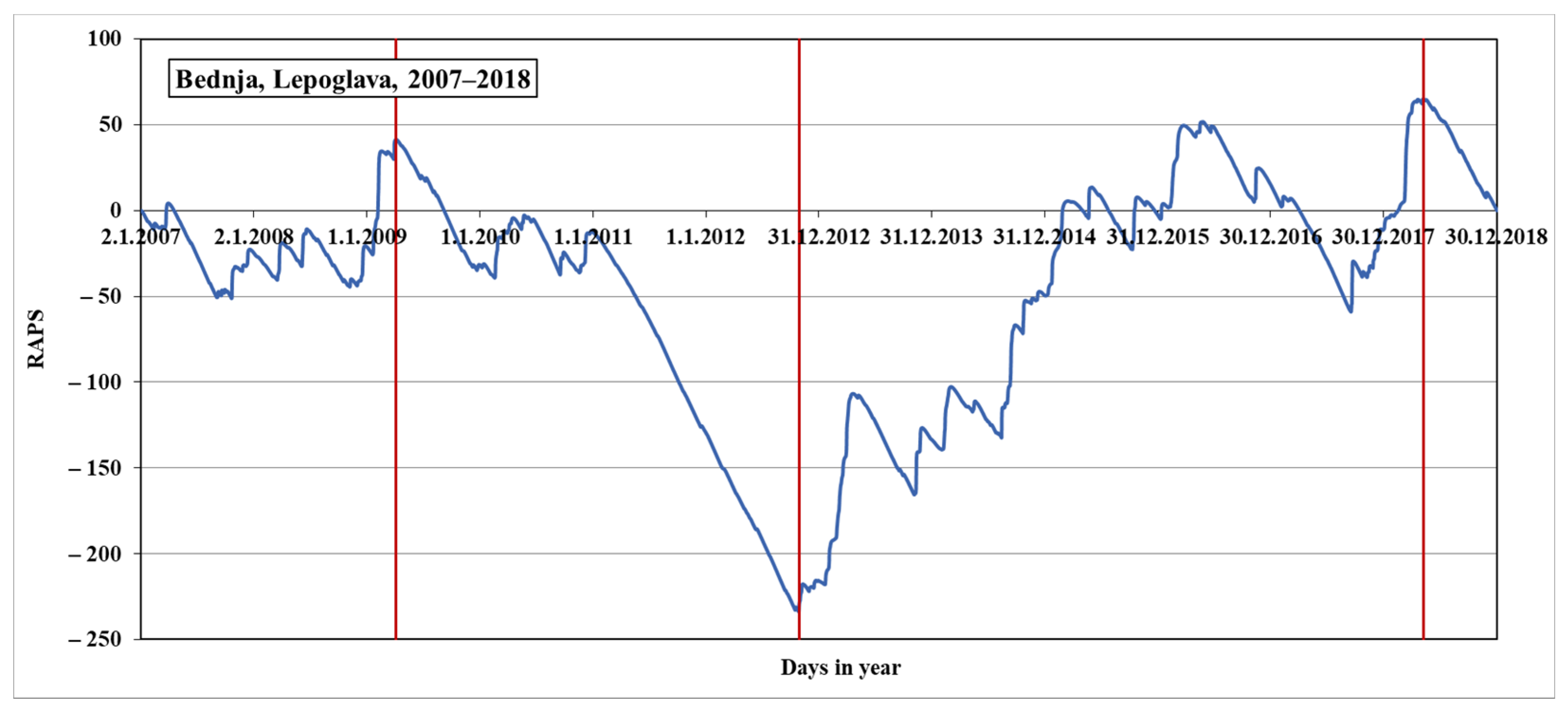
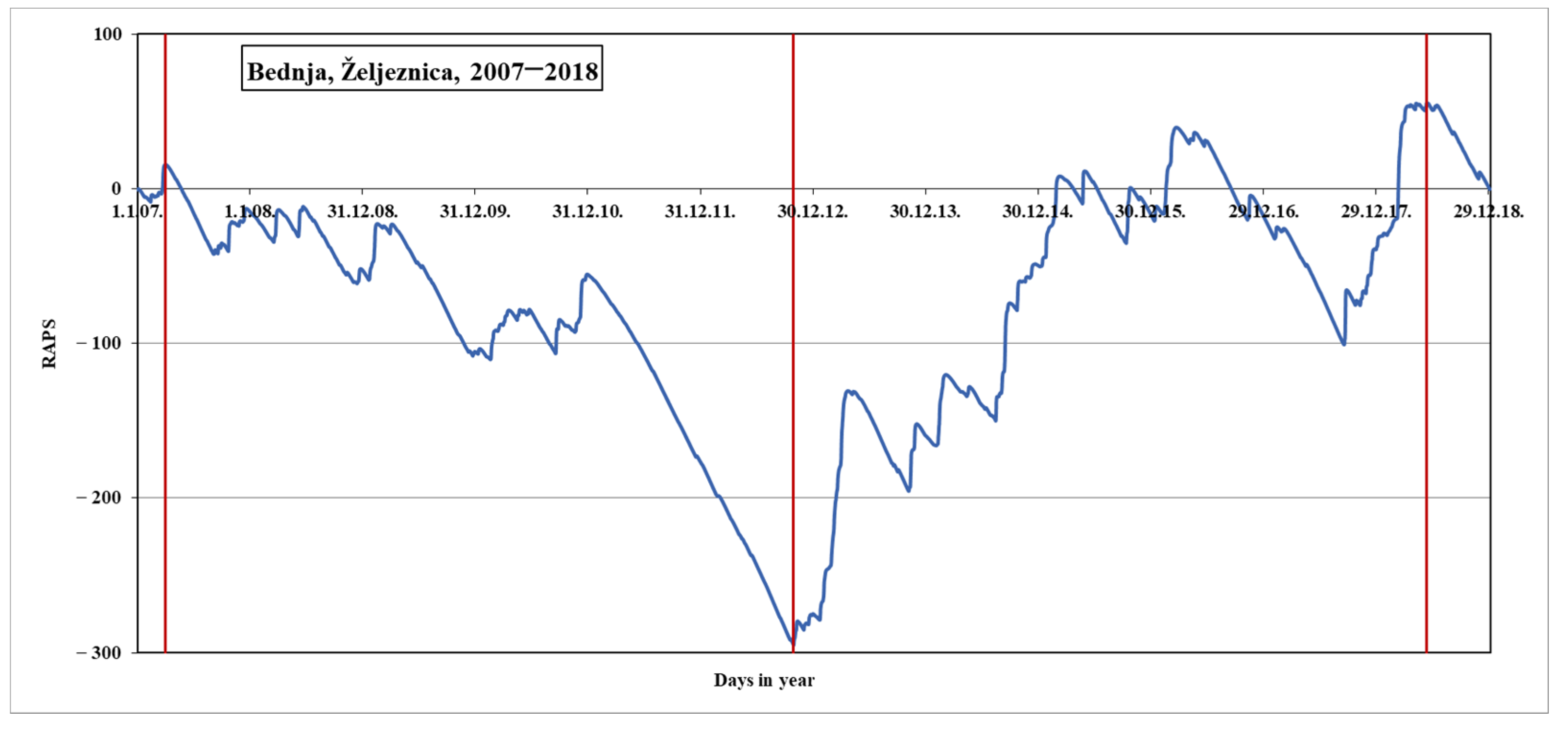
The second step is a RAPS analysis of the particular time series of the average daily flow, for each of the five analyzed measuring stations. This part of the research intends to determine any possible interruptions in the original time series of the flow. Additionally, obtained results, as well as conclusions, will give additional information about the characteristics of the river Bednja. Some discordances should be determined in the first step of the methodology.
The third step of the methodology is a RAPS analysis of the average daily flow values between all the measuring stations. This will be provided to see if the subseries obtained in the RAPS analysis from the second step have mutual correlations between the measuring stations.
The methodology conducted in this research consists of observing river flow data at five consecutive measurement stations to create the best possible input data set for the RAPS analysis.
RAPS will be made on collected and cleaned data sets of river flow to prepare a visualization concerning time. This will provide a diagram of the calculated values, so the stationarity of the flow series can be observed. This will lead to a better understanding of the series nature and give the possibility to extract insight into the river flow prediction.
RAPS is a widely used method for analyzing river flow [
22] and other research areas [
23,
24]. RAPS gives a visual determination of subseries from input data series using frequent statistical parameters. It provides insight into the occurrence of the trends, data grouping, fluctuations, and similar appearances during the time, using average value and standard deviations of the input data from the observed time series:
where
Yt is the value of the analyzed member (parameter) of the considered time series,
Y is the average value of the regarded time series,
Sy is the standard deviation of the supposed time series,
n is the number of members of the considered time series, and
k = 1, 2, …,
n, where
n is a counter during summation.
The data provided with the RAPS method will be used in correlation analysis to observe the association between data from five different measurement stations. In correlated data, the change in the magnitude of 1 variable is associated with a difference in the importance of another variable, either in the exact (positive correlation) or the opposite (negative correlation) direction [
25]. In this research, the Pearson correlation coefficient is used on RAPS values. The Pearson coefficient ranges from −1 to +1, where 0 indicates no linear association, and the relationship becomes stronger as the coefficient value approaches an absolute value of 1.
5. Conclusions
River flow behavior prediction is the subject of much research, given the frequent floods caused by climate changes and the anthropogenic use of rivers. New approaches to preparing the data for forecasting methodologies are needed to better understand the connection between the values of river flows through the whole river, from its spring till the end. RAPS methodology gives the visual division of low and high flow periods in time series, using average values and standard deviations. The results of an application of the RAPS method on data sets from five consecutive measurement stations on River Bednja provide information about the similarities in the duration of subperiods at most of the stations. Still, some irregularities also raise the need for additional analysis. Correlation analysis shows the connection between all five stations according to the last (downstream) station on the river Bednja flow, Ludbreg. The given values of the correlation coefficient, especially the RAPS correlation coefficients, show a significant connection between all stations. As such, it is essential for predicting flow intensity regarding flood protection, assessing hydro-technical facilities, and monitoring the flow.