Hydraulic Conditions of Incipient Rill by Raindrop-Induced Overland Flow on Steep Slopes of Sandy Soil
Abstract
:1. Introduction
2. Rainfall Simulation
2.1. Experimental Condition
2.2. Rill Erosion
3. Results and Discussion
3.1. Rill Evolution
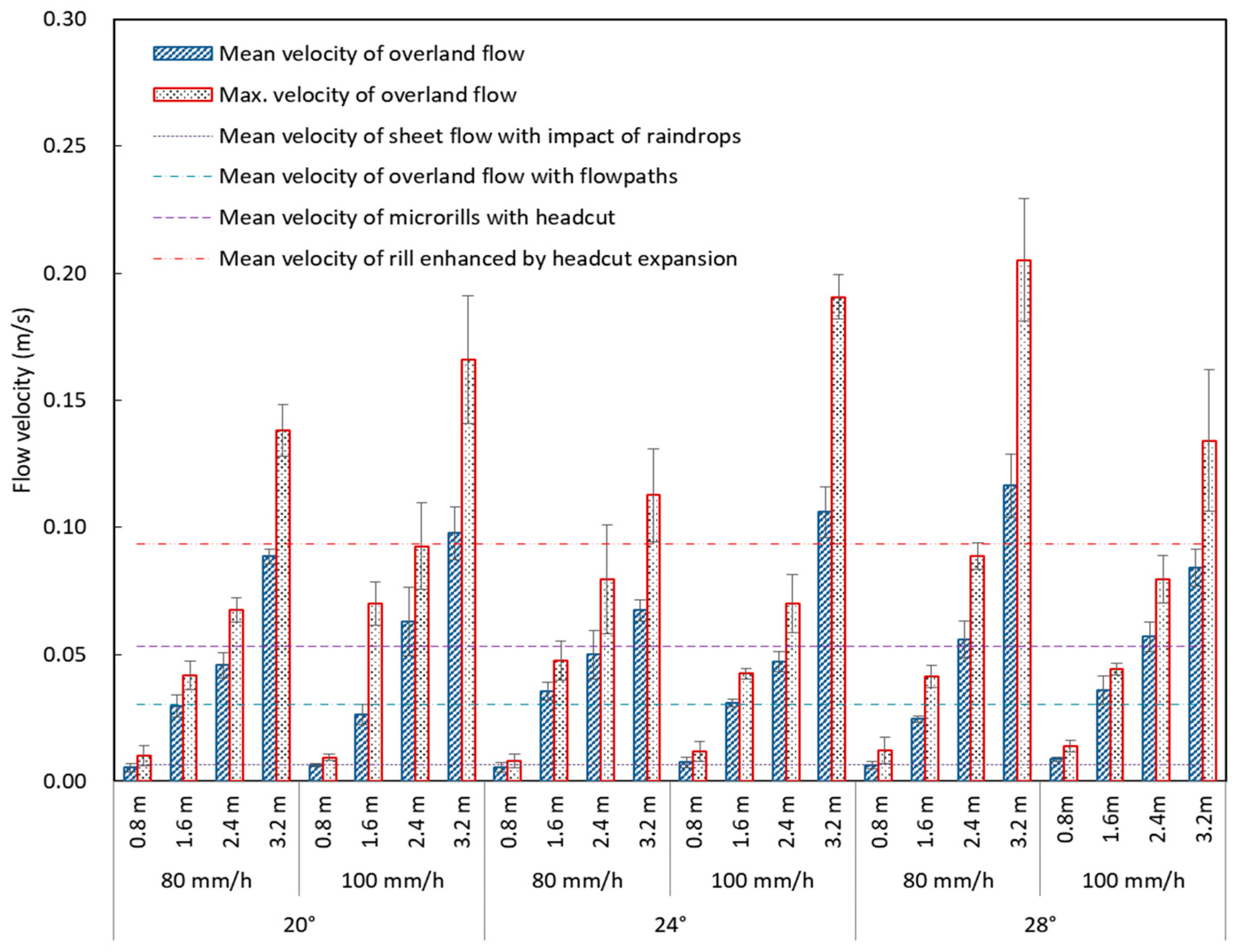
3.2. Velocity of Overland Flow
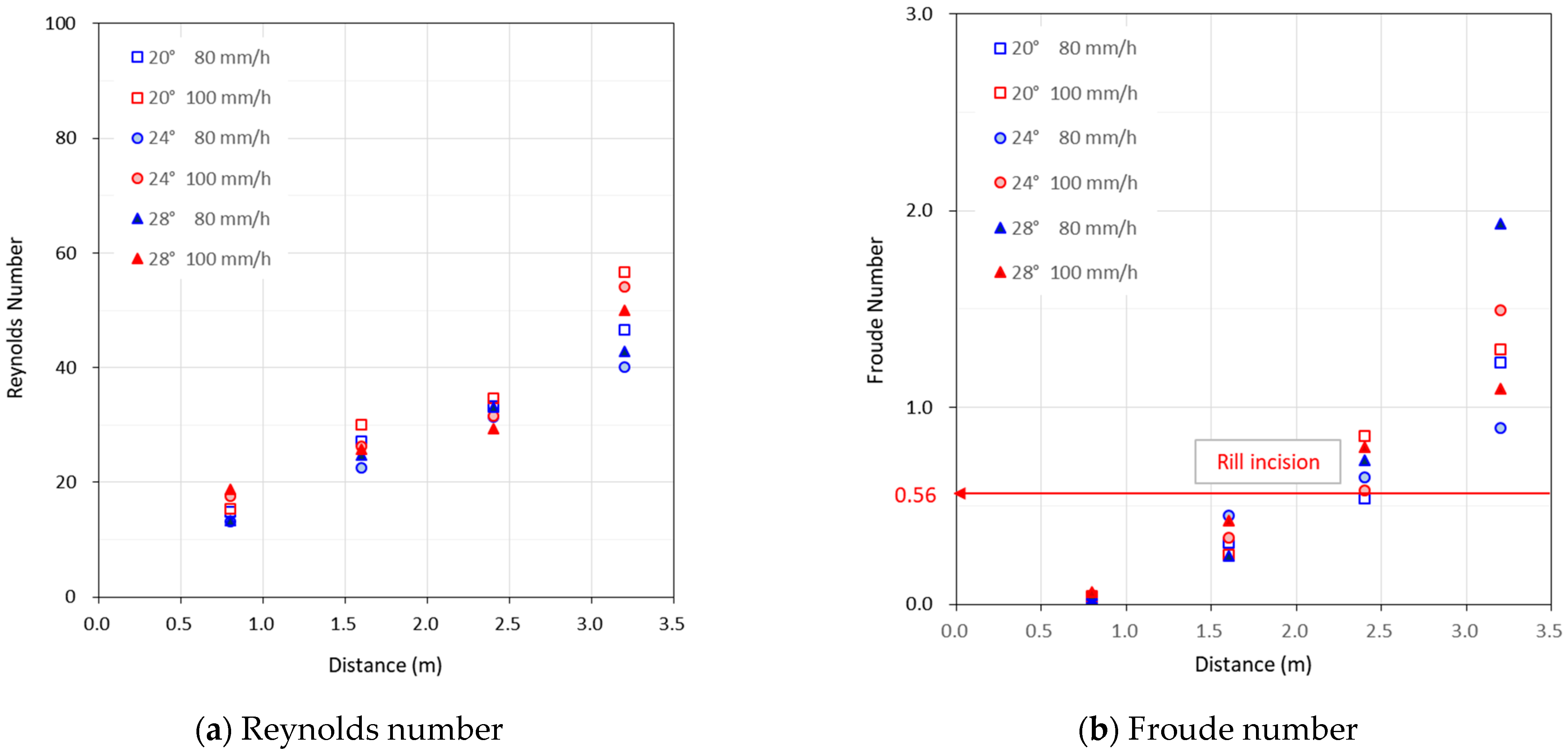
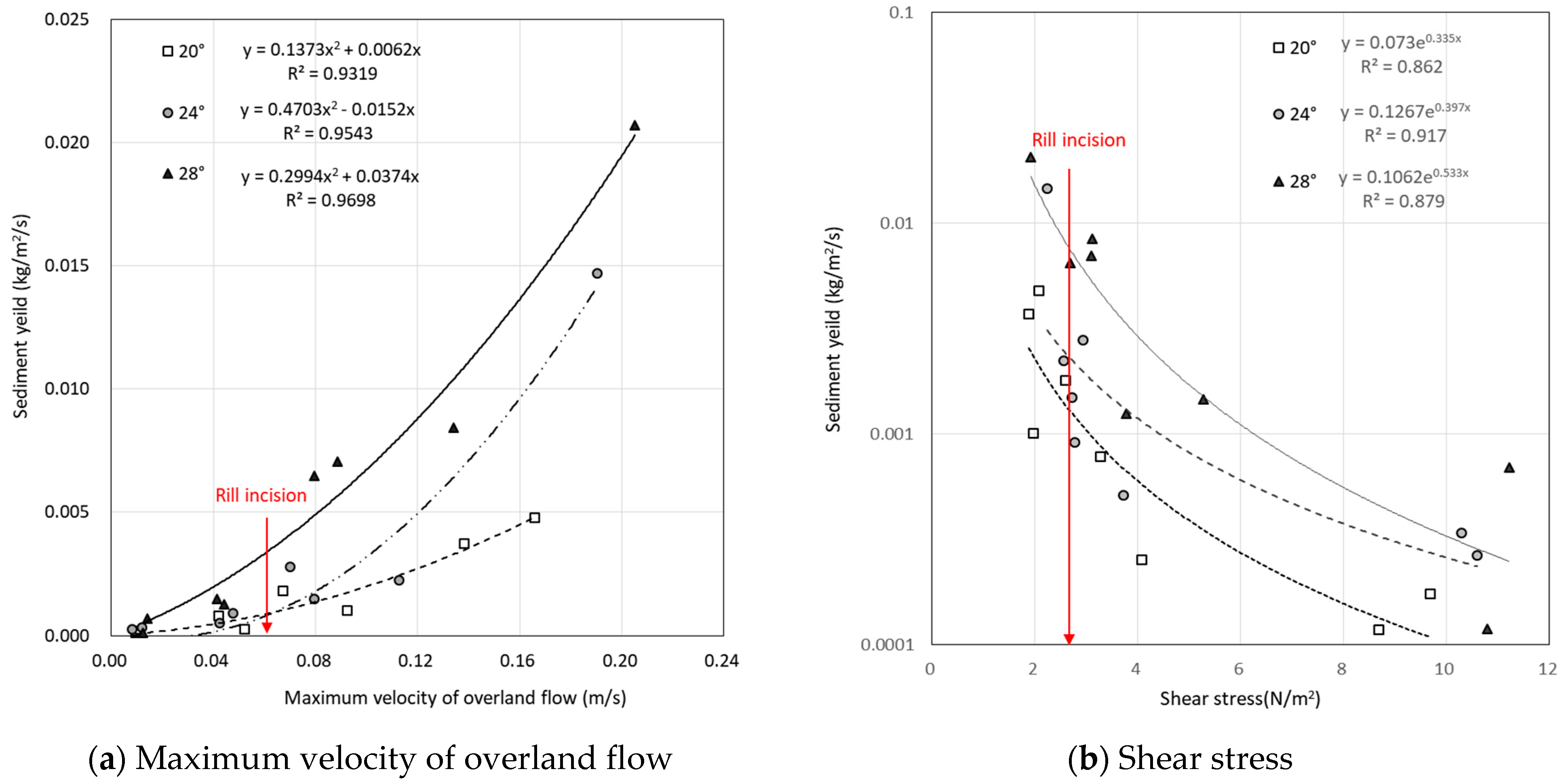
3.3. Hydrodynamic for Rill Incipience
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korean Statistical Information Service (KOSIS). Slope Distribution by Location, National Forest Inventory; Korean Statistical Information Service: Daejeon, South Korea, 2010. [Google Scholar]
- Miura, S.; Yoshinaga, S.; Yamada, T. Protective effect of floor cover against soil erosion on steep slopes forested with chamaecyparis obtusa (hinoki) and other species. J. For. Res. 2003, 8, 27–35. [Google Scholar] [CrossRef]
- Shakesby, R.A.; Doerr, S.H. Wildfire as a hydrological and geomorphological agent. Earth-Sci. Rev. 2006, 74, 269–307. [Google Scholar] [CrossRef]
- Cerdà, A.; Doerr, S.H. The effect of ash and needle cover on surface runoff and erosion in the immediate post-fire period. CATENA 2008, 74, 256–263. [Google Scholar] [CrossRef]
- Ghahramani, A.; Ishikawa, Y.; Gomi, T.; Shiraki, K.; Miyata, S. Effect of ground cover on splash and sheetwash erosion over a steep forested hillslope: A plot-scale study. CATENA 2011, 85, 34–47. [Google Scholar] [CrossRef]
- Nearing, M.A.; Norton, L.D.; Bulgakov, D.A.; Larionov, G.A.; West, L.T.; Dontsova, K.M. Hydraulics and erosion in eroding rills. Water Resour. Res. 1997, 33, 865–876. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion in the United Kingdom: Field Studies in the Silsoe Area 1973–1975; Occasional Paper No. 4; National College of Agricultural Engineering: London, UK, 1977. [Google Scholar]
- Govers, G.; Rauws, G. Transporting capacity of overland flow on plane and irregular beds. Earth Surf. Proc. Landf. 1986, 11, 515–524. [Google Scholar] [CrossRef]
- Zheng, F.L.; Tang, K.L. Rill erosion process on steep slope land of the Loess Plateau. Int. J. Sediment Res. 1997, 12, 52–59. [Google Scholar]
- Bewket, W.; Sterk, G. Assessment of soil erosion in cultivated fields using a survey methodology for rills in the Chemoga watershed, Ethiopia. Agric. Ecosyst. Environ. 2003, 97, 81–93. [Google Scholar] [CrossRef]
- Zheng, F.; He, X.; Gao, X.; Zhang, C.; Tang, K. Effects of erosion patterns on nutrient loss following deforestation on the Loess Plateau of China. Agric. Ecosyst. Environ. 2005, 108, 85–97. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Jia, L.; Gong, H.; Cai, Q. Experimental study of Rill Evolution Processes and Relation-ships between Runoff and Erosion on Clay Loam and Loess. Soil Sci. Soc. Am. J. 2014, 78, 1716–1725. [Google Scholar] [CrossRef]
- Govers, G.; Poesen, J. Assessment of the interrill and rill contributions to total soil loss from an upland field plot. Geomorphology 1988, 1, 343–354. [Google Scholar] [CrossRef]
- Shen, H.; Zheng, F.; Wen, L.; Lu, J.; Jiang, Y. An experimental study of rill erosion and morphology. Geomorphology 2015, 231, 193–201. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, H.; Yao, W.; Zhang, N.; Xizhi, L.V. Experimental investigation of morphological characteristics of rill evolution on loess slope. CATENA 2016, 137, 536–544. [Google Scholar] [CrossRef]
- Shin, S.S.; Sim, Y.J.; Son, S.J.; Park, S.D. Micromorphological changes of rill developed by simulated rainfall and inflow on steep slopes. KSCE J. Civ. Eng. 2023, 43, 21–32. [Google Scholar]
- Lee, J.Y.; Yang, D.Y.; Kim, J.Y.; Chung, G.S. Application of landsat ETM image to estimate the distribution of soil types and erosional pattern in the wildfire area of Gangneung, Gangwon province, Korea. J. Korean Earth Sci. Soc. 2004, 25, 764–773. [Google Scholar]
- Kim, K.T.; Kim, J.H. Analysis of soil erosion hazard zone by cropland. J. Korean Wetl. Soc. 2005, 7, 107–117. [Google Scholar]
- Lee, H.H.; Joo, J.D. Characteristics of soil erosion on the forest fired sites by using rainfall simulator. J. Korean For. Soc. 2006, 95, 649–656. [Google Scholar]
- Kim, C.G.; Shin, K.; Joo, K.Y.; Lee, K.S.; Shin, S.S.; Choung, Y. Effects of soil conservation measures in a partially vegetated area after forest fires. Sci. Total Environ. 2008, 399, 158–164. [Google Scholar] [CrossRef]
- Shin, S.S.; Park, S.D.; Cho, J.W.; Lee, K.S. Effect of vegetation recovery for surface runoff and soil erosion in burned mountains, Yangyang. KSCE J. Civ. Eng. 2008, 28, 393–403. [Google Scholar]
- Seo, J.I.; Chun, K.W.; Kim, S.W.; Kim, M.S. Rainfall pattern regulating surface erosion and its effect on variation in sediment yield in post-wildfire area. J. Korean Soc. For. Sci. 2010, 99, 534–545. [Google Scholar]
- Shin, S.S.; Park, S.D.; Lee, K.S. Sediment and hydrological response to vegetation recovery following wildfire on hillslopes and the hollow of a small watershed. J. Hydrol. 2013, 499, 154–166. [Google Scholar] [CrossRef]
- Jeong, J.G.; Seo, B.M.; Ha, S.H.; Lee, D.W. A measurement of hydraulic conductivity of disturbed sandy soils by particle analysis and falling head method. J. Eng. Geol. 2006, 16, 15–21. [Google Scholar]
- Park, S.D.; Lee, K.S.; Shin, S.S. Statistical soil erosion model for burnt mountain areas in Korea - RUSLE approach. J. Hydrol. Eng. ASCE 2012, 17, 292–304. [Google Scholar] [CrossRef]
- Shin, S.S.; Park, S.D.; Pierson, F.B.; Williams, C.J. Evaluation of physical erosivity factor for interrill erosion on steep vegetated hillslopes. J. Hydrol. 2019, 571, 559–572. [Google Scholar] [CrossRef]
- Savat, J. Laboratory experiments on erosion and deposition of loess by laminar sheet flow and turbulent rill flow. In Agricultural Soil Erosion in Temperate Non Mediterranean Climate; Université de Strasbourg: Strasbourg, France, 1979; pp. 139–144. [Google Scholar]
- Merritt, E. The identification of four stages during micro-rill development. Earth Surf. Process. Landf. 1984, 9, 493–496. [Google Scholar] [CrossRef]
- Rauws, G.; Govers, G. Hydraulic and soil mechanical aspects of rill generation on agricultural soils. J. Soil Sci. 1988, 39, 111–124. [Google Scholar] [CrossRef]
- Bryan, R.B.; Poesen, J. Laboratory experiments on the influence of slope length on runoff, percolation and rill development. Earth Surf. Process. Landf. 1989, 14, 211–231. [Google Scholar] [CrossRef]
- Govers, G. Empirical relationships for the transport capacity of overland flow. Eros. Transp. Depos. Process. IAHS Publ. 1990, 189, 45–63. [Google Scholar]
- Slattery, M.; Bryan, R. Hydraulic conditions for rill incision under simulated rainfall: A laboratory experiment. Earth Surf. Process. Landf. 1992, 17, 127–146. [Google Scholar] [CrossRef]
- Abrahams, A.D.; Li, G. Rill hydraulics on a semiarid hillslope, southern Arizona. Earth Surf. Process-Es Landf. 1996, 21, 35–47. [Google Scholar] [CrossRef]
- Giménez, R.; Govers, G. Interaction between bed roughness and flow hydraulics in eroding rills. Water Resour. Res. 2001, 37, 791–799. [Google Scholar] [CrossRef]
- Wells, R.R.; Bennett, S.J.; Alonso, C.V. Modulation of headcut soil erosion in rills due to upstream sediment loads. Water Resour. Res. 2010, 46, W12531. [Google Scholar] [CrossRef]
- Li, G.; Zheng, F.; Lu, J.; Xu, X.; Hu, W.; Han, Y. Inflow rate impact on hillslope erosion processes and flow hydrodynamics. Soil Sci. Soc. Am. J. 2016, 80, 711–719. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhao, Y.; Mi, H.; Mo, B. Estimating rill erosion process from eroded morphology in flume experiments by volume replacement method. CATENA 2016, 136, 135–140. [Google Scholar] [CrossRef]
- Nearing, M.A.; Simanton, J.R.; Norton, L.D.; Bulygin, S.J.; Stone, J. Soil erosion by surface water flow on a stony, semiarid hillslope. Earth Surf. Process. Landf. 1999, 24, 677–686. [Google Scholar] [CrossRef]
- Lei, T.W.; Zhang, Q.W.; Zhao, J.; Xia, W.S.; Pan, Y.H. Soil detachment rates for sediment loaded flow in rills. Trans. ASAE 2002, 45, 1897–1903. [Google Scholar]
- Yao, C.; Lei, T.; Elliot, W.J.; McCool, D.K.; Zhao, J.; Chen, S. Critical conditions for rill initiation. Trans. ASABE 2008, 51, 107–114. [Google Scholar] [CrossRef] [Green Version]
- Berger, C.; Schulze, M.; Rieke-Zapp, D.; Schlunegger, F. Rill development and soil erosion: A laboratory study of slope and rainfall intensity. Earth Surf. Process. Landf. 2010, 35, 1456–1467. [Google Scholar] [CrossRef]
- Tian, P.; Xu, X.; Pan, C.; Hsu, K.; Yang, T. Impacts of rainfall and inflow on rill formation and erosion processes on steep hillslopes. J. Hydrol. 2017, 548, 24–39. [Google Scholar] [CrossRef]
- Jiang, F.; Zhan, Z.; Chen, J.; Lin, J.; Wang, M.K.; Ge, H.; Huang, Y. Rill erosion processes on a steep colluvial deposit slope under heavy rainfall in flume experiments with artificial rain. CATENA 2018, 169, 46–58. [Google Scholar] [CrossRef]
- Tian, P.; Pan, C.; Xu, X.; Wu, T.; Yang, T.; Zhang, L. A field investigation on rill development and flow hydrodynamics under different upslope inflow and slope gradient conditions. Hydrol. Res. 2020, 51, 1201–1220. [Google Scholar] [CrossRef]
- Niu, Y.; Gao, Z.; Li, Y.; Lou, Y.; Zhang, S.; Zhang, L.; Due, J.; Zhang, X.; Luo, K. Characteristics of rill erosion in spoil heaps under simulated inflow: A field runoff plot experiment. Soil Tillage Res. 2020, 202, 104655. [Google Scholar] [CrossRef]
- Kou, P.; Xu, Q.; Yunus, A.P.; Dong, X.; Zhong, Y.; Chen, L.; Fang, S.; Luo, X.; Jin, Z. Rill development and its change rate: A field experiment under constant rainfall intensity. CATENA 2021, 199, 105112. [Google Scholar] [CrossRef]
- Moody, J.A.; Smith, J.D.; Ragan, B.W. Critical shear stress for erosion of cohesive soils subjected to temperatures typical of wildfires. J. Geophys. Res. 2005, 110, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Zheng, F.; Wen, L.; Han, Y.; Hu, W. Impacts of rainfall intensity and slope gradient on rill erosion processes at loessial hillslope. Soil Tillage Res. 2016, 155, 429–436. [Google Scholar] [CrossRef]
- Qin, C.; Zheng, F.; Xu, X.; Wu, H.; Shen, H. A laboratory study on rill network development and morphological characteristics on loessial hillslope. J. Soils Sediments 2017, 18, 1679–1690. [Google Scholar] [CrossRef]
- Shih, H.M.; Yang, C.T. Estimating overland flow erosion capacity using unit stream power. Int. J. Sediment Res. 2009, 24, 46–62. [Google Scholar] [CrossRef]
- Shi, Z.H.; Fang, N.F.; Wu, F.Z.; Wang, L.; Yue, B.J.; Wu, G.L. Soil erosion processes and sediment sorting associated with transport mechanisms on steep slopes. J. Hydrol. 2012, 454–455, 123–130. [Google Scholar] [CrossRef]
- Govers, G. Relationship between discharge, velocity and flow area for rills eroding loose, non-layered materials. Earth Surf. Process. Landf. 1992, 17, 515–528. [Google Scholar] [CrossRef]
- Zhuang, X.; Wang, W.; Ma, Y.; Huang, X.; Lei, T. Spatial distribution of sheet flow velocity along slope under simulated rainfall conditions. Geoderma 2018, 321, 1–7. [Google Scholar] [CrossRef]
- Savat, J. Common and uncommon selectivity in the process of fluid transportation: Field observations and laboratory experiments on bare surfaces. CATENA Suppl. 1982, 1, 139–160. [Google Scholar]
- Loch, R.J.; Thomas, E.C. Resistance to rill erosion: Observations on the efficiency of rill erosion on a tilled clay soil under simulated rain and run-on water. CATENA Suppl. 1987, 8, 71–83. [Google Scholar]
- Shin, S.S.; Park, S.D.; Lee, S.K.; Nam, M.J. Soil Erosion Experimental Equipment; 10-2016-0085990; Korean Intellectual Property Office: Daejeon, Republic of Korea, 2016. [Google Scholar]
- Nam, M.J.; Park, S.D.; Lee, S.K.; Shin, S.S. Interaction between raindrops splash and sheet flow in interrill erosion of steep hillslopes. J. Korea Water Resour. Assoc. 2015, 48, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Shin, S.S.; Park, S.D.; Hwang, Y. Erodibility evaluation of sandy soils for sheet erosion on steep slopes. J. Korea Water Resour. Assoc. 2022, 55, 291–300. [Google Scholar]
- Park, S.D.; Shin, S.S.; Kim, S.J.; Chio, B. Effects of surface compaction treatment on soil loss from disturbed bare slopes under simulated rainfalls. J. Korea Water Resour. Assoc. 2013, 46, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Moss, A.; Green, P.; Hutka, J. Small channels: Their formation, nature and significance. Earth Surf. Process. Landf. 1982, 7, 401–415. [Google Scholar] [CrossRef]
- Torri, D.; Sfalanga, M.; Del Sette, M. Splash detachment: Runoff depth and soil cohesion. CATENA 1987, 14, 149–155. [Google Scholar] [CrossRef]
- Govers, G. Spatial and temporal variability in rill development processes at the Huldenberg experimental Site. CATENA Suppl. 1987, 8, 17–33. [Google Scholar]
- Bagnold, R.A. An approach to the sediment transport problem form general physics; U.S., Geological Survey Professional Paper, 422-J; U.S. Government Printing Office: Washington, DC, USA, 1966.
- Yang, C.T. Unit stream power and sediment transport. J. Hydraul. Div. (ASCE) 1972, 98, 1805–1826. [Google Scholar] [CrossRef]
- Planchon, O.; Fritsch, E.; Valentin, C. Rill development in a wet Savannah environment. CATENA Suppl. 1987, 8, 55–70. [Google Scholar]
- Govers, G. Selectivity and transport capacity of thin flows in relation with rill erosion. CATENA 1985, 12, 35–49. [Google Scholar] [CrossRef]
- Foster, G. Modelling the soil erosion process. In Hydrologic Modelling of Small Watersheds; Haan, C., Johnson, H., Brakensiek, D., Eds.; American Society of Agricultural Engineers Monograph: St. Joseph, MI, USA, 1982; Volume 5, pp. 940–947. [Google Scholar]
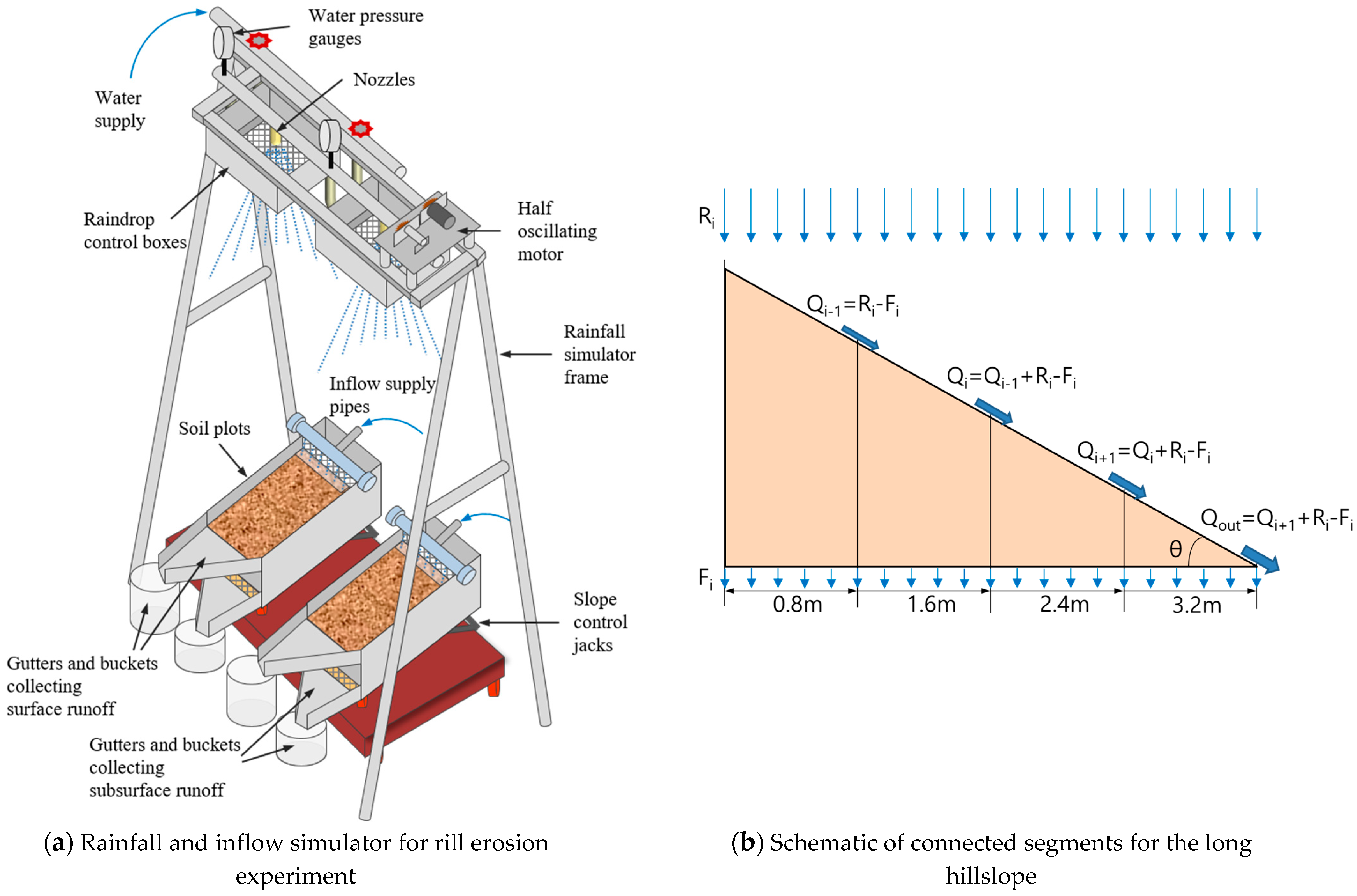
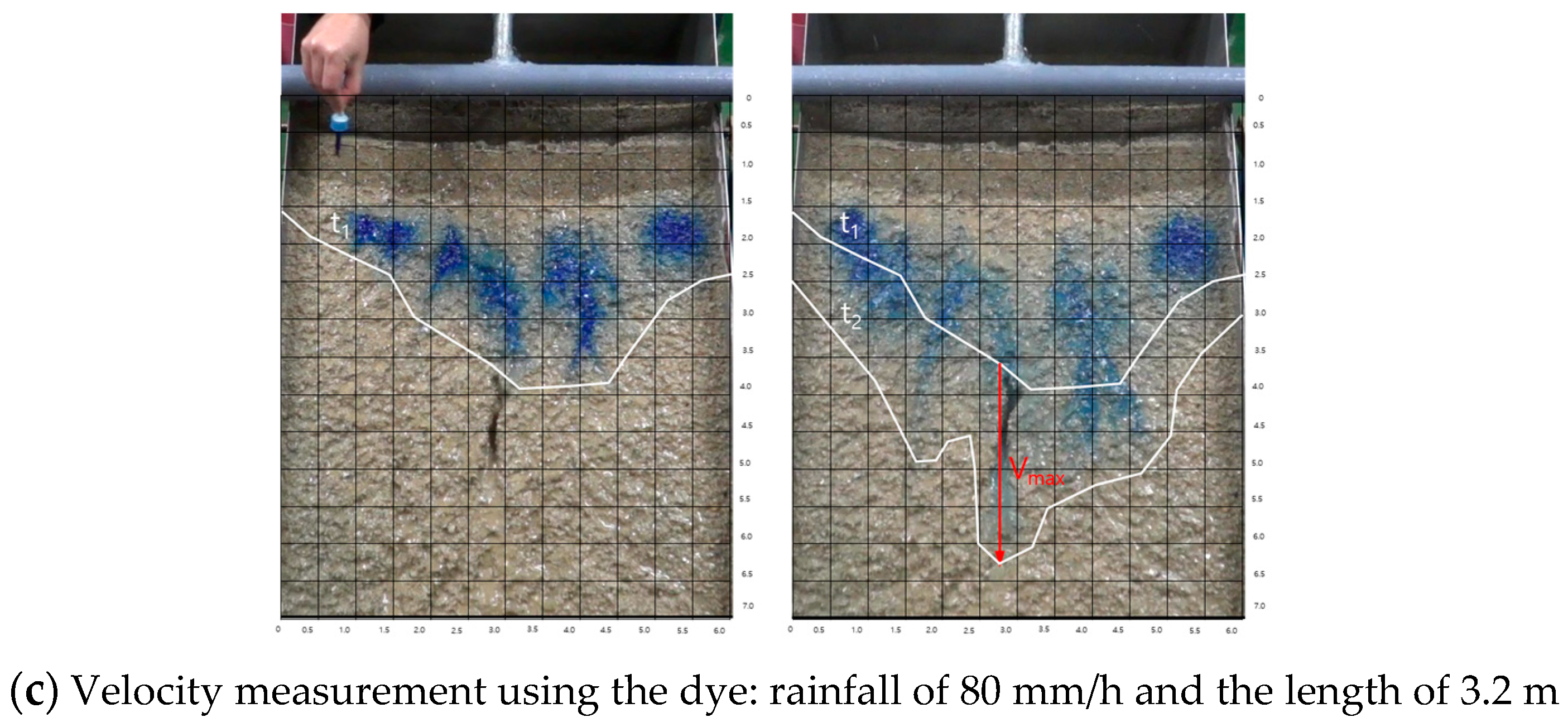




| Factors | Subfactors | Range |
|---|---|---|
| Erosivity | Rainfall intensity, I (mm/h) | 80.0 ± 1.2, 100.0 ± 1.8 |
| Inflow discharge, Qin (ml/s) | 0.0, 8.8 ± 1.1, 17.5 ± 2.2, 26.3 ± 3.3 | |
| Duration of simulation (min) | 10 | |
| Topography | Length, L (m) | 0.8 |
| Width, W (m) | 0.6 | |
| Slope, S (°) | 20, 24, 28 | |
| Erodibility | Clay (%) | 1.1 |
| Silt (%) | 3.9 | |
| Sand (%) | 73.3 | |
| Gravel (%) | 21.7 | |
| Mean diameter, Dm (mm) | 0.936 | |
| Bulk density, ρs (g/cm3) | 1.78 | |
| Organic matter content, Om (%) | 2.05 ± 0.08 | |
| Share strength, τs (kg/cm2) | 0.312 ± 0.033 |
| Slope (°) | Rainfall Intensity, I (mm/h) | Segment Distance, Seg (m) | Inflow Rate, Qin (ml/s) | Unit Flow Rate, Qout (10−5 m2/s) | Runoff Coefficient, C | Flow Velocity, V (m/s) |
|---|---|---|---|---|---|---|
| 20 | 80 | 0.8 | 0.0 | 1.49 | 0.81 | 0.006 |
| 1.6 | 8.0 | 2.72 | 0.86 | 0.030 | ||
| 2.4 | 15.8 | 3.35 | 0.75 | 0.046 | ||
| 3.2 | 26.0 | 4.68 | 0.76 | 0.089 | ||
| 100 | 0.8 | 0.0 | 1.55 | 0.68 | 0.006 | |
| 1.6 | 11.0 | 3.01 | 0.73 | 0.026 | ||
| 2.4 | 19.3 | 3.48 | 0.64 | 0.063 | ||
| 3.2 | 31.0 | 5.69 | 0.77 | 0.098 | ||
| 24 | 80 | 0.8 | 0.0 | 1.33 | 0.75 | 0.005 |
| 1.6 | 7.9 | 2.26 | 0.73 | 0.036 | ||
| 2.4 | 15.9 | 3.15 | 0.71 | 0.051 | ||
| 3.2 | 23.0 | 4.02 | 0.71 | 0.068 | ||
| 100 | 0.8 | 0.0 | 1.78 | 0.79 | 0.008 | |
| 1.6 | 9.8 | 2.65 | 0.69 | 0.031 | ||
| 2.4 | 19.7 | 3.17 | 0.58 | 0.047 | ||
| 3.2 | 30.0 | 5.43 | 0.75 | 0.106 | ||
| 28 | 80 | 0.8 | 0.0 | 1.34 | 0.75 | 0.006 |
| 1.6 | 7.5 | 2.49 | 0.82 | 0.025 | ||
| 2.4 | 15.1 | 3.33 | 0.78 | 0.056 | ||
| 3.2 | 23.0 | 4.30 | 0.76 | 0.116 | ||
| 100 | 0.8 | 0.0 | 1.88 | 0.84 | 0.009 | |
| 1.6 | 9.7 | 2.60 | 0.66 | 0.036 | ||
| 2.4 | 18.8 | 2.94 | 0.55 | 0.057 | ||
| 3.2 | 29.0 | 5.03 | 0.71 | 0.084 |
| Factors | Sediment Yield (kg/m2/s) | Sediment Concentration (kg/m3) |
|---|---|---|
| Slope steepness, S (°) | 0.346 | 0.427 * |
| Shear strength of soil, τs(kg/cm2) | −0.124 | −0.138 |
| Inflow discharge, Qin (ml/sec) | 0.628 ** | 0.572 ** |
| Rainfall intensity, I (mm/hr) | 0.023 | −0.023 |
| Supply water discharge, Qsup (ml/sec) | 0.615 ** | 0.555 ** |
| Overland flow discharge, Oout (ml/sec) | 0.640 ** | 0.555 ** |
| Runoff coefficient, C | −0.049 | −0.111 |
| Mean velocity of overland flow, V (m/s) | 0.797 ** | 0.743 ** |
| Maximum velocity of overland flow, Vmax (m/s) | 0.831 ** | 0.766 ** |
| Mean water depth, h (mm) | −0.481 * | −0.492 * |
| Reynolds number | 0.640 ** | 0.555 ** |
| Froude number | 0.849 ** | 0.803 ** |
| Shear stress, τ (N/m2) | −0.442 * | −0.440 * |
| Ratio of shear stress for shear strength, τ/τs | −0.411 * | −0.409 * |
| Stream power, W (N/m/s) | 0.817 ** | 0.749 ** |
| Unit stream power, VS (m/s) | 0.916 ** | 0.873 ** |
| Authors | Soil | Slope Length | Supply Water (Rainfall + Inflow) | Runoff | Velocity of Rill | Hydrodynamic |
|---|---|---|---|---|---|---|
| Torri et al. [61] | Sandy (flume) | 0.5°–17° 2.0 m | I = 30–60 mm/h | - | - | τcr = 0.45–0.50 Pa |
| Govers [31] | Silt to coarse sand(flume) | 1–12° 6.0 m | Qin = 0.023–0.117 L/s | - | Vcr = 0.03–0.035 m/s | τcr = 0.2–0. 35 Pa VcrS = 0.004 m/s |
| Yao et al. [40] | Silt loam(flume) | 20°, 25° 8.0 m | I = 100 mm/h | Qout = 0.048–0.071 L/s | Vcr = 0.048–0.052 m/s | τcr = 1.41–1.76 Pa VcrS= 0.017–0.024 m/s |
| Shen et al. [48] | Silt loam(flume) | 20° 10 m | I = 85–100 mm/h | - | Vave = 0.240–0.246 m/s | - |
| Tian et al. [42] | Sandy loam(field) | 26° 5.0 m | I = 60 mm/h Qin = 0.1–0.6 L/s | - | Vcr = 0.21 m/s | τcr = 2.76 Pa W = 0.15 N/m/s VcrS = 0.06 m/s |
| Jiang et al. [43] | Sandy loam(field) | 20° 5.0 m | I = 100–120 mm/h | Qout = 0.106–0.113 L/s | Vave = 0.10–0.13 m/s | τ = 17–23 Pa VS = 0.03–0.04 m/s |
| Zhuang et al. [53] | Coarse-sand loamy(flume) | 20° 8.0 m | I = 80–120 mm/h | - | Vcr = 0.073–0.079 m/s | VcrS = 0.027–0.029 m/s |
| In this study | Sandy(flume) | 20°– 28° 3.2 m | I = 80–100 mm/h Qin = 8.8–0.31 L/s | Qout = 0.08–0.34 L/s | Vcr = 0.065 m/s | τcr = 2.67 Pa W = 0.12 N/m/s VcrS = 0.024 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, S.S.; Park, S.D.; Sim, Y.J.; Ryu, J.H. Hydraulic Conditions of Incipient Rill by Raindrop-Induced Overland Flow on Steep Slopes of Sandy Soil. Water 2023, 15, 502. https://doi.org/10.3390/w15030502
Shin SS, Park SD, Sim YJ, Ryu JH. Hydraulic Conditions of Incipient Rill by Raindrop-Induced Overland Flow on Steep Slopes of Sandy Soil. Water. 2023; 15(3):502. https://doi.org/10.3390/w15030502
Chicago/Turabian StyleShin, Seung Sook, Sang Deog Park, Young Ju Sim, and Jae Hyeon Ryu. 2023. "Hydraulic Conditions of Incipient Rill by Raindrop-Induced Overland Flow on Steep Slopes of Sandy Soil" Water 15, no. 3: 502. https://doi.org/10.3390/w15030502
APA StyleShin, S. S., Park, S. D., Sim, Y. J., & Ryu, J. H. (2023). Hydraulic Conditions of Incipient Rill by Raindrop-Induced Overland Flow on Steep Slopes of Sandy Soil. Water, 15(3), 502. https://doi.org/10.3390/w15030502






