Coil System Design for Multi-Frequency Resistivity Logging Tool Based on Numerical Simulation
Abstract
:1. Introduction
2. Principle and Method
2.1. Measuring Principle
2.2. Simulation Method
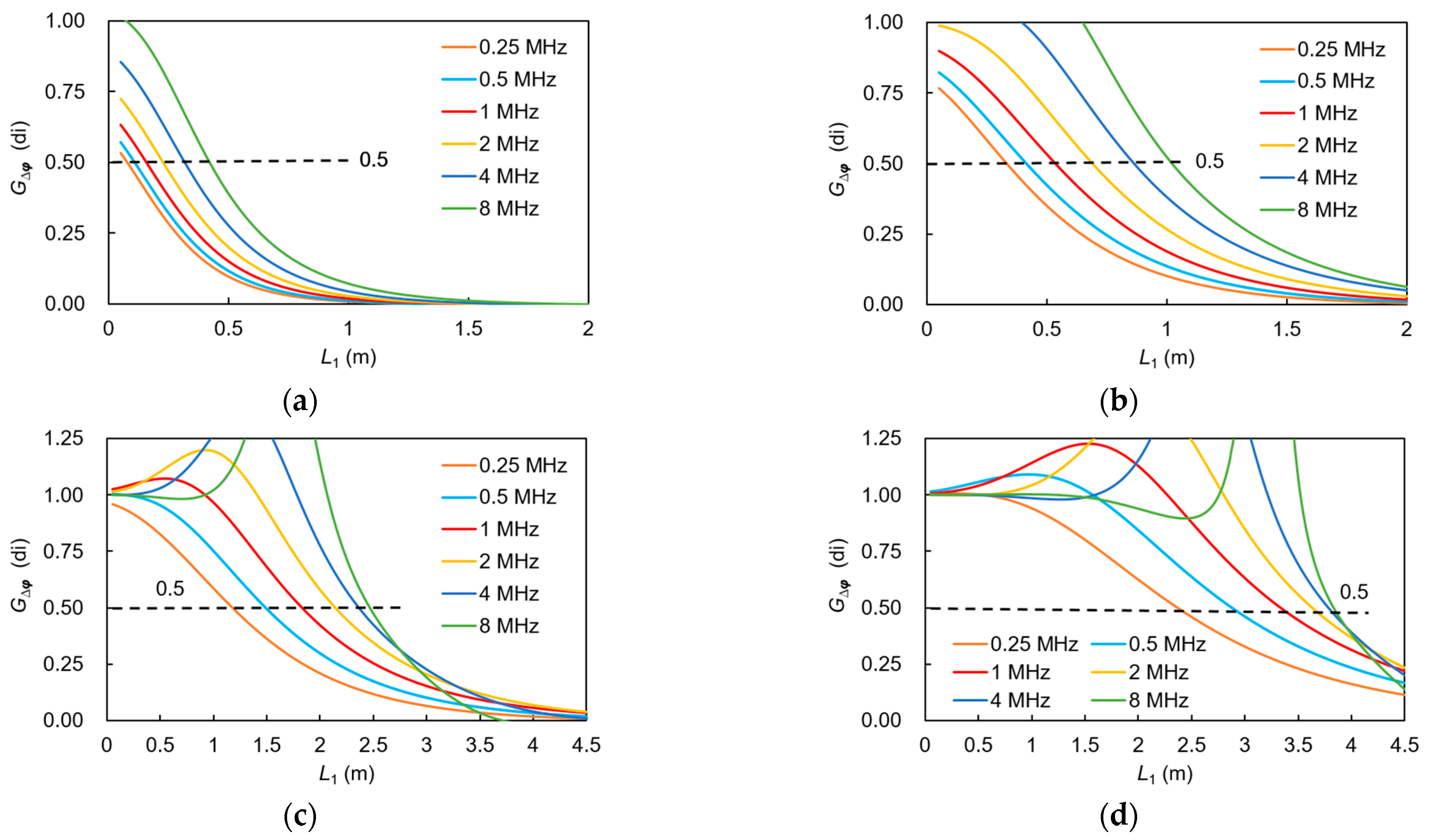
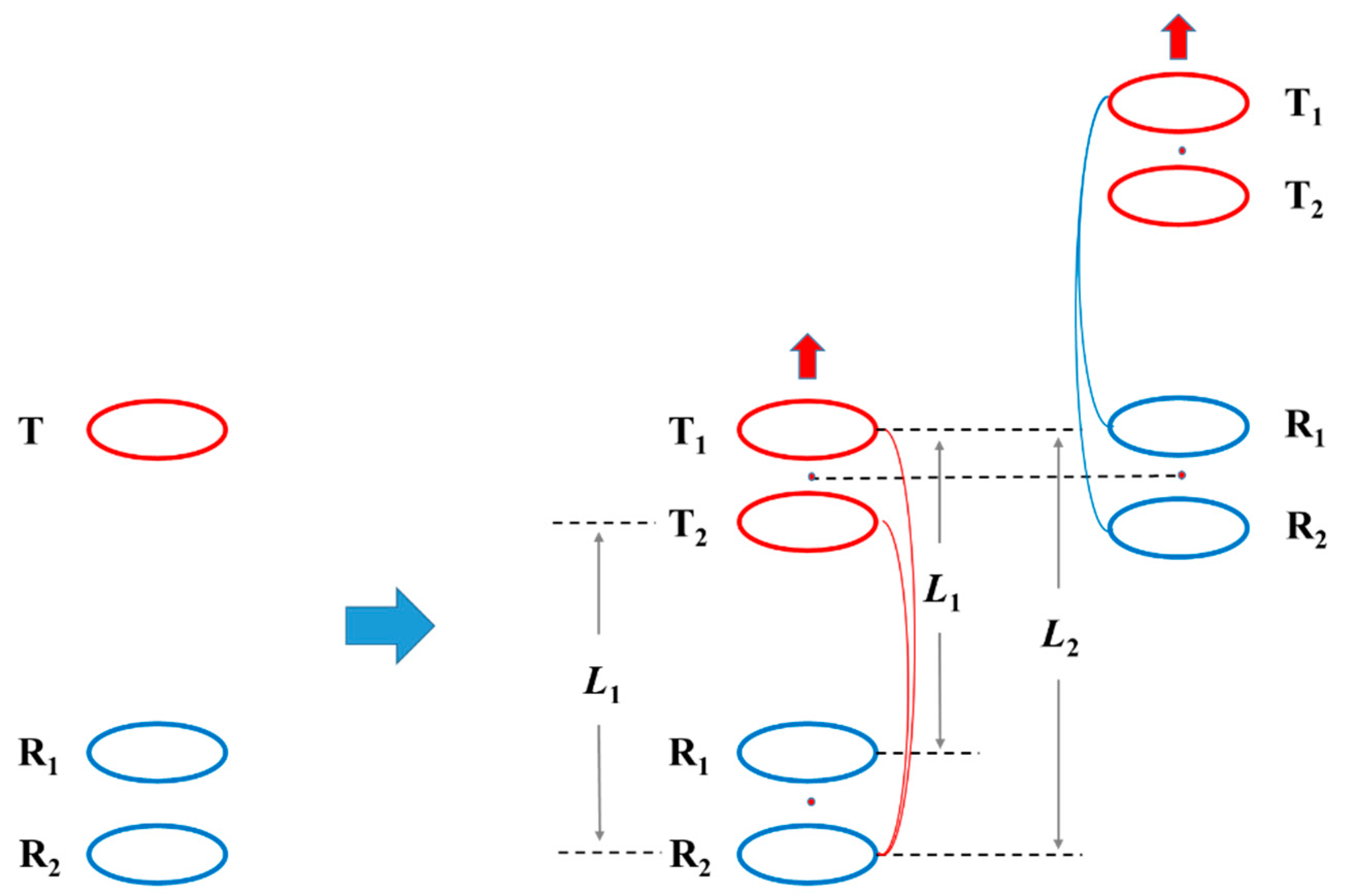
2.3. Determine the Source-Receiver Distance
3. Result and Discussion
3.1. Structure of Coil Systems
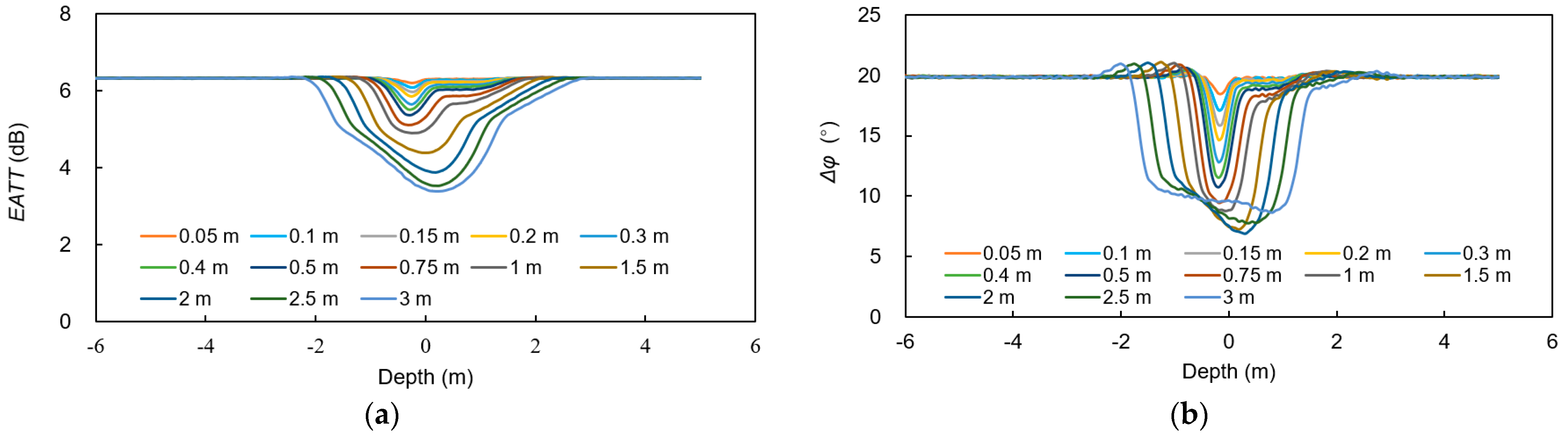
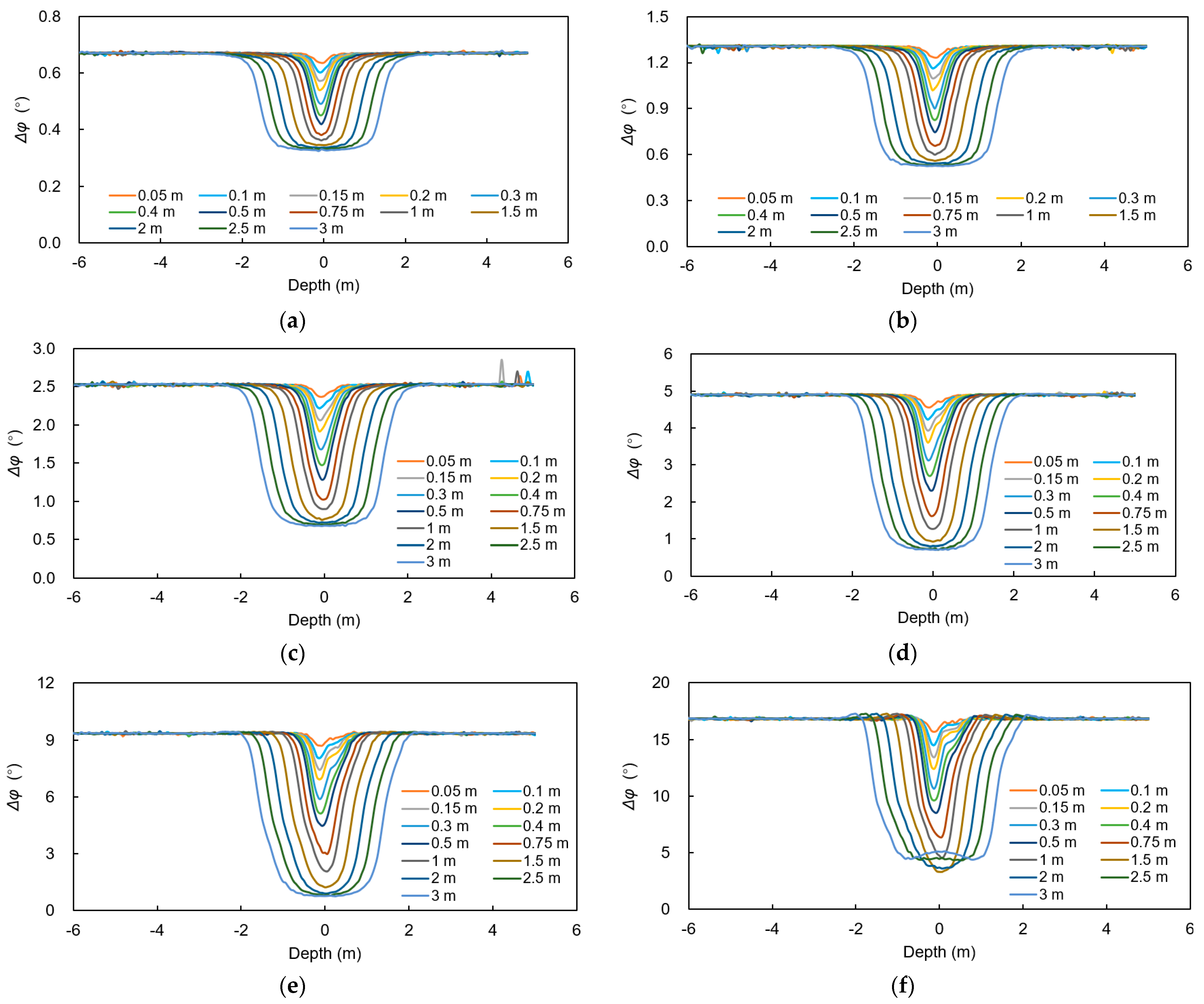
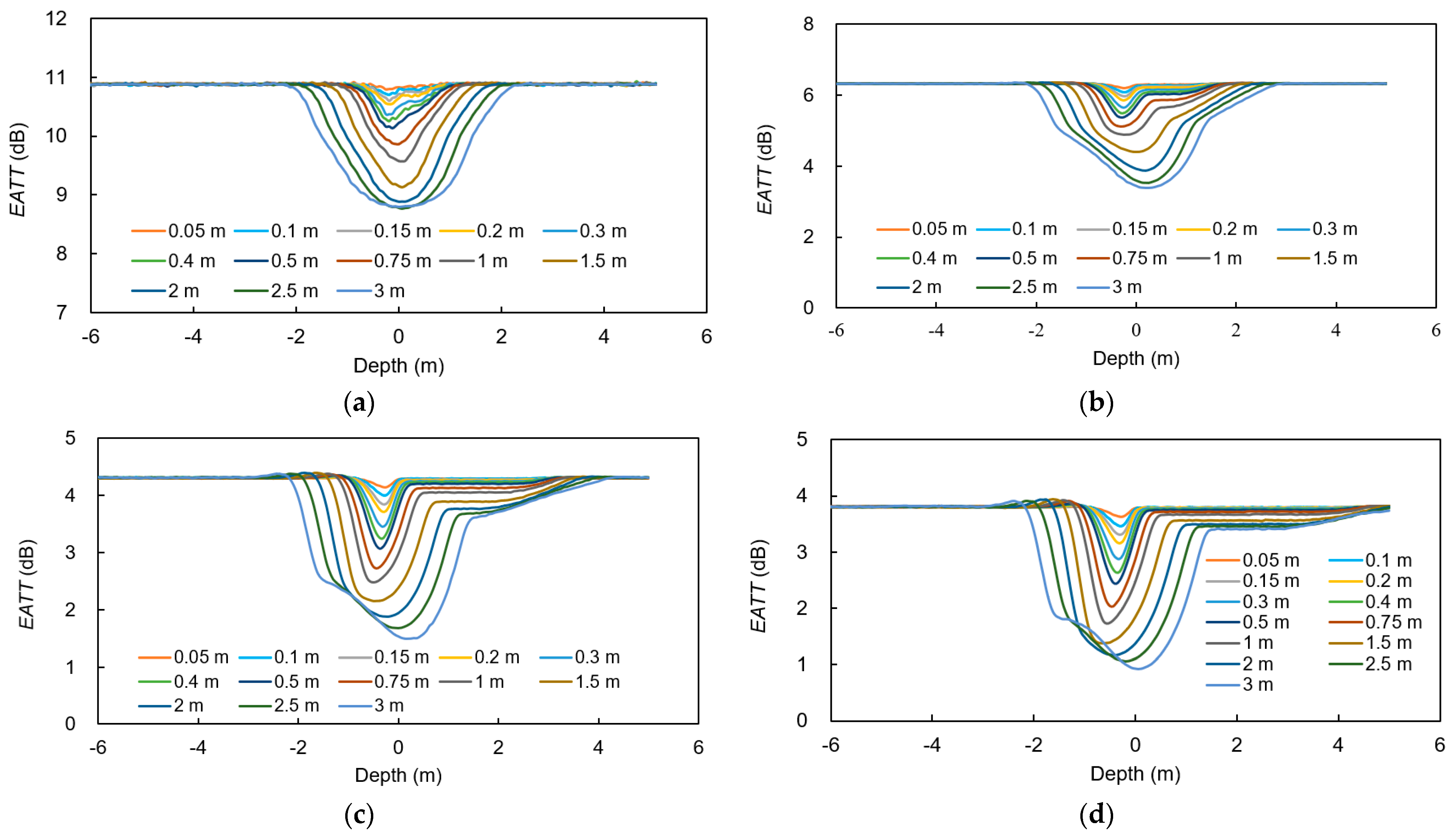
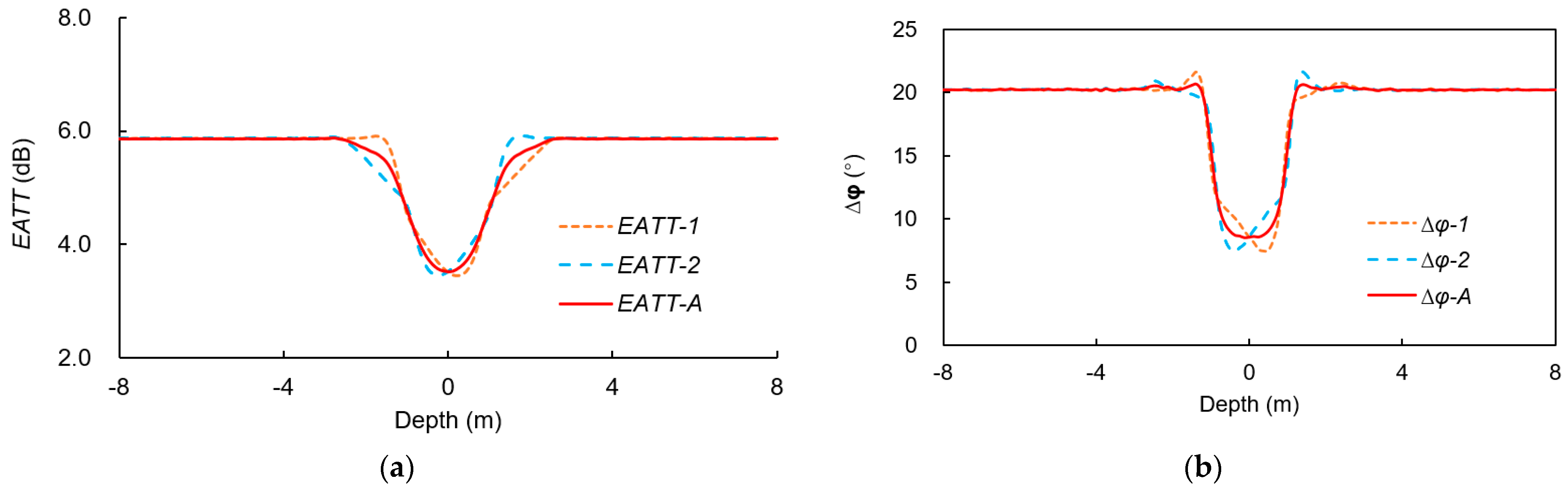
3.2. Vertical Resolution
3.3. Structure Improvement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, J.; Zhao, J.; Jiao, S.; Song, R.; Tang, T. Multi-point resistivity measurement system for full-diameter long cores during fluid displacement. Rev. Sci. Instrum. 2022, 93, 124502. [Google Scholar] [CrossRef] [PubMed]
- Snyder, D.D.; Merkel, R.; Williams, J. Complex formation resistivity- the forgotten half of the resistivity log. In Proceedings of the Spwla 18th Annual Logging Symposium, Houston, TX, USA, 5–8 June 1977. [Google Scholar]
- Zisser, N.; Kemna, A.; Nover, G. Relationship between low-frequency electrical properties and hydraulic permeability of low-permeability sandstones. Geophysics 2010, 75, E131–E141. [Google Scholar] [CrossRef]
- Zisser, N.; Nover, G. Anisotropy of permeability and complex resistivity of tight sandstones subjected to hydrostatic pressure. J. Appl. Geophys. 2009, 68, 356–370. [Google Scholar] [CrossRef]
- Khairy, H.; Harith, Z.Z.T. Interfacial, pore geometry and saturation effect on complex resistivity of shaly sandstone: Dispersion and laboratory investigation. Geosci. J. 2011, 15, 395–415. [Google Scholar] [CrossRef]
- Kavian, M.; Slob, E.; Mulder, W. A new empirical complex electrical resistivity model. Geophysics 2012, 77, E185–E191. [Google Scholar] [CrossRef]
- Li, J.; Ke, S.; Yin, C.; Kang, Z.; Jia, J.; Ma, X. A laboratory study of complex resistivity spectra for predictions of reservoir properties in clear sands and shaly sands. J. Pet. Sci. Eng. 2019, 177, 983–994. [Google Scholar] [CrossRef]
- Jia, J.; Ke, S.; Rezaee, R.; Li, J.; Wu, F. The frequency exponent of artificial sandstone’s complex resistivity spectrum. Geophys. Prospect. 2021, 69, 856–871. [Google Scholar] [CrossRef]
- Tong, M.; Tao, H. Permeability estimating from complex resistivity measurement of shaly sand reservoir. Geophys. J. Int. 2008, 173, 733–739. [Google Scholar] [CrossRef]
- Liu, H.; Jie, T.; Li, B.; Youming, D.; Chunning, Q. Study of the low-frequency dispersion of permittivity and resistivity in tight rocks. J. Appl. Geophys. 2017, 143, 141–148. [Google Scholar] [CrossRef]
- Jia, J.; Ke, S.; Li, J.; Kang, Z.; Ma, X.; Li, M.; Guo, J. Estimation of permeability and saturation based on imaginary component of complex resistivity spectra: A laboratory study. Open Geosci. 2020, 12, 299–306. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Y.; Li, T.; Yi, S.; Li, N. A Universal Multi-Frequency Micro-Resistivity Array Imaging Method for Subsurface Sensing. Remote Sens. 2022, 14, 3116. [Google Scholar] [CrossRef]
- Bittar, M.S.; Bartel, R. Multi-Frequency Electromagnetic Wave Resistivity Tool with Improved Calibration Measurement. US Patent 6,218,842, 17 April 2001. [Google Scholar]
- Bittar, M.S. Compensated Multi-Mode Elctromagnetic Wave Resistivity Tool. Google Patents. US Patent 6,538,447, 25 March 2003. [Google Scholar]
- Epov, M.; Yeltsov, I.; Zhmaev, S.; Petrov, A.; Ulyanov, V.; Glinskikh, V. Vikiz Method for Logging Oil and Gas Boreholes; Branch “Geo” of the Publishing House of the SB RAS: Novosibirsk, Russia, 2002. [Google Scholar]
- Maurer, H.-M.; Beard, D.R. Multiple Depths of Investigation Using Two Transmitters. US Patent 8,547,103, 1 October 2013. [Google Scholar]
- Wang, H.; Poppitt, A. The broadband electromagnetic dispersion logging data in a gas shale formation: A case study. In Proceedings of the Spwla 54th Annual Logging Symposium, New Orleans, LA, USA, 22–26 June 2013. [Google Scholar]
- Hizem, M.; Budan, H.; Deville, B.; Faivre, O.; Mosse, L.; Simon, M. Dielectric dispersion: A new wireline petrophysical measurement. In Proceedings of the Spe Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Bean, C.; Cole, S.; Boyle, K.; Kho, D.; Neville, T.J. New wireline dielectric dispersion logging tool result in fluvio-deltaic sands drilled with oil-based mud. In Proceedings of the Spwla 54th Annual Logging Symposium, New Orleans, LA, USA, 22–26 June 2013. [Google Scholar]
- Seleznev, N.V.; Habashy, T.M.; Boyd, A.J.; Hizem, M. Formation properties derived from a multi-frequency dielectric measurement. In Proceedings of the Spwla 47th Annual Logging Symposium, Veracruz, Mexico, 4–7 June 2006. [Google Scholar]
- Al Qarshubi, I.; Trabelsi, A.; Akinsanmi, M.; Polinski, R.; Faivre, O.; Hizem, M.; Mosse, L. Quantification of remaining oil saturation using a new wireline dielectric dispersion measurement-a case study from dukhan field arab reservoirs. In Proceedings of the Spe Middle East Oil and Gas Show and Conference, Manama, Bahrain, 25–28 September 2011. [Google Scholar]
- Al-Yaarubi, A.; Al-Mjeni, R.; Bildstein, J.; Al-Ani, K.; Mikhasev, M.; Legendre, F.; Hizem, M. Applications of dielectric dispersion logging in oil-based mud. In Proceedings of the Spwla 55th Annual Logging Symposium, Abu Dhabi, United Arab Emirates, 18–22 May 2014. [Google Scholar]
- Jiang, M.; Ke, S.; Kang, Z. Measurements of complex resistivity spectrum for formation evaluation. Measurement 2018, 124, 359–366. [Google Scholar] [CrossRef]
- Ke, S. An electric parameter measurement system with coil sonde for big diameter core. Well Logging Technol. 2007, 2, 116–117+123. (In Chinese) [Google Scholar]
- Kang, Z.; Qin, H.; Zhang, Y.; Hou, B.; Hao, X.; Chen, G. Coil optimization of ultra-deep azimuthal electromagnetic resistivity logging while drilling tool based on numerical simulation. J. Pet. Explor. Prod. Technol. 2023, 13, 787–801. [Google Scholar] [CrossRef]
- Yiren, F.; Xufei, H.; Shaogui, D.; Xiyong, Y.; Haitao, L. Logging while drilling electromagnetic wave responses in inclined bedding formation. Pet. Explor. Dev. 2019, 46, 711–719. [Google Scholar]
- Chu, Z.H.; Huang, L.J.; Gao, J.; Xiao, L.Z. Geophysical Logging Methods and Principles; Petroleum Industry Press: Beijing, China, 2008; Volume 1. (In Chinese) [Google Scholar]
- Kang, Z.; Ke, S.; Yin, C.; Jia, J.; Li, M.; Li, J.; Ma, X. Introduction of the coil-type complex resistivity spectrum logging method. In Proceedings of the Seg Technical Program Expanded Abstracts, Anaheim, CA, USA, 14–19 October 2018. [Google Scholar]
- Xu, W.; Ke, S.Z.; Li, A.Z.; Chen, P.; Zhu, J.; Zhang, W. Response simulation and theoretical calibration of a dual-induction resistivity lwd tool. Appl. Geophys. 2014, 11, 31–40. [Google Scholar] [CrossRef]
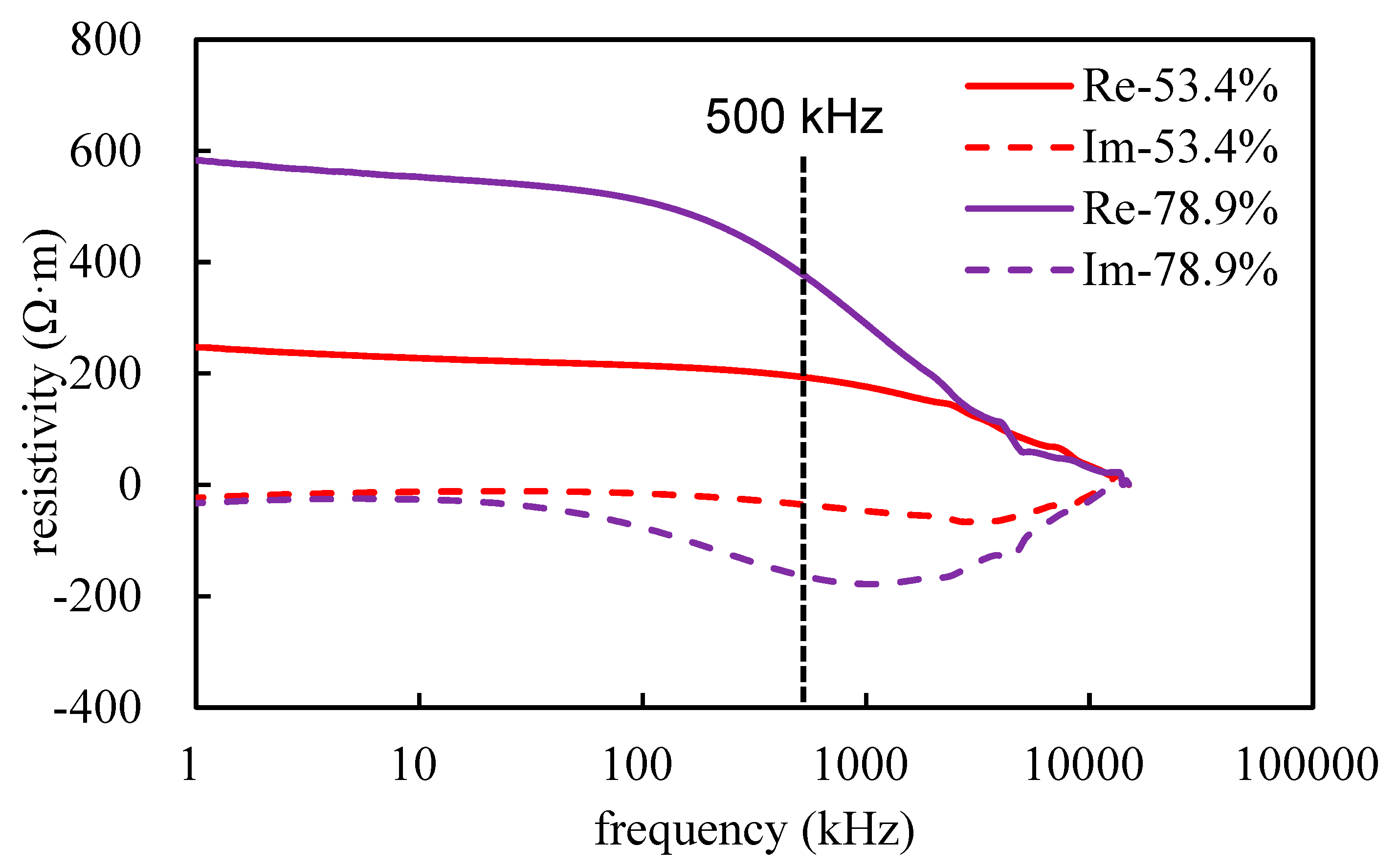
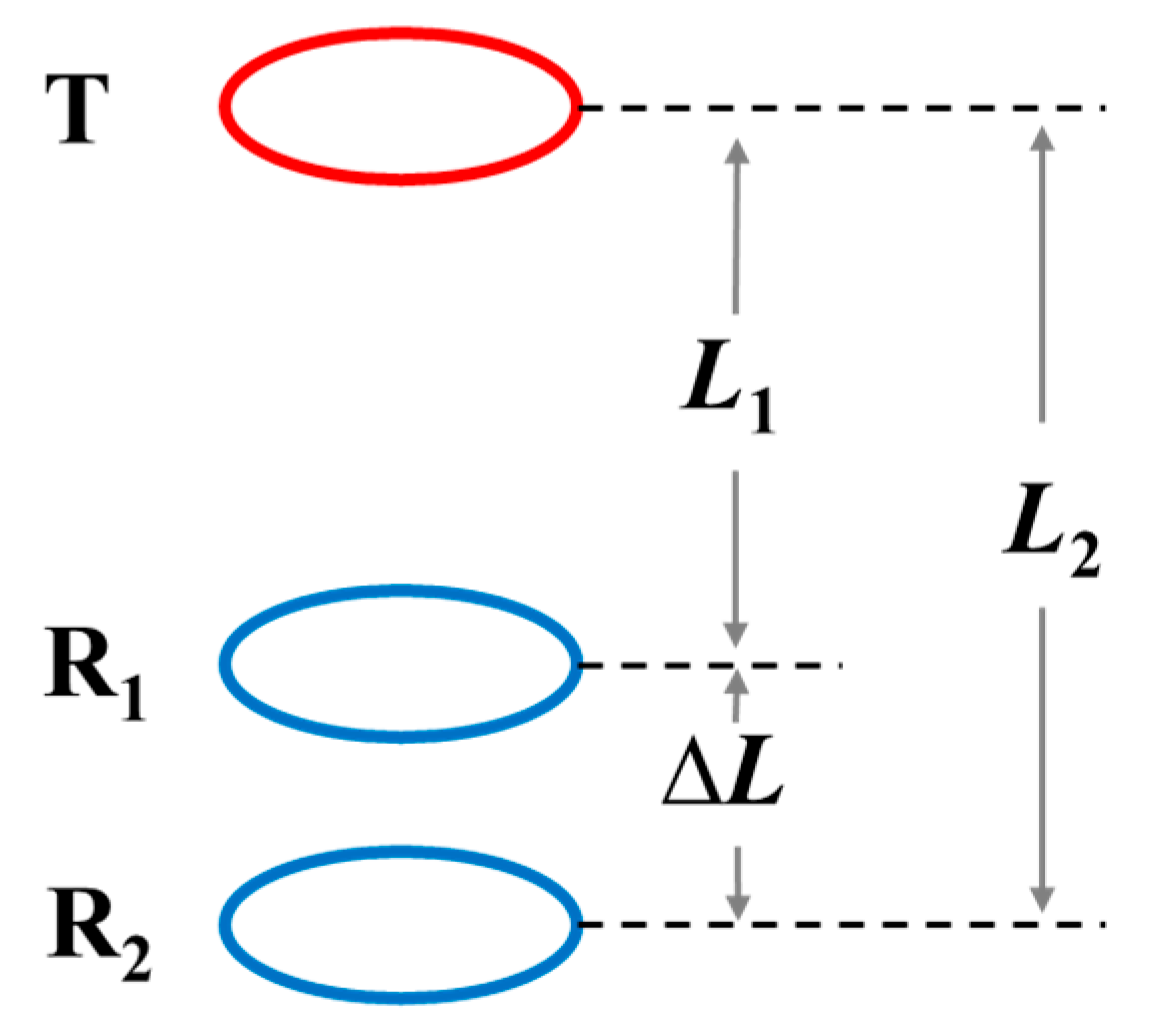
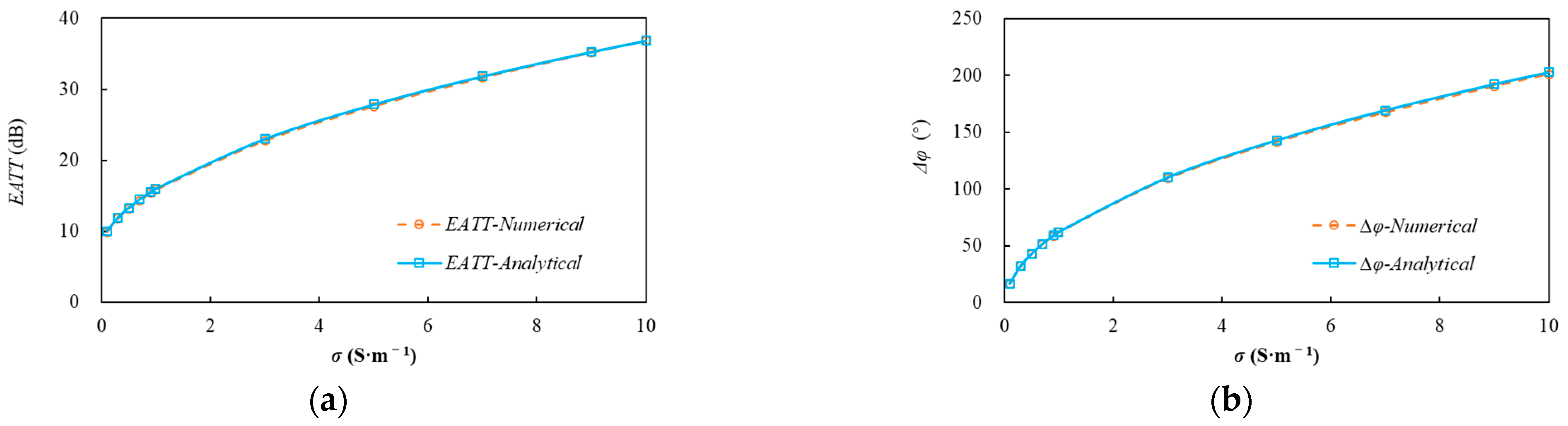
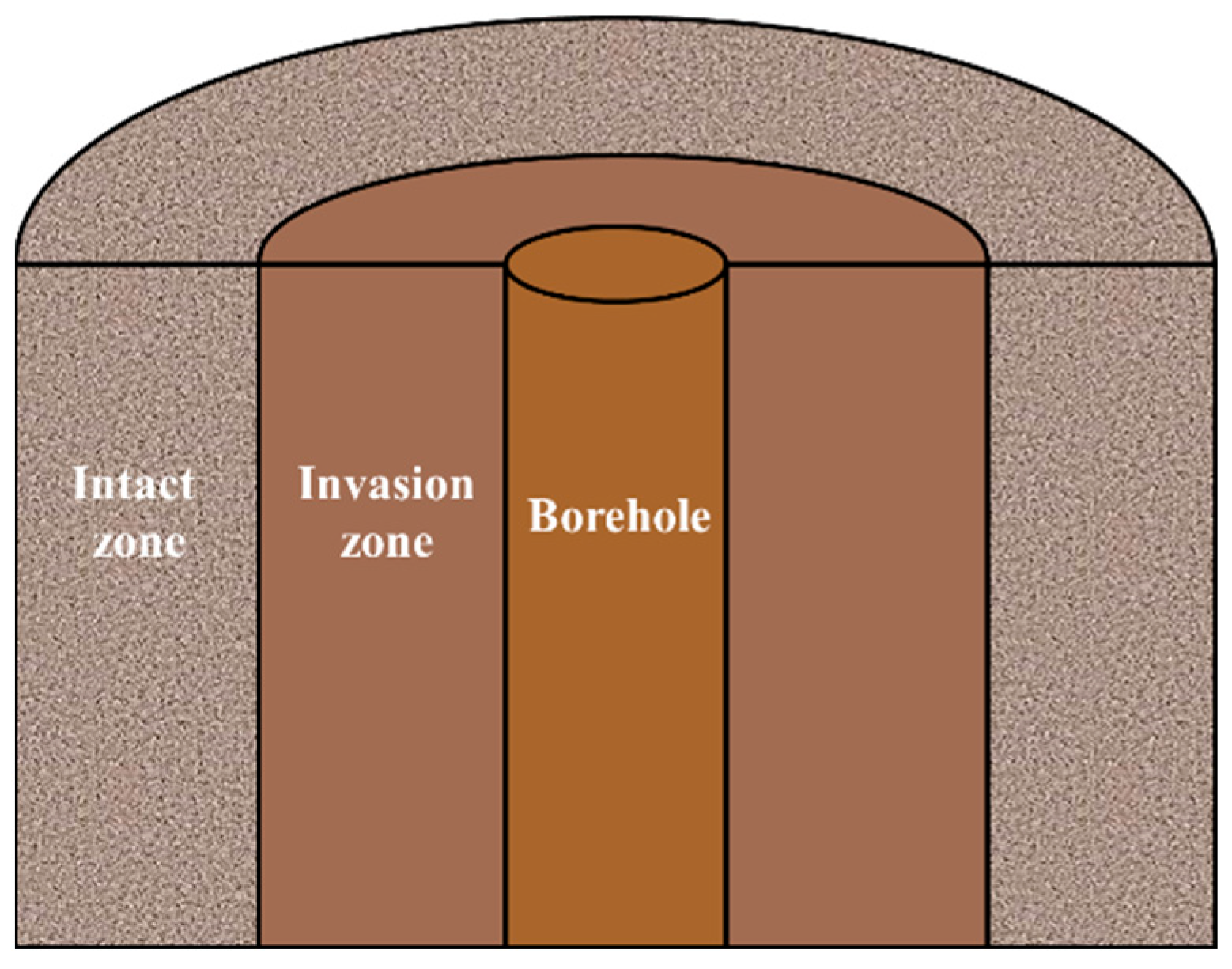


| Parameters | Borehole | Invasion Zone | Intact Zone |
|---|---|---|---|
| Inner radius (m) | 0 | 0.054 | DOI |
| Outer radius (m) | 0.054 | DOI | 25 |
| Relative magnetic permeability | 1 | 1 | 1 |
| Relative permittivity | 75 | 50 | 30 |
| Conductivity (S/m) | 1 | 0.5 | 0.1 |
| Frequency (MHz) | DOI = 0.3 m | DOI = 0.5 m | DOI = 1 m | DOI = 1.5 m | ||||
|---|---|---|---|---|---|---|---|---|
| L1 (m) | L2 (m) | L1 (m) | L2 (m) | L1 (m) | L2 (m) | L1 (m) | L2 (m) | |
| 0.25 | 0.08 | 0.28 | 0.33 | 0.53 | 1.18 | 1.38 | 2.37 | 2.57 |
| 0.5 | 0.11 | 0.31 | 0.41 | 0.61 | 1.49 | 1.69 | 2.88 | 3.08 |
| 1 | 0.16 | 0.36 | 0.53 | 0.73 | 1.83 | 2.03 | 3.34 | 3.54 |
| 2 | 0.23 | 0.43 | 0.69 | 0.89 | 2.15 | 2.35 | 3.63 | 3.83 |
| 4 | 0.32 | 0.52 | 0.86 | 1.06 | 2.36 | 2.56 | 3.78 | 3.98 |
| 8 | 0.42 | 0.62 | 1.02 | 1.22 | 2.47 | 2.67 | 3.83 | 4.03 |
| DOI/m | Coil System Structure |
|---|---|
| 0.3 | T1-0.10-T2-0.09-T3-0.07-T4-0.05-T5-0.03-T6-0.08-R1-0.20-R2 (m) |
| 0.5 | T1-0.16-T2-0.17-T3-0.16-T4-0.12-T5-0.08-T6-0.33-R1-0.20-R2 (m) |
| 1 | T1-0.11-T2-0.21-T3-0.32-T4-0.34-T5-0.31-T6-1.18-R1-0.20-R2 (m) |
| 1.5 | T1-0.05-T2-0.15-T3-0.29-T4-0.46-T5-0.51-T6-2.37-R1-0.20-R2 (m) |
| Parameters | Borehole | Target Layer | Surrounding Layer |
|---|---|---|---|
| Inner radius (m) | 0 | 0.054 | 0.054 |
| Outer radius (m) | 0.054 | 25 | 25 |
| Relative magnetic permeability | 1 | 1 | 1 |
| Relative permittivity | 75 | 65 | 30 |
| Conductivity (S/m) | 1 | 0.001 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Ke, S.; Rezaee, R. Coil System Design for Multi-Frequency Resistivity Logging Tool Based on Numerical Simulation. Water 2023, 15, 4213. https://doi.org/10.3390/w15244213
Jia J, Ke S, Rezaee R. Coil System Design for Multi-Frequency Resistivity Logging Tool Based on Numerical Simulation. Water. 2023; 15(24):4213. https://doi.org/10.3390/w15244213
Chicago/Turabian StyleJia, Jiang, Shizhen Ke, and Reza Rezaee. 2023. "Coil System Design for Multi-Frequency Resistivity Logging Tool Based on Numerical Simulation" Water 15, no. 24: 4213. https://doi.org/10.3390/w15244213
APA StyleJia, J., Ke, S., & Rezaee, R. (2023). Coil System Design for Multi-Frequency Resistivity Logging Tool Based on Numerical Simulation. Water, 15(24), 4213. https://doi.org/10.3390/w15244213







