1. Introduction
Errors in model inputs, structure, and parameters often lead to unsatisfactory predictions in hydrological flood forecasting [
1]. Consequently, the introduction of error correction methods becomes crucial for improving the accuracy of forecasted outcomes. One such method is the System Differential Response Curve (SRC), proposed by Weimin Bao, with several advantages, including a simple structure, the absence of additional parameters, clear physical interpretation, and no loss of foresight [
2,
3]. Currently, this method is widely applied in various research areas, such as parameter calibration, correction of streamflow error], correction of a real mean rainfall error, and correction of state variables. [
4,
5,
6,
7] The hydrological model is regarded as a system in the context of the SRC analysis. In this framework, the model’s input corresponds to the independent variable, while the model’s output represents the dependent variable. To perform inverse analysis and rectify the model’s input, a functional relationship called the response matrix is established, which characterizes the relationship between the model’s input and output. During the process of inverse analysis, the response matrix may suffer from multicollinearity, which arises when the vectors of the response matrix exhibit strong linear dependencies. The presence of multicollinearity results in the response matrix becoming ill-conditioned, making it impossible to calculate the corrected value of the independent variable. Furthermore, insufficient information in the response matrix can lead to significant amplification of small errors, thereby endangering the stability of the solution [
8]. In order to address the issue of ill-conditioning in the response matrix and avoid excessive correction of the model’s input, Bao et al. [
8] proposed the ridge estimation-SRC method by incorporating ridge estimation into the SRC method. Ridge estimation [
9,
10] is a regression analysis technique used to handle the problem of multicollinearity. In ordinary least squares estimation, when the design matrix (also known as the independent variable matrix) exhibits multicollinearity, the inverse matrix of the design matrix cannot be computed. To address this issue, ridge estimation sacrifices the unbiasedness of ordinary least squares estimation by introducing a bias term to the design matrix. This trade-off allows for obtaining more reliable regression coefficients at the cost of sacrificing some information from the design matrix and reducing estimation precision when multicollinearity is present. Thus, ridge estimation solves the problem of the non-invertibility of the design matrix in ordinary least squares estimation [
9,
11,
12]. Furthermore, ridge estimation serves the purpose of introducing a penalty function that constrains the range of the estimated parameter.
Currently, there are several methods available for automatically selecting the ridge parameter in ridge estimation, such as the ridge trace method, the generalized cross-validation method (GCV) [
13,
14], and the L-curve method [
15,
16], among others. The ridge trace method determines the optimal ridge parameter by plotting curves of different ridge parameters against the corresponding regression coefficient components. The subjective nature of this approach hinders its efficiency, especially when dealing with a large number of variables in the design matrix. As the number of variables increases, the creation of ridge trace plots becomes more time-consuming and challenging due to the need for manual intervention. The GCV method determines the optimal ridge parameter by minimizing the cross-validation error. However, locating the minimum of the GCV function can sometimes be challenging due to its flatness, and it is prone to overfitting [
17]. Hansen et al. [
18,
19] proposed the L-curve method as a more robust approach for determining the optimal ridge parameter in ill-conditioned matrices, especially in the presence of measurement errors. Compared to the two methods mentioned above, the L-curve has rigorous mathematical derivation and clear mathematical significance. It exhibits good applicability in solving the problem of ill-conditioning in the design matrix. The L-curve method calculates the estimated parameters and model’s residuals using least squares by selecting multiple sets of different ridge parameters. By plotting the value of the model’s residuals on the X-axis and the value of the estimated parameters on the Y-axis, a curve is fitted to determine the optimal value of the ridge parameter. This method takes into account the fluctuations in the residuals and estimated parameters, enabling accurate identification of the optimal ridge parameter in general scenarios. Currently, the L-curve method is extensively employed for selecting ridge parameters [
20,
21]. The L-curve criterion aims to minimize the sum of the model’s residuals and estimated terms. The residual term represents the error between observed and simulated values, while the estimated term represents the parameters that need to be estimated. The traditional L-curve method considers the change in the estimated term and emphasizes that a good estimation should limit this change, achieving an appropriate size for the estimated terms while minimizing the residual term. This perspective is persuasive in hydrological studies. However, the traditional L-curve method does not incorporate the physical meaning of the estimated parameters and fails to capture information about the parameters’ range of the estimated term. When coupled with SRC, the selected optimal ridge parameters often exhibit a bias towards smaller values. This bias can result in certain components of the estimated term exceeding the allowable parameter range during calculations, thereby resulting in poorer fitting accuracy between the measured and simulated data after correction. To address this issue, this study proposes the constrained L-curve (CL-curve) method, which incorporates a constraint term to consider the physical interpretation of the model parameters. By introducing this constraint, it restricts the variation in the estimated term, ensuring that the estimated parameters remain within a reasonable range. In addition, coupling the CL-curve with the SRC aims to enhance the accuracy of updating streamflow for the SRC.
Accurate hydrological models play a crucial role in water resource planning and management, reservoir operation planning, and flood control management. As a result, they have become a highly sought-after research topic in the field of hydrology. Moreover, the development of these models contributes to a deeper understanding of ongoing hydrological processes within watersheds. Generally, hydrological models can be categorized into two groups: (a) conceptual and physically based models, such as the Xin-Anjiang (XAJ) model and the Soil and Water Assessment Tool (SWAT) model; and (b) empirical or data-driven models, including support vector machines (SVM) and artificial neural networks (ANN). A thorough review of these hydrological models can be found in the literature [
22,
23]. Conceptual and physically-based models are widely utilized in hydrological studies due to their ability to effectively simulate the hydrological processes of watersheds while considering the physical mechanisms and hydrological characteristics. The SWAT model, developed by the US Department of Agriculture, is a distributed hydrological model that incorporates strong physical mechanisms. This model utilizes geographic information systems and remote sensing to simulate the hydrological processes of a basin based on spatial information and surface characteristics. It comprehensively accounts for the influence of underlying surfaces on streamflow, making it a widely applied tool in the simulation of streamflow and sediment in large basins. Consequently, in this study, the SWAT model is used as the research model to simulate daily streamflow in this study area.
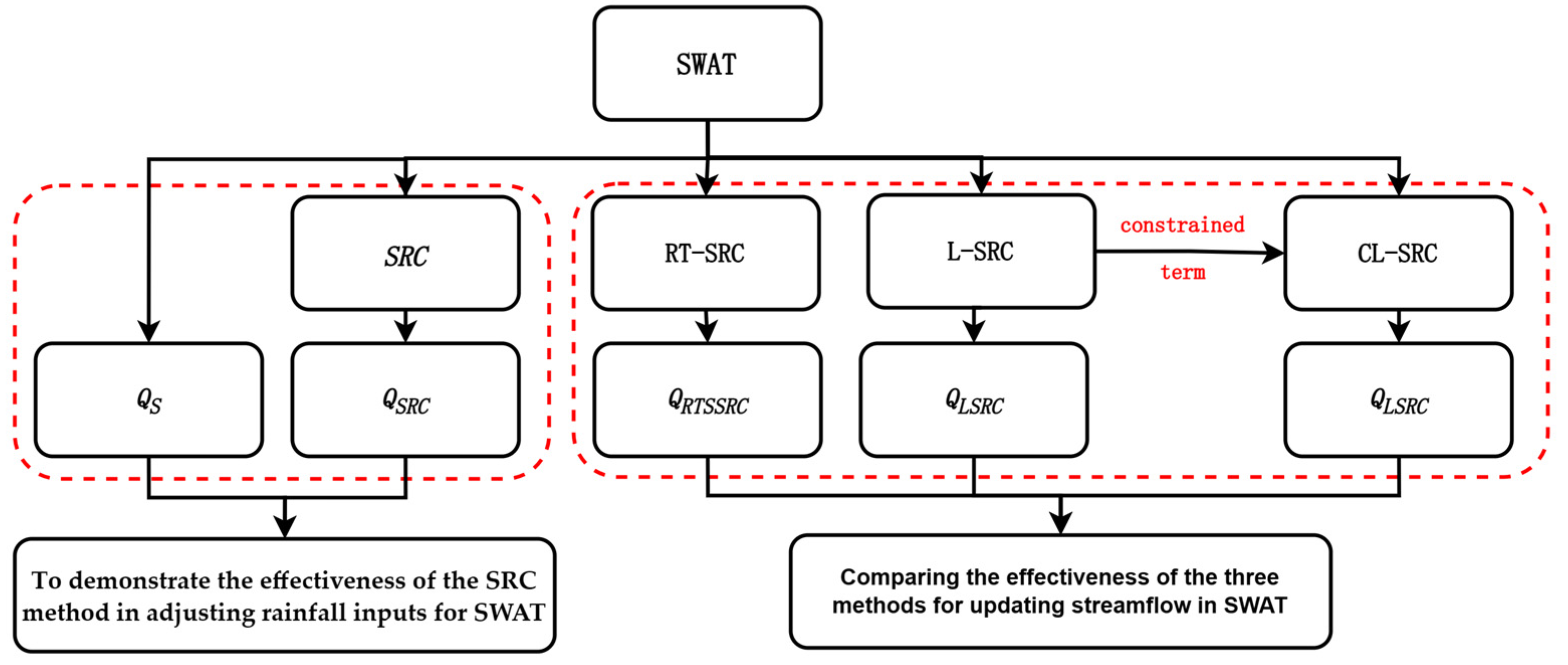
This study selects the Jianyang basin of the Minjiang River as this study area and presents the Constrained L-curve-SRC(CL-SRC) method for verification. The main objectives of this research are as follows: (1) To establish an ideal model that tests the effectiveness of the SRC in modeled correcting streamflow by adjusting areal mean rainfall. (2) Introducing ridge estimation solves the issue of the inability to invert the matrix in the SRC method when there is multicollinearity in the design matrix. Additionally, a comparative analysis is conducted between the ridge trace method and the traditional L-curve method to evaluate the strengths and weaknesses of selecting ridge parameters. (3) Through an analysis of the issues inherent in the L-curve and drawing on the physical implications of the estimated parameters, this study proposes a constrained L-curve method by incorporating a constraint term. The purpose is to enhance the accuracy and suitability of selecting the optimal ridge parameter. Additionally, the ridge trace method, L-curve method, and constrained L-curve method are coupling with the SRC, comparing their respective effects on updating streamflow.
2. Materials and Methods
This study focuses on the Jianyang basin as the study area and utilizes the SWAT model to simulate daily streamflow. In the first step, the SRC method is applied to update the streamflow and analyze any existing issues. Subsequently, the CL-Curve, RT, L-Curve, and SRC are coupled to form three methods: CL-SRC, RT-SRC, and L-SRC. The paper compares the corrective effects of the three methods that have been constructed. The specific research framework is shown in
Figure 1.
2.1. Study Area
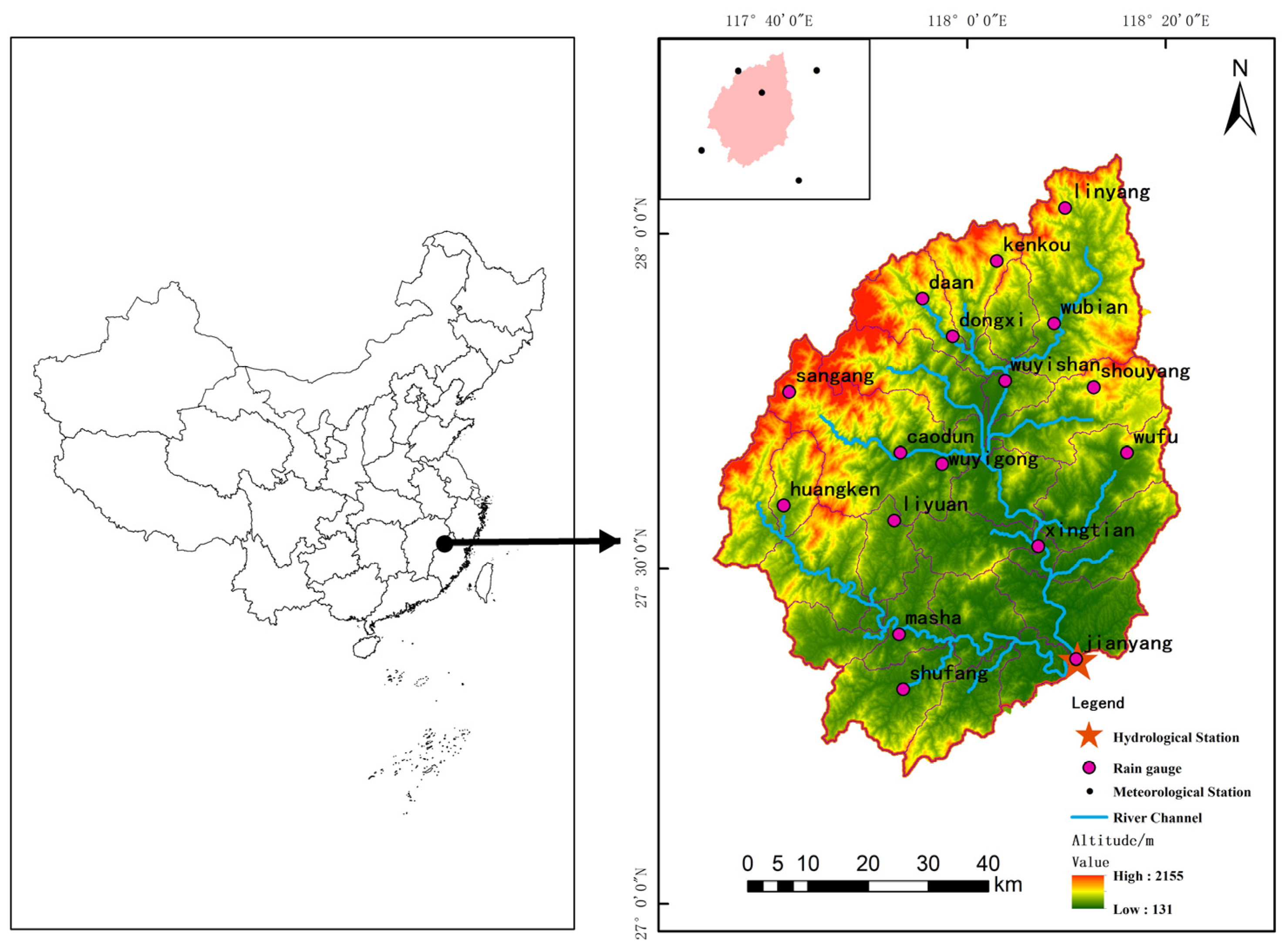
The Jianyang Basin, situated in Fujian Province, China, is positioned in the upstream region of the Minjiang River, with coordinates ranging from 117°31′ to 118°19′ east longitude and 27°10′ to 28°5′ north latitude. This basin encompasses a drainage area of 4848 km
2, with an average annual rainfall of 1702 mm and an annual streamflow coefficient ranging from 0.5 to 0.6. It experiences a subtropical monsoon humid climate, characterized by substantial vegetation coverage and shallow groundwater depths. Rainfall within the basin exhibits significant interannual variability and a spatial distribution that generally decreases from north to south. Earlier studies have effectively employed the SWAT model for runoff simulation in this basin [
24]. For this study, meteorological data from nearby stations, including Shaowu, Qixianshan, Wuyishan, Pucheng, and Jianou meteorological stations were utilized. Furthermore, rainfall data were collected from 17 rainfall stations located within the basin, as depicted in
Figure 2.
2.2. Data
The hydrological data used in this study were obtained from the measured daily data of the Jianyang Station in the Hydrological Yearbook from 1993 to 2000. The topographic data utilized the 30 m resolution original elevation data from the Geospatial Data Cloud SRTMDEM (
https://www.gscloud.cn, accessed on 16 July 2022). The meteorological data were sourced from the China Surface Climate Data Set (V3.0) (
https://data.tpdc.ac.cn, accessed on 20 March 2022). The soil data were selected from the Second National Land Survey Data of Nanjing Soil Research Institute (
http://www.ncdc.ac.cn, accessed on 10 November 2021) with a resolution of 1 km x 1 km. The land use data were acquired from the Research Center for Resources and Environment Science Data of the Chinese Academy of Sciences (
https://www.resdc.cn, accessed on 10 November 2021) for the year 1995 at a resolution of 1 km × 1 km. For more details, please refer to
Table 1.
2.3. Least Squares Method
Assuming that the observation equation can be expressed as:
where
represents the design matrix,
represents the parameter to be estimated,
represents the observed value, and Δ represents the observed error, which follows a zero-mean white noise distribution.
At this juncture, the estimation criterion can be expressed as:
The estimated item can be calculated by the least squares method as:
The fluctuation of the estimated item, measured by the mean square error, can be represented as:
where
represents expectation, Equation (4) can be expressed after equation transformation as:
where
represents the sum of the variance of the estimated item, reflecting the fluctuation of the parameter to be estimated;
is the sum of the squares of the deviations of the estimated quantity
from the observed value
, reflecting the difference between the estimated item and the true value and the deviation is 0 in the unbiased estimation.
2.4. System Differential Response Curve (SRC)
The precision of hydrological forecasts is greatly affected by the accuracy of rainfall, which is the most crucial input for basin hydrological models. Thus, this paper primarily focuses on improving the accuracy of simulated streamflow by correcting rainfall data.
The SRC method considers the hydrological model as a system. By perturbing the input (an independent variable) and studying the response of the output (a dependent variable) to this perturbation, the relationship between the response and the perturbation is then formulated as a function. Subsequently, the correction of the independent variable is obtained through the inversion of this function, thus achieving the correction of the output.
To simplify the calculations, this paper only considers rainfall as the input error and simplifies the hydrological system into the following functional relationship:
where
denotes the observed rainfall series and serves as input for the model, while
represents the model’s simulated streamflow series and serves as output for the model.
Assuming that the observed rainfall series is represented by
, and the measured streamflow series is represented by
, By taking the areal mean rainfall as the independent variable and performing differentiation on Equation (1), the differential equation for the relationship between streamflow and areal mean rainfall can be represented as:
where
represents the differential response of the streamflow with respect to the areal mean rainfall.
The differentiation of rainfall for each time period is calculated using Equation (7), then the relationship between rainfall and streamflow can be written in matrix form as follows:
where
represents the streamflow error series,
denotes the areal mean rainfall error series,
is the residual series, and
U is the system response matrix, Specifically,
, where each
is the differential response at time
when the independent variable
changes by one unit. More precisely,
, as defined previously [
1].
By utilizing the least squares method to solve Equation (8), the value of the corrected error series
for areal mean rainfall can be formulated as follows:
where
represents the value of the corrected error for the areal mean rainfall, and
represents the difference between measured streamflow and simulated streamflow. The process of calculation involves a large number of variables, which can potentially cause the designed matrix
to become ill-conditioned. Furthermore, the inclusion of harmful information in the
matrix can cause oscillations in the process of correction.
In order to rectify the aforementioned issue, ridge estimation has been incorporated into the process of solution; thus, the estimated term can be represented as follows:
where
represents the ridge parameter [
8], and
represents the Identity matrix with the same dimensions as the U matrix.
According to Equation (10), the corrected value of areal mean rainfall in the basin can be represented as:
where
represents the areal mean rainfall series after corrected.
2.5. The Ideal Model
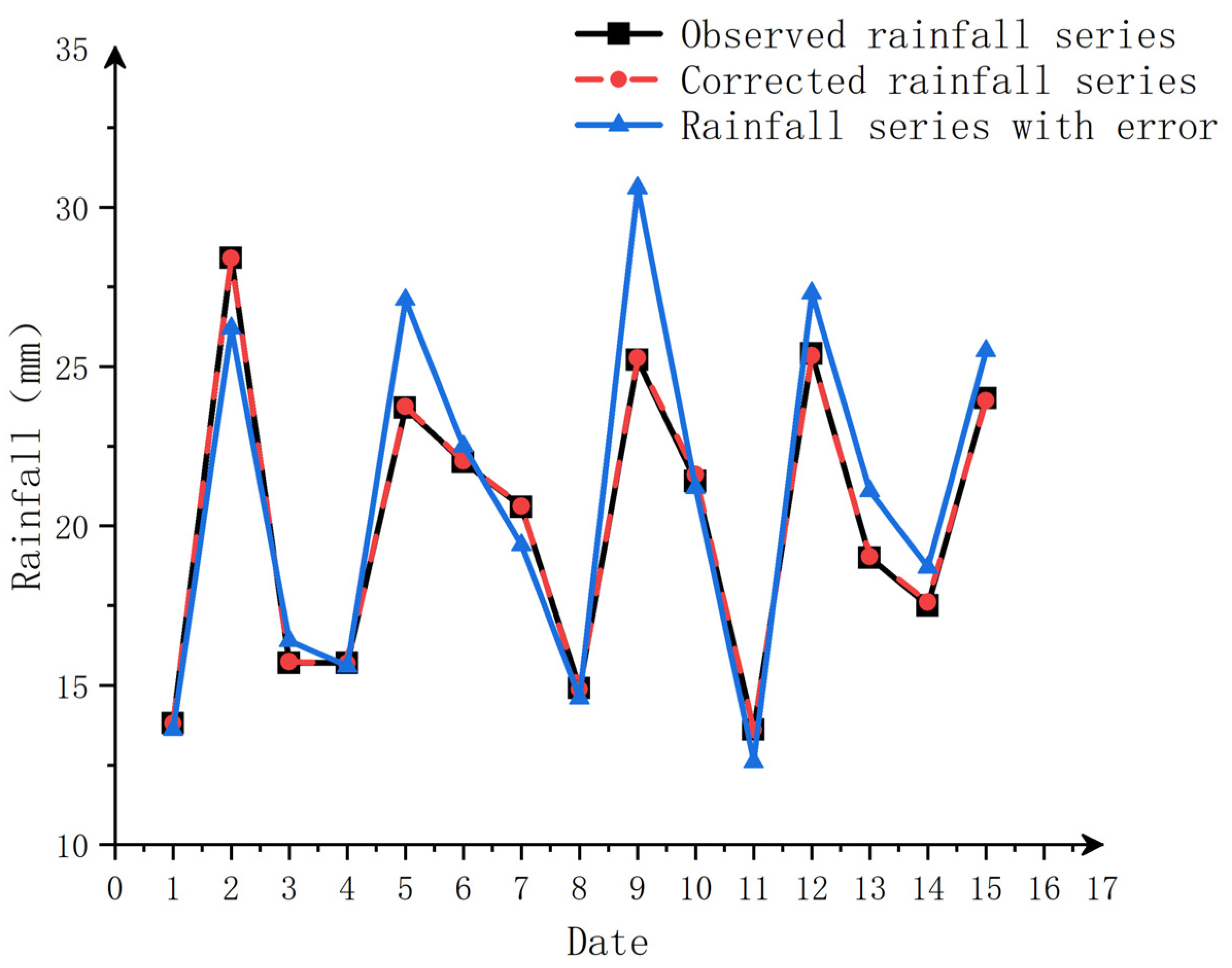
Due to the inherent complexity and uncertainty of practical hydrological basins, hydrological models are bound to contain errors in their inputs, structures, and parameters. This complexity, coupled with the multitude of sources of error, complicates the identification of essential components and key variables for error analysis. An “ideal” model, in this context, refers to a model in which the inputs, structure, and parameters are accurately known, which can be further studied through targeted research by deliberately introducing parameter errors. In this paper, an ideal model was constructed using SWAT to evaluate the effectiveness of the SRC method. The ideal model was utilized to evaluate the performance of the SRC method by intentionally introducing errors in areal mean rainfall series, and it provides a comprehensive explanation of the SRC.
2.6. Method for Selecting Ridge Parameters
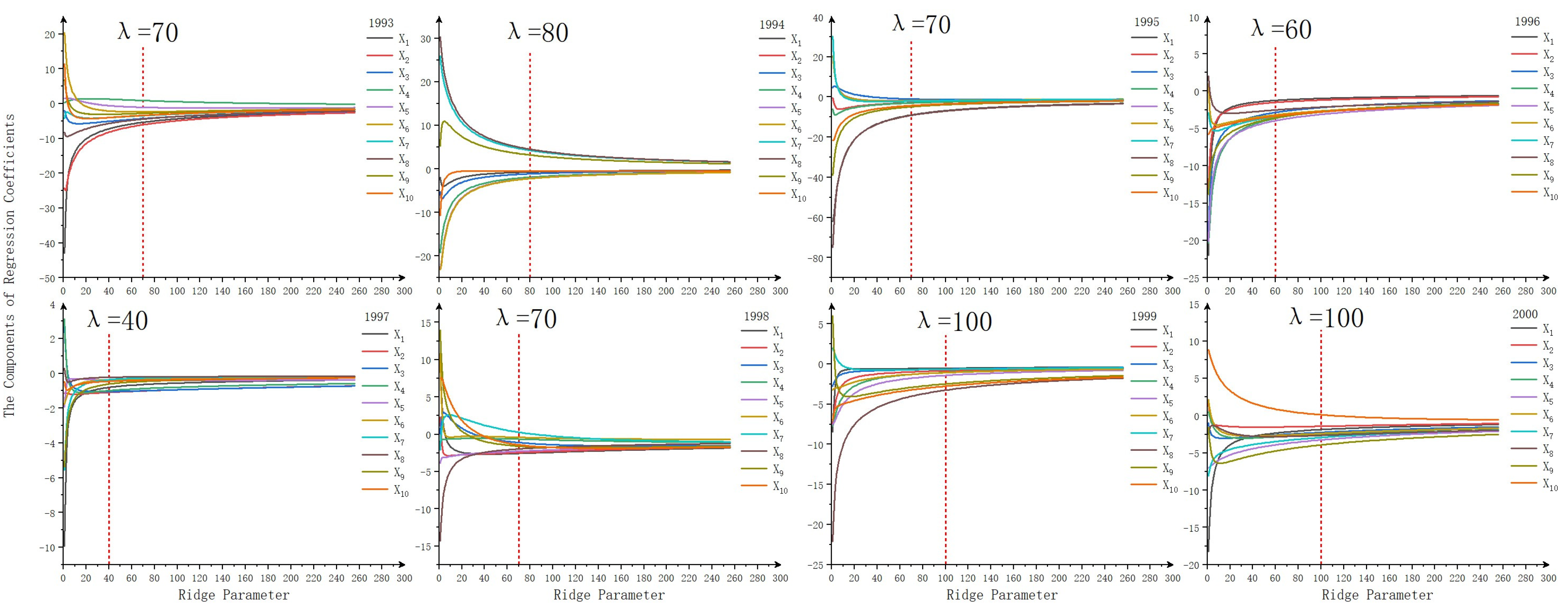
2.6.1. Ridge Trace Method
The regression coefficient for the ridge trace method is defined as:
where
represents the regression coefficient.
The ridge trace method involves setting multiple sets of different ridge parameters to obtain the corresponding regression coefficients () by using Equation (12). The resulting ridge traces are depicted with as the X-axis and (the component of ) as the Y-axis. The optimal ridge parameter is identified at the point of convergence where all components of the regression coefficients converge to a steady state. In this study, the initial value of the ridge parameter was set to 0.01, the iteration step was set to 0.1, and the maximum value was set to 400. These values were chosen to facilitate the calculation of the regression coefficient components for each ridge parameter.
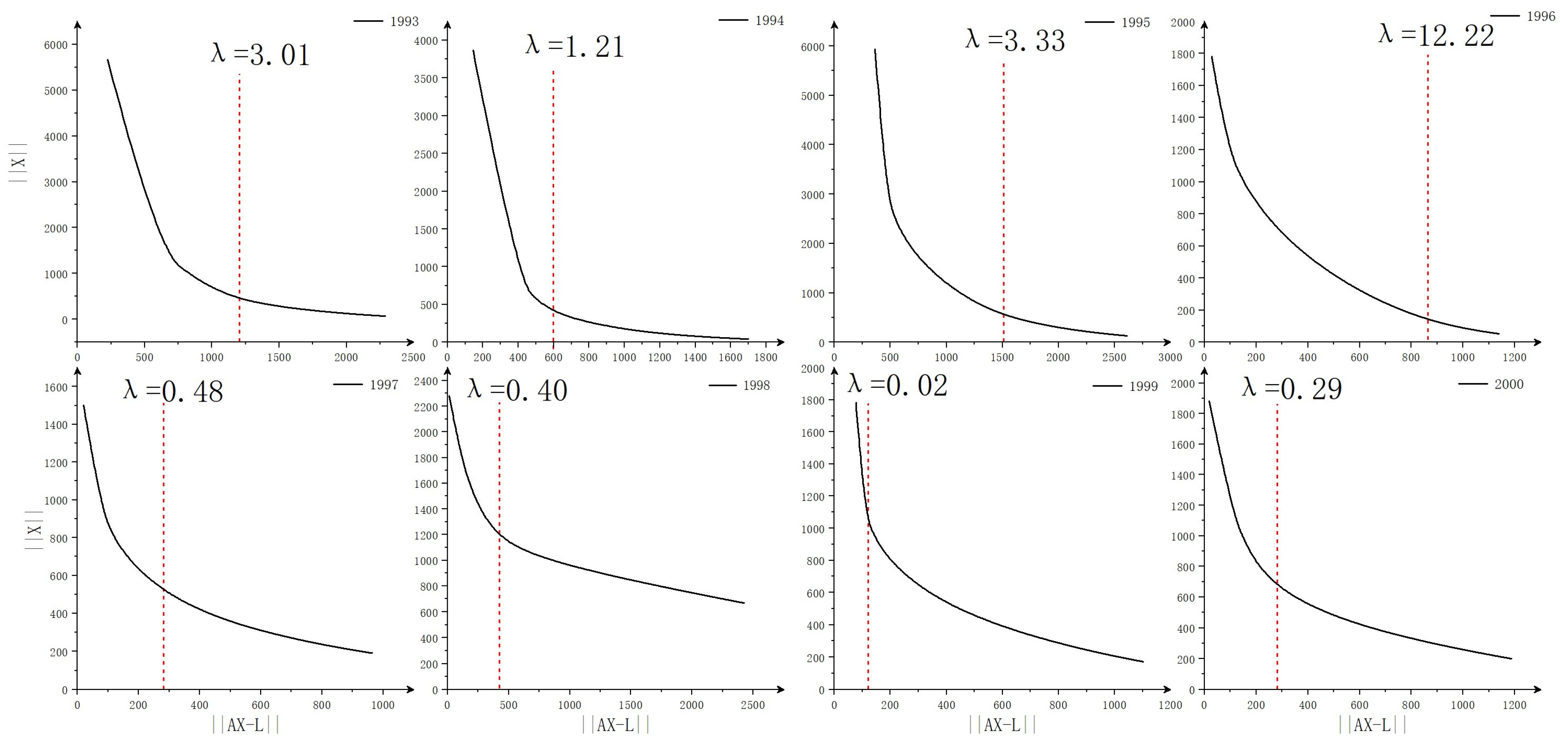
2.6.2. L-Curve
When the condition number of the designed matrix in Equation (9) is large, it may make matrix Ill-conditioned and the designed matrix cannot be properly inverted. In order to tackle this problem, a ridge parameter, also known as L2 regularization, is introduced. This, in turn, reformulates Equation (3) as follows:
where
represents the ridge parameter, which can improve the problem of ill-conditioned. At the same time, adding a penalty function can restrict adjustments to the model and prevent the estimated parameters from exceeding a reasonable range. Smaller values of
will produce estimates that are closer to being unbiased.
The introduction of the ridge estimation leads to a modified estimation criterion, which is given by:
where
all denote 2-norms,
represents the residual term, and
represents the estimated term.
According to the definition provided by the L-curve [
19], it is evident that as
approaches 0, the penalty function has a diminished impact, leading to an estimate that is nearly unbiased. At this point, the curve is characterized by a vertical segment dominated by the condition of the matrix. As
gradually increases, the ridge parameter begins to exert its influence, causing the curve to transition into a horizontal segment that is predominantly governed by the ridge parameter.
The steps to determine the optimal ridge parameter using the L-curve are as follows:
- (1)
Selecting different ridge parameters and calculating the corresponding and . In this study, the minimum ridge parameter is set to 0.001, the maximum value is set to 200, and the iteration step size is set to 0.01.
- (2)
Plotting the residual item () on the horizontal axis and the estimated norm () on the vertical axis. Subsequently, fitting the points into a curve will yield the computed L-curve.
- (3)
Calculating the curvature of the curve and the ridge parameter corresponding to the point with the maximum curvature of the curve is the optimal ridge parameter.
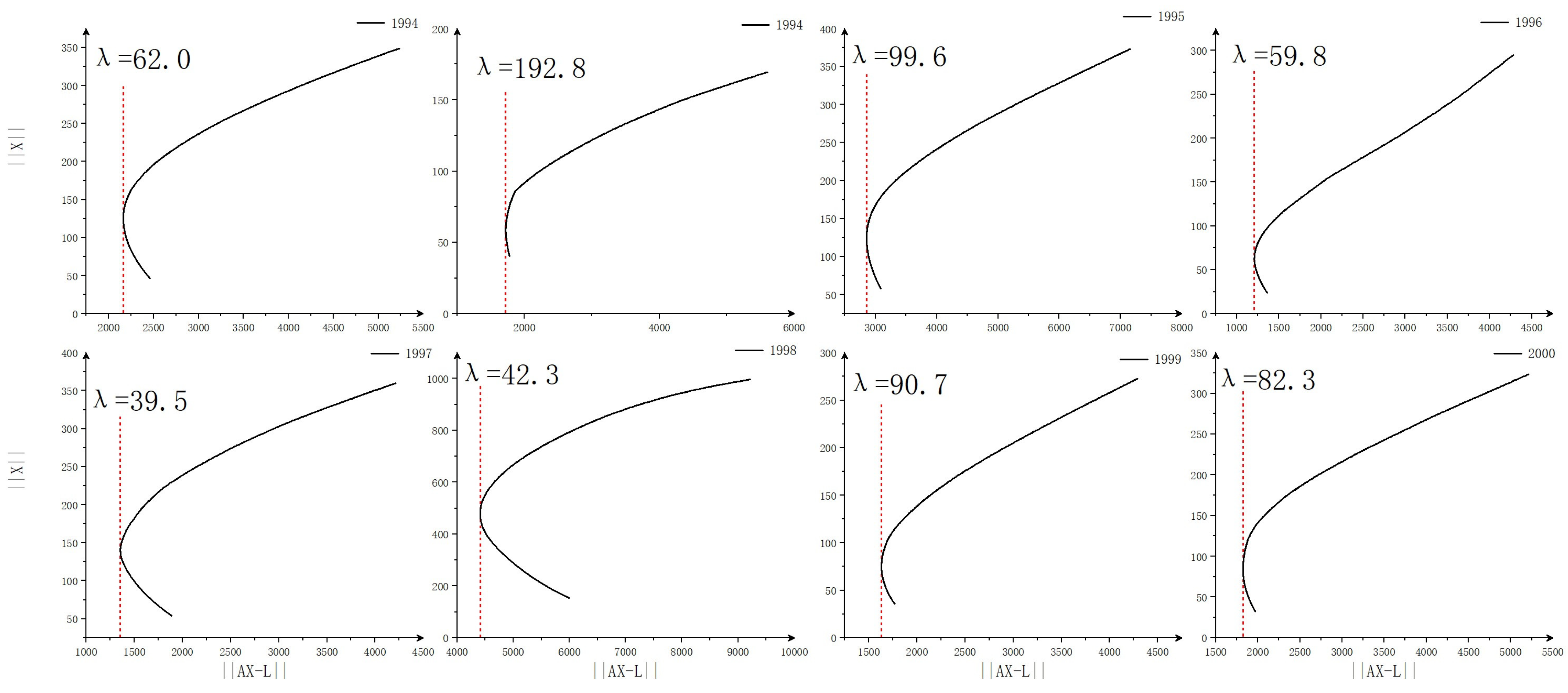
2.6.3. Constrained L-Curve (CL-Curve)
Although the traditional L-curve method takes into account the change of the estimated parameters during the process of selection, it does not consider the physical meaning of the model’s parameters and ignores information about the range of values for these parameters. By using the optimal ridge parameter in the SRC, it can lead to excessive correction of the estimated parameters, exceeding the parameter range, and ultimately reducing the accuracy of the simulated streamflow. Therefore, the optimal ridge parameter is not necessarily the actual optimal point. To tackle these challenges, this paper suggests enhancements to the L-curve method. Specifically, the estimated parameter in this study pertains to areal mean rainfall, a quantity with a clear physical interpretation. It is essential to note that areal mean rainfall must always possess values greater than or equal to 0. Therefore, a constraint term
is introduced to limit the range of variation for the estimated parameter. Based on the
, Equation (10) yields the corrected rainfall series
. By comparing
with
, it is determined that the absolute value of the negative values in
is always less than or equal to the corresponding values in
. After incorporating the constraint term, the estimated parameter term is denoted as
.
Based on the steps of the L-curve mentioned above, the actual optimal ridge parameter of the CL-curve can be obtained.
At this point, the constrained L-curve exhibits the following traits:
- (1)
If all the constraint terms are greater than or equal to the absolute value of the negative of , which means that the constraints are not in effect, then the L-curve can be obtained, and the result of the optimal ridge parameter is consistent with the traditional L-curve.
- (2)
When the constraint term comes into effect and approaches 0, the left side is no longer a line close to being perpendicular. Instead, as gradually increases, and decrease until a turning point appears in the fitted curve. This is different from the traditional L curve. Subsequently, as continues to increase, keeps decreasing while starts to increase.
- (3)
The graph of the constrained L-curve is no longer an “L” shape. Instead, it assumes a U-shaped form that tilts towards the right.
2.7. SWAT Model
2.7.1. The Theory of Model
The SWAT (Soil and Water Assessment Tool) model is a distributed hydrological model developed by the United States Department of Agriculture with a strong physical mechanism. The model is based on geographic information systems and remote sensing, using spatial information and land surface information from the study watershed to simulate hydrological processes [
25,
26,
27]. The model includes modules for meteorology, hydrology, sediment transport, vegetation growth, nutrients, pollutants, and crop management. This study mainly applies the hydrological simulation module of the model, and its water balance equation is as follows:
where
represents the soil water content in mm on day
, while
represents the initial soil water content in mm on day
,
denotes rainfall in mm on day
,
represents the surface runoff in mm on day
,
indicates the evapotranspiration loss in mm on day
,
refers to the infiltration of soil profile in mm on day
, and
represents the volume of water from return flow in mm on day
.
2.7.2. Configuration of the SWAT Model
(1) The collected land use data and soil data were reclassified. The SPAW is utilized to calculate the soil properties of the basin. The properties of land use are derived from the corresponding data in the SWAT database to construct the basin-specific SWAT database. Meteorological station data are employed to compute rainfall, solar radiation, temperature, wind speed, and dew point with the assistance of SWAT Weather software. A weather generator is constructed based on the calculated data.
(2) According to the hydrological data obtained from the Jianyang basin, this study divided the basin into 31 sub-basins with a threshold of 10,000 hm
2. The outlet was identified in sub-basin number 28, as shown in
Figure 3. By applying a threshold of 10%, this paper overlaid and analyzed the spatial data, resulting in the division of the basin into 274 Hydrologic Response Units (HRUs). Subsequently, a SWAT model was constructed to simulate daily streamflow.
2.7.3. Parameter Calibration of the SWAT Model
The Jianyang basin was divided into three periods for modeling: a warm-up period in 1992, a calibration period from 1993 to 1998, and a validation period from 1998 to 2000. For parameter calibration, the SWAT-CUP software was used in conjunction with the SUFI2 algorithm, which facilitated the selection of 11 sensitive parameters that exerted a significant influence on streamflow. Each iteration included 500 cycles, resulting in a total of 2000 iterations performed to identify the optimal parameters. The results of the parameter calibration are presented in
Table 2.
2.7.4. Evaluation Criteria
In this study, the accuracy of simulated streamflow was evaluated through the use of three metrics: the Nash-Sutcliffe efficiency coefficient (NSE), relative error (RE), and mean square error (MSE).
(1)
is used to measure the degree of fit between the simulated and measured values, with a value closer to 1 indicating a better simulation.
is calculated as follows:
where
denotes the length of the streamflow series;
represents the measured value;
represents the simulated value;
is the average value of the measured values obtained in the experiment.
(2)
reflects the error between simulated and measured values, and can be calculated using the following formula:
(3)
is a metric utilized to quantify the degree of data variability by measuring the “average error”. A smaller MSE indicates a higher level of precision in the calculated values of the model. The formula for calculating MSE is as follows:
where
represents the corrected value.
4. Discussion
In
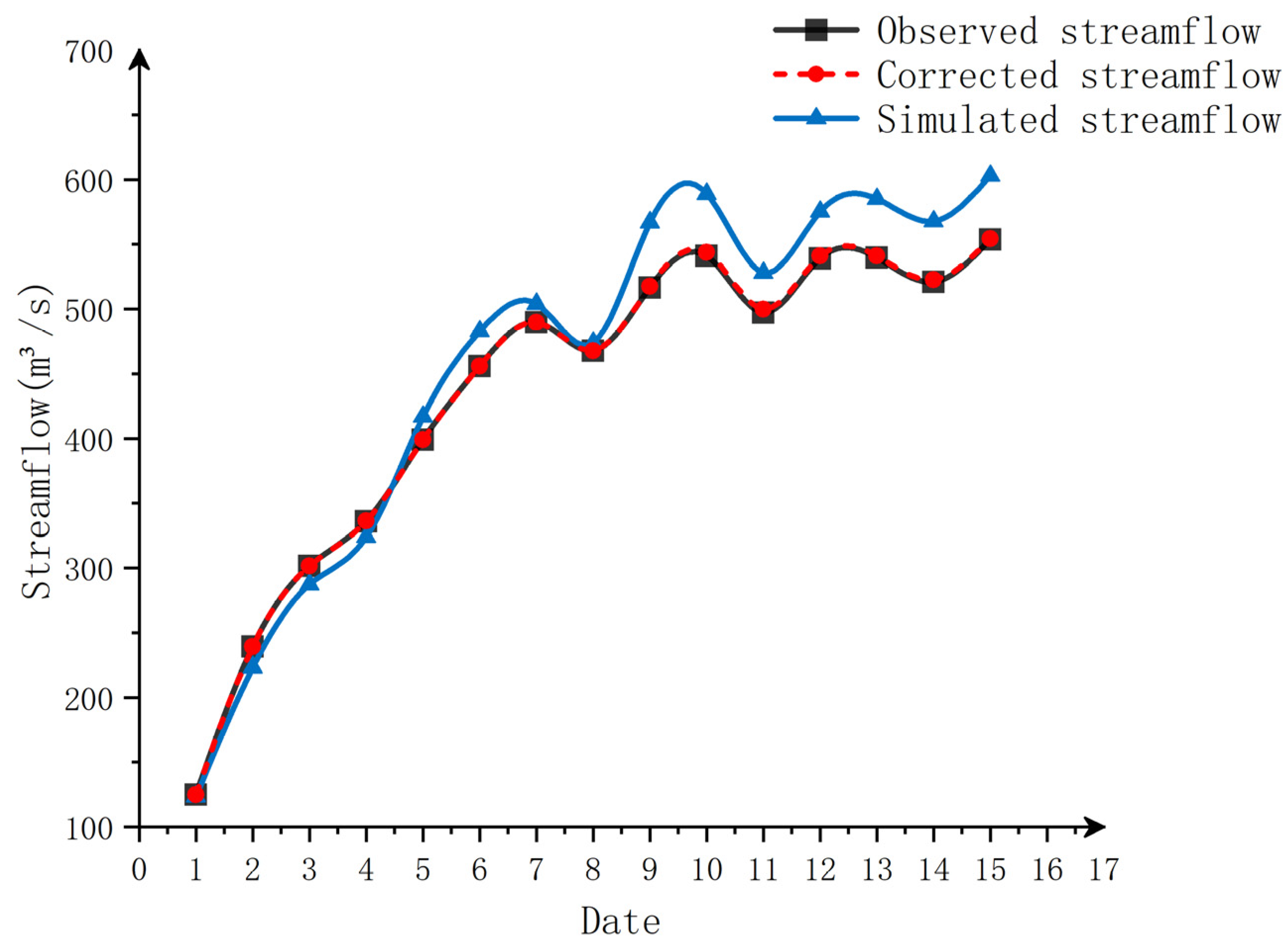
Section 3.1 of this paper, an ideal model was constructed, and the results showed that SRC can accurately identify errors in rainfall series and improve the accuracy of simulated streamflow by reducing rainfall errors. According to the result of the simulated streamflow in
Section 3.2, it can be concluded that SWAT performs well in the Jianyang basin, with only a lower fitting accuracy in 1998. Upon analysis, it is revealed that the anomalous performance in 1998 can be attributed to a severe flood that ravaged southern China. The Jianyang basin, positioned upstream of the Min River in Fujian Province, was significantly impacted by this catastrophic event, resulting in suboptimal simulation outcomes for that particular year.
The SRC method encounters two issues during the computational process: The ill-condition of the designed matrix and the inability to constrain the fluctuation of the estimated parameters. When applied to estimated parameters in hydrological models, this method tends to excessively adjust the estimated parameters, leading to a degradation of the fitting accuracy. In
Section 3.3, the aforementioned two issues are encountered, resulting in a phenomenon of decreasing accuracy in simulated streamflow after correction. The phenomenon of reverse correction in the SRC can be examined from three perspectives: (1) The SRC method relies on a first-order Taylor series expansion to approximate the response functions of the input and output. While this approximation works well for linear systems, it leads to larger errors for highly nonlinear systems like the SWAT model. This larger approximation error contributes to the phenomenon of reverse correction. (2) When calculating the response matrix for input and output, errors originating from input data, the model’s structure, and the model’s parameters are introduced. These errors contaminate the response matrix with detrimental information, resulting in significant biases when applying the least squares method for estimation. As a consequence, the SRC method, driven by its aim to maximize the accuracy of the fit, induces oscillations in the estimated parameters, thereby leading to a reduction in the accuracy of the fit. (3) The SRC method does not take into account the changes in the estimated parameters when solving for the values of correction. It focuses solely on achieving better accuracy of the simulated streamflow without considering the impact on the estimated parameters. This approach leads to substantial fluctuations in the estimated parameters, some of which may exceed their valid ranges after correction. By imposing constraints on the estimated parameters within predefined upper and lower bounds and subsequently incorporating them into the SWAT model, a certain degree of parameter information is forfeited, contributing to the phenomenon of reverse correction.
To summarize, the absence of constraints on the changes in estimated parameters is the main factor contributing to reverse correction. In order to address this problem, ridge estimation is introduced, which serves a dual purpose. Firstly, it resolves the issue of the non-invertibility of the response matrix. Secondly, the ridge parameter functions as a penalty function, effectively constraining fluctuations in the estimated parameters, limiting their values to a reasonable range, and enhancing the robustness of the SRC.
In
Section 3.4,
Section 3.5 and
Section 3.6, this paper respectively constructs three methods, namely RT-SRC, L-SRC, and CL-SRC, to update the simulated streamflow. From the analysis of the three methods for selecting the optimal ridge parameter discussed above, it can be concluded that the presence of multicollinearity in the design matrix leads to a large MSE for the least squares estimate, resulting in unstable performance. Although the least squares estimate is unbiased in this case, it does not satisfy the criteria of MSE. However, by introducing ridge estimation, although it becomes a biased estimate, the MSE is smaller compared to the unbiased estimate, making the estimated results more acceptable. When the ridge parameter is set to a large value, the estimates become stable, yet the bias of the ridge estimate becomes substantial, deviating from the unbiased estimate, which is also unreasonable. Therefore, the selection of an appropriate ridge parameter is of utmost importance in ridge estimation. The ridge trace method is used to determine the optimal ridge parameter by evaluating the stability of the components of the regression coefficients. At this point, the application of RT-SRC has demonstrated its effectiveness in enhancing the accuracy of simulated streamflow. Following the correction, there was a notable improvement in the NSE for all years. However, it should be noted that the correction also resulted in an increase in the RE of streamflow depth. This disparity can be attributed to the fact that the SWAT model developed for this basin has a higher base flow and a lower peak flow. These characteristics result in an elevation of average mean rainfall after correction and, subsequently, an increase in the error of streamflow. Also, the ridge trace method currently only allows for identifying the unclear range of the optimal ridge parameter, and selecting the precise ridge parameter is susceptible to subjective interference, resulting in a lack of accuracy in choosing the optimal ridge parameter. Furthermore, if there are numerous components of the regression coefficients, plotting the ridge trace becomes complicated and burdensome. The coupled L-curve and SRC approaches demonstrate unsatisfactory performance in updating streamflow. While the L-curve effectively addresses the problem of an ill-conditioned design matrix, it ultimately diminishes the accuracy of the simulated streamflow after correction. Further examination of the estimated parameters highlights the limitations of the traditional L-curve method. While it considers the fluctuation of the estimated parameters, it also assumes that these parameters should not be excessively large. However, the traditional L-curve solely focuses on selecting the numerically optimal point as the optimal ridge parameter, disregarding the physical significance of the estimated parameters in the actual hydrological model. As a result, the valid range of the estimated parameters is neglected in the computation process, leading some estimated parameters to exceed their valid range when employed in the SRC. Consequently, these factors have resulted in a decrease in the fitting accuracy of simulated streamflow after being updated. The CL-curve, unlike the traditional L-curve, considers the physical significance of estimated parameters. As a result, it accurately identifies the optimal ridge parameter of the model and ensures that the estimated parameters are adjusted within a reasonable range. This approach prevents excessive corrections during the modification of independent variables, which could lead to poor simulation results in the dependent variable. In terms of the system differential response curve, the CL-curve demonstrates superior applicability compared to the traditional L-curve, making it more suitable for practical problems.
6. Impacts and Limitations
Despite variations in hydrological characteristics and climatic conditions across different regions, the CL-SRC method incorporates the evolving hydrological processes of the specific region and model when calculating the response matrix of independent and dependent variables. This adaptability enables the CL-SRC method to enhance the accuracy of simulated streamflow for diverse models and regions. In subsequent studies, enhancing the precision of simulated streamflow can also result in improved accuracy in simulating pollutants such as sediment, nitrogen, phosphorus, and others.
Moreover, it is important to acknowledge that when employing the CL-SRC method in models like SWAT, which exhibit less pronounced linear characteristics, a progressive approximation principle should be adopted through multiple adjustments. Furthermore, errors can stem from various sources, including the model’s structure and parameters. However, the CL-SRC method assumes that errors solely arise from input variables, such as rainfall. Consequently, this may lead to residual errors even after correction, impeding a complete alignment with the observed streamflow. The aforementioned data further corroborates this assertion.