Flood Detection in Polarimetric SAR Data Using Deformable Convolutional Vision Model
Abstract
:1. Introduction
- (1)
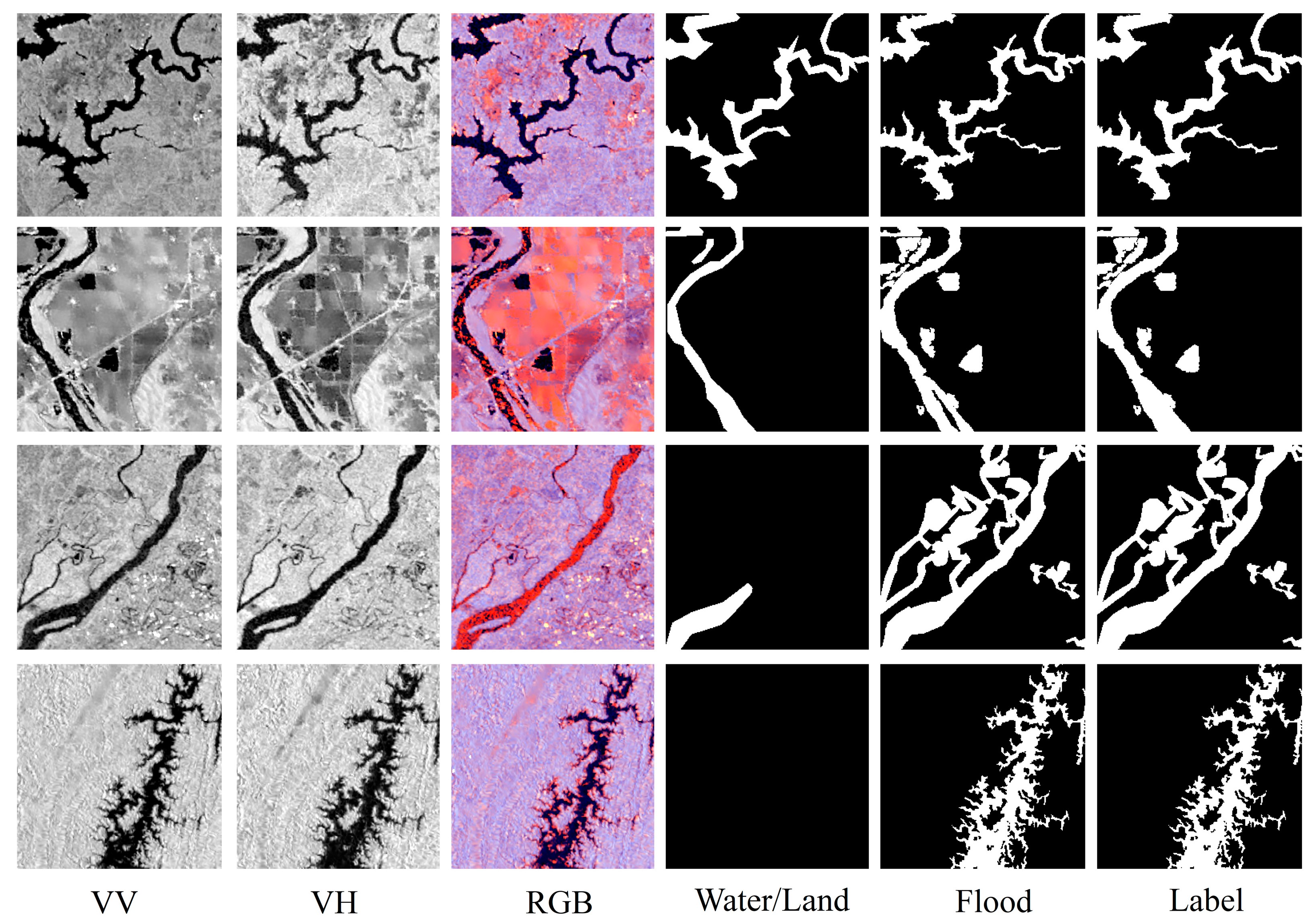
- Introducing the |VV|/|VH| Ratio to Enhance Data Features. Given the limitations of dual-polarized data in Sentinel-1, and the |VV|/|VH| ratio’s significant capability to enhance the reflective properties of water bodies, causing them to exhibit relatively higher pixel values in the ratio image. In this study, polarimetric data VV, VH, and |VV|/|VH|ratio, which was combined into an RGB image using band combination, was used as an input to the model, so that the model could better capture the reflectance change of the flood boundary.
- (2)
- The introduction of this method contributes to the improvement of the performance of flood detection models, enhancing their sensitivity to changes in the flood region.
- (3)
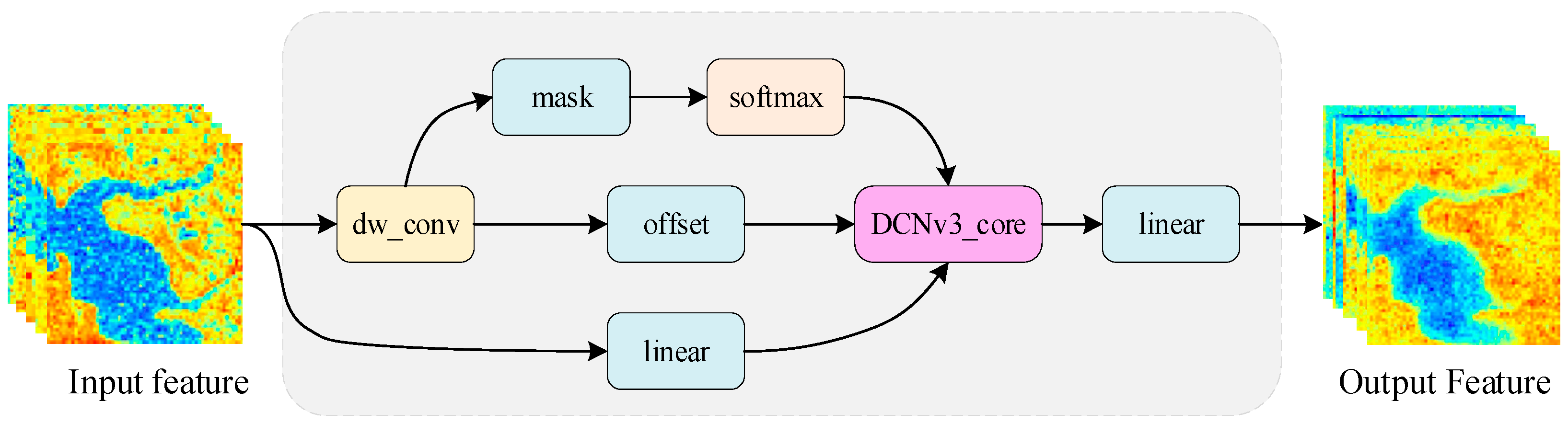
- A flood detection network model (FWSARNet) is proposed. In the encoder part, the FWSARNet model proposed in this paper introduced deformable convolution as the core operator, and deformable convolution (DCNv3) was used to replace the MHSA (Multi-Head Self-Attention) module in ViT, which could better capture the local details and spatial variations of the flood boundary present in the SAR image while reducing the parameters, thus, realizing the adequate extraction of local details and spatial variation features of the flood boundary.
- (4)
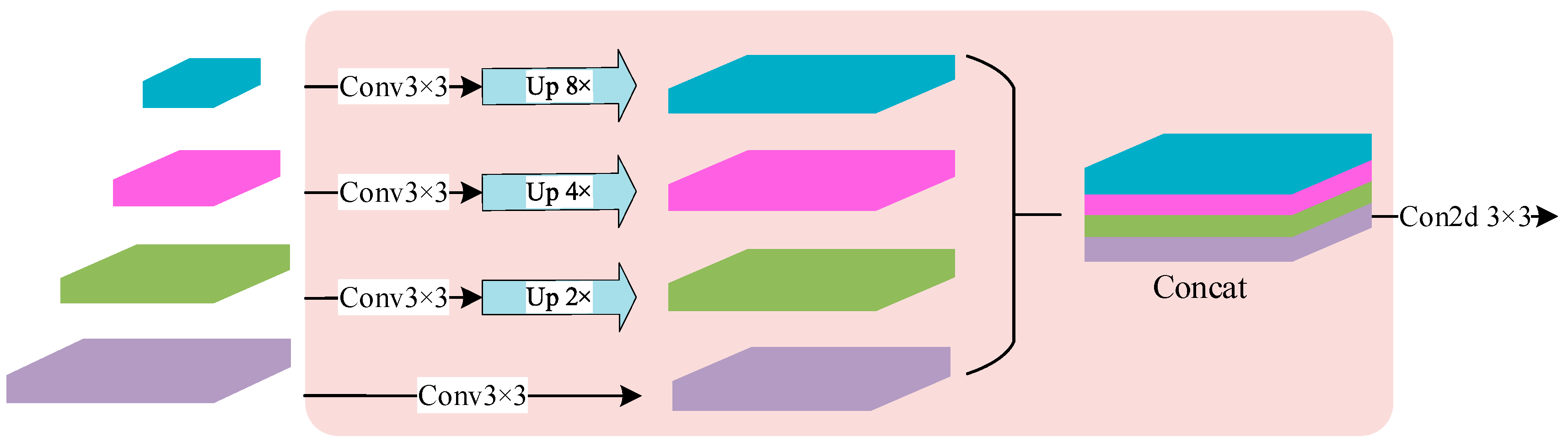
- In the decoder part, the model adopted the method of multi-level feature map fusion, which carried out multi-scale feature fusion and up-sampling operations on different levels of feature maps, combining different levels of feature information in the detection process could retain more semantic and detailed information, which further improved the recognition ability of fine water bodies.
2. Methods
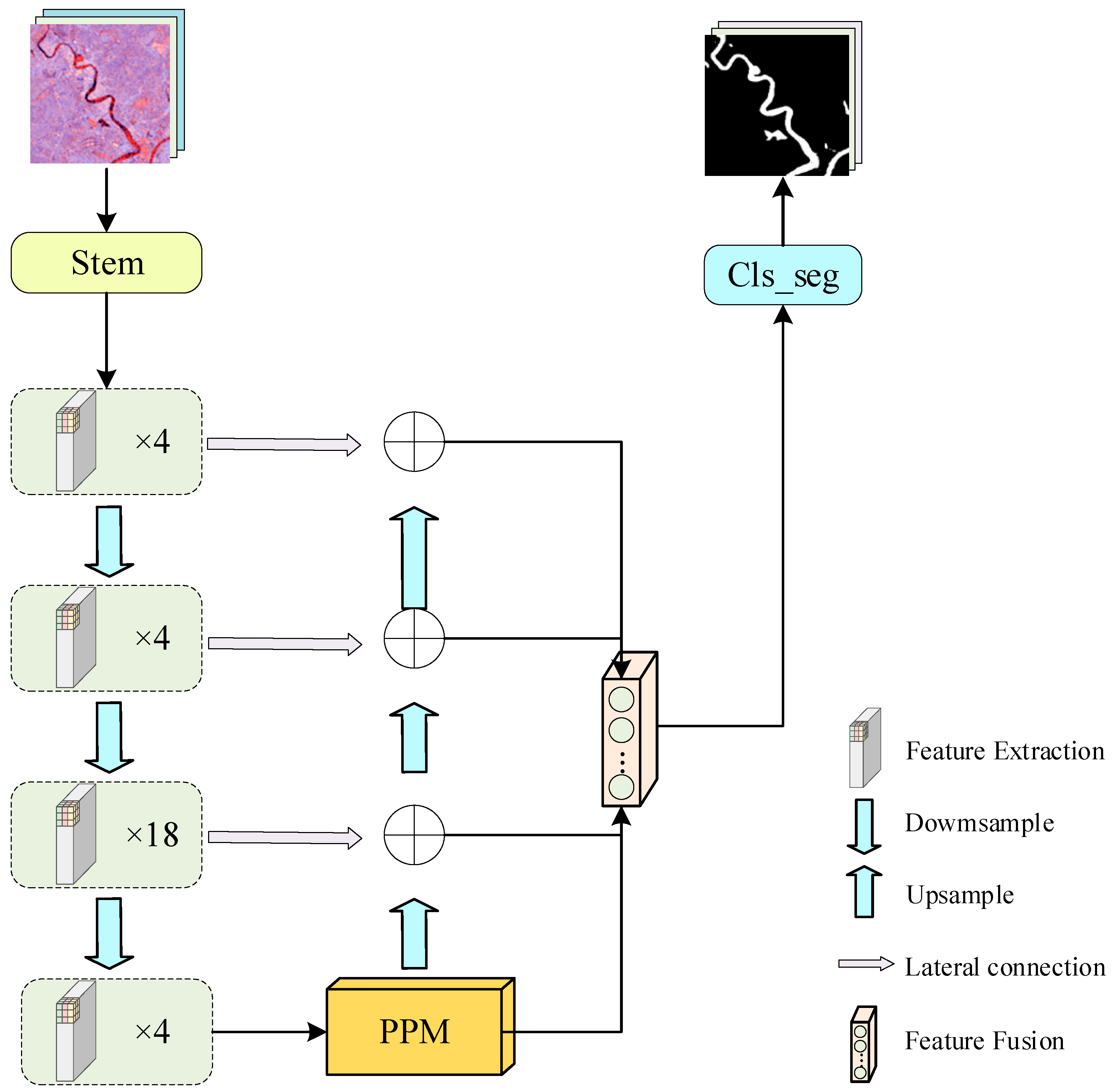
2.1. Encoder
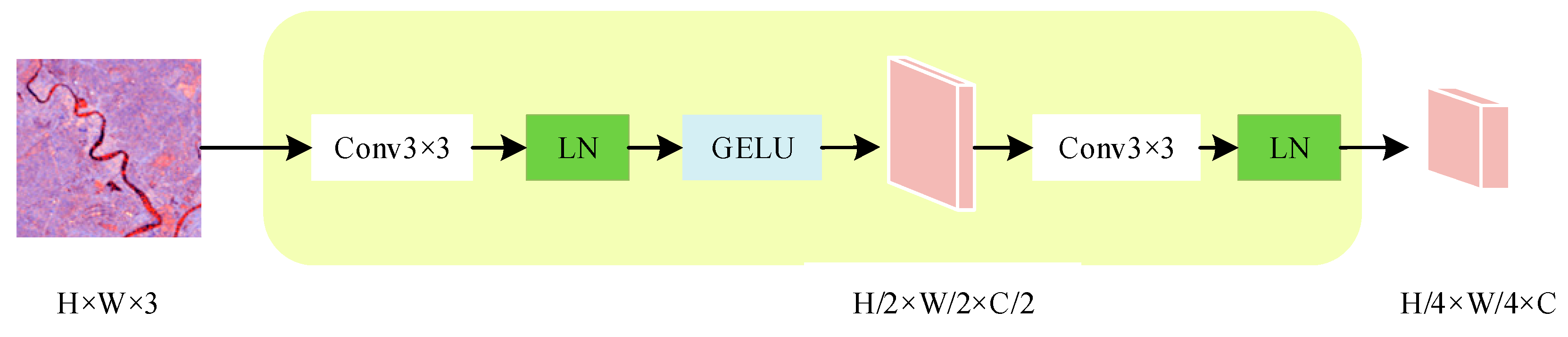
2.1.1. Stem and Downsample Layers
2.1.2. Feature Extraction Module
2.2. Decoder
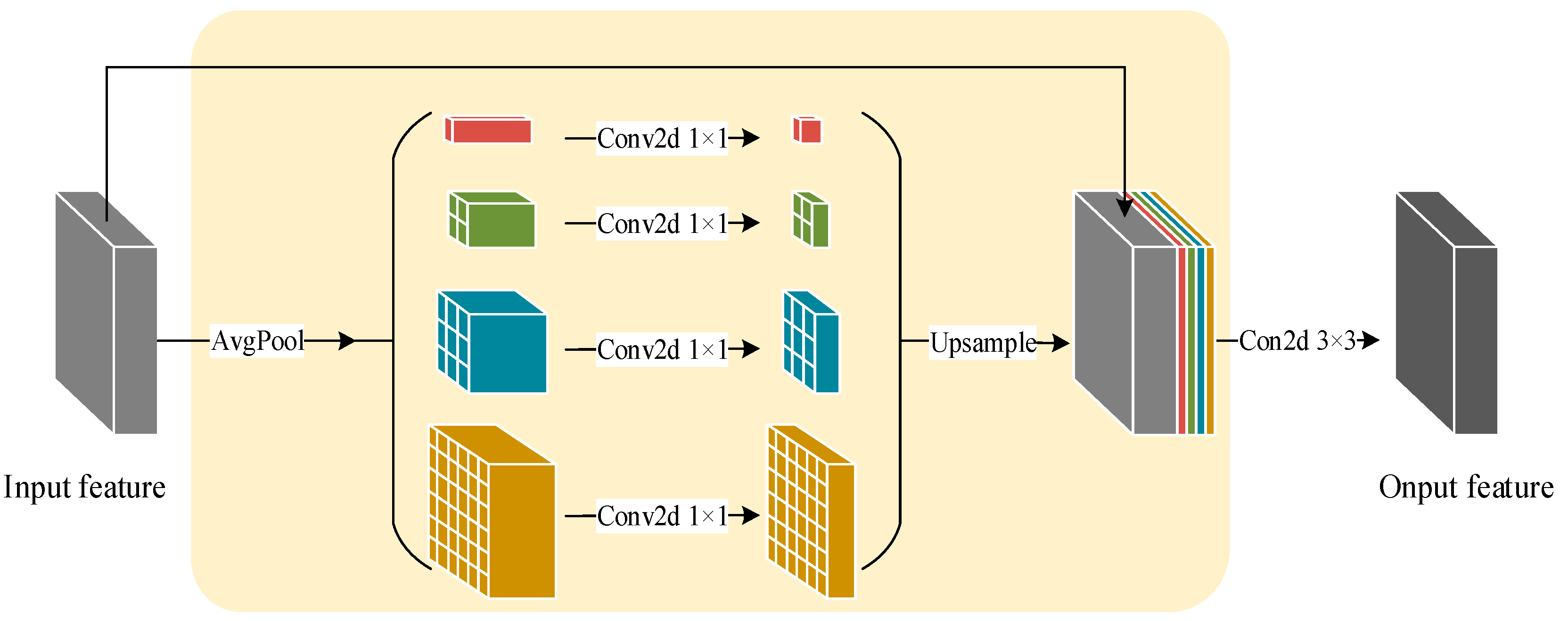
2.2.1. Pyramid Pool Module
2.2.2. Feature Fusion Module
2.3. Experimental Metrics
3. Experiments
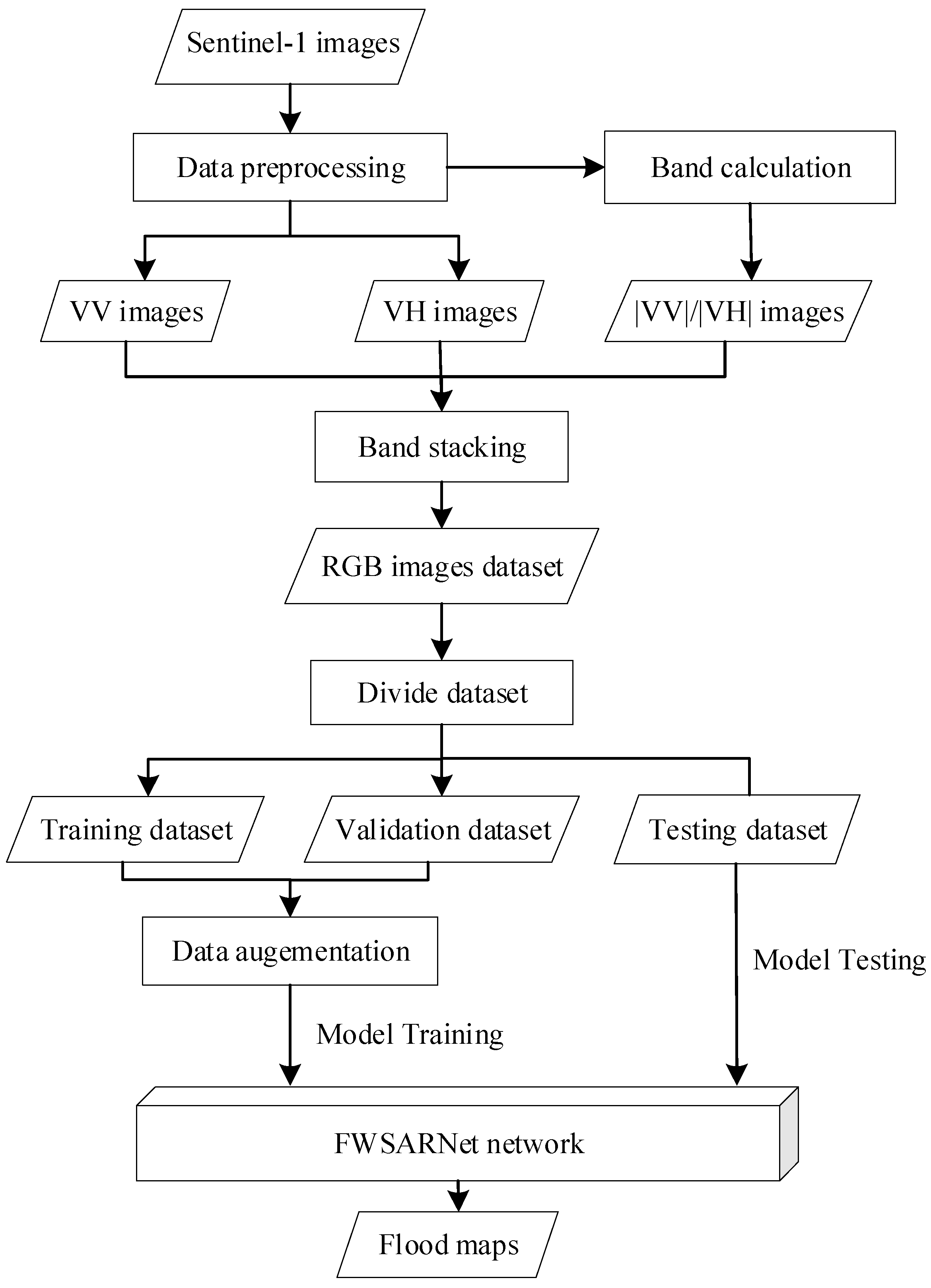
3.1. Dataset and Preprocessing
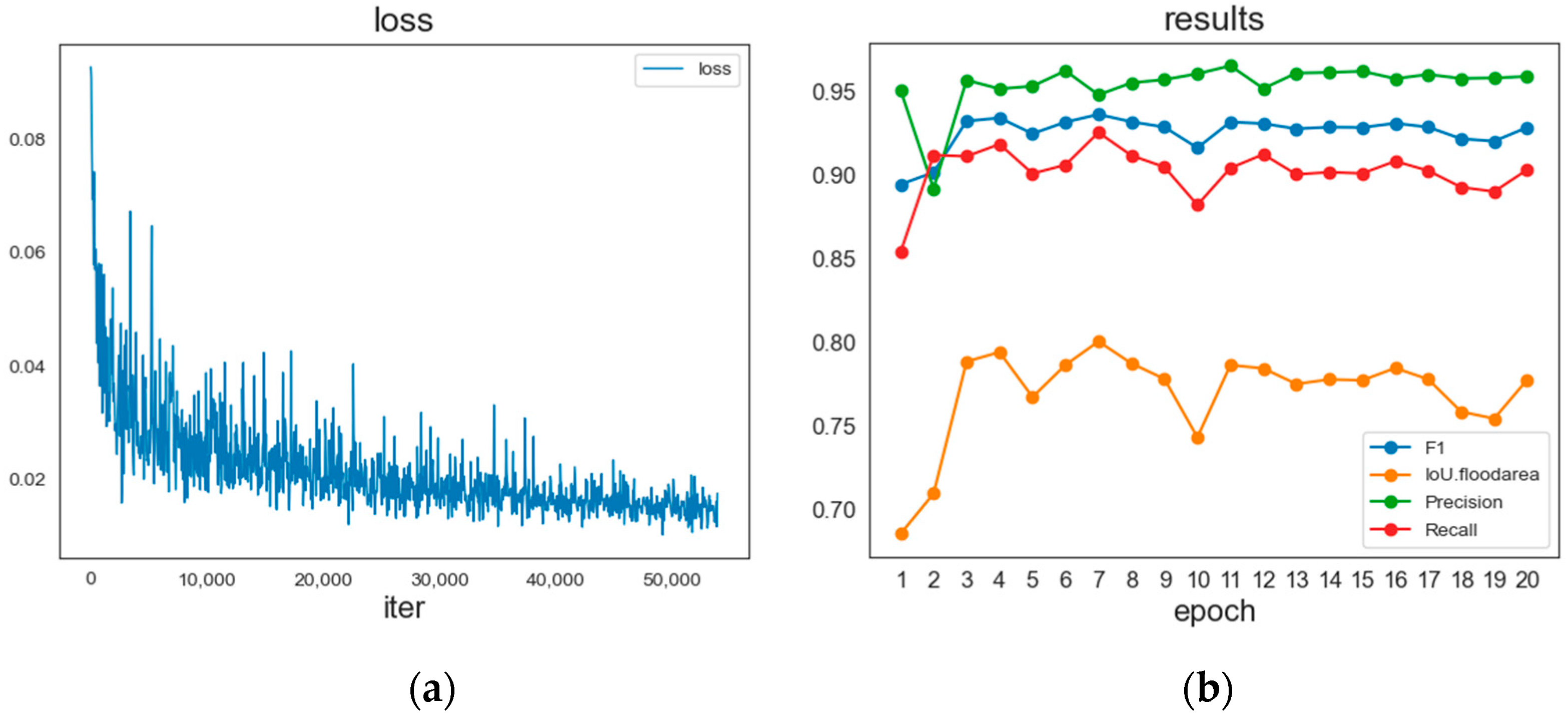
3.2. Model Training
3.3. Results
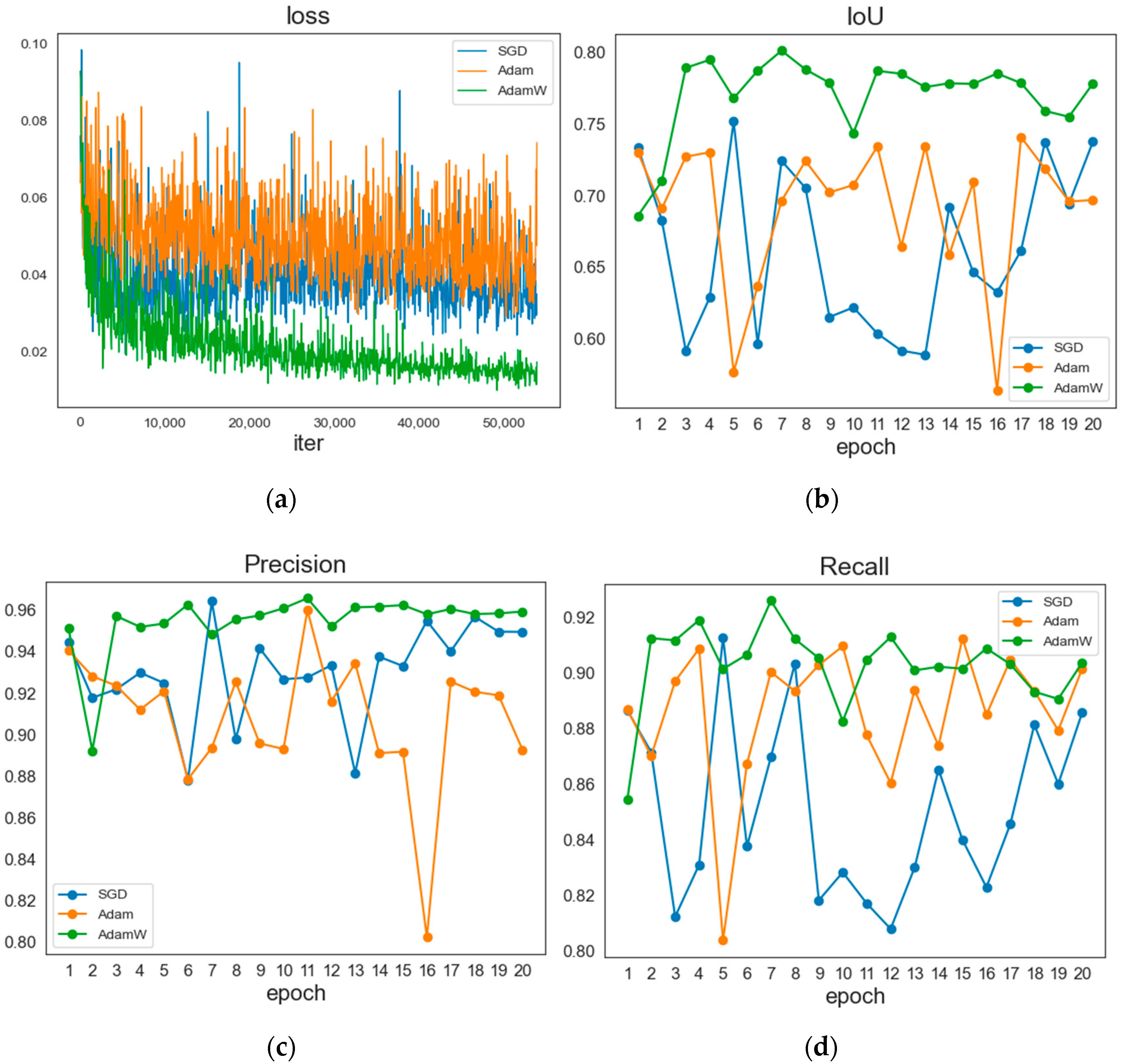
3.3.1. Optimizer Analysis
3.3.2. Comparison of Different Backbone Models
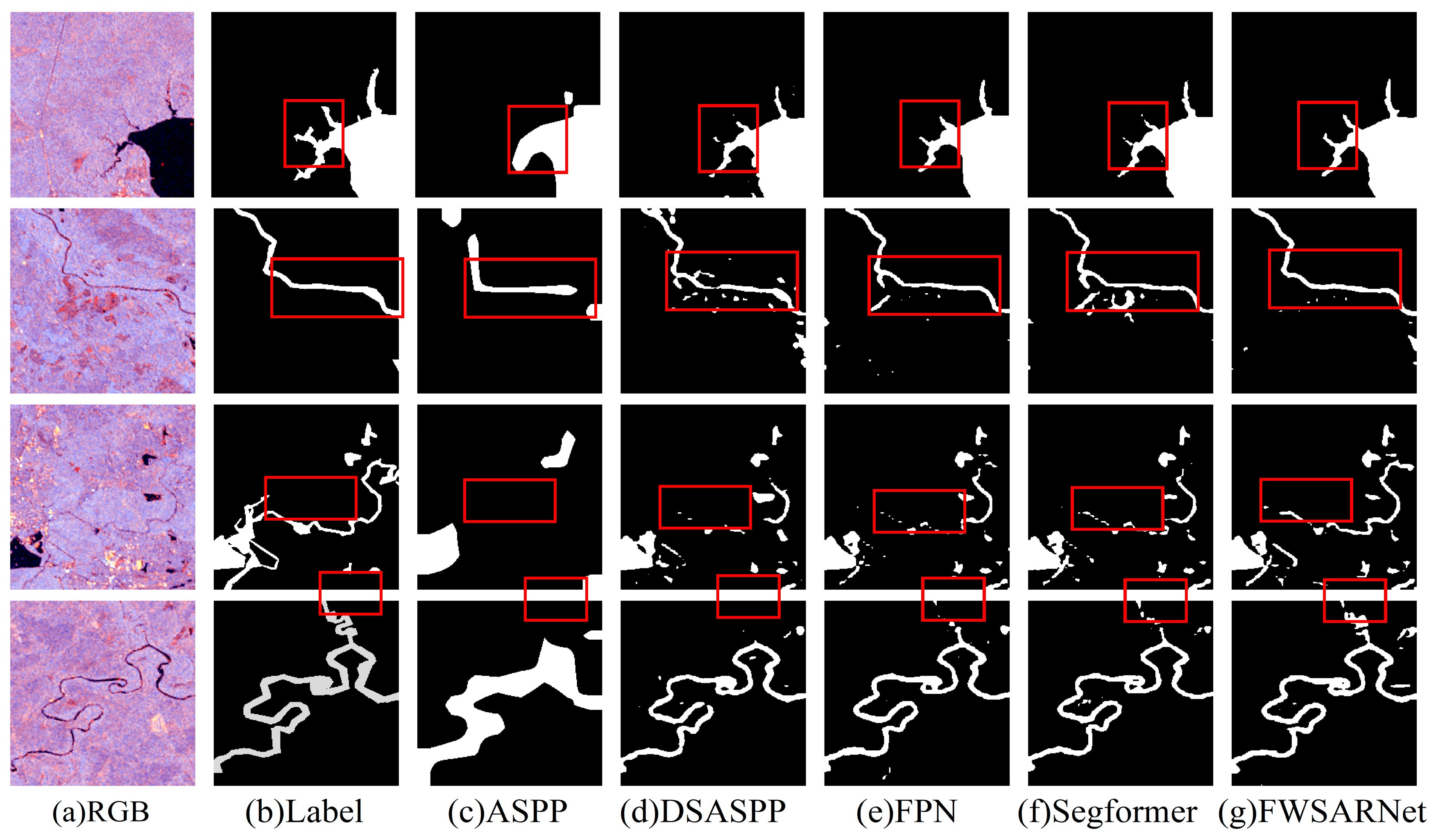
3.3.3. Comparison of Different Decoder Models
4. Discussion
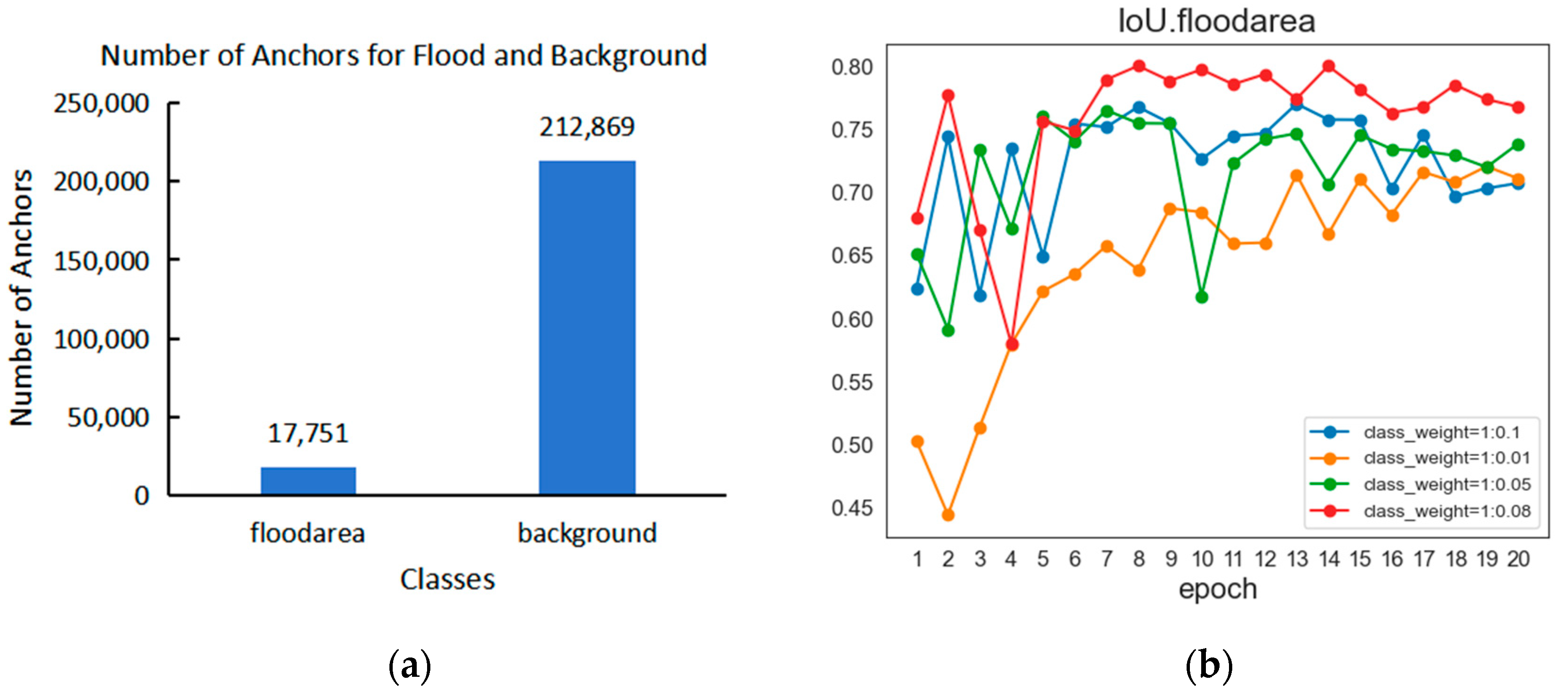
4.1. Analysis of Data Category Weights
4.2. Model Efficiency Analysis
4.3. Comparison with Other SOTA Models
4.4. Comparison of Different Features
4.5. Generalization Experiment
5. Conclusions
6. Limitations and Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorenzo, A.; Berny, B.; Francesco, D.; Gustavo, N.; Ad, D.R.; Peter, S.; Klaus, W.; Luc, F. Global projections of river flood risk in a warmer world. Earth’s Future 2017, 5, 171–182. [Google Scholar]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite imaging reveals increased proportion of population exposed to floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Wenchao, K.; Yuming, X.; Feng, W.; Ling, W.; Hongjian, Y. Flood Detection in Gaofen-3 SAR Images via Fully Convolutional Networks. Sensors 2018, 18, 2915. [Google Scholar]
- Chen, Y.; Huang, J.; Song, X.; Gao, P.; Wan, S.; Shi, L.; Wang, X. Spatiotemporal Characteristics of Winter Wheat Waterlogging in the Middle and Lower Reaches of the Yangtze River, China. Adv. Meteorol. 2018, 2018, 3542103. [Google Scholar] [CrossRef]
- Munawar, H.S.; Hammad, A.W.A.; Waller, S.T. Remote Sensing Methods for Flood Prediction: A Review. Sensors 2022, 22, 960. [Google Scholar] [CrossRef]
- Kugler, Z.; De Groeve, T. The Global Flood Detection System. 2007. Available online: https://www.researchgate.net/publication/265746365_The_Global_Flood_Detection_System (accessed on 20 May 2022).
- Lin, Y.; Zhang, T.; Ye, Q.; Cai, J.; Wu, C.; Khirni, S.A.; Li, J. Long-term remote sensing monitoring on LUCC around Chaohu Lake with new information of algal bloom and flood submerging. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102413. [Google Scholar] [CrossRef]
- Lin, L.; Di, L.; Tang, J.; Yu, E.; Zhang, C.; Rahman, M.; Shrestha, R.; Kang, L. Improvement and Validation of NASA/MODIS NRT Global Flood Mapping. Remote Sens. 2019, 11, 205. [Google Scholar] [CrossRef]
- Mateo, G.G.; Veitch, M.J.; Smith, L.; Oprea, S.V.; Schumann, G.; Gal, Y.; Baydin, A.G.; Backes, D. Towards global flood mapping onboard low cost satellites with machine learning. Sci. Rep. 2021, 11, 7249. [Google Scholar] [CrossRef]
- Tottrup, C.; Druce, D.; Meyer, R.P.; Christensen, M.; Riffler, M.; Dulleck, B.; Rastner, P.; Jupova, K.; Sokoup, T.; Haag, A.; et al. Surface Water Dynamics from Space: A Round Robin Intercomparison of Using Optical and SAR High-Resolution Satellite Observations for Regional Surface Water Detection. Remote Sens. 2022, 14, 2410. [Google Scholar] [CrossRef]
- Murfitt, J.; Duguay, C.R. 50 years of lake ice research from active microwave remote sensing: Progress and prospects. Remote Sens. Environ. 2021, 264, 112616. [Google Scholar] [CrossRef]
- Martinis, S. Automatic Near Real-Time Flood Detection in High Resolution X-Band Synthetic Aperture Radar Satellite Data Using Context-Based Classification on Irregular Graphs. Ph.D. Thesis, Faculty of Geosciences, LMU Munich, Munich, Germany, 2010. [Google Scholar]
- Ian, G. Polarimetric Radar Imaging: From Basics to Applications; Lee, J.-S., Pottier, E., Eds.; CRC Press: Boca Raton, FL, USA, 2012; Volume 33. [Google Scholar]
- Bao, L.; Lv, X.; Yao, J. Water Extraction in SAR Images Using Features Analysis and Dual-Threshold Graph Cut Model. Remote Sens. 2021, 13, 3465. [Google Scholar] [CrossRef]
- Shen, G.; Guo, H.; Liao, J. Object oriented method for detection of inundation extent using multi-polarized synthetic aperture radar image. J. Appl. Remote Sens. 2008, 2, 23512–23519. [Google Scholar] [CrossRef]
- Tong, X.; Luo, X.; Liu, S.; Xie, H.; Chao, W.; Liu, S.; Liu, S.; Makhinov, A.N.; Makhinova, A.F.; Jiang, Y. An approach for flood monitoring by the combined use of Landsat 8 optical imagery and COSMO-SkyMed radar imagery. ISPRS J. Photogramm. Remote Sens. 2018, 136, 144–153. [Google Scholar] [CrossRef]
- D’Addabbo, A.; Refice, A.; Pasquariello, G.; Lovergine, F.P.; Capolongo, D.; Manfreda, S. A Bayesian Network for Flood Detection Combining SAR Imagery and Ancillary Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3612–3625. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Garcia-Rodriguez, J. A Review on Deep Learning Techniques Applied to Semantic Segmentation. arXiv 2017, arXiv:1704.06857. [Google Scholar]
- Deng, J.; Xuan, X.; Wang, W.; Li, Z.; Yao, H.; Wang, Z. A review of research on object detection based on deep learning. J. Phys. Conf. Ser. 2020, 1684, 12028. [Google Scholar] [CrossRef]
- Abu, M.A.; Indra, N.H.; Rahman, A.H.A.; Sapiee, N.A.; Ahmad, I. A study on Image Classification based on Deep Learning and Tensorflow. Int. J. Eng. Res. Technol. 2019, 12, 563–569. [Google Scholar]
- Guo, H.; He, G.; Jiang, W.; Yin, R.; Yan, L.; Leng, W. A Multi-Scale Water Extraction Convolutional Neural Network (MWEN) Method for GaoFen-1 Remote Sensing Images. ISPRS Int. J. Geo-Inf. 2020, 9, 189. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Olaf, R.; Philipp, F.; Thomas, B. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015, Proceedings, Part III 18; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Chen, L.; Papandreou, G.; Schroff, F.; Hartwig, A. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. arXiv 2018, arXiv:1807.10165. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5686–5696. [Google Scholar]
- Ng, K.W.; Huang, Y.F.; Koo, C.H.; Chong, K.L.; El-Shafie, A.; Najah Ahmed, A. A review of hybrid deep learning applications for streamflow forecasting. J. Hydrol. 2023, 625, 130141. [Google Scholar] [CrossRef]
- Essam, Y.; Huang, Y.F.; Ng, J.L.; Birima, A.H.; Ahmed, A.N.; El-Shafie, A. Predicting streamflow in Peninsular Malaysia using support vector machine and deep learning algorithms. Sci. Rep. 2022, 12, 3883. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Fan, R.; Yang, X.; Wang, J.; Latif, A. Extraction of Urban Water Bodies from High-Resolution Remote-Sensing Imagery Using Deep Learning. Water 2018, 10, 585. [Google Scholar] [CrossRef]
- He, Y.; Yao, S.; Yang, W.; Yan, H.; Zhang, L.; Wen, Z.; Zhang, Y.; Liu, T. An Extraction Method for Glacial Lakes Based on Landsat-8 Imagery Using an Improved U-Net Network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 6544–6558. [Google Scholar] [CrossRef]
- Zhong, H.; Sun, H.; Han, D.; Li, Z.; Jia, R. Lake water body extraction of optical remote sensing images based on semantic segmentation. Appl. Intell. 2022, 52, 17974–17989. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, X.; Zhang, Y.; Zhao, G. MSLWENet: A Novel Deep Learning Network for Lake Water Body Extraction of Google Remote Sensing Images. Remote Sens. 2020, 12, 4140. [Google Scholar] [CrossRef]
- Edoardo, N.; Joseph, B.; Samir, B.; Lars, B. Fully Convolutional Neural Network for Rapid Flood Segmentation in Synthetic Aperture Radar Imagery. Remote Sens. 2020, 12, 2532. [Google Scholar]
- Peng, B.; Huang, Q.; Vongkusolkit, J.; Gao, S.; Wright, D.B.; Fang, Z.N.; Qiang, Y. Urban Flood Mapping With Bitemporal Multispectral Imagery Via a Self-Supervised Learning Framework. Ieee J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 2001–2016. [Google Scholar] [CrossRef]
- Yuan, K.; Zhuang, X.; Schaefer, G.; Feng, J.; Guan, L.; Fang, H. Deep-Learning-Based Multispectral Satellite Image Segmentation for Water Body Detection. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 7422–7434. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł. Attention Is All You Need. 2017. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html (accessed on 16 July 2023).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Abed, M.; Imteaz, M.A.; Ahmed, A.N.; Huang, Y.F. A novel application of transformer neural network (TNN) for estimating pan evaporation rate. Appl. Water Sci. 2023, 13, 31. [Google Scholar] [CrossRef]
- Ma, D.; Jiang, L.; Li, J.; Shi, Y. Water index and Swin Transformer Ensemble (WISTE) for water body extraction from multispectral remote sensing images. Giscience Remote Sens. 2023, 60, 2251704. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ding, X.; Zhang, X.; Zhou, Y.; Han, J.; Ding, G.; Sun, J. Scaling Up Your Kernels to 31 × 31: Revisiting Large Kernel Design in CNNs. arXiv 2022, arXiv:2203.06717. [Google Scholar]
- Chen, F.; Wu, F.; Xu, J.; Gao, G.; Ge, Q.; Jing, X. Adaptive deformable convolutional network. Neurocomputing 2021, 453, 853–864. [Google Scholar] [CrossRef]
- Wang, W.; Dai, J.; Chen, Z.; Huang, Z.; Li, Z.; Zhu, X.; Hu, X.; Lu, T.; Lu, L.; Li, H.; et al. InternImage: Exploring Large-Scale Vision Foundation Models with Deformable Convolutions. arXiv 2023, arXiv:2211.05778. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. arXiv 2017, arXiv:1612.01105. [Google Scholar]
- Aldahoul, N.; Momo, M.A.; Chong, K.L.; Ahmed, A.N.; Huang, Y.F.; Sherif, M.; El-Shafie, A. Streamflow classification by employing various machine learning models for peninsular Malaysia. Sci. Rep. 2023, 13, 14574. [Google Scholar] [CrossRef]
- Woodworth, B.; Patel, K.K.; Stich, S.U.; Dai, Z.; Bullins, B.; Mcmahan, H.B.; Shamir, O.; Srebro, N. Is Local SGD Better than Minibatch SGD? arXiv 2020, arXiv:2002.07839. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2019, arXiv:1711.05101. [Google Scholar]
- Llugsi, R.; Yacoubi, S.E.; Fontaine, A.; Lupera, P. Comparison between Adam, AdaMax and Adam W optimizers to implement a Weather Forecast based on Neural Networks for the Andean city of Quito. In Proceedings of the 2021 IEEE Fifth Ecuador Technical Chapters Meeting (ETCM), Cuenca, Ecuador, 12–15 October 2021; pp. 1–6. [Google Scholar]
- Chu, X.; Tian, Z.; Wang, Y.; Zhang, B.; Ren, H.; Wei, X.; Xia, H.; Shen, C. Twins: Revisiting the Design of Spatial Attention in Vision Transformers. arXiv 2021, arXiv:2104.13840. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Tsung-Yi, L.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. arXiv 2017, arXiv:1612.03144. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. arXiv 2021, arXiv:2105.15203. [Google Scholar]
- Sayak, P.; Ganju, S. Flood Segmentation on Sentinel-1 SAR Imagery with Semi-Supervised Learning. arXiv 2021, arXiv:2107.08369. [Google Scholar]
- Ghosh, B.; Garg, S.; Motagh, M. Automatic Flood Detection from Sentinel-1 Data Using Deep Learning Architectures. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, V-3-2022, 201–208. [Google Scholar] [CrossRef]
- Garg, S.; Ghosh, B.; Motagh, M. Automatic Flood Detection from Sentinel-1 Data Using Deep Learning: Demonstration of NASA-ETCI Benchmark Datasets. 2022. Available online: https://ui.adsabs.harvard.edu/abs/2021AGUFM.H55A0739G/abstract (accessed on 16 July 2023).



| Backbone | Iou (%) | mIou (%) | F1 (%) | Precision (%) | Recall (%) |
|---|---|---|---|---|---|
| ViT | 68.21 | 81.44 | 89.18 | 91.42 | 87.26 |
| ResNet | 76.21 | 86.17 | 92.26 | 94.25 | 90.51 |
| Swin Transformer | 77.08 | 86.68 | 92.58 | 94.59 | 90.81 |
| Twins_svt | 77.80 | 87.13 | 92.86 | 95.38 | 90.69 |
| FWSARNet | 80.10 | 88.47 | 93.67 | 94.84 | 92.59 |
| Decoder | Iou (%) | mIou (%) | F1 (%) | Precision (%) | Recall (%) |
|---|---|---|---|---|---|
| ASPP | 71.39 | 83.25 | 90.4 | 90.53 | 90.28 |
| DSASPP | 77.52 | 87.07 | 92.81 | 96.54 | 89.81 |
| FPN | 77.99 | 87.3 | 92.96 | 95.84 | 90.53 |
| Segformer | 79.32 | 88.07 | 93.42 | 95.95 | 91.25 |
| FWSARNet | 80.1 | 88.47 | 93.67 | 94.84 | 92.59 |
| Model | Flops (G) | Params (M) | Test Time (s) | Train Time (min) |
|---|---|---|---|---|
| ViT | 98.51 | 144.06 | 267 | 409.96 |
| ResNet | 99.17 | 66.4 | 182 | 318.07 |
| Swin Transformer | 66.39 | 81.15 | 225 | 272.27 |
| Twins_svt | 63.33 | 87.61 | 232 | 286.22 |
| FWSARNet | 58.75 | 58.96 | 140 | 263.23 |
| DATA | VV | VH | |VV|/|VH| | IoU (%) |
|---|---|---|---|---|
| ETCI2021 | + | − | − | 76.18 |
| − | + | − | 78.14 | |
| + | + | − | 78.25 | |
| + | + | + | 80.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Wang, R.; Li, P.; Zhang, P. Flood Detection in Polarimetric SAR Data Using Deformable Convolutional Vision Model. Water 2023, 15, 4202. https://doi.org/10.3390/w15244202
Yu H, Wang R, Li P, Zhang P. Flood Detection in Polarimetric SAR Data Using Deformable Convolutional Vision Model. Water. 2023; 15(24):4202. https://doi.org/10.3390/w15244202
Chicago/Turabian StyleYu, Haiyang, Ruili Wang, Pengao Li, and Ping Zhang. 2023. "Flood Detection in Polarimetric SAR Data Using Deformable Convolutional Vision Model" Water 15, no. 24: 4202. https://doi.org/10.3390/w15244202





