Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI
Abstract
:1. Introduction
2. Materials and Methods
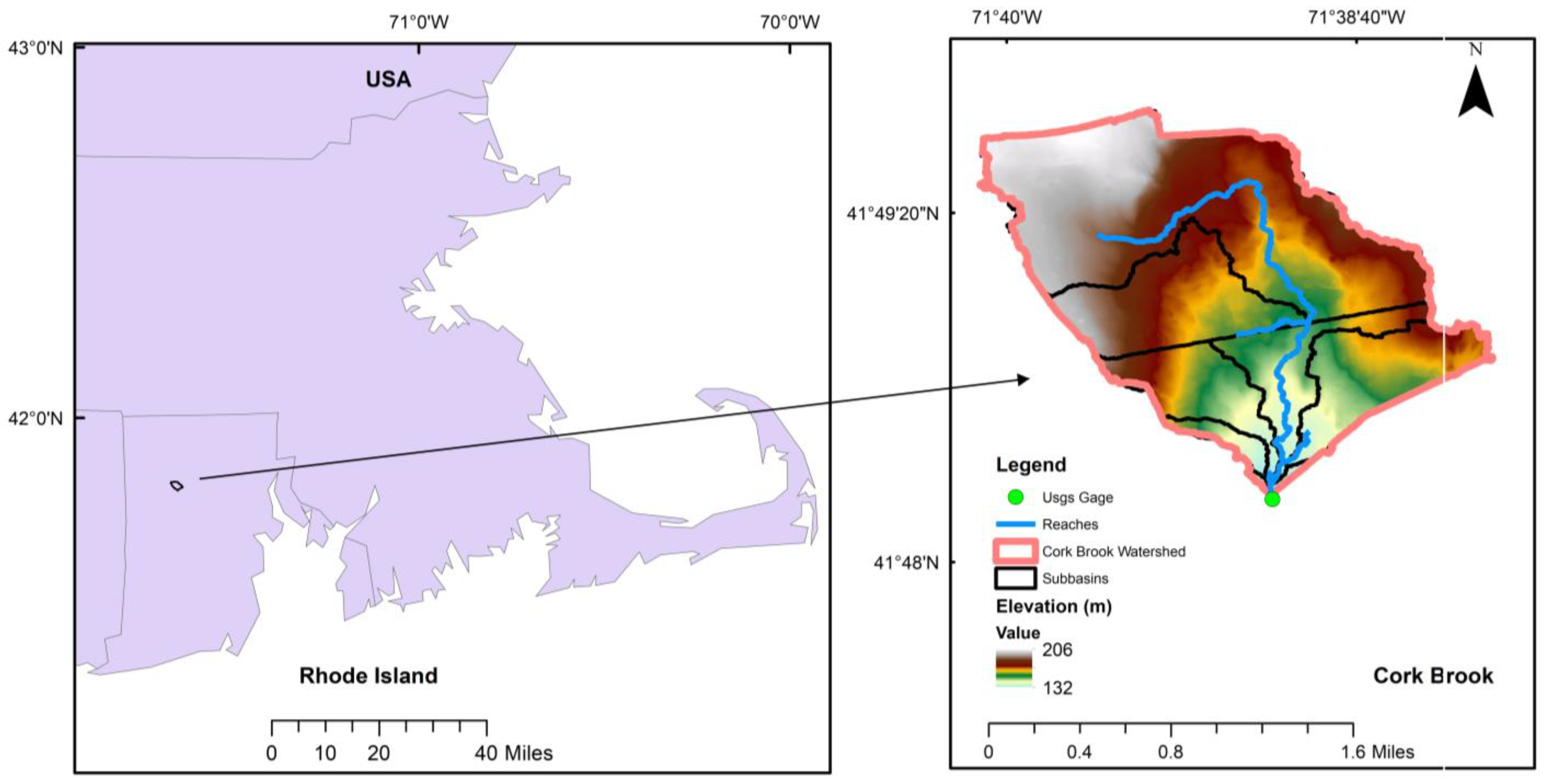
2.1. Study Area
2.2. Model
2.2.1. SWAT
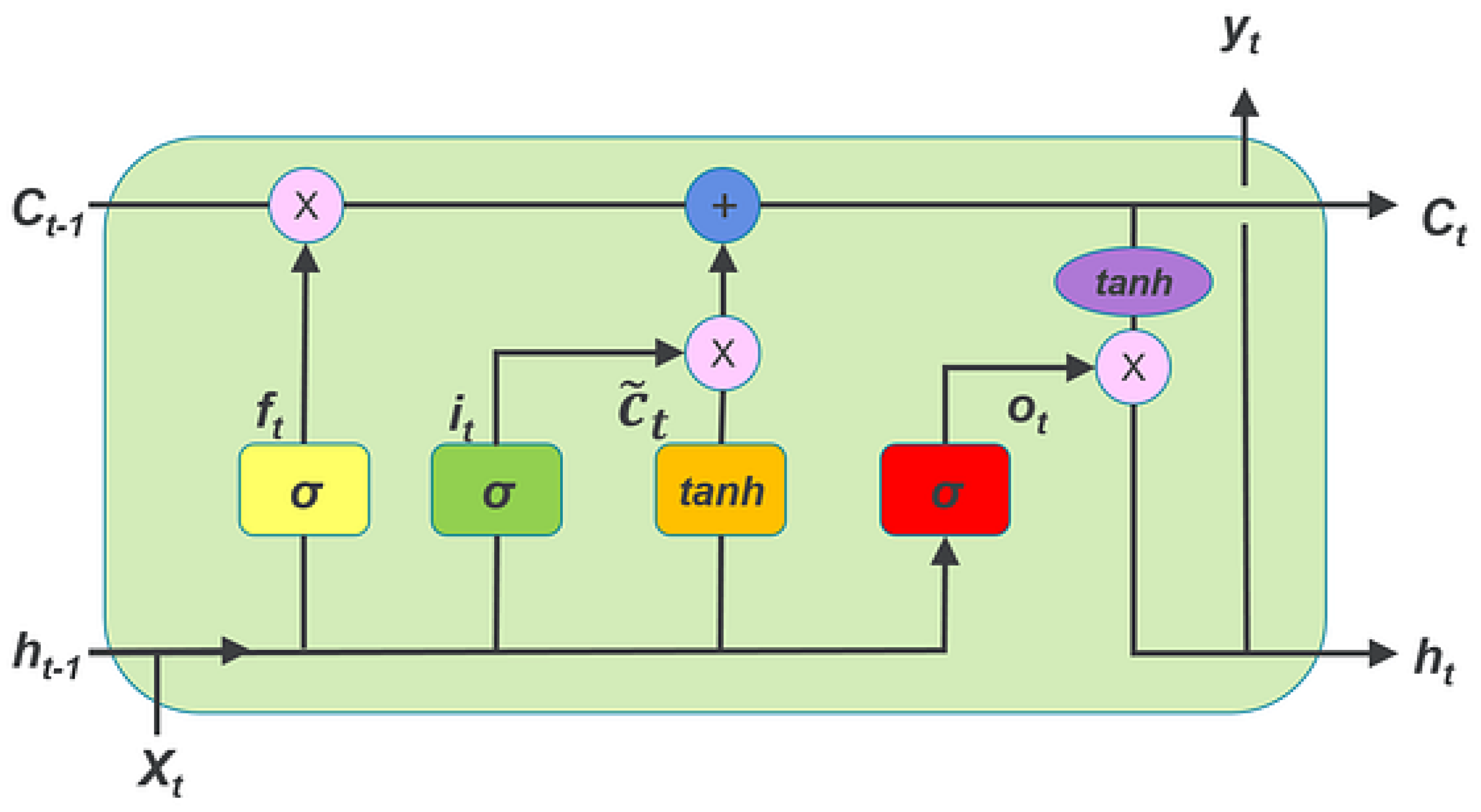
2.2.2. LSTM
2.2.3. Methodology
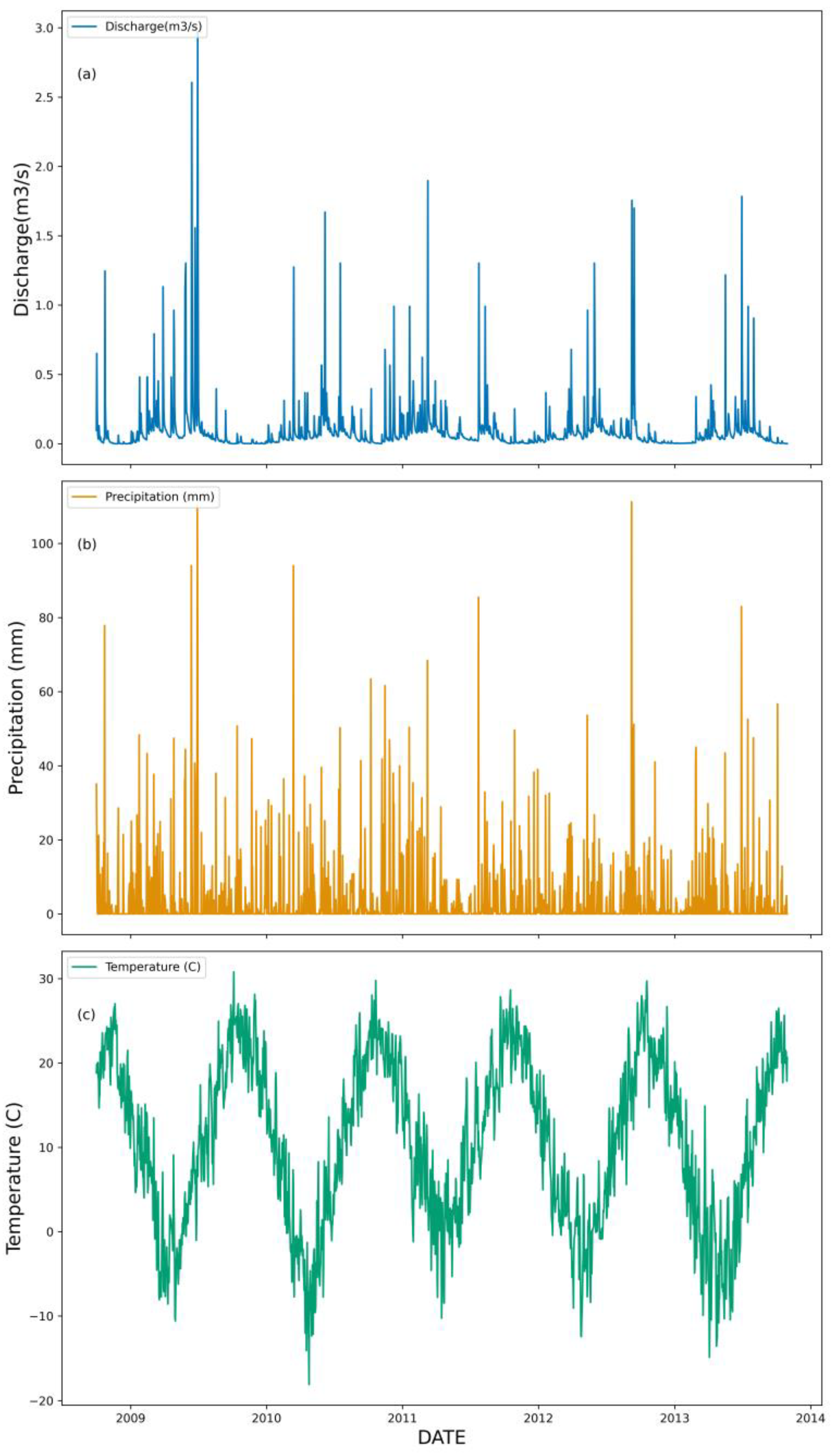
2.2.4. Feature Selection and Data Preprocessing
2.2.5. LSTM Model Structure and Hyperparameter Tuning
2.2.6. Model Evaluation
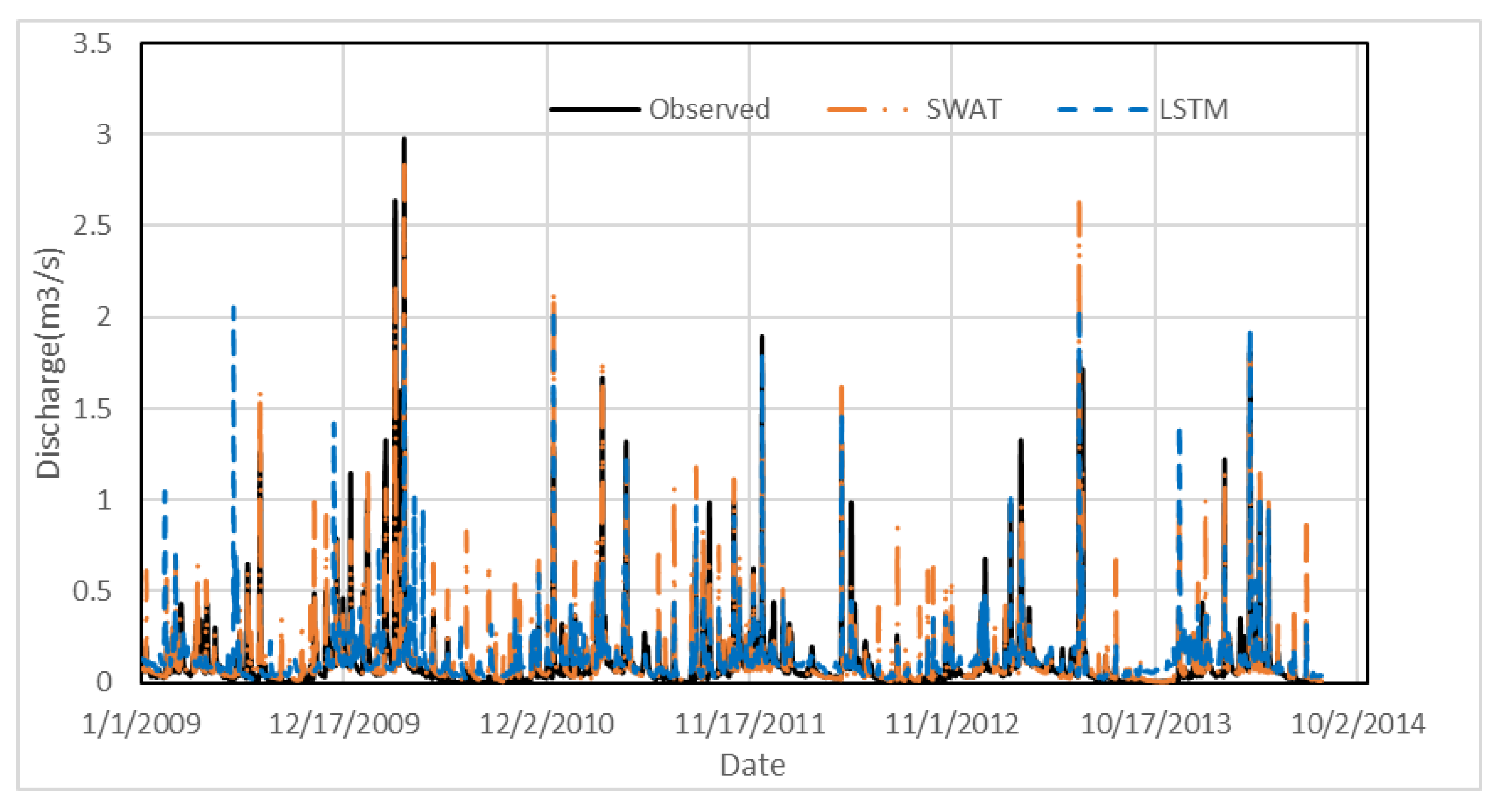
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beven, K.; Lamb, R.; Quinn, P.; Romanowicz, R.; Freer, J. Topmodel. Comput. Models Watershed Hydrol. 1995, 627–668. [Google Scholar]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M.; Woodward, C.S.; Smith, S.; Vanderborght, J.; Vereecken, H.; Simmer, C. Proof of concept of regional scale hydrologic simulations at hydrologic resolution utilizing massively parallel computer resources. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a catchment-aware long short-term memory network (LSTM) for large-scale hydrological modeling. Hydrol. Earth Syst. Sci. Discuss 2019, 2019, 1–32. [Google Scholar]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; Van Beek, L.P.H.; Bierkens, M.F.; Blyth, E.; Whitehead, P. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Adams, T.E.; Pagano, T.C. Flood Forecasting: A Global Perspective; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Herrnegger, M.; Senoner, T.; Nachtnebel, H.-P. Adjustment of spatio-temporal precipitation patterns in a high Alpine environment. J. Hydrol. 2018, 556, 913–921. [Google Scholar] [CrossRef]
- Wesemann, J.; Herrnegger, M.; Schulz, K. Hydrological modelling in the anthroposphere: Predicting local runoff in a heavily modified high-alpine catchment. J. Mt. Sci. 2018, 15, 921–938. [Google Scholar] [CrossRef]
- Razavi, S. Deep learning, explained: Fundamentals, explainability, and bridgeability to process-based modelling. Environ. Model. Softw. 2021, 144, 105159. [Google Scholar] [CrossRef]
- Remesan, R.; Mathew, J. Hydrological Data Driven Modelling; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Solomatine, D.; See, L.M.; Abrahart, R.J. Data-driven modelling: Concepts, approaches and experiences. Pract. Hydroinform. Comput. Intell. Technol. Dev. Water Appl. 2008, 68, 17–30. [Google Scholar]
- Halff, A.H.; Halff, H.M.; Azmoodeh, M. Predicting runoff from rainfall using neural networks. In Proceedings of the Engineering Hydrology, ASCE, San Francisco, CA, USA, 25–30 July 1993. [Google Scholar]
- Kumar, D.N.; Raju, K.S.; Sathish, T. River flow forecasting using recurrent neural networks. Water Resour. Manag. 2004, 18, 143–161. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking data-driven rainfall–runoff models in Great Britain: A comparison of long short-term memory (LSTM)-based models with four lumped conceptual models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Frame, J.M.; Kratzert, F.; Klotz, D.; Gauch, M.; Shalev, G.; Gilon, O.; Qualls, L.M.; Gupta, H.V.; Nearing, G.S. Deep learning rainfall–runoff predictions of extreme events. Hydrol. Earth Syst. Sci. 2022, 26, 3377–3392. [Google Scholar] [CrossRef]
- Schmidhuber, J.; Hochreiter, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Saha, G.K.; Rahmani, F.; Shen, C.; Li, L.; Cibin, R. A deep learning-based novel approach to generate continuous daily stream nitrate concentration for nitrate data-sparse watersheds. Sci. Total. Environ. 2023, 878, 162930. [Google Scholar] [CrossRef] [PubMed]
- Ma, K.; Feng, D.; Lawson, K.; Tsai, W.P.; Liang, C.; Huang, X.; Shen, C. Transferring hydrologic data across continents–leveraging data-rich regions to improve hydrologic prediction in data-sparse regions. Water Resour. Res. 2021, 57, e2020WR028600. [Google Scholar] [CrossRef]
- Yang, T.; Sun, F.; Gentine, P.; Liu, W.; Wang, H.; Yin, J.; Du, M.; Liu, C. Evaluation and machine learning improvement of global hydrological model-based flood simulations. Environ. Res. Lett. 2019, 14, 114027. [Google Scholar] [CrossRef]
- Tao, Y.; Gao, X.; Hsu, K.; Sorooshian, S.; Ihler, A. A deep neural network modeling framework to reduce bias in satellite precipitation products. J. Hydrometeorol. 2016, 17, 931–945. [Google Scholar] [CrossRef]
- Ley, A.; Bormann, H.; Casper, M. Intercomparing LSTM and RNN to a Conceptual Hydrological Model for a Low-Land River with a Focus on the Flow Duration Curve. Water 2023, 15, 505. [Google Scholar] [CrossRef]
- Nifa, K.; Boudhar, A.; Ouatiki, H.; Elyoussfi, H.; Bargam, B.; Chehbouni, A. Deep Learning Approach with LSTM for Daily Streamflow Prediction in a Semi-Arid Area: A Case Study of Oum Er-Rbia River Basin, Morocco. Water 2023, 15, 262. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Sungmin, O.; Dutra, E.; Orth, R. Robustness of process-based versus data-driven modeling in changing climatic conditions. J. Hydrometeorol. 2020, 21, 1929–1944. [Google Scholar]
- Hunt, K.M.R.; Matthews, G.R.; Pappenberger, F.; Prudhomme, C. Using a long short-term memory (LSTM) neural network to boost river streamflow forecasts over the western United States. Hydrol. Earth Syst. Sci. 2022, 26, 5449–5472. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Hettiarachchi, P.; Hall, M.J.; Minns, A.W. The extrapolation of artificial neural networks for the modelling of rainfall—Runoff relationships. J. Hydroinformatics 2005, 7, 291–296. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L.; Isik, S. Water quality prediction using SWAT-ANN coupled approach. J. Hydrol. 2020, 590, 125220. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Pmlr, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Essam, Y.; Huang, Y.F.; Ng, J.L.; Birima, A.H.; Ahmed, A.N.; El-Shafie, A. Predicting streamflow in Peninsular Malaysia using support vector machine and deep learning algorithms. Sci. Rep. 2022, 12, 383. [Google Scholar] [CrossRef]
- Klotz, D.; Kratzert, F.; Gauch, M.; Sampson, A.K.; Brandstetter, J.; Klambauer, G.; Hochreiter, S.; Nearing, G. Uncertainty estimation with deep learning for rainfall–runoff modeling. Hydrol. Earth Syst. Sci. 2022, 26, 1673–1693. [Google Scholar] [CrossRef]
- Liang, W.; Chen, Y.; Fang, G.; Kaldybayev, A. Machine learning method is an alternative for the hydrological model in an alpine catchment in the Tianshan region, Central Asia. J. Hydrol. Reg. Stud. 2023, 49, 101492. [Google Scholar] [CrossRef]
- Feng, D.; Beck, H.E.; Lawson, K.; Shen, C. The suitability of differentiable, physics-informed machine learninghydrologic models for ungauged regions and climate change impact assessment. Hydrol. Earth Syst. Sci. 2023, 17, 2357–2373. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G.; Parajka, J. Spatio-temporal variability of event runoff coefficients. J. Hydrol. 2006, 331, 591–604. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States–representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Addy, K.; Gold, A.J.; Loffredo, J.A.; Schroth, A.W.; Inamdar, S.P.; Bowden, W.B.; Kellogg, D.Q.; Birgand, F. Stream response to an extreme drought-induced defoliation event. Biogeochemistry 2018, 140, 199–215. [Google Scholar] [CrossRef]
- Krysanova, V.; Arnold, J.G. Advances in ecohydrological modelling with SWAT—A review. Hydrol. Sci. J. 2008, 53, 939–947. [Google Scholar] [CrossRef]
- Walega, A.; Amatya, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 100645. [Google Scholar] [CrossRef]
- Marin, M.; Clinciu, I.; Tudose, N.C.; Ungurean, C.; Adorjani, A.; Mihalache, A.L.; Davidescu, A.A.; Davidescu, O.; Dinca, L.; Cacovean, H. Assessing the vulnerability of water resources in the context of climate changes in a small forested watershed using SWAT: A review. Environ. Res. 2020, 184, 109330. [Google Scholar] [CrossRef] [PubMed]
- Im, S.; Lee, J.; Kuraji, K.; Lai, Y.-J.; Tuankrua, V.; Tanaka, N.; Gomyo, M.; Inoue, H.; Tseng, C.-W. Soil conservation service curve number determination for forest cover using rainfall and runoff data in experimental forests. J. For. Res. 2020, 25, 204–213. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Alizadeh, B.; Bafti, A.G.; Kamangir, H.; Zhang, Y.; Wright, D.B.; Franz, K.J. A novel attention-based LSTM cell post-processor coupled with bayesian optimization for streamflow prediction. J. Hydrol. 2021, 601, 126526. [Google Scholar] [CrossRef]
- Man, Y.; Yang, Q.; Shao, J.; Wang, G.; Bai, L.; Xue, Y. Enhanced LSTM model for daily runoff prediction in the upper huai river basin, China. Engineering 2022, 24, 229–238. [Google Scholar] [CrossRef]
- Zulqarnain, M.; Ghazali, R.; Hassim, Y.M.M.; Aamir, M. An Enhanced gated recurrent unit with auto-encoder for solving text classification problems. Arab. J. Sci. Eng. 2021, 46, 8953–8967. [Google Scholar] [CrossRef]
- Joseph, V.R. Optimal ratio for data splitting. Stat. Anal. Data Min. ASA Data Sci. J. 2022, 15, 531–538. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Jha, M.K. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44, 1–18. [Google Scholar] [CrossRef]
- Chambers, B.M.; Pradhanang, S.M.; Gold, A.J. Simulating Climate change induced thermal stress in coldwater fish habitat using SWAT model. Water 2017, 9, 732. [Google Scholar] [CrossRef]
- Gupta, A.; Govindaraju, R. Propagation of structural uncertainty in watershed hydrologic models. J. Hydrol. 2019, 575, 66–81. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of hydrological model uncertainties and advances in their analysis. Water 2020, 13, 28. [Google Scholar] [CrossRef]
- Li, H.; Sivapalan, M. Effect of spatial heterogeneity of runoff generation mechanisms on the scaling behavior of event runoff responses in a natural river basin. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Brantley, S.L.; Lebedeva, M.I.; Balashov, V.N.; Singha, K.; Sullivan, P.L.; Stinchcomb, G. Toward a conceptual model relating chemical reaction fronts to water flow paths in hills. Geomorphology 2017, 277, 100–117. [Google Scholar] [CrossRef]
- Rempe, D.M.; Dietrich, W.E. A bottom-up control on fresh-bedrock topography under landscapes. Proc. Natl. Acad. Sci. USA 2014, 111, 6576–6581. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward Improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Hong, N.-M.; Wu, P.-J.; Lin, C.-J. Modeling and assessing land-use and hydrological processes to future land-use and climate change scenarios in watershed land-use planning. Environ. Geol. 2007, 53, 623–634. [Google Scholar] [CrossRef]
- Guo, W.; Yu, L.; Huang, L.; He, N.; Chen, W.; Hong, F.; Wang, B.; Wang, H. Ecohydrological response to multi-model land use change at watershed scale. J. Hydrol. Reg. Stud. 2023, 49, 101517. [Google Scholar] [CrossRef]
- Dixon, B.; Earls, J. Effects of urbanization on streamflow using SWAT with real and simulated meteorological data. Appl. Geogr. 2012, 35, 174–190. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Xie, J. Simulating runoff under changing climatic conditions: A comparison of the long short-term memory network with two conceptual hydrologic models. J. Hydrol. 2021, 592, 125779. [Google Scholar] [CrossRef]
- Yan, L.; Chen, C.; Hang, T.; Hu, Y. A stream prediction model based on attention-LSTM. Earth Sci. Inform. 2021, 14, 723–733. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arxiv 2015, arXiv:1506.00019. [Google Scholar]


| Parameter | Definition | Range | Units |
|---|---|---|---|
| CN2.mgt | SCS runoff curve number | 60–75 | - |
| ALPHA_BF.gw | Baseflow alpha factor | 0.0–0.10 | 1/Days |
| GW_DELAY.gw | Groundwater delay | 0.0–7.0 | Days |
| GWQMN.gw | Depth of water in shallow aquifer for return flow | 0–1000 mm | mm |
| SMTMP.bsn | Snowmelt base temperature | −0.5–2.0 | °C |
| ESCO.hru | Soil evaporation compensation factor 0.15–0.65 - | 0.15–0.65 | - |
| ALPHA_BNK | Baseflow alpha factor for bank storage | 0.0–7.0 | Days |
| SLSOIL.hru | Slope length for lateral subsurface flow | 0.0–15 | m |
| Layer (Type) | Output Shape | Param # |
|---|---|---|
| Lstm_1 (LSTM) | (None, 10, 75) | 23,400 |
| Dropout_1 (Dropout) | (None, 10, 75) | 0 |
| Lstm_2 (LSTM) | (None, 10, 75) | 45,300 |
| Dropout_2 (Dropout) | (None, 10, 75) | 0 |
| Lstm_3 (LSTM) | (None, 10, 75) | 45,300 |
| Dropout_3 (Dropout) | (None, 10, 75) | 0 |
| Lstm_4 (LSTM) | (None, 10, 75) | 45,300 |
| Dropout_4 (Dropout) | (None, 10, 75) | 0 |
| Lstm_5 (LSTM) | (None, 75) | 45,300 |
| Dense_1 (Dense) | (None, 75) | 5700 |
| Dense_2 (Dense) | (None, 1) | 76 |
| Total Params: 210376 |
| Calibration (2009–2013) | Validation (2013–2014) | |||
|---|---|---|---|---|
| SWAT | LSTM | SWAT | LSTM | |
| NSE | 0.65 | 0.77 | 0.63 | 0.60 |
| R2 | 0.68 | 0.78 | 0.68 | 0.65 |
| Deviation (%) | ||
|---|---|---|
| Percentile | SWAT | LSTM |
| 2 | 5 | −7 |
| 5 | 4 | −3 |
| 10 | 0 | 1 |
| 20 | −9 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, S.G.; Pradhanang, S.M. Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI. Water 2023, 15, 4194. https://doi.org/10.3390/w15234194
Shrestha SG, Pradhanang SM. Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI. Water. 2023; 15(23):4194. https://doi.org/10.3390/w15234194
Chicago/Turabian StyleShrestha, Shiva Gopal, and Soni M. Pradhanang. 2023. "Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI" Water 15, no. 23: 4194. https://doi.org/10.3390/w15234194
APA StyleShrestha, S. G., & Pradhanang, S. M. (2023). Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI. Water, 15(23), 4194. https://doi.org/10.3390/w15234194







