Research on Subsidence Prediction Method of Water-Conducting Fracture Zone of Overlying Strata in Coal Mine Based on Grey Theory Model
Abstract
:1. Introduction
2. Prediction Method of Mining-Induced Overburden Subsidence Based on Grey Theory
2.1. Basic Principle of Grey Theory Model
2.2. Model Accuracy Test
- (1)
- Posteriori error test
- (2)
- Grey correlation degree test
2.3. Grey Theory Prediction Method of Overburden Subsidence Based on Distributed Strain Monitoring
3. Similar Material Model Test of Mining Overburden Deformation
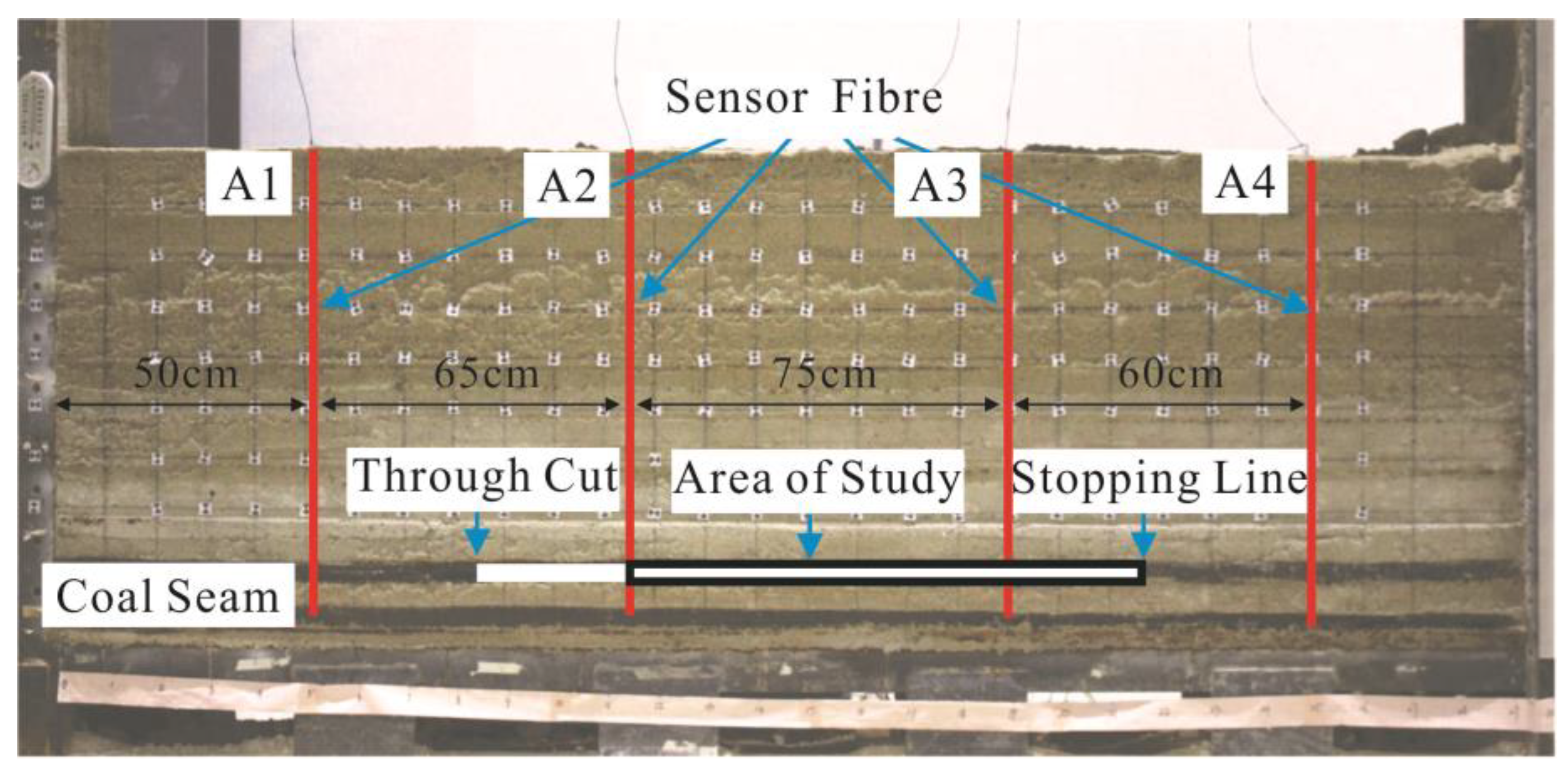
3.1. The Scheme of Similar Material Model Test
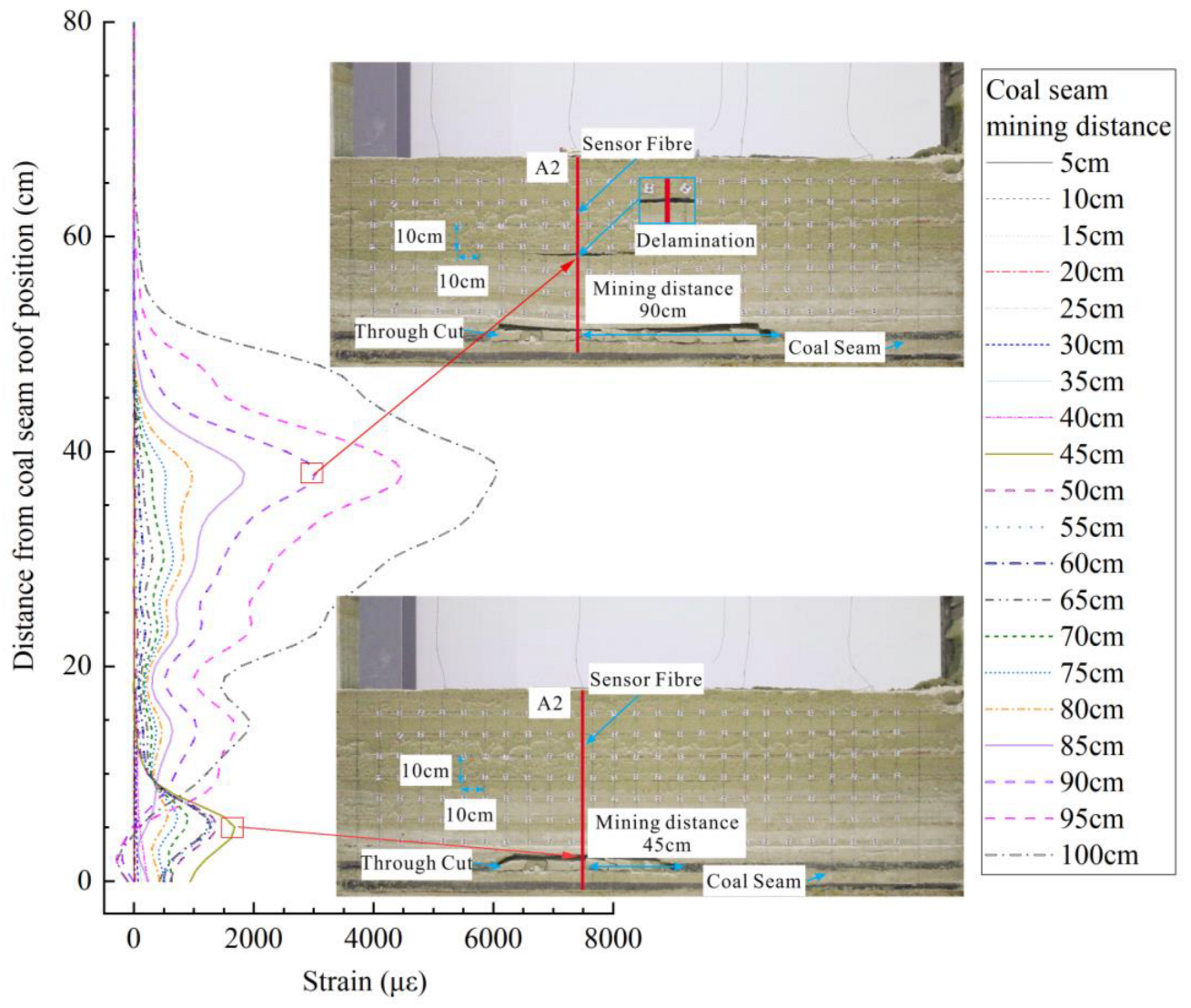
3.2. The Strain Distribution Characteristics of Mining Overburden Rock and the Height Determination of Water-Conducting Fractured Zone
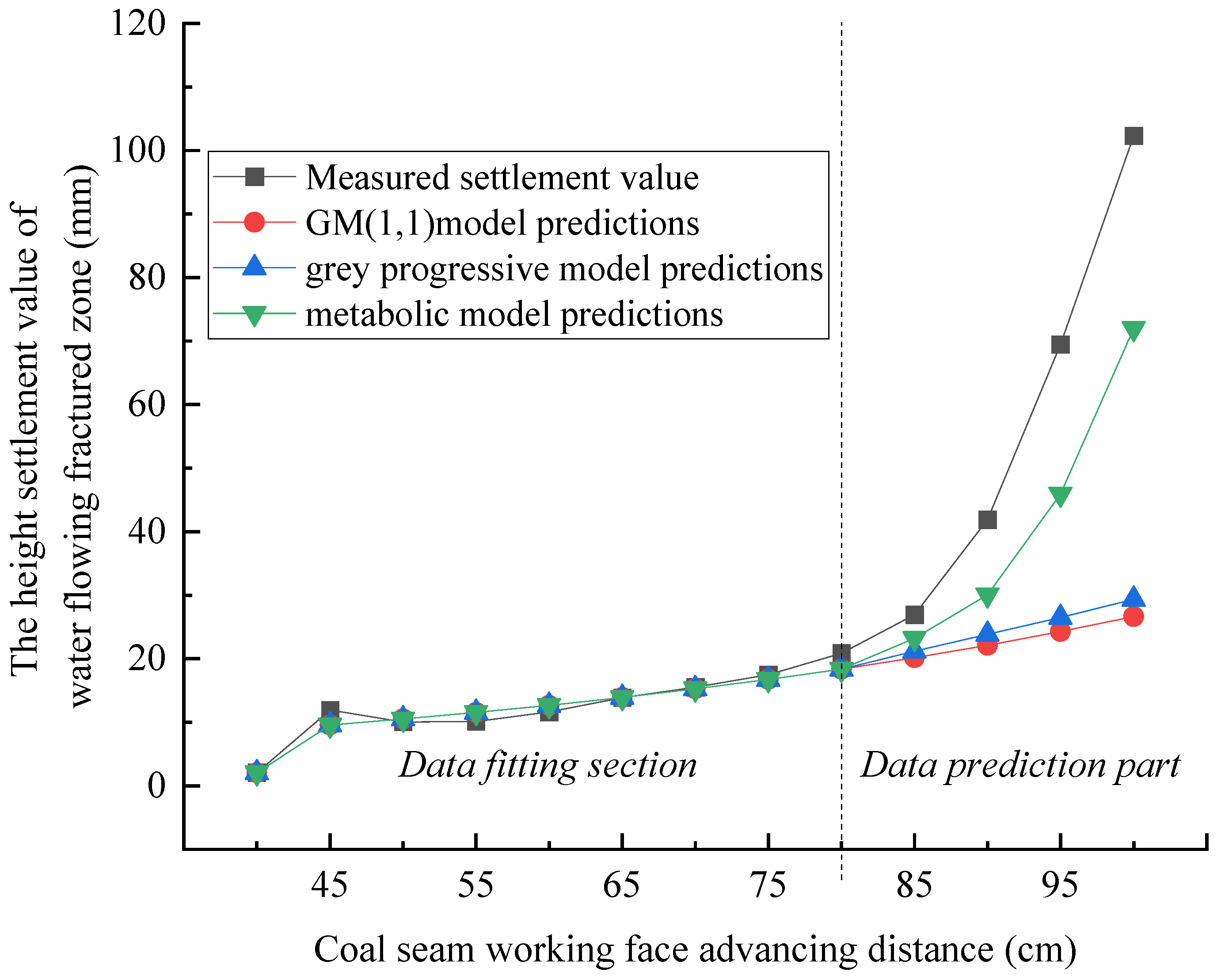
3.3. Grey Model Prediction of Mining Overburden Deformation
4. Parameter Optimization Evaluation Method of Grey Theory Prediction Model
- (1)
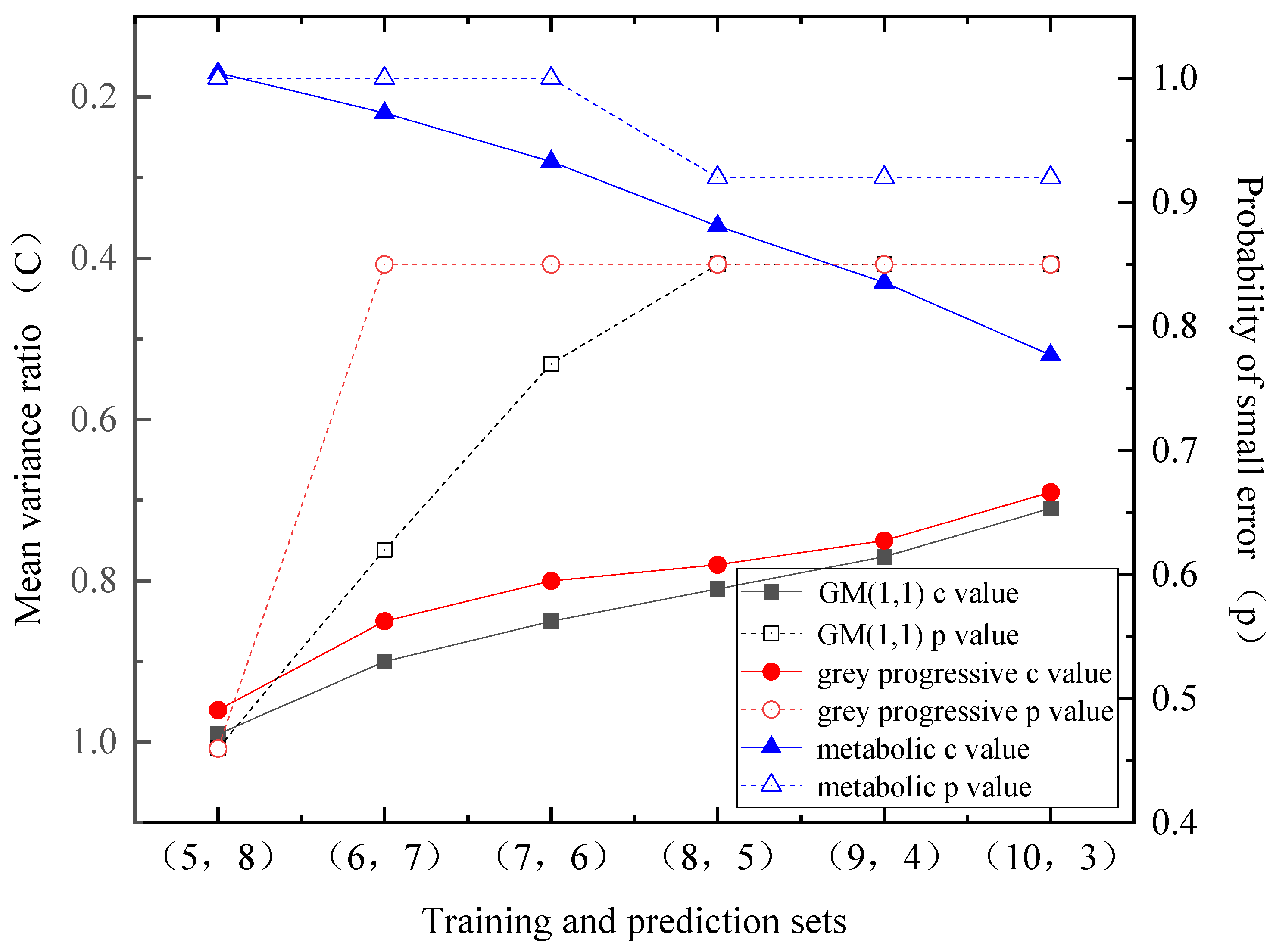
- Precision evolution characteristics of the grey model
- (2)
- Prediction accuracy analysis and evaluation of the grey model
5. Conclusions
- (1)
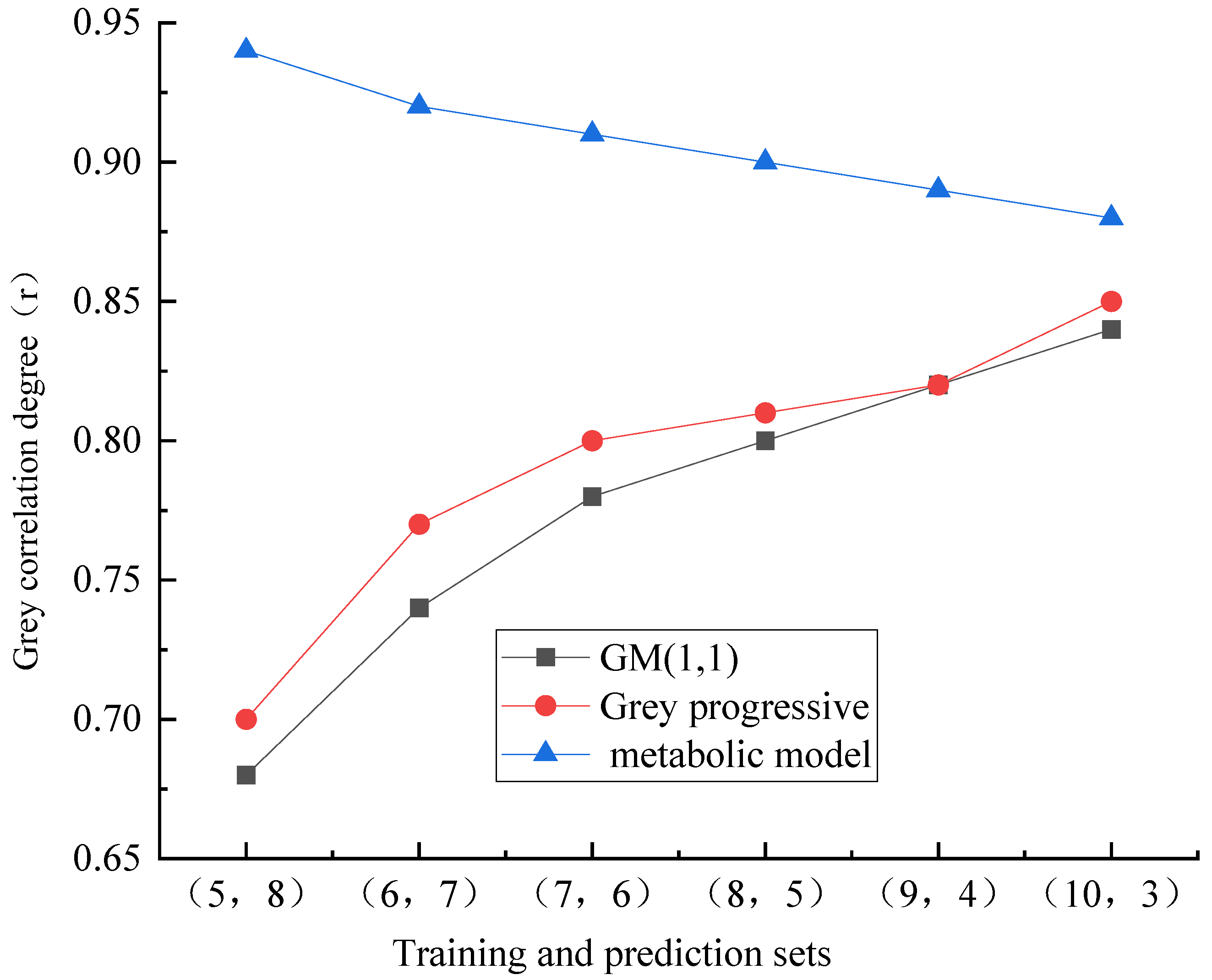
- The subsidence prediction model of the water-conducting fracture zone is established by combining the equidistant sampling data of mining overburden strata of Brillouin optical time domain technology with the GM (1, 1) model. Six kinds of subsidence prediction schemes of mining overburden strata are designed by introducing a grey progressive model and metabolic model, and the subsidence of the water-conducting fracture zone of overburden strata in the mining process of coal seam working face is predicted.
- (2)
- For the metabolic model, the prediction model is related to the mutation of the settlement of the water-conducting fracture zone caused by the breaking of the key stratum of the overlying rock. As for predicting the settlement of the water-conducting fracture zone in the overlying strata of the Shendong Coal Mine, the optimal number of model training is 7 to 8, and the number of predictions is 5 to 6 times. In this case, the prediction accuracy can reach level 1.
- (3)
- The prediction method of overlying strata settlement based on the GM (1, 1) model and grey progressive model is not suitable for the settlement prediction of the water-conducting fracture zone because the model data sequence is too long and the prediction accuracy in the middle and late stage of coal seam mining is gradually reduced.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adhikary, D.P.; Guo, H. Measurement of Longwall Mining Induced Strata Permeability. Geotech. Geol. Eng. 2014, 32, 617–626. [Google Scholar] [CrossRef]
- Teng, Y.H.; Yi, S.H.; Zhu, W.; Jing, S. Development Patterns of Fractured Water-Conducting Zones under Fully Mechanized Mining in Wet-Collapsible Loess Area. Water 2023, 15, 22. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, X.W.; Chen, Y.F.; Wang, X.L.; Tan, S.H. Numerical modelling of fractures induced by coal mining beneath reservoirs and aquifers in china. Q. J. Eng. Geol. Hydrogeol. 2013, 46, 237–244. [Google Scholar] [CrossRef]
- Cheng, G.W.; Ma, T.H.; Tang, C.A.; Liu, H.; Wang, S. A zoning model for coal mining-induced strata movement based on microseismic monitoring. Int. J. Rock Mech. Min. Sci. 2017, 94, 123–138. [Google Scholar] [CrossRef]
- Zheng, D.Q.; Wang, K.Y.; Yang, Z.Q.; Zhao, W.Q.; Wang, Y. Height development law of water-conducting fracture zone in super-thick coal seam under repeated mining. Contemp. Chem. Res. 2023, 11, 52–54. (In Chinese) [Google Scholar]
- Wang, Q.; Pan, R.; Jiang, B.; Li, S.C.; He, M.C.; Sun, H.B.; Wang, L.; Qin, Q.; Yu, H.C.; Luan, Y.C. Study on Failure Mechanism of Roadway with Soft Rock in Deep Coal Mine and Confined Concrete Support System. Eng. Fail. Anal. 2017, 81, 155–177. [Google Scholar] [CrossRef]
- Guo, X.M.; Liu, Y.F.; Gu, Z.X. Detection and calculation of water-conducting fracture zone height in coal seam mining in Binchang mining area. J. Min. Strat. Control Eng. 2023, 5, 91–100. (In Chinese) [Google Scholar]
- Lin, C.G.; Deng, J.; Wang, Q.Z.; Li, C.F.; Wang, J.W.; Huang, H.F.; Liu, Q. Study on the height of water flowing fractured zone in the second panel of Gaojiapu mine field. Coal Technol. 2023, 10, 1–5. (In Chinese) [Google Scholar]
- Li, C.; Gao, H.; Qiu, J.; Yang, Y.; Qu, X.; Wang, Y.; Bi, Z. Grey Model Optimized by Particle Swarm Optimization for Data Analysis and Application of Multi-Sensors. Sensors 2018, 18, 2503. [Google Scholar] [CrossRef]
- Jiao, A.R. Determination of height of water flowing fractured zone in 15,102 working face of Zhangshigou Coal Mine. Shanxi Metall. 2023, 46, 151–153. (In Chinese) [Google Scholar]
- Booth, C.J.; Greer, C.B. Application of MODFLOW using TMR and discrete-step modification of hydraulic properties to simulate the hydrogeologic impact of longwall mining subsidence on overlying shallow aquifers. In Proceedings of the 11th International Mine Water Association Congress—Mine Water—Managing the Challenges, Aachen, Germany, 4–11 September 2011; pp. 211–216. [Google Scholar]
- Xu, S.Y.; Zhang, Y.B.; Shi, H.; Wang, K.; Geng, Y.; Chen, J. Physical Simulation of Strata Failure and Its Impact on Overlying Unconsolidated Aquifer at Various Mining Depths. Water 2018, 10, 650. [Google Scholar] [CrossRef]
- Piao, C.D.; Li, J.J.; Wang, D.L.; Qiao, W. A DOFS-Based Approach to Calculate the Height of Water-Flowing Fractured Zone in Overlying Strata under Mining. Geofluids 2021, 2021, 8860600. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Yang, X.; Xu, F.Q. Distributed optical fiber monitoring technology for height of water-conducting fracture zone in fully mechanized caving face. China Min. Ind. 2022, 31, 108–114. (In Chinese) [Google Scholar]
- Li, X.J.; Chi, M.B.; Wu, B.Y.; Jv, Z.Y. Study on the law of overburden fracture development between layers of underground reservoirs in coal mines based on distributed optical fiber monitoring. China Coal 2022, 48, 49–56. (In Chinese) [Google Scholar]
- Hou, G.Y.; Hu, Z.Y.; Li, Z.X.; Zhao, Q.R.; Feng, D.X.; Cheng, C.; Zhou, H. The application status and prospect of distributed optical fiber and fiber grating sensing technology in coal mine safety monitoring. Coal J. 2023, 48, 96–110. (In Chinese) [Google Scholar]
- Cheng, G.; Wang, Z.X.; Shi, B.; Zhu, W.; Li, T. Research on the construction of multi-field optical fiber neural perception and safety guarantee system for mining-induced overburden deformation. Coal Sci. Technol. 2023, 10, 5947. (In Chinese) [Google Scholar]
- Li, W.P.; Li, T.; Shang, R. Study on structural variation and permeability change of overlying strata in coal mining of large mining area in northern Shaanxi. J. Eng. Geol. 2012, 20, 294–299. (In Chinese) [Google Scholar]
- Deng, Z.; Ke, Y.H.; Gong, H.L.; Li, X.; Li, Z. Land subsidence prediction in Beijing based on PS-InSAR technique and improved Grey-Markov model. GIScience Remote Sens. 2017, 54, 797–818. [Google Scholar] [CrossRef]
- Wang, H.Z.; Zhang, D.S.; Wang, X.F.; Zhang, W. Visual Exploration of the Spatiotemporal Evolution Law of Overburden Failure and Mining-Induced Fractures: A Case Study of the Wangjialing Coal Mine in China. Minerals 2017, 7, 35. [Google Scholar] [CrossRef]
- Jiang, G.; Lin, L.; Liu, Z.D.; Wang, Z. Grey prediction model of slope deformation. Rock Soil Mech. 2000, 3, 53–55. [Google Scholar]
- Wang, Z.S.; Deng, K.Z. Discrete grey prediction model of residual settlement in old goaf. J. China Coal Soc. 2010, 35, 1084–1088. (In Chinese) [Google Scholar]
- Huang, R.; Fu, X.; Pu, Y. A Novel Fractional Accumulative Grey Model with GA-PSO Optimizer and Its Application. Sensors 2023, 23, 636. [Google Scholar] [CrossRef] [PubMed]
- Mi, J.W.; Fan, L.B.; Duan, X.C.; Qiu, Y.Y. Short-Term Power Load Forecasting Method Based on Improved Exponential Smoothing Grey Model. Math. Probl. Eng. 2018, 2018, 3894723. [Google Scholar] [CrossRef]
- Shi, B.; Gu, K.; Wei, G.Q.; Wu, J.H. Full-section distributed optical fiber monitoring technology for ground subsidence drilling. J. Eng. Geol. 2018, 26, 356–364. (In Chinese) [Google Scholar]
- Liu, S.P.; Shi, B.; Gu, K.; Zhang, C.C.; Yang, J.L.; Zhang, S.; Yang, P. Land subsidence monitoring in sinking coastal areas using distributed fiber optic sensing: A case study. Nat. Hazards 2020, 103, 3043–3061. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, Z.X.; Shi, B. Research progress of DFOS in safety mining monitoring of mines. J. China Coal Soc. 2022, 47, 2923–2949. (In Chinese) [Google Scholar]
- Gilbert, P.; Konietzky, H.; Diering, M. Similarity considerations for mining induced subsidence prediction. Int. J. Rock Mech. Min. Sci. 2005, 42, 576–585. [Google Scholar]
- Mitri, H.S.; Severin, J. Physical modelling of rockbolting in coal mines: A review of current status and future needs. Int. J. Rock Mech. Min. Sci. 2014, 70, 318–328. [Google Scholar]
- Gharehdash, N.S.; Abd Aziz, S.M. Physical modeling for prediction of strata behavior during longwall mining under weak geological conditions. Geotech. Geol. Eng. 2014, 32, 333–344. [Google Scholar]
- Liu, Y.Y.; Song, X.M.; Wang, Z.L. Calculation of periodic breaking step distance of thick and hard rock strata and analysis of influencing factors. Coal Eng. 2020, 52, 106–111. (In Chinese) [Google Scholar]
- Sun, Q.X.; Chen, Q.T.; Li, H.J.; Mou, Y. Study on the mechanism of the advance effect of key stratum breaking on surface movement and deformation. Coal Eng. 2023, 55, 105–109. (In Chinese) [Google Scholar]

| Accuracy Grade | Mean Square Deviation Ratio | Probability of Small Error | Correlation Degree |
|---|---|---|---|
| Grade 1 (good) | C ≤ 0.35 | p ≥ 0.95 | r ≥ 0.9 |
| Grade 2 (qualified) | 0.35 < C ≤ 0.5 | 0.8 ≤ p < 0.95 | r ≥ 0.8 |
| Grade 3 (barely) | 0.5 < C ≤ 0.65 | 0.7 ≤ p < 0.8 | r ≥ 0.7 |
| Grade 4 (unqualified) | C > 0.65 | p < 0.7 | r ≥ 0.6 |
| Lithology | Prototype | Model | |||||
|---|---|---|---|---|---|---|---|
| Thickness (m) | Volume Weight (kN/m3) | Compressive Strength (MPa) | Thickness (cm) | Volume Weight (kN/m3) | Compressive Strength (kPa) | Proportion Number | |
| Loose layer | 40 | 17 | 0.7 | 40 | 11.3 | 4.67 | 11:1:0 |
| Sandy mudstone | 6 | 24.1 | 17.2 | 6 | 16.1 | 114.7 | 8:6:4 |
| Fine sandstone | 5 | 28 | 36.5 | 5 | 18.7 | 243.3 | 3:5:5 |
| Sandy mudstone | 7 | 24.1 | 17.2 | 7 | 16.1 | 114.7 | 8:6:4 |
| Mudstone | 9 | 24.3 | 15.3 | 9 | 16.2 | 102 | 10:5:5 |
| Fine sandstone | 13.5 | 28 | 36.5 | 13.5 | 18.7 | 243.3 | 3:5:5 |
| Sandy mudstone | 6 | 24.1 | 17.2 | 6 | 16.1 | 114.7 | 8:6:4 |
| 2−2 coal | 4.2 | 13 | 15 | 4.2 | 8.7 | 100 | 6:5:5 |
| Sandy mudstone | 6 | 24.1 | 17.2 | 6 | 16.1 | 114.7 | 8:6:4 |
| 2−3 coal | 4.2 | 13 | 15 | 4.2 | 8.7 | 100 | 6:5:5 |
| Sandy mudstone | 5 | 24.1 | 17.2 | 5 | 16.1 | 114.7 | 8:6:4 |
| Advancing Distance | Measured Displacement Values Based on Photogrammetry (mm) | GM(1,1) Model | Grey Progressive Model | Metabolic Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Predicted Value (mm) | Residual Error (mm) | Relative Residual (%) | Predicted Value (mm) | Residual Error (mm) | Relative Residual (%) | Predicted Value (mm) | Residual Error (mm) | Relative Residual (%) | ||
| 80 | 20.88 | 18.37 | −2.50 | 11.99 | 18.37 | −2.50 | 11.99 | 18.37 | −2.5 | 11.99 |
| 85 | 26.94 | 20.16 | −6.77 | 25.15 | 21.18 | −5.76 | 21.38 | 23.22 | −3.71 | 13.78 |
| 90 | 41.89 | 22.12 | −19.76 | 47.18 | 23.85 | −18.04 | 43.06 | 30.04 | −11.85 | 28.29 |
| 95 | 69.47 | 24.28 | −45.19 | 65.04 | 26.50 | −42.97 | 61.85 | 45.91 | −23.56 | 33.91 |
| 100 | 102.31 | 26.65 | −75.66 | 73.95 | 29.35 | −72.96 | 71.31 | 72 | −30.3 | 29.62 |
| Quantity of Training Sets (Number) | Working Face Advancing Range (cm) | Quantity of Prediction Sets (Number) | Representation Methods |
|---|---|---|---|
| 5 | 40~60 | 8 | (5, 8) |
| 6 | 40~65 | 7 | (6, 7) |
| 7 | 40~70 | 6 | (7, 6) |
| 8 | 40~75 | 5 | (8, 5) |
| 9 | 40~80 | 4 | (9, 4) |
| 10 | 40~85 | 3 | (10, 3) |
| Number of Training Sets | Number of Predictions | Mean Square Deviation Ratio | Probability of Small Error | Grey Correlation Degree | Accuracy Grade |
|---|---|---|---|---|---|
| 5 | 8 | 0.99 | 0.46 | 0.68 | Level 4 (unqualified) |
| 6 | 7 | 0.9 | 0.62 | 0.74 | Level 4 (unqualified) |
| 7 | 6 | 0.85 | 0.77 | 0.78 | Level 4 (unqualified) |
| 8 | 5 | 0.81 | 0.85 | 0.80 | Level 4 (unqualified) |
| 9 | 4 | 0.77 | 0.85 | 0.82 | Level 4 (unqualified) |
| Number of Training Sets | Number of Predictions | Mean Square Deviation Ratio | Probability of Small Error | Grey Correlation Degree | Accuracy Grade |
|---|---|---|---|---|---|
| 5 | 8 | 0.17 | 1.00 | 0.94 | Level 1 (excellent) |
| 6 | 7 | 0.22 | 1.00 | 0.92 | Level 1 (excellent) |
| 7 | 6 | 0.28 | 1.00 | 0.91 | Level 1 (excellent) |
| 8 | 5 | 0.36 | 0.92 | 0.90 | Level 2 (good) |
| 9 | 4 | 0.43 | 0.92 | 0.89 | Level 2 (good) |
| 10 | 3 | 0.52 | 0.92 | 0.88 | Level 3 (qualified) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; He, Z.; Piao, C.; Chi, W.; Lu, Y. Research on Subsidence Prediction Method of Water-Conducting Fracture Zone of Overlying Strata in Coal Mine Based on Grey Theory Model. Water 2023, 15, 4177. https://doi.org/10.3390/w15234177
Li J, He Z, Piao C, Chi W, Lu Y. Research on Subsidence Prediction Method of Water-Conducting Fracture Zone of Overlying Strata in Coal Mine Based on Grey Theory Model. Water. 2023; 15(23):4177. https://doi.org/10.3390/w15234177
Chicago/Turabian StyleLi, Jinjun, Zhihao He, Chunde Piao, Weiqi Chi, and Yi Lu. 2023. "Research on Subsidence Prediction Method of Water-Conducting Fracture Zone of Overlying Strata in Coal Mine Based on Grey Theory Model" Water 15, no. 23: 4177. https://doi.org/10.3390/w15234177
APA StyleLi, J., He, Z., Piao, C., Chi, W., & Lu, Y. (2023). Research on Subsidence Prediction Method of Water-Conducting Fracture Zone of Overlying Strata in Coal Mine Based on Grey Theory Model. Water, 15(23), 4177. https://doi.org/10.3390/w15234177





