Study on Cascade Density of the Impeller Based on Response Surface Analysis
Abstract
:1. Introduction
2. Calculation Model and Numerical Method
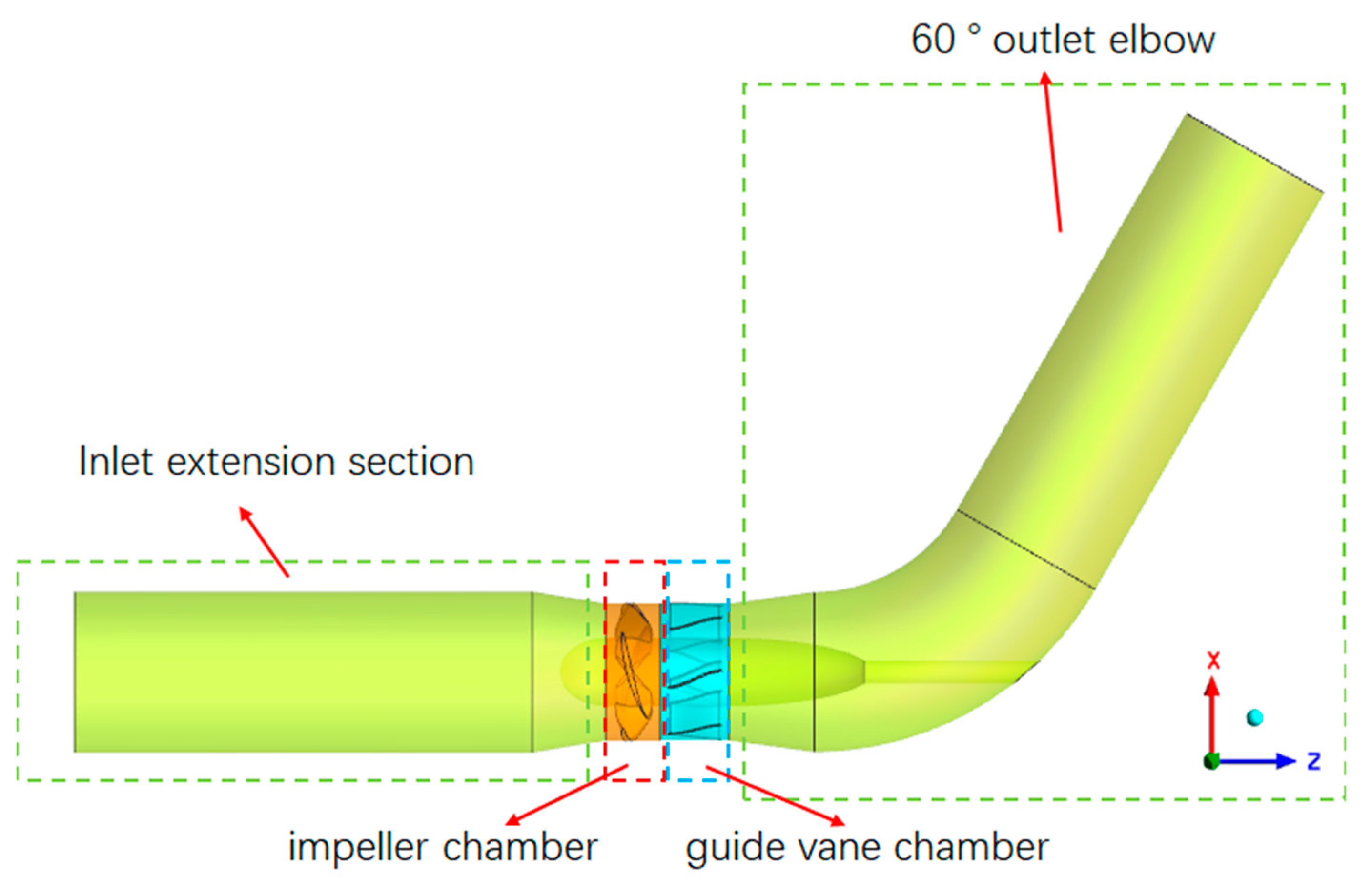
2.1. Calculation Model and Control Parameters
2.2. Numerical Simulation Method
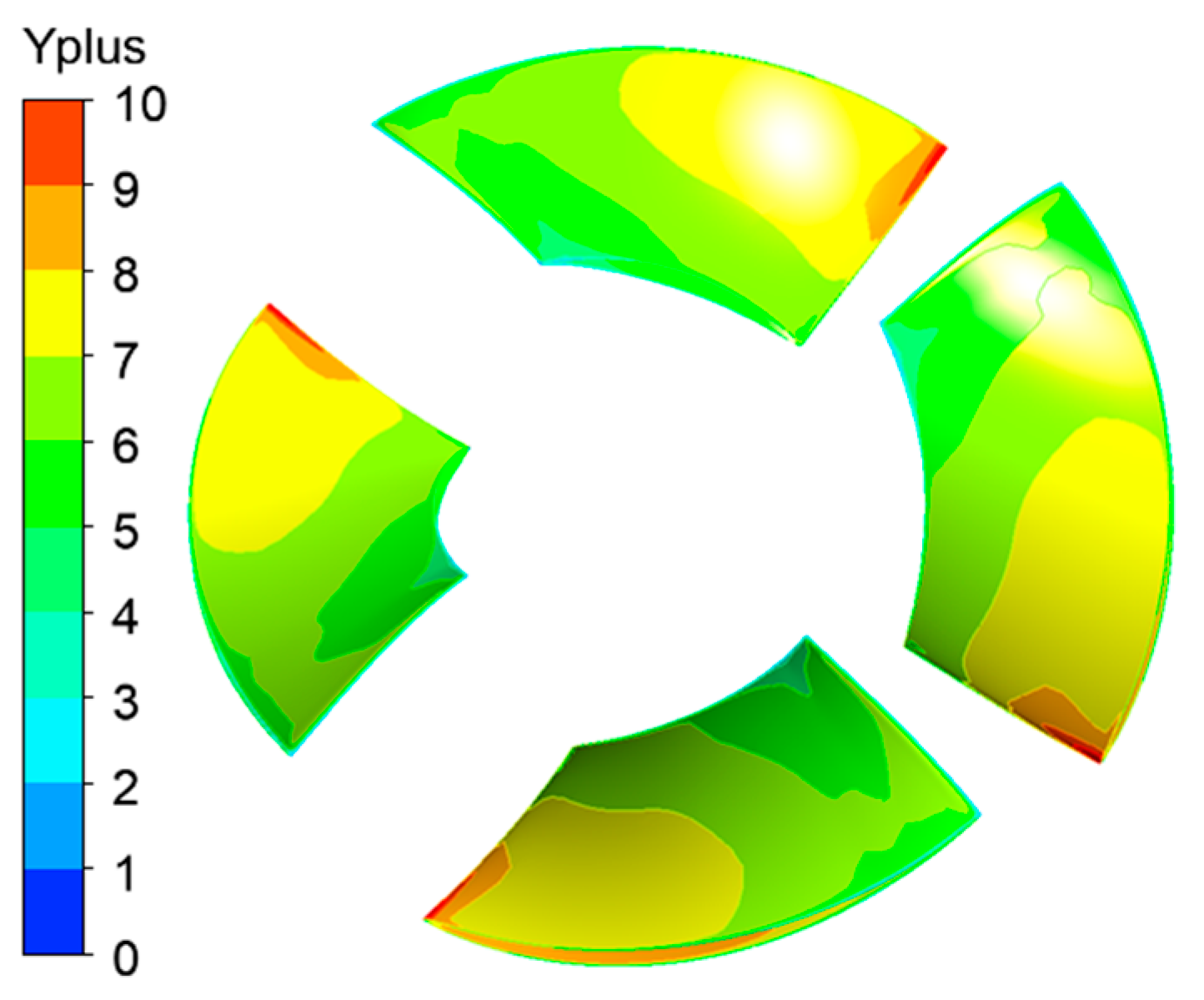
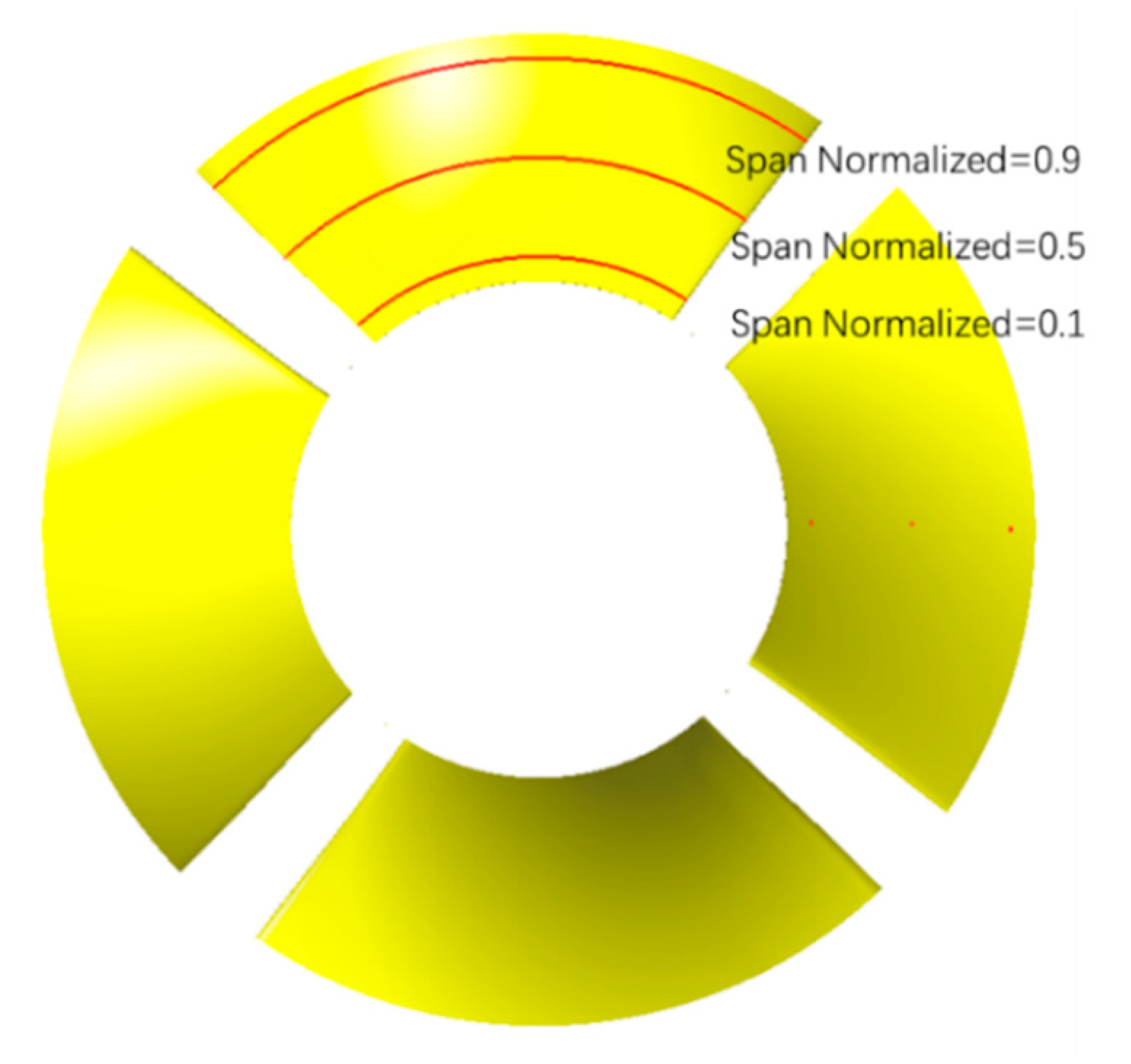
2.3. Grid Division and Independence Analysis
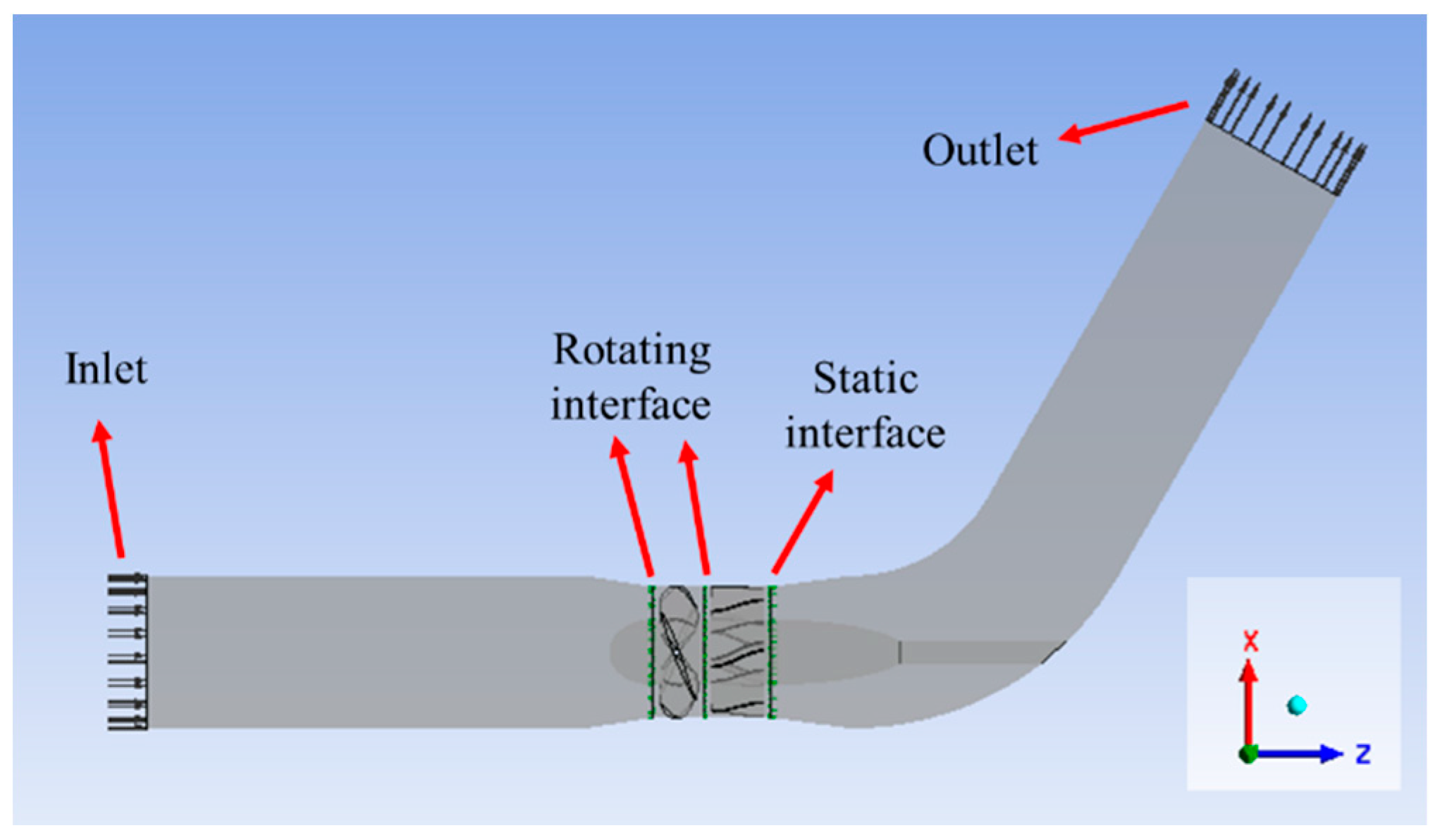
2.4. Boundary Condition Setting
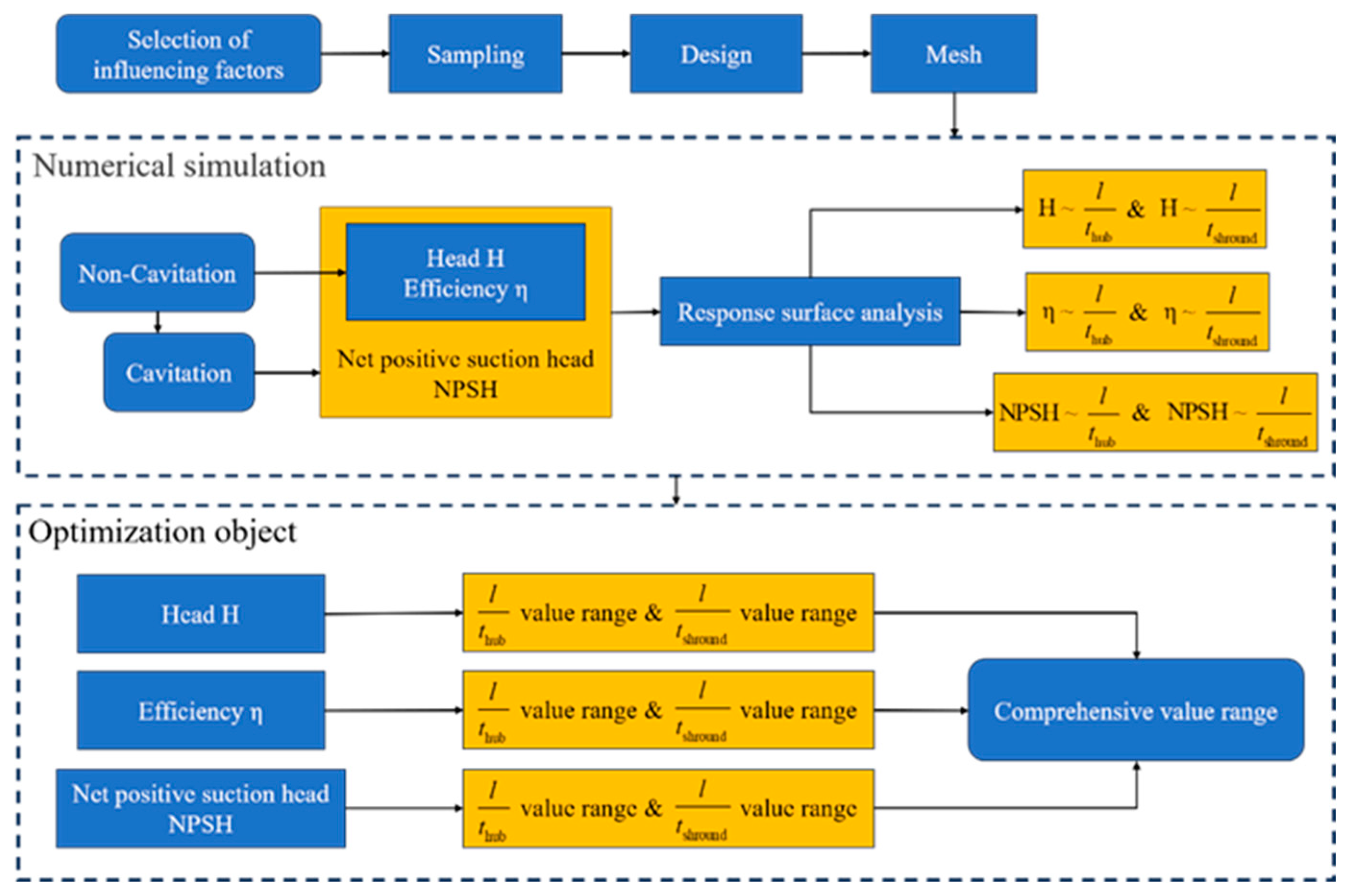
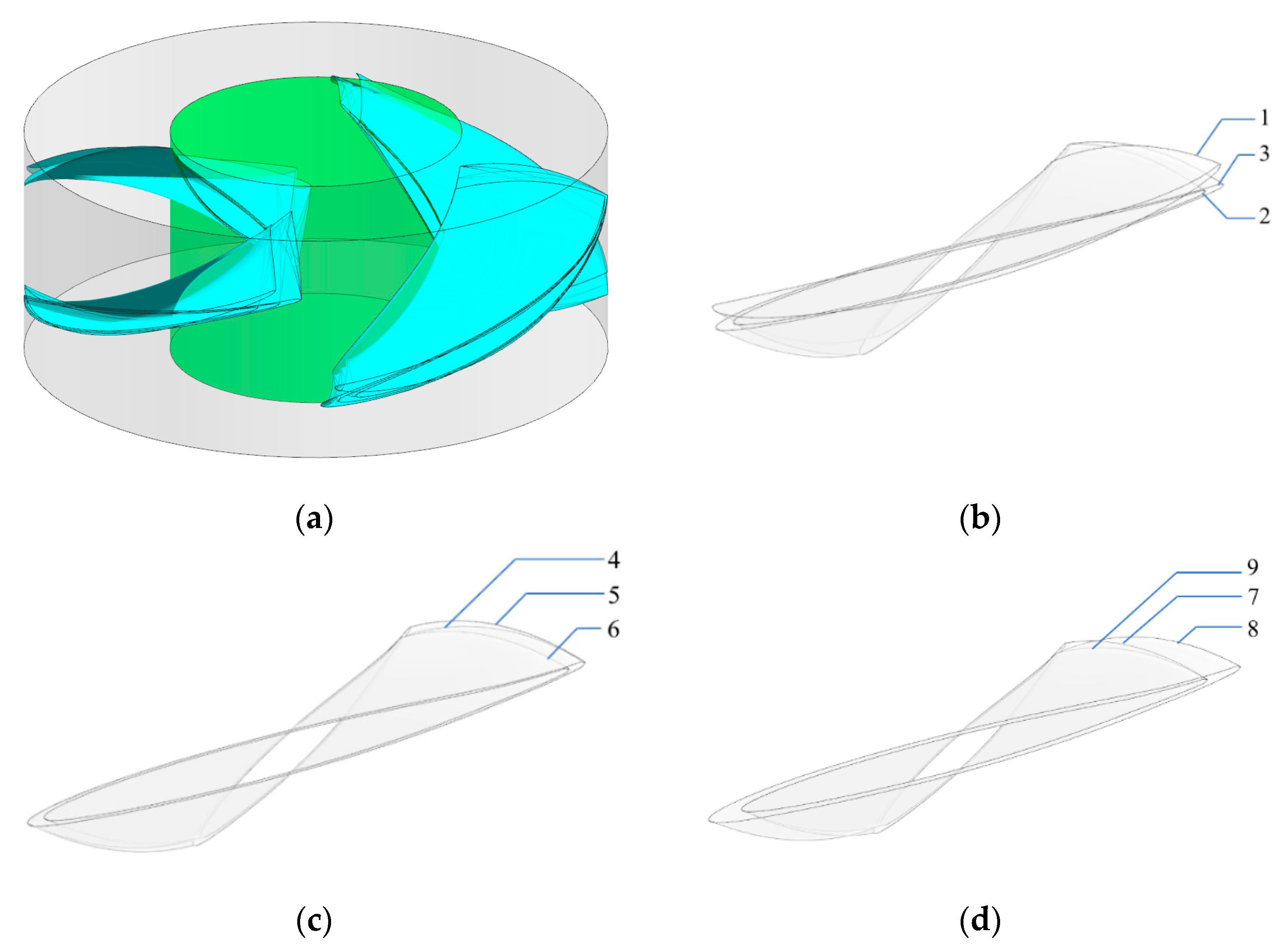
3. Scheme Design
4. Analysis of Calculation Results
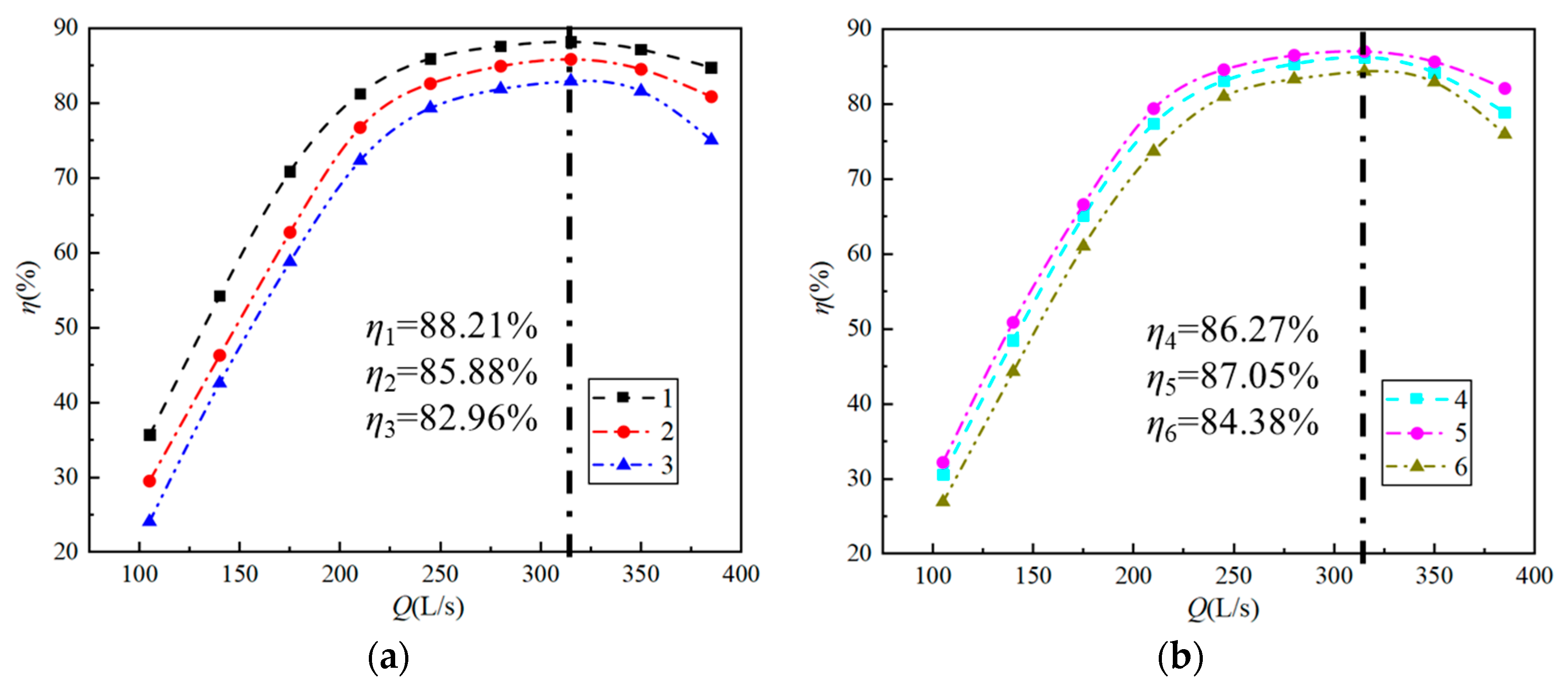
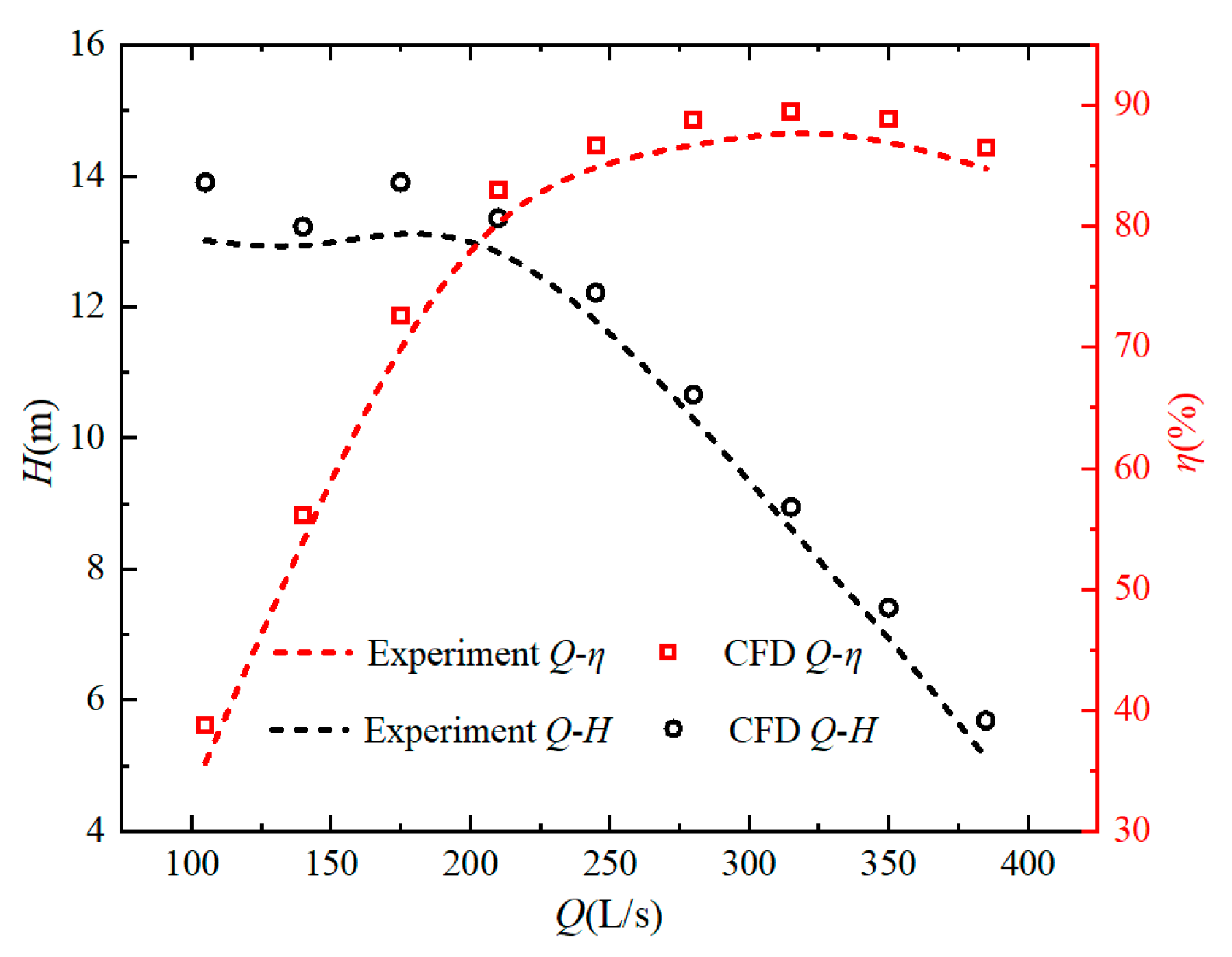
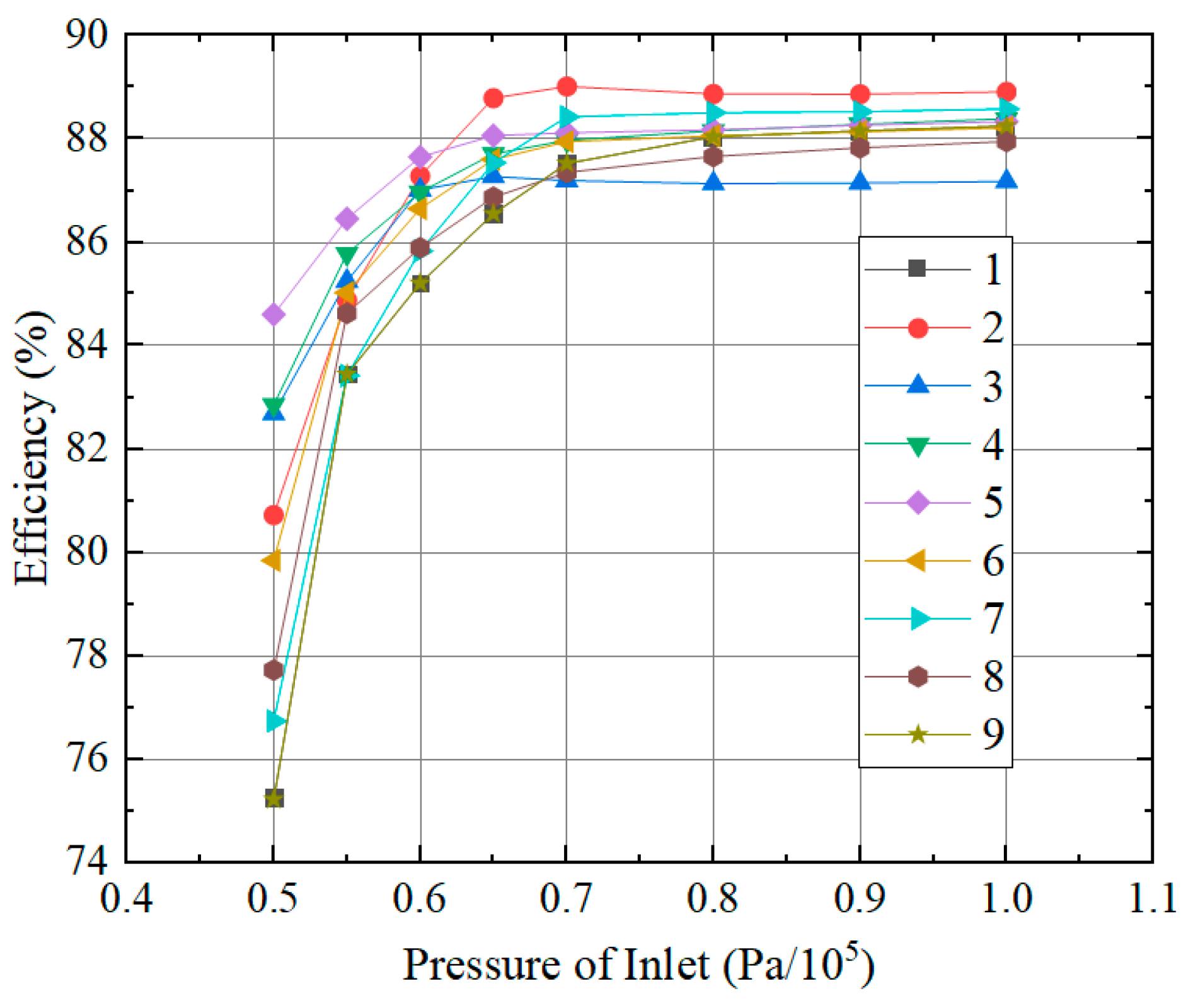
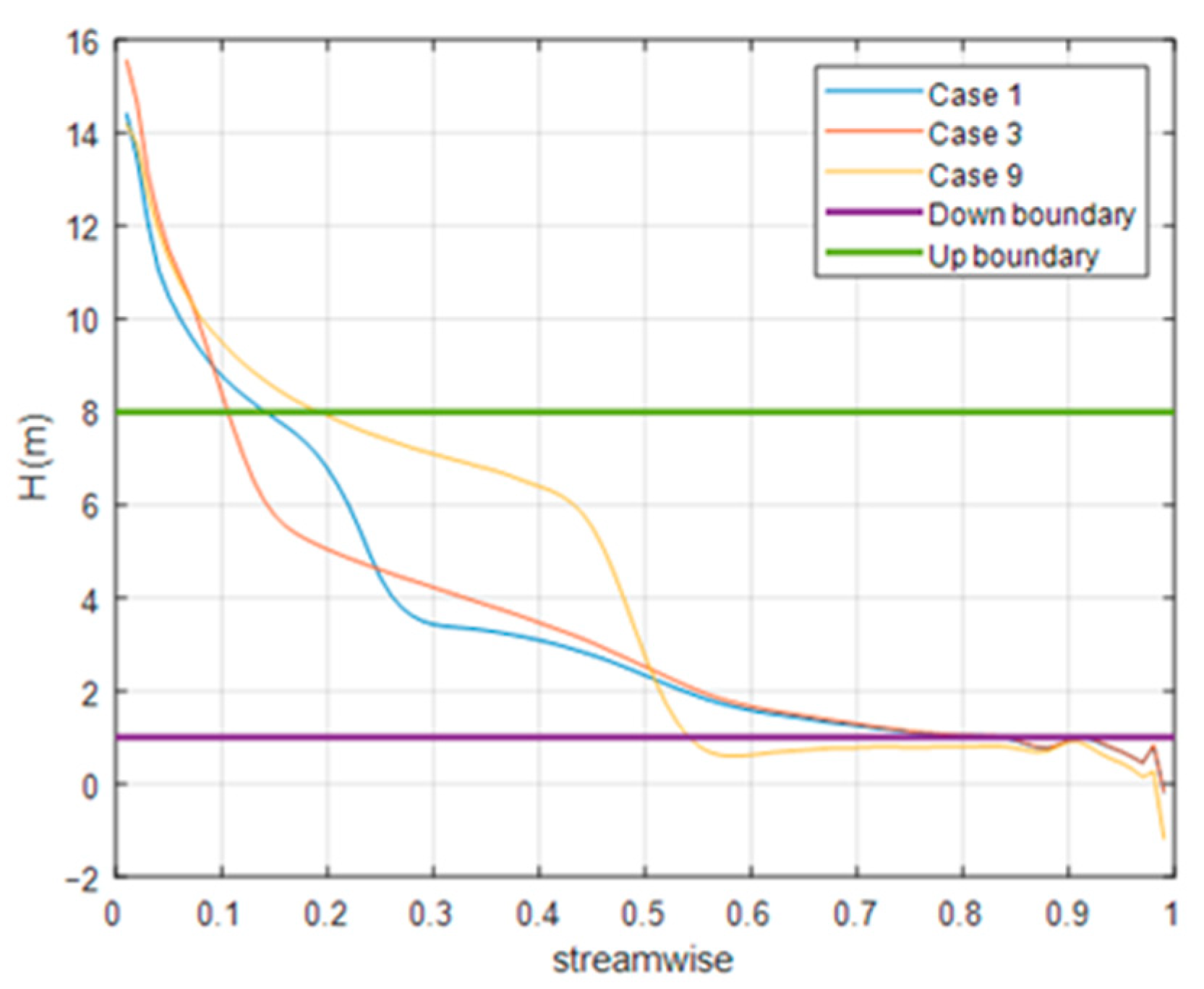
4.1. External Characteristic Analysis
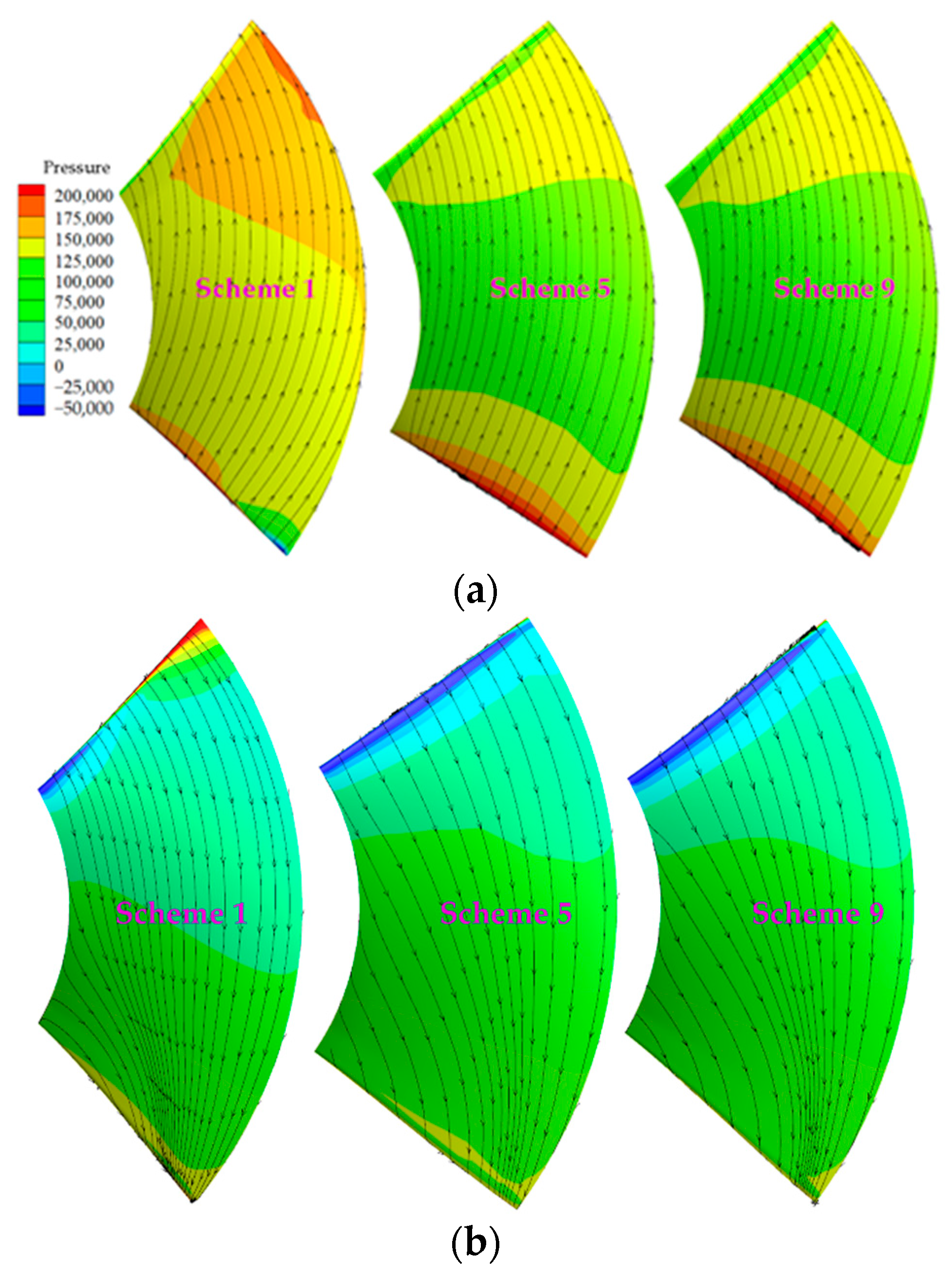
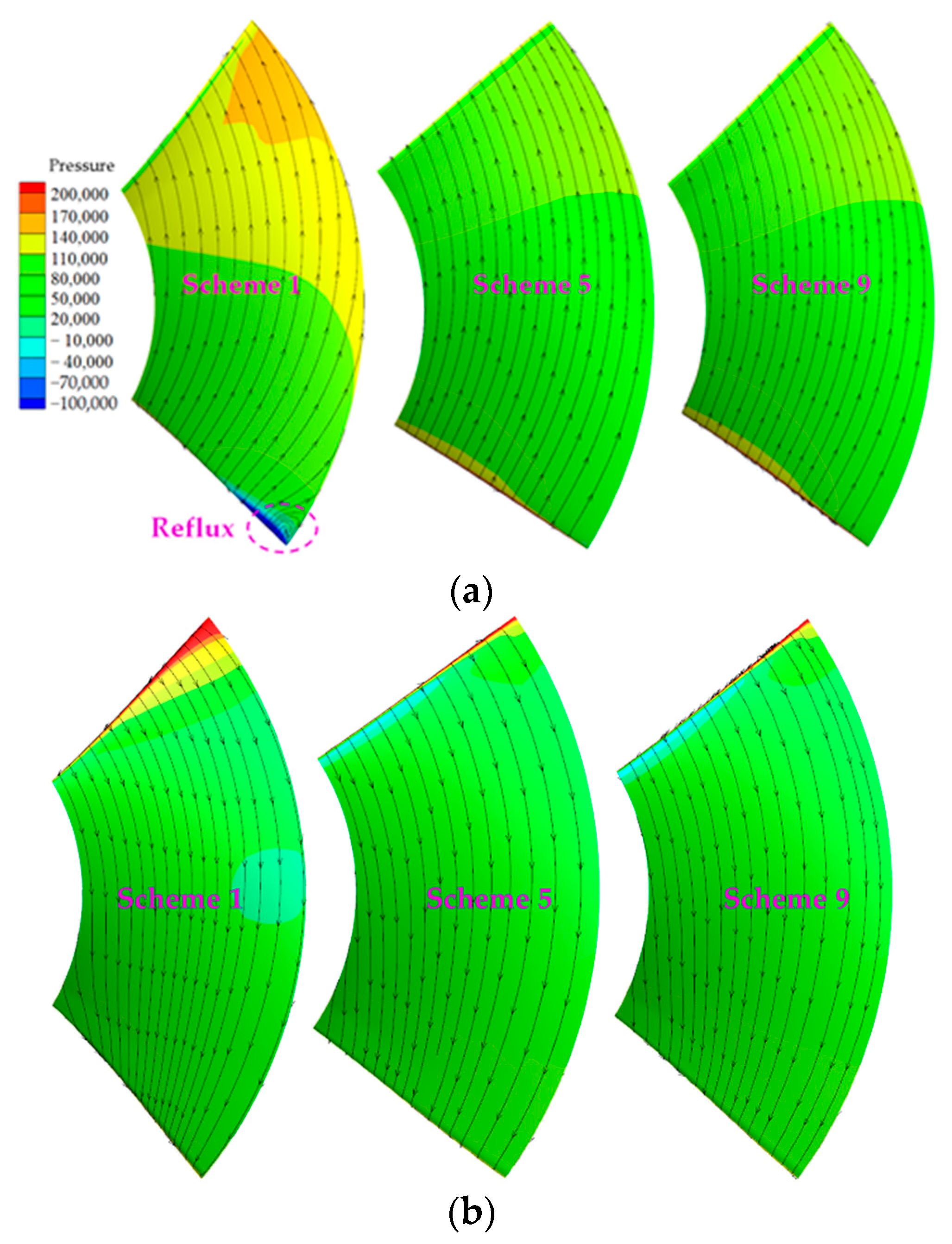
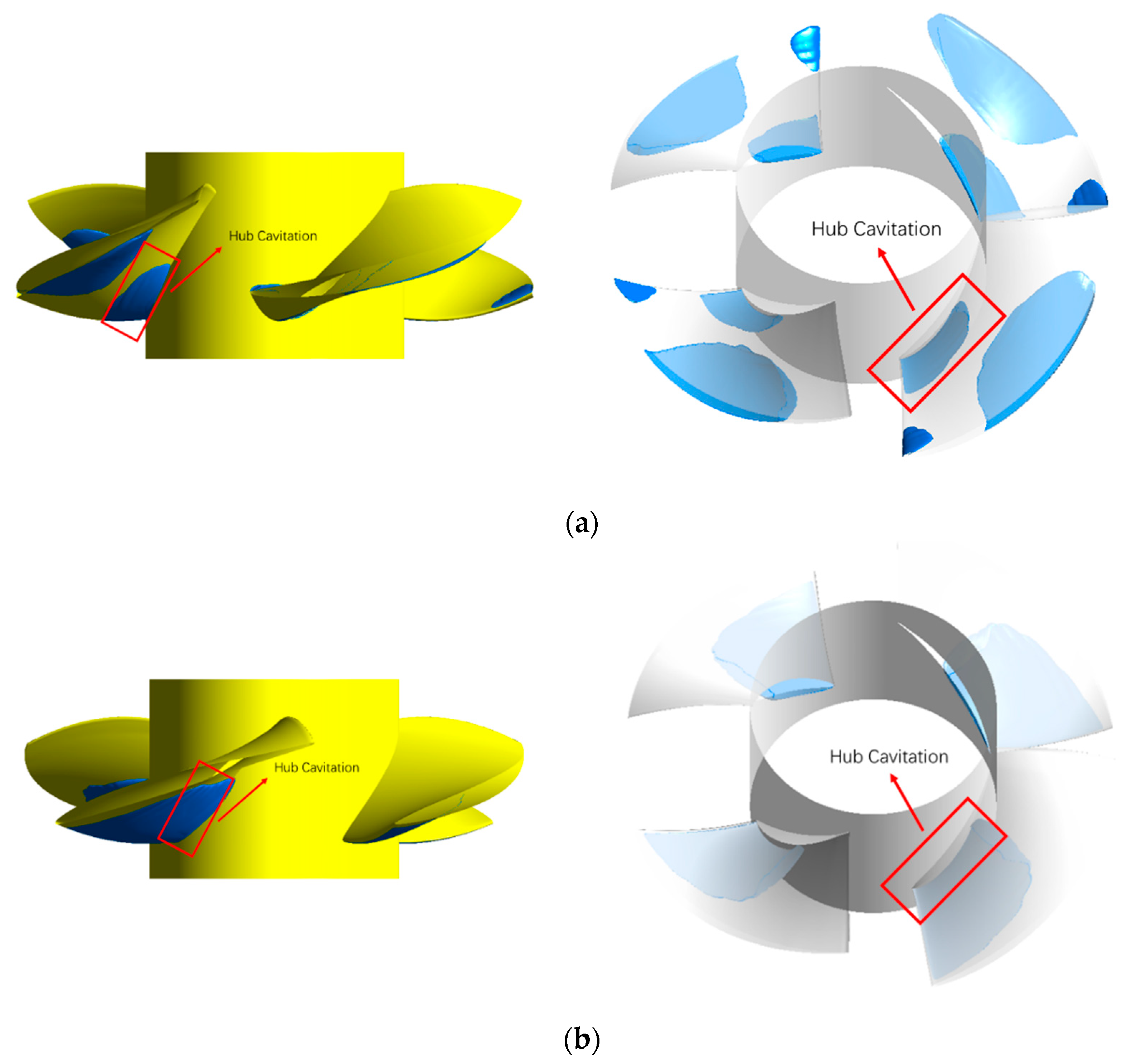
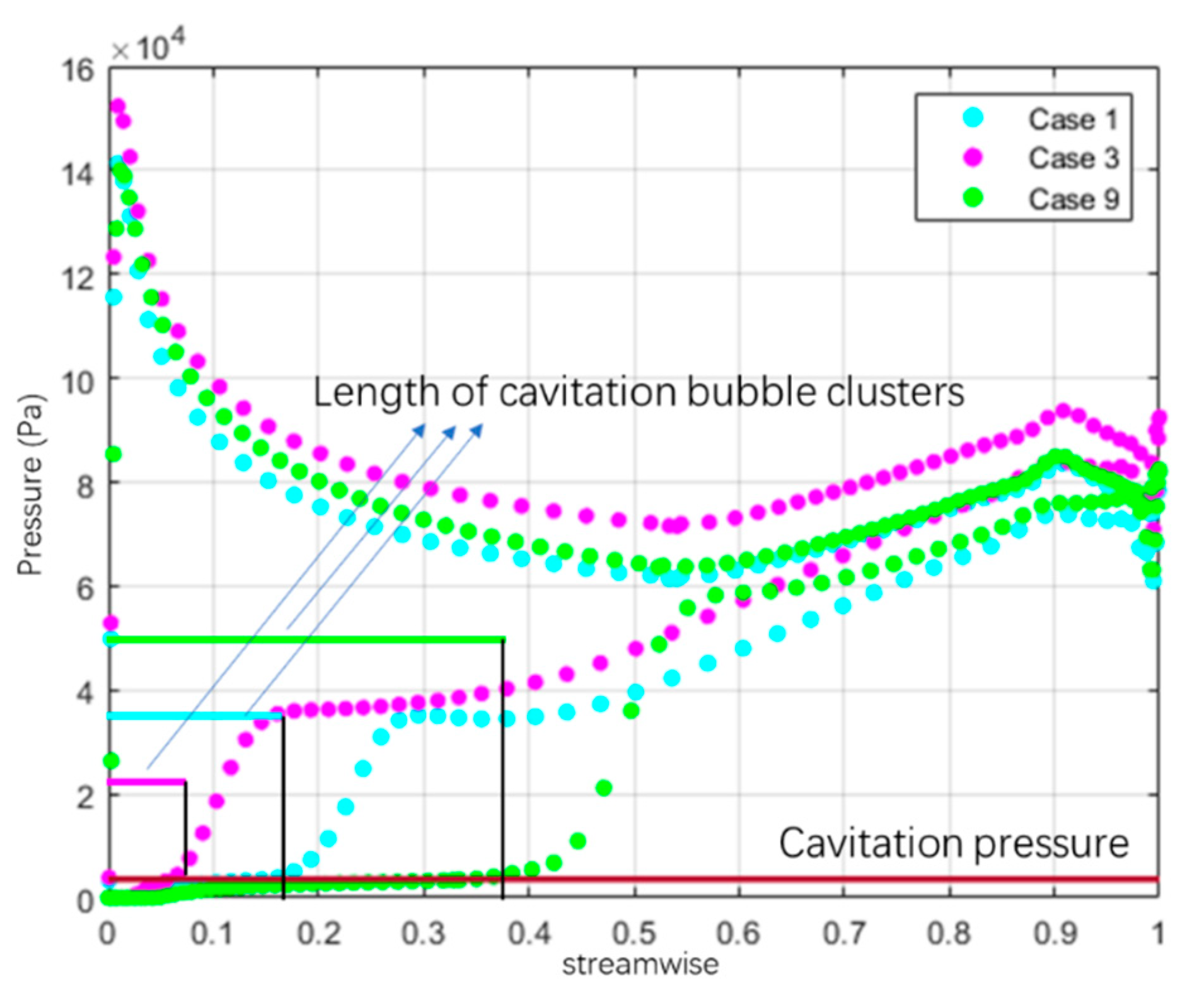
4.2. Flow Analysis
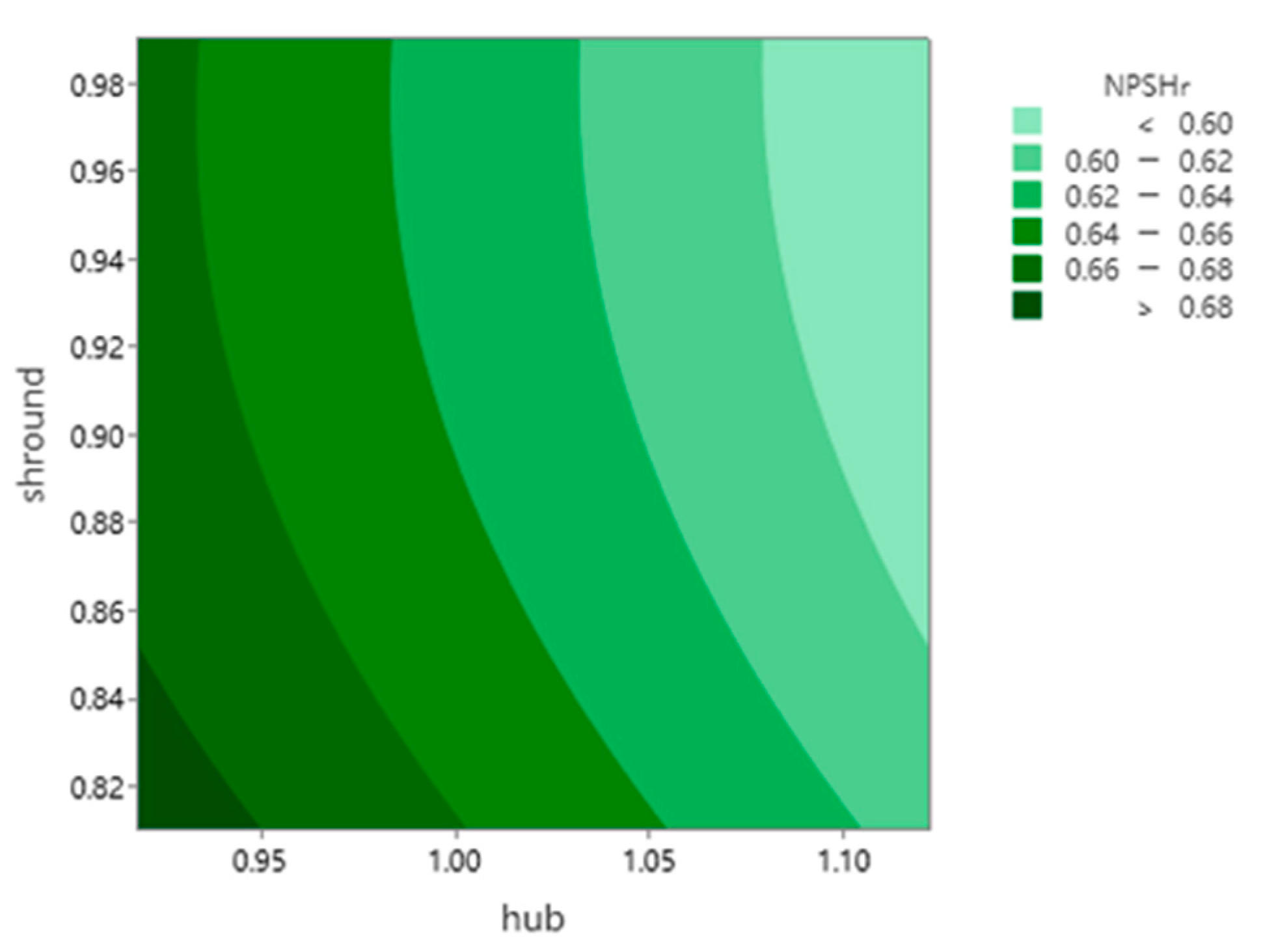
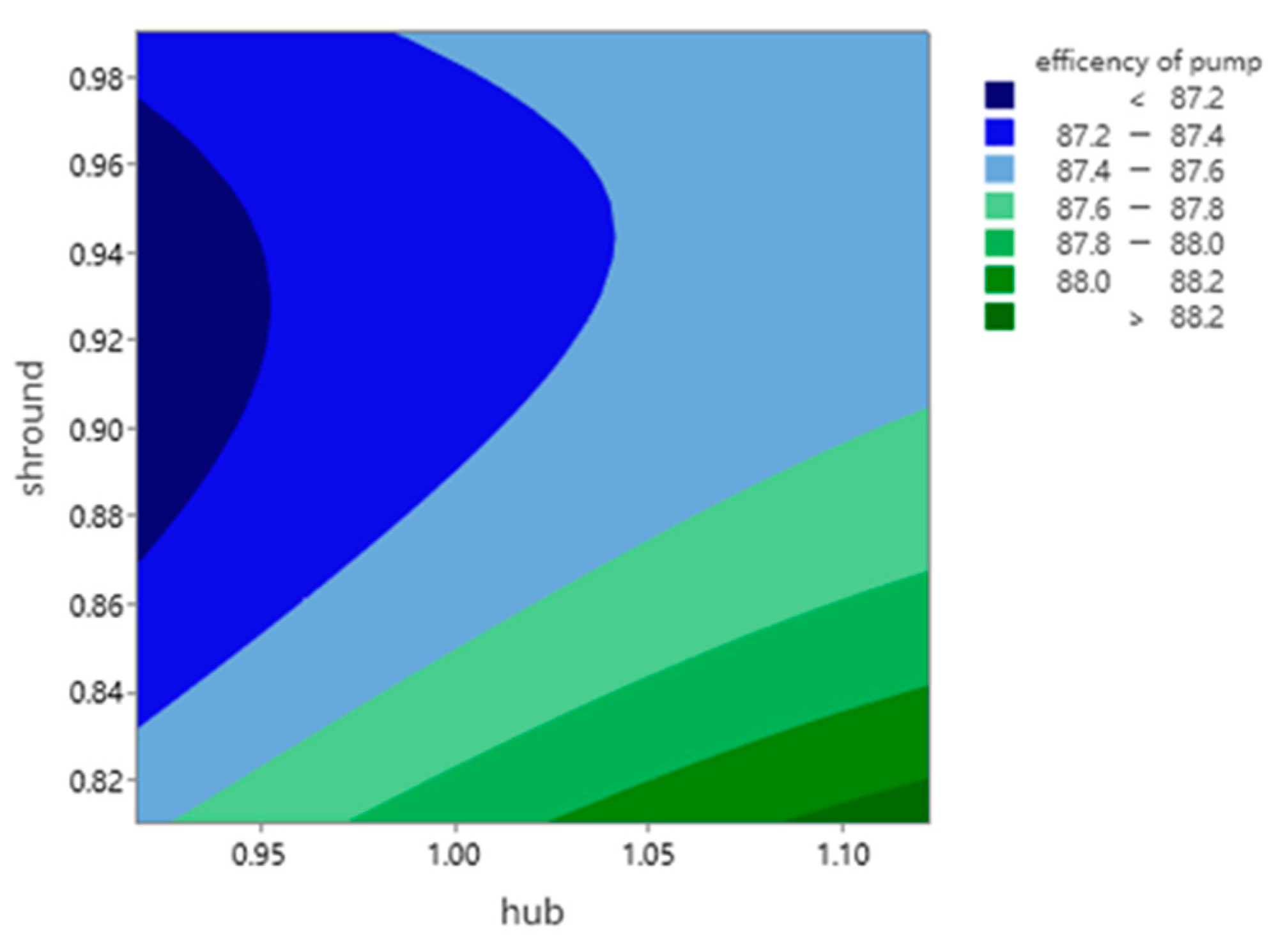
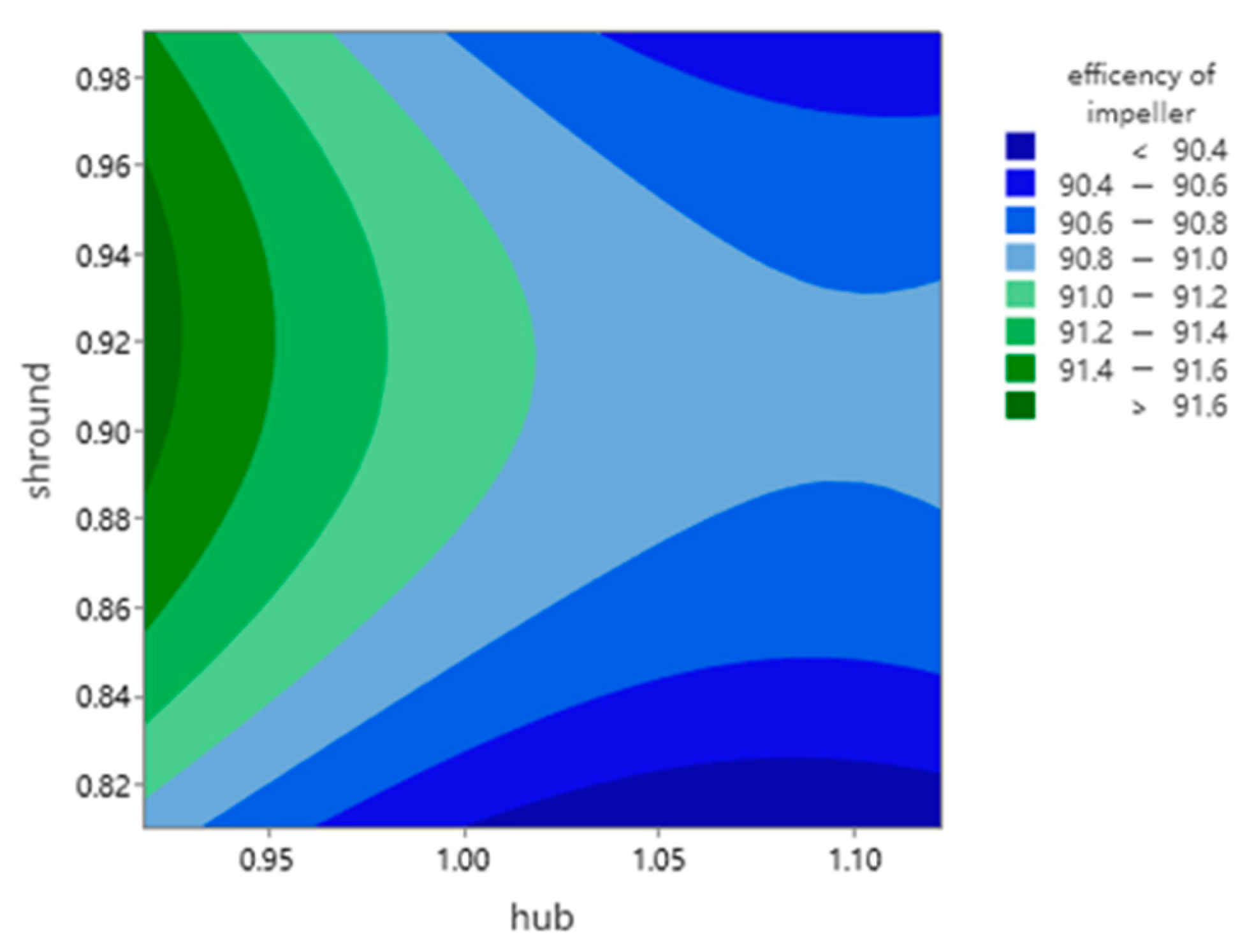
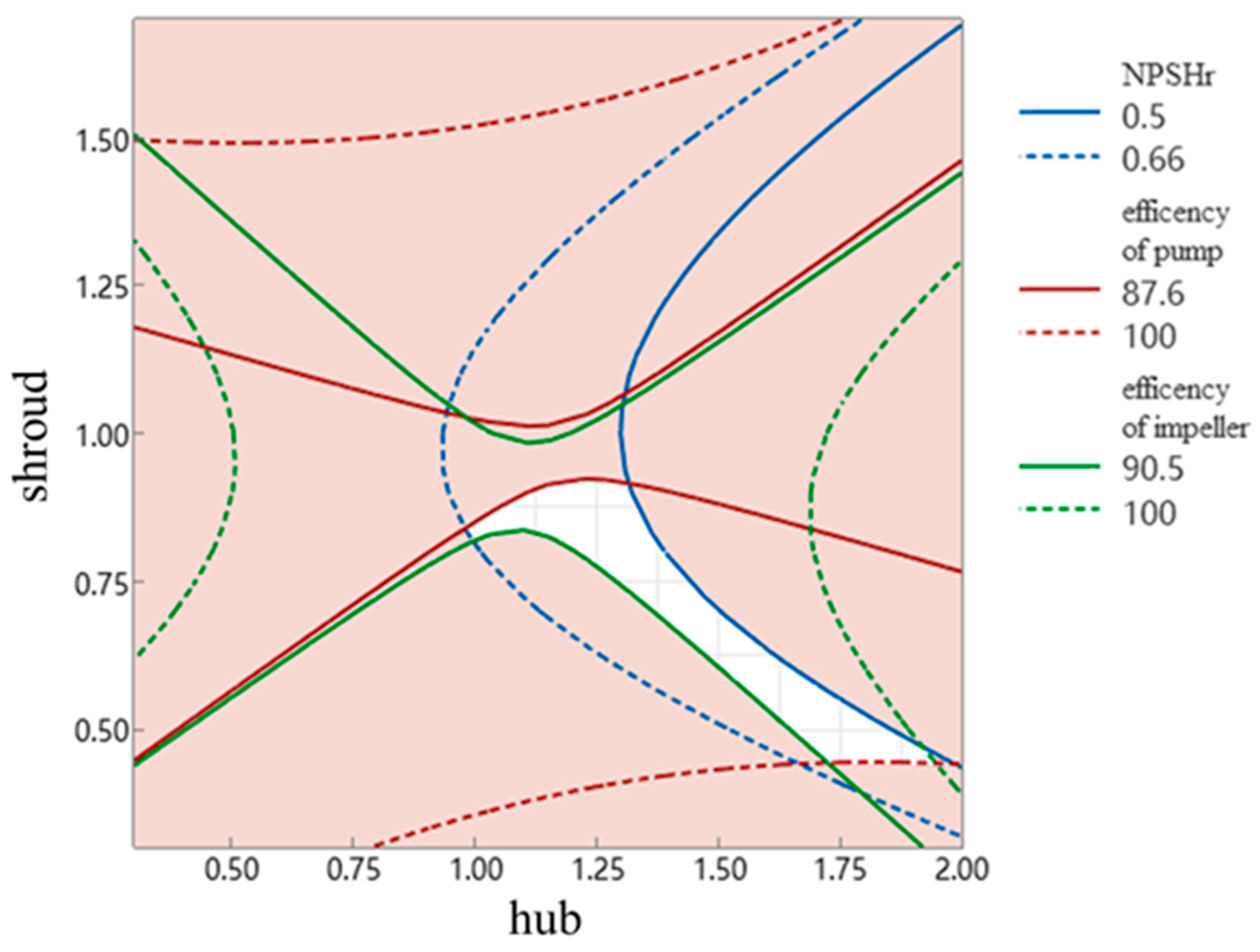
5. Optimization Analysis
6. Conclusions
- (1)
- The influence of cascade density on the hydraulic performance and cavitation performance of an axial flow pump section is analyzed by CFD numerical simulation. The accuracy of numerical simulation is ensured by grid independence analysis. The hydraulic characteristics and cavitation characteristics of a three-dimensional twisted hydrofoil under different cascade densities are analyzed;
- (2)
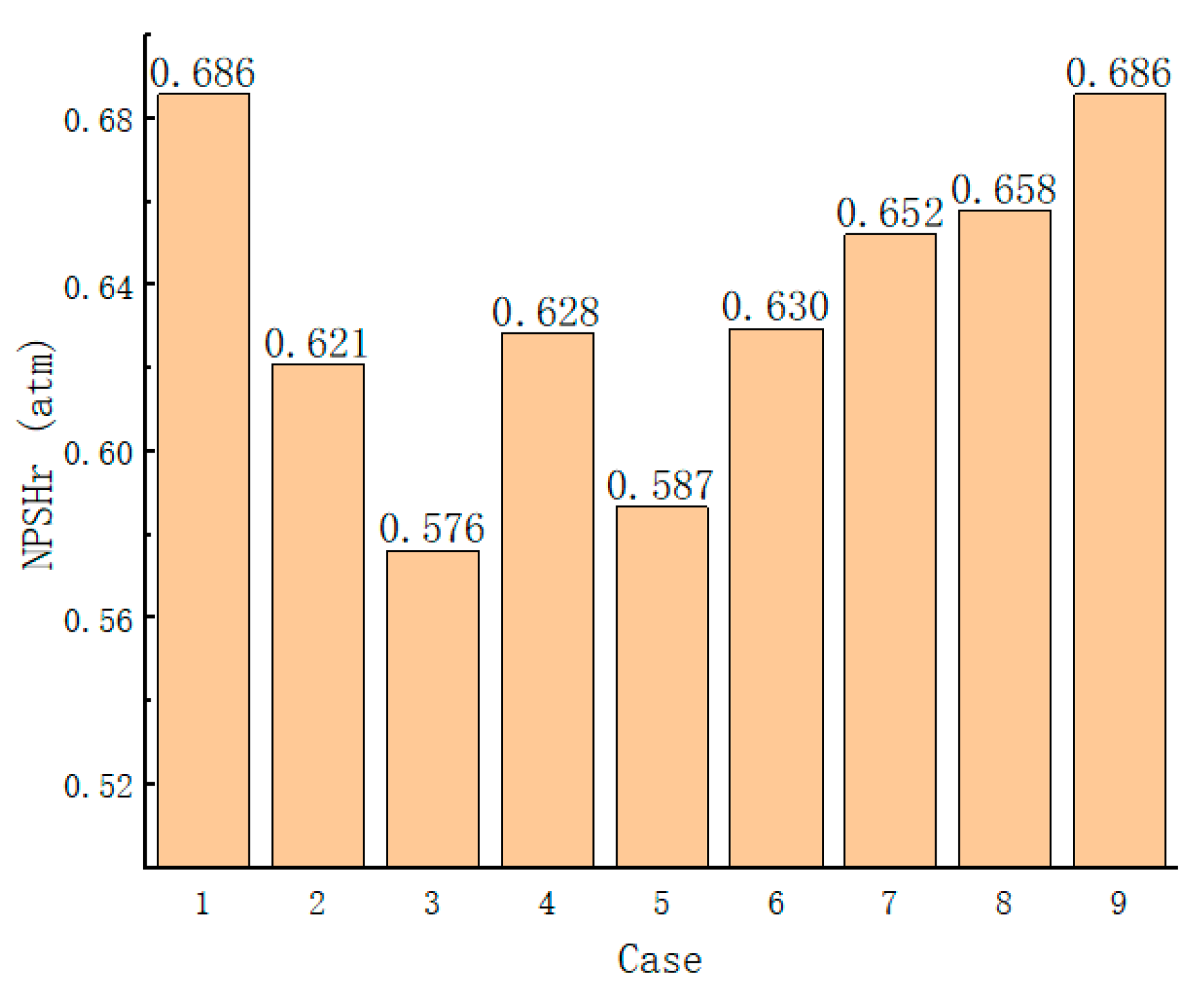
- From the perspective of flow pattern and external characteristics, the impeller flow pattern of scheme 1 is the best under small flow condition and design condition. However, under the condition of large flow rate, the impeller flow state of scheme 5 and scheme 9 is better; from the perspective of cavitation, the density of the cascade at the hub has a great influence on the cavitation performance. Especially when the density of the cascade at the hub is small, the lift coefficient is high, resulting in too large a flow velocity and too small a pressure, which is prone to cause cavitation;
- (3)
- Through the method of response surface analysis, the effective response surface of a single target parameter and cascade density is obtained, and the influence of cascade density on a three-dimensional hydrofoil is analyzed. According to the corresponding range of comprehensive target parameters, the range of cascade density of the comprehensive target parameters is obtained.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, Z.L.; You, B.G.; Lu, R. Study on effects of impact angle and cascade density on internal flow characteristics of axial flow pump. Pump Technol. 2022, 6, 23–26. [Google Scholar]
- Ning, C.; Yuan, S.Q.; Li, Y.; Xu, H.; Zheng, F. Influence of blade number on flow field in compound impeller with same cascade density. J. Mech. Eng. 2022, 58, 320–327. [Google Scholar]
- Lin, Y.; Kadivar, E.; el Moctar, O.; Neugebauer, J.; Schellin, T.E. Experimental investigation on the effect of fluid–structure interaction on unsteady cavitating flows around flexible and stiff hydrofoils. Phys. Fluids 2022, 34, 083308. [Google Scholar] [CrossRef]
- Zhang, H.-S.; Guo, Z.-P.; Wu, Q.; Zhang, H.-Z.; Wang, G.-Y. Experimental Investigation of fluid-structure interaction of composite hydrofoils in cavitating flow. J. Hydrodyn. 2022, 34, 207–213. [Google Scholar] [CrossRef]
- Podnar, A.; Hočevar, M.; Novak, L.; Dular, M. Analysis of bulb turbine hydrofoil cavitation. Appl. Sci. 2021, 11, 2639. [Google Scholar] [CrossRef]
- Custodio, D.; Henoch, C.; Johari, H. Cavitation on hydrofoils with leading edge protuberances. Ocean Eng. 2018, 162, 196–208. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, J.; Yu, S.; Mou, C.; Li, Z.; He, C.; Wu, D.; Mou, J.; Ren, Y. Unsteady numerical simulation method of hydrofoil surface cavitation. Int. J. Mech. Sci. 2022, 228, 107490. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wu, Q.; Yao, Z.; Huang, B.; Wang, G. Bend-twist coupling effects on the cavitation behavior and hydroelastic response of composite hydrofoils. Int. J. Multiph. Flow 2023, 158, 104286. [Google Scholar] [CrossRef]
- Park, K.; Sun, H.; Lee, S. The effect of leading-edge droop on the performance of cavitating hydrofoil in an oscillating environment. J. Mech. Eng. Sci. 2009, 223, 2331–2339. [Google Scholar] [CrossRef]
- Conesa, F.R.; Liem, R.P. Slotted hydrofoil design optimization to minimize cavitation in amphibious aircraft application: A numerical simulation approach. Adv. Aircr. Spacecr. Sci. 2020, 7, 309. [Google Scholar]
- Dular, M.; Bachert, R.; Schaad, C.; Stoffel, B. Investigation of a re-entrant jet reflection at an inclined cavity closure line. Eur. J. Mech.-B/Fluids 2007, 26, 688–705. [Google Scholar] [CrossRef]
- Ghadimi, A.; Ghassemi, H. Comparative assessment of hydrodynamic performance of two-dimensional Naca0012 and Naca6612 hydrofoils under different cavitation and non-cavitation conditions. Int. J. Hydromechatronics 2020, 3, 349. [Google Scholar] [CrossRef]
- Zhi, Y.; Huang, R.; Qiu, R.; Wang, Y.; Huang, C. LES investigation into the cavity shedding dynamics and cavitation–vortex interaction around a surface-piercing hydrofoil. Phys. Fluids 2022, 34, 123314. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Q.; Tang, T.; Lu, S.; Yi, Q.; Wang, X. Numerical study of the impact of water injection holes arrangement on cavitation flow control. Sci. Prog. 2020, 103, 273–328. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Dong, S.; Liu, Y.; Huang, H.; Zhang, G. Physical investigation of transient dynamic behaviors of cavitation-induced vibration over a flexible hydrofoil. Phys. Fluids 2021, 33, 113303. [Google Scholar] [CrossRef]
- Gao, Y.; Li, W.; Ji, L.; Cao, W.; Chen, Y. Optimization Design of Centrifugal Pump Auxiliary Blades Based on Orthogonal Experiment and Grey Correlation Analysis. Water 2023, 15, 2465. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, W.; Hang, J.; Shi, W.; Yan, H.; Zhu, Y. Numerical Investigation of a High-Speed Electrical Submersible Pump with Different End Clearances. Water 2020, 12, 1116. [Google Scholar] [CrossRef]
- Feng, H.M. Water Pump; Water Power Press: Zhengzhou, Henan, 1991. [Google Scholar]
- Ben, S.M.; Heyd, B.; Danzart, M.; Ducauze, C.J. D-optimal designs: An approach to reduce the number of products in preference mapping. Sci. Aliment. 1998, 18, 471–483. [Google Scholar]
- Balaji, D.; Vetrivel, M.; Ekambaram, M. Optimization of Wear Reduction on Al–TiO2–Gr Powder Metallurgy Composites Using D-Optimal Method. J. Hydrodyn. 2020, 7, 667–674. [Google Scholar]
- Peter, J.; Lars, D. A Full Multigrid Method Applied to Turbulent Flow using the SIMPLEC Algorithm Together with a Collocated Arrangement. J. Hydrodyn. 1994, 116, 245–256. [Google Scholar]
- De Giorgi, M.G.; Ficarella, A.; Fontanarosa, D. Numerical investigation of nonisothermal cavitating flows on hydrofoils by means of an extended Schnerr-Sauer model coupled with a nucleation model. J. Eng. Gas Turbines Power 2020, 142, 041003. [Google Scholar] [CrossRef]
- Zhai, Z.; Chen, T.; Li, H. Evaluation of mass transport cavitation models for unsteady cavitating flows. Mod. Phys. Lett. B 2020, 34, 2050020. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, L.-J.; Wang, Z.-W.; Jiang, X.-Y.; Zhou, X.-J.; Ding, J.-H.; Han, W.-F. Numerical investigation of the cavitation dynamic parameters in a Francis turbine draft tube with columnar vortex rope. J. Hydrodyn. 2019, 31, 931–939. [Google Scholar] [CrossRef]
- Han, C.-Z.; Xu, S.; Cheng, H.-Y.; Ji, B.; Zhang, Z.-Y. LES method of the tip clearance vortex cavitation in a propelling pump with special emphasis on the cavitation-vortex interaction. J. Hydrodyn. 2020, 32, 1212–1216. [Google Scholar] [CrossRef]
- Moghaddam, A.H.; Kutschelis, B.; Holz, F.; Börjesson, T.; Skoda, R. Three-dimensional flow simulation of a twin-screw pump for the analysis of gap flow characteristics. J. Fluids Eng. 2022, 144, 031202. [Google Scholar] [CrossRef]





| Samples | Hub | Shroud |
|---|---|---|
| 1 | 0.918 | 0.900 |
| 2 | 1.122 | 0.810 |
| 3 | 1.122 | 0.900 |
| 4 | 1.020 | 0.990 |
| 5 | 1.122 | 0.990 |
| 6 | 1.020 | 0.900 |
| 7 | 1.020 | 0.810 |
| 8 | 0.918 | 0.990 |
| 9 | 0.918 | 0.810 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Cheng, L. Study on Cascade Density of the Impeller Based on Response Surface Analysis. Water 2023, 15, 4101. https://doi.org/10.3390/w15234101
Gao M, Cheng L. Study on Cascade Density of the Impeller Based on Response Surface Analysis. Water. 2023; 15(23):4101. https://doi.org/10.3390/w15234101
Chicago/Turabian StyleGao, Mengxing, and Li Cheng. 2023. "Study on Cascade Density of the Impeller Based on Response Surface Analysis" Water 15, no. 23: 4101. https://doi.org/10.3390/w15234101
APA StyleGao, M., & Cheng, L. (2023). Study on Cascade Density of the Impeller Based on Response Surface Analysis. Water, 15(23), 4101. https://doi.org/10.3390/w15234101






