Exploring Climate Sensitivity in Hydrological Model Calibration
Abstract
:1. Introduction
2. Materials and Methods
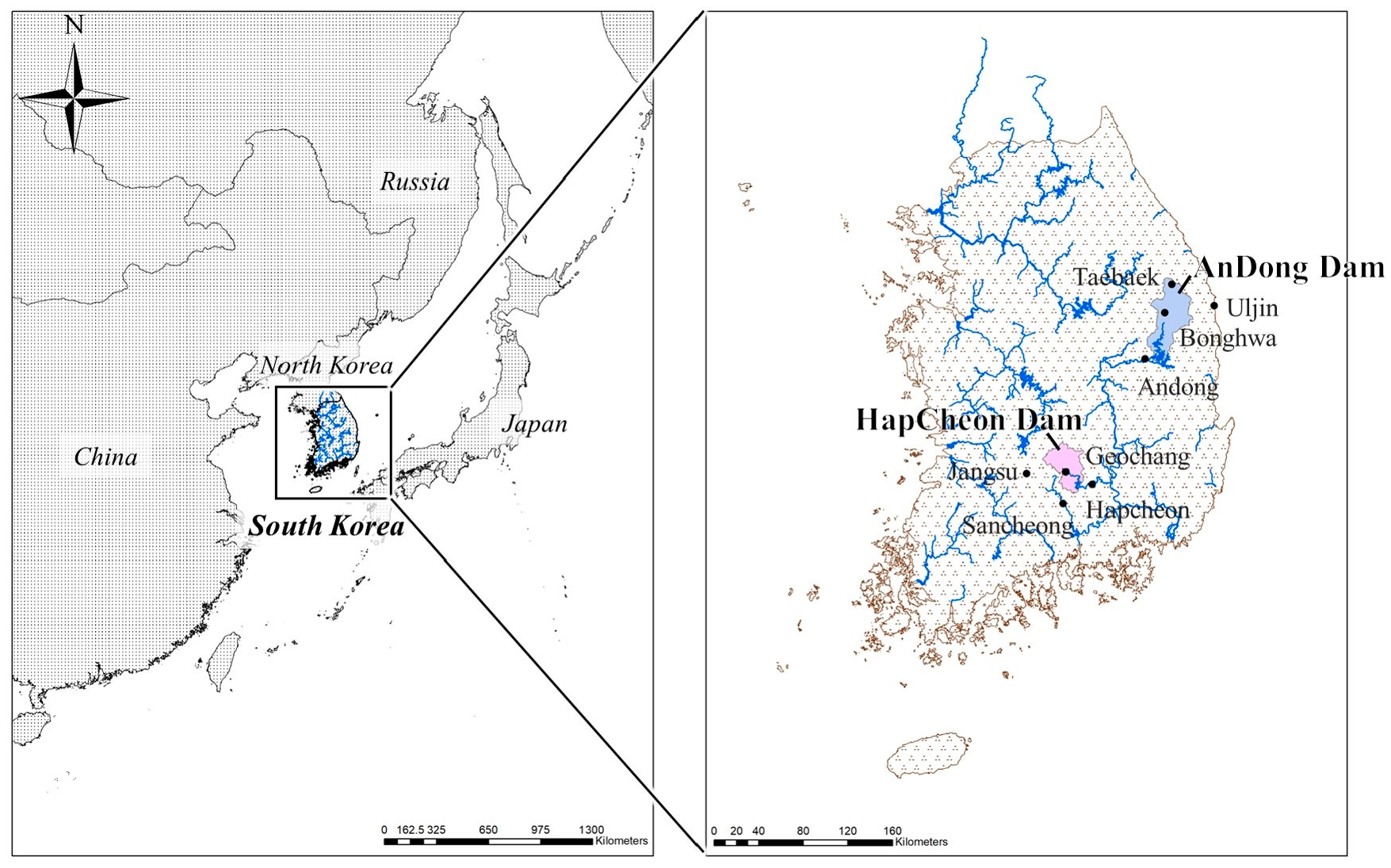
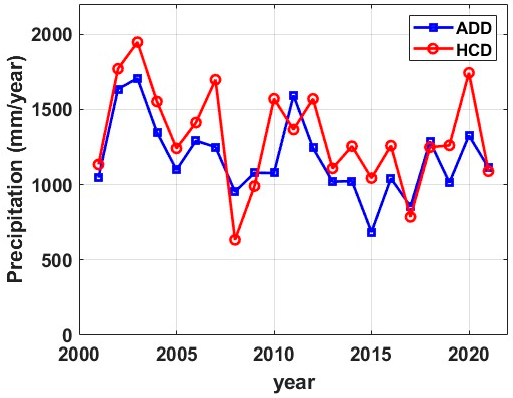
2.1. Study Area and Data
2.2. Conceptual Hydrologic Partitioning Model
2.3. Parameter Estimation Using Markov Chain Monte Carlo (MCMC) Technique
- (1)
- A candidate parameter is sampled from the proposal distribution
- (2)
- The adoption threshold value, Tc, is calculated.
- (3)
- If the uniform random number u between 0 and 1 satisfies the min(1, Tc) > u, it becomes ; otherwise, it becomes .
2.4. Model Predictive Performance Evaluation and Uncertainty Analysis
3. Results and Discussion
3.1. Segmentation of Hydrological Model Calibration and Validation Periods Based on Climatic Conditions
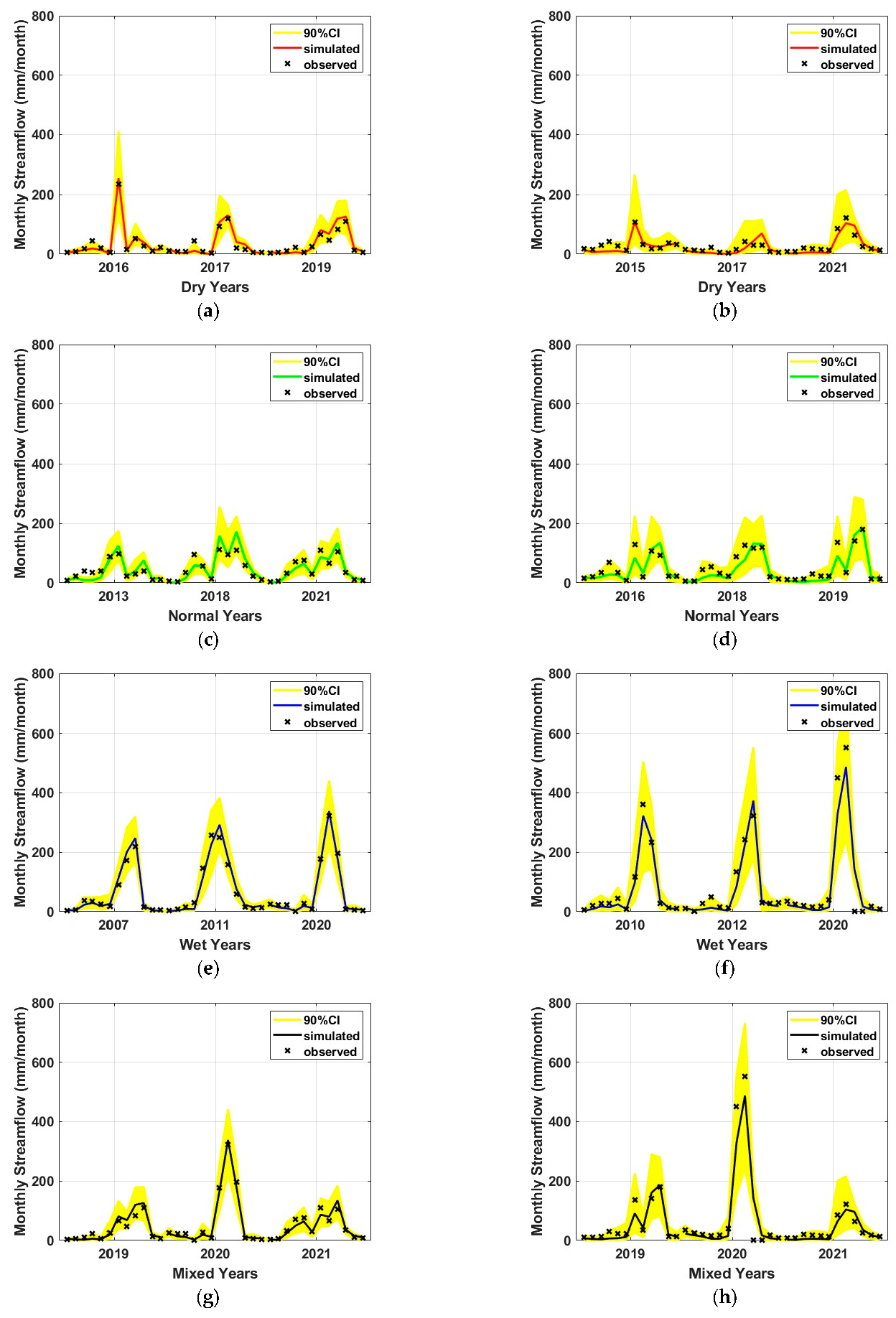
3.2. Calibration Results by Climatic Condition and Discussion
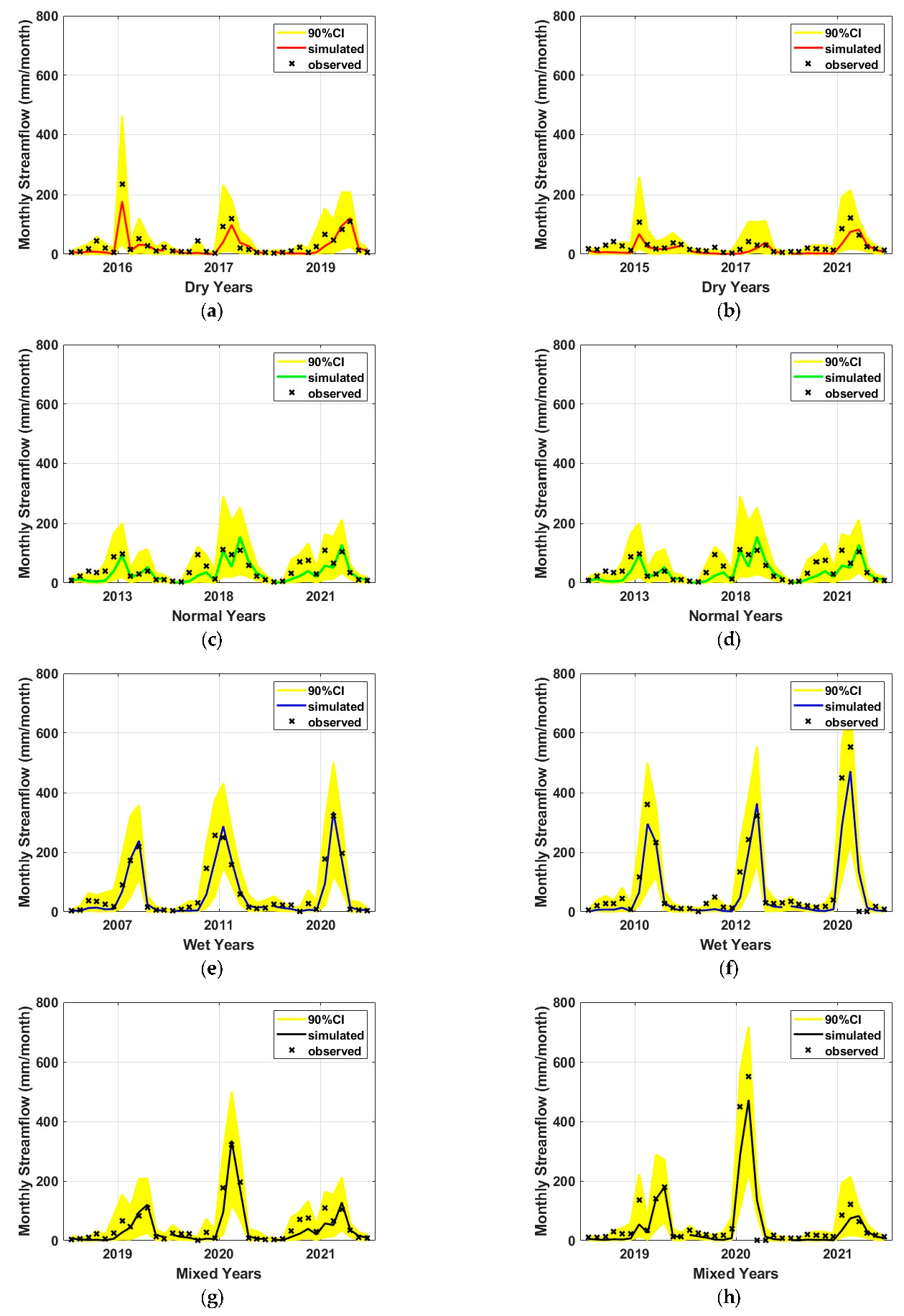
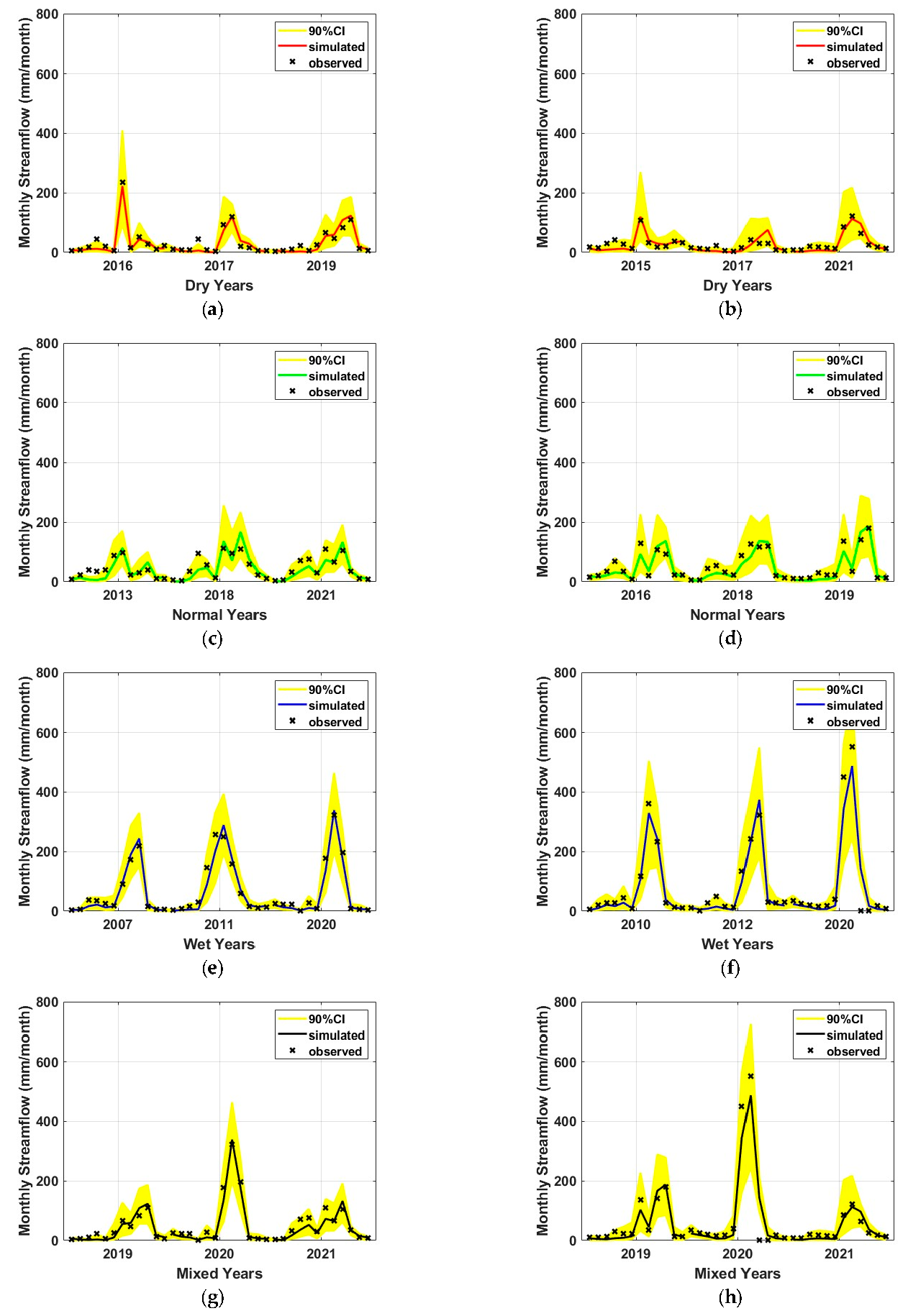
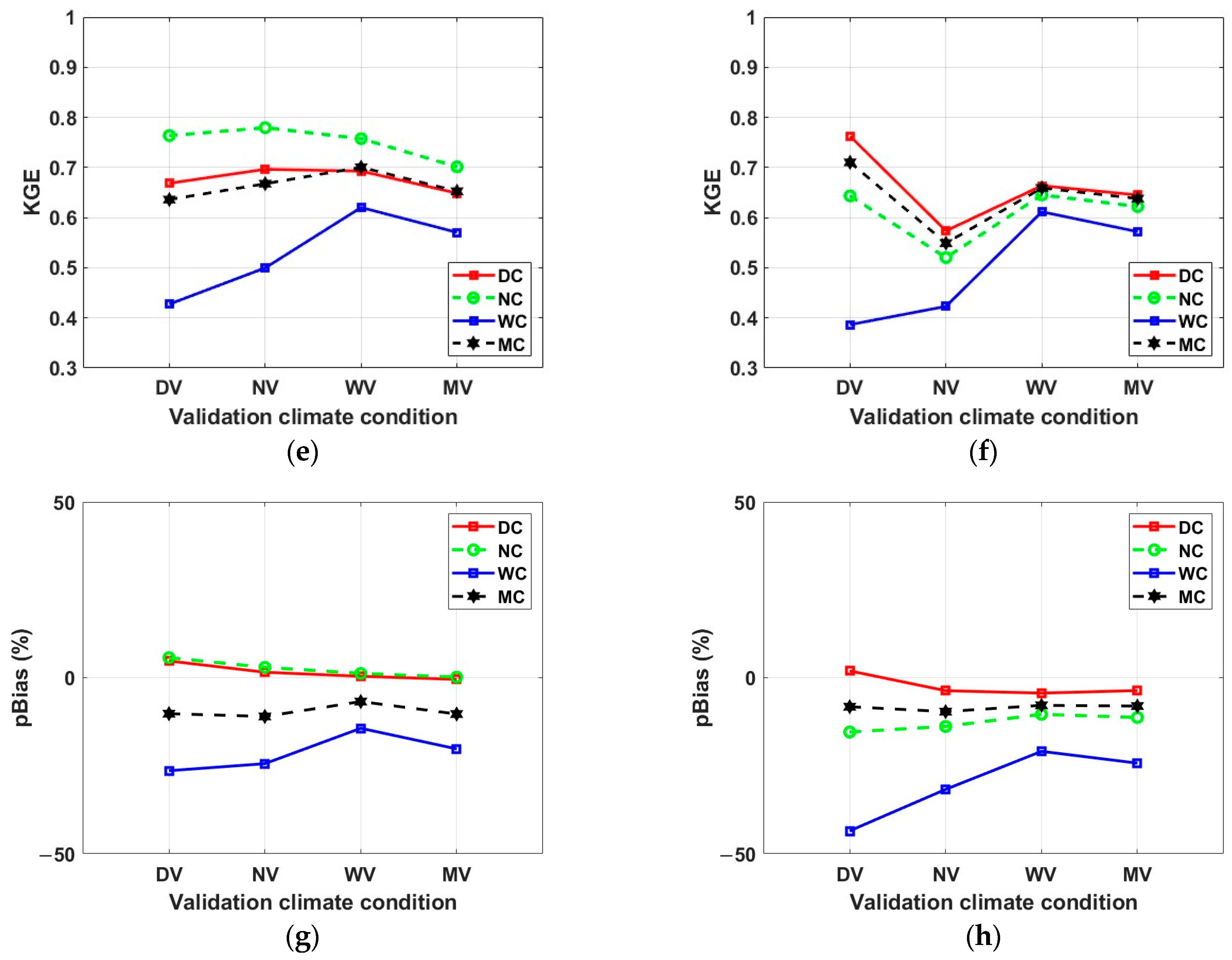
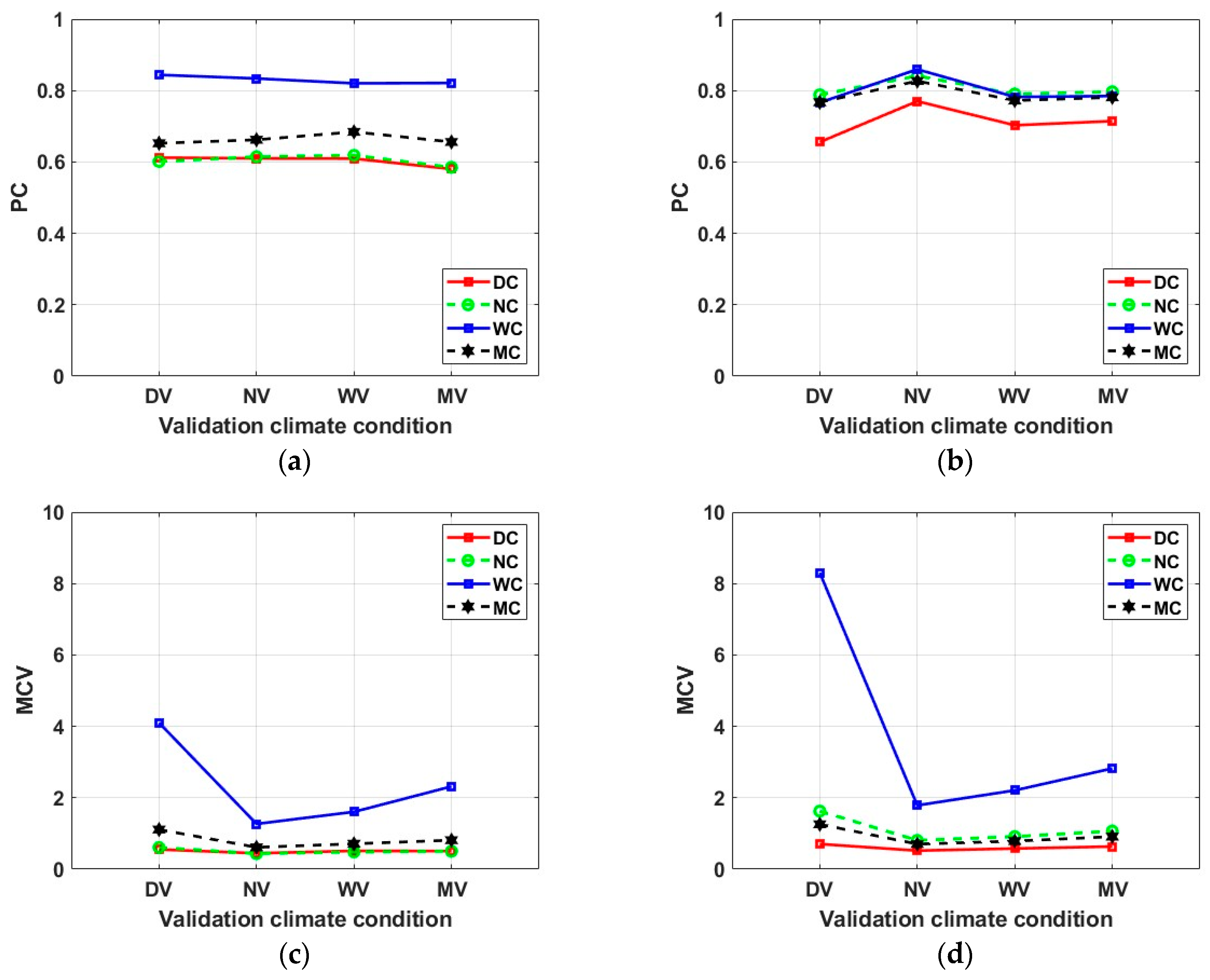
3.3. Validation Results by Climatic Condition and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of high streamflow extremes in climate change studies: How do we calibrate hydrological models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S.K. Robust estimation of hydrological model parameters. Hydrol. Earth Syst. Sci. 2008, 12, 1273–1283. [Google Scholar] [CrossRef]
- Kavetski, D.; Fenicia, F. Elements of a flexible approach for conceptual hydrological modeling: 2. Applications experimental insights. Water Resour. Res. 2011, 47, 1–19. [Google Scholar] [CrossRef]
- Singh, S.K.; Kanga, S.; Gulati, B.; Raič, M.; Sajan, B.; Đurin, B.; Singh, S. Spatial and Temporal Analysis of Hydrological Modelling in the Beas Basin Using SWAT + Model. Water 2023, 15, 3338. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Tu, Y.; Dong, R.; Ma, Q.; Liu, C. Research on Parameter Regionalization of Distributed Hydrological Model Based on Machine Learning. Water 2023, 15, 518. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.; Liu, J.; Yan, D.; Yu, F.; Zhang, L. Effect of calibration data series length on performance and optimal parameters of hydrological model. Water Sci. Eng. 2010, 3, 378–393. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.; Wang, D.; Zhang, X. Multi-period calibration of a semidistributed hydrological model based on hydroclimatic clustering. Adv. Water Resour. 2011, 34, 1292–1303. [Google Scholar] [CrossRef]
- Yen, H.; Wang, X.; Fontane, D.; Harmel, R.; Arabi, M. A framework for propagation of uncertainty contributed by parameterization, input data, model structure, and calibration/validation data in watershed modeling. Environ. Model. Softw. 2014, 54, 211–221. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Huang, G.; Chen, X.; Bao, A. Assessment of parameter uncertainty in hydrological model using a Markov-Chain-Monte-Carlo-based multilevel-factorial analysis method. J. Hydrol. 2016, 538, 471–486. [Google Scholar] [CrossRef]
- Beneyto, C.; Vignes, G.; Aranda, J.Á.; Francés, F. Sample Uncertainty Analysis of Daily Flood Quantiles Using a Weather Generator. Water 2023, 15, 3489. [Google Scholar] [CrossRef]
- Brown, I.; McDougall, K.; Chadalavada, S.; Alam, M.J. An Alternative Method for Estimating the Peak Flow for a Regional Catchment Considering the Uncertainty via Continuous Simulation. Water 2023, 15, 3355. [Google Scholar] [CrossRef]
- Motavita, D.; Chow, R.; Guthke, A.; Nowak, W. The comprehensive differential split-sample test: A stress-test for hydrological model robustness under climate variability. J. Hydrol. 2019, 573, 501–515. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gupta, V.; Fulton, J. Evaluation of maximum likelihood parameter estimation techniques for conceptual rainfall runoff models: Influence of calibration data variability and length on model credibility. Water Resour. Res. 1983, 19, 251–259. [Google Scholar] [CrossRef]
- Anctil, F.; Perrin, C.; Andreassian, V. Impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. Environ. Model. Softw. 2004, 19, 357–368. [Google Scholar] [CrossRef]
- Xia, Y.; Yang, Z.; Jackson, C.; Stoffa, P.; Sen, M. Impacts of data length on optimal parameter and uncertainty estimation of a land surface model. J. Geophys. Res.-Atmos. 2004, 109, 1–13. [Google Scholar] [CrossRef]
- Perrin, C.; Oudin, L.; Andreassian, V.; Rojas-Serna, C.; Michel, C.; Mathevet, T. Impact of limited streamflow data on the efficiency and the parameters of rainfall runoff models. Hydrol. Sci. J. 2007, 52, 131–151. [Google Scholar] [CrossRef]
- Shen, H.; Tolson, B.A.; Mai, J. Time to update the split-sample approach in hydrological model calibration. Water Resour. Res. 2022, 58, e2021WR031523. [Google Scholar] [CrossRef]
- Wagener, T.; McIntyre, N.; Lees, M.; Wheater, H.; Gupta, H. Towards reduced uncertainty in conceptual rainfall-runoff modelling: Dynamic identifiability analysis. Hydrol. Process 2003, 17, 455–476. [Google Scholar] [CrossRef]
- Abebe, N.; Ogden, F.; Pradhan, N. Sensitivity and uncertainty analysis of the conceptual HBV rainfall-runoff model: Implications for parameter estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
- Refsgaard, J.; Knudsen, J. Operational validation and intercomparison of different types of hydrological models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Hartmann, G.; Bárdossy, A. Investigation of the transferability of hydrological models and a method to improve model calibration. Adv. Geosci. 2005, 5, 83–87. [Google Scholar] [CrossRef]
- Seibert, J.; Rodhe, A.; Bishop, K. Simulating interactions between saturated and unsaturated storage in a conceptual runoff model. Hydrol. Process 2003, 17, 379–390. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L.; Peterson, T. Simulating runoff under changing climatic conditions: Revisiting an apparent deficiency of conceptual rainfall runoff models. Water Resour. Res. 2016, 52, 1820–1846. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Ruelland, D.; Tramblay, Y.; Bargaoui, Z. Evaluating the robustness of conceptual rainfall-runoff models under climate variability in northern Tunisia. J. Hydrol. 2017, 550, 201–217. [Google Scholar] [CrossRef]
- Wagener, T.; Reinecke, R.; Pianosi, F. On the evaluation of climate change impact models. Wiley Interdiscip. Rev. Clim. Chang. 2022, 13, e772. [Google Scholar] [CrossRef]
- Yapo, P.; Gupta, H.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Gan, T.; Dlamini, E.; Biftu, G. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Klemes, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Wu, K.; Johnston, C. Hydrologic response to climatic variability in a great lakes watershed: A case study with the swat model. J. Hydrol. 2007, 337, 187–199. [Google Scholar] [CrossRef]
- Ruelland, D.; Hublart, P.; Tramblay, Y. Assessing uncertainties in climate change impacts on runoff in Western Mediterranean basins. Proc. Int. Assoc. Hydrol. Sci. 2015, 371, 75–81. [Google Scholar] [CrossRef]
- Vaze, J.; Post, D.; Chiew, F.; Perraud, J.; Viney, N.; Teng, J. Climate non-stationarity: Validity of calibrated rainfall runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F.; Perrin, C. Multimodel evaluation of twenty lumped hydrological models under contrasted climate conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1171–1189. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Martel, J.; Brissette, F. Uncertainty of hydrological model components in climate change studies over two Nordic Quebec catchments. J. Hydrometeorol. 2018, 19, 27–46. [Google Scholar] [CrossRef]
- Ahn, K.H.; de Padua, V.M.N.; Kim, J.; Yi, J. Impact of Diverse Configuration in Multivariate Bias Correction Methods on Large-Scale Hydrological Modelling under Climate Change. J. Hydrol. 2023, 627, 130406. [Google Scholar] [CrossRef]
- Ashu, A.B.; Lee, S.-I. Multi-Site Calibration of Hydrological Model and Spatio-Temporal Assessment of Water Balance in a Monsoon Watershed. Water 2023, 15, 360. [Google Scholar] [CrossRef]
- Lee, E.; Sadeghi, S.M.M.; Deljouei, A.; Cohen, M.J. A multi-decadal national scale assessment of reference evapotranspiration methods in continental and temperate climate zones of South Korea. J. Hydrol. 2023, 625, 130021. [Google Scholar] [CrossRef]
- Lee, O.; Choi, J.; Sim, I.; Won, J.; Kim, S. Stochastic Parsimonious Hydrologic Partitioning Model under East Asia Monsoon Climate and Its Application to Climate Change. Water 2020, 12, 25. [Google Scholar] [CrossRef]
- Choi, J.; Kim, R.; Kim, S. Development of parsimonious semi-distributed hydrolgic partitioning model based on soil moisture storages. J. Korean Soc. Water Environ. 2020, 36, 229–244. [Google Scholar] [CrossRef]
- Galletti, A.; Avesani, D.; Bellin, A.; Majone, B. Detailed simulation of storage hydropower systems in large Alpine watersheds. J. Hydrol. 2021, 603, 127125. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models–Part 1: Problem definition and representation of water demand. Hydrol. Earth Syst. Sci. 2015, 19, 33–61. [Google Scholar] [CrossRef]
- Lee, O.; Kim, H.; Kim, S. Hydrological simple water balance modeling for increasing geographically isolated doline wetland functions and its application to climate change. Ecol. Eng. 2020, 149, 105812. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; ISBN 978-92-5-104219-9. [Google Scholar]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef]
- United States Department for Agriculture Soil Conservation Service. Urban Hydrology for Small Watersheds TR-55. Technical Release; United States Department for Agriculture Soil Conservation Service: Washington, DC, USA, 1986. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Brooks, S.; Gelman, A. General Methods for Monitoring Convergence of Iterative Simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar]
- Liu, X.; Xia, C.; Tang, Y.; Tu, J.; Wang, H. Parameter optimization and uncertainty assessment for rainfall frequency modeling using an adaptive Metropolis–Hastings algorithm. Water Sci. Technol. 2021, 83, 1085–1102. [Google Scholar] [CrossRef] [PubMed]
- Box, G.; Cox, D. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Kuczera, G. Improved parameter inference in catchment models: 1. Evaluating parameter uncertainty. Water Resour. Res. 1983, 19, 1151–1162. [Google Scholar] [CrossRef]
- Kim, R.; Won, J.; Choi, J.; Lee, O.; Kim, S. Application of Bayesian Approach to Parameter Estimation of TANK Model: Comparison of MCMC and GLUE Methods. J. Korean Soc. Water Environ. 2020, 36, 300–313. [Google Scholar] [CrossRef]
- Engel, B.; Srinivasan, R.; Arnold, J.; Rewerts, C.; Brown, S. Nonpoint-source (NPS) pollution modeling using models integrated with geographic information systems (GIS). Water Sci. Technol. 1993, 28, 685–690. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ritter, A.; Munoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Gupta, H.; Kling, H.; Yilmaz, K.; Martinez, G. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Patil, S.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef]
- Sorooshian, S.; Duan, Q.; Gupta, V. Calibration of rainfall-runoff models: Application of global optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Budyko, M. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]





| Parameter | Unit | Lower Bound | Upper Bound |
|---|---|---|---|
| nZr | mm | 5 | 2000 |
| s* | - | 0.01 | 0.99 |
| Ks | mm/day | 15 | 500 |
| - | 1 | 20 | |
| - | 0.01 | 0.99 | |
| ds | mm | 1 | 20 |
| Mean | Std (Standard Deviation) | Min | Max | Dry Year (2015) | Normal Year (2005) | Wet Year (2003) | ||
|---|---|---|---|---|---|---|---|---|
| AnDong Dam watershed | Annual Precipitation (mm) | 1175 | 254 | 684 | 1707 | 684 | 1097 | 1707 |
| Annual Potential Evapotranspiration (mm) | 993 | 39.5 | 923 | 1050 | 1044 | 967 | 929 | |
| Dryness Index | 0.889 | 0.224 | 0.545 | 1.53 | 1.53 | 0.882 | 0.545 | |
| HapCheon Dam watershed | Annual Precipitation (mm) | 1318 | 332 | 633 | 1947 | 633 | 1240 | 1947 |
| Annual Evapotranspiration (mm) | 1060 | 36.7 | 958 | 1127 | 1112 | 1085 | 958 | |
| Dryness Index | 0.870 | 0.292 | 0.492 | 1.76 | 1.76 | 0.874 | 0.492 | |
| Calibration Condition | Parameter | PCV | R2 | NSE | KGE | MCV | |
|---|---|---|---|---|---|---|---|
| Dry | nZr | 478 | 0.583 | 0.743 | 0.729 | 0.706 | 0.663 |
| s* | 0.586 | 0.444 | |||||
| Ks | 307 | 0.338 | |||||
| β | 3.55 | 0.445 | |||||
| α | 0.713 | 0.280 | |||||
| ds | 8.50 | 0.554 | |||||
| Normal | nZr | 364 | 0.504 | 0.632 | 0.603 | 0.757 | 0.527 |
| s* | 0.607 | 0.407 | |||||
| Ks | 346 | 0.312 | |||||
| β | 3.53 | 0.461 | |||||
| α | 0.759 | 0.228 | |||||
| ds | 9.45 | 0.488 | |||||
| Wet | nZr | 469 | 0.754 | 0.603 | 0.565 | 0.480 | 1.40 |
| s* | 0.628 | 0.422 | |||||
| Ks | 300 | 0.421 | |||||
| β | 5.98 | 0.787 | |||||
| α | 0.650 | 0.354 | |||||
| ds | 9.14 | 0.569 | |||||
| Mixed | nZr | 386 | 0.666 | 0.734 | 0.729 | 0.741 | 0.969 |
| s* | 0.599 | 0.436 | |||||
| Ks | 316 | 0.379 | |||||
| β | 4.45 | 0.583 | |||||
| α | 0.680 | 0.323 | |||||
| ds | 9.95 | 0.528 | |||||
| Calibration Condition | Parameter | PCV | R2 | NSE | KGE | MCV | |
|---|---|---|---|---|---|---|---|
| Dry | nZr | 526 | 0.519 | 0.795 | 0.793 | 0.809 | 1.11 |
| s* | 0.623 | 0.376 | |||||
| Ks | 250 | 0.548 | |||||
| β | 4.47 | 0.386 | |||||
| α | 0.648 | 0.357 | |||||
| ds | 8.42 | 0.626 | |||||
| Normal | nZr | 589 | 0.587 | 0.780 | 0.755 | 0.679 | 1.17 |
| s* | 0.672 | 0.366 | |||||
| Ks | 274 | 0.499 | |||||
| β | 5.80 | 0.619 | |||||
| α | 0.643 | 0.373 | |||||
| ds | 9.15 | 0.593 | |||||
| Wet | nZr | 651 | 0.586 | 0.736 | 0.731 | 0.775 | 2.48 |
| s* | 0.646 | 0.403 | |||||
| Ks | 285 | 0.466 | |||||
| β | 8.28 | 0.594 | |||||
| α | 0.660 | 0.345 | |||||
| ds | 9.40 | 0.576 | |||||
| Mixed | nZr | 561 | 0.597 | 0.756 | 0.748 | 0.735 | 0.832 |
| s* | 0.665 | 0.371 | |||||
| Ks | 270 | 0.513 | |||||
| β | 5.37 | 0.605 | |||||
| α | 0.646 | 0.373 | |||||
| ds | 8.52 | 0.599 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Choi, J.; Seo, J.; Won, J.; Kim, S. Exploring Climate Sensitivity in Hydrological Model Calibration. Water 2023, 15, 4094. https://doi.org/10.3390/w15234094
Lee J, Choi J, Seo J, Won J, Kim S. Exploring Climate Sensitivity in Hydrological Model Calibration. Water. 2023; 15(23):4094. https://doi.org/10.3390/w15234094
Chicago/Turabian StyleLee, Jeonghoon, Jeonghyeon Choi, Jiyu Seo, Jeongeun Won, and Sangdan Kim. 2023. "Exploring Climate Sensitivity in Hydrological Model Calibration" Water 15, no. 23: 4094. https://doi.org/10.3390/w15234094
APA StyleLee, J., Choi, J., Seo, J., Won, J., & Kim, S. (2023). Exploring Climate Sensitivity in Hydrological Model Calibration. Water, 15(23), 4094. https://doi.org/10.3390/w15234094







