Insights into CFD Modelling of Water Hammer
Abstract
:1. Introduction
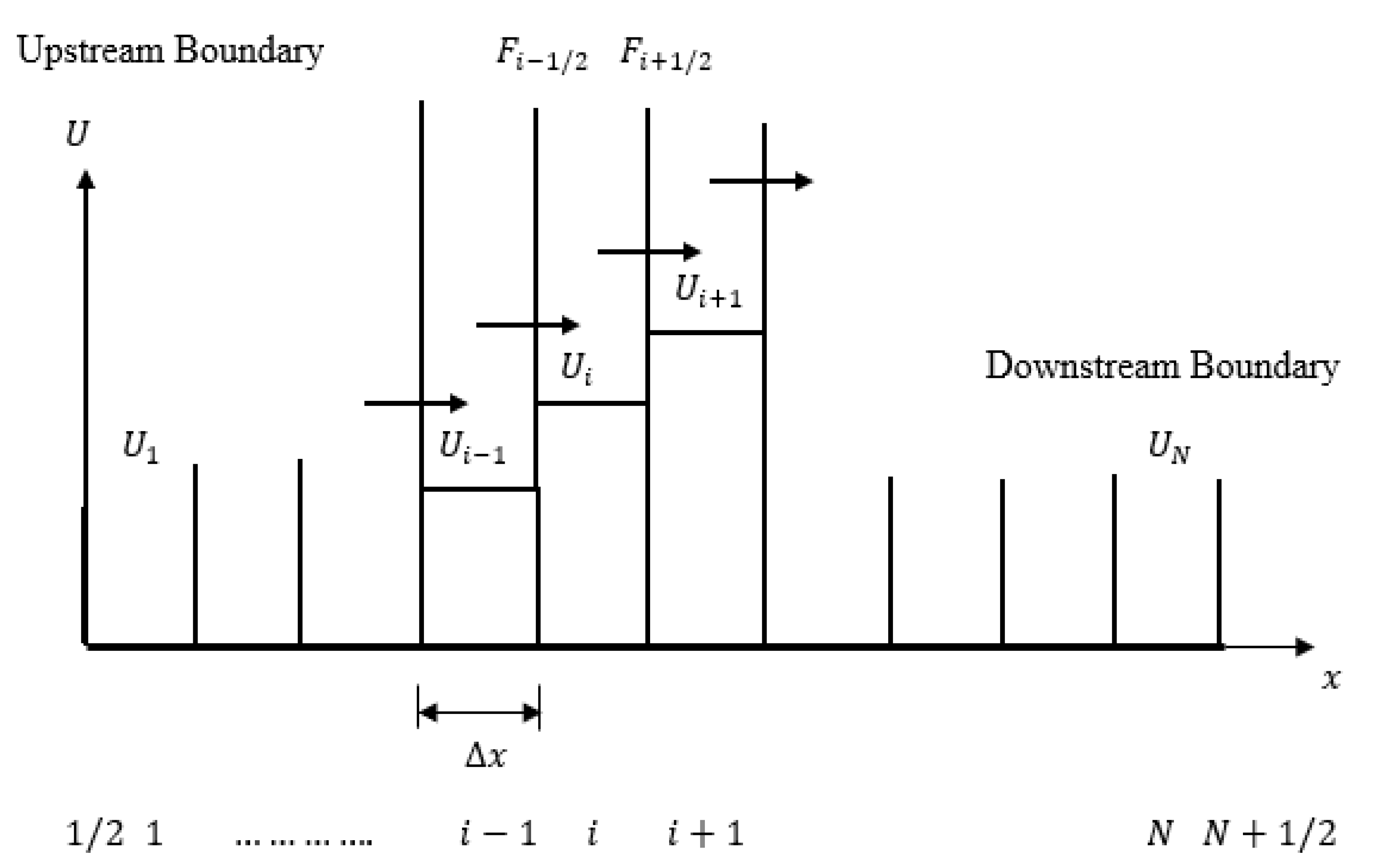
2. The Finite Volume Approach
2.1. Water Hammer Equation with Unsteady Friction
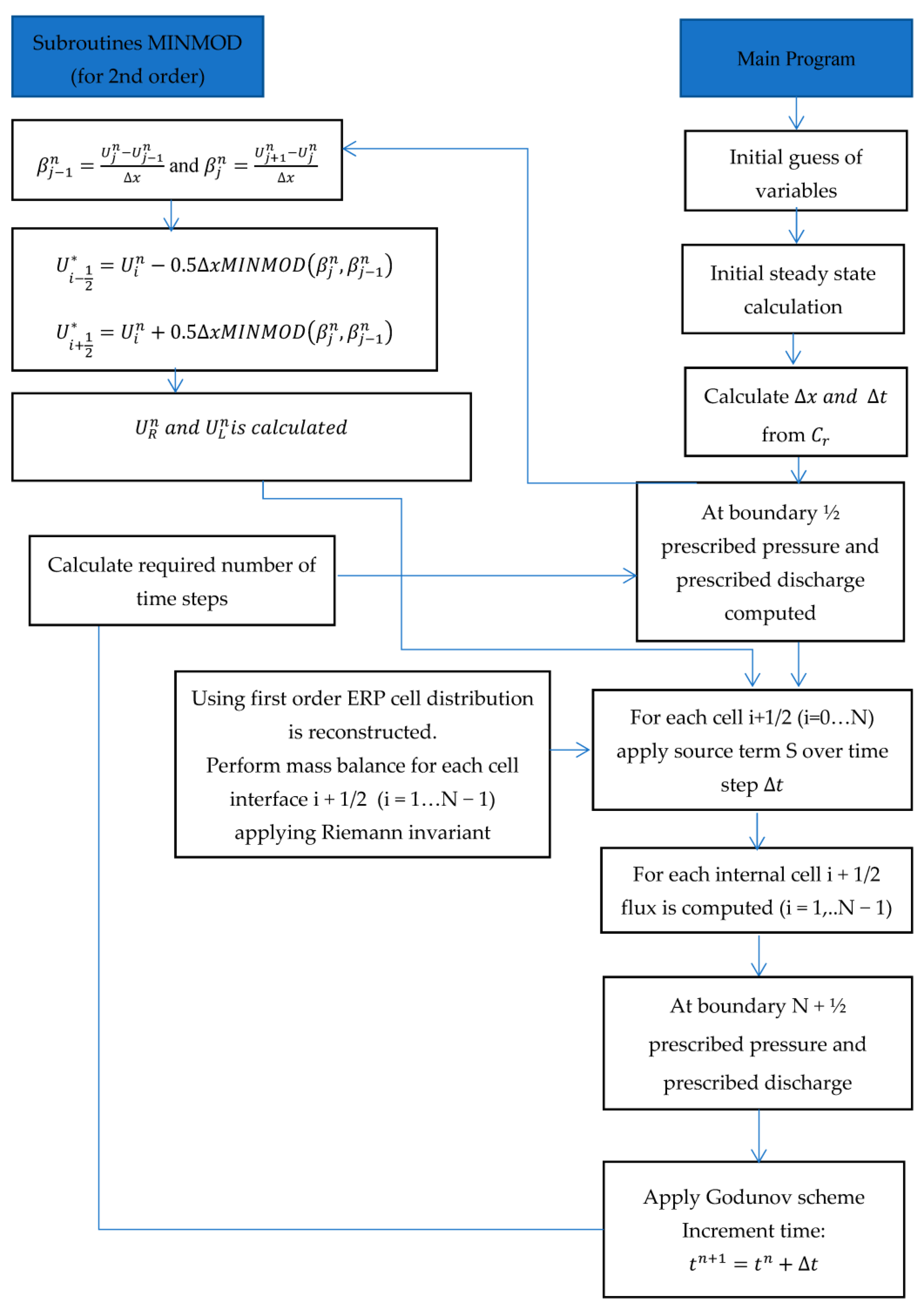
2.2. Numerical Solution with Second-Order Finite Volume Method
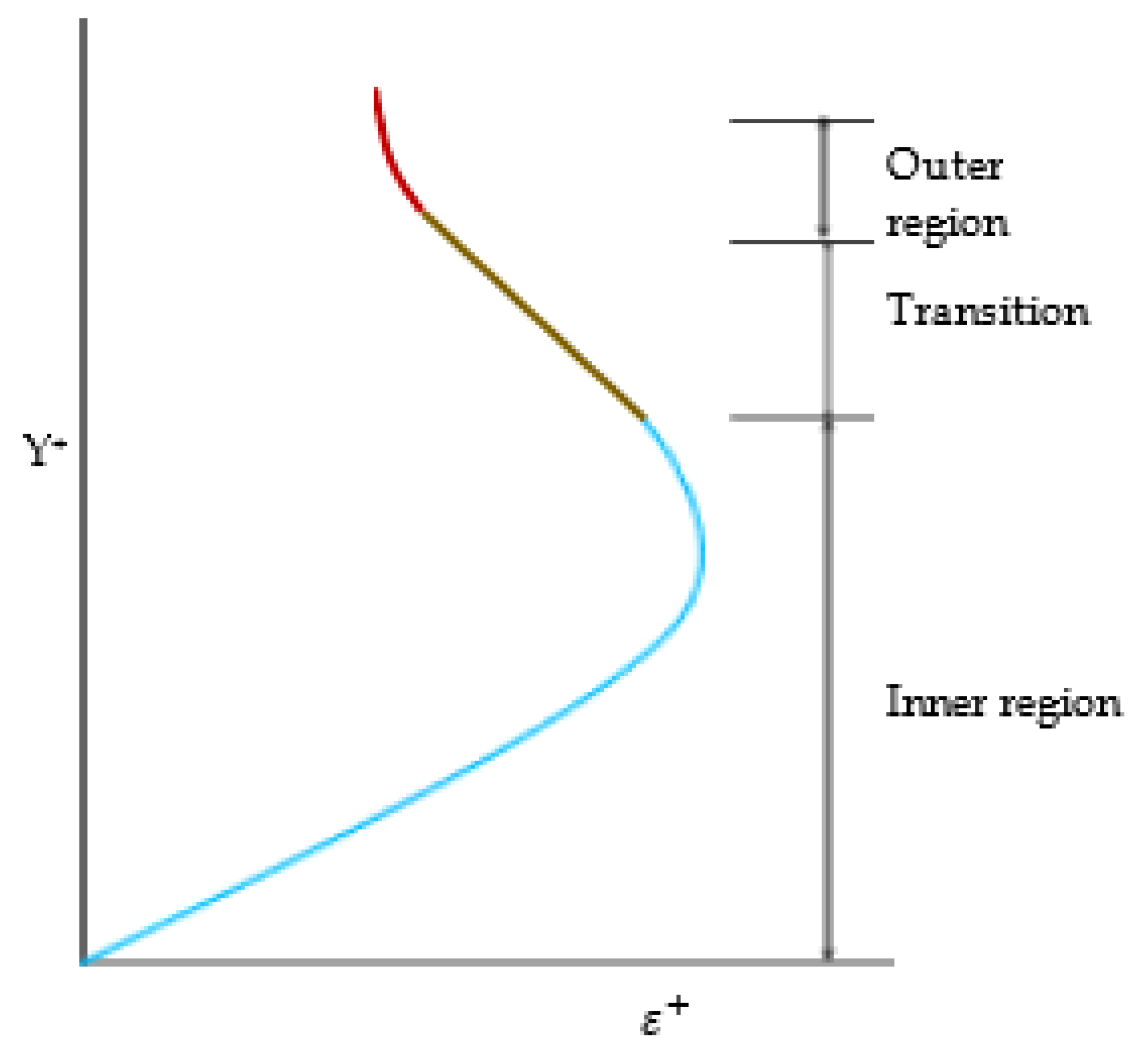
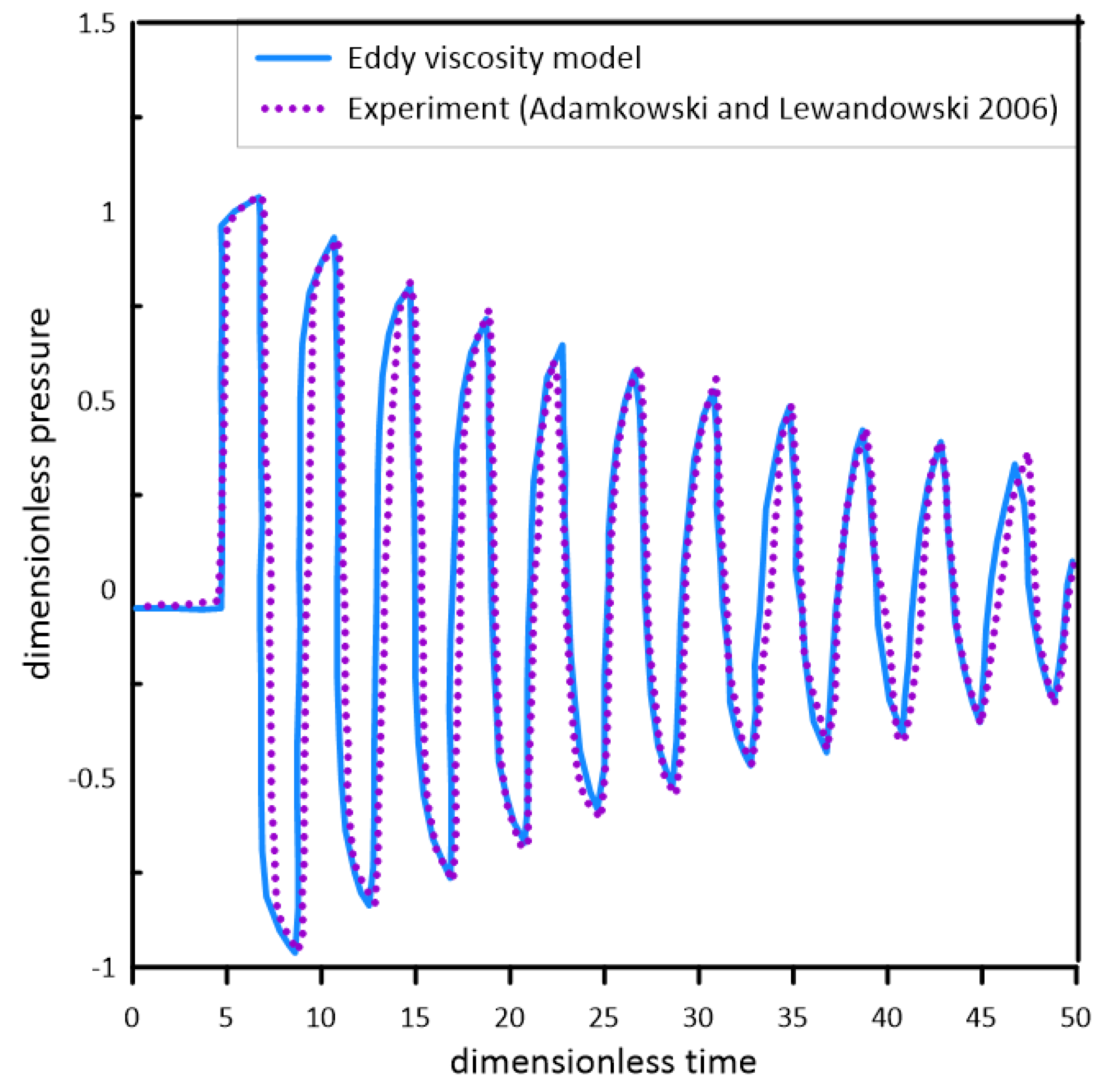
3. Quasi-2-D Eddy Viscosity Model
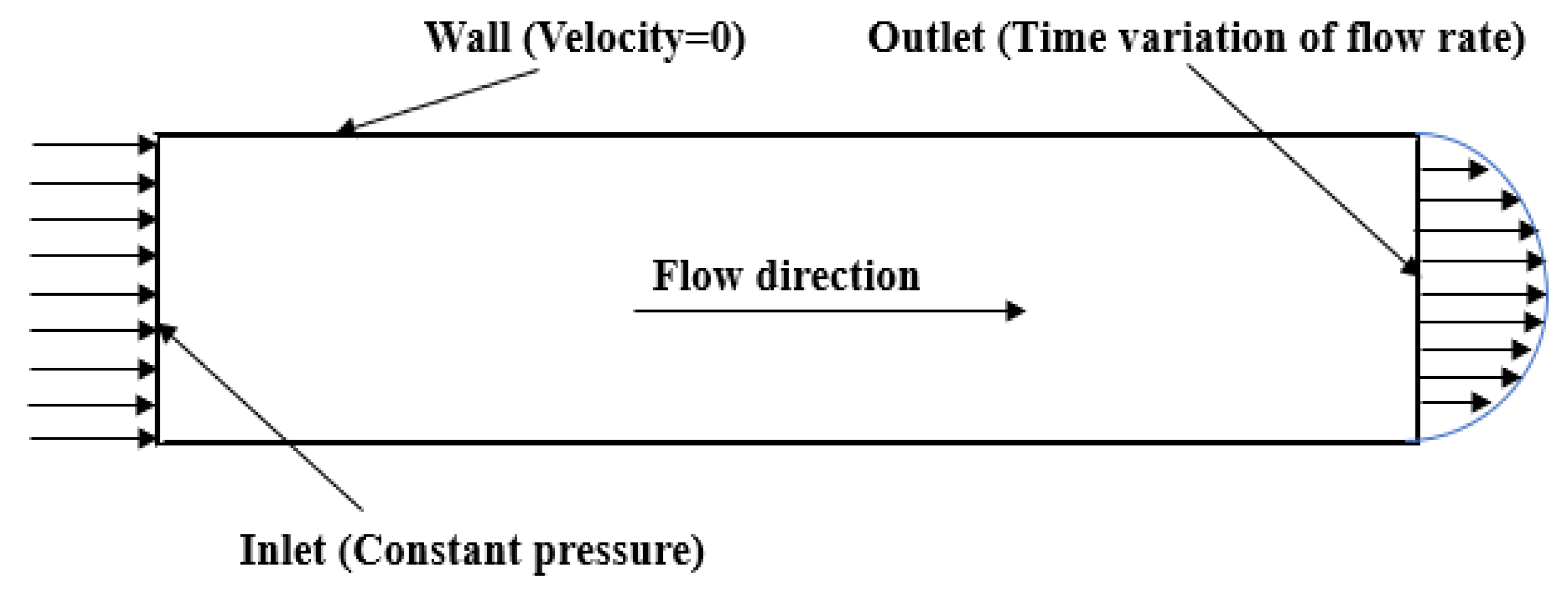
4. Three-Dimensional CFD Modelling
4.1. Governing Equations for 3-D CFD Model
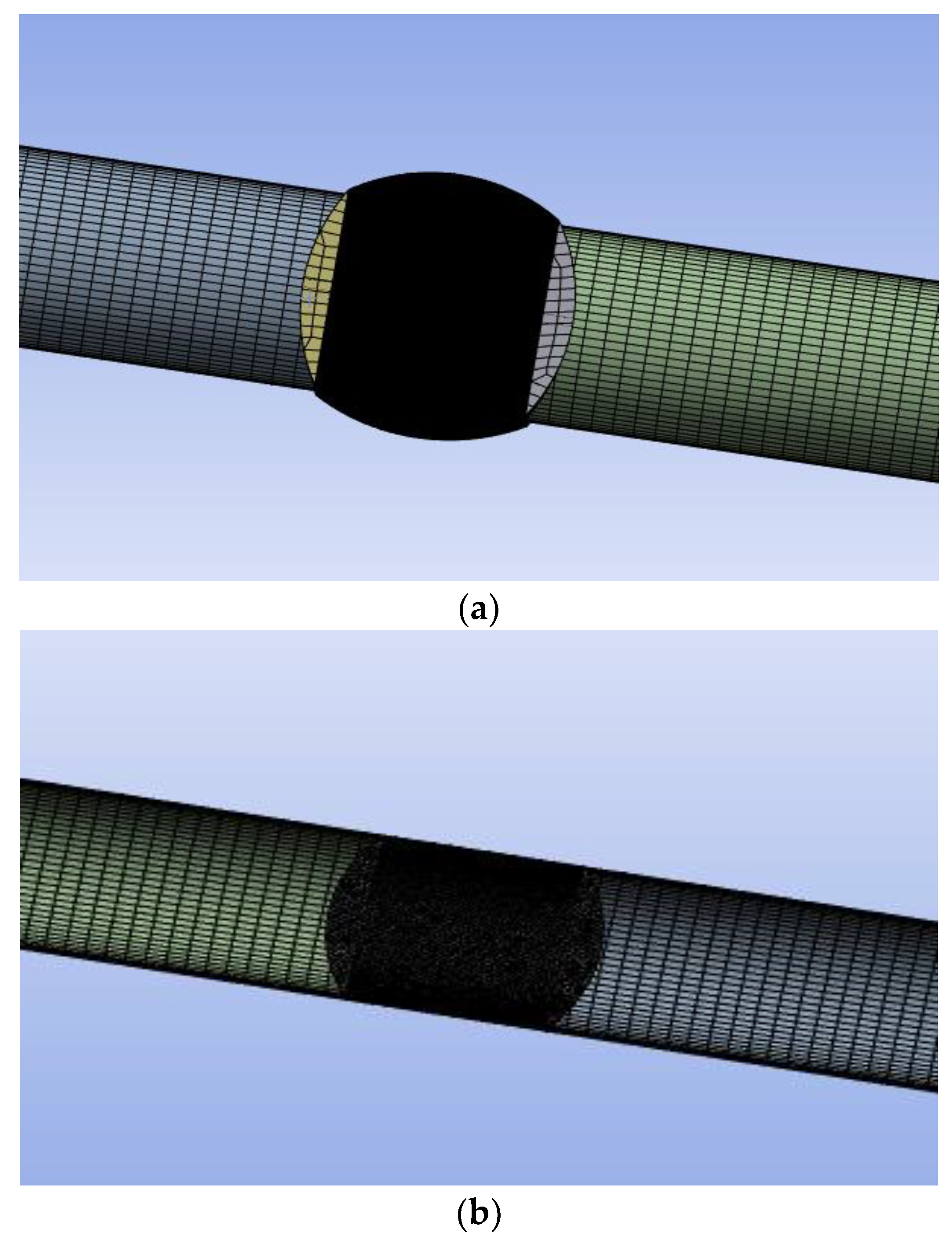
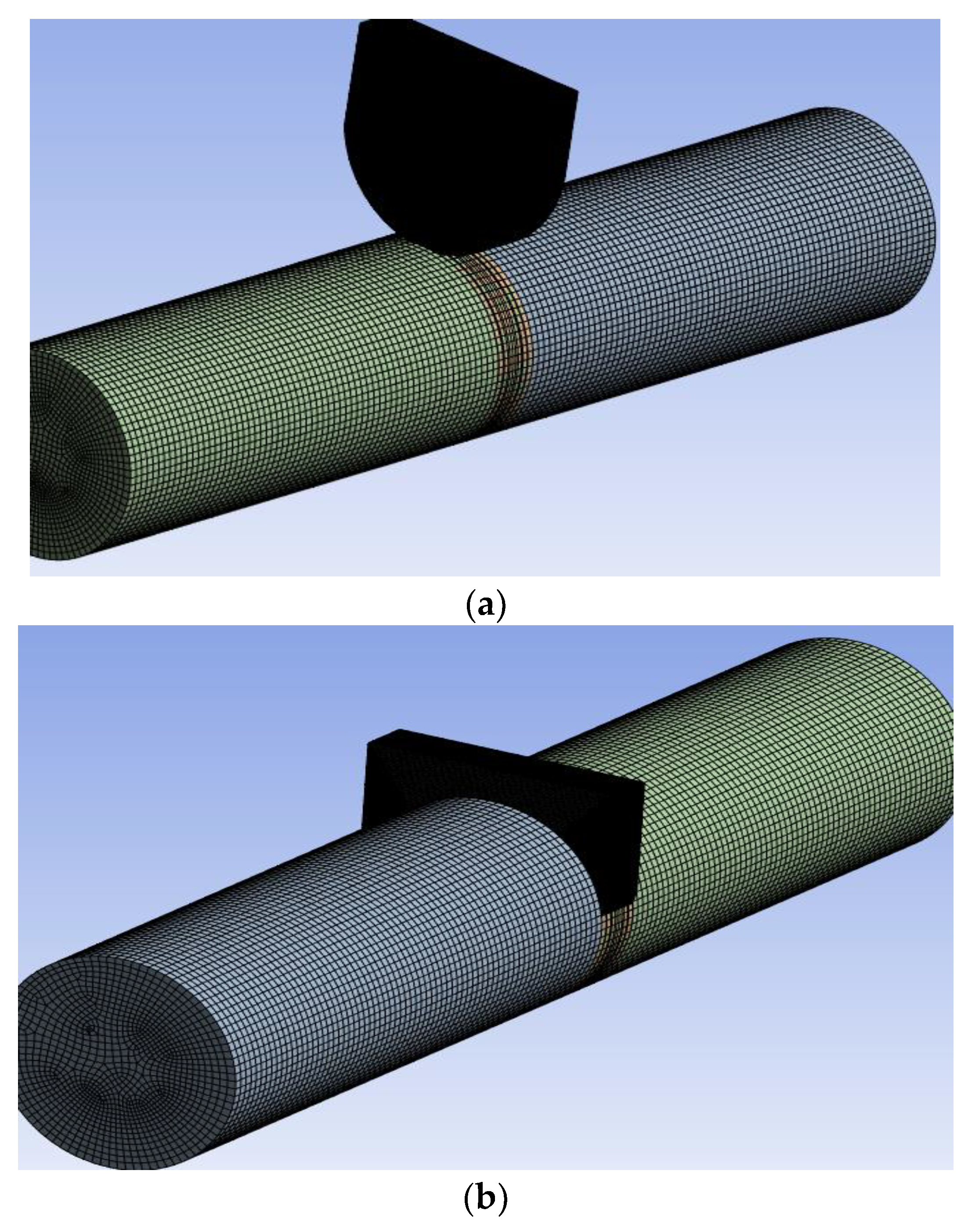
4.2. Mesh Analysis
4.3. Turbulence Modelling
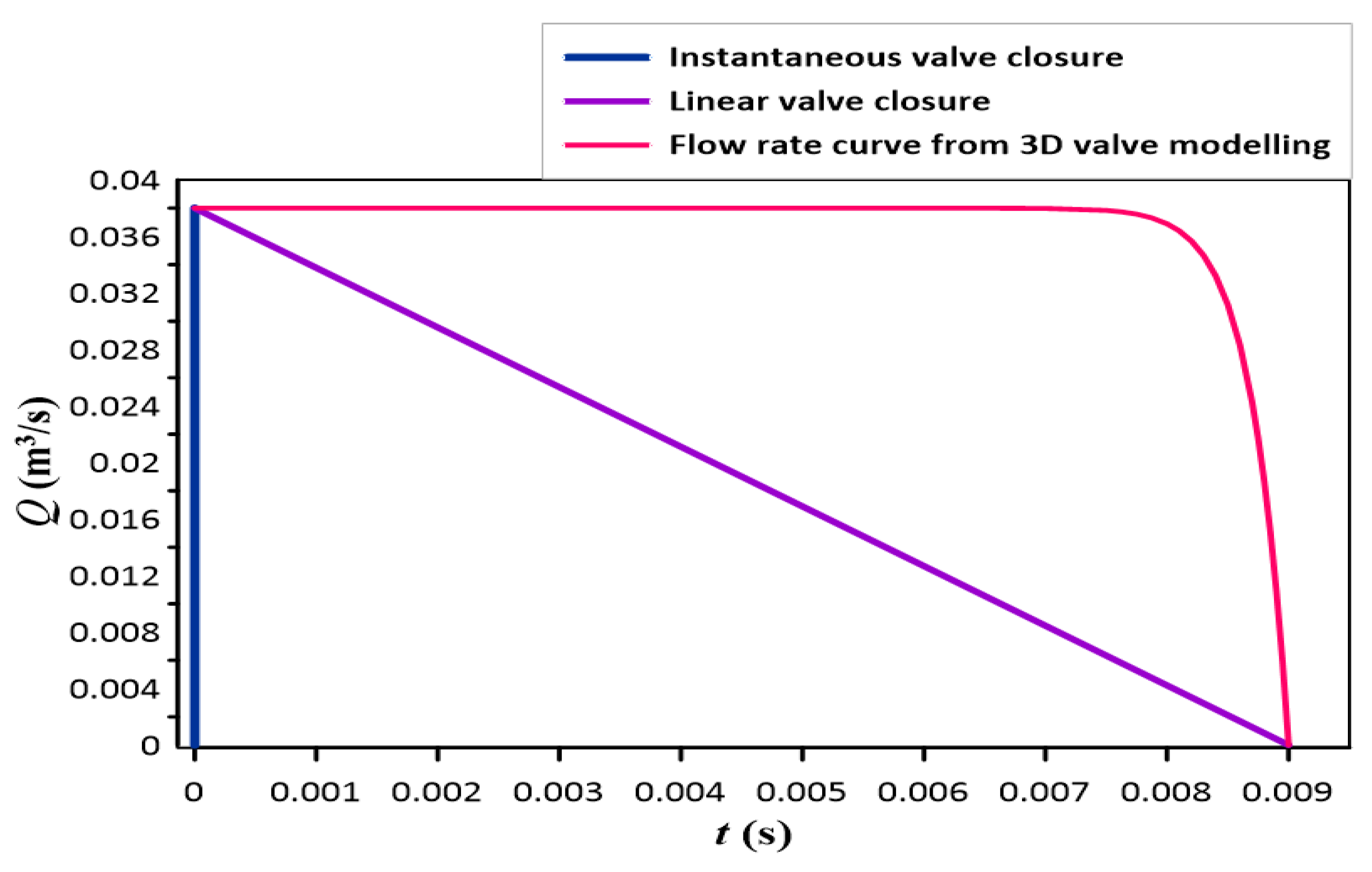
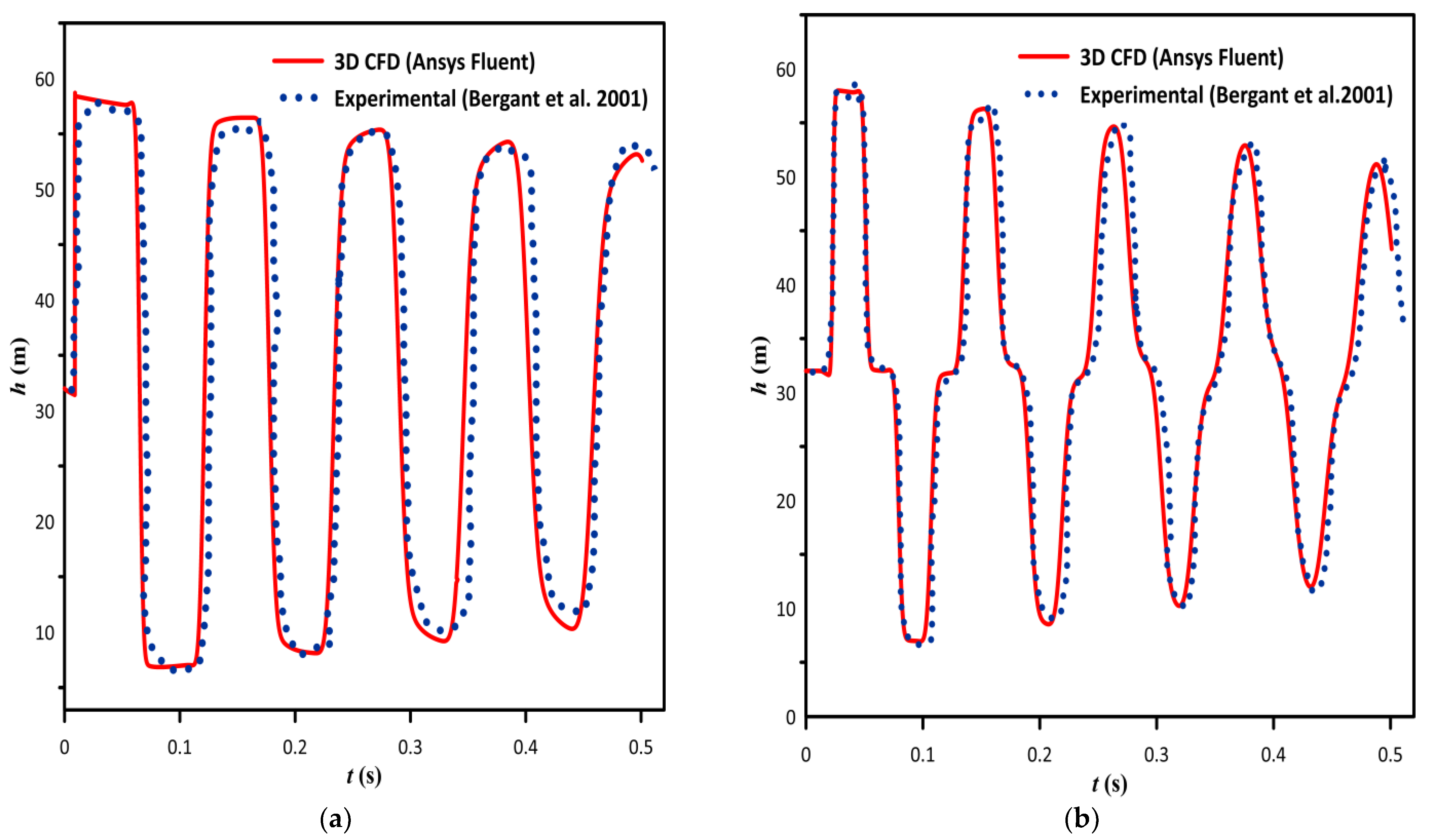
4.4. Various 3-D CFD Approaches in Water Hammer Modelling
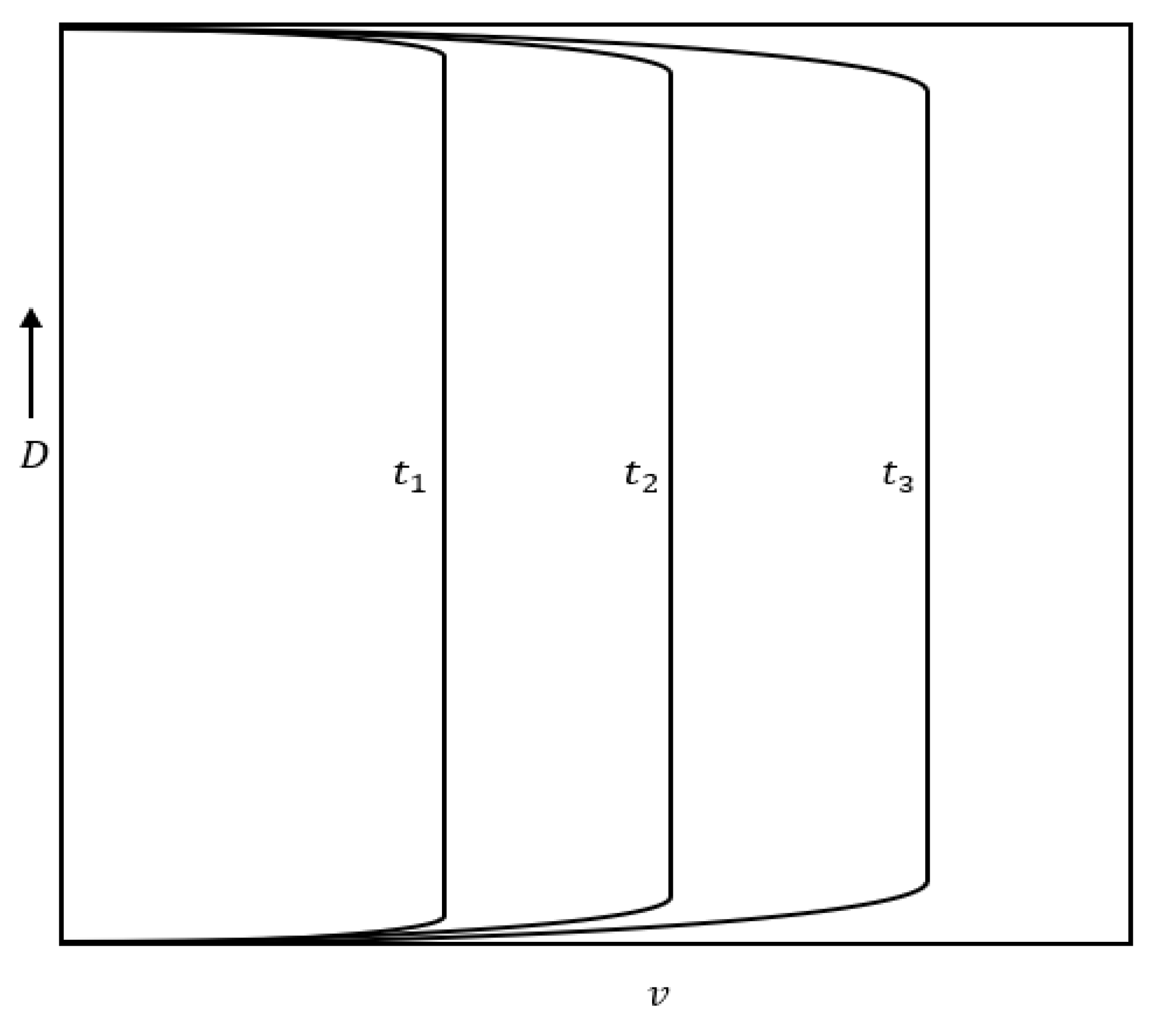
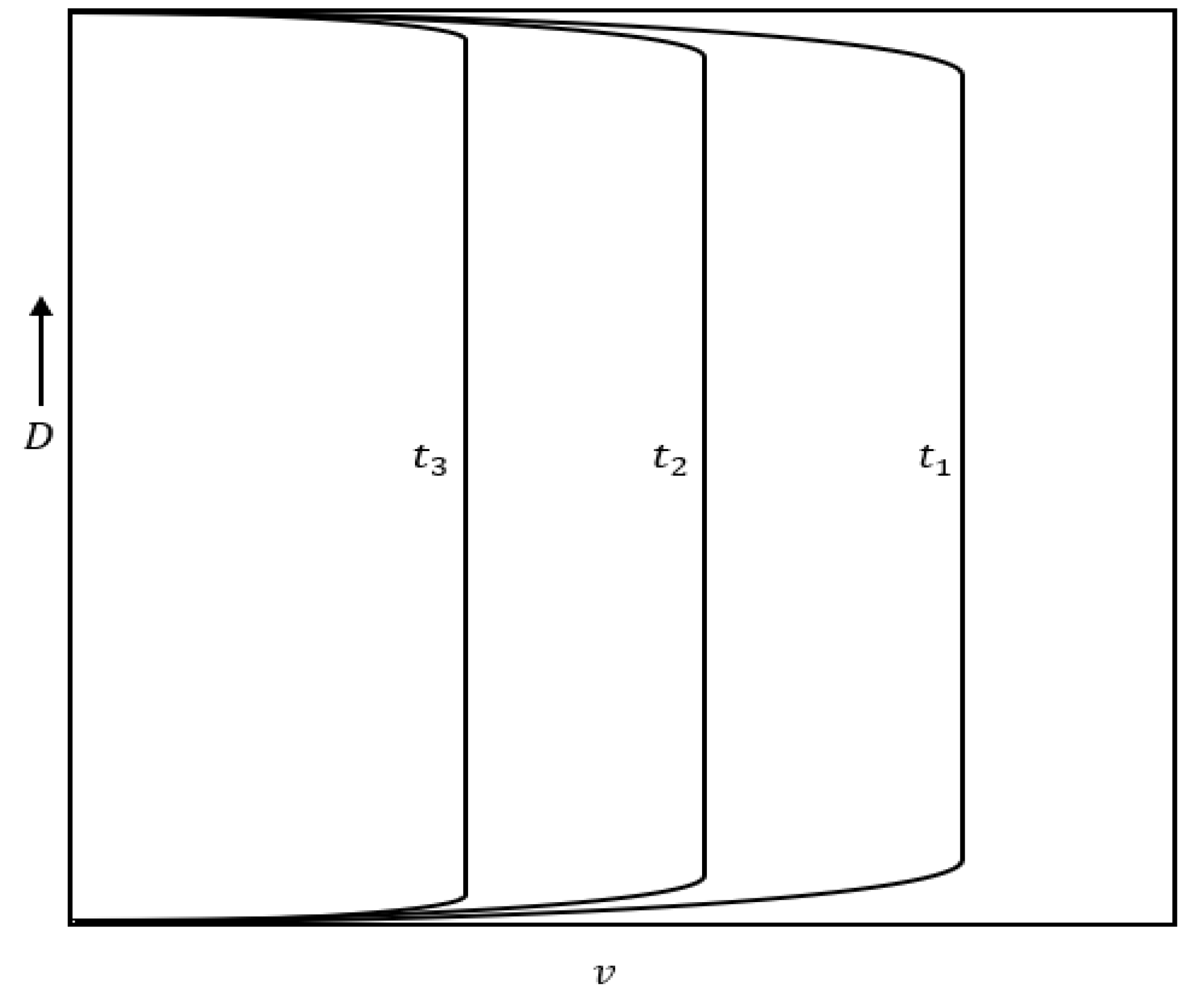
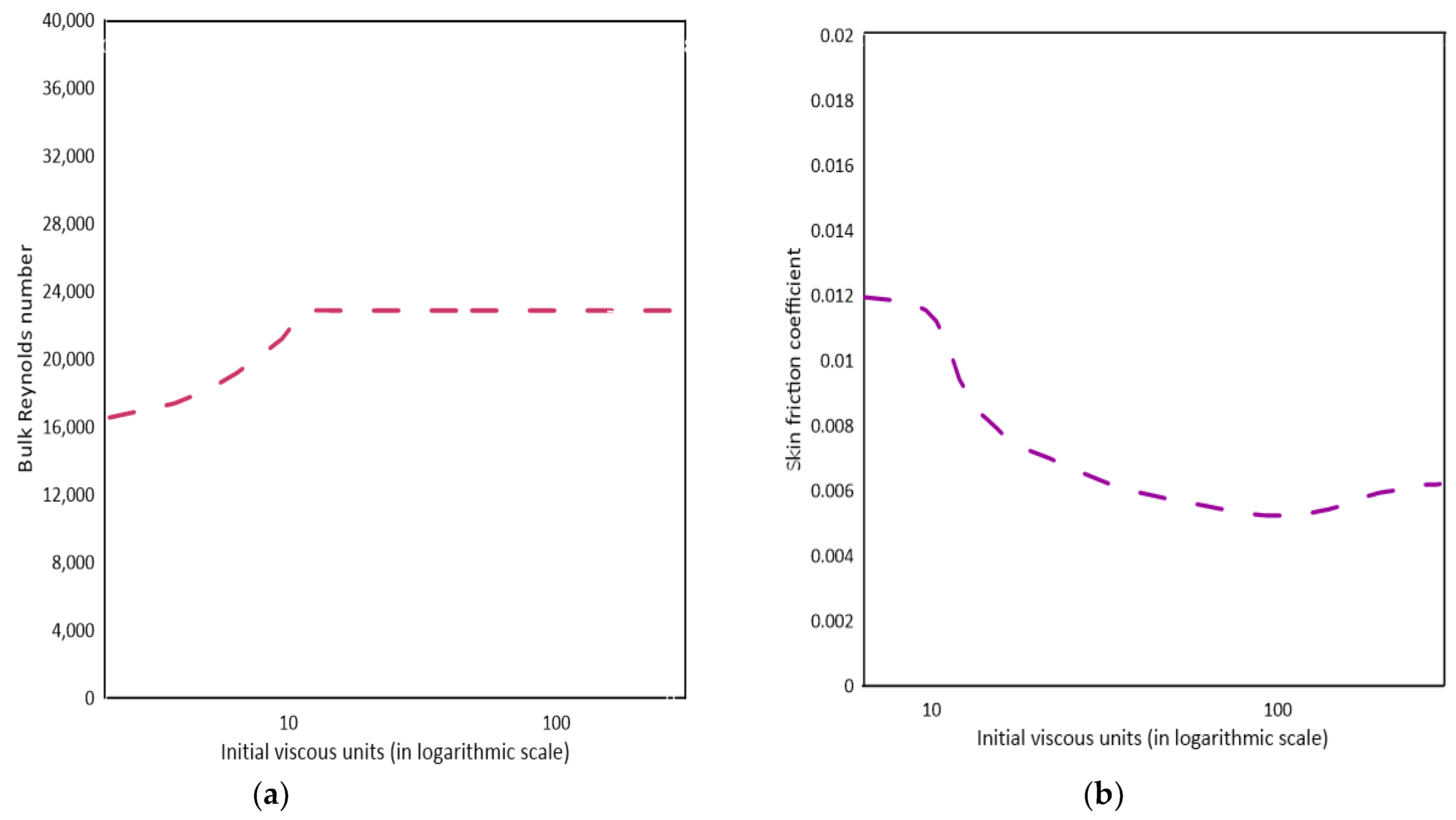
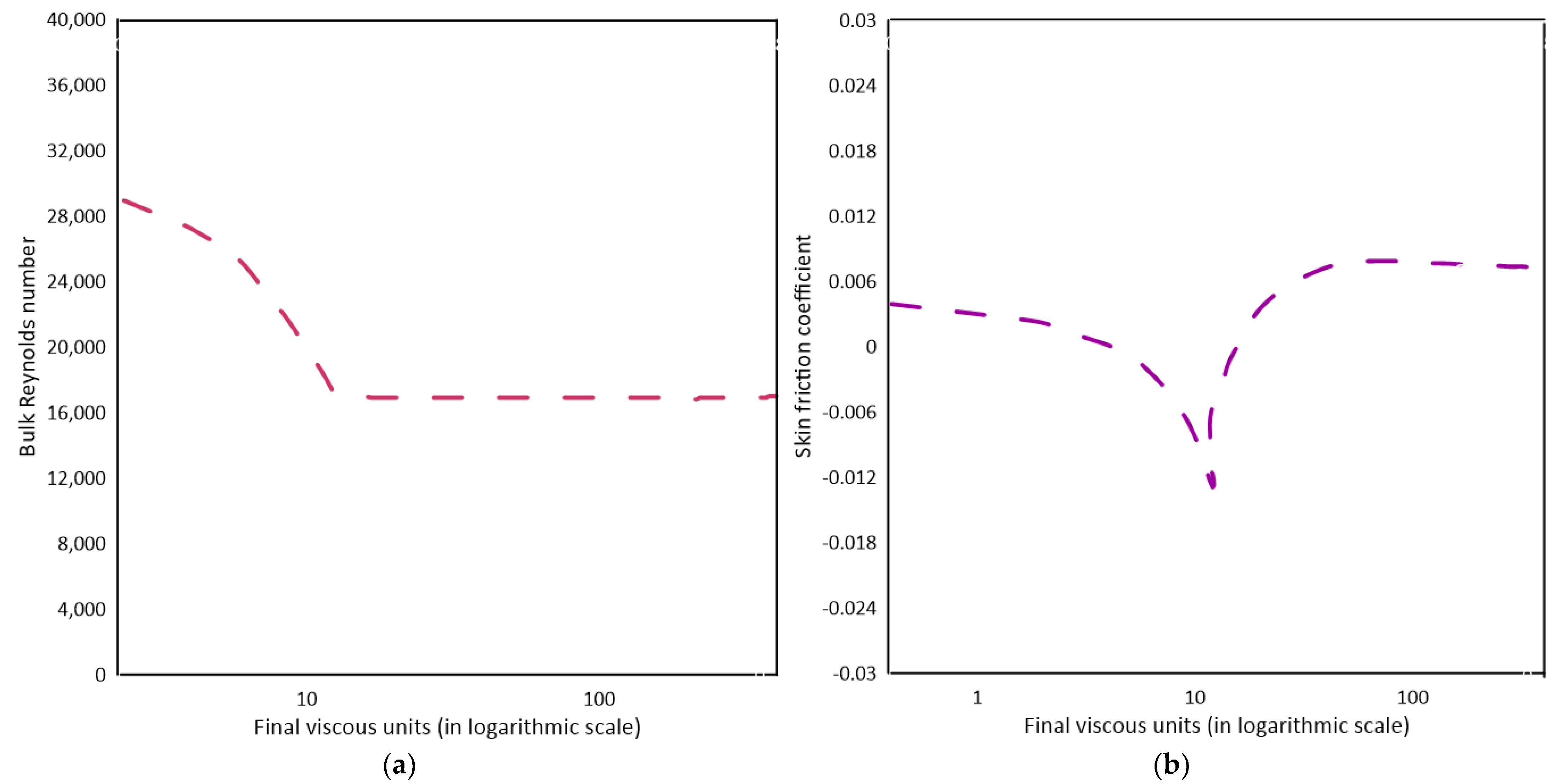
5. Turbulence Structures in Accelerating and Decelerating Flows
5.1. Accelerating Flows
5.2. Decelerating Flows
6. Future Research Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Wu, D.; Lai, Z.; Du, T. Three-Dimensional Computational Fluid Dynamics Simulation of Valve-Induced Water Hammer. J. Mech. Eng. Sci. 2017, 231, 2263–2274. [Google Scholar] [CrossRef]
- Ghidaoui, M.S.; Asce, M.; Sameh; Mansour, G.S.; Zhao, M. Applicability of Quasisteady and Axisymmetric Turbulence Models in Water Hammer. J. Hydraul. Eng. 2002, 128, 917–924. [Google Scholar] [CrossRef]
- Lohrasbi, A.R.; Attarnejad, R. Water Hammer Analysis by Characteristic Method. Am. J. Eng. Appl. Sci. 2008, 1, 287–294. [Google Scholar] [CrossRef]
- Meniconi, S.; Ferrante, M. In-Line Partially Closed Valves: How to Detect by Transient Tests. In Proceedings of the World Environment and Water Resource Congress, Kansas City, MO, USA, 17–21 May 2009; pp. 135–144. [Google Scholar]
- Pal, S.; Hanmaiahgari, P.R.; Karney, B.W. An Overview of the Numerical Approaches to Water Hammer Modelling: The Ongoing Quest for Practical and Accurate Numerical Approaches. Water 2021, 13, 1597. [Google Scholar] [CrossRef]
- Pu, J.H.; Shao, S.; Huang, Y. Numerical and Experimental Turbulence Studies on Shallow Open Channel Flows. J. Hydro-Environ. Res. 2014, 8, 9–19. [Google Scholar] [CrossRef]
- Hui Pu, J.; Shao, S.; Huang, Y.; Hussain, K. Evaluations of SWEs and SPH Numerical Modelling Techniques for Dam Break Flows. Eng. Appl. Comput. Fluid Mech. 2013, 7, 544–563. [Google Scholar] [CrossRef]
- Pu, J.H.; Cheng, N.S.; Tan, S.K.; Shao, S. Source Term Treatment of SWEs Using Surface Gradient Upwind Method. J. Hydraul. Res. 2012, 50, 145–153. [Google Scholar] [CrossRef]
- Pu, J.H.; Pandey, M.; Li, J.; Satyanaga, A.; Kundu, S.; Hanmaiahgari, P.R. Editorial: The Urban Fluvial and Hydro-Environment System. Front. Environ. Sci. 2022, 10, 1075282. [Google Scholar] [CrossRef]
- Brunone, B.; Ferrante, M.; Cacciamani, M. Decay of Pressure and Energy Dissipation in Laminar Transient Flow. ASME J. Fluids Eng. 2004, 126, 928–934. [Google Scholar] [CrossRef]
- Riasi, A.; Nourbakhsh, A.; Raisee, M. Energy Dissipation in Unsteady Turbulent Pipe Flows Caused by Water Hammer. Comput. Fluids 2013, 73, 124–133. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Energy Dissipation and Pressure Decay during Transients in Viscoelastic Pipes with an In-Line Valve. J. Fluids Struct. 2014, 45, 235–249. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Brunone, B.; Meniconi, S.; Ramos, H.M.; Covas, D.I.C. CFD and 1D Approaches for the Unsteady Friction Analysis of Low Reynolds Number Turbulent Flows. J. Hydraul. Eng. 2017, 143, 04017050. [Google Scholar] [CrossRef]
- Silva-Araya, W.F.; Chaudhry, M.H. Computation of Energy Dissipation in Transient Flow. J. Hydraul. Eng. 1997, 123, 108–115. [Google Scholar] [CrossRef]
- Reddy, H.P.; Asce, M.; Walter; Silva-Araya, F.; Chaudhry, M.H.; Asce, F. Estimation of Decay Coefficients for Unsteady Friction for Instantaneous, Acceleration-Based Models. J. Hydraul. Eng. 2012, 138, 260–271. [Google Scholar] [CrossRef]
- Wang, L.Q.; Li, Z.F.; Wu, D.Z.; Hao, Z.R. Transient Flow around an Impulsively Started Cylinder Using a Dynamic Mesh Method. Int. J. Comut Fluid. Dyn. 2007, 21, 127–135. [Google Scholar] [CrossRef]
- Godunov, S.K. A Difference Method for the Numerical Calculation of Discontinuous Solutions of Hydrodynamic Equations. Mat. Sb. 1959, 89, 271–306. [Google Scholar]
- Pal, S.; Kottam, R.R.; Lambert, M.F.; Hanmaiahgari, P.R. Estimation of Deposit Thickness in Single-Phase Liquid Flow Pipeline Using Finite Volume Modelling. J. Pipeline Sci. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Pu, J.H. Turbulence Modelling of Shallow Water Flows Using Kolmogorov Approach. Comput. Fluids 2015, 115, 66–74. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, Bergen, NJ, USA, 1993. [Google Scholar]
- Adamkowski, A.; Lewandowski, M. Experimental Examination of Unsteady Friction Models for Transient Pipe Flow Simulation. ASME J. Fluids Eng. 2006, 128, 1351–1363. [Google Scholar] [CrossRef]
- Zielke, W. Frequency-Dependent Friction in Transient Pipe Flow. J. Basic. Eng. Trans. ASME 1968, 90, 109–115. [Google Scholar] [CrossRef]
- Trikha, A.K. An Efficient Method for Simulating Frequency Dependent Friction in Transient Liquid Flow. ASME J. Fluids Eng. 1975, 97, 97–105. [Google Scholar] [CrossRef]
- Kagawa, T. High Speed and Accurate Computing Method of Frequency-Dependent Friction in Laminar Pipe Flow for Characteristic Method. JSME Int. J. Ser. B 1983, 49, 2638–2644. [Google Scholar] [CrossRef]
- Suzuki; Takayuki Taketomi, K.; Sato, S. Improving Zielke’s Method of Simulating Frequency-Dependent Friction in Laminar Liquid Pipe Flow. ASME J. Fluids Eng. 1991, 113, 569–573. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Transient, Turbulent, Smooth Pipe. J. Hydraul. Res. 1995, 33, 435–456. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Transient Turbulent Friction in Smooth Pipe Flows. J. Sound Vib. 2003, 259, 1011–1036. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B. Transient Turbulent Friction in Fully Rough Pipe Flows. J. Sound. Vib. 2004, 270, 233–257. [Google Scholar] [CrossRef]
- Pal, S.; Hanmaiahgari, P.R.; Lambert, M.F. Efficient Approach toward the Application of the Godunov Method to Hydraulic Transients. J. Hydroinformatics 2020, 22, 1370–1390. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Bergant, A.; Simpson, A.R.; Asce, M.; Lambert, M.F. Systematic Evaluation of One-Dimensional Unsteady Friction Models in Simple Pipelines. J. Hydraul. Eng. 2006, 132, 696–708. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients; Springer: New York, NY, USA, 2014. [Google Scholar]
- Carstens, M.R.; Rollers, J.E. Boundary-Shear Stress in Unsteady Turbulent Pipe Flow. J. Hydraul. Div. 1959, 85, 67–81. [Google Scholar] [CrossRef]
- Brunone, B.; Golia, U.M.; Greco, M. Some Remarks on the Momentum Equation for Fast Transients. In Proceedings of the International Meeting on Hydraulic Transients with Water Column Separation (9th Round Table of the IAHR Group), Valencia, Spain, 4–6 September 1991; pp. 201–209. [Google Scholar]
- Bergant, A.; Simpson, A.R.; Vítkovský, J. Developments in Unsteady Pipe Flow Friction Modelling. J. Hydraul. Res. 2001, 39, 249–257. [Google Scholar] [CrossRef]
- Ramos, H.; Covas, D.; Borga, A.; Loureiro, D. Surge Damping Analysis in Pipe Systems: Modelling and Experiments. J. Hydraul. Res. 2004, 42, 413–425. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Lambert, M.F.; Simpson, A.R.; Bergant, A. Advances in Unsteady Friction Modelling in Transient Pipe Flow. In Proceedings of the 8th International Conference on Pressure Surges, The Hague, The Netherlands, 12–14 April 2000. Water Distribution Networks Optimization View Project Acoustic Methods for Leak Detection in Water Networks View Project. [Google Scholar]
- Vítkovský, J.; Stephens; Mark; Bergant, A.; Simpson, A.; Asce, M.; Lambert, M. Numerical Error in Weighting Function-Based Unsteady Friction Models for Pipe Transients. J. Hydraul. Eng. 2006, 132, 709–721. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Zhao, Y.; Ou, C.; Zhao, Y. An Accurate and Efficient Scheme Involving Unsteady Friction for Transient Pipe Flow. J. Hydroinformatics 2021, 23, 879–896. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Liu, D.; Ma, J.; Wang, P.; Xia, L. A Second-Order Finite Volume Method for Pipe Flow with Water Column Separation. J. Hydro-Environ. Res. 2017, 17, 47–55. [Google Scholar] [CrossRef]
- Zhao, M.; Ghidaoui, M.S.; Asce, M. Godunov-Type Solutions for Water Hammer Flows. J. Hydraul. Eng. 2004, 130, 341–348. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Pezzinga, G. Quasi-2D Model for Unsteady Flow in Pipe Networks. J. Hydraul. Eng. 1999, 125, 676–685. [Google Scholar] [CrossRef]
- Hanmaiahgari, P.R.; Maji, S. Eddy Viscosity Turbulence Model for Incompressible Fluid Flow in Closed Conduits. In Proceedings of the 19th IAHR-APD Congress, Hanoi, Vietnam, 21 September 2014. [Google Scholar]
- Granville, P.S. A Modified Van Driest Formula for the Mixing Length of Turbulent Boundary Layers in Pressure Gradients. ASME J. Fluid Eng. 1990, 12, 777–849. [Google Scholar] [CrossRef]
- Araya, W.F.S. Silva-Araya Energy Dissipation in Transient Flow. Ph.D. Thesis, Washington State University, Pullman, WA, USA, 1993. [Google Scholar]
- SaemI, S.; Raisee, M.; Cervantes, M.J.; Nourbakhsh, A. Computation of Two- and Three-Dimensional Water Hammer Flows. J. Hydraul. Res. 2019, 57, 386–404. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Soares, A.K.; Ramos, H.M.; Covas, D.I.C. CFD Modeling of Transient Flow in Pressurized Pipes. Comput. Fluids 2016, 126, 129–140. [Google Scholar] [CrossRef]
- Korteweg, D.J. Ueber Die Fortpflanzungsgeschwindigkeit des Schalles in Elastischen Röhren; Wiely: Hoboken, NJ, USA, 1878. [Google Scholar]
- Martins, N.M.C.; Carriço, N.J.G.; Ramos, H.M.; Covas, D.I.C. Velocity-Distribution in Pressurized Pipe Flow Using CFD: Accuracy and Mesh Analysis. Comput. Fluids 2014, 105, 218–230. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, L.; Ou, C.; Fang, H.; Liu, D. 3D CFD Simulation and Analysis of Transient Flow in a Water Pipeline. Aqua Water Infrastruct. Ecosyst. Soc. 2022, 71, 751–767. [Google Scholar] [CrossRef]
- Fursikov, A.V.; Imanuvilov, O.Y. Exact Controllability of the Navier-Stokes and Boussinesq Equations. Russ. Math. Surv. 1999, 54, 565–618. [Google Scholar] [CrossRef]
- Kyle Anderson, W.; Newman, J.C.; Whitfield, D.L.; Nielsen, E.J. Sensitivity Analysis for Navier-Stokes Equations on Unstructured Meshes Using Complex Variables. AIAA J. 2001, 39, 56–63. [Google Scholar] [CrossRef]
- FLUENT 6.3 User’s Guide. Available online: https://www.academia.edu/35464626/FLUENT_6_3_Users_Guide (accessed on 11 September 2023).
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of Turbulence Models for Shear Flows by a Double Expansion Technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Saemi, S.D.; Raisee, M.; Cervantes, M.J.; Nourbakhsh, A. Computation of Laminar and Turbulent Water Hammer Flows. In Proceedings of the 1th World Congress on Computational Mechanics (WCCM XI), 5th European Conference on Computational Mechanics (ECCM V), 6th European Conference on Computational Fluid Dynamics (ECFD VI), Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Martin, N.M.C.; Wahba, E.M. On the Hierarchy of Models for Pipe Transients: From Quasi-Two-Dimensional Water Hammer Models to Full Three-Dimensional Computational Fluid Dynamics Models. ASME J. Press. Vessel. Technol. 2022, 144, 021402. [Google Scholar] [CrossRef]
- Wu, D.; Yang, S.; Wu, P.; Wang, L. MOC-CFD Coupled Approach for the Analysis of the Fluid Dynamic Interaction between Water Hammer and Pump. J. Hydraul. Eng. 2015, 141, 06015003. [Google Scholar] [CrossRef]
- Ferreira, J.P.B.C.C.; Martins, N.M.C.; Covas, D.I.C. Ball Valve Behavior under Steady and Unsteady Conditions. J. Hydraul. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Riasi, A.; Nourbakhsh, A.; Raisee, M. Unsteady Velocity Profiles in Laminar and Turbulent Water Hammer Flows. ASME J. Fluids Eng. 2009, 131, 1212021–1212028. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Liu, D.; Karney, B.; Wang, P.; Xia, L.; Ma, J.; Xu, C. CFD Approach for Column Separation in Water Pipelines. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Kalantar, M.; Jonsson, P.; Dunca, G.; Cervantes, M.J. Numerical Investigation of the Pressure-Time Method. IOP Conf. Ser. Earth Environ. Sci. Inst. Phys. 2022, 1079, 012075. [Google Scholar] [CrossRef]
- Saemi, S.; Raisee, M.; Cervantes, M.J.; Nourbakhsh, A. Numerical Investigation of the Pressure-Time Method Considering Pipe with Variable Cross Section. ASME J. Fluids Eng. 2018, 140, 44–58. [Google Scholar] [CrossRef]
- Mandair, S.; Magnan, R.; Morissette, J.-F.; Karney, B. Energy-Based Evaluation of 1D Unsteady Friction Models for Classic Laminar Water Hammer with Comparison to CFD. J. Hydraul. Eng. 2020, 146. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transient; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Neyestanaki, M.K.; Dunca, G.; Jonsson, P.; Cervantes, M.J. A Comparison of Different Methods for Modelling Water Hammer Valve Closure with CFD. Water 2023, 15, 1510. [Google Scholar] [CrossRef]
- Simindhokt, S.; Mehrdad, R. Numerical Investigation of the Pressure Time Method. Flow Meas. Instrum. 2017, 55, 44–58. [Google Scholar]
- Simindokht, S. Raisee Mehrdad Evaluation of Transient Effects in the Pressure-Time Method. Flow. Meas. Instrum. 2019, 68, 101581. [Google Scholar]
- Han, Y.; Shi, W.; Xu, H.; Wang, J.; Zhou, L. Effects of Closing Times and Laws on Water Hammer in a Ball Valve Pipeline. Water 2022, 14, 1497. [Google Scholar] [CrossRef]
- Yoon, Y.; Park, B.H.; Shim, J.; Han, Y.O.; Hong, B.J.; Yun, S.H. Numerical Simulation of Three-Dimensional External Gear Pump Using Immersed Solid Method. Appl. Therm. Eng. 2017, 118, 539–550. [Google Scholar] [CrossRef]
- He, S.; Ariyaratne, C.; Vardy, A.E. A Computational Study of Wall Friction and Turbulence Dynamics in Accelerating Pipe Flows. Comput. Fluids 2008, 37, 674–689. [Google Scholar] [CrossRef]
- Vardy, A.E.; Brown, J.M.B.; He, S.; Ariyaratne, C.; Gorji, S. Applicability of Frozen-Viscosity Models of Unsteady Wall Shear Stress. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Guerrero, B.; Lambert, M.F.; Chin, R.C. Extreme Wall Shear Stress Events in Turbulent Pipe Flows: Spatial Characteristics of Coherent Motions. J. Fluid Mech. 2020, 904. [Google Scholar] [CrossRef]
- Guerrero, B.; Lambert, M.F.; Chin, R.C. Transient Dynamics of Accelerating Turbulent Pipe Flow. J. Fluid Mech. 2021, 917, A43. [Google Scholar] [CrossRef]
- Maruyama, T.; Kuribayashf, T.; Mizushina, T. The Structure of the Turbulence in Transient Pipe Flow. J. Chem. Eng. Jpn. 1976, 9, 431–439. [Google Scholar] [CrossRef]
- Jackson, H. A Study of Turbulence under Conditions of Transient Flow in a Pipe. J. Fluid Mech. 2000, 408, 1–38. [Google Scholar]
- Greenblatt, D.; Moss, E.A. Rapid Temporal Acceleration of a Turbulent Pipe Flow. J. Fluid Mech. 2004, 514, 65–75. [Google Scholar] [CrossRef]
- Jung, S.Y.; Chung, Y.M. Large-Eddy Simulation of Accelerated Turbulent Flow in a Pipe. In PProceedings of the 6th International Symposium on Turbulence and Shear Flow Phenomena, TSFP 2009, International Symposium on Turbulence and Shear Flow Phenomena, TSFP, Seoul, Republic of Korea, 22–24 June 2009; pp. 277–282. [Google Scholar]
- He, S.; Seddighi, M. Turbulence in Transient Channel Flow. J. Fluid Mech. 2013, 715, 60–102. [Google Scholar] [CrossRef]
- Guala, M.; Tomkins, C.D.; Christensen, K.T.; Adrian, R.J. Vortex Organization in a Turbulent Boundary Layer Overlying Sparse Roughness Elements. J. Hydraul. Res. 2012, 50, 465–481. [Google Scholar] [CrossRef]
- Dey, S.; Lambert, M.F. Reynolds Stress and Bed Shear in Nonuniform Unsteady Open-Channel Flow. J. Hydraul. Eng 2005, 131, 610–614. [Google Scholar] [CrossRef]
- Ariyaratne, C.; He, S.; Vardy, A.E. Wall Friction and Turbulence Dynamics in Decelerating Pipe Flows. J. Hydraul. Res. 2010, 48, 810–821. [Google Scholar] [CrossRef]
- Mathur, A.; Gorji, S.; He, S.; Seddighi, M.; Vardy, A.E.; O’Donoghue, T.; Pokrajac, D. Temporal Acceleration of a Turbulent Channel Flow. J Fluid Mech. 2018, 835, 471–490. [Google Scholar] [CrossRef]
- Chung, Y.M. Unsteady Turbulent flow with Sudden Pressure Gradient Changes. Int. J. Numer. Meth. Fluids 2005, 47, 925–930. [Google Scholar] [CrossRef]
- Joel Sundstrom, L.R.; Cervantes, M.J. Laminar Similarities between Accelerating and Decelerating Turbulent Flows. Int. J. Heat Fluid Flow 2018, 71, 13–26. [Google Scholar] [CrossRef]
- Seddighi, M.; He, S.; Orlandi, P.; Vardy, A.E. A Comparative Study of Turbulence in Ramp-up and Ramp-down Unsteady Flows. Flow. Turbul. Combust 2011, 86, 439–454. [Google Scholar] [CrossRef]
- Guerrero, B.; Lambert, M.F.; Chin, R.C. Transient Behaviour of Decelerating Turbulent Pipe Flows. J. Fluid Mech. 2023, 962, A44. [Google Scholar] [CrossRef]
- Meng, W.; Cheng, Y.; Wu, J.; Yang, Z.; Zhu, Y.; Shang, S. GPU Acceleration of Hydraulic Transient Simulations of Large-Scalewater Supply Systems. Appl. Sci. 2018, 9, 91. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, M.R.A.; Pu, J.H.; Hanmaiahgari, P.R.; Lambert, M.F. Insights into CFD Modelling of Water Hammer. Water 2023, 15, 3988. https://doi.org/10.3390/w15223988
Kumar MRA, Pu JH, Hanmaiahgari PR, Lambert MF. Insights into CFD Modelling of Water Hammer. Water. 2023; 15(22):3988. https://doi.org/10.3390/w15223988
Chicago/Turabian StyleKumar, M. R. Ajith, Jaan H. Pu, Prashanth R. Hanmaiahgari, and Martin F. Lambert. 2023. "Insights into CFD Modelling of Water Hammer" Water 15, no. 22: 3988. https://doi.org/10.3390/w15223988




