Experimental Study on Flow Structure Characteristics of Gap Flow Boundary Layer Based on PIV
Abstract
:1. Introduction
2. Experimental Program
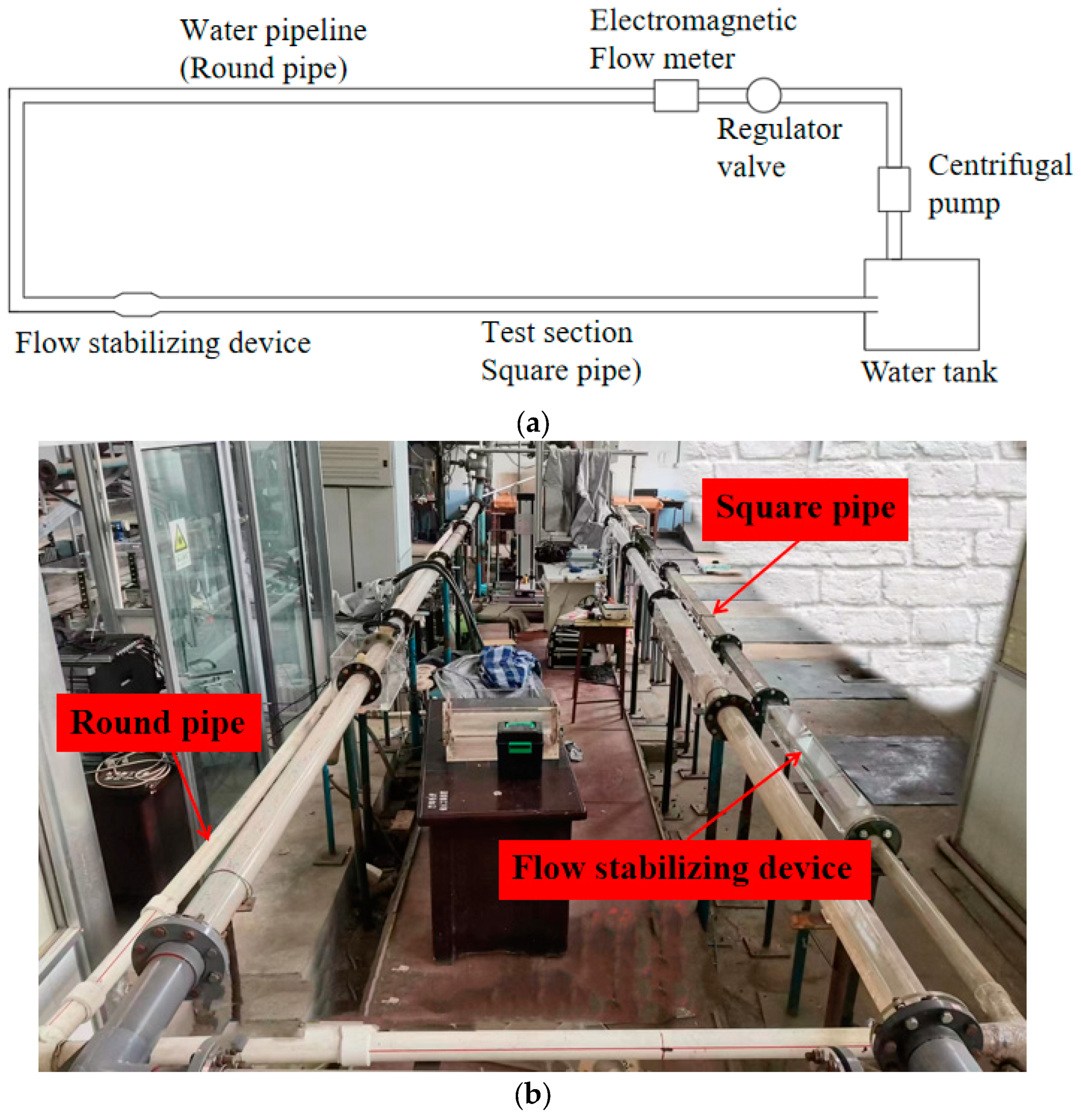
2.1. Experimental System
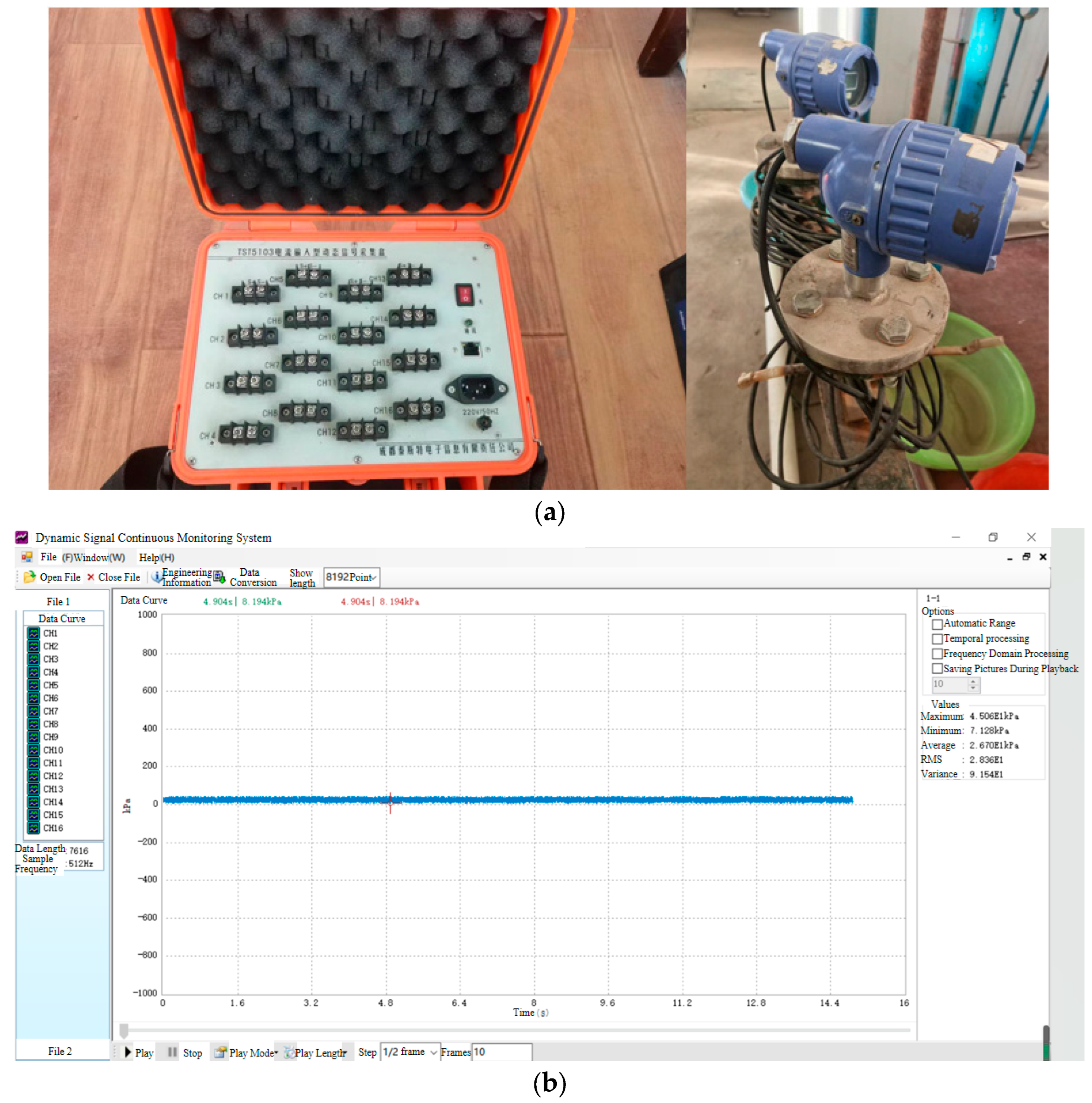
2.2. Measuring Device
2.3. Experimental Program Design
2.3.1. Test Conditions
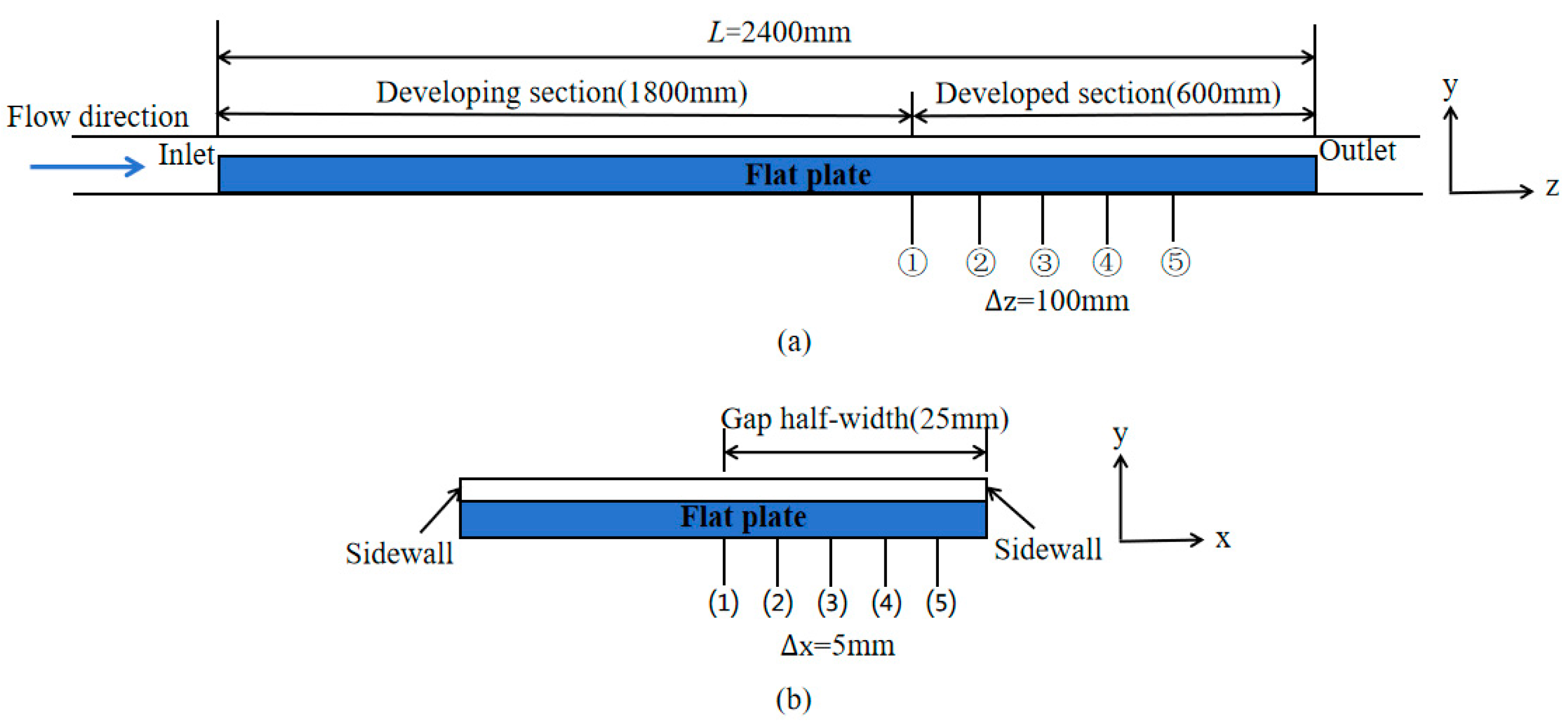
2.3.2. Arrangement of Test Sections and Test Lines
3. Results
3.1. Calculation of Wall Friction Velocity
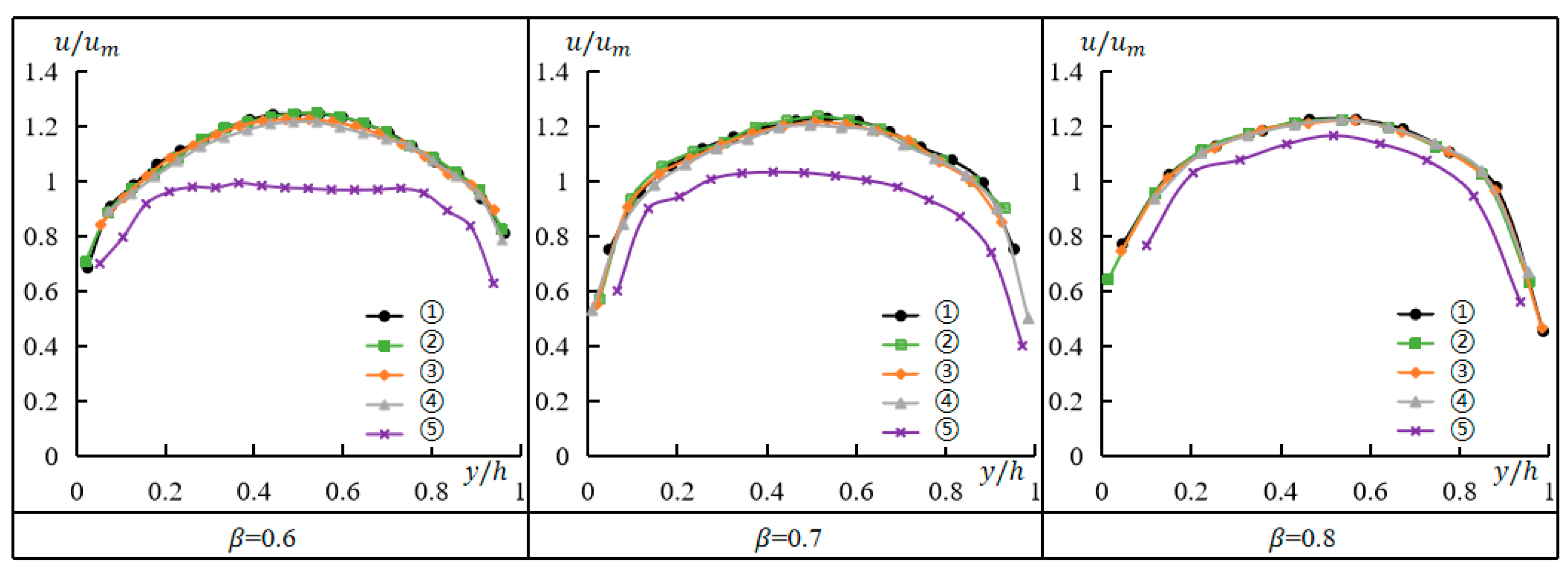
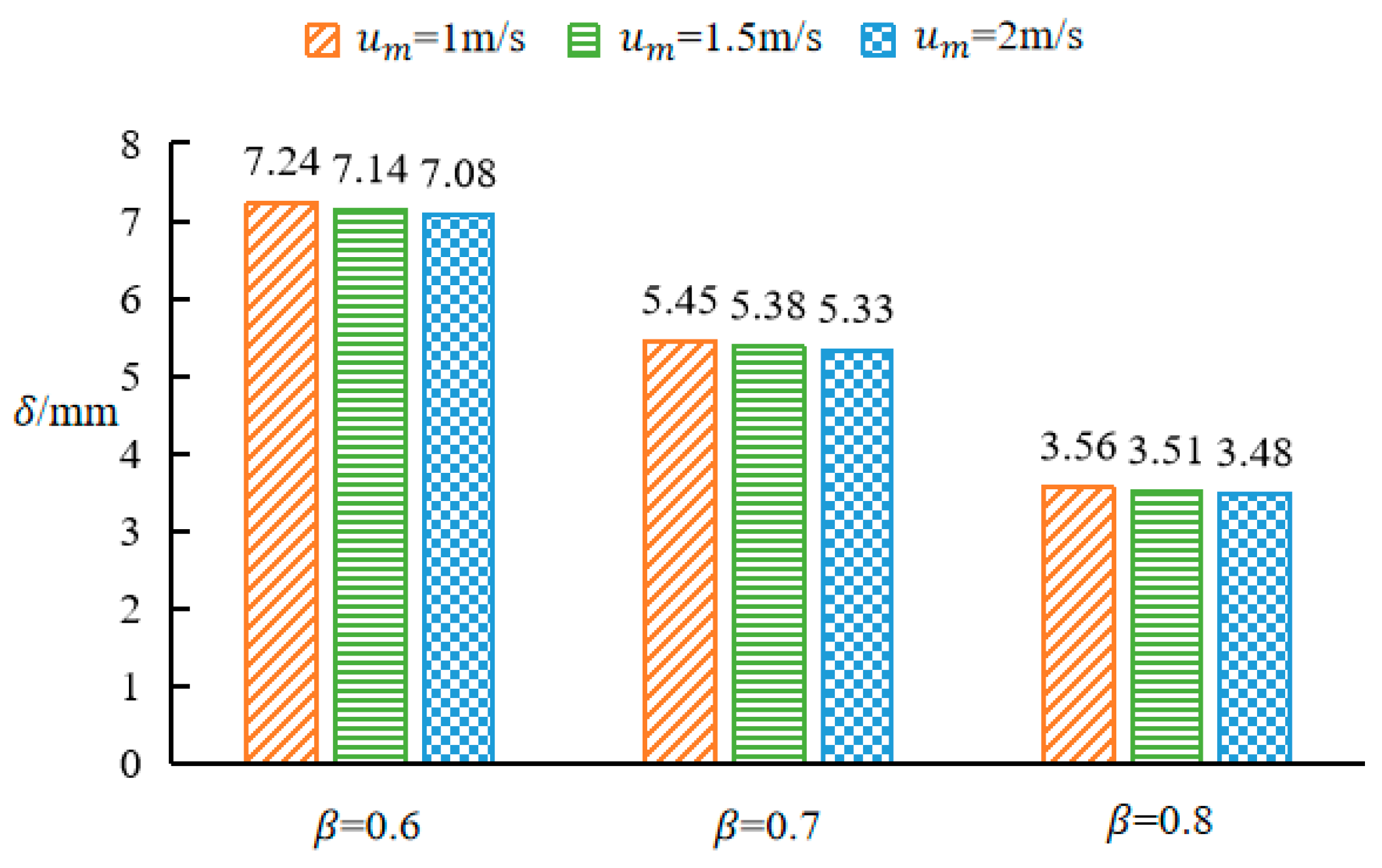
3.2. Boundary Layer Thickness
3.3. Wall Function
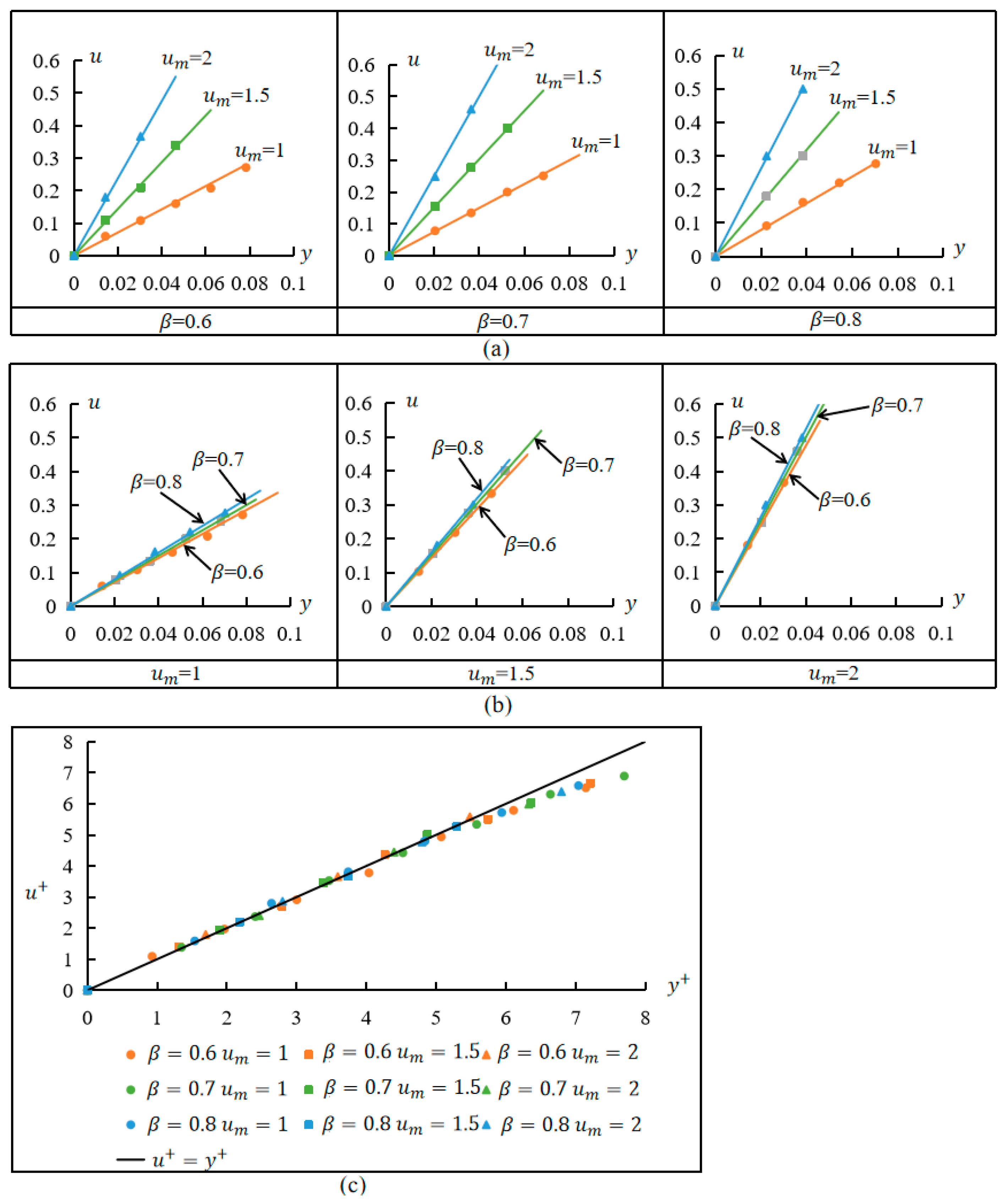
3.3.1. Viscous Sub-Layer
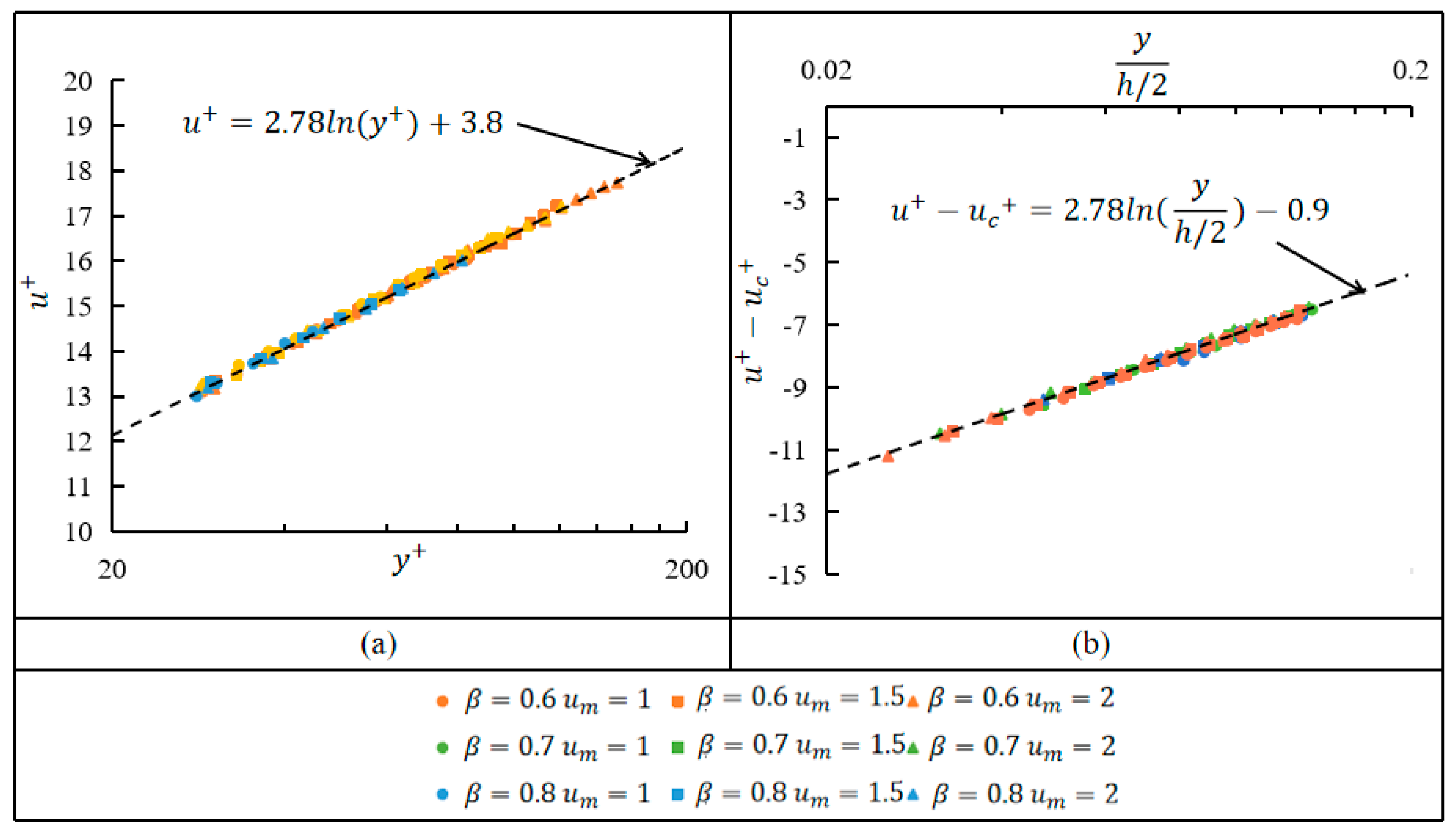
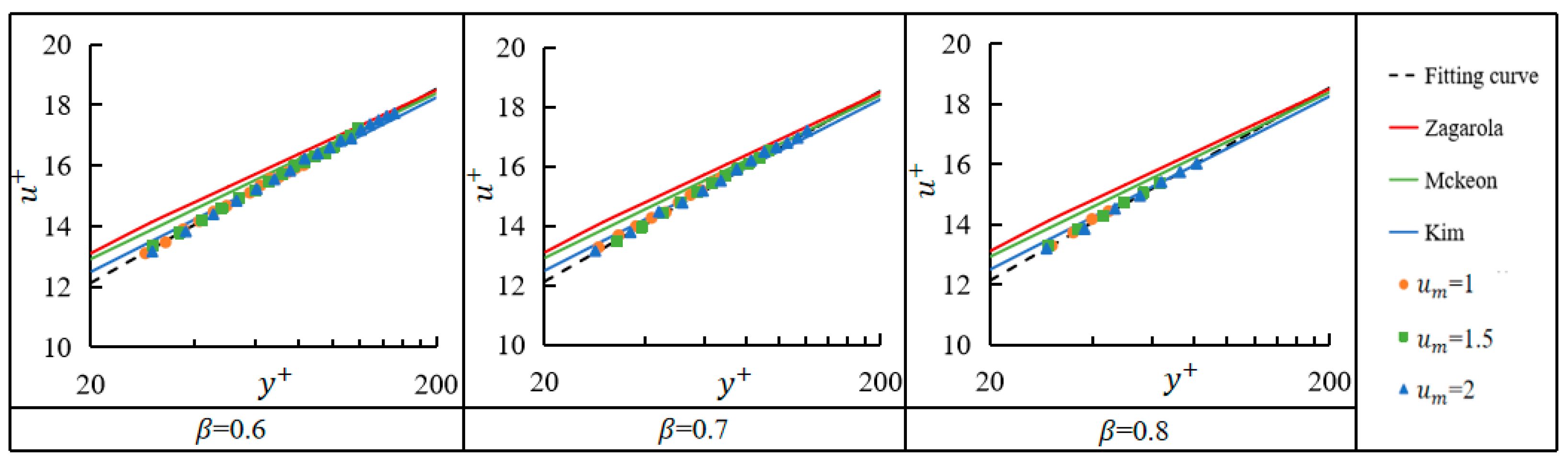
3.3.2. Logarithmic Layer
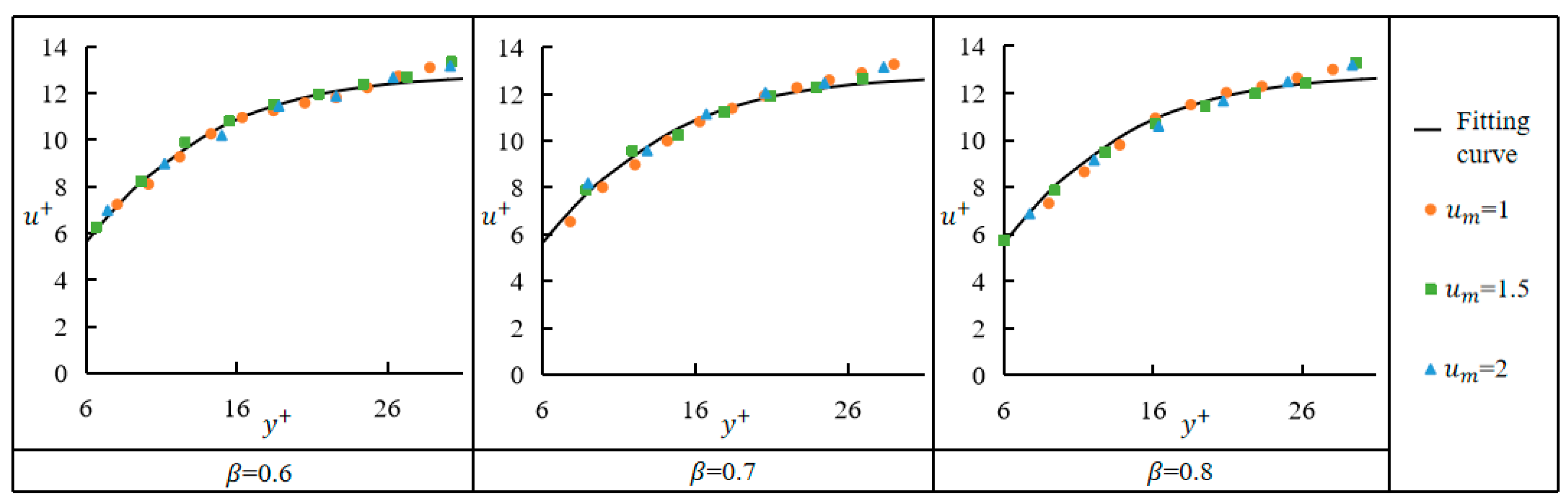
3.3.3. Transition Layer
4. Discussion
5. Conclusions
- (1)
- In this study, two methods were used to calculate the wall friction velocity, the results of the two methods were very similar, and the maximum relative error did not exceed 5%, which indicates that using PIV to measure the velocity profile in the viscous sub-layer to solve the wall friction velocity had good precision.
- (2)
- The boundary layer thickness of the gap flow was inversely proportional to both the mean velocity of the gap flow and the gap ratio, and the ratio of the boundary layer thickness to the gap half-height was constant for all the conditions investigated in this study.
- (3)
- The boundary layer data were nondimensionalized by using the wall friction velocity and the wall position to obtain the wall function of the boundary layer of the gap flow; it was expressed as
- (4)
- In the viscous sub-layer, the velocity gradient was proportional to both the mean velocity of the gap flow and the gap ratio, and thus, the wall friction velocity was also proportional to the mean velocity of the gap flow and the gap ratio; the experimental data in the transition region satisfied the hyperbolic tangent function well; and the logarithmic region satisfied both the logarithmic law and the law of defects, and was therefore also known as the overlap region.
- (5)
- The thickness of the logarithmic region increased with the increase in the mean velocity of the gap flow and decreased with the increase in the gap ratio. The range of the inner region of the gap flow boundary layer was 0.18 or 0.13(/2).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qianqian, L.; Chengwei, H.; Jian, R. The gap flow resistance of start and its influence of 2D servo valve. Mach. Tool Hydraul. 2023, 51, 39–44. [Google Scholar]
- Jian, H.; Kaiqiang, W.; Chao, W.; Lang, G.; Chunyu, G. Prediction of hydrodynamic performance of pump jet propulsor considering the effect of gap flow model. Ocean Eng. 2021, 233, 109162. [Google Scholar] [CrossRef]
- Guangjie, P.; Shiming, H.; Hao, C.; Fengyi, F.; Yiyang, Z.; Peng, S. Numerical and experimental research on the influence of clearance between impeller and cover on the pump performance. Mechanika 2022, 28, 67–72. [Google Scholar]
- Xiaoneng, J.; Xihuan, S.; Yongye, L. Numerical simulation of annular gap flow field of static pipeline vehicle under different Reynolds numbers. J. Vib. Shock. 2021, 3, 10–18. [Google Scholar]
- Shunfang, H.; Xianzhi, D. Several problems in the teaching of boundary layer theory. J. Nav. Univ. Eng. 1983, 3, 93–97. [Google Scholar]
- Von Karman, T. Lanminare und Turbulente Reibung. Z. Angew. Math. Mech. 1921, 1, 235. [Google Scholar]
- Prandtl, L. Bericht über neuere Untersuchungen über das Verhalten der laminaren Reibungsschicht, insbesondere den laminar-turbulenten Umschlag. Luftfahrtforschung 1942, 2, 141–147. [Google Scholar]
- Nikuradse, J. GesetmäBigkeiten der Turbulenten Strömung in Glatten Rohren. Forschungsheft 356, Augabe B Band 3; VDI-Verlag: Berlin, German, 1932. [Google Scholar]
- Jinyin, Z. Experimental Investigation and Numerical Simulation of Turbulent Pipe Flow and the Tripping Effects; Dalian University of Technology: Dalian, China, 2002. [Google Scholar]
- Zagarola, M.V.; Smits, A.J. Mean-flow scaling of turbulent pipe flow. Fluid Mech. 1998, 373, 33–79. [Google Scholar] [CrossRef]
- Zengnan, D.; Changzhi, C.; Xinyu, L. State of the research of open-channel turbulence. Hydrodynamics 1994, 9, 8–22. [Google Scholar]
- Jianzhong, L.; Xiurong, Z. The Study of Turbulent Boundary Layer on the Outlet Structure. Hydraul. Eng. 1985, 8, 19–25. [Google Scholar]
- Wenping, W. The Problem of Turbulent Boundary Layer in Hydraulic Structure—Theory and Application; Xi’an University of Technology: Xi’an, China, 2007. [Google Scholar]
- Bingbo, W. The development and application of Computational Fluid Dynamics. Mech.-Electron. Appl. Tech. 2018, 49, 145. [Google Scholar]
- Afra, B.; Karimnejad, S.; Delouei, A.A.; Tarokh, A. Flow control of two tandem cylinders by a highly flexible filament: Lattice spring IB-LBM. Ocean Eng. 2022, 250, 111025. [Google Scholar] [CrossRef]
- Delouei, A.A.; Karimnejad, S.; He, F.L. Direct Numerical Simulation of pulsating flow effect on the distribution of non-circular particles with increased levels of complexity: IB-LBM. Comput. Math. Appl. 2022, 121, 115–130. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- Moser, R.D.; Kim, J.; Mansour, N.N. Direct numerical simulation of turbulent channel flow up to Reτ = 590. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Minwei, W. Numerical Research on Turbulent Pipe Flow; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Chunxiao, X. Direct Numerical Simulation on Channel Turbulence; Tsinghua University Press: Beijing, China, 1995. [Google Scholar]
- Johansson, A.V.; Alfredsson, P.H. Effects of imperfect spatial resolution on measurement of wall-bounded turbulent shear flows. Fluid Mech. 1983, 137, 409. [Google Scholar] [CrossRef]
- Xuan, Z.; Xue, S.; Yukui, T.; Hailang, S.; Hua, X.; Nan, Z. Experimental and Numerical Investigations of the Boundary Layer Parameters of an Underwater Flat Plate Model. J. Exp. Fluid Mech. 2017, 31, 26–31. [Google Scholar]
- Yonghao, Z.; Xiaoyong, Y.; Luguo, L.; Shouxu, Q.; Sichao, T. Visualization Experiment of Velocity Boundary Layer in Rectangular Channel Using PIV Technique. At. Energy Sci. Technol. 2023, 57, 503–513. [Google Scholar]
- Weiyi, Y.; Wenhai, Q.; Jinbiao, X.; Tengfei, Z.; Xiang, C.; Xiaojing, L. PIV flow measurement in a Rectangular Narrow Channel with Inlet Blockage. Nucl. Sci. Eng. 2021, 41, 1016–1022. [Google Scholar]
- Zhanmin, L.; Maozhu, Y. The LDA Measurement of Turbulent Flow in Square Duct and the Comparison of Some Flow Characteristics with Pipe Flow. Chin. J. Theor. Appl. Mech. 1986, 18, 267–275. [Google Scholar]
- Kangjun, W.; Jianxia, B.; Zhanqi, T.; Nan, J. Comparative Study of Turbulent Boundary Layer Wall Friction Velocity Measured by Average Velocity Profile Method. J. Exp. Mech. 2019, 34, 209–216. [Google Scholar]
- Millikan, C.B. A Critical Discussion of Turbulent Flows in Channels and Circle Tubes. In Proceedings of the Fifth International Congress of Applied Mechanics, New York, NY, USA, 28 October 1939. [Google Scholar]
- Rannie, W.D. Heat Transfer in Turbulent Shear Flow. J. Aeronaut. Sci. 1956, 23, 485. [Google Scholar] [CrossRef]
- Tardu, S.F.; Brunton, S.L.; Noack, B.R. Active Control of the Turbulent Drag by a Localized Periodical Blowing Dissymmetric in Time. Exp. Fluids 2009, 47, 19–26. [Google Scholar] [CrossRef]
- Von Karman, T. The Analogy between Fluid Friction and Heat Transfer. Trans. ASME 1939, 61, 705–710. [Google Scholar] [CrossRef]
- Spalding, D.B. A Single Formula for the “Law of the Wall”. J. Appl. Mech. 1961, 28, 455–458. [Google Scholar] [CrossRef]
- Zagarola, M.V.; Smits, A.J. Scaling of the Mean Velocity Profile for Turbulent Pipe Flow. Phys. Rev. Lett. 1997, 78, 239–242. [Google Scholar] [CrossRef]
- Mckeon, B.J.; Li, J.; Jiang, W.; Morrison, J.F.; Smits, A.J. Further Observations on the Mean Velocity in Fully-developed Pipe Flow. J. Fluid Mech. 2004, 501, 135–147. [Google Scholar] [CrossRef]
- Wangyi, W. Fluid Mechanics, 18th ed.; Peking University Press: Beijing, China, 2019; pp. 370–372. [Google Scholar]
- Zengmin, D. Experimental Study on the Lateral Velocity Derivative in a Turbulent Boundary Layer; Harbin Institute of Technology: Harbin, China, 2017. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Nezu, I.; Rodi, W. Open-channel Flow Measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Cardoso, A.H.; Graf, W.H.; Gust, G. Uniform Flow in a Smooth Open Channel. J. Hydraul. Res. 1989, 27, 603–616. [Google Scholar] [CrossRef]
- Roussinova, V.; Biswas, N.; Balachandar, R. Revisiting Turbulence in Smooth Uniform Open Channel Flow. J. Hydraul. Res. 2008, 46, 36–48. [Google Scholar] [CrossRef]
- Qiang, Z.; Fengchuan, Z.; Yuchen, Y.; Zhaoyu, D. Diagnostic Function Analysis of the Logarithmic Law in Open Channel Turbulence. J. Tsinghua Univ. Sci. Technol. 2019, 59, 999–1005. [Google Scholar]




| Gap Ratio | Plate Height | Square Pipe Height | Square Pipe Width (Gap Width) | Gap Height |
|---|---|---|---|---|
| 0.6 | 30 | 50 | 50 | 20 |
| 0.7 | 35 | 50 | 50 | 15 |
| 0.8 | 40 | 50 | 50 | 10 |
| Gap Ratio | Mean Velocity of Gap Flow | Reynolds Number of Gap Flow |
|---|---|---|
| 0.6 | 1 | 28,435 |
| 1.5 | 42,652 | |
| 2 | 56,870 | |
| 0.7 | 1 | 22,967 |
| 1.5 | 34,450 | |
| 2 | 45,933 | |
| 0.8 | 1 | 16,587 |
| 1.5 | 24,880 | |
| 2 | 33,174 |
| = 0.6 | |||
| =1 m/s | = 1.5 m/s | = 2 m/s | |
| Method 1 | 0.0568 | 0.0820 | 0.1056 |
| Method 2 | 0.0549 | 0.0781 | 0.1004 |
| Relative error | 3.35% | 4.76% | 4.92% |
| = 0.7 | |||
| = 1 m/s | = 1.5 m/s | = 2 m/s | |
| Method 1 | 0.0577 | 0.0836 | 0.1084 |
| Method 2 | 0.0567 | 0.0806 | 0.1035 |
| Relative error | 1.73% | 3.59% | 4.52% |
| = 0.8 | |||
| = 1 m/s | = 1.5 m/s | = 2 m/s | |
| Method 1 | 0.0580 | 0.0838 | 0.1088 |
| Method 2 | 0.0577 | 0.0817 | 0.1049 |
| Relative error | 0.52% | 2.51% | 3.58% |
| 1 m/s | 1.5 m/s | 2 m/s | |||
|---|---|---|---|---|---|
| 0.6 | 59/0.126 | 94/0.143 | 129/0.154 | ||
| 0.7 | 41/0.114 | 66/0.131 | 95/0.148 | ||
| 0.8 | 18/0.074 | 40/0.117 | 55/0.127 | ||
| 1 m/s | 1.5 m/s | 2 m/s | |||
|---|---|---|---|---|---|
| K | |||||
| 0.6 | 0.0708 | 0.0695 | 0.0716 | ||
| 0.7 | 0.0717 | 0.0704 | 0.0711 | ||
| 0.8 | 0.0715 | 0.0713 | 0.0712 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Sun, X.; Li, Y.; Wang, C. Experimental Study on Flow Structure Characteristics of Gap Flow Boundary Layer Based on PIV. Water 2023, 15, 3989. https://doi.org/10.3390/w15223989
Sun L, Sun X, Li Y, Wang C. Experimental Study on Flow Structure Characteristics of Gap Flow Boundary Layer Based on PIV. Water. 2023; 15(22):3989. https://doi.org/10.3390/w15223989
Chicago/Turabian StyleSun, Lei, Xihuan Sun, Yongye Li, and Cheng Wang. 2023. "Experimental Study on Flow Structure Characteristics of Gap Flow Boundary Layer Based on PIV" Water 15, no. 22: 3989. https://doi.org/10.3390/w15223989
APA StyleSun, L., Sun, X., Li, Y., & Wang, C. (2023). Experimental Study on Flow Structure Characteristics of Gap Flow Boundary Layer Based on PIV. Water, 15(22), 3989. https://doi.org/10.3390/w15223989





