Abstract
Our study focuses on the dynamic transient analysis of arched beam bridges over rivers, which face unique geohazards and challenges, including vibrations and dynamic loads that can affect structural integrity. The finite element software ANSYS v. 19.3 was employed to assess acceleration time histories at various bridge positions. Using MATLAB, we conducted wavelet packet decomposition to extract insights from the data, specifically isolating river-induced influences. In this article, the introduction of the wavelet packet rate index (WPERI) is presented as a novel metric for the detection of cracks in the curved bridge segments over rivers. The WPERI proves reliable in accounting for the river environment’s impact on structural integrity. Our findings highlight the sensitivity and precision of the WPERI in accurately detecting cracks and vulnerabilities in these riverine bridges. By combining WPT, finite element analysis, and signal decomposition, our research offers insights into tailored crack detection methods for riverine bridges. This study underscores the potential of WPT as a tool for identifying and characterizing cracks in curved bridge elements over rivers. The innovative WPERI provides a holistic approach to addressing structural issues, thus enhancing bridge durability amid changing environmental conditions. It contributes significantly to structural engineering and paves the way for the further exploration of river-specific crack detection techniques.
1. Introduction
During the operational lives of structural elements such as beam-type constructions, expansive bridges, and skyscrapers, the gradual accumulation of localized damage poses a risk of progressive failure. To address this issue, a four-tiered classification system for damage identification has been developed. The system involves (i) detecting the presence of damage, (ii) pinpointing its location, (iii) quantifying the severity of damage, and (iv) forecasting the remaining structural serviceability [1]. Structural damage often results in alterations toa structure’s dynamic behavior, which are prominently reflected in changes in natural frequencies and mode shapes. These variations can be valuable for identifying damage. Various methods exist for assessing and tracking these changes, each with its own strengths and weaknesses. Additionally, the application of Fourier transformation allows the conversion of signals between the time and frequency domains. In summary, as structures like bridges and skyscrapers age, the gradual accumulation of damage can lead to progressive failure. A classification system has been developed to systematically identify and assess this damage, primarily through changes in a structure’s dynamic behavior, which can be measured using techniques like Fourier transformation [2,3].
To address this issue, the short-time Fourier transform (STFT) was introduced. STFT divides a signal into smaller, equallysized segments and creates a two-dimensional representation of time and frequency. However, STFT has limitations when it comes to providing precise information about both time and frequency due to the fixed window size, making it challenging to balance time and frequency resolution [4]. In contrast, the wavelet transform (WT) offers a fresh approach to signal analysis, overcoming the constraints of traditional signal processing methods. Wavelets have the unique ability to conduct localized analyses of a signal, allowing a focused examination of specific time or space intervals. This characteristic significantly enhances the precision in terms of identifying structural irregularities within complex domains [5,6]. The use of wavelet analysis introduces a more nuanced dimension into structural health assessment, providing a powerful tool for detecting and understanding evolving conditions within intricate structures. In essence, wavelet analysis overcomes the trade-off between temporal and spectral precision, enabling a more refined understanding of structural dynamics and the manifestation of damage. The WT is a potent mathematical tool used for analyzing signals or data simultaneously in the time and frequency domains. It excels when dealing with signals containing transient or localized features. Unlike the STFT, which only provides frequency information, the wavelet transform captures both temporal and frequency details. The key concept involved in the wavelet transform is breaking down a signal into a set of wavelet functions, or wavelets, known for their compact and localized waveform nature. These wavelets are derived from a foundational mother wavelet function through dilation and translation operations. Dilation controls the wavelet’s scale or frequency, while translation determines its temporal position [7]. In practice, the wavelet transform divides the original signal into various scales or resolutions, each representing a distinct spectrum of frequencies. Within each scale, it calculates a set of wavelet coefficients that reveal how the wavelets contribute to the signal in that particular scale. These coefficients provide insights into the signal’s temporal localization and frequency components [8,9].
Wavelet transform (WT) and wavelet packet transform (WPT) are valuable signal processing techniques with applications in various fields. WT allows signal decomposition into different scales, offering both high- and low-frequency component analysis using wavelets. These localized, short-duration waveforms provide a time–frequency trade-off, enabling the capture of transient features in signals. The continuous wavelet transform (CWT) operates on a continuous range of scales, while the discrete wavelet transform (DWT) simplifies the process with discrete scales and translations, commonly used in tasks like data compression and denoising. On the other hand, WPT extends the DWT by allowing both high- and low-frequency components to be further subdivided into sub-bands, resulting in a more detailed signal decomposition. This flexibility and adaptability make WPT a powerful tool for applications requiring a comprehensive analysis of signal frequency content, such as speech recognition, image processing, and biomedical signal analysis. By offering enhanced decomposition and the option to choose specific wavelet bases for each sub-band, WPT provides a richer representation of signals, particularly useful for feature extraction tasks. In the realm of the WPT, the process initiates with the division of the signal into sub-bands, achieved via a dedicated wavelet filter. However, the WPT diverges from its predecessor, the wavelet transform, by granting the liberty for multiple sub-bands to coexist at each tier of decomposition. This enrichment results in a deeper and more intricate decomposition, amplifying the WPT’s capacity to encapsulate nuanced intricacies and variations within the signal [10,11]. Distinct filters are employed to split the signal into its various sub-bands, culminating in a tree-like representation where each node corresponds to a particular sub-band. This branching tree structure, akin to a network of signal components, providesa comprehensive means of dissecting and interpreting the signal’s attributes. This recursive process of decomposition can be pursued until the desired level of signal intricacy is achieved. The merit of the WPT is firmly grounded in its ability to present a holistic and in-depth portrayal of a signal. By accommodating varied scales and frequencies, the WPT meticulously captures multifaceted information, thereby enriching the signal representation [12].
The WT delivers a multiresolution analysis, presenting acapacity to identify cracks across various scales or resolutions. Within the context of arched beams, the introduction of cracks can introduce high-frequency elements into the signal. Here, the WT thrives by adeptly capturing these high-frequency features, thereby establishing its efficacy in the detection and localization of cracks [13,14]. Its intrinsic time–frequency localization properties serve as a pivotal asset in singling out transient or localized crack attributes, a crucial step in distinguishing them from other signal constituents. Moreover, the WT’s unique ability to segment the signal into both approximation and detail coefficients facilitates the extraction of crack-related insights from the signal [15,16]. On the other hand, the WPT extends its advantage by offering more detailed signal decomposition compared to the WT. Armed with multiple sub-bands at each level, the WPT possesses the prowess to capture intricate nuances and fluctuations within the signal [17]. This attribute becomes especially beneficial in the realm of crack identification for arched beams, where the nature of cracks might exhibit multifaceted patterns and variations. The WPT’s configuration, resembling a tree-like structure, introduces flexibility into the analysis—each sub-band can be independently examined [18]. This inherent flexibility gains significance in the realm of arched beams, where cracks might manifest distinct characteristics and arise at diverse locations. The meticulous decomposition offered by the WPT facilitates a comprehensive grasp of the intricacies inherent to crack features, culminating in the precise identification and assessment of crack severity [19,20]. Table 1 provides a summary of the advantages and limitations of the WT and WPT methods compared to traditional methods (e.g., classic analytic method, numerical modeling, etc.).

Table 1.
A comparison between the advantages and limitations of this study using traditional methods.
WT and WPT find valuable applications in the analysis of structural elements like beam-type constructions, particularly in the domains of structural health monitoring, damage detection, and vibration analysis. When dealing with beam-type structures, such as those commonly found in construction, these techniques play pivotal roles in understanding their behavior and integrity. WT, for instance, proves its worth by offering insights into the dynamic characteristics of beams. It is instrumental in vibration analysis, allowing the assessment of natural frequencies and mode shapes. Through dynamic loading or monitoring responses to external forces, WT helps to identify alterations in the vibration patterns, which can serve as early indicators of structural issues. Furthermore, it excels in detecting damage, as structural changes often lead to shifts in the dynamic behavior of beams. By analyzing changes in the frequency response, WT can effectively pinpoint cracks, deformations, or other structural anomalies. In contrast, WPT, as an extension of WT, takes structural analysis a step further. Its ability to perform a granular multi-resolution analysis is particularly beneficial for complex structural systems. WPT meticulously breaks down the structural response into numerous sub-bands, enabling a more detailed examination of structural behavior. It excels at localized damage detection, offering pinpoint accuracy in terms of identifying the specific locations of structural issues. Moreover, WPT’s adaptability allows the selection of specific wavelet bases for each sub-band, enhancing its accuracy in damage detection and localization tasks. In summary, WT and WPT are indispensable tools for evaluating the dynamic characteristics and structural health of beam-type constructions, offering both general and detailed insights into their behavior and integrity, with WPT being particularly valuable for complex structural systems and precise damage detection. The WPT is an advanced mathematical technique that extends the capabilities of the wavelet transform. It facilitates a detailed, step-by-step decomposition of a signal, allowing in-depth analysis. One application of WPT is the estimation of the WPERI, which serves as an indicator of structural damage in simple structures subjected to well-defined input loads.
However, real-world scenarios often pose challenges, particularly in the case of large structures, where it is not feasible to introduce a known excitation. In such practical situations, effective damage detection methods should be able to identify structural issues based on ambient excitation, providing a more robust approach to structural health monitoring. An innovative dimension can be introduced to the WPERI by crafting a methodology that transcends the conventional reliance on known input loads for gauging structural damage. This novel approach revolves around tapping into ambient data to appraise structural well-being in real-world contexts, particularly in scenarios featuring intricate or large-scale structures. The crux of this innovation encompasses the following concepts:
Highlighting Ambient Excitation: elevating WPERI to adeptly identify structural damage under the influence of ambient vibrations and forces, thus eliminating the need for predetermined excitation sources.
Data-Driven Strategies: Making use of data-driven methodologies such as machine learning and artificial intelligence to decipher insights from strategically placed sensors. These techniques adapt to the distinct characteristics of the structure and discern patterns linked to damage.
Multi-Sensor Integration: Employing a network of sensors strategically placed to capture diverse ambient data, including accelerations, strains, and temperature fluctuations. Integrating data from diverse sensors ensures a comprehensive understanding of the structure’s condition.
Real-Time Surveillance: Forging a real-time monitoring system that continuously processes sensor data, dynamically updating the WPERI or a similar metric. This enables swift detection and response to structural alterations or damage.
Anomaly Detection: Implementing methods for anomaly detection that swiftly identify deviations from the anticipated structural behavior, thereby acting as early warning signals for further investigation.
Versatile Applicability: Ensuring that this innovative approach is adaptable for a broad spectrum of structures, from rudimentary to complex, making it a versatile asset for myriad engineering and infrastructure undertakings.
This pioneering perspective on WPERI endows structural health monitoring systems with the capability to thrive in practical scenarios where controlled excitation might not be viable. It establishes a powerful tool for the early identification of structural issues, significantly contributing to the security and long-term endurance of a wide array of structures.
The research at hand capitalizes on the advantageous aspects of both the WPT and the WT, presenting an insightful approach to crack identification within arched beams. The inherent strengths of these techniques lie in their ability to encapsulate the distinctive attributes and features intrinsic to cracks within this specific structural configuration. Concurrently, the WT’s multifaceted approach of multiresolution analysis and time–frequency localization introduces a distinct avenue for singling out crack-associated high-frequency elements and transient attributes. By harnessing the innovative capacities of both the WPT and WT, the accuracy and effectiveness of crack identification within arched beams experience a substantial elevation. This synergistic amalgamation of techniques not only furthers our understanding of crack-related phenomena within the intricate framework of arched beams but also augments our ability to identify, assess, and ultimately address these structural anomalies. The primary objective of this study is to explore the application of WT and WPT as powerful tools for dynamic transient analysis in the context of arched beam bridges located over rivers. This study aims to leverage these methodologies to detect and characterize structural damage, particularly cracks, unique to riverine environments. The central focus is on enhancing the precision and sensitivity of structural health assessment by introducing the innovative WPERI. On the other hand, the motivation for this paper arises from the growing need to develop more effective and refined techniques for assessing the structural integrity of arched beam bridges in river settings. These structures face distinctive geohazards, such as vibrations and dynamic loads, which demand specialized analysis methods. The motivation also stems from the potential to make a significant contribution to the field of structural engineering by introducing a novel approach, the WPERI, which promises enhanced accuracy in terms of detecting and mitigating structural issues. Furthermore, this study’s motivation lies in addressing the practical challenges associated with the conventional limitations of methodologies like STFT in terms of identifying structural vulnerabilities in riverine environments. By synergizing WPT, finite element analysis, and signal decomposition, this study seeks to establish a foundation for the development of more robust and tailored crack detection techniques that can ultimately reinforce the durability of riverine bridges under varying environmental conditions.
2. River-Spanning Bridges
River-spanning bridges are vital components of infrastructure, facilitating efficient transportation and fostering economic growth [21]. These complex engineering marvels demand careful design to ensure not only safety and structural integrity but also operational efficiency. Diverse bridge designs, including arches, suspensions, cable-stays, and beam/girders, are tailored to the unique demands of each river crossing [22,23]. River dynamics introduce intricate challenges into the design equation, as factors like weather conditions and seasonal variations can cause fluctuating water levels and flow rates [24]. The creation of bridges resilient enough to withstand the forces of fast-moving water, potential debris, and even ice during colder months is imperative. Moreover, the ever-present threat of floods mandates the engineering of flood-resistant structures capable of enduring hydraulic forces and preventing scour erosion [25,26].
Arched beam bridges that elegantly stretch over rivers epitomize the fusion of engineering prowess with architectural elegance (see Figure 1). This distinctive bridge construction style seamlessly amalgamates the stability inherent to arches with the load-bearing proficiency of beams, giving rise to bridges that not only traverse water bodies but also stand as enduring symbols of structural efficiency and aesthetic grace [27,28]. The arched component of these bridges, characterized by its gracefully curved form, assumes a pivotal role in the distribution of loads [29]. By transforming vertical forces into lateral ones that are absorbed by abutments or supports at the bridge’s ends, arches ensure unwavering stability while simultaneously facilitating uninterrupted water flow [30]. Overarching the arches, beams provide further reinforcement, deftly shouldering the weight of the bridge deck and distributing it uniformly throughout the entire structure [31,32].
Figure 1.
The various types of river-side arched beam bridges (Reprinted from Ref. [32]).
Arched beam bridges, sometimes simply referred to as arch bridges, are a fascinating and enduring type of bridge design characterized by their gracefully curved arches. These arches are the fundamental structural elements that span the distance the bridge needs to cover. What makes arch bridges remarkable is their natural ability to distribute loads efficiently. When weight, such as that of vehicles or pedestrians, is applied to the bridge, the arch shape redirects the forces downward and outward along the curve. This design feature allows the bridge to efficiently transfer the load to its supports, typically abutments or piers, resulting in exceptional stability. As a result, arch bridges are often preferred for spanning rivers, valleys, and gorges, where a long, unobstructed span is essential. These bridges can be constructed using a variety of materials, from traditional stone and brick masonry in historic bridges to modern choices like reinforced concrete or steel. What sets arch bridges apart is not only their structural prowess but also their aesthetic appeal. They have a timeless and elegant appearance that has been appreciated for centuries. This combination of strength and beauty has made arch bridges iconic architectural structures that often become landmarks. Some of the most famous examples include the Pont du Gard in France and the Ponte Vecchio in Italy, each of which has its own unique historical and architectural significance. Building arch bridges, both in the past and the present, involves tackling engineering challenges related to designing the arch’s curvature and calculating load-bearing capacities, making them a testament to human ingenuity and architectural achievement. Arched beam bridges extending over rivers are susceptible to an array of geohazards, i.e., natural geological processes that carry the potential to compromise their integrity and safety. Among these, the looming risk of riverbank erosion emerges as a critical concern, gradually undermining the foundations on which these bridges stand [33,34].
With regard to Figure 1 and Figure 2, it can be stated that the riverside bridges hold significant importance due to their multifaceted roles in society. They primarily serve as vital transportation links, connecting communities and enabling the efficient movement of people, goods, and services across rivers. This enhanced connectivity not only reduces travel times but also fosters economic growth, trade, and cultural integration. Additionally, riverside bridges play critical roles in emergency response, environmental preservation, and urban development, contributing to the overall well-being and resilience of the regions that they serve. Their strategic planning, construction, and maintenance are fundamental to realizing these wide-ranging benefits. Controlling cracks in riverside arched beam bridges is imperative for both structural stability and safety. Firstly, cracks can compromise the load-bearing capacity of the arches and other bridge components, potentially leading to structural failure. Ensuring the structural integrity of these bridges is paramount to avoid accidents, injuries, and fatalities. Moreover, addressing cracks at an early stage through preventive measures, such as sealing or repairing cracks, can significantly extend the bridge’s lifespan and reduce the overall maintenance cost. Additionally, controlling cracks is environmentally beneficial, as it minimizes the risk of pollution from bridge materials and ensures the continuity of transportation and trade over these essential river crossings. Ultimately, effective crack control measures are critical for preserving the safety, durability, and functionality of riverside arched beam bridges.

Figure 2.
Several examples of failure on river-side arched beam bridges (photographs adapted from Google Images, 2023).
Leveraging the WT and WPT in the analysis of arched beam bridges offers a host of distinctive advantages. Both transforms serve as conduits for multi-resolution analysis, greatly facilitating the identification and understanding of various structural behaviors and stress distributions. A particular forte lies in their adeptness at event localization, rendering them invaluable tools for pinpointing critical instances within the dynamics of a bridge. Furthermore, these transforms play pivotal roles in noise reduction, thereby elevating the precision of data interpretation. By extracting key features such as natural frequencies and stress concentrations, a holistic comprehension of the bridge’s overall condition can be facilitated. However, it is essential to note that the application of WT and WPT also has limitations. The intricate nature of the transformed outcomes could pose challenges for those unversed in the intricacies of signal processing.
Accurate analysis hinges on the quality of sensor data, underscoring the criticality of meticulous data acquisition. Prudent scale selection becomes paramount, as ill-suited choices may lead to incomplete analyses. Additionally, the computational demands associated with these techniques can be substantial, potentially influencing real-time monitoring capabilities. Lastly, the underlying assumptions of linearity and stationarity might not align seamlessly with the dynamic behaviors exhibited by arched beam bridges. When addressing the analysis of cracks within arched beam bridges, the application of WT and WPT is indispensable due to the nuanced intricacies of bridge structures and the utmost necessity for accurate crack assessment. These transforms, with their multi-scale approaches, empower the identification of cracks at varying depths and extents within the bridge components. Their adaptability to the dynamic behaviors characteristic of arched beam bridges enables the capture of temporal changes, facilitating early detection and the implementation of timely preventive measures. In essence, the amalgamation of WT and WPT introduces an expansive and sophisticated toolkit for the analysis of cracks. This amalgamation substantially augments the accuracy of assessments, playing a pivotal role in enhancing the overall safety and durability of arched beam bridges.
3. Materials and Methods
3.1. Wavelet Packet Energy Rate Index
Wavelet packets encompass an ensemble of customary wavelet functions that are linearly amalgamated. Inherent in wavelet packets are attributes like orthonormality and time–frequency localization, which are passed down from their corresponding wavelet functions. A wavelet packet is represented by a function with three distinct indices, namely i, j, and k, and these integers symbolize the modulation, scale, and translation parameters, respectively [35].
The wavelet functions can be obtained from the following recursive relationships:
The first wavelet is a so-called mother wavelet function and defined as follows:
The discrete filters h(k) and g(k) encompass the quadrature mirror filters that stand in conjunction with the scaling function and the foundational wavelet function. An array of mother wavelets has been documented in the literature, with many being tailored to meet crucial properties such as invertibility and orthogonality. Throughout research, these wavelets have been a focal point of discussion, with the Db5 function often emerging as a recommended choice for the mother wavelet function due to its favorable characteristics when juxtaposed with other options [35]. In the WT, each level contributes one high-frequency term and one low-frequency residual from the ultimate level of decomposition. In contrast, the WPT takes a different approach, achieving a comprehensive decomposition at every level, consequently allowing enhanced resolution within the high-frequency spectrum. The inter-relationship between the components of the jth and (j + 1)th levels adheres to recursive relationships as follows [36]:
where H and G are the filtering–decimation operators related to the discrete filters h(k) and g(k) in a wayakin that discussed in [35]:
after j level of decomposition, the original signal f(t) can be expressed as described in [36]:
The wavelet packet component signal can be represented by a linear combination of wavelet packet functions as follows [36]:
where the wavelet packet coefficients can be obtained from Equation (12). Also, Equation (13) ensures that the wavelet packet functions are orthogonal.
In this study, the wavelet packet energy index is proposed to identify the locations and severity of damage. To take that step, the signal energy Ef at j level is first defined as described in [37]:
substituting Equation (11) into Equation (14) and using the orthogonal condition Equation (13) yields the method used in [37]:
where the wavelet packet component energy can be the energy stored in the component signal , which is presented as described in [37]:
The component signal is a superposition of wavelet functions of the same scale as j but translated into the time domain . This means that the component energy is the energy stored in a frequency band determined via the wavelet functions . Equation (15) illustrates that the total signal energy can be decomposed into a summation of wavelet packet component energies that correspond to different frequency bands. So, the wavelet packet energy rate index (WPERI) is believed to indicate the structural damage. The rate of signal wavelet packet energy at j level is defined as described in [37]:
where is the component signal energy level without damage, and is the component signal energy El’ with some damage. It is postulated that structural damage would affect the wavelet packet component energies and subsequently alter this damage indicator. It is desirable to select the WPERI that is sensitive to the changes in the signal characteristics.
3.2. Damage Identification Procedures
Outlined below is a procedure for damage identification hinging on the novel wavelet packet rate index (WPERI). This methodology operates under two key assumptions: (1) the availability of dependable structural models for both the undamaged and damaged configurations, and (2) the application of the same impulse load at a designated location across both scenarios. Initial stages involve the processing of vibration signals collected from sensors (the sensors represent the primary recording instruments strategically placed within the arch beams to assess deformations in the bridge structure), a process that involves the utilization of the wavelet packet transform (WPT). To ascertain the most suitable level of wavelet packet decomposition, a trial-and-error sensitivity analysis was undertaken that utilized both the intact and compromised structural models. Subsequently, the calculation of wavelet packet energy rates was conducted upon the signals [35,38]. If n stands for the total number of all sensors distributed in the structure, a total of n-WPERIs can be obtained after performing the wavelet packet decomposition. As the mean values and the standard deviations of the WPERIs are expressed as and , the one-side (1−α) upper confidence limit for the WPERI can be governed via the equation used in [39,40,41,42]:
In this context, Zα represents the value within the standard normal distribution characterized by a mean of zero and a variance of one, such that its cumulative probability equals 100(1−α). This establishment serves as a critical benchmark, akin to a threshold, to gauge potential anomalies in the wavelet packet rate index (WPERI), signifying a prospective damage indicator [43]. A notable advantage of this damage identification approach lies in its foundation upon the statistical attributes of the damage indicator observed through sensors [44,45]. Any indicator that surpasses this predefined threshold triggers a damage alarm, effectively creating a resilient mechanism even when multiple instances of damage are in play [46]. Remarkably, the proposed method remains effective regardless of the presence of numerous damages. The locations of sensors showcasing WPERI values surpassing the threshold provide crucial insights into the precise areas where potential damage may have occurred [47].
The identification procedure for evaluating crack behavior in the curved segments of arched beam bridges over river spans is a comprehensive process. It commences with the collection of pertinent data, which can stem from a variety of sources, including structural measurements, sensor data, or results obtained via finite element analysis (FEA) simulations in ANSYS. Ensuring the integrity of the data is crucial, and, therefore, preprocessing becomes the next critical step. During this phase, the collected data undergo rigorous cleaning and conditioning to eliminate any noise, outliers, or undesired artifacts. This data preparation stage is essential to ensure that the subsequent analysis is based on reliable and accurate information. To delve deeper into the structural behavior and assess the presence of cracks, an excitation signal is defined. This signal serves as a representative input to simulate various dynamic loading or environmental conditions that impact the bridge’s response. It could mimic traffic loads, wind forces, or seismic events, depending on the specific analysis objectives. The MATLAB environment is employed for the WT analysis, a technique that decomposes the preprocessed data into different scales and time–frequency components. This decomposition provides valuable insights into how the bridge’s response evolves over time. Selecting an appropriate wavelet basis and the scale parameters tailored to the unique characteristics of the bridge’s response is vital for obtaining meaningful results.
For a more detailed assessment, the WPT, an extension of WT, was employed. WPT further decomposes the data into sub-bands and nodes, offering enhanced time–frequency resolution. This higher granularity is particularly advantageous when scrutinizing complex structural behaviors like crack propagation. Following the WT or WPT analysis, the identified features or patterns were examined to pinpoint indicators of crack behavior. These indicators included shifts in frequency, variations in signal amplitude, or changes in the signal’s time–frequency distribution. Detecting these patterns aided us in locating and evaluating the presence and severity of cracks within the bridge’s curved segments. For a comprehensive understanding of the structural implications of identified cracks, the findings were integrated back into ANSYS if FEA simulations were utilized. This integration enabled the evaluation of how the identified cracks impact structural elements such as stress concentrations or alterations in vibration characteristics. The results were rigorously validated by comparing them to known crack locations or benchmark data. The interpretation of these findings was crucial to assess the significance of the identified crack behavior in the context of the bridge’s safety and structural integrity. Ultimately, the entire assessment procedure, including methodologies, parameters, and results, were meticulously documented. Recommendations for necessary repairs, maintenance, or further investigations based on the crack behavior assessment were provided, aiding us in undertaking informed decision-making regarding the safety and upkeep of arched beam bridges spanning rivers.
3.3. Modeling of the Arced Beam
In this study, an arced beam configuration measuring 8 m in length and 5 m in height, supported with a simple support mechanism, was meticulously modeled. The representation of this setup is shown in Figure 3. The material properties encompassed a mass density of 7850 kg/m3 and a modulus of elasticity of 2.11 × 1011 Pa. Additionally, the beam’s cross-sectional area and moment of inertia were set at 0.05 m2 and 1.66 × 10−4 m4, respectively. For the application of an impulse load, exemplified by a triangular load, a force-time history was introduced to the beam at distances of 2, 3, 5, and 6 m from the left support. Employing transient dynamic analysis in ANSYS, acceleration and displacement time histories were computed. Subsequently, the acquired signals from each loading sequence underwent distinct wavelet packet decomposition, followed by cumulative integration of the outcomes. To gauge the efficacy of the proposed crack identification approach, an intact model was established alongside six damaged models, encompassing varying crack locations and magnitudes. The intensity of each crack was quantified by reducing the stiffness of the corresponding element, as detailed in Table 2. This comprehensive assessment served as a robust testbed for evaluating the capacity of the proposed method across different damage scenarios.
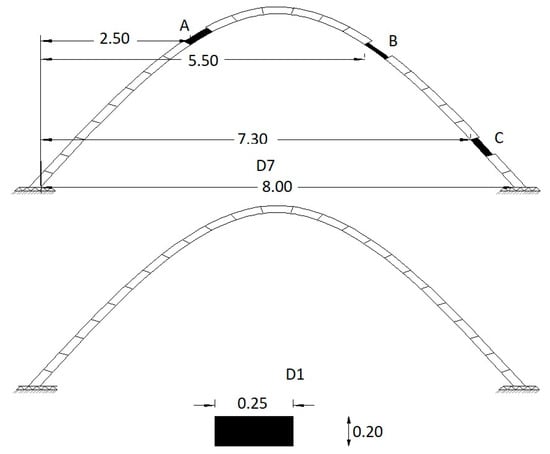
Figure 3.
A simulated simply supported beam (Note: A–C points are survey locations).

Table 2.
Characteristics of local and intensity cracks in all simulated specimens.
4. Results
The main principle of this study is based on that introduced by Han et al. [48]. The model was used to simulate a crack behavior (with consideration of the reduction in the stiffness of the components) in curved segments of arched beam bridges spanning rivers using optimized wavelet and wavelet packet transform techniques. In this regard, the dynamic loading was assessed based on the river flow’s impact on structure and modeled using ANSYS finite element software. Also, for WPERI simulation, the MATLAB programming language was utilized. In Figure 4, the acceleration of the time history data offers a comprehensive view of how the models respond over time. The focus is particularly directed towards a specific point located 3.5 m away from the left support, where the load was initially applied 2 m from the same support. This choice of observation point allows a detailed analysis of the dynamic behavior of the models, specifically in relation to potential cracks. Interestingly, when comparing the acceleration time histories across the different models, noticeable disparities become apparent. These differences in acceleration patterns serve as indicators of the structural changes introduced by cracks. It should be noted that in the numerical model, damage is simulated through a process that involves reducing the stiffness of the various components within the structure. This means that the simulated damage is not explicitly modeled as cracks using ANSYS or any other specialized crack modeling technique. Instead of creating crack-like features in the model, the approach taken here involves diminishing the structural stiffness of the components to mimic the effects of damage. This can be a practical way to assess how the structure responds to changes in stiffness, which may result from damage, without explicitly simulating the presence of cracks via finite element analysis software like ANSYS. It is a valuable approach for understanding how structural behavior is affected by reduced stiffness, which can be a precursor to more extensive damage in other scenarios. Moving forward, after processing the signals and decomposing them into wavelet packet components, the WPERI is calculated using Equation (17). The process involves analyzing the energy distribution across different scales and locations within the signal. This index encapsulates valuable information about the presence and intensity of cracks. Its values are plotted in Figure 5, Figure 6 and Figure 7.
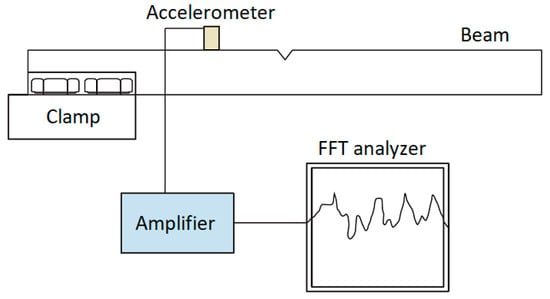
Figure 4.
A verification procedure implemented by Abu-Hamdeh et al. (Reprinted from Ref. [49]).
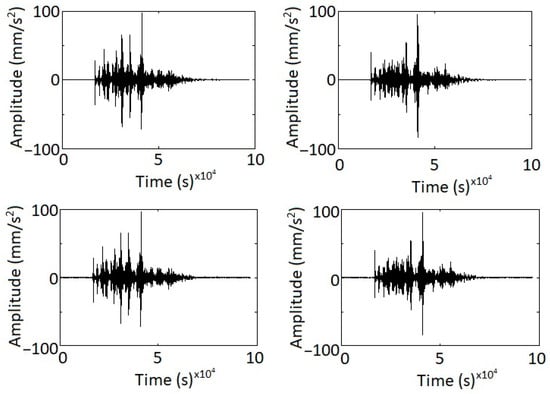
Figure 5.
Acceleration–time history for all the specimens.
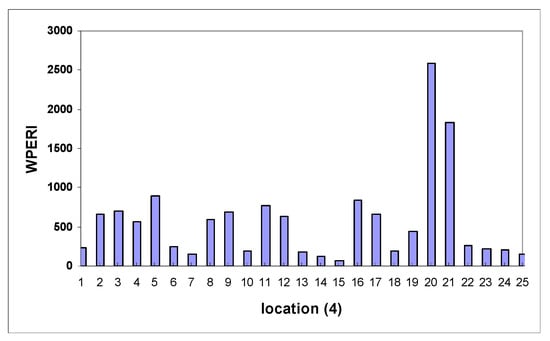
Figure 6.
Histogram of wavelet packet energy rate index in location A.
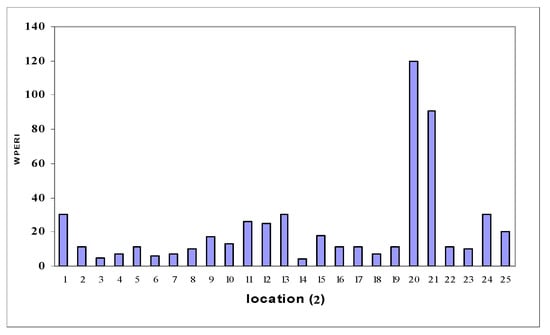
Figure 7.
Histogram of wavelet packet energy rate index in location B.
Table 3 provides the estimated energy component regarding Efj shift in the frequency of the harmonic function using the WT, WPT, and WPERI models. In an ideal scenario, these highly responsive component energies present themselves as promising candidates for unveiling signal characteristics. Hence, the introduction of the WPERI is suggested as a means to signify structural damage. Examining these figures, a distinct pattern emerges. The highest values of the WPERI are observed at the exact locations where the cracks are simulated. This alignment between high index values and crack locations underscores the methodology’s ability to accurately identify and pinpoint cracks within the structure. Meanwhile, in regions without cracks, the index values remain considerably lower. Furthermore, the methodology’s sensitivity to crack intensity becomes evident. As the intensity of the simulated crack increases, there is a non-linear rise in the corresponding WPERI values. This demonstrates that the methodology can not only detect the presence of cracks but also gauge their severity. Utilizing Equation (18) with a chosen confidence level (α = 0.02) results in values that help to establish a threshold for crack identification. These values are illustrated in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, indicating the point at which the index value crosses the threshold and signifies the presence of a crack. This threshold provides a reliable criterion for declaring the presence of structural damage. Collectively, the visual representations in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 illustrate the methodology’s robustness in terms of crack identification. The index values remain consistently at zero for undamaged regions, ensuring a clear differentiation between the healthy and damaged portions of the structure. In Figure 9, for instance, the distinct emergence of the wavelet packet rate index between nodes 20 and 21 (corresponding to element C in model 3) reinforces the methodology’s precision in localizing cracks. In conclusion, this comprehensive methodology combines wavelet analysis, energy distribution, and statistical thresholds to effectively detect and locate cracks in the structural system. Its ability to discern subtle changes in behavior due to cracks, sensitivity to crack intensity, and robustness in terms of differentiating between healthy and damaged regions make it a powerful tool for assessing the structural integrity and health of arched beam bridges.

Table 3.
The energy of components at the third level where WT, WPT, and WPERI undergo assessment to determine a shift (Efj) in the frequency of the harmonic function.
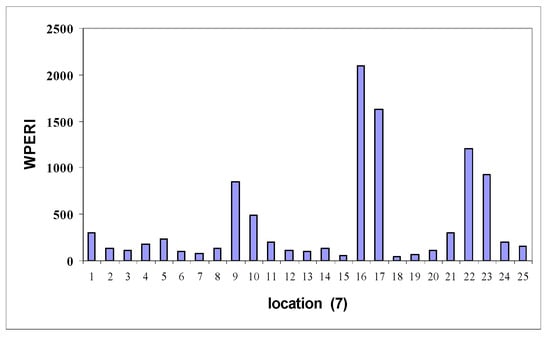
Figure 8.
Histogram of wavelet packet energy rate index in location C.
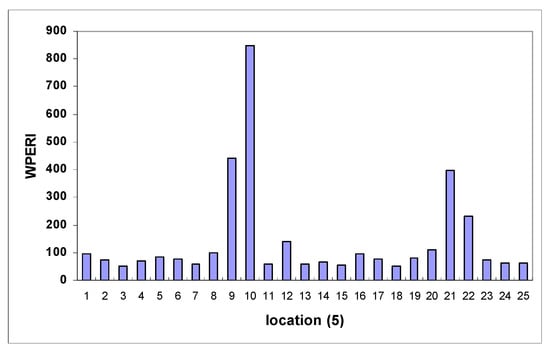
Figure 9.
Histogram of wavelet packet energy rate index in location D.
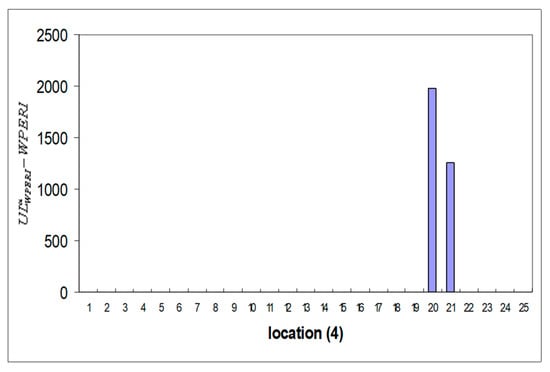
Figure 10.
Histogram after considering crack threshold in location A.
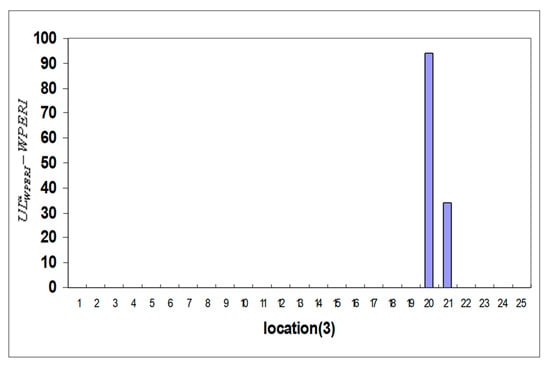
Figure 11.
Histogram after considering crack threshold in location B.
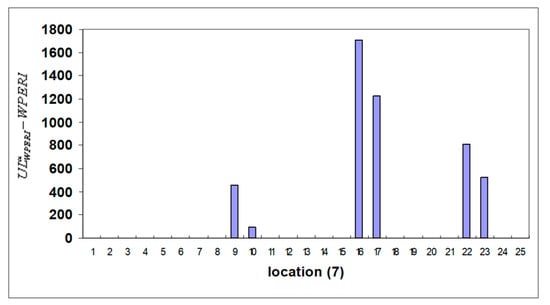
Figure 12.
Histogram after considering crack threshold in location C.
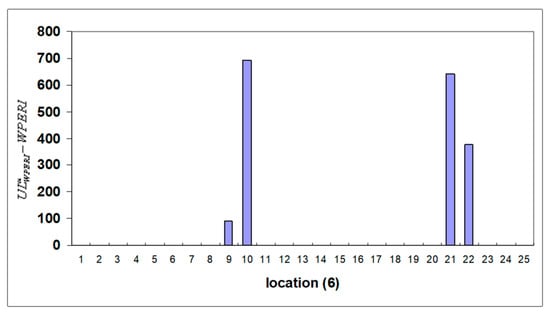
Figure 13.
Histogram after considering crack threshold in location D.
The utilization of the WPERI serves as a vital and sophisticated approach in the field of structural health assessment, particularly for detecting and characterizing potential cracks within complex systems like arched beam bridges. The WPERI holds significant advantages related to its ability to capture intricate changes in signal behavior, allowing for the precise identification of damage locations and intensities. Unlike traditional methods that solely rely on individual signal parameters or statistical thresholds, the WPERI integrates wavelet analysis and energy distribution across multiple scales and locations within a signal. This holistic approach provides a comprehensive perspective on the dynamic response of the structure, enabling the detection of subtle variations induced by cracks. The WPERI effectively translates these nuanced changes into a quantifiable index, facilitating an objective evaluation of structural health.
By employing a threshold derived from statistical properties, the methodology establishes a clear demarcation between normal and abnormal conditions, making it a robust tool for early crack detection and accurate assessment. Ultimately, the implementation of WPERI enhances the reliability of structural health monitoring, offering a proactive strategy for maintaining the integrity and safety of arched beam bridges and other intricate systems. Table 4 provides first two natural frequencies (Hz) for different damage scenarios. These scenarios are identified in Figure 3.

Table 4.
The initial pair of resonance frequencies (in Hertz) across various damage situations.
Regarding model verification, the applied WT and WPT were verified using the results of the experimental study presented by Abu-Hamdeh et al. [49]. A minimal crack location was identified by analyzing the mode shapes affected by the crack, and [49] treated the uncracked beams as an experimental task. Aluminum specimens were prepared, and their material properties were characterized as follows: the modulus of elasticity (E) was measured as 70 GPa, and the mass density (ρ) was determined to be 2700 kg/m3.Various crack positions and sizes were investigated using wire-cut machining. An assembled fixture, which included a substantial base plate for securing the specimen, was employed. The overall experimental arrangement is depicted in Figure 4. A result of the model verification is illustrated in Table 5. Also, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 provide information regarding modeling with WT, WPT, and WPERI.

Table 5.
The verification model calculated for the different depths and positions of a 16mm crack.
5. Discussion
The task of identifying cracks within arced beams presents a formidable challenge, demanding adept modeling techniques. Within this comprehensive discourse, the manifold advantages and considerations inherent in employing the wavelet packet transform (WPT) and the wavelet transform (WT) for the intricate endeavor of crack identification within arched beams are explored. Initially, the WPT stands out for its intricate modeling capacity, offering a superior approach to crack identification when compared to the WT. Through the intricate process of decomposing the signal into multiple sub-bands at each hierarchical level, the WPT unfolds a panoramic canvas for the analysis of crack-induced characteristics. In this realm, the WPT’s prowess comes to the fore, deftly unmasking intricate intricacies and variations that simpler models may inadvertently overlook. This granular dissection bestowed by the WPT resonates as a powerful instrument for capturing even the most intricate crack features, culminating in an accurate portrayal of both the pattern and severity of cracks. A boon for modeling arced beams, this heightened capability proves particularly instrumental where cracks manifest as complex and irregular patterns.
Contrastingly, the WT offers a streamlined modeling avenue that remains steadfast in providing valuable insights into the realm of crack identification within arced beams. Rooted in the concept of multiresolution analysis, the WT excels in promptly uncovering high-frequency constituents tied to cracks. Such prowess takes center stage in the context of arced beams, where the presence of cracks frequently injects high-frequency elements into the signal. Fueled by its time–frequency localization attributes, the WT empowers the discernment of transient or localized features attributed to cracks, thereby facilitating their differentiation from other signal elements. The WT’s hallmark simplicity and efficiency render it an astute selection for crack identification modeling, especially when confronted with constraints such as computational resources or temporal limitations. However, employing WPT and WT for crack identification modeling within arced beams necessitates thoughtful consideration of the trade-offs. While the WPT’s detailed decomposition augments modeling finesse, it simultaneously ushers in computational intricacies, potentially demanding more substantial computational resources and elongating modeling duration. This consideration holds significance in scenarios where the optimization of computational efficiency is imperative. In essence, the choice between WPT and WT for crack identification modeling in arced beams entails a nuanced evaluation of intricacies, resources, and temporal demands to ascertain the most fitting approach for the specific modeling context.
In light of these results, the choice between WPT and WT for crack identification modeling becomes a matter of context and priorities. The detailed modeling prowess of the WPT becomes a clear advantage when precision in the detection of intricate crack features is crucial. This is particularly relevant when dealing with arced beams, where cracks can adopt complex patterns that demand meticulous analysis. Conversely, the WT’s efficiency and ability to promptly identify high-frequency components make it a pragmatic choice when timely assessments are necessary. The trade-off lies in computational demands; while the WPT’s thorough decomposition requires more resources, the WT’s simpler approach could be more suited to situations where resource optimization is key. Ultimately, these results underscore the versatility of the WPT and WT as tools for crack identification within arced beams. The ability to tailor the modeling approach based on the specific characteristics of the structure, available resources, and the urgency of the assessment offers a strategic advantage. By judiciously leveraging the strengths of both methods, engineers and researchers can make informed decisions that strike a balance between precision and efficiency, thereby enhancing the accuracy and effectiveness of crack identification strategies in arced beam structures.
As depicted in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, multiple positions were identified for the investigation of crack history and WPERI values within the structural body, as illustrated in Figure 3. These histograms serve to enhance our understanding of the behavior of cracks in the curved segments of arched beam bridges spanning rivers.
On the other hand, it is worth noting that the wavelet transform (WT) offers a more straightforward approach to crack identification, albeit potentially at the cost of capturing the nuanced intricacies and variations that the wavelet packet transform (WPT) can reveal. Deciding on the most suitable modeling technique requires careful consideration of specific application requirements, available computational resources, and the desired level of detail in crack detection. When implementing these models within MATLAB, the process involves a series of crucial steps to prepare the signal obtained from the arched beam. The initial phase focuses on enhancing the signal quality by eliminating noise and artifacts. In this regard, MATLAB offers a comprehensive suite of signal processing functions, including filtering, noise removal, and data normalization, all of which prove to be invaluable. Following the preprocessing stage, the wavelet analysis techniques are applied. For WT implementation, MATLAB’s Wavelet Toolbox provides functions like ‘cwt’ for continuous wavelet transform or ‘wavedec’ for discrete wavelet decomposition. These functions meticulously break down the signal into different scales or levels, resulting in approximation and detail coefficients that encapsulate distinct frequency components. Conversely, when applying the WPT, the ‘wptree’ function constructs a wavelet packet tree. This process results ina more granular decomposition into numerous sub-bands at each level, providing an even more detailed and localized view of the signal’s characteristics. Therefore, the choice between WT and WPT is contingent upon the specific needs of the analysis, where WT may be favored for a more straightforward overview, and WPT can be advantageous when fine-grained detail is required.
It should be noted that both the T and WPT are versatile signal processing techniques that are inherently 1D in nature. They are primarily designed for analyzing and decomposing one-dimensional signals, such as time series data, audio signals, or 1D images. These transforms provide a powerful tool for understanding the time–frequency characteristics of such signals. However, in practical applications, it is not uncommon to extend these techniques to two-dimensional signals, such as images. This is achieved by applying the 1D WT or WPT independently to the rows and columns of the 2D data. This process is known as the separable 2D wavelet transform. The extension to 2D allows the analysis of spatial frequency content in images, which is valuable in image processing, compression, and feature extraction. By applying the 1D wavelet transforms in both dimensions, it is possible to capture both horizontal and vertical variations in the data. This approach can reveal details in images, detect edges, and provide a multi-resolution representation that is useful in various computer vision tasks. In summary, while WT and WPT are inherently 1D, they can be extended to effectively analyze 2D data by separately applying the 1D transform to the rows and columns. This extension is valuable for image analysis and processing.
6. Conclusions
In conclusion, the wavelet transform (WT) has proven itself as an invaluable tool in the field of crack identification, adeptly capturing subtle structural changes arising from damage. Its proficiency in crack detection and localization has solidified its reputation as a dependable metric for assessing localized deterioration in structures. The newly introduced WT-based energy rate index, developed through a streamlined three-step computational process, presents a promising solution for such assessments. Looking ahead, the potential applications of this conclusion are vast. The proposed damage identification procedure stands out for its user-friendly implementation and time-efficient characteristics, making it particularly suitable for real-time use when reference data arereadily available. Furthermore, the wavelet packet energy rate index (WPERI) exhibits a non-linear response that correlates with increasing crack severity, indicating its sensitivity to variations in damage intensity. It is worth noting, however, that careful selection of the scale and decomposition level remains crucial in wavelet packet analysis to maintain optimal crack identification effectiveness, especially when operating below a scale of four. Of particular interest is the WPERI’s ability to detect an increased number of cracks, showcasing its effectiveness in scenarios involving multiple instances of damage. These collective findings underscore the pivotal role of the WT and the innovative WPERI index in advancing crack identification methodologies, providing a practical and reliable means of assessing structural health, particularly in the context of arced beams. Looking forward, the combined potential of WT and WPERI holds great promise in terms of enhancing our understanding of structural integrity and promoting effective damage management practices in complex configurations. Future research may explore the integration of machine learning algorithms to further refine and automate the crack identification process, ultimately contributing to safer and more resilient structural designs and maintenance procedures.
Author Contributions
L.C., D.D. and M.K.: conceptualization, methodology, software, formal analysis, investigation, data curation, writing—original draft preparation. X.L. and Y.M.: validation, supervision, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Improvement Projects of Guangdong Province (2022ZDJS048) and the Technology Plan Projects with No. of 220607154531533.
Data Availability Statement
All data are available within the article.
Acknowledgments
The authors would like to thank the anonymous reviewers for providing invaluable review comments and recommendations for improving the scientific level of the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 2018, 30, 91–105. [Google Scholar] [CrossRef]
- Gurley, K.; Kareem, A. Application of wavelet transform in earthquake, wind and ocean engineering. Eng. Struct. 2010, 21, 149–167. [Google Scholar]
- Hou, Z.; Noori, M.; Amand, S.R. Wavelet-based approach for structural damage detection. J. Struct. Eng. ASCE 2018, 12, 677–683. [Google Scholar] [CrossRef]
- Wang, W.J.; McFadden, P.D. Application of wavelets to gearbox vibration signals for fault detection. J. Sound Vib. 2010, 192, 927–939. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics; Department of Mathematics, University of Lowell, MA, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016. [Google Scholar]
- Goldaran, R.; Kouhdaragh, M. Crack Identification of Curved-Elements Using Wavelet Packet. Adv. Sci. Technol. 2021, 105, 144–150. [Google Scholar]
- Yang, Z.; Chen, X.; He, Y.; He, Z.; Zhang, J. The analysis of curved beam using B-spline wavelet on interval finite element method. Shock Vib. 2014, 2014, 738162. [Google Scholar] [CrossRef]
- Zupan, E.; Zupan, D.; Saje, M. The wavelet-based theory of spatial naturally curved and twisted linear beams. Comput. Mech. 2009, 43, 675–686. [Google Scholar] [CrossRef]
- Saravanan, V.; Ramachandran, M.; Selvam, M.; Nanjundan, P. Investigation of Non Linear Analysis WRT Dynamic Relaxation. Data Anal. Art. Intell. 2022, 2, 197–203. [Google Scholar]
- Lotfollahi-Yaghin, M.A.; Koohdaragh, M. Examining the function of wavelet packet transform (WPT) and continues wavelet transform (CWT) in recognizing the crack specification. KSCE J. Civil Eng. 2011, 15, 497–506. [Google Scholar] [CrossRef]
- Kumar, M.; Moinuddin, S.Q.; Kumar, S.S.; Sharma, A. Discrete wavelet analysis of mutually interfering co-existing welding signals in twin-wire robotic welding. J. Manufact. Proc. 2021, 63, 139–151. [Google Scholar] [CrossRef]
- Elefante, A.; Nilsen, M.; Sikström, F.; Christiansson, A.K.; Maggipinto, T.; Ancona, A. Detecting beam offsets in laser welding of closed-square-butt joints by wavelet analysis of an optical process signal. Opt. Laser Technol. 2019, 109, 178–185. [Google Scholar] [CrossRef]
- Machorro-Lopez, J.M.; Hernandez-Figueroa, J.A.; Carrion-Viramontes, F.J.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Crespo-Sanchez, S.E.; Martinez-Trujano, L.A. Analysis of acoustic emission signals processed with wavelet transform for structural damage detection in concrete beams. Mathematics 2023, 11, 719. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, Q. Application of wavelet theory for crack identification in structures. J. Eng. Mech. 1998, 124, 152–157. [Google Scholar] [CrossRef]
- Pacheco-Chérrez, J.; Cárdenas, D.; Probst, O. Measuring Crack-type Damage Features in Thin-walled Composite Beams using De-noising and a 2D Continuous Wavelet Transform of Mode Shapes. J. Appl. Comput. Mech. 2021, 7, 355–371. [Google Scholar]
- Taha, M.R.; Noureldin, A.; Lucero, J.L.; Baca, T.J. Wavelet transform for structural health monitoring: A compendium of uses and features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Rezaifar, O.; Gholhaki, M.; Khanahmadi, M.; Amiri, Y. A review of structural health monitoring and damage detection using wavelet transform: The case study of damage detection in cantilever beams. J. Vib. Sound 2022, 11, 157–171. [Google Scholar]
- Liu, J.; Zhu, W.D.; Charalambides, P.G.; Shao, Y.M.; Xu, Y.F.; Fang, X.M. A dynamic model of a cantilever beam with a closed, embedded horizontal crack including local flexibilities at crack tips. J. Sound Vib. 2016, 382, 274–290. [Google Scholar] [CrossRef]
- Pentaris, F.P.; Stonham, J.; Makris, J.P. A novel approach of Structural health monitoring by the application of FFT and wavelet transform using an index of frequency dispersion. Int. J. Geol. 2013, 7, 39–48. [Google Scholar]
- Wang, S.; Liu, X.; Yang, T.; Wu, X. Panoramic crack detection for steel beam based on structured random forests. IEEE Access 2018, 6, 16432–16444. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, Z. Development of a novel type of open-web continuous reinforced-concrete rigid-frame bridge. J. Bridge Eng. 2020, 25, 05020005. [Google Scholar] [CrossRef]
- Boothroyd, R.J.; Williams, R.D.; Hoey, T.B.; Tolentino, P.L.; Yang, X. National-scale assessment of decadal river migration at critical bridge infrastructure in the Philippines. Sci. Total Environ. 2021, 768, 144460. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Roy, M.B.; Roy, P.K.; Mukherjee, S. Assessing the nature of sediment transport with bridge scour by 1D sediment transport model in the sub-catchment basin of Bhagirathi–Hooghly river. Model. Earth Syst. Environ. 2021, 7, 2823–2845. [Google Scholar] [CrossRef]
- Fan, Z.; Huang, Q.; Ren, Y.; Xu, X.; Zhu, Z. Real-time dynamic warning on deflection abnormity of cable-stayed bridges considering operational environment variations. J. Perform. Construct. Facil. 2021, 35, 04020123. [Google Scholar] [CrossRef]
- Tan, H.; Hu, X.; Wu, X.; Zeng, Y.; Tu, X.; Xu, X.; Qian, J. Initial crack propagation of integral joint in steel truss arch bridges and its fatigue life accession. Eng. Fail. Anal. 2021, 130, 105777. [Google Scholar] [CrossRef]
- Badroddin, M.; Chen, Z. Lifetime resilience measurement of river-crossing bridges with scour countermeasures under multiple hazards. J. Eng. Mech. 2021, 147, 04021058. [Google Scholar] [CrossRef]
- Nicoletti, V.; Martini, R.; Carbonari, S.; Gara, F. Operational Modal Analysis as a Support for the Development of Digital Twin Models of Bridges. Infrastructures 2023, 8, 24. [Google Scholar] [CrossRef]
- Nicoletti, V.; Quarchioni, S.; Tentella, L.; Martini, R.; Gara, F. Experimental tests and numerical analyses for the dynamic characterization of a steel and wooden cable-stayed footbridge. Infrastructures 2023, 8, 100. [Google Scholar] [CrossRef]
- Badroddin, M.; Billah, A.M. Multi-state functionality restoration of highway bridges using stochastic process. Eng. Struct. 2023, 293, 116623. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A. Vulnerability of bridges to individual and multiple hazards-floods and earthquakes. Reliab. Eng. Syst. Saf. 2021, 210, 107564. [Google Scholar] [CrossRef]
- Ayele, Y.Z.; Aliyari, M.; Griffiths, D.; Droguett, E.L. Automatic crack segmentation for UAV-assisted bridge inspection. Energies 2020, 13, 6250. [Google Scholar] [CrossRef]
- Parke, G.; Hewson, N. ICE Manual of Bridge Engineering, 2nd ed.; Thomas Telford Publishing: London, UK, 2008. [Google Scholar]
- Malone, A.; Santi, P.; Cabana, Y.C.; Smith, N.M.; Manning, J.; Zeballos, E.Z.; Zhou, W. Cross-validation as a step toward the integration of local and scientific knowledge of geologic hazards in rural Peru. Int. J. Disaster Risk Reduct. 2022, 67, 102682. [Google Scholar] [CrossRef]
- Filizadeh, R.; Hernandez, E.; Rosowsky, D. Time-Dependent Damage Evolution of Reinforced Concrete Bridge Piers: Implications for Multihazard Analysis. ASCE-ASME J. Risk Uncertain. Eng. Syst. 2023, 9, 04022066. [Google Scholar] [CrossRef]
- Zhao, B.; Lei, D.; Fu, J.; Yang, L.; Xu, W. Experimental study on micro-damage identification in reinforced concrete beam with wavelet packet and DIC method. Construct. Build. Mater. 2019, 210, 338–346. [Google Scholar] [CrossRef]
- Benffey, J.P. An Introduction to Reliability and Quality Engineering; Longman Scientific & Technical, Longman Group UK Limited: London, UK, 2014. [Google Scholar]
- Ang, A.H.S.; Tang, W.H. Probability Concepts in Engineering Planning and Design; John Wiley & Sons, Inc.: New York, NY, USA, 2018. [Google Scholar]
- Azarafza, M.; Feizi-Derakhshi, M.R.; Azarafza, M. Computer modeling of crack propagation in concrete retaining walls: A case study. Comput. Concr. 2017, 19, 509–514. [Google Scholar] [CrossRef]
- Deng, T.; Huang, J.; Cao, M.; Li, D.; Bayat, M. Seismic damage identification method for curved beam bridges based on wavelet packet norm entropy. Sensors 2021, 22, 239. [Google Scholar] [CrossRef]
- Zhang, Z.; Hamata, O.; Akiduki, T.; Mashimo, T.; Saito, T.; Hayashi, K. Cracks in bridge floor detected by 2-dimensional complex discrete wavelet packet transform. Int. J. Innov. Comput. Inform. Control 2020, 16, 2007–2019. [Google Scholar]
- Yang, T.; Li, Y.; Lin, X. Foundation scour identification method based on vehicle braking excitation and wavelet packet energy analysis for continuous beam bridges. China J. High. Trans. 2021, 34, 51. [Google Scholar]
- Shahsavari, V.; Mehrkash, M.; Santini-Bell, E. Damage detection and decreased load-carrying capacity assessment of a vertical-lift steel truss bridge. J. Perform. Construct. Facil. 2020, 34, 04019123. [Google Scholar] [CrossRef]
- Farajpour, M.; Najafabadi, M.A. Investigation of crack propagation in filament wound composite samples of Mode-I by using acoustic emission technique. J. Comp. Mater. 2023, 57, 3979–3989. [Google Scholar] [CrossRef]
- Zamorano, M.; Gómez, M.J.; Castejón, C. Optimal Selection of the Mother Wavelet in WPT Analysis and Its Influence in Cracked Railway Axles Detection. Machines 2023, 11, 493. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Li, J.; Hao, H.; Ma, H. Analysis of ultrasonic nonlinearity for bolt hole crack detection in rail joints by wavelet packet decomposition. Adv. Struct. Eng. 2023, 26, 1395–1409. [Google Scholar] [CrossRef]
- Gomez, M.J.; Castejon, C.; Corral, E.; Cocconcelli, M. Railway Axle Early Fatigue Crack Detection through Condition Monitoring Techniques. Sensors 2023, 23, 6143. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Geng, P.; Chen, J.; He, C. Dynamic discrimination method of seismic damage in tunnel portal based on improved wavelet packet transform coupled with Hilbert-Huang transform. Mech. Syst. Signal Proc. 2023, 188, 110023. [Google Scholar] [CrossRef]
- Han, J.G.; Ren, W.X.; Sun, Z.S. Wavelet packet based damage identification of beam structures. Int. J. Solids Struct. 2005, 42, 6610–6627. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Daqrouq, K.; Mebarek-Oudina, F. Simulation and Analysis with Wavelet Transform Technique and the Vibration Characteristics for Early Revealing of Cracks in Structures. Math. Prob. Eng. 2021, 2021, 6626232. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).