Hydraulic Transient Impact on Surrounding Rock Mass of Unlined Pressure Tunnels
Abstract
:1. Introduction
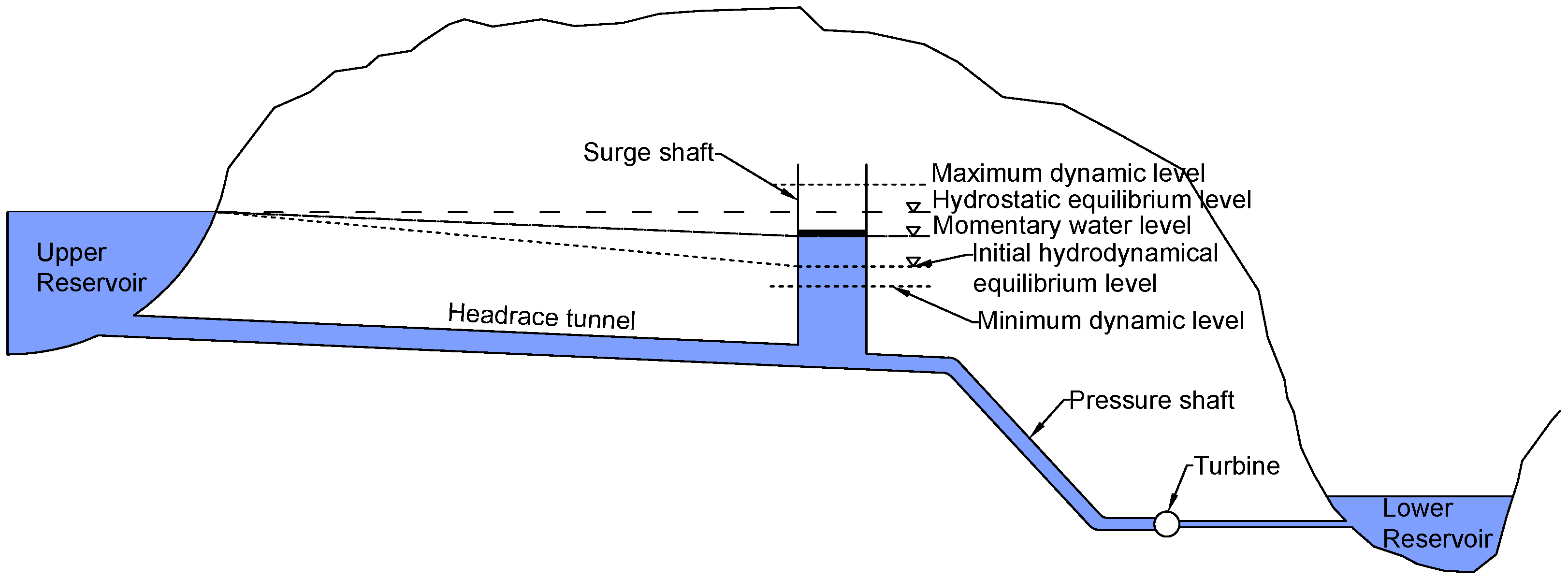
2. Hydraulic Transients in Hydropower Plants
3. Fluid Flow in the Rock Mass
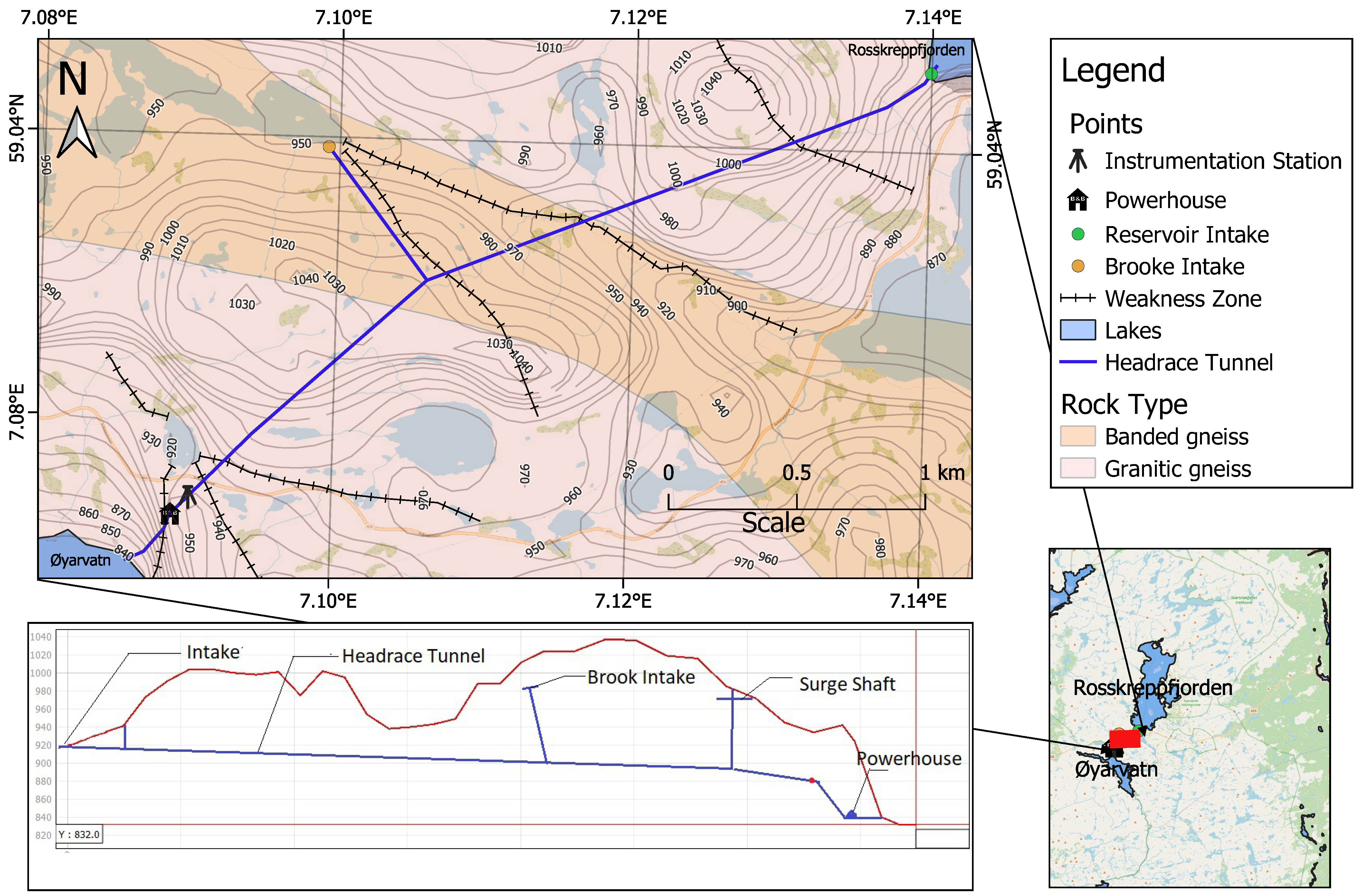
4. Case Study at Roskrepp Power Plant
5. Analysis
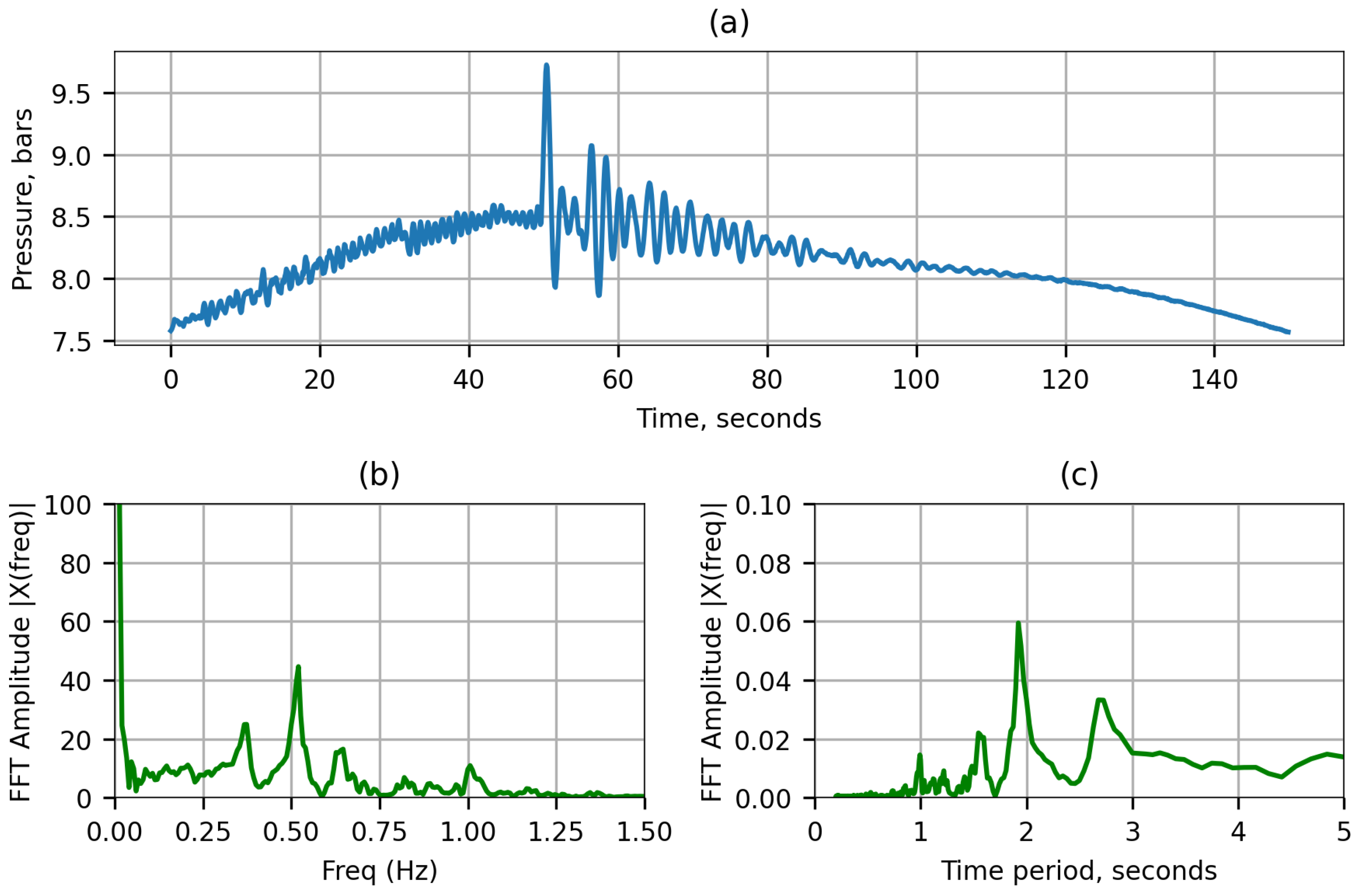
5.1. Finding Pressure Peaks in the Data
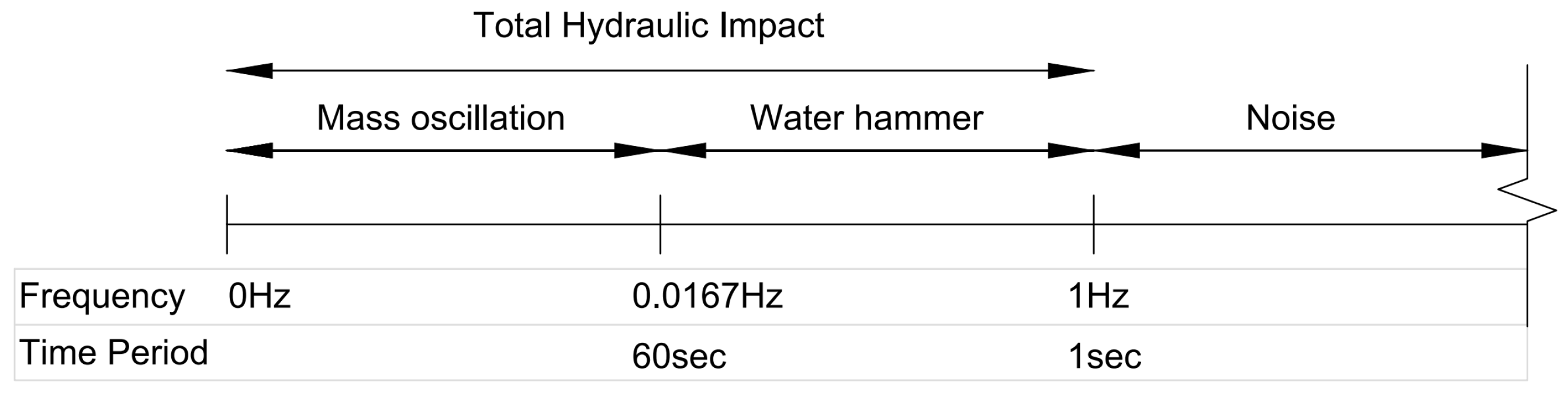
5.2. Natural Frequency of Oscillation
5.3. Shutdown Procedure and Duration
5.4. Quantifying the Hydraulic Impact
5.5. Method of Calculating HI and MPD
6. Results
6.1. Pore Pressure Response
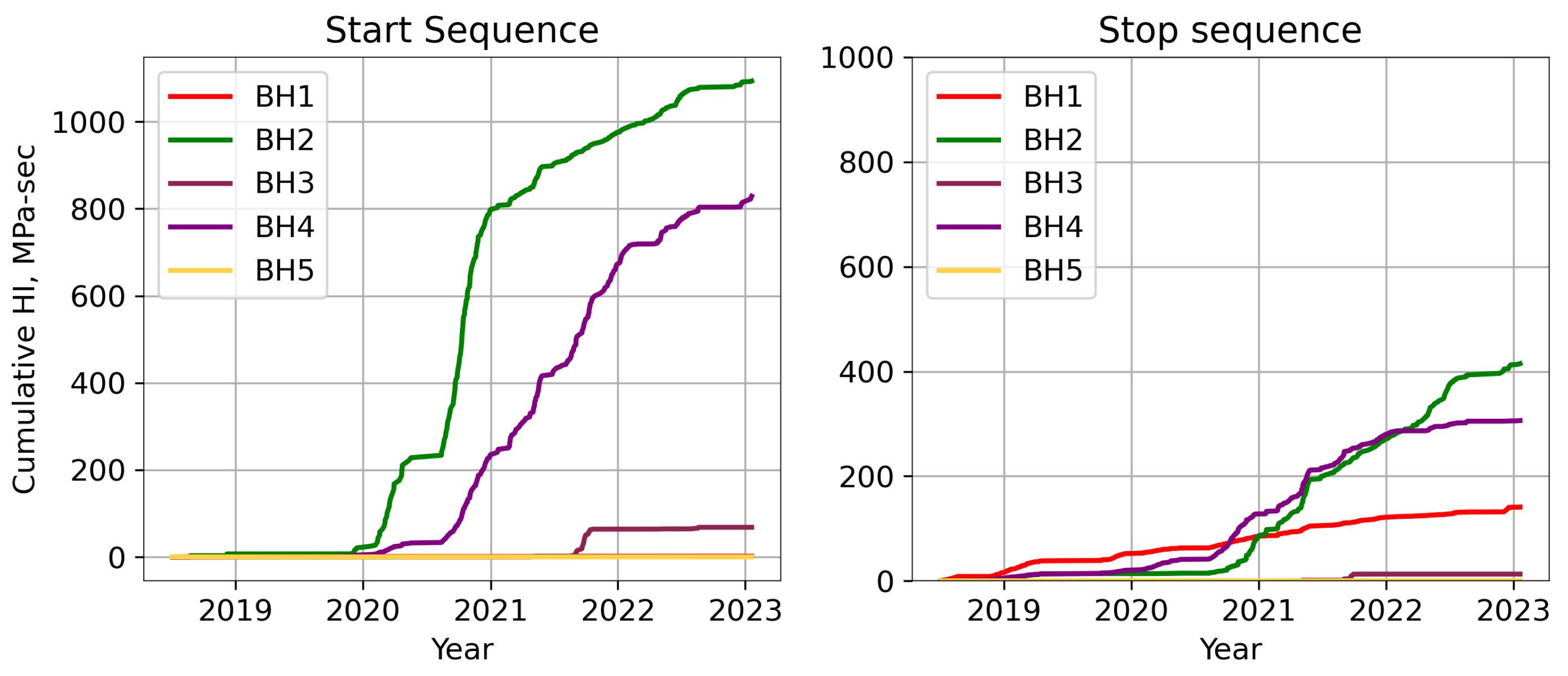
6.2. Start and Stop Sequence
6.3. Effect of Shutdown Duration
7. Discussion
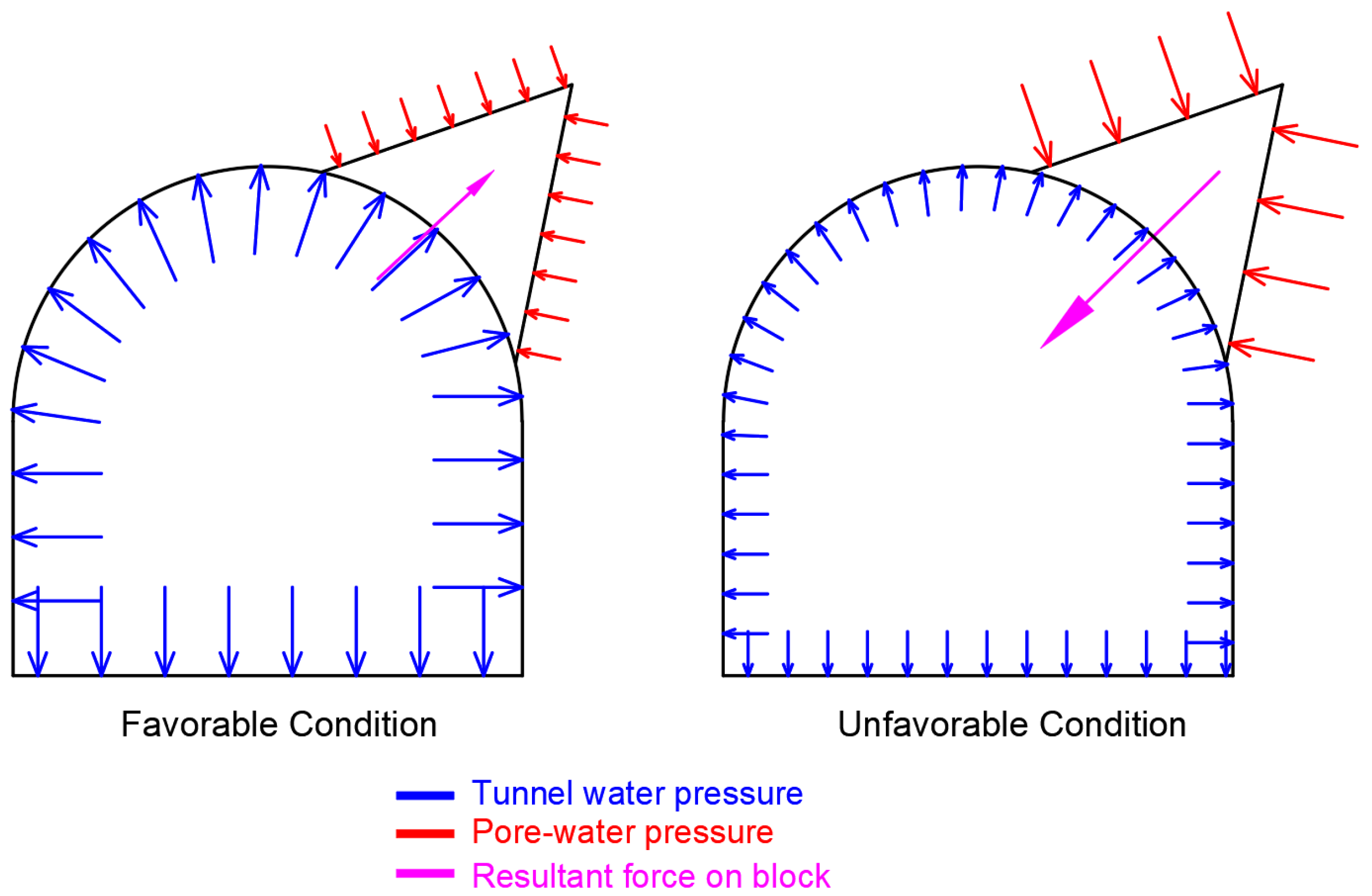
7.1. Joint Characteristics
7.2. Behavior of Monitored Boreholes
7.3. Natural, Cutoff and Sampling Frequency
7.4. Design Practice
7.5. Operational Requirements
8. Conclusions and Recommendations
- The impact of the start sequences on the rock mass due to transient-induced cyclic loading is greater than the impact of the stop sequences. The analysis suggests that start sequences produce three times as much HI as the stop sequences in the operation of a hydropower plant under hydropeaking.
- The analysis of pore pressure data reveals that the shutdown duration has a direct influence on HI. When the shutdown duration is reduced by half, the HI increases by five times.
- The response of pore pressure in the rock joints is greatly influenced by the properties of joints like joint wall opening (aperture), roughness, infilling condition, joint spacing and persistence.
- HI and MPD can be used as complementary values to quantify the impact of hydraulic transient in unlined pressure tunnels.
- A water hammer can travel into a rock mass and cause a difference in the pressure inside the rock mass. So, it cannot be neglected in the design of unlined pressure tunnels since it will have long-term operational impacts.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Panthi, K.K.; Basnet, C.B. State-of-the-art design guidelines in the use of unlined pressure tunnels/shafts for hydropower scheme. In Proceedings of the ISRM International Symposium—10th Asian Rock Mechanics Symposium, ARMS 2018, Singapore, 29 October–3 November 2018. [Google Scholar]
- Rancourt, A.J. Guidelines for Preliminary Design of Unlined Pressure Tunnels. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2010. [Google Scholar]
- Bye, T.; Hope, E. Deregulation of Electricity Markets: The Norwegian Experience. Econ. Political Wkly. 2005, 40, 5269–5278. [Google Scholar]
- Eurelectric. Hydro in Europe: Powering Renewables; Technical Report; Eurelectric: Brussels, Belgium, 2011. [Google Scholar]
- Skar, C.; Jaehnert, S.; Tomasgard, A.; Midthun, K.; Fodstad, M. Norway’s role as a flexibility provider in a renewable Europe. In A Position Paper Prepared by FME CenSES; CenSES Centre for Sustainable Energy Studies: Trondheim, Norway, 2018; Volume 80. [Google Scholar]
- Egging, R.; Tomasgard, A. Norway’s role in the European energy transition. Energy Strategy Rev. 2018, 20, 99–101. [Google Scholar] [CrossRef]
- Neupane, B.; Vereide, K.; Panthi, K.K. Operation of Norwegian hydropower plants and its effect on block fall events in unlined pressure tunnels and shafts. Water 2021, 13, 1567. [Google Scholar] [CrossRef]
- Bråtveit, K.; Bruland, A.; Brevik, O. Rock falls in selected Norwegian hydropower tunnels subjected to hydropeaking. Tunn. Undergr. Space Technol. 2016, 52, 202–207. [Google Scholar] [CrossRef]
- Neupane, B.; Panthi, K.K.; Vereide, K. Cyclic fatigue in unlined hydro tunnels caused by pressure transients. Int. J. Hydropower Dams 2021, 28, 46–54. [Google Scholar]
- Palmström, A.; Broch, E. The design of unlined hydropower tunnels and shafts: 100 years of Norwegian experience. Int. J. Hydropower Dams 2017, 24, 72–79. [Google Scholar]
- Benson, R.P. Design of unlined and lined pressure tunnels. Tunn. Undergr. Space Technol. Inc. Trenchless 1989, 4, 155–170. [Google Scholar] [CrossRef]
- Neupane, B. Long-Term Impact on Unlined Tunnels of Hydropower Plants Due to Frequent Start/Stop Sequences. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2021. [Google Scholar]
- Chaudhry, H. Applied Hydraulic Transients Third Edition; Springer: Columbia, SC, USA, 2014. [Google Scholar]
- Jaeger, C. Present Trends in Surge Tank Design. Proc.-Mech. Eng. 1953, 168, 91–124. [Google Scholar] [CrossRef]
- Khilqa, S.S.E. Damping in Transient Pressurized Flows Damping in Transient Pressurized Flows. Ph.D. Thesis, University of South Carolina, Columbia, CS, USA, 2019. [Google Scholar]
- Vítkovský, J.P.; Bergant, A.; Simpson, A.R.; Lambert, M.F. Systematic Evaluation of One-Dimensional Unsteady Friction Models in Simple Pipelines. J. Hydraul. Eng. 2006, 132, 696–708. [Google Scholar] [CrossRef]
- Parmakian, J. Waterhammer Analysis; Dover Publications, Inc.: New York, NY, USA, 1963. [Google Scholar]
- Hakami, E. Aperture Distribution of Rock Fractures. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 1995. [Google Scholar]
- Louis, C. Study of Groundwater Flow in Jointed Rock and Its Influence on the Stability of Rock Masses; Imperial College of Science and Technology: London, UK, 1969; pp. 1–90. [Google Scholar]
- Panthi, K.K.; Basnet, C.B. Fluid Flow and Leakage Assessment Through an Unlined/Shotcrete Lined Pressure Tunnel: A Case from Nepal Himalaya. Rock Mech. Rock Eng. 2021, 54, 1687–1705. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Berg, S.S.; Lyslo, K.B.; Skurtveit, E. Fracture networks and fluid transport in active fault zones. J. Struct. Geol. 2001, 23, 343–353. [Google Scholar] [CrossRef]
- Holmøy, K.H. Significance of Geological Parameters for Predicting Water Leakage in Hard Rock Tunnels. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2008. [Google Scholar]
- Neupane, B.; Panthi, K.K.; Vereide, K. Effect of Power Plant Operation on Pore Pressure in Jointed Rock Mass of an Unlined Hydropower Tunnel: An Experimental Study. Rock Mech. Rock Eng. 2020, 53, 3073–3092. [Google Scholar] [CrossRef]
- Lévesque, L. Nyquist sampling theorem: Understanding the illusion of a spinning wheel captured with a video camera. Phys. Educ. 2014, 49, 697–705. [Google Scholar] [CrossRef]
- Guo, W.; Wang, B.; Yang, J.; Xue, Y. Optimal control of water level oscillations in surge tank of hydropower station with long headrace tunnel under combined operating conditions. Appl. Math. Model. 2017, 47, 260–275. [Google Scholar] [CrossRef]
- Pröll, Samuel. Finding Peaks in Noisy Signals (With Python and JavaScript). Available online: https://www.samproell.io/posts/signal/peak-finding-python-js/ (accessed on 20 March 2023).
- Lyons, R. Understanding Digital Signal Processing; Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mosonyi, E. High-Head Power Plants; Akadémiai Kiadó: Budapest, Hungary, 1991; Volume Two/A. [Google Scholar]
- Neupane, B.; Panthi, K.K. Evaluation on the Effect of Pressure Transients on Rock Joints in Unlined Hydropower Tunnels Using Numerical Simulation. Rock Mech. Rock Eng. 2021, 54, 2975–2994. [Google Scholar] [CrossRef]
- Bhattarai, K.P.; Zhou, J.; Palikhe, S.; Pandey, K.P.; Suwal, N. Numerical Modeling and Hydraulic Optimization of a Surge Tank Using Particle Swarm Optimization. Water 2019, 11, 715. [Google Scholar] [CrossRef]
- Preisig, G.; Eberhardt, E.; Smithyman, M.; Preh, A.; Bonzanigo, L. Hydromechanical rock mass fatigue in deep-seated landslides accompanying seasonal variations in pore pressures. Rock Mech. Rock Eng. 2016, 49, 2333–2351. [Google Scholar] [CrossRef]
- Bakken, T.H.; Harby, A.; Forseth, T.; Ugedal, O.; Sauterleute, J.F.; Halleraker, J.H.; Alfredsen, K. Classification of hydropeaking impacts on Atlantic salmon populations in regulated rivers. River Res. Appl. 2021, 39, 313–325. [Google Scholar] [CrossRef]
- Ki-Bok, M.; Rutqvist, J.; Tsang, C.F.; Jing, L. Stress-dependent permeability of fractured rock masses: A numerical study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
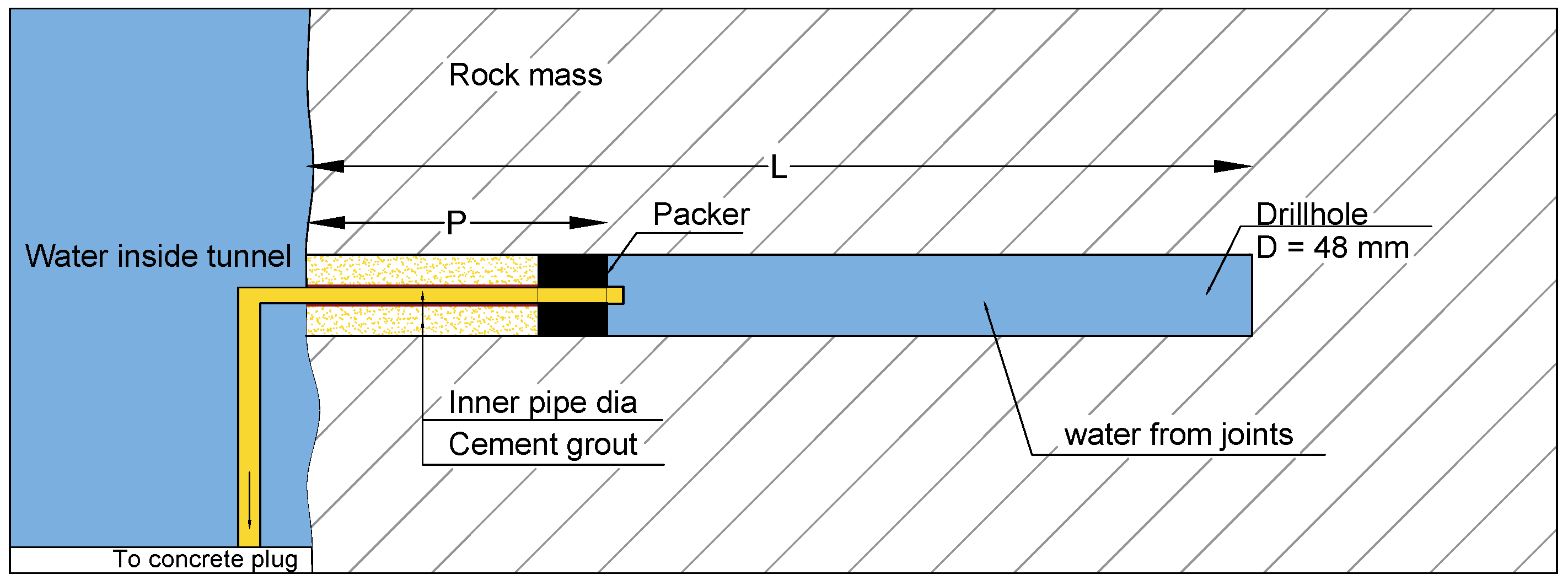
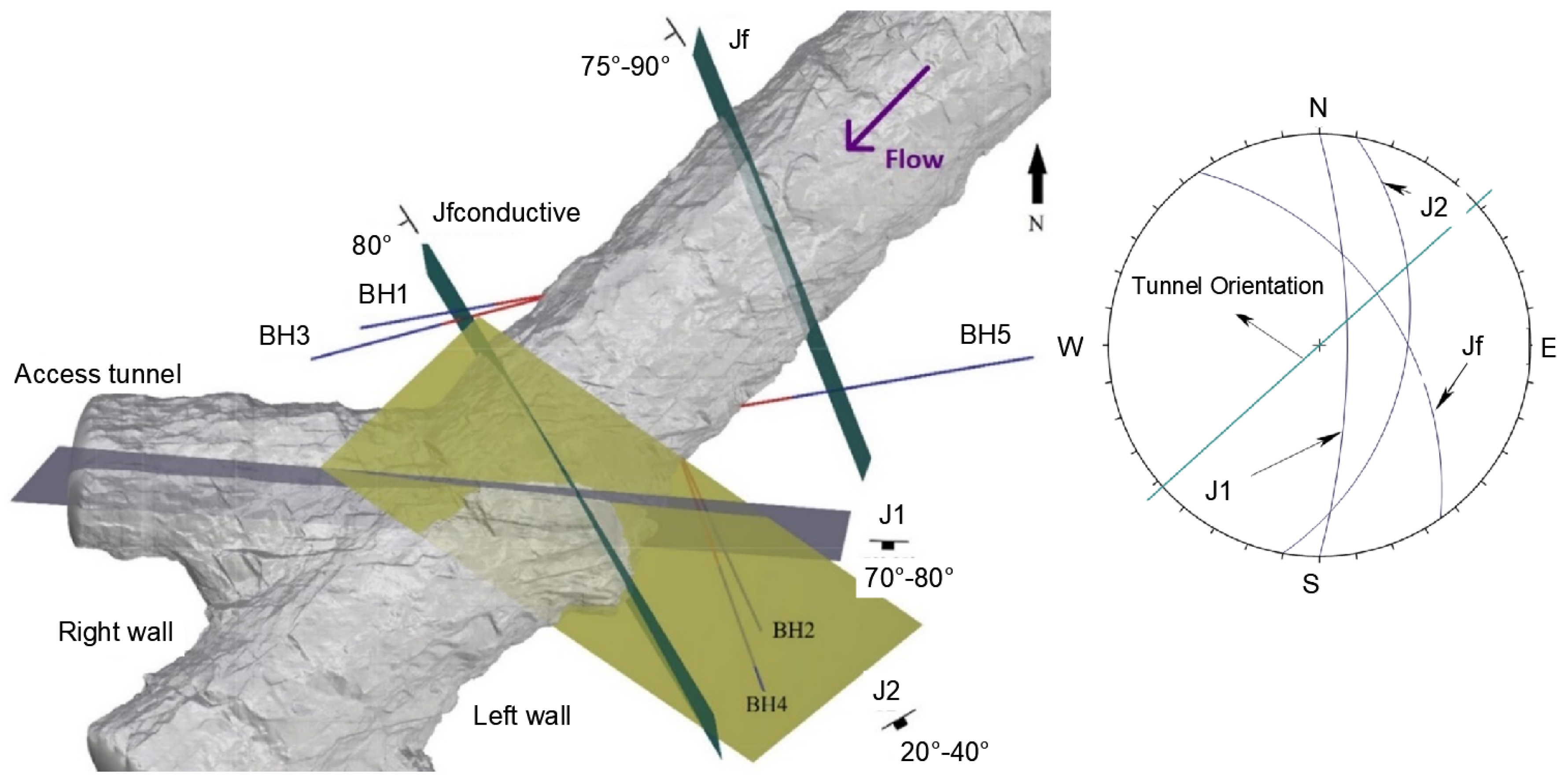







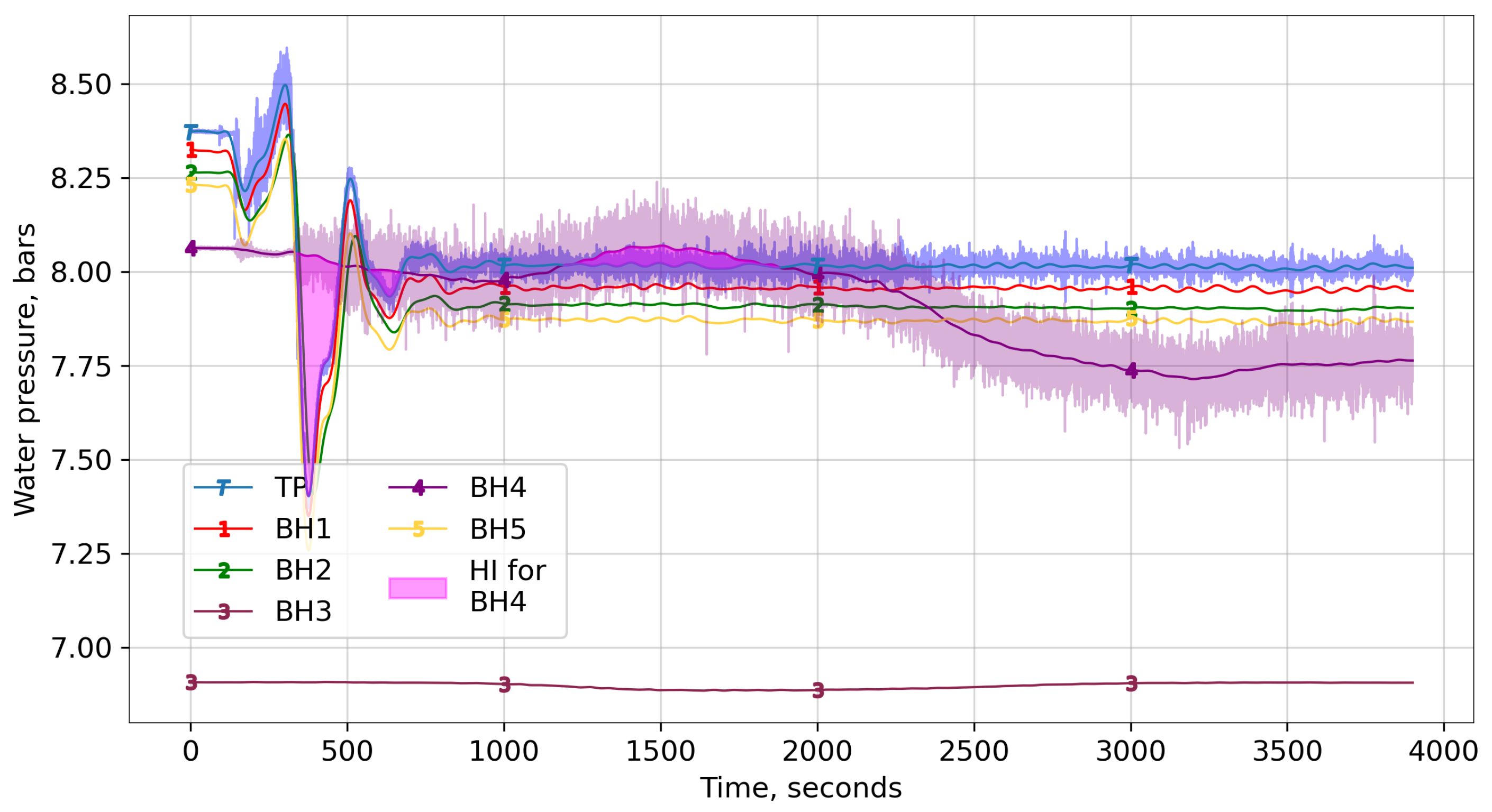
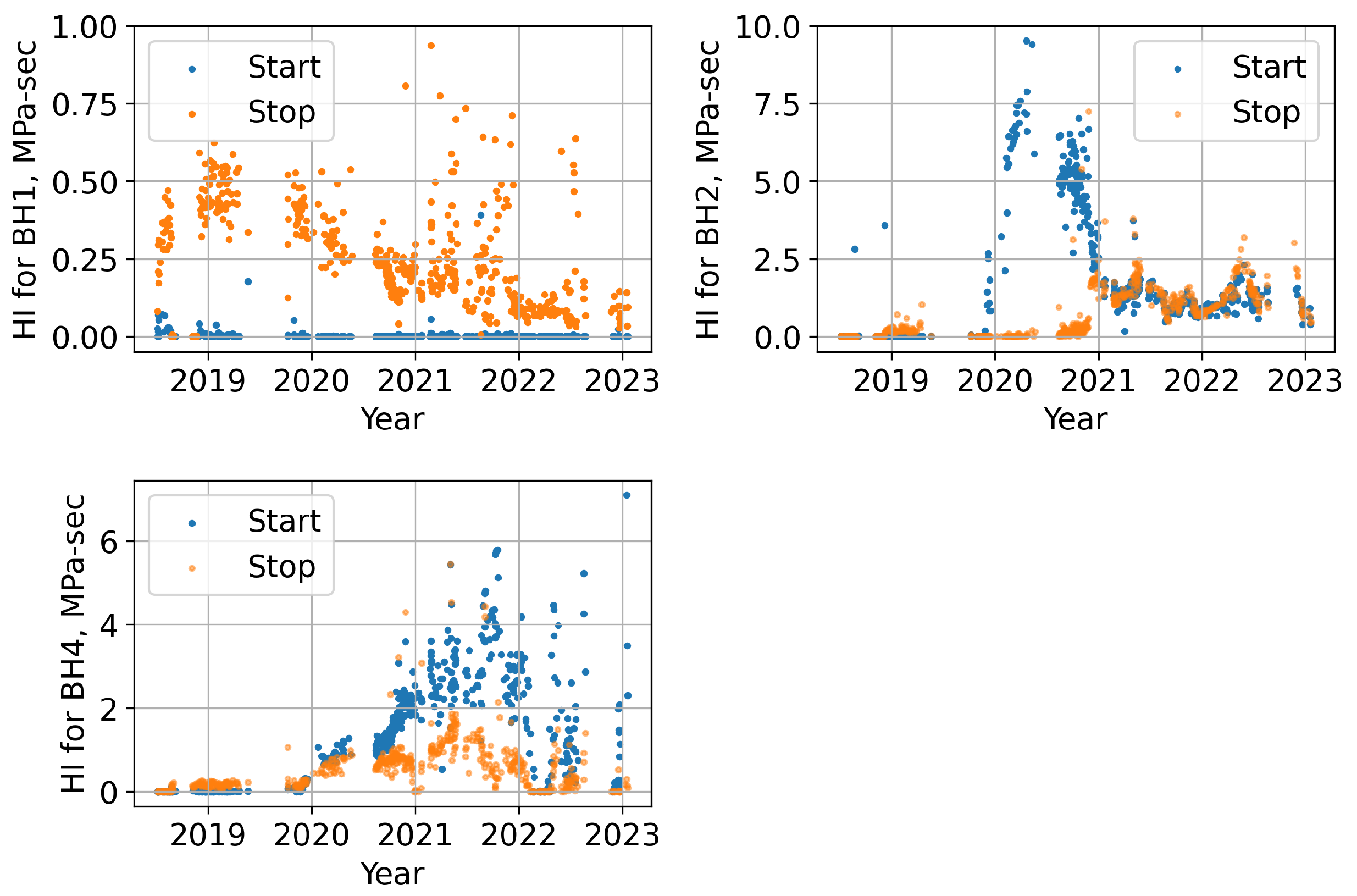


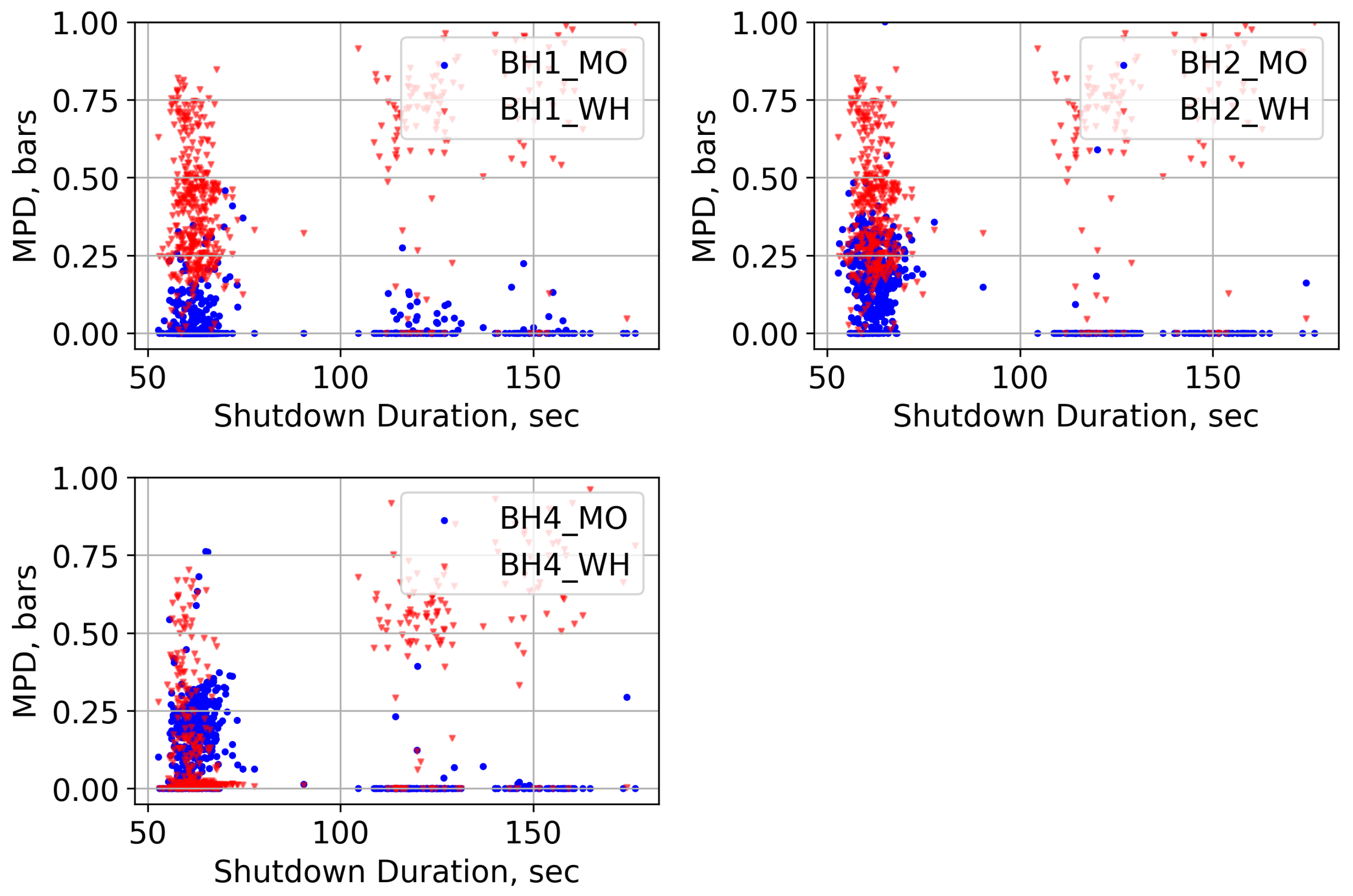

| Borehole | BH1 | BH2 | BH3 | BH4 | BH5 |
|---|---|---|---|---|---|
| Trend/plunge | 255°/10° | 155°/10° | 260°/10° | 160°/10° | 80°/10° |
| Location | Right wall | Left wall | Right wall | Left wall | Left wall |
| Borehole length (L), m | 7 | 7 | 9 | 9 | 11 |
| Depth of packer from tunnel wall (P), m | 2 | 2 | 4 | 4 | 2 |
| Effective length | 5 | 5 | 5 | 5 | 9 |
| Joint Set | Jf | Jfconductive | J1 | J2 |
|---|---|---|---|---|
| Strike | N 140°–160° E | N 150° E | N 80°–100° E | N 60°–75° E |
| Dip | 75°–90° SW | 80° SW | 70°–85° SW | 20°–40° SE |
| Persistence (m) | 3–10 | More than 10 m | 3–10 m | 3–10 m |
| Joint wall weathering | Fresh (W1) | Slightly weathered (W2) | Fresh (W1) | Slightly weathered (W2) |
| Joint roughness | Rough planar JRC 4–6 | Rough undulating JRC 14–18 | Rough planar JRC 4–6 | Smooth undulating JRC 10–14 |
| Joint aperture (mm) | Tight (0.1–0.25 mm) | Partly open (0.25–1 mm) | Tight (0.1–0.25 mm) | Partly open (0.25–1 mm) |
| Joint infilling condition | Clay | Washed out | Clay | Washed out |
| Seepage | Damp but no dripping or following water present | Continuous flow | Wet with occasional drops of water | Continuous flow |
| Typical spacing (m) | 1–2 m | More than 10 m | 1–2 m | More than 10 m |
| Borehole Type | Borehole | Remarks |
|---|---|---|
| Highly responsive | BH5 (after March 2020) | No HI and MPD due to MO and WH |
| Responsive | BH1 | HI and MPD only due to WH but less HI due to MO |
| Moderately responsive | BH2 (after September 2019) and BH4 | HI and MPD due to both WH and MO |
| Non responsive | BH2 (before September 2019), BH3, BH5 (before March 2020) | No HI due to both WH and MO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, S.; Panthi, K.K.; Vereide, K. Hydraulic Transient Impact on Surrounding Rock Mass of Unlined Pressure Tunnels. Water 2023, 15, 3894. https://doi.org/10.3390/w15223894
Ghimire S, Panthi KK, Vereide K. Hydraulic Transient Impact on Surrounding Rock Mass of Unlined Pressure Tunnels. Water. 2023; 15(22):3894. https://doi.org/10.3390/w15223894
Chicago/Turabian StyleGhimire, Sanyam, Krishna Kanta Panthi, and Kaspar Vereide. 2023. "Hydraulic Transient Impact on Surrounding Rock Mass of Unlined Pressure Tunnels" Water 15, no. 22: 3894. https://doi.org/10.3390/w15223894
APA StyleGhimire, S., Panthi, K. K., & Vereide, K. (2023). Hydraulic Transient Impact on Surrounding Rock Mass of Unlined Pressure Tunnels. Water, 15(22), 3894. https://doi.org/10.3390/w15223894








