A Beach Profile Evolution Model Driven by the Hybrid Shock-Capturing Boussinesq Wave Solver
Abstract
:1. Introduction
2. Model Development
2.1. Wave Module
2.2. Wave Boundary Layer Module
2.3. Morphology Module
3. Hydrodynamic Validations
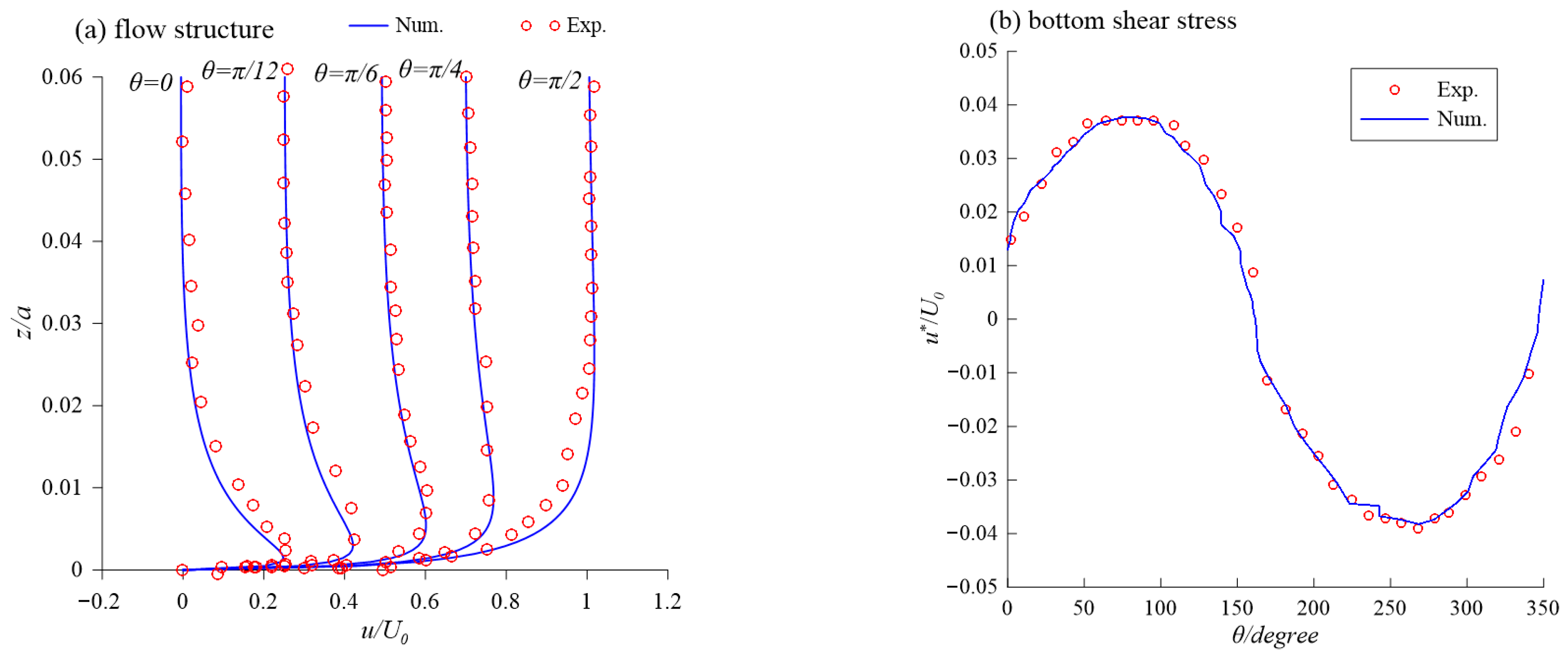
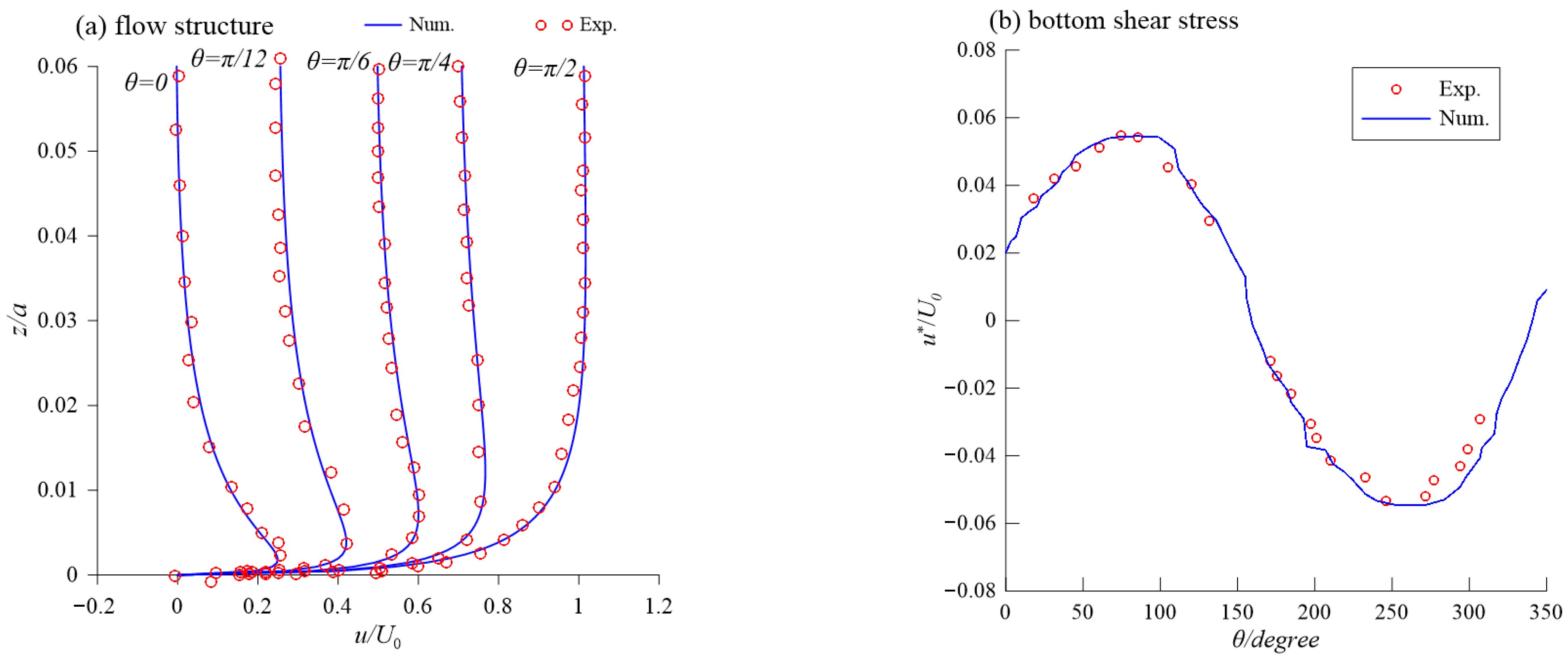
3.1. Validations of Wave Boundary Layer
3.2. Validations of Solitary Wave
4. Morphology Validations
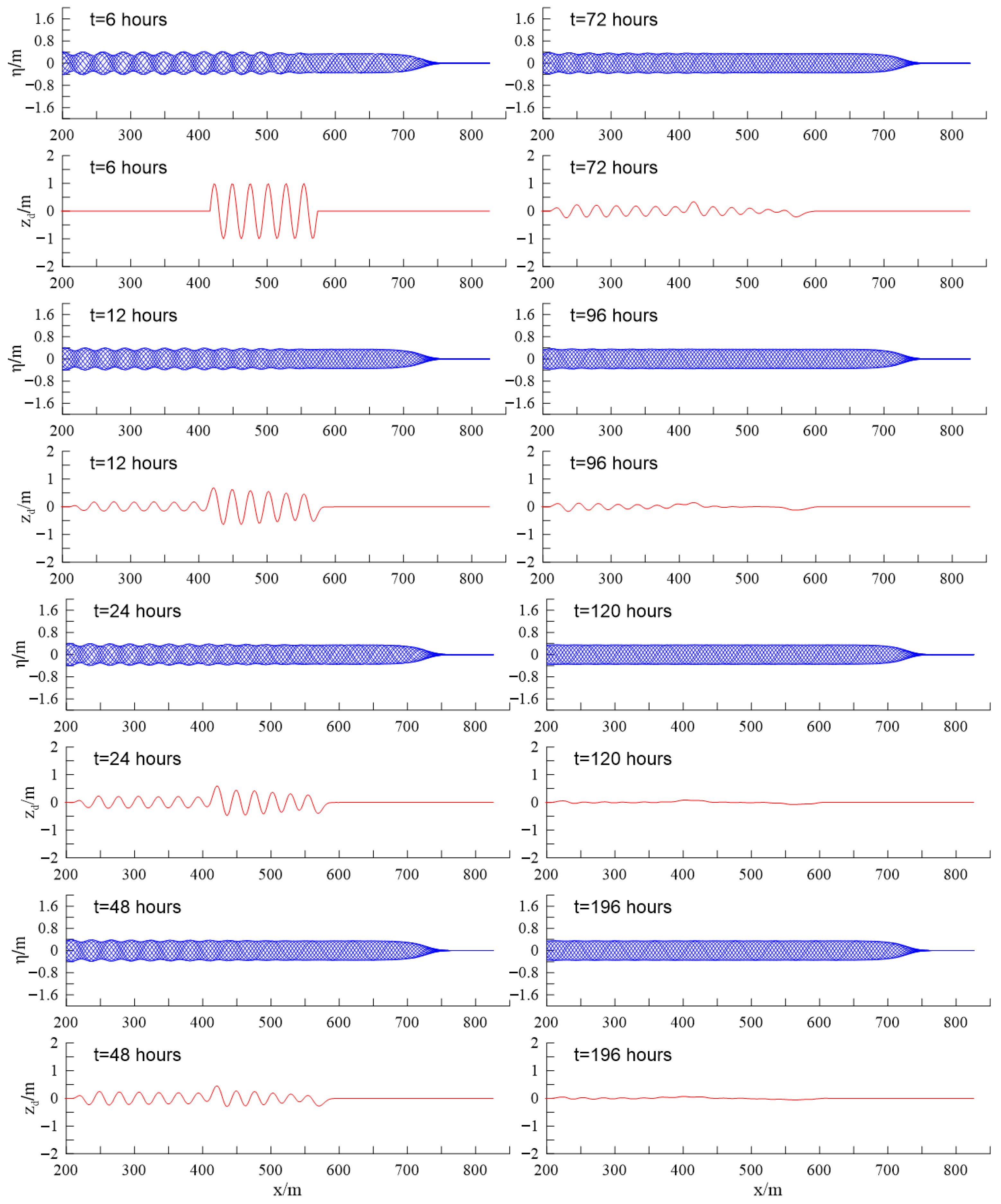
4.1. Sandbar Evolution under Bragg Resonance
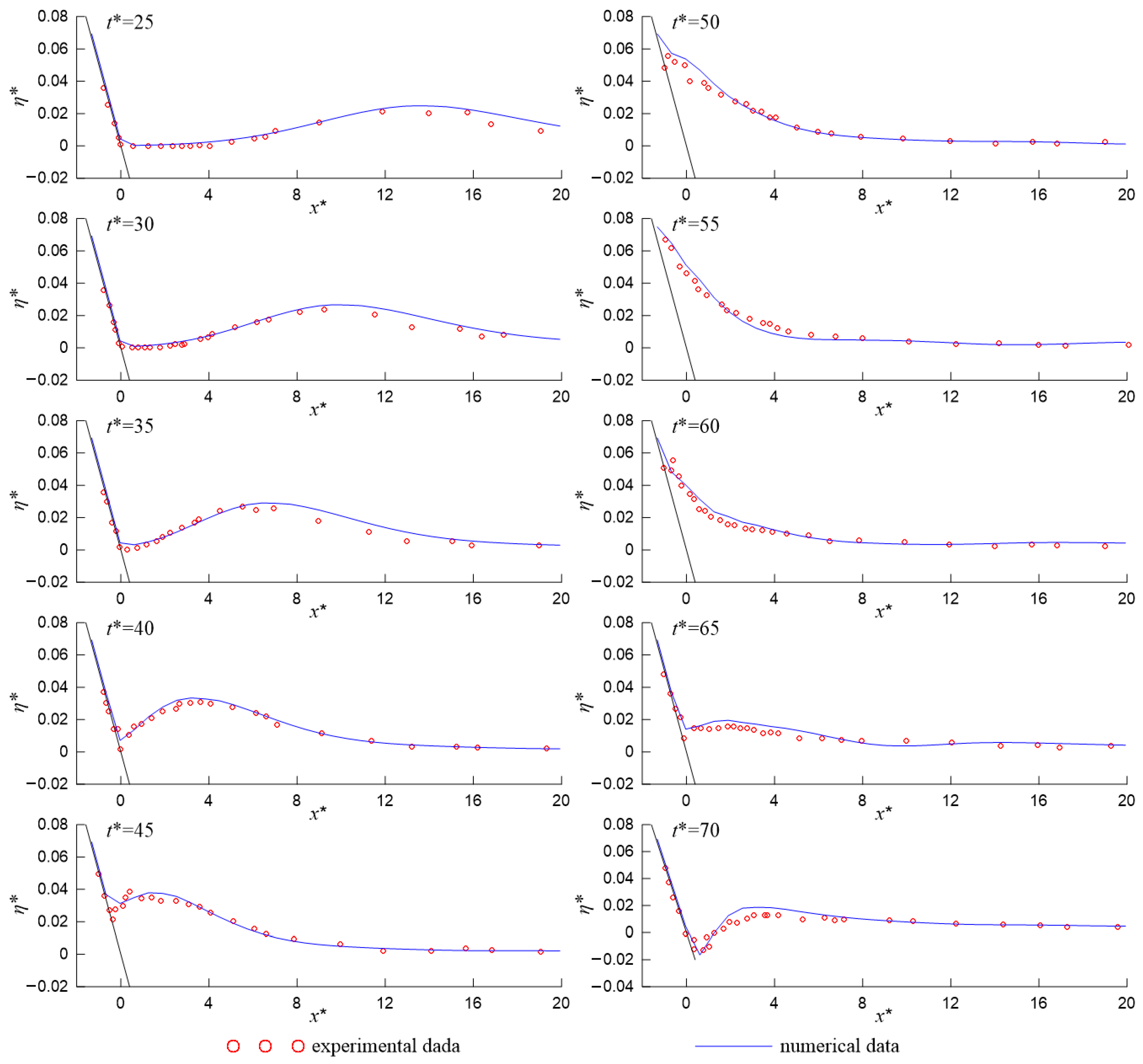
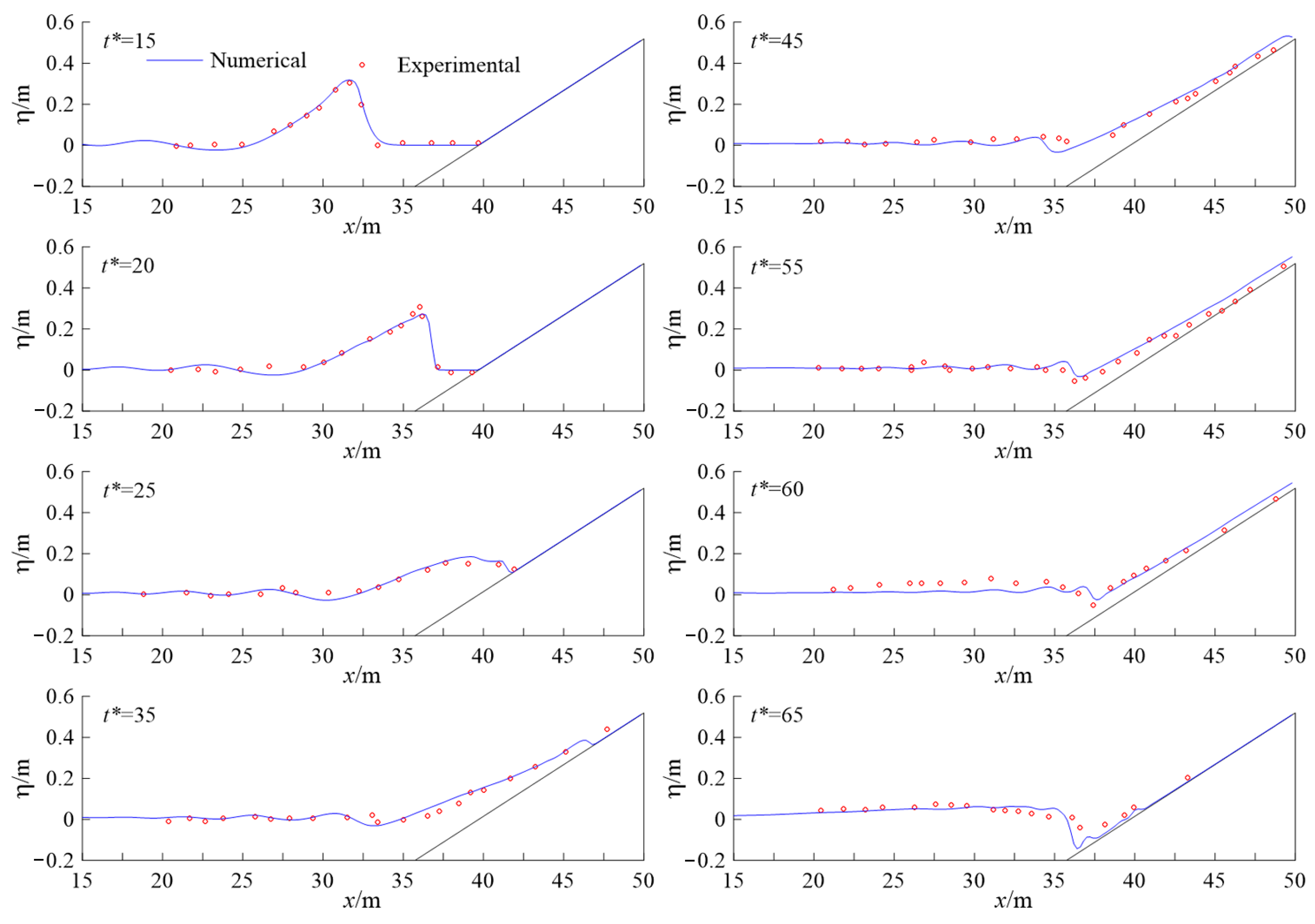
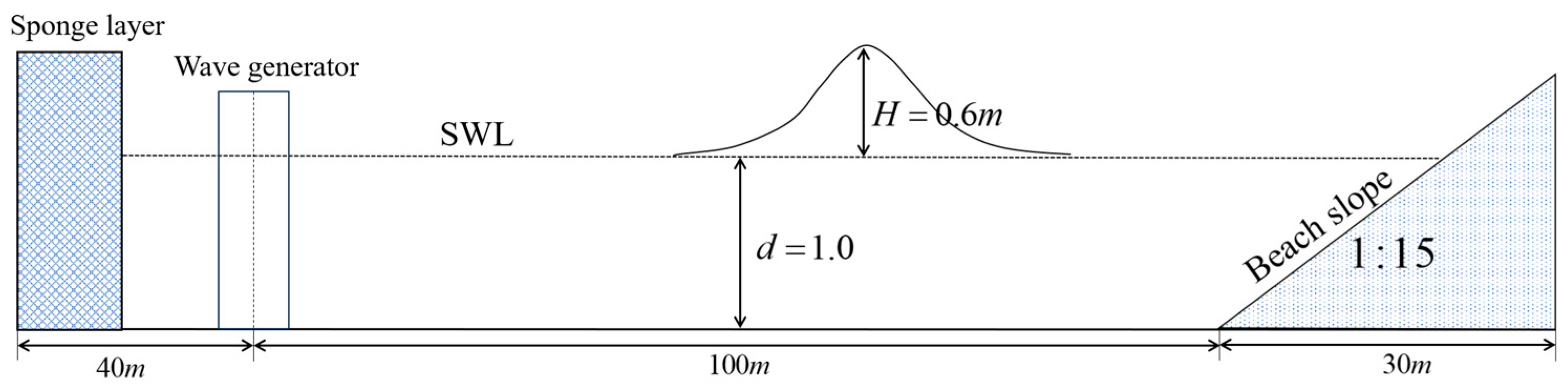
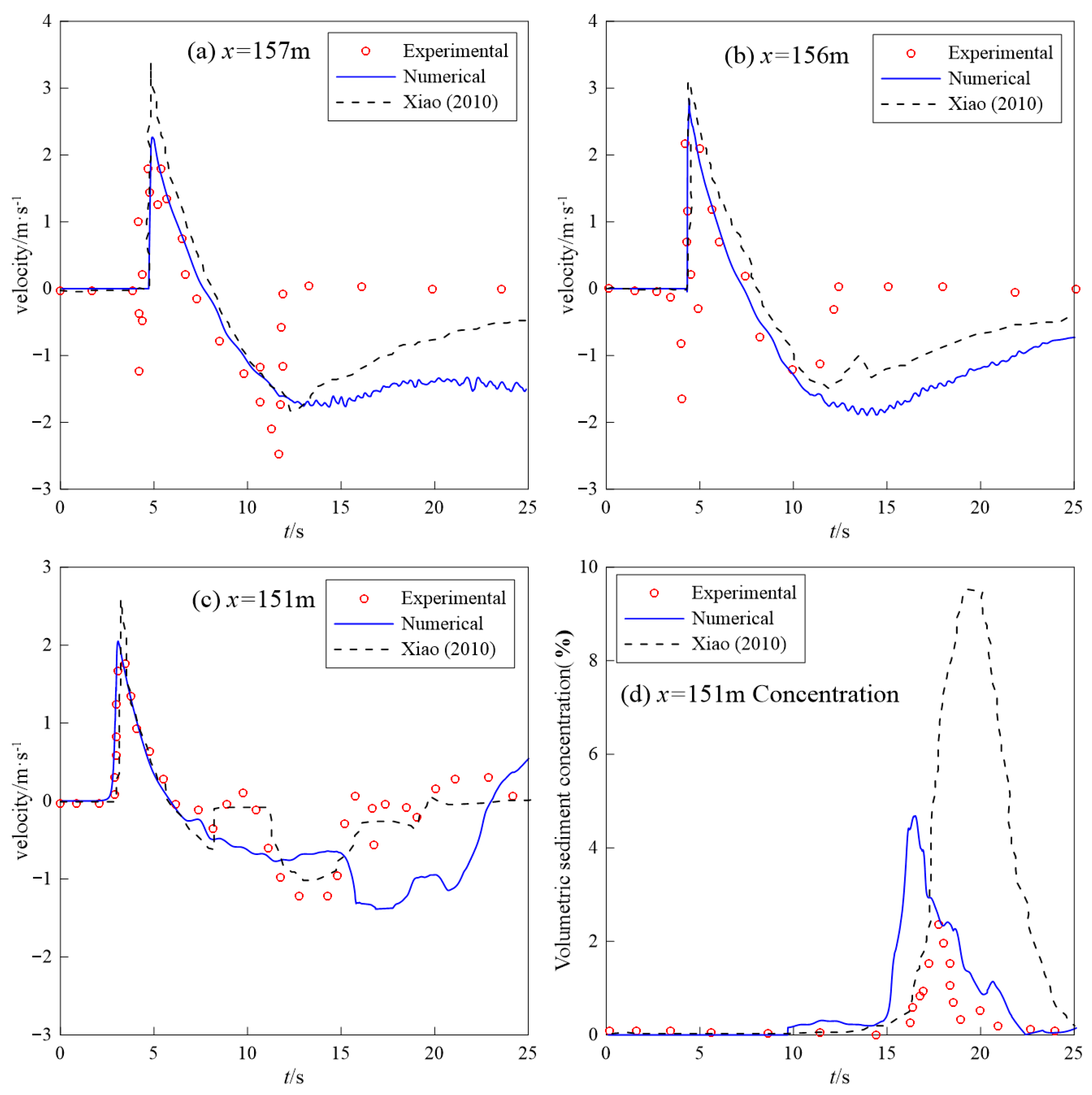
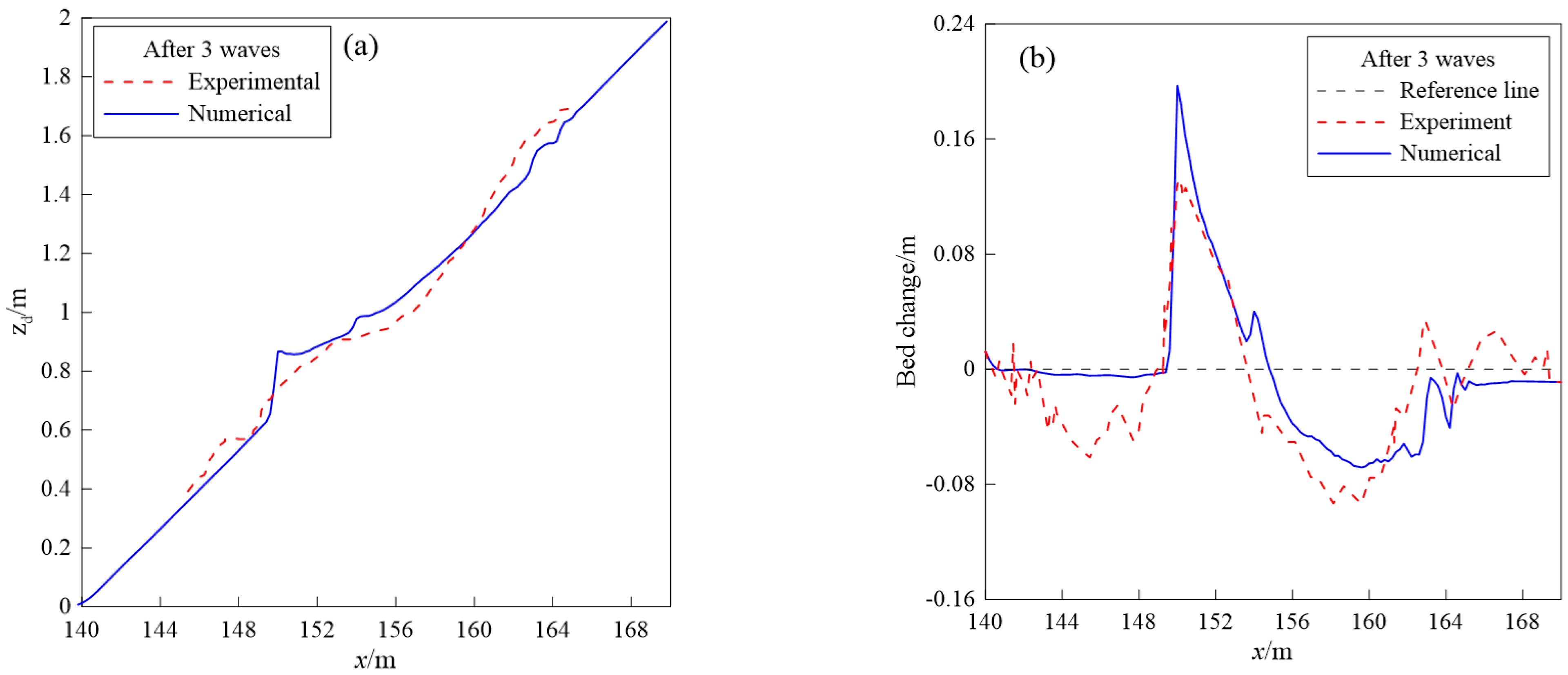
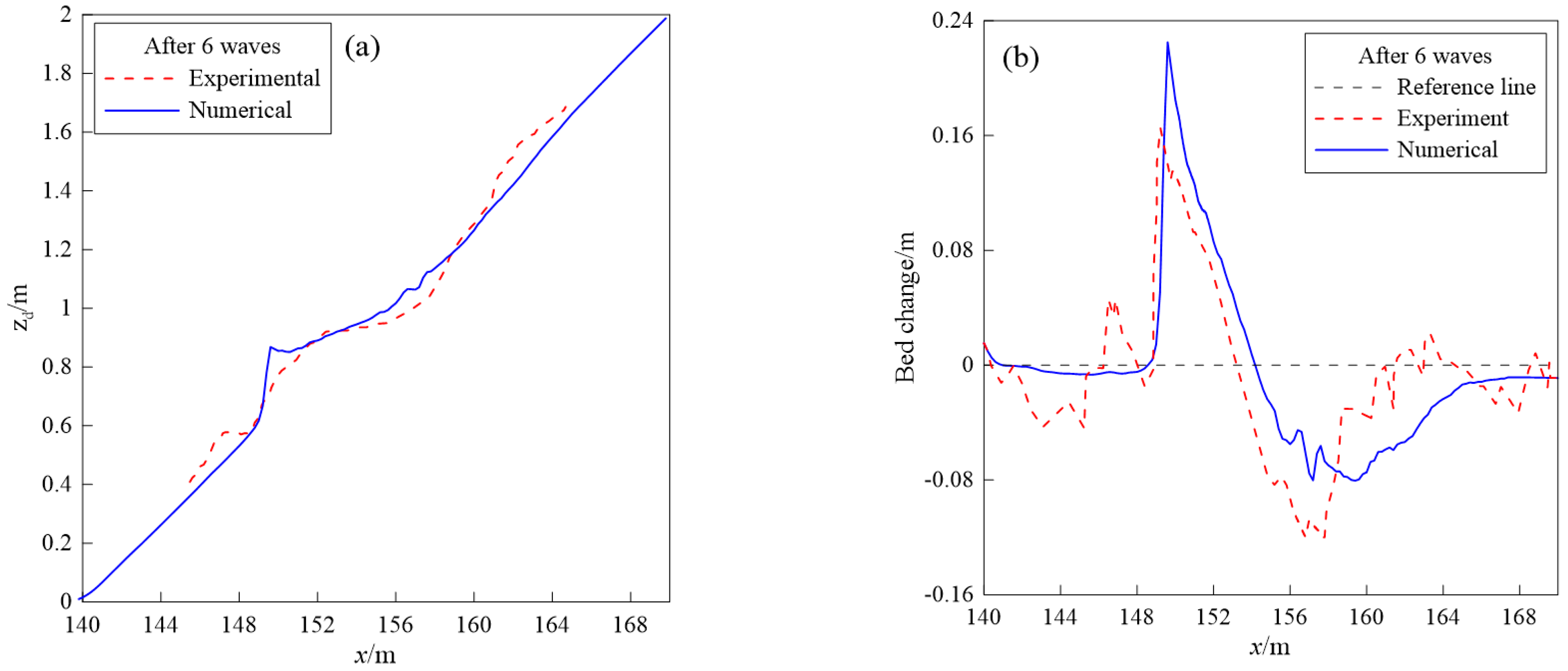
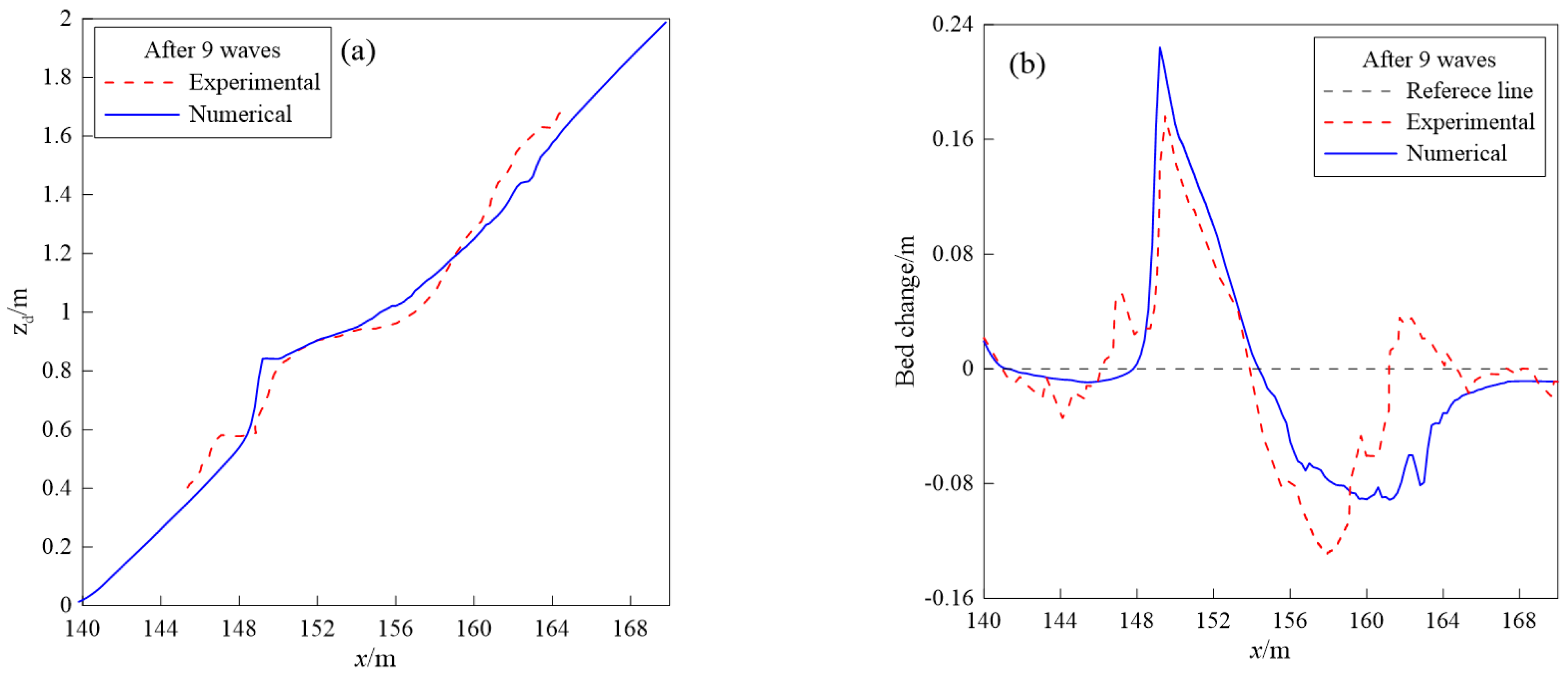
4.2. Sandbar Generation under Solitary Waves
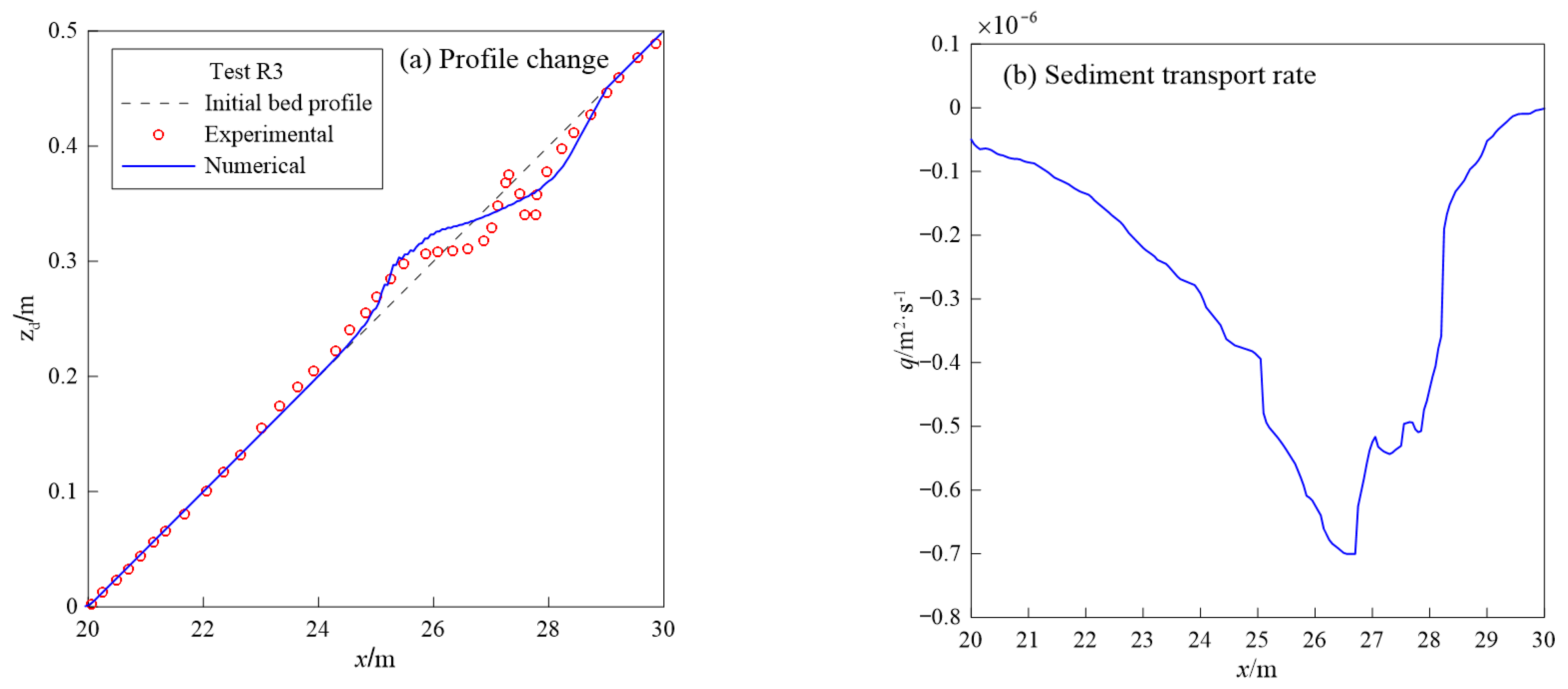
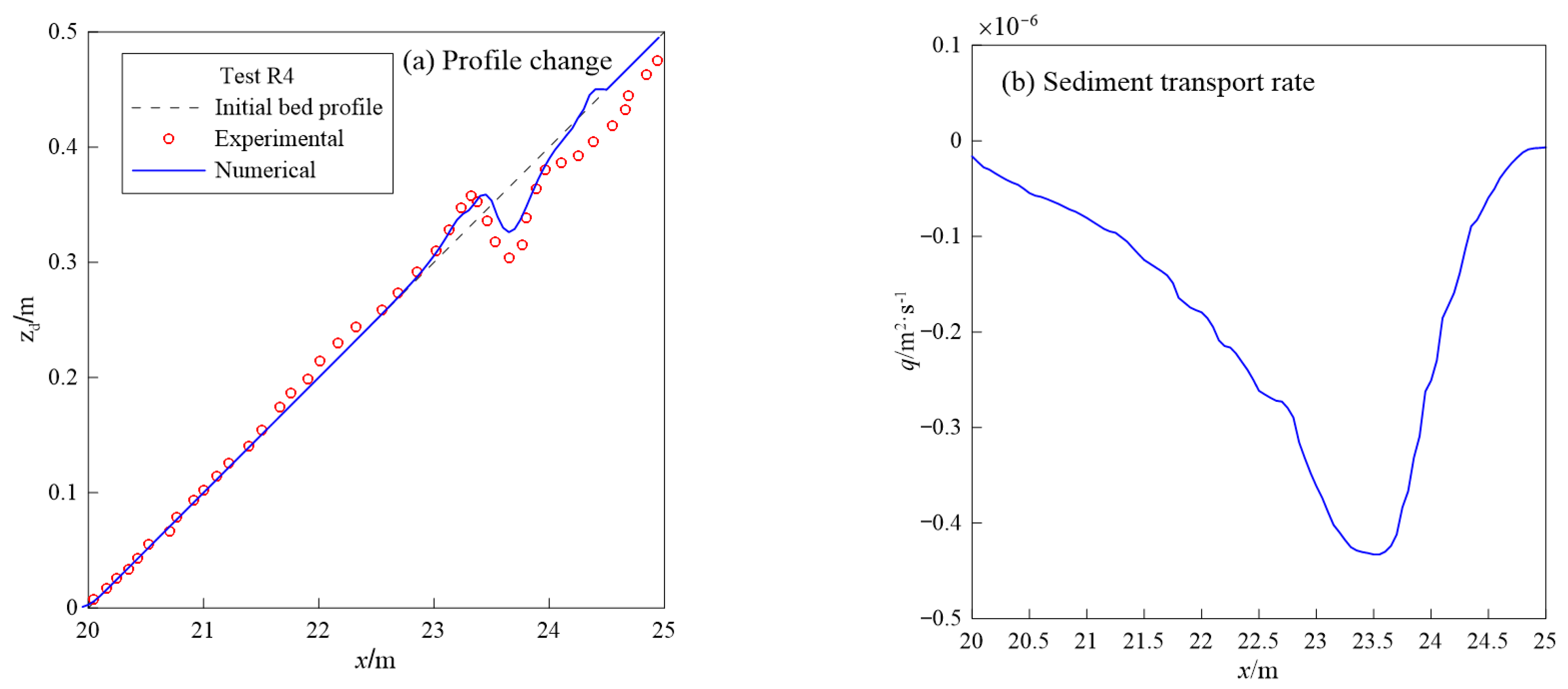
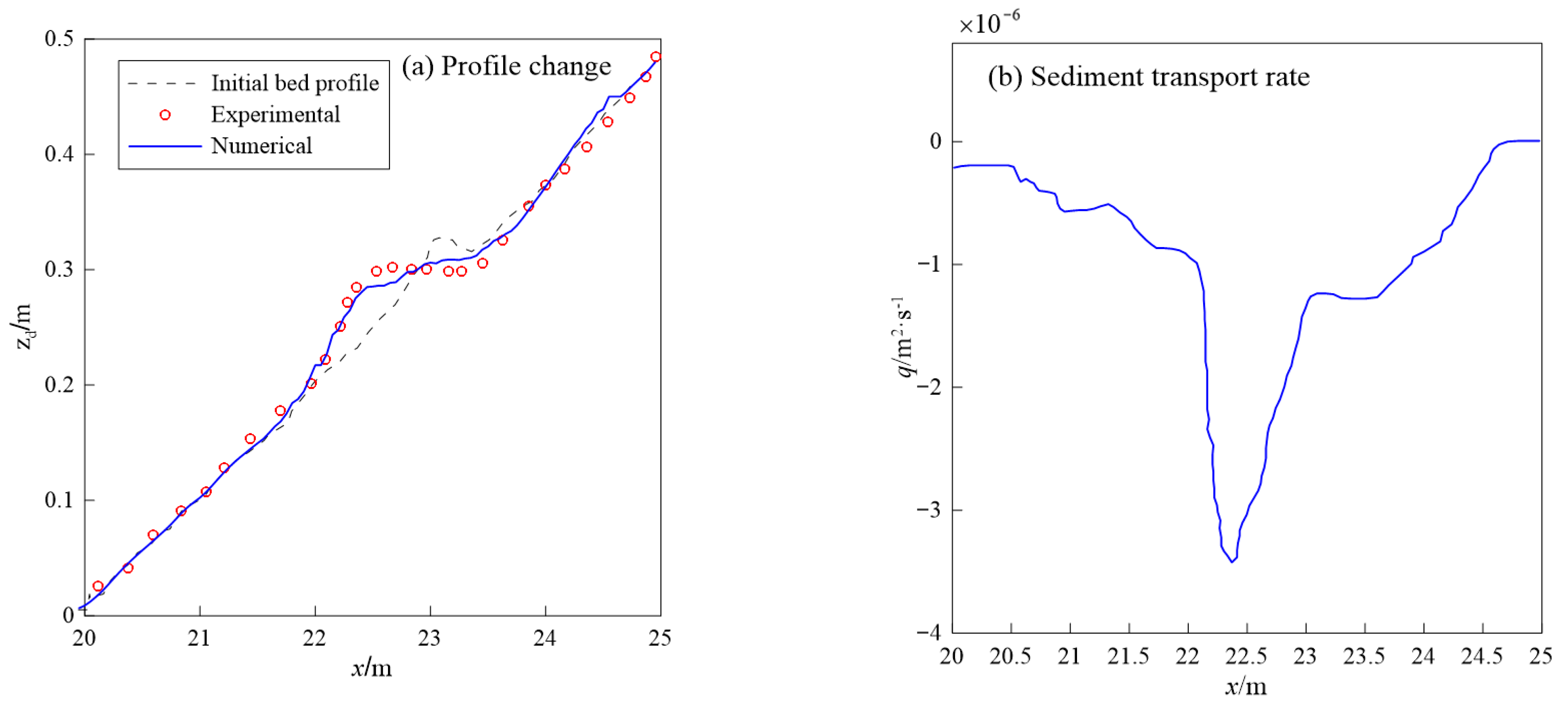
4.3. Sandbar Generation and Migration under Regular Waves
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fredsøe, J.; Andersen, O.H.; Silberg, S. Distribution of suspended sediment in large waves. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 1041–1059. [Google Scholar] [CrossRef]
- Deigaard, R.; Fredsoe, J.; Hedegaard, I.B. Suspended sediment in the surf zone. J. Waterw. Port Coast. Ocean Eng. 1986, 112, 115–128. [Google Scholar] [CrossRef]
- Shibayama, T.; Nistor, I. Modelling of time-dependent sand transport at the bottom boundary layer in the surf zone. Coast. Eng. 1998, 40, 241. [Google Scholar] [CrossRef]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; World Scientific: Singapore, 1992. [Google Scholar]
- Kubo, H.; Sunamura, T. Large-scale turbulence to facilitate sediment motion under spilling breakers. In Proceedings of the Fourth Conference on Coastal Dynamics, Lund, Sweden, 11–15 June 2001; pp. 212–221. [Google Scholar]
- Ting, F.C.K. Large-scale turbulence under a solitary wave. Coast. Eng. 2006, 53, 441–462. [Google Scholar] [CrossRef]
- Ting, F.C.K. Large-scale turbulence under a solitary wave. Part 2: Forms and evolution of coherent structures. Coast. Eng. 2008, 55, 522–536. [Google Scholar] [CrossRef]
- Sun, J.W.; Fang, K.Z.; Liu, Z.B.; Fan, H.X.; Sun, Z.C.; Wang, P. A review on the theory and application of Boussinesq-type equations for water waves. Haiyang Xuebao 2020, 42, 1–11. (In Chinese) [Google Scholar]
- Gao, J.L.; Ma, X.Z.; Zang, J.; Dong, G.H.; Ma, X.J.; Zhu, Y.Z.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Gao, J.L.; Zhou, X.J.; Zhou, L.; Zang, J.; Chen, H.Z. Numerical investigation on effects of fringing reefs on low-frequency oscillations within a harbor. Ocean Eng. 2019, 172, 86–95. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Chen, H.Z.; Zang, J.; Dong, G.H. On hydrodynamic characteristics of transient harbor resonance excited by double solitary waves. Ocean Eng. 2021, 219, 108345. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T. Time-dependent numerical code for extended boussinesq equations. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 251–261. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Liu, Z.B.; Han, P.X.; Fang, K.Z.; Liu, Y. A high-order nonlinear Boussinesq-type model for internal waves over a mildly-sloping topography in a two-fluid system. Ocean Eng. 2023, 285, 115283. [Google Scholar] [CrossRef]
- Gao, J.L.; Shi, H.B.; Zang, J.; Liu, Y.Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Dong, G.H.; Chen, H.Z.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Rakha, K.A.; Deigaard, R.; Brøker, I. A phase-resolving cross-shore transport model for beach evolution. Coast. Eng. 1997, 31, 231–261. [Google Scholar] [CrossRef]
- Karambas, T.V.; Koutitas, C. Surf and swash zone morphology evolution induced by nonlinear waves. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 102–113. [Google Scholar] [CrossRef]
- Long, W.; Kirby, J.T. Cross-shore sediment transport model based on the Boussinesq equations and an improved Bagnold formula. In Proceedings of the Coastal Sediments ’03, Clearwater Beach, FL, USA, 18–23 May 2003. [Google Scholar]
- Rakha, K.A. A quasi-3D phase-resolving hydrodynamic and sediment transport model. Coast. Eng. 1998, 34, 277–311. [Google Scholar] [CrossRef]
- Karambas, T.V.; Karathanassi, E.K. Longshore sediment transport by nonlinear waves and currents. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 277–286. [Google Scholar] [CrossRef]
- Fang, K.Z.; Dong, P.; Zou, Z.L. A phase-resolving beach evolution model based on fully nonlinear Boussinesq equations. In Proceedings of the 21th International Offshore and Polar Engineering Conference (ISOPE), Beijing, China, 20–25 June 2010; pp. 1069–1074. [Google Scholar]
- Wenneker, I.; van Dongeren, A.; Lescinski, J.; Roelvink, D.; Borsboom, M. A Boussinesqtype wave driver for a morphodynamical model to predict short-term morphology. Coast. Eng. 2011, 58, 66–84. [Google Scholar] [CrossRef]
- Karambas, T.V. Design of detached breakwaters for coastal protection: Development and application of an advanced numerical model. In Proceedings of the 33rd International Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012; Volume 1. [Google Scholar]
- Rahman, S.; Mano, A.; Udo, K. Quasi-2D sediment transport model combined with Bagnold-type bed load transport. In Proceedings of the 12th International Coastal Symp, Plymouth, UK, 8–12 April 2013; Volume 1, pp. 368–373. [Google Scholar]
- Lynett, P.J. Nearshore wave modeling with high order Boussinesq-type equations. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 348–357. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean. Model. 2012, 43, 36–51. [Google Scholar] [CrossRef]
- Orszaghova, J.; Borthwick, A.G.L.; Taylor, P.H. From the paddle to the beach-a Boussinesq shallow water numerical wave tank based on madsen and Sørensen’s equations. J. Comput. Phys. 2012, 231, 328–344. [Google Scholar] [CrossRef]
- Roeber, V.; CHEUNG, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Fang, K.Z.; Zhang, Z.; Zou, Z.L.; Liu, Z.B.; Sun, J.W. Modelling of 2-D extended Boussinesq equations using a hybrid numerical scheme. J. Hydrodyn. 2014, 26, 187–198. [Google Scholar] [CrossRef]
- Cienfuegos, R. A fourth-order compact finite volume scheme for fully nonlinear and weakly dispersive Boussinesq-type equations. Part II: Boundary conditions and validation. Int. J. Numer. Methods Fluids 2007, 53, 1423–1455. [Google Scholar] [CrossRef]
- Dutykh, D.; Katsaounis, T.; Mistotakis, D. Finite volume scheme for dispersive wave propagation and runup. J. Comput. Phys. 2011, 230, 3035–3061. [Google Scholar] [CrossRef]
- USACE. Shore Protection Manual, 4th ed.; Department of the Army, U.S. Corps of Engineers: Washington, DC, USA, 1984.
- Simpson, G.; Castelltort, S. Coupled model of surface water flow, sediment transport and morphological evolution. Comput. Geosci. 2006, 32, 1600–1614. [Google Scholar] [CrossRef]
- Madsen, O.S.; Durham, W.M. Pressure-induced subsurface sediment transport in the surf zone. In Proceedings of the Coastal Sediments ’07, ASCE, New Orleans, LA, USA, 13–17 May 2007; pp. 82–95. [Google Scholar]
- Young, Y.L.; Xiao, H.; Maddux, T. Hydro- and morpho-dynamic modeling of breaking solitary waves over a fine sand beach. Part I: Experimental study. Mar. Geol. 2010, 269, 107–118. [Google Scholar] [CrossRef]
- Xiao, H.; Young, Y.L.; Jean, H. Prévost.Hydro- and morpho-dynamic modeling of breaking solitary waves over a fine sand beach. Part II: Numerical simulation. Mar. Geol. 2010, 269, 119–131. [Google Scholar] [CrossRef]
- Sabaruddin, R.; Akira, M.; Keiko, U. Coupling of boussinesq and sediment transport model in a wave flume. J. Jpn. Soc. Civ. Eng. Ser. B1 2012, 68, 259–264. [Google Scholar]
- Francesco, G.; Giovanni, C.; Oriana, D.G.; Simone, S. Modeling Bed Evolution Using Weakly Coupled Phase-Resolving Wave Model and Wave-Averaged Sediment Transport Model. Coast. Eng. J. 2016, 58, 1650011. [Google Scholar]
- Georgios, T.K.; Constantine, D.M.; Nils, K.D.; Rolf, D. Boussinesq-Type Modeling of Sediment Transport and Coastal Morphology. Coast. Eng. J. 2017, 2, 1750007. [Google Scholar]
- Meyer-Peter, E.; Müller, R. Formulas of bed-load transport. In Proceedings of the 2nd Meeting, IAHR, Stockholm, Sweden, 7–9 June 1948; pp. 39–64. [Google Scholar]
- Kim, G.; Lee, C.; Suh, K. Extended Boussinesq equations for rapidly varying topography. Ocean Eng. 2009, 36, 842–851. [Google Scholar] [CrossRef]
- Fang, K.Z.; Zou, Z.L.; Dong, P.; Liu, Z.B.; Gui, Q.Q.; Yin, J.W. An efficient shock capturing algorithm to the extended Boussinesq wave Equations. Appl. Ocean Res. 2013, 43, 11–20. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F.; Kobayashi, M.H. Shock-capturing Boussinesq-type model for nearshore wave processes. Coast. Eng. 2010, 57, 407–423. [Google Scholar] [CrossRef]
- Toro, E.F. Musta: A multi-stage numerical flux. Appl. Numer. Math. 2006, 56, 464–1479. [Google Scholar] [CrossRef]
- Guo, W.; Lai, J.; Lin, G. Finite-volume multi-stage schemes for shallow-water flow simulations. Int. J. Numer. Methods Fluids 2008, 57, 177–204. [Google Scholar] [CrossRef]
- Long, W. Boussinesq Modeling of Wave, Eurrent and Sediment Transport; University of Delaware: Newark, DE, USA, 2006. [Google Scholar]
- Hsu, T.; Hanes, D.M. Effects of wave shape on sheet flow sediment transport. J. Geophys. Res. Part C Ocean. 2004, 109, C5025. [Google Scholar] [CrossRef]
- Hsu, T.; Elgar, S.; Guza, R.T. Wave-induced sediment transport and onshore sandbar migration. Coast. Eng. 2006, 53, 817–824. [Google Scholar] [CrossRef]
- Ribberink, J.S. Bed-load transport for steady flows and unsteady oscillatory flows. Coast. Eng. 1998, 34, 59–82. [Google Scholar] [CrossRef]
- Jensen, J.H.; Fredsøe, J. Oblique Flow over Dredged Channels. II: Sediment Transport and Morphology. J. Hydraul. Eng. 1999, 125, 1190–1198. [Google Scholar] [CrossRef]
- Synolakis, C.E. The run-up of solitary waves. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Yin, J. Experimental and Numerical Researches of Sandbar Migration. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2012. (In Chinese). [Google Scholar]


| Case | Slope | Depth/ | Height/ | Period/s |
|---|---|---|---|---|
| Test R3 | 1:20 | 0.45 | 0.11 | 1.2 |
| Test R4 | 1:10 | 0.45 | 0.13 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Fang, K.; Liu, Z.; Sun, J.; Zhou, L. A Beach Profile Evolution Model Driven by the Hybrid Shock-Capturing Boussinesq Wave Solver. Water 2023, 15, 3799. https://doi.org/10.3390/w15213799
Wang P, Fang K, Liu Z, Sun J, Zhou L. A Beach Profile Evolution Model Driven by the Hybrid Shock-Capturing Boussinesq Wave Solver. Water. 2023; 15(21):3799. https://doi.org/10.3390/w15213799
Chicago/Turabian StyleWang, Ping, Kezhao Fang, Zhongbo Liu, Jiawen Sun, and Long Zhou. 2023. "A Beach Profile Evolution Model Driven by the Hybrid Shock-Capturing Boussinesq Wave Solver" Water 15, no. 21: 3799. https://doi.org/10.3390/w15213799





