Prediction for the Sluice Deformation Based on SOA-LSTM-Weighted Markov Model
Abstract
:1. Introduction
2. Statistical Model of Sluice Deformation
3. SOA-LSTM Network Model
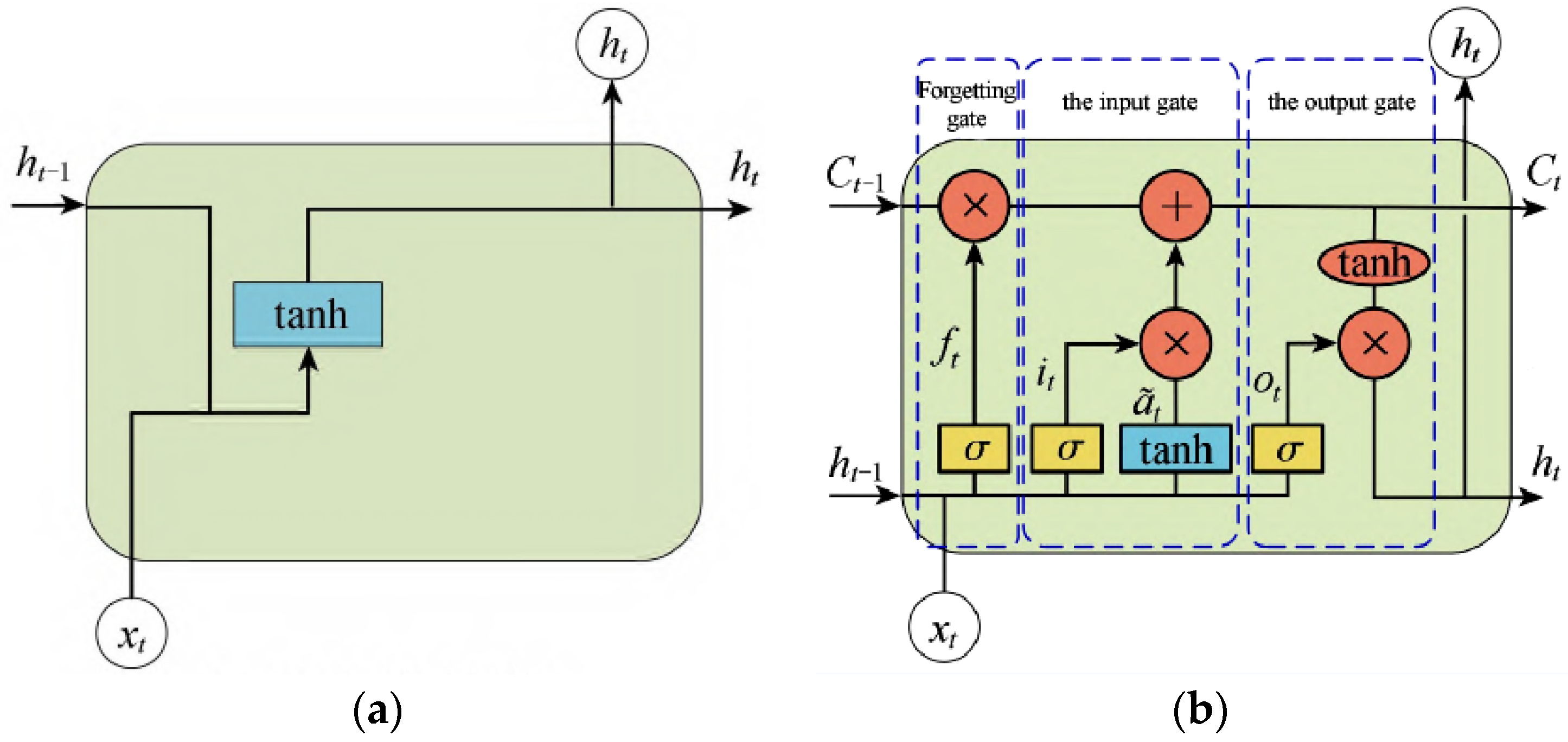
3.1. Principles of (Long Short-Term Memory) LSTM Neural Network
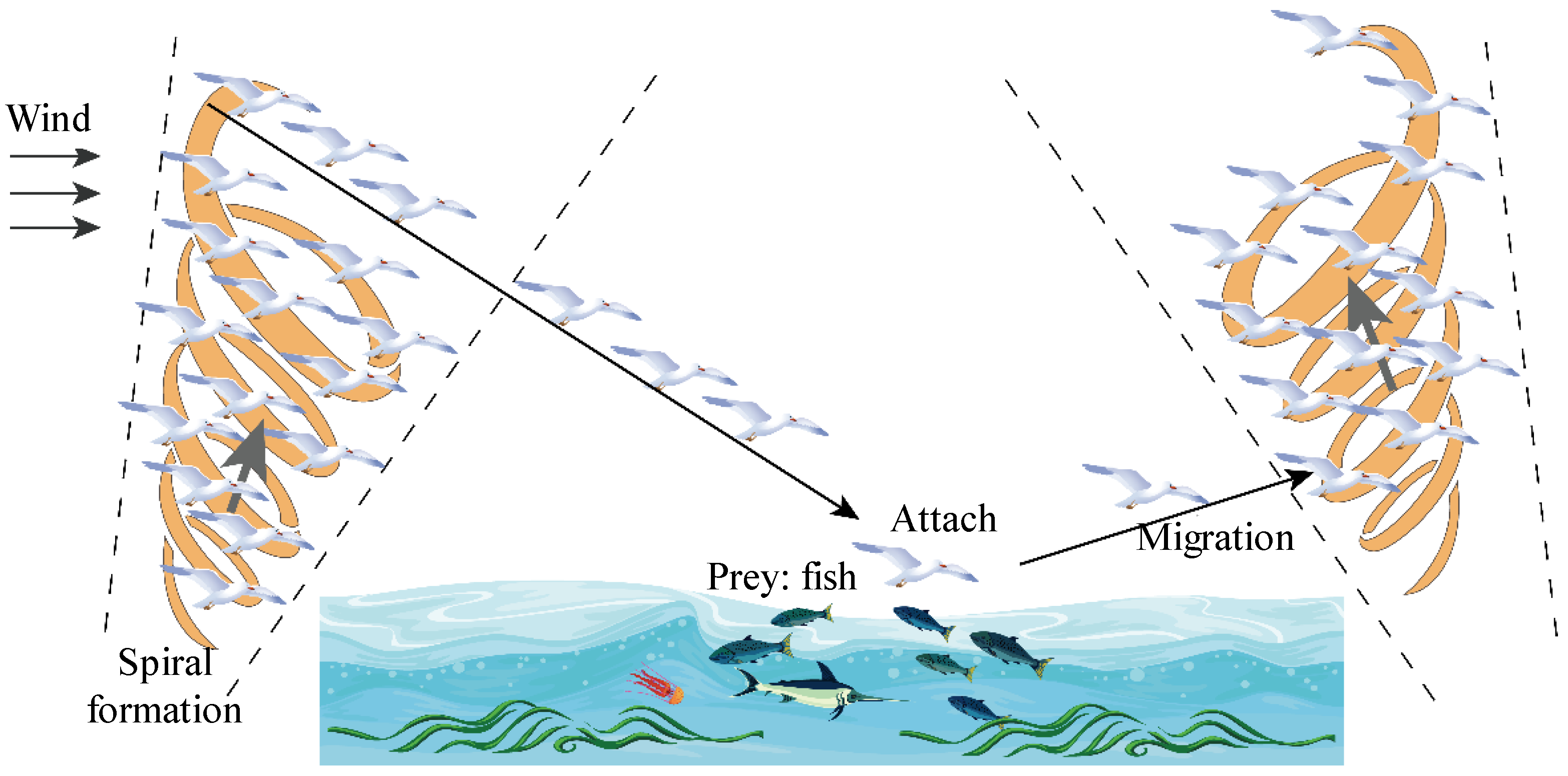
3.2. Principles of Seagull Optimization Algorithm (SOA)
- (1)
- Migration behavior (global search)During the seagull migration process, a seagull moves from one position to another. The above migration behavior should satisfy the following three conditions:
- (1)
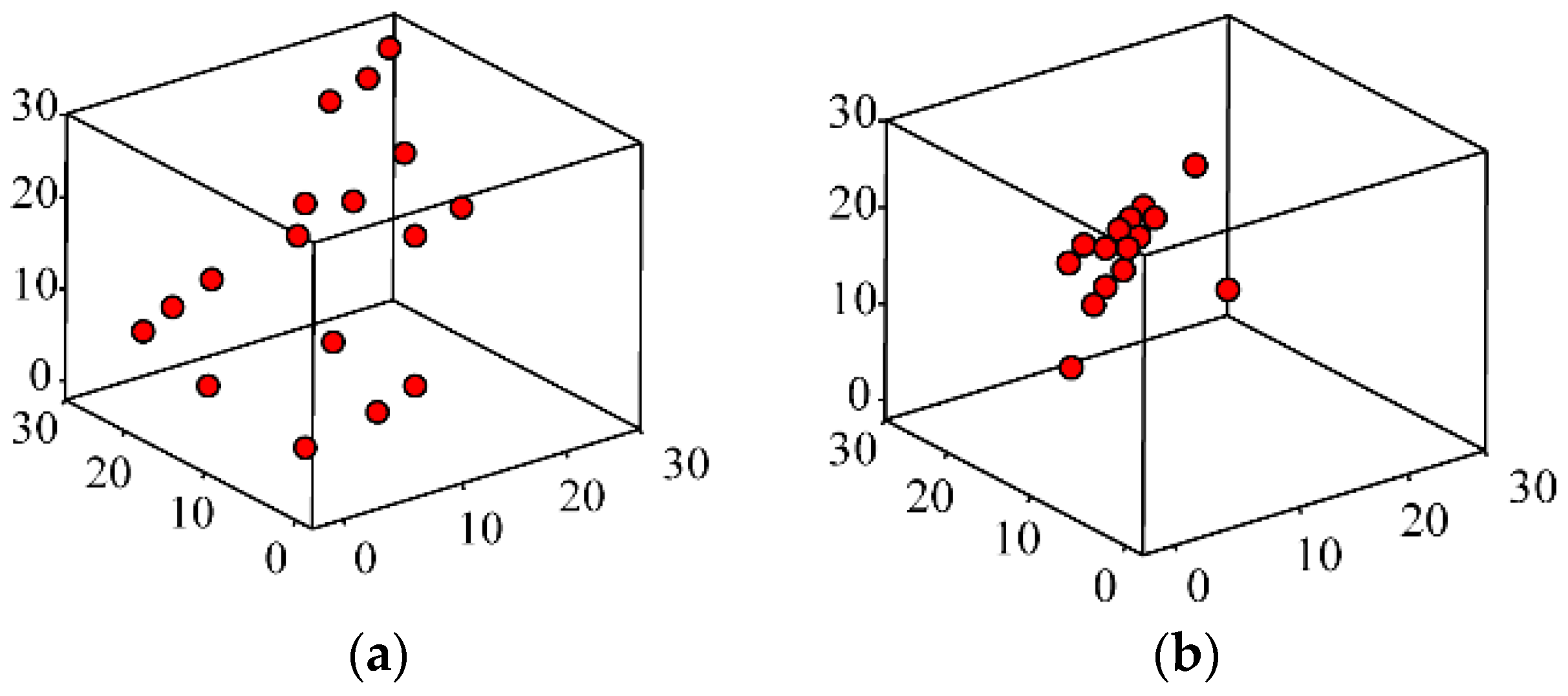
- Avoiding collision. To avoid collisions between adjacent seagulls, an additional variable A is introduced to update the position of the seagull during the iterative calculation, as shown in Figure 3a.where is the new position; is the current position of the seagull; i is the number of the current iteration; A is the additional variable representing the movement of seagull in the given search space. The calculation method of A is as follows.where is the control frequency of variable A, its range is [0, ]. Typically, is set to 2; i is the number of current iterations, ; is the maximum number of iterations.
- (2)
- Moving towards the best neighbor. After avoiding collisions between adjacent seagulls, a seagull moves towards the direction of the best neighbor, as illustrated in Figure 3b.where represents the direction in which the seagull moves from its original position to the position of the best neighboring seagull ; B is a random parameter used to balance the global and local search, and its calculation formula can be denoted as:where rd is a random value between 0 and 1.
- (3)
- Moving towards the best position. Finally, the seagull updates its own position based on the best position, as depicted in Figure 3c.where represents the distance between the current position and the global best position.
- (2)
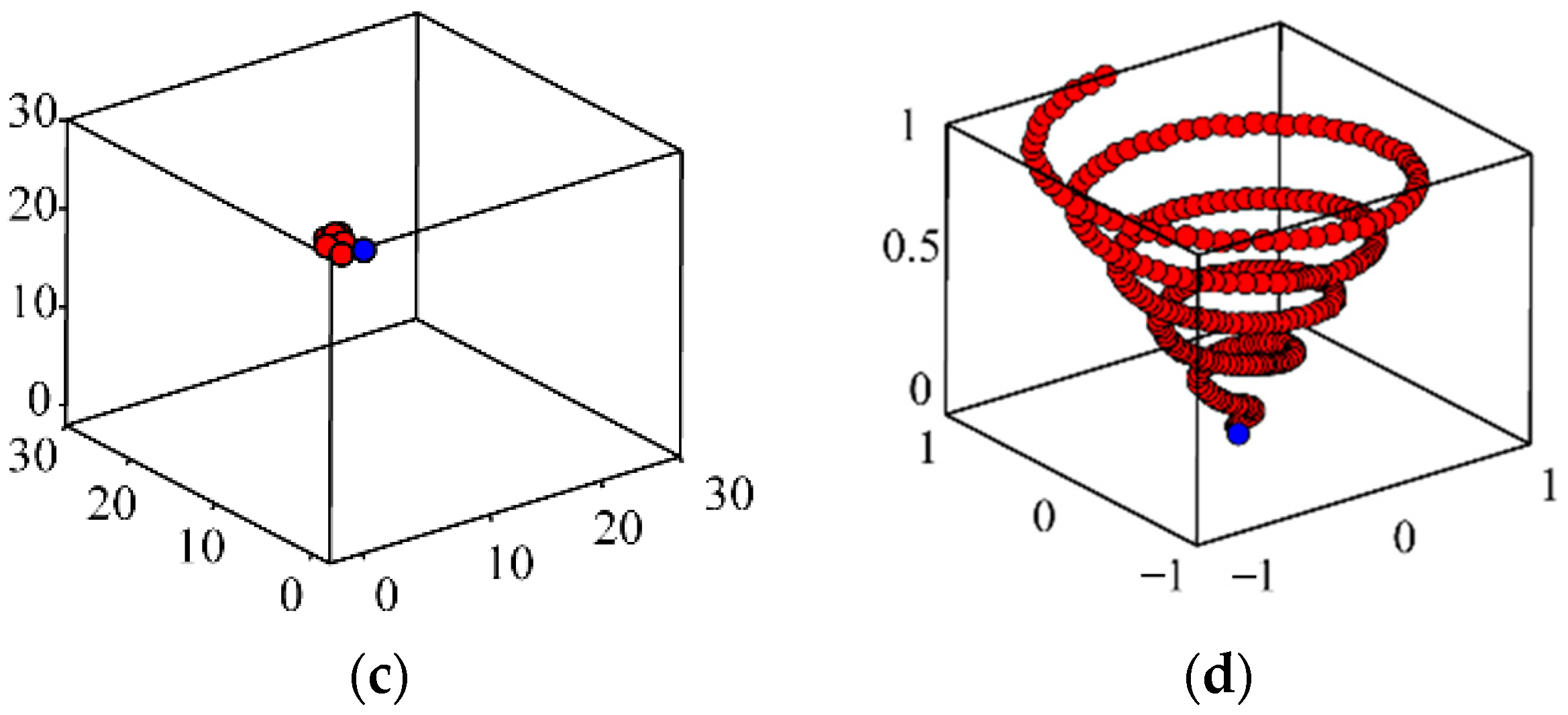
- Aggressive behavior (local search)When a seagull needs to attack its prey during flight, it forms a spiral formation in the air, as shown in Figure 3d. This behavior can be described in the xyz three-dimensional plane as follows.where r denotes the spiral radius formed by the seagull swarm; k is a random angle within the range [0, 2π]; v and u are constants that determine the spiral shape; e denotes the base of the natural logarithm.Considering both seagull migration and aggressive behaviors, the calculation formula of seagull location updating can be obtained based on Equation (12) to Equation (16) as follows.where is the attack position of the seagull, which is denoted as its final location is updated.
3.3. SOA Optimized LSTM
- (1)
- Data processing. First, the data set is normalized, and 80% of the data in the monitoring sequence is selected as the training set, and 20% of the data in the monitoring sequence is selected as the test set.
- (2)
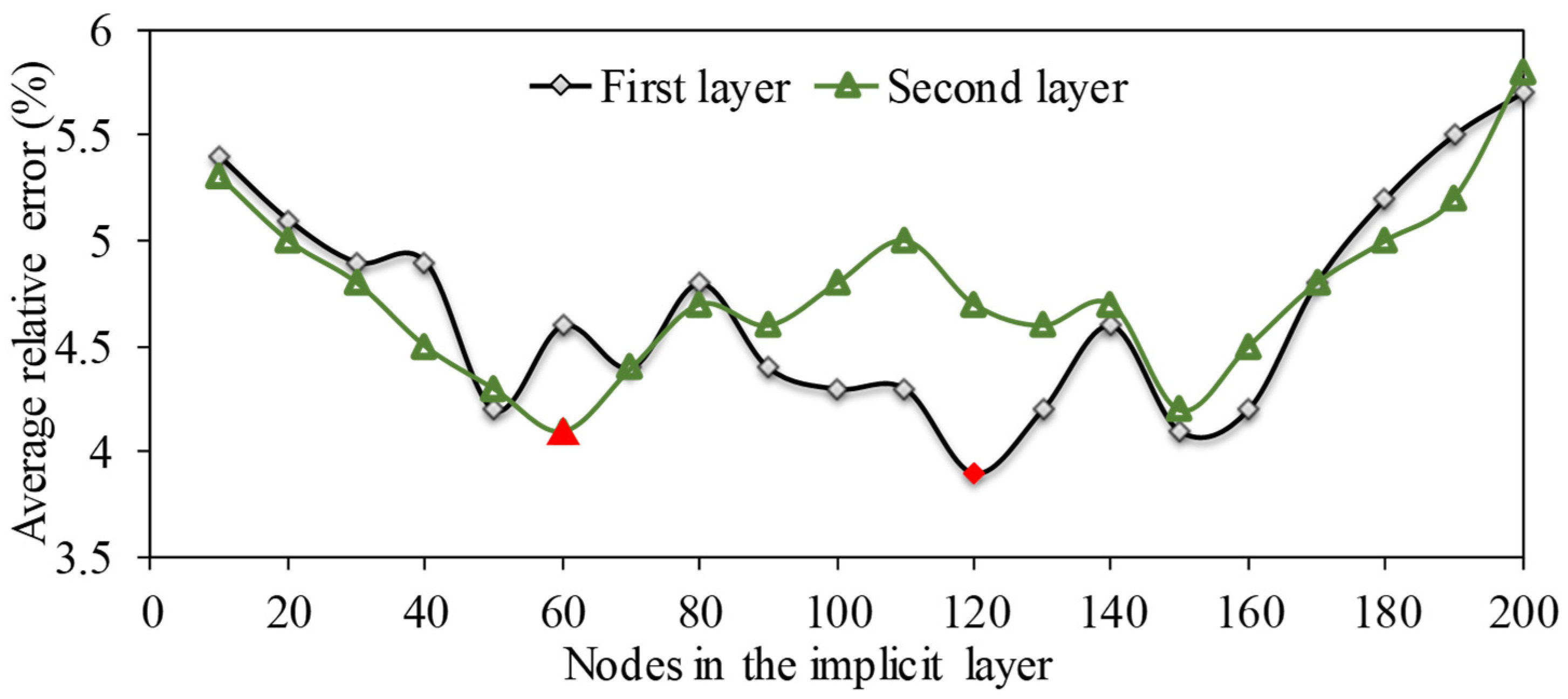
- Single LSTM model structure design. The LSTM model results are designed in terms of the number of network layers, the number of neurons in the input and hidden layers, the optimizer, and the loss function of the LSTM, and the multivariate multidimensional single-step LSTM network model with an initial input of nine dimensions, a time step of one, and an output of one dimension is constructed.
- (3)
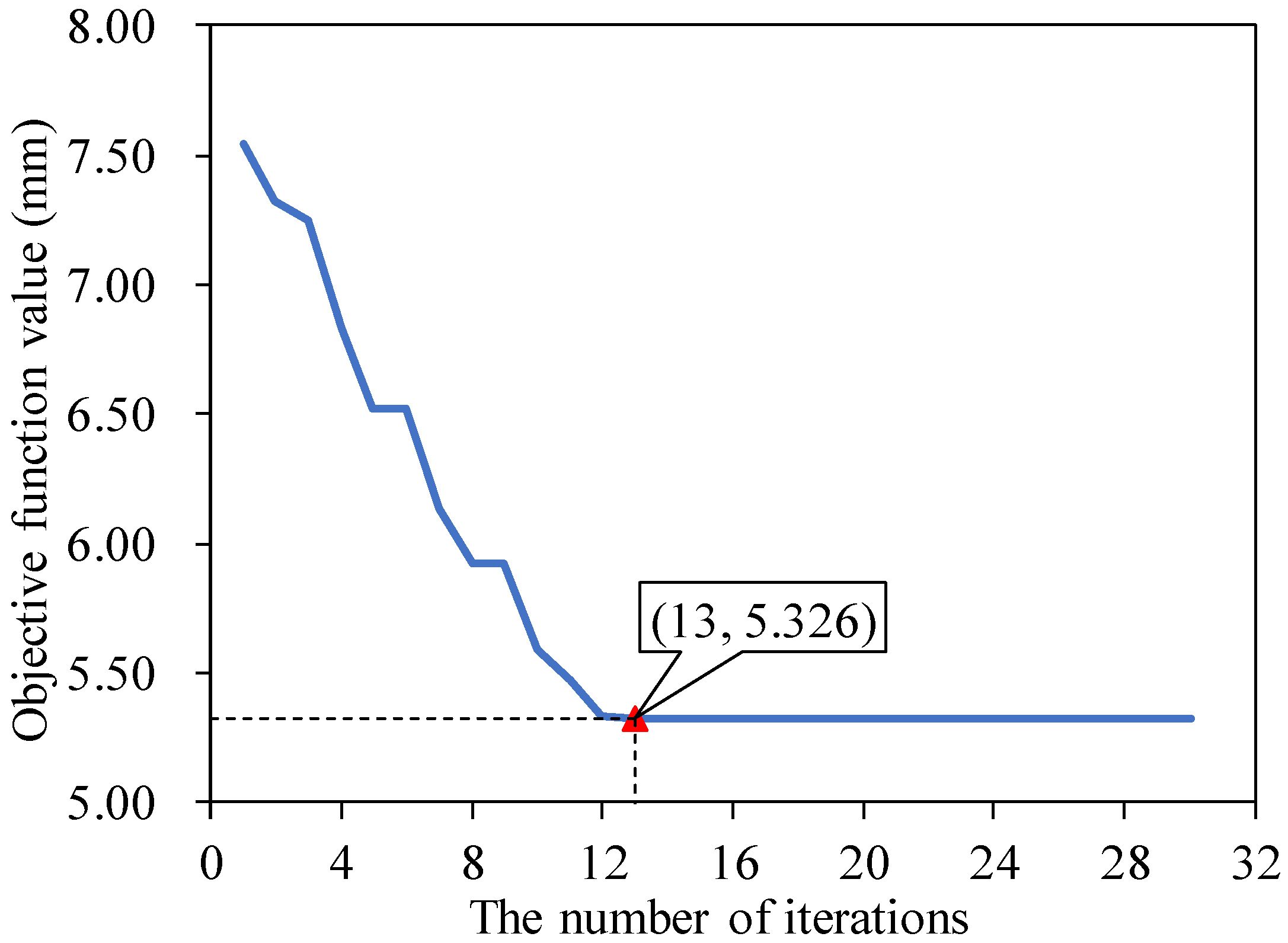
- Construction of SOA LSTM model. The LSTM hyper-parameters to be optimized, such as the number of neurons in the hidden layer, the initial learning rate, the maximum number of iterations, the minimum number of batches, the time step, and the regularization parameter, are used as the solution objectives of the seagull optimization algorithm, and the root mean square error (RMSE) on the training set is taken as the fitness function to obtain the SOA-LSTM model. The computational formula is given by:where n is the number of data in the training set; is the measured value of data in training set; is the fitted value of data in training set.
- (4)
- Model training and prediction. The training data are applied to train the SOA-LSTM model, the test data are input into the trained model, and finally obtain the predicted values.
- (5)
- Model comparison. The prediction results are utilized to calculate the prediction accuracy evaluation index to test the model effect.
4. SOA-LSTM-Weighted Markov Model for Sluice Deformation Prediction
4.1. Weighted Markov Model-Based Sluice Deformation Prediction
- (1)
- State classification. The mean square deviation method is proposed to classify the values of random sequence indicator into five state intervals.
- (2)
- Markovianity test. For discrete sluice deformation sequences, the chi-square statistic can be constructed to test for Markovianity.
- (3)
- State transition probability matrix. The one-step state transition frequency matrix with different lags (k is the step size) and the one-step state transition probability matrix should be calculated, separately.
- (4)
- Autocorrelation coefficients and transfer weights of each order. After selecting the lag time, the autocorrelation coefficient and transfer weight of each order should be calculated, separately.
- (5)
- Prediction table preparation. The sluice deformation of several years before the prediction year should be taken as the initial state, and then the sluice deformation should be combined with the transfer probability matrix of the corresponding lag time to obtain the probability of each order state in the prediction year. Afterwards, the predicted state probabilities of each year of the same state are weighted and summed, which is the average probability of being in each state in the prediction year. The above calculations can be compiled into a prediction table, and the state corresponding to the maximum probability value in the prediction table is taken and predicted by using the weighted Markov model.
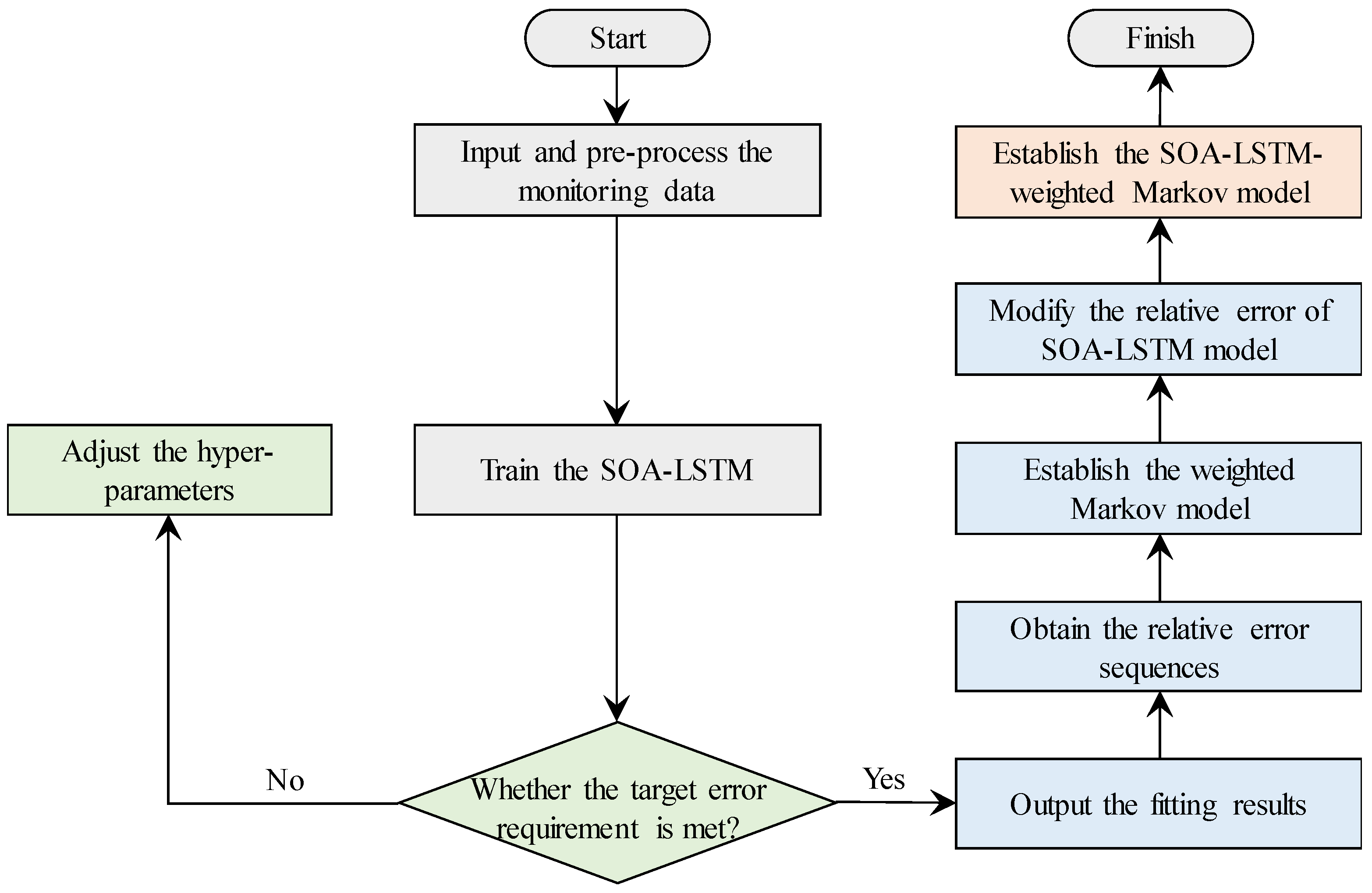
4.2. Sluice Deformation Prediction Procedure of SOA-LSTM-Weighted Markov Model
- (1)
- Based on the training set, the SOA-LSTM network model is established.
- (2)
- After comparing the measured data with the fitted value, the error sequence can be obtained.
- (3)
- The weighted Markov model is constructed according to the steps in Section 3.1.
- (4)
- The sluice deformation prediction model based on the SOA-LSTM-weighted Markov model can be established.
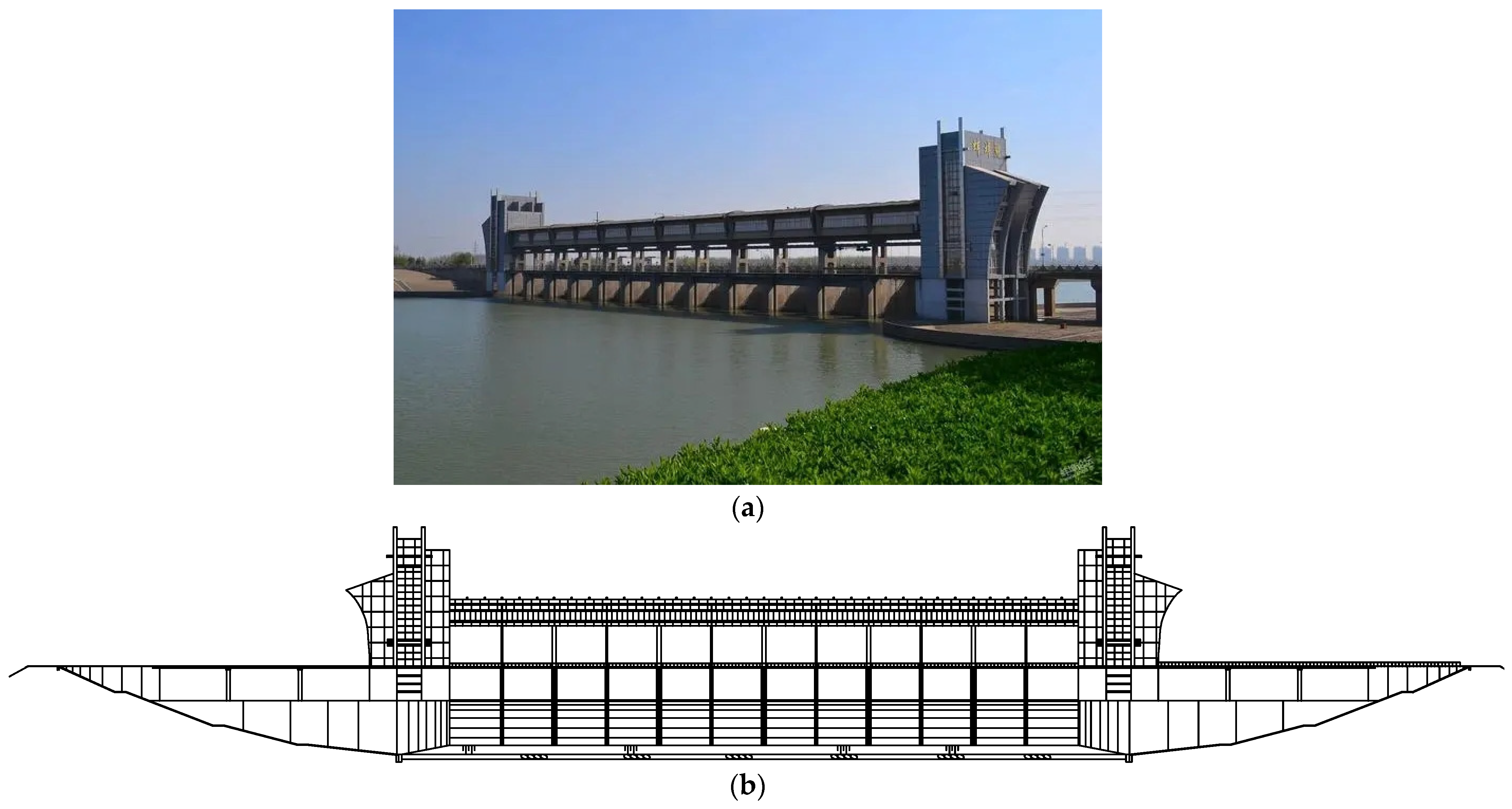
5. Project Overview
6. Results and Discussions
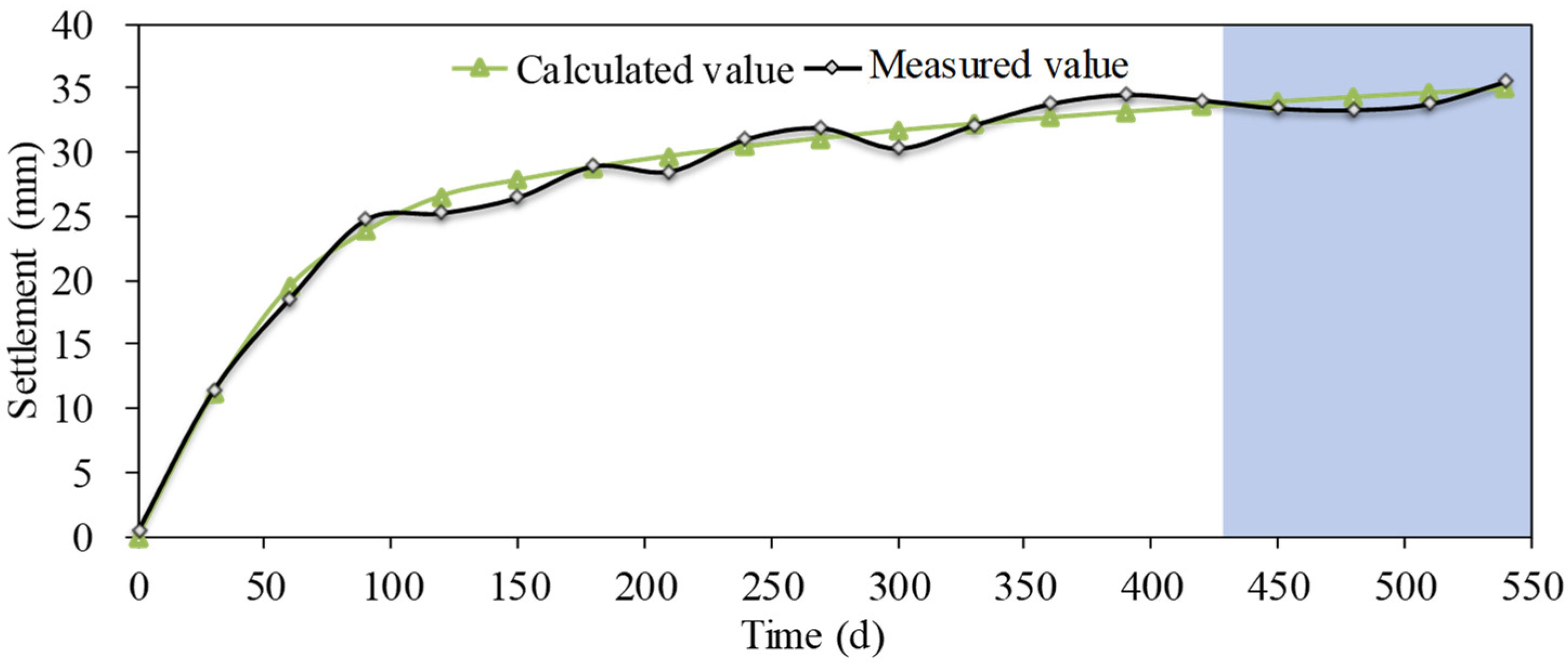
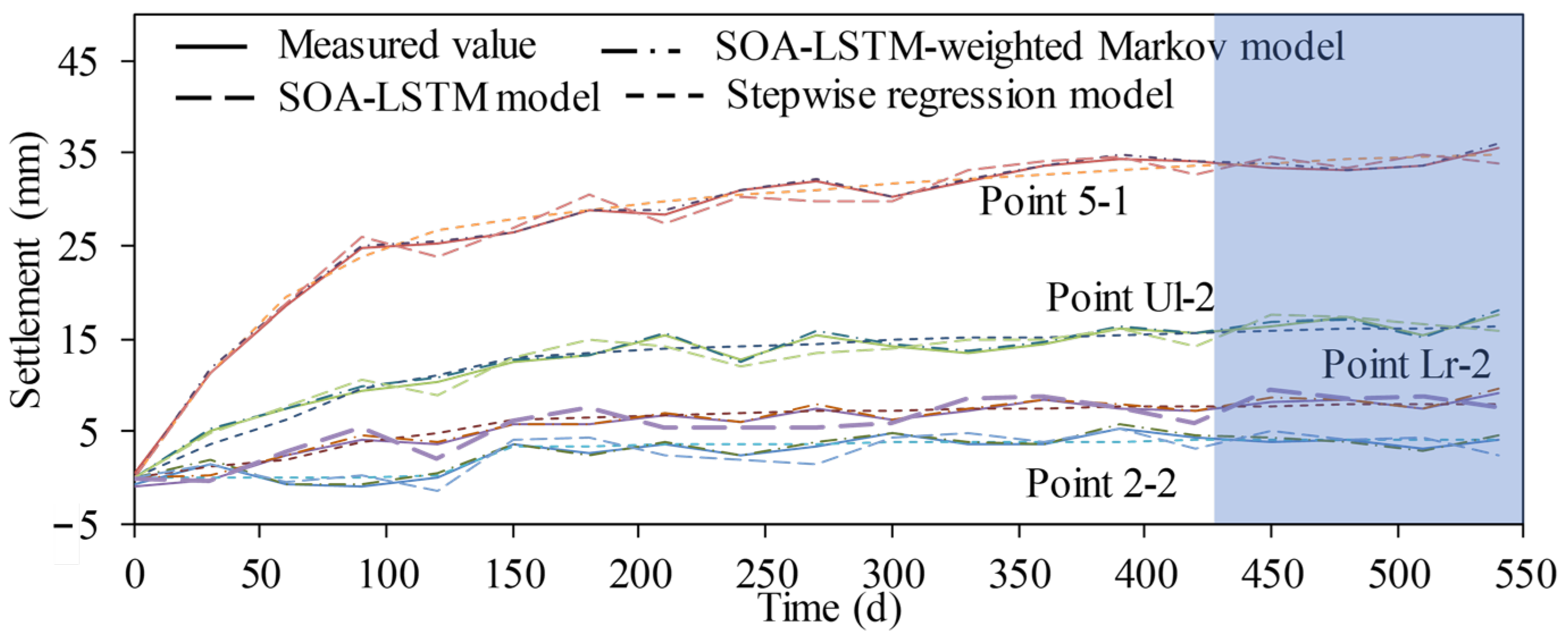
6.1. Fitted and Predicted Results of the Stepwise Regression Model
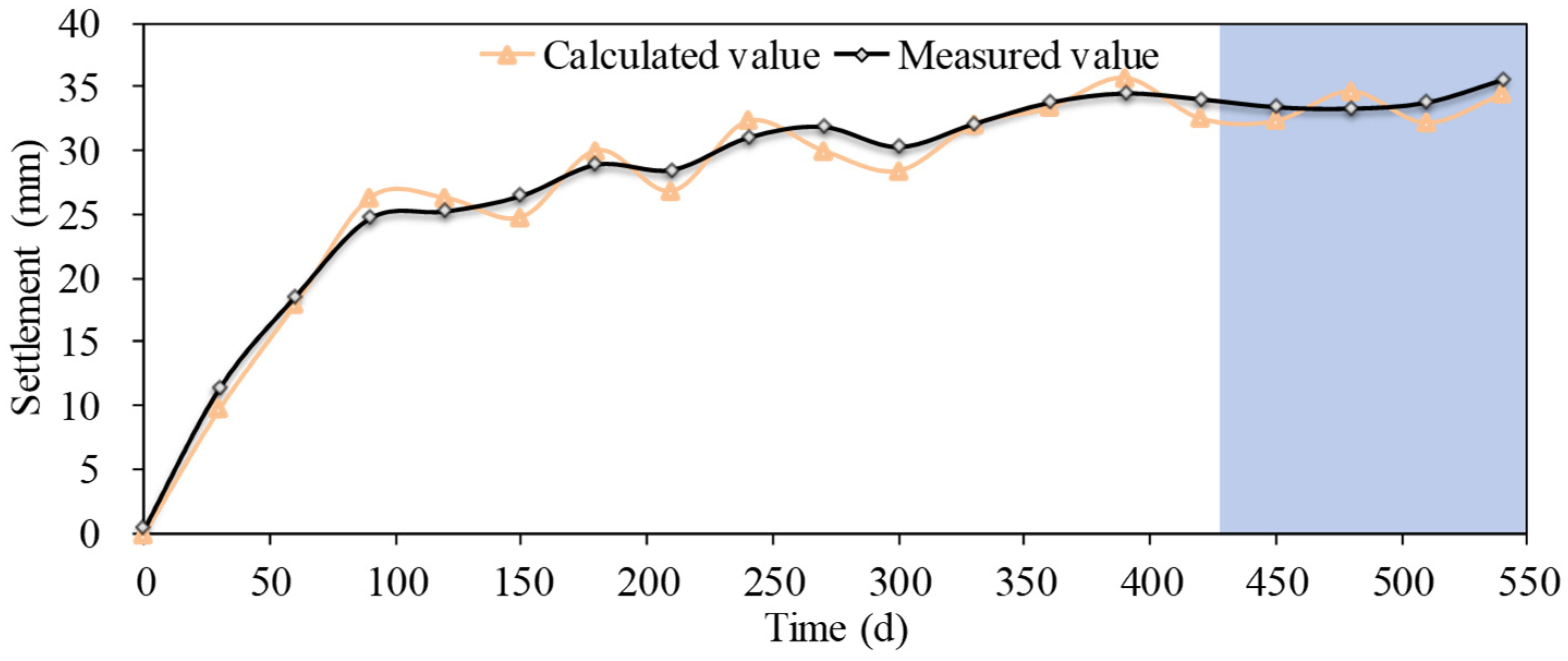
6.2. Fitted and Predicted Results of the SOA-LSTM Network Model
6.3. Fitted and Predicted Results of the SOA-LSTM-Weighted Markov Model
- (1)
- State classification. The relative error series has a mean of 75% and a root mean square error of 7.64%, which is classified into five states corresponding to the intervals of (−22.44%, −9.16%), (−9.16%, −4.58%), (−4.58%, 3.07%), (3.07%, 7.65%) and (7.65%, 24.20%), respectively.
- (2)
- Markovianity test. The one-step transfer frequency matrix , one-step transfer probability matrix , and marginal probability and chi-square statistics were calculated, and the calculation results are described in Table 5. The value of the calculated statistic is 109.9, and given the significance level, . Then . Because , the random sequence is highly significant in terms of Markovianity, and can be predicted by the weighted Markov model.
- (3)
- The state transition probability matrix determination. The relative errors of the fitted values of the SOA-LSTM model were taken as a random sequence, and the one-step state transfer probability matrixes with the step size of 2, 3, 4, and 5, respectively.
- (4)
- Calculation of the autocorrelation coefficients and transfer weights of each order. The autocorrelation coefficients (rk) and transmission weights (wk) of each order are shown in Table 6.
- (5)
- Prediction table preparation. According to the relative errors of the SOA-LSTM model, the corresponding state transfer probability is weighted and calculated to predict the relative error state of test set. Table 7 illustrates a subset of the weighted prediction results of the relative error state of the test set. The state S with the maximum probability value in the prediction table was determined, E was taken as the median value of the corresponding state interval. xSL was selected as the predicted value of the SOA-LSTM network model. xSlM was selected as the predicted value of the SOA-LSTM-weighted Markov model. Therefore, the corrected predicted value can be expressed as:
7. Conclusions
- (1)
- The stepwise regression model is more suitable for dealing with linear problems; it has some limitations in fitting and predicting nonlinear and fluctuating monitoring sequences. By contrast, the proposed model shows obvious superiority in dealing with monitoring data with fluctuation.
- (2)
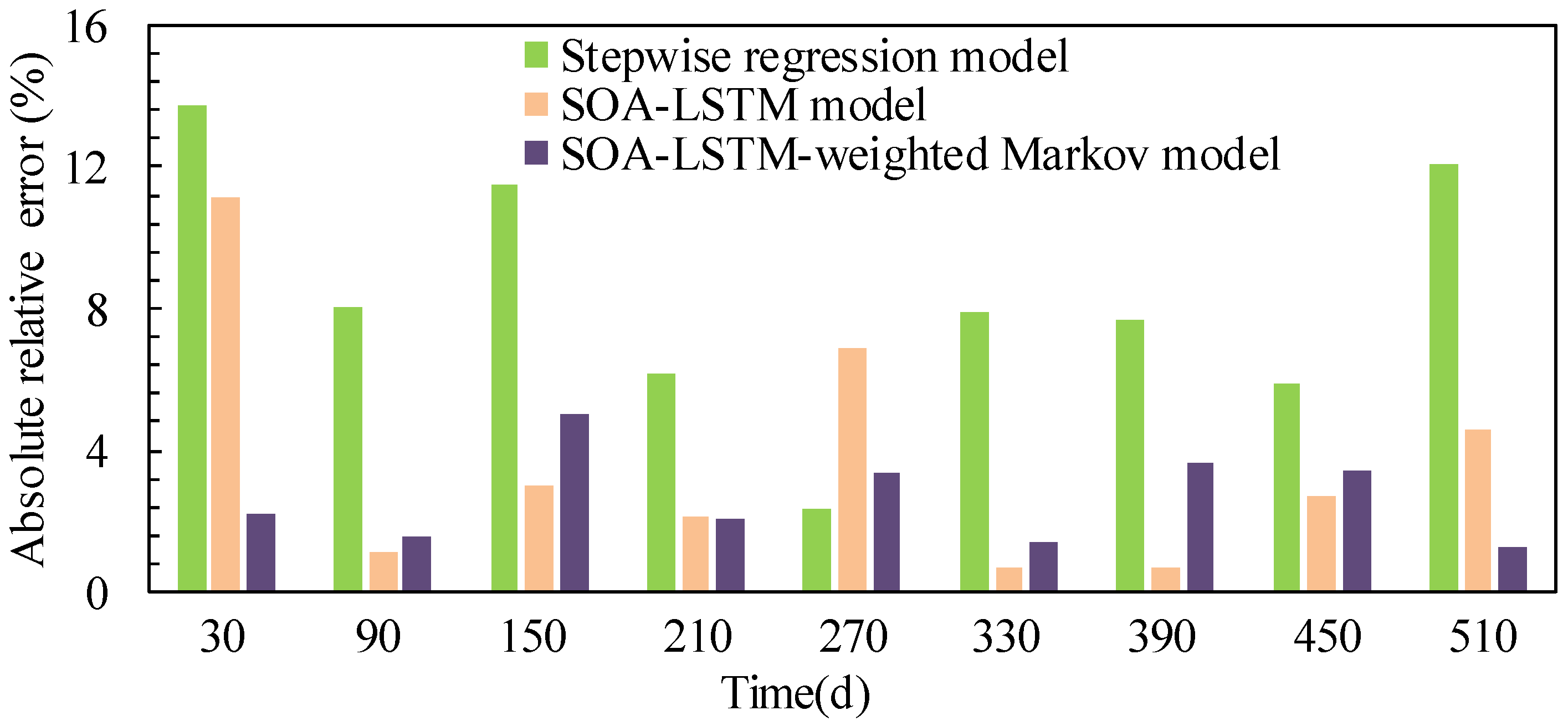
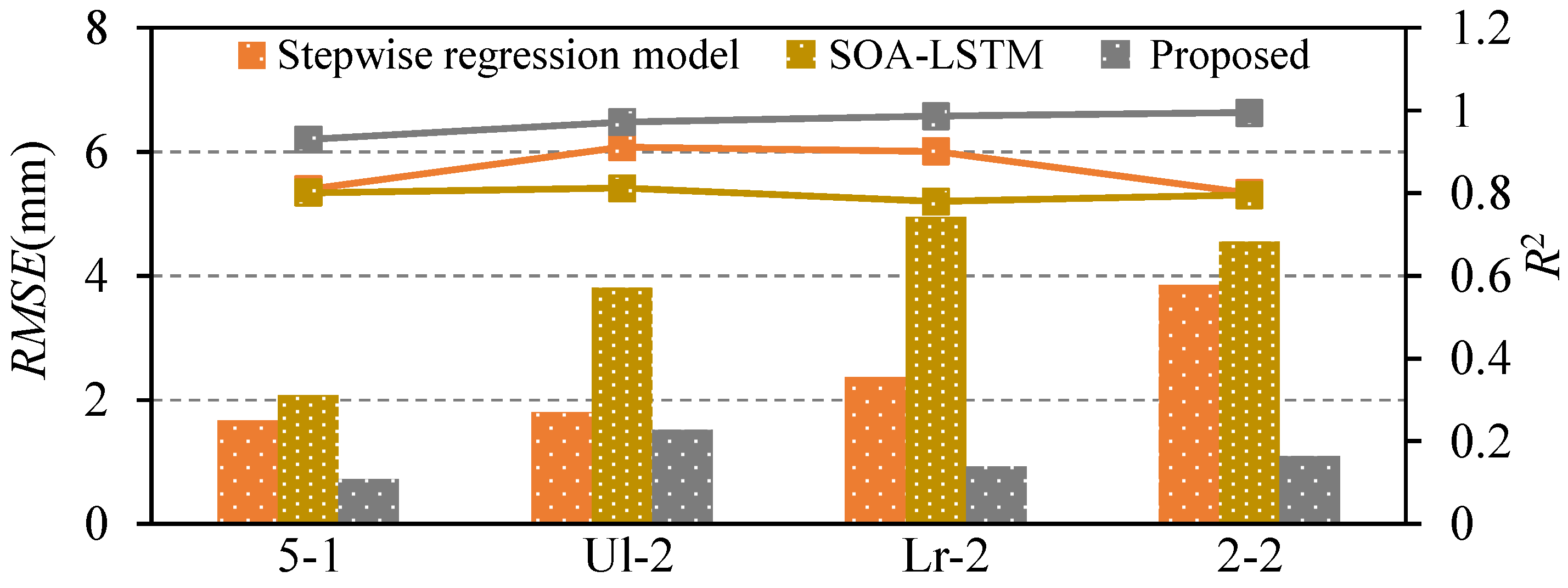
- The SOA improves the training efficiency of the neural network hyper-parameters of the LSTM model. The SOA-LSTM model can more accurately reflect the nonlinear change rule of the sluice settlement, and the weighted Markov model takes into account the strength of the dependency relationship between different lags, which can fully utilize the information of the training set, significantly reduce the model prediction error, and improve the model prediction accuracy. As listed in Table 1, the maximum settlement variation ranges from 1.73 mm to 31.59 mm, which indicates the apparent fluctuation of sluice settlement monitoring data. On the basis of the fitted results, predicted results and absolute relative errors, the proposed model demonstrates the largest values of R2 and the smallest values of RMSE for the monitoring data of four monitoring points. Therefore, the SOA-LSTM-weighted Markov model is especially suitable for fitting and predicting the larger fluctuation of the sluice settlement, it is also especially suitable for dealing with the more volatile settlement monitoring data.
- (3)
- Due to the better regularity of the actual data series selected in this paper, the prediction accuracy of the SOA-LSTM model and the SOA-LSTM-weighted Markov model is higher. When more monitoring data are obtained, the prediction model should be trained and adjusted in time, and then the subsequent dynamic prediction of the sluice settlement can be carried out, which will be able to better describe the settlement law of the sluice. To our knowledge, the proposed model expresses the stable and accurate results in predicting long sequenced monitoring data. In view of the practical application performance in the case study, the proposed model is supposed to applied extensively in deformation prediction of more sluice projects to improve safety monitoring efficiency, which provides a new aid for structural engineers involved in the real-time health assessment and safety monitoring in sluices. The study in this paper focuses mainly on the data-driven sluice deformation prediction model. A further study should pay more attention to investigating the physics-data double-driven intelligent prediction model, and the proposed method will have prospective applications in sluice structural behavior safety monitoring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, Z.; Cao, X.; Liu, G.; Lu, W. Optimizing operation rules of sluices in river networks based on knowledge-driven and data-driven mechanism. Water Resour. Manag. 2014, 28, 3455–3469. [Google Scholar] [CrossRef]
- He, X.; Wang, Y.P.; Zhu, Q.; Zhang, Y.; Zhang, D.; Zhang, J.; Yang, Y.; Gao, J. Simulation of sedimentary dynamics in a small-scale estuary: The role of human activities. Environ. Earth Sci. 2015, 74, 869–878. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, H. Automatic damage detection and diagnosis for hydraulic structures using drones and artificial intelligence techniques. Remote Sens. 2023, 15, 615. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.; Marel, H.; Bavec, M. Coupling of GPS/GNSS and radar interferometric data for a 3D surface displacement monitoring of landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Tu, R.; Liu, J.; Lu, C.; Zhang, R.; Zhang, P.; Lu, X. Cooperating the BDS, GPS, GLONASS and strong-motion observations for real-time deformation monitoring. Geophys. J. Int. 2017, 209, 1408–1417. [Google Scholar] [CrossRef]
- De Lacy, M.C.; Ramos, M.I.; Gil, A.J.; Franco, Ó.D.; Herrera, A.M.; Avilés, M.; Domínguez, A.; Chical, J.C. Monitoring of vertical deformations by means high-precision geodetic levelling. Test case: The Arenoso dam (South of Spain). J. Appl. Geod. 2017, 11, 31–41. [Google Scholar] [CrossRef]
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perissin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space geodetic monitoring of engineered structures: The ongoing destabilization of the Mosul dam, Iraq. Sci. Rep. 2016, 6, 37408. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, P.; Yan, X.; Zhao, X. Middle displacement monitoring of medium–small span bridges based on laser technology. Struct. Control Health Monit. 2020, 27, e2509. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, H.; Yu, Y.; Xu, X.; Hu, W.; Li, M.; Ou, J. Bridge displacement monitoring method based on laser projection-sensing technology. Sensors 2015, 15, 8444–8463. [Google Scholar] [CrossRef]
- Rodriguez, A.; Comeron, A.; Mesalles, E. Performance assessment of a homodyne laser radar for surface displacement monitoring. Opt. Eng. 2001, 40, 2812–2821. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating. Earth Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Wang, Y.; Wu, L. Use of SAR/InSAR in mining deformation monitoring, parameter inversion, and forward predictions: A review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 71–90. [Google Scholar] [CrossRef]
- Yang, X.; Wang, D.; Xu, Y.; Hou, M.; Wang, Z. Performance assessment of Insar-based vertical displacement monitoring of sluices in coastal soft soil area. KSCE J. Civ. Eng. 2022, 26, 371–380. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, C.; Guo, G.; Li, L.; Zhao, Y.; Li, H.; Gong, Y. Monitoring sluice health in vibration by monocular digital photography and a measurement robot. KSCE J. Civ. Eng. 2019, 23, 2666–2678. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagallim, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Peng, M.; Zhang, L.M. Analysis of human risks due to dam break floods—Part 2: Application to Tangjiashan landslide dam failure. Nat. Hazards 2012, 64, 1899–1923. [Google Scholar] [CrossRef]
- Kalkan, Y.; Potts, L.V.; Bilgi, S. Assessment of vertical deformation of the Atatürk dam using geodetic observations. J. Surv. Eng. 2016, 142, 04015011. [Google Scholar] [CrossRef]
- Li, W.; Ye, Y.; Hu, N.; Wang, X.; Wang, Q. Real-time warning and risk assessment of tailings dam disaster status based on dynamic hierarchy-grey relation analysis. Complexity 2019, 2019, 5873420. [Google Scholar] [CrossRef]
- Shao, C.; Gu, C.; Yang, M.; Xu, Y.; Su, H. A novel model of dam displacement based on panel data. Struct. Control Health Monit. 2018, 25, e2037. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, M.; Zhang, K.; Li, Z. A dam deformation residual correction method for high arch dams using phase space reconstruction and an optimized long short-term memory network. Mathematics 2023, 11, 2010. [Google Scholar] [CrossRef]
- Zheng, S.; Gu, C.; Shao, C.; Hu, Y.; Xu, Y.; Huang, X. A novel prediction model for seawall deformation based on CPSO-WNN-LSTM. Mathematics 2023, 11, 3752. [Google Scholar] [CrossRef]
- Li, M.; Wang, J. An empirical comparison of multiple linear regression and artificial neural network for concrete dam deformation modelling. Math. Prob. Eng. 2019, 2019, 7620948. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, D.J.; Liu, Y.T.; Chen, Z.Y.; Chen, X.Q. Temporal convolution network-based time frequency domain integrated model of multiple arch dam deformation and quantification of the load impact. Struct. Control Health Monit. 2022, 29, e3090. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, S.C.; Li, Y.H. Application of dynamic gray forecast model in dam deformation monitoring and forecast. J. Xi’an Univ. Sci. Technol. 2005, 3, 014. [Google Scholar]
- Huang, C.; Zhou, L.; Liu, F.; Cao, Y.; Liu, Z.; Xue, Y. Deformation prediction of dam based on optimized grey verhulst model. Mathematics 2023, 11, 1729. [Google Scholar] [CrossRef]
- Chu, C.; Xu, G. Application of grey deformation prediction model optimized by double coefficient for tailings dam. Math. Prob. Eng. 2022, 2022, 6103860. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, C.; Gu, C.; Meng, Z. Concrete dam displacement prediction based on an ISODATA-GMM clustering and random coefficient model. Water 2019, 11, 714. [Google Scholar] [CrossRef]
- Chen, W.; Wang, X.; Cai, Z.; Liu, C.; Zhu, Y.; Lin, W. DP-GMM clustering-based ensemble learning prediction methodology for dam deformation considering spatiotemporal differentiation. Knowl.-Based Syst. 2021, 222, 106964. [Google Scholar] [CrossRef]
- Hu, J.; Ma, F. Zoned deformation prediction model for super high arch dams using hierarchical clustering and panel data. Eng. Comput. 2020, 37, 2999–3021. [Google Scholar] [CrossRef]
- Lin, C.; Weng, K.; Lin, Y.; Zhang, T.; He, Q.; Su, Y. Time series prediction of dam deformation using a hybrid STL–CNN–GRU model based on sparrow search algorithm optimization. Appl. Sci. 2022, 12, 11951. [Google Scholar] [CrossRef]
- Shao, C.; Zheng, S.; Gu, C.; Hu, Y.; Qin, X. A novel outlier detection method for monitoring data in dam engineering. Expert Syst. Appl. 2022, 193, 116476. [Google Scholar] [CrossRef]
- Xing, Y.; Chen, Y.; Huang, S.; Wang, P.; Xiang, Y. Research on dam deformation prediction model based on optimized SVM. Processes 2022, 10, 1842. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Altan, A.; Karasu, S.; Zio, E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 2021, 100, 106996. [Google Scholar] [CrossRef]
- Song, S.; Zhou, Q.; Zhang, T.; Hu, Y. Automatic concrete dam deformation prediction model based on TPE-STL-LSTM. Water 2023, 15, 2090. [Google Scholar] [CrossRef]
- Hu, Y.; Gu, C.; Meng, Z.; Shao, C.; Min, Z. Prediction for the settlement of concrete face rockfill dams using optimized LSTM model via correlated monitoring data. Water 2022, 14, 2157. [Google Scholar] [CrossRef]
- Si, H.Y.; Chen, M. Three dimensional structural analysis of complex sluice chamber structures. Appl. Mech. Mater. 2012, 170, 1971–1976. [Google Scholar] [CrossRef]
- Ding, Q.; Huang, Y.; Xie, T.; Li, F.; Gao, L. Prediction of horizontal displacement of sluice gate based on BP neural network weighted Markov model. J. Water Resour. Water 2020, 31, 187–193. [Google Scholar]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Y.; Zhang, G.; Jermsittiparsert, K.; Razmjooy, N. Experimental modeling of PEM fuel cells using a new improved seagull optimization algorithm. Energy Rep. 2019, 5, 1616–1625. [Google Scholar] [CrossRef]

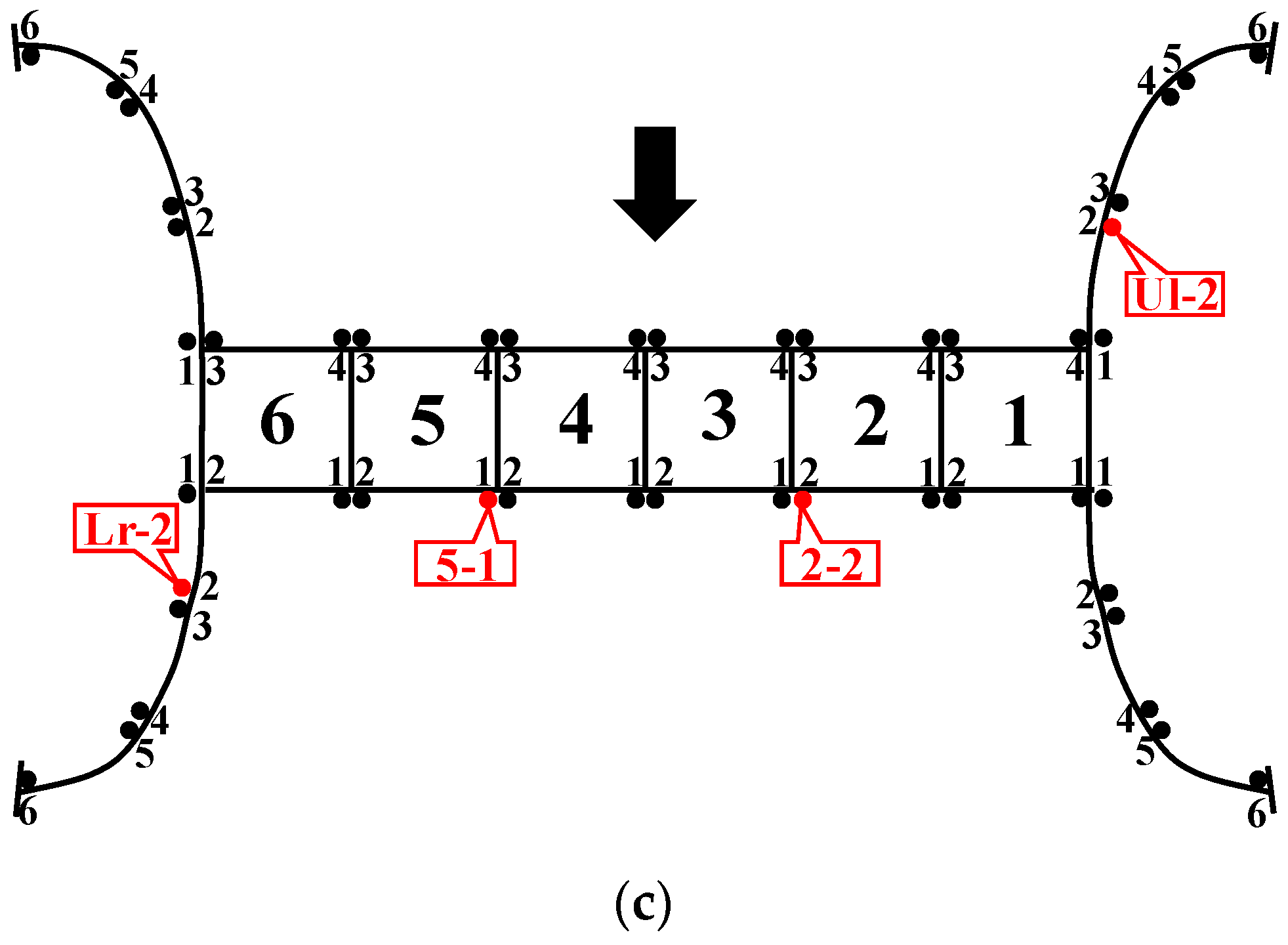
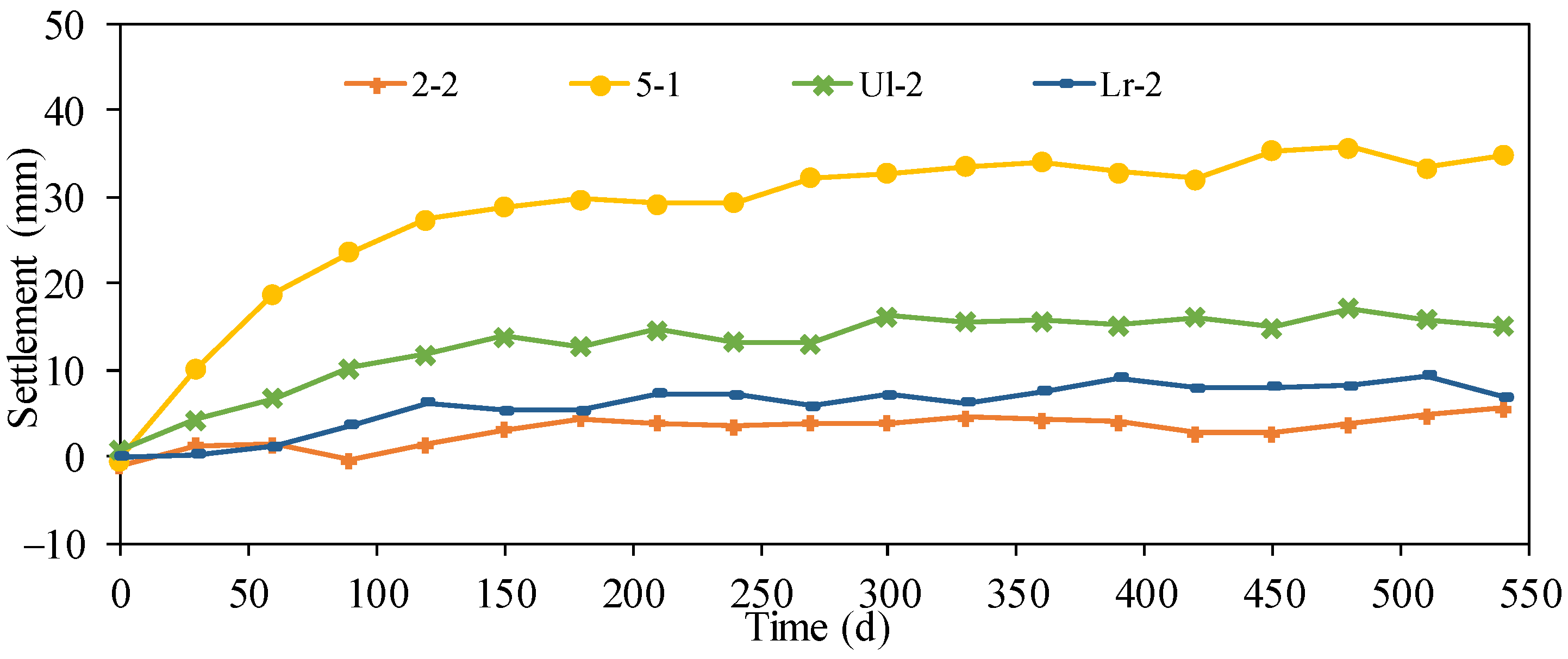

| Project Site | Maximum Average Variation (mm) | Minimum Settlement (mm) | Maximum Settlement (mm) | Maximum Settlement Variation (mm) | ||
|---|---|---|---|---|---|---|
| Point | Settlement | Point | Settlement | |||
| Upper left-wing wall | −14.99 | Ul-6 | −12.71 | Ul-2 | −16.33 | 3.62 |
| Lower left-wing wall | −14.95 | Ll-6 | −9.80 | Ll-4 | −17.82 | 8.02 |
| Upper right-wing Wall | −16.80 | Ur-1 | −14.14 | Ur-2 | −18.37 | 4.23 |
| Lower right-wing wall | −18.11 | Lr-2 | −8.03 | Lr-5 | −28.71 | 20.68 |
| Upper sluice pier | −13.52 | 1-3 | −0.21 | 3-4 | −31.80 | 31.59 |
| Lower sluice pier | −14.30 | 2-2 | −4.19 | 5-1 | −35.75 | 31.56 |
| Abutment pier | −8.45 | Right pier | −7.59 | Left pier | −9.32 | 1.73 |
| Time (d) | Monitoring Data (mm) | Time (d) | Monitoring Data (mm) | Time (d) | Monitoring Data (mm) |
|---|---|---|---|---|---|
| 0 | 1.43 | 210 | 29.14 | 420 | 34.71 |
| 30 | 11.72 | 240 | 30.83 | 450 | 33.20 |
| 60 | 17.74 | 270 | 29.32 | 480 | 33.43 |
| 90 | 23.85 | 300 | 29.72 | 510 | 36.25 |
| 120 | 26.79 | 330 | 32.21 | 540 | 35.75 |
| 150 | 28.95 | 360 | 34.41 | ||
| 180 | 28.56 | 390 | 33.06 |
| Time (d) | Monitoring Data | Predicted Value (mm) | Relative Error (%) | Time | Monitoring Data | Predicted Value (mm) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 0 | 1.43 | 1.431 | 0 | 300 | 29.72 | 29.17 | −1.85 |
| 30 | 11.72 | 10.87 | −7.23 | 330 | 32.21 | 29.66 | −7.91 |
| 60 | 17.74 | 17.99 | 1.46 | 360 | 34.41 | 30.10 | −12.53 |
| 90 | 23.85 | 21.93 | −8.01 | 390 | 33.06 | 30.51 | −7.69 |
| 120 | 26.79 | 24.48 | −8.61 | 420 | 34.71 | 30.89 | −11.00 |
| 150 | 28.95 | 25.63 | −11.48 | 450 | 33.20 | 31.24 | −5.89 |
| 180 | 28.56 | 26.56 | −7.02 | 480 | 33.43 | 31.57 | −5.56 |
| 210 | 29.14 | 27.35 | −6.16 | 510 | 36.25 | 31.88 | −12.04 |
| 240 | 30.83 | 28.03 | −9.09 | 540 | 35.75 | 32.18 | −10.01 |
| 270 | 29.32 | 28.63 | −2.33 |
| Time (d) | Hidden Layers | Nodes in First Layer | Nodes in Second Layer | Learning Rate |
|---|---|---|---|---|
| Upper bound | 10 | 200 | 200 | 0.1 |
| Lower bound | 1 | 10 | 10 | 0.001 |
| Optimized parameters | 2 | 120 | 60 | 0.005 |
| Status | Marginal Probability | Total | |||||
|---|---|---|---|---|---|---|---|
| 1 | 0.127 | 10.768 | 5.410 | 1.94 | 0.961 | 0.000 | 19.079 |
| 2 | 0.158 | 0.575 | 0.062 | 2.010 | 0.867 | 0.851 | 4.365 |
| 3 | 0.436 | 2.083 | 0.972 | 7.210 | 0.439 | 1.836 | 12.54 |
| 4 | 0.157 | 0.000 | 0.087 | 1.521 | 0.247 | 1.957 | 3.842 |
| 5 | 0.122 | 0.723 | 0.000 | 2.513 | 4.984 | 6.745 | 14.965 |
| Total | 1 | 14.149 | 6.531 | 15.194 | 7.498 | 11.389 | 54.761 |
| Project | Order | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| rk | 0.568 | 0.354 | 0.248 | 0.126 | 0.139 |
| wk | 0.416 | 0.245 | 0.168 | 0.081 | 0.105 |
| Initial Time (d) | Status | Lag Time | Weights | Status | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||
| 60 | 3 | 1 | 0.4106 | 0.0771 | 0.1328 | 0.5587 | 0.1528 | 0.0759 |
| 120 | 3 | 2 | 0.2514 | 0.0979 | 0.1757 | 0.4892 | 0.1363 | 0.0978 |
| 180 | 3 | 3 | 0.1659 | 0.1000 | 0.2000 | 0.4785 | 0.1000 | 0.1207 |
| 240 | 4 | 4 | 0.0824 | 0.1581 | 0.0000 | 0.6296 | 0.1043 | 0.1062 |
| 300 | 5 | 5 | 0.1021 | 0.0657 | 0.0657 | 0.4000 | 0.2678 | 0.1985 |
| Pj (Weighted sum) | 0.0922 | 0.1315 | 0.5249 | 0.0901 | 0.1447 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Xie, W.; Wu, Y.; Sun, X.; Zhang, C.; Gu, H.; Zhu, M.; Zheng, S. Prediction for the Sluice Deformation Based on SOA-LSTM-Weighted Markov Model. Water 2023, 15, 3724. https://doi.org/10.3390/w15213724
Peng J, Xie W, Wu Y, Sun X, Zhang C, Gu H, Zhu M, Zheng S. Prediction for the Sluice Deformation Based on SOA-LSTM-Weighted Markov Model. Water. 2023; 15(21):3724. https://doi.org/10.3390/w15213724
Chicago/Turabian StylePeng, Jianhe, Wei Xie, Yan Wu, Xiaoran Sun, Chunlin Zhang, Hao Gu, Mingyuan Zhu, and Sen Zheng. 2023. "Prediction for the Sluice Deformation Based on SOA-LSTM-Weighted Markov Model" Water 15, no. 21: 3724. https://doi.org/10.3390/w15213724
APA StylePeng, J., Xie, W., Wu, Y., Sun, X., Zhang, C., Gu, H., Zhu, M., & Zheng, S. (2023). Prediction for the Sluice Deformation Based on SOA-LSTM-Weighted Markov Model. Water, 15(21), 3724. https://doi.org/10.3390/w15213724






