The Cr(III) Exchange Mechanism of Macroporous Resins: The Effect of Functionality and Chemical Matrix, and the Statistical Verification of Ion Exchange Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cr (III)-Containing Solutions
2.2. Conversion of H+ Form of Resins into Na+ Form
2.3. Analysis of Cr (III)
2.4. Ion Exchange Studies
2.5. Statistical Verification of Adsorption Data and Isotherm Models
2.6. FT-IR Analysis
3. Results
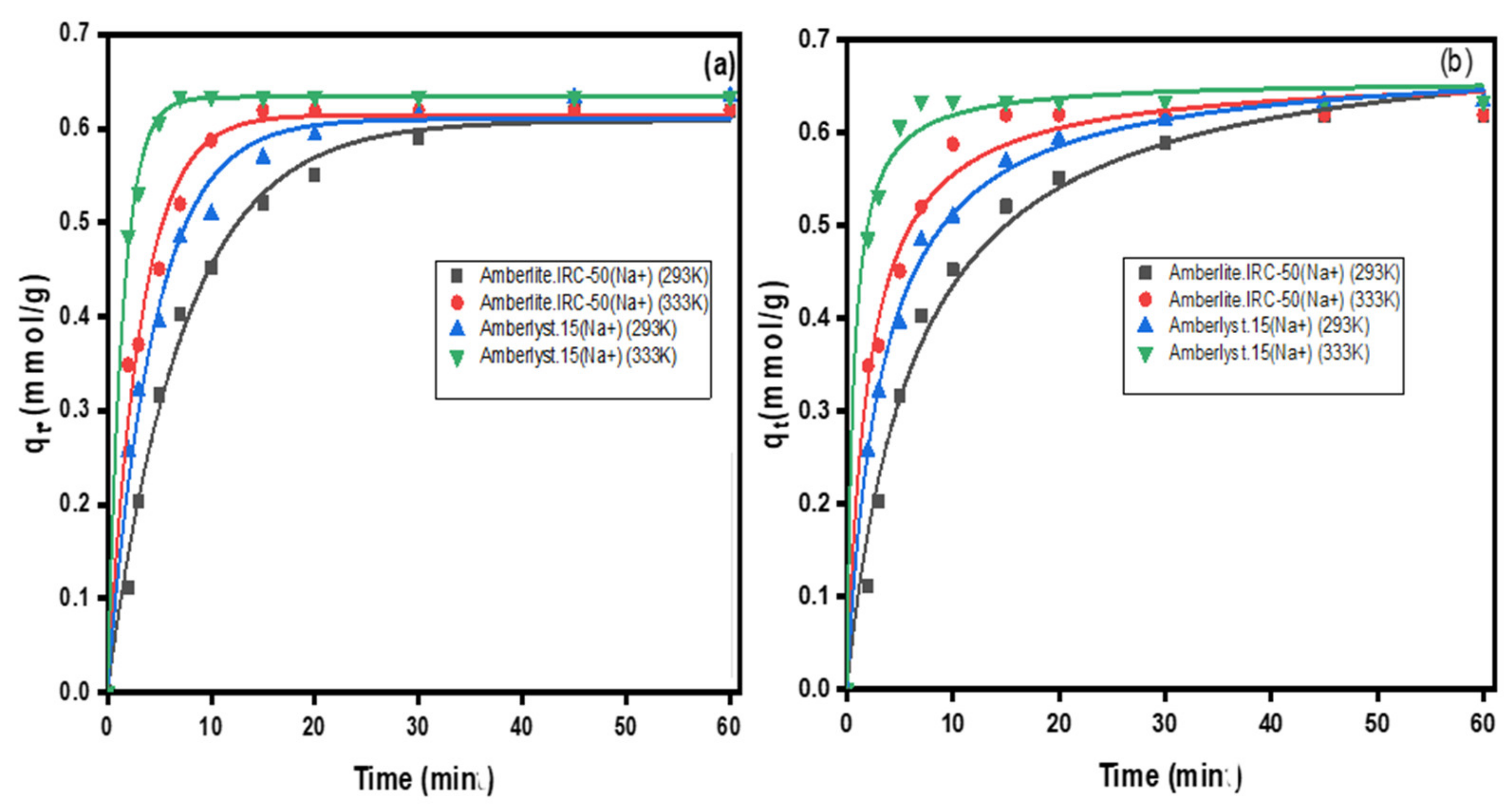
3.1. Exchange Kinetics
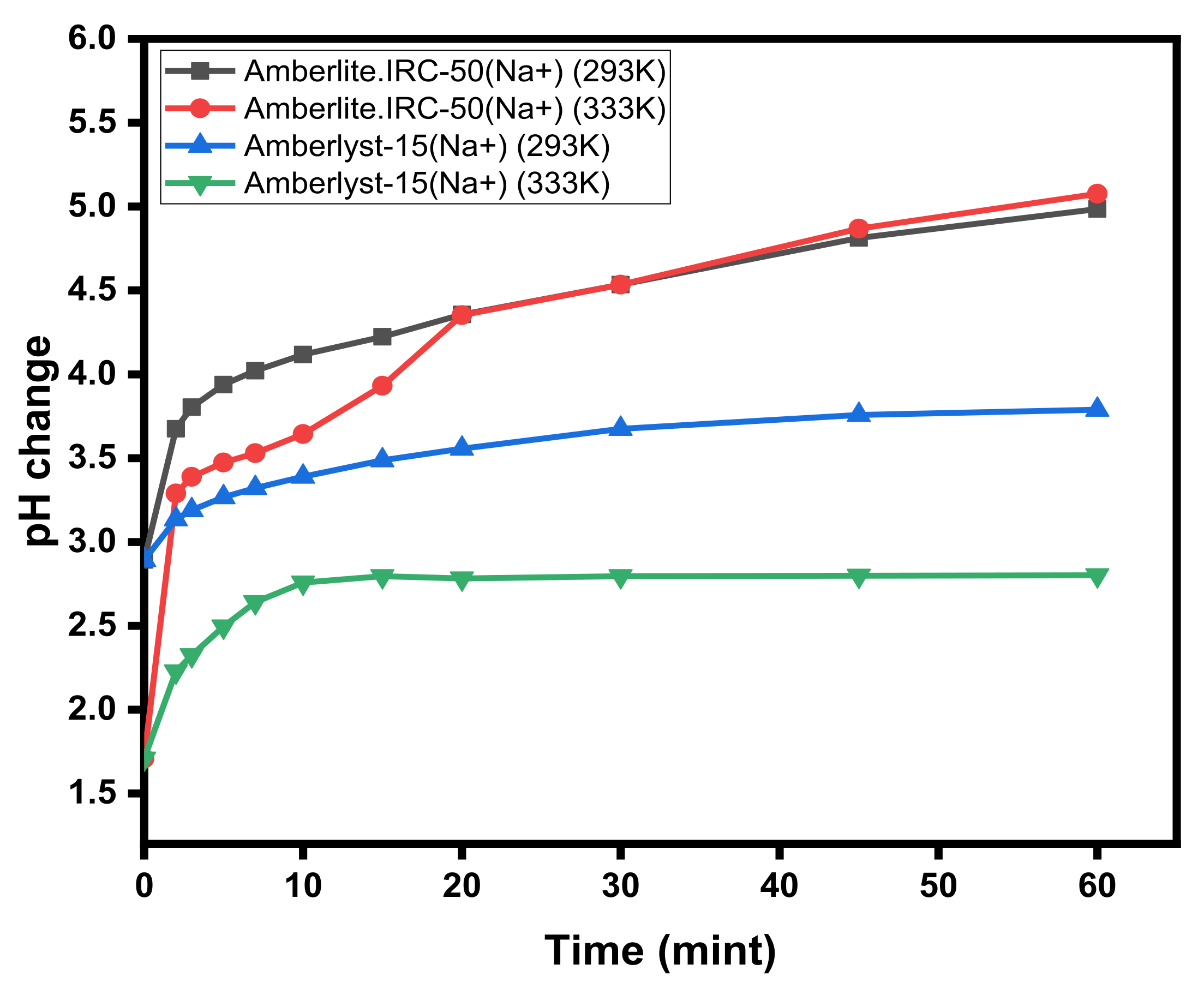
3.2. Changes in pH Values during Exchange Studies
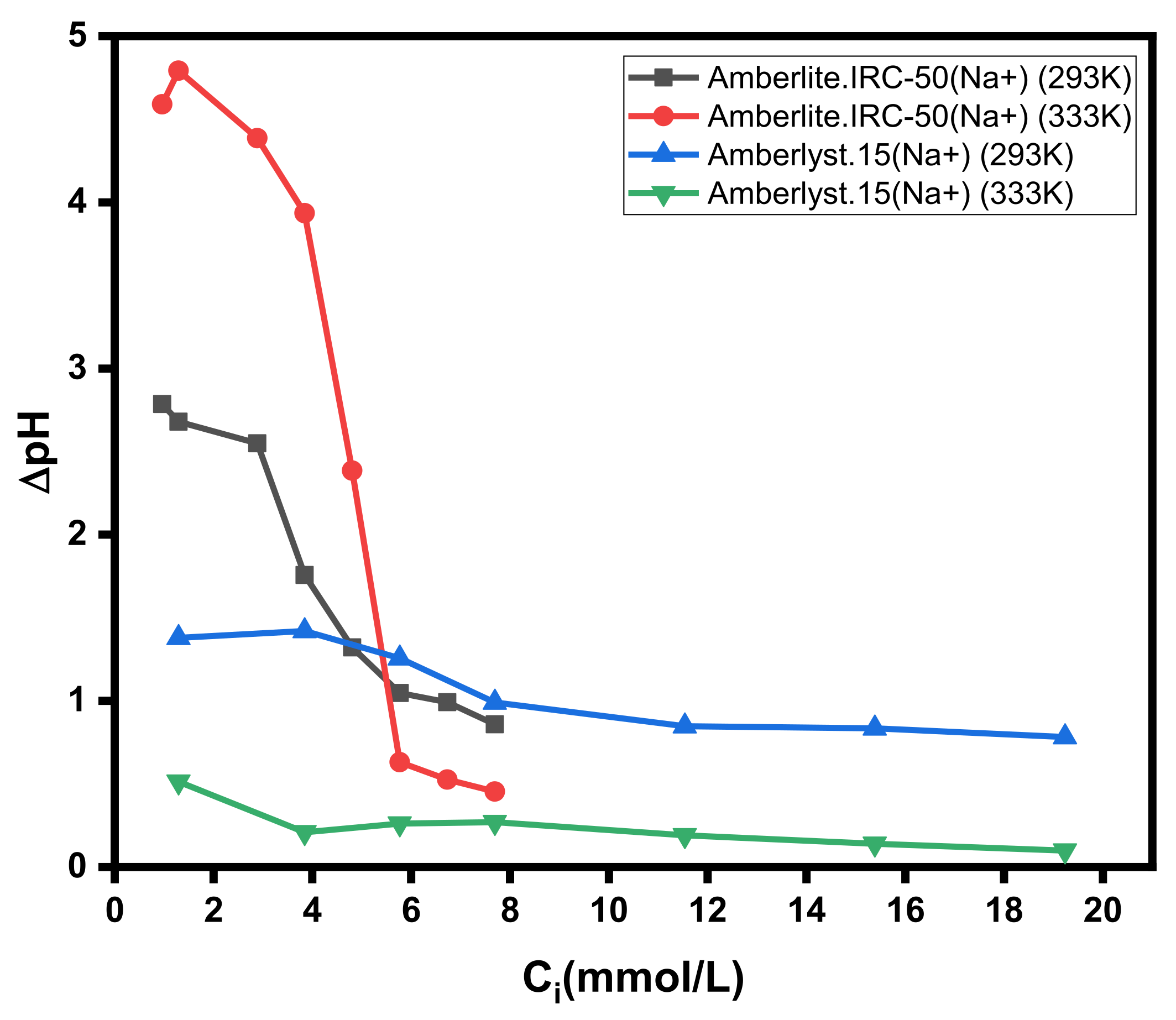
3.3. Influence of Concentration and Temperature
3.4. Influence of H+ Ions Co-Sorption
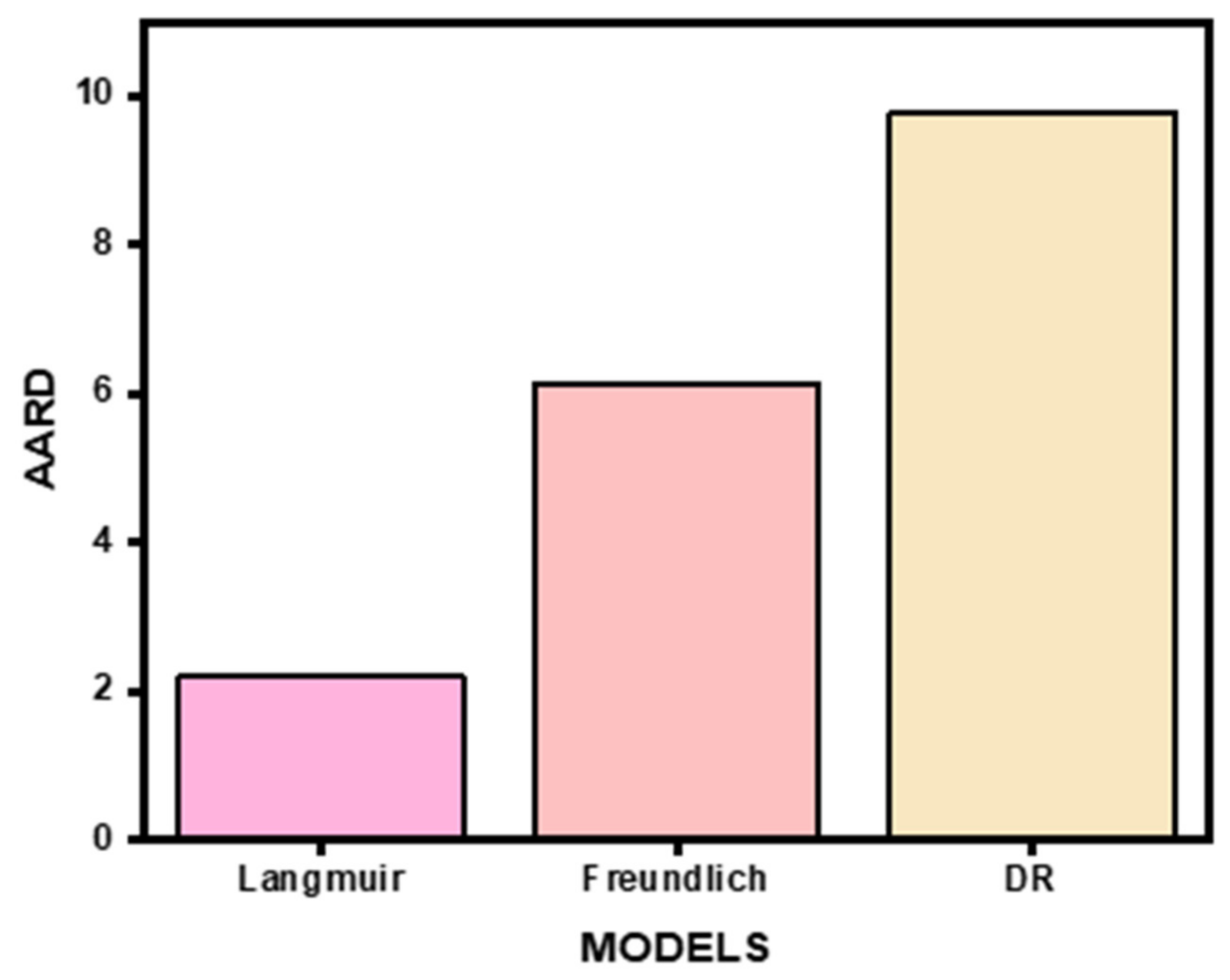
3.5. Ion Exchange Data Modeling
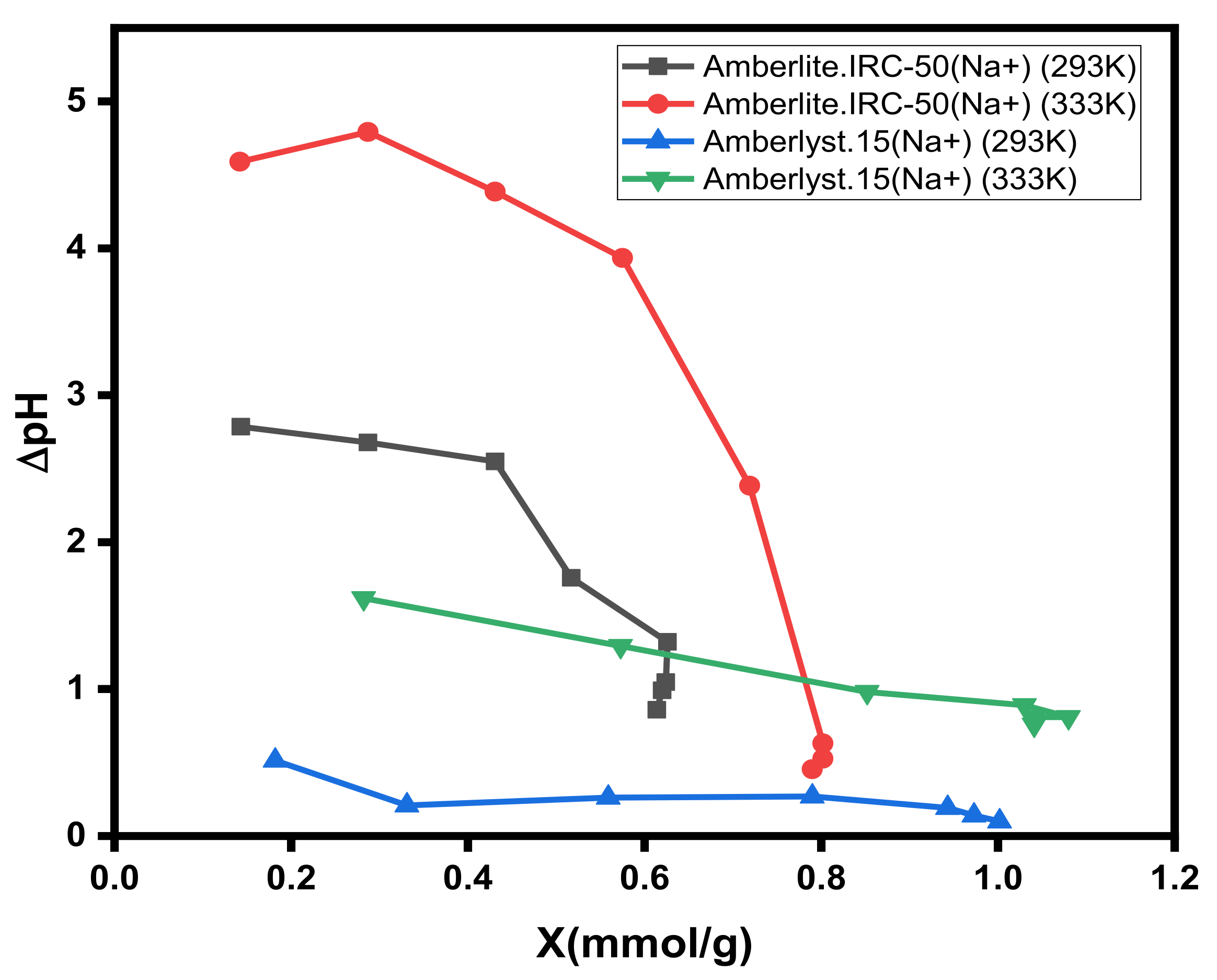
3.6. Adsorption Isotherm Parameters
3.7. Kinetic Data Modeling
3.8. Rate Constant and Activation Energy Parameters
3.9. FT-IR Analysis of Cr(III) Exchange Mechanism
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Z.; Chen, K.; Zhang, Y.; Wang, Y.; Wang, F.; Zhang, G.; Dionysiou, D.D. Magnetically recoverable MgFe2O4/conjugated polyvinyl chloride derivative nanocomposite with higher visible-light photocatalytic activity for treating Cr (VI)-polluted water. Sep. Purif. Technol. 2020, 236, 116272. [Google Scholar] [CrossRef]
- Ge, T.; Shen, L.; Li, J.; Zhang, Y.; Zhang, Y. Morphology-controlled hydrothermal synthesis and photocatalytic Cr (VI) reduction properties of α-Fe2O3. Colloids Surf. A Physicochem. Eng. Asp. 2022, 635, 128069. [Google Scholar] [CrossRef]
- Hsueh, Y.-H.; Lin, K.-S.; Wang, Y.-T.; Chiang, C.-L. Copper, nickel, and zinc cations biosorption properties of Gram-positive and Gram-negative MerP mercury-resistance proteins. J. Taiwan Inst. Chem. Eng. 2017, 80, 168–175. [Google Scholar] [CrossRef]
- Yadav, S.K.; Sinha, S.; Singh, D.K. Chromium (VI) removal from aqueous solution and industrial wastewater by modified date palm trunk. Environ. Prog. Sustain. Energy 2015, 34, 452–460. [Google Scholar] [CrossRef]
- Naushad, M.; Al-Othman, Z.A.; Islam, M. Adsorption of cadmium ion using a new composite cation-exchanger polyaniline Sn (IV) silicate: Kinetics, thermodynamic and isotherm studies. Int. J Environ. Sci. Technol. 2013, 10, 567–578. [Google Scholar] [CrossRef]
- Frei, R.; Polat, A. Chromium isotope fractionation during oxidative weathering—Implications from the study of a Paleoproterozoic (ca. 1.9 Ga) paleosol, Schreiber Beach, Ontario, Canada. Precambrian Res. 2013, 224, 434–453. [Google Scholar]
- Khan, S.A.; Abbasi, N.; Hussain, D.; Khan, T.A. Sustainable mitigation of paracetamol with a novel dual-functionalized pullulan/kaolin hydrogel nanocomposite from simulated wastewater. Langmuir 2022, 38, 8280–8295. [Google Scholar] [CrossRef]
- Khan, S.A.; Siddiqui, M.F.; Khan, T.A. Ultrasonic-assisted synthesis of polyacrylamide/bentonite hydrogel nanocomposite for the sequestration of lead and cadmium from aqueous phase: Equilibrium, kinetics and thermodynamic studies. Ultrason. Sonochemistry 2020, 60, 104761. [Google Scholar] [CrossRef]
- Bleotu, I.; Dragoi, E.N.; Mureşeanu, M.; Dorneanu, S.A. Removal of Cu (II) ions from aqueous solutions by an ion-exchange process: Modeling and optimization. Environ. Prog. Sustain. Energy 2018, 37, 605–612. [Google Scholar] [CrossRef]
- Jadbabaei, N.; Zhang, H. Sorption mechanism and predictive models for removal of cationic organic contaminants by cation exchange resins. Environ. Sci. Technol. Lett. 2014, 48, 14572–14581. [Google Scholar] [CrossRef]
- Alvarado, L.; Torres, I.R.; Chen, A. Integration of ion exchange and electrodeionization as a new approach for the continuous treatment of hexavalent chromium wastewater. Sep. Purif. Technol. 2013, 105, 55–62. [Google Scholar] [CrossRef]
- Xiao, K.; Han, G.; Li, J.; Dan, Z.; Xu, F.; Jiang, L.; Duan, N. Evaluation of polyacrylic anion exchange resins on the removal of Cr (VI) from aqueous solutions. RSC Adv. 2016, 6, 5233–5239. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Yuan, S.; Sun, J.; Zheng, S. Effect of resin charged functional group, porosity, and chemical matrix on the long-term pharmaceutical removal mechanism by conventional ion exchange resins. Chemosphere 2016, 160, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Zhang, M.; Liu, F.; Shuang, C.; Zhu, C.; Zhang, Y.; Li, A. Effect of polymeric matrix on the adsorption of reactive dye by anion-exchange resins. J. Taiwan Inst. Chem. Eng. 2016, 62, 98–103. [Google Scholar] [CrossRef]
- Murtaza, B.; Naseer, A.; Imran, M.; Shah, N.S.; Al-Kahtani, A.A.; ALOthman, Z.A.; Shahid, M.; Iqbal, J.; Abbas, G.; Natasha, N. Chromium removal from aqueous solution using bimetallic Bi0/Cu0-based nanocomposite biochar. Environ. Geochem. Health 2023, 1–14. [Google Scholar] [CrossRef]
- Murtaza, B.; Bilal, S.; Imran, M.; Shah, N.S.; Shahid, M.; Iqbal, J.; Khan, Z.U.H.; Ahmad, N.; Al-Kahtani, A.A.; ALOthman, Z.A. The Study of Removal Chromium (VI) ions from Aqueous Solution by Bimetallic ZnO/FeO Nanocomposite with Siltstone: Isotherm, Kinetics and Reusability. Inorg. Chem. Commun. 2023, 154, 110891. [Google Scholar] [CrossRef]
- Edebali, S.; Pehlivan, E. Evaluation of chelate and cation exchange resins to remove copper ions. Powder Technol. 2016, 301, 520–525. [Google Scholar] [CrossRef]
- Ren, J.; Zheng, Y.; Lin, Z.; Han, X.; Liao, W. Macroporous resin purification and characterization of flavonoids from Platycladus orientalis (L.) Franco and their effects on macrophage inflammatory response. Food Funct. 2017, 8, 86–95. [Google Scholar] [CrossRef]
- Riveros, P. The extraction of Fe (III) using cation-exchange carboxylic resins. Hydrometallurgy 2004, 72, 279–290. [Google Scholar] [CrossRef]
- Cavaco, S.A.; Fernandes, S.; Augusto, C.M.; Quina, M.J.; Gando-Ferreira, L.M. Evaluation of chelating ion-exchange resins for separating Cr (III) from industrial effluents. J. Hazard. Mater. 2009, 169, 516–523. [Google Scholar] [CrossRef]
- Özmetin, C.; Aydın, Ö.; Kocakerim, M.M.; Korkmaz, M.; Özmetin, E. An empirical kinetic model for calcium removal from calcium impurity-containing saturated boric acid solution by ion exchange technology using Amberlite IR–120 resin. Chem. Eng. J. 2009, 148, 420–424. [Google Scholar] [CrossRef]
- Vargas, A.M.; Cazetta, A.L.; Kunita, M.H.; Silva, T.L.; Almeida, V.C. Adsorption of methylene blue on activated carbon produced from flamboyant pods (Delonix regia): Study of adsorption isotherms and kinetic models. Chem. Eng. J. 2011, 168, 722–730. [Google Scholar] [CrossRef]
- Babaei, A.A.; Baboli, Z.; Jaafarzadeh, N.; Goudarzi, G.; Bahrami, M.; Ahmadi, M. Synthesis, performance, and nonlinear modeling of modified nano-sized magnetite for removal of Cr (VI) from aqueous solutions. Desalin. Water Treat. 2015, 53, 768–777. [Google Scholar] [CrossRef]
- Thitame, P.V.; Shukla, S.R. Removal of lead (II) from synthetic solution and industry wastewater using almond shell activated carbon. Enviorn. Prog. Sustain. Energy 2017, 36, 1628–1633. [Google Scholar] [CrossRef]
- Ng, C.; Losso, J.N.; Marshall, W.E.; Rao, R.M. Freundlich adsorption isotherms of agricultural by-product-based powdered activated carbons in a geosmin–water system. Bioresour. Technol. 2002, 85, 131–135. [Google Scholar] [CrossRef]
- Brdar, M.; Šćiban, M.; Takači, A.; Došenović, T. Comparison of two and three parameters adsorption isotherm for Cr (VI) onto Kraft lignin. Chem. Eng. J. 2012, 183, 108–111. [Google Scholar] [CrossRef]
- Vijayakumar, G.; Tamilarasan, R.; Dharmendirakumar, M. Adsorption, Kinetic, Equilibrium and Thermodynamic studies on the removal of basic dye Rhodamine-B from aqueous solution by the use of natural adsorbent perlite. J. Mater. Environ. Sci. 2012, 3, 157–170. [Google Scholar]
- Dubinin, M. The equation of the characteristic curve of activated charcoal. Proc. USSR Acad. Sci. 1947, 55, 327–329. [Google Scholar]
- Sadeghalvad, B.; Khosravi, S.; Azadmehr, A.R. Nonlinear isotherm and kinetics of adsorption of copper from aqueous solutions on bentonite. Russ. J. Phys. Chem. A 2016, 90, 2285–2291. [Google Scholar] [CrossRef]
- Ahmadi, S.; Igwegbe, C.A.; Rahdar, S.; Asadi, Z. The survey of application of the linear and nonlinear kinetic models for the adsorption of nickel (II) by modified multi-walled carbon nanotubes. Appl. Water Sci. 2019, 9, 98. [Google Scholar] [CrossRef]
- Rivas, B.L.; Pooley, S.A.; Maturana, H.A.; Villegas, S. Metal ion uptake properties of acrylamide derivative resins. Macromol. Chem. Phys. 2001, 202, 443–447. [Google Scholar] [CrossRef]
- Gode, F.; Pehlivan, E. A comparative study of two chelating ion-exchange resins for the removal of chromium (III) from aqueous solution. J. Hazard. Mater. 2003, 100, 231–243. [Google Scholar] [CrossRef] [PubMed]
- Dubey, S.; Gusain, D.; Sharma, Y.C. Kinetic and isotherm parameter determination for the removal of chromium from aqueous solutions by nanoalumina, a nanoadsorbent. J. Mol. Liq. 2016, 219, 1–8. [Google Scholar] [CrossRef]
- Ho, Y.-S.; McKay, G. Sorption of dye from aqueous solution by peat. Chem. Eng. 1998, 70, 115–124. [Google Scholar] [CrossRef]
- Markandeya, S.; Kisku, G. Linear and non-linear kinetic modeling for adsorption of disperse dye in batch process. Res. J. Environ. Toxicol. 2015, 9, 320–331. [Google Scholar]
- Fei, W.; Wang, L.-J.; Li, J.-S.; Sun, X.-Y.; Han, W.-Q. Adsorption behavior and mechanism of cadmium on strong-acid cation exchange resin. Trans. Nonferrous Met. Soc. China 2009, 19, 740–744. [Google Scholar]
- Jha, M.K.; Van Nguyen, N.; Lee, J.-c.; Jeong, J.; Yoo, J.-M. Adsorption of copper from the sulphate solution of low copper contents using the cationic resin Amberlite IR 120. J. Hazard. Mater. 2009, 164, 948–953. [Google Scholar] [CrossRef]
- Salem, I.A. Activation of H2O2 by Amberlyst-15 resin supported with copper (II)-complexes towards oxidation of crystal violet. Chemosphere 2001, 44, 1109–1119. [Google Scholar] [CrossRef]



| Models | Amberlite IRC-50 (Na+) | Amberlyst-15 (Na+) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature | Temperature | ||||||||
| 293 K | 313 K | 323 K | 333 K | 293 K | 313 K | 323 K | 333 K | ||
| Langmuir | qe,exp | 0.62 | 0.65 | 0.72 | 0.80 | 0.97 | 1.12 | 1.18 | 1.23 |
| qe,cal | 0.60 | 0.67 | 0.74 | 0.80 | 1.29 | 1.40 | 1.45 | 1.49 | |
| KL | 80.077 | 377.14 | 104.02 | 0.71 | 0.373 | 0.57 | 0.67 | 0.79 | |
| R2 | 0.874 | 0.811 | 0.710 | 0.685 | 0.76 | 0.82 | 0.86 | 0.88 | |
| RMSE | 0.073 | 0.107 | 0.149 | 0.152 | 0.093 | 0.076 | 0.081 | 0.099 | |
| SSE | 0.05 | 0.104 | 0.178 | 0.210 | 0.076 | 0.046 | 0.054 | 0.079 | |
| Freundlich | |||||||||
| qe,cal | 0.64 | 0.69 | 0.73 | 0.79 | 0.96 | 1.10 | 1.18 | 1.24 | |
| KF | 0.56 | 0.65 | 0.69 | 0.75 | 0.40 | 0.54 | 0.59 | 0.64 | |
| N | 2.49 | 10.95 | 9.40 | 8.29 | 2.49 | 2.79 | 2.87 | 2.99 | |
| R2 | 0.85 | 0.77 | 0.65 | 0.64 | 0.70 | 0.76 | 0.79 | 0.81 | |
| RMSE | 0.078 | 0.118 | 0.155 | 0.16 | 0.131 | 0.129 | 0.136 | 1.146 | |
| SSE | 0.056 | 0.12 | 1.20 | 0.23 | 0.138 | 0.135 | 1.148 | 1.171 | |
| D-R | |||||||||
| Qe, cal | 0.61 | 0.69 | 0.74 | 0.81 | 1.03 | 1.15 | 1.20 | 1.26 | |
| E | 8.88 | 12.51 | 8.08 | 8.87 | 0.90 | 1.39 | 1.58 | 1.81 | |
| R2 | 0.87 | 0.81 | 0.70 | 0.70 | 0.95 | 0.97 | 0.97 | 0.95 | |
| RMSE | 0.28 | 0.33 | 0.29 | 0.39 | 0.56 | 0.61 | 0.65 | 0.68 | |
| SSE | 0.74 | 1.00 | 0.69 | 1.56 | 2.58 | 3.03 | 3.38 | 3.72 | |
| Kinetic Model | T (K) | k1 (min)−1 | R2 | SSE | RMSE |
|---|---|---|---|---|---|
| Pseudo-Ist-order | |||||
| Amberlite IRC-50 (Na+) | 293 | 0.13 | 0.99 | ||
| 333 | 0.31 | 0.98 | 0.01 | 0.11 | |
| Amberlyst-15 (Na+) | 293 | 0.22 | 0.98 | ||
| 333 | 0.67 | 0.99 | 0.02 | 0.15 | |
| Pseudo-IInd-order | T (K) | k2(mmolg−1∙min−1) | R2 | SSE | RMSE |
| Amberlite IRC-50 (Na+) | 293 | 0.21 | 0.98 | ||
| 333 | 0.75 | 0.98 | 0.05 | 0.23 | |
| Amberlyst-15 (Na+) | 293 | 0.44 | 0.99 | ||
| 333 | 2.47 | 0.99 | 0.04 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, K.H.; Shah, N.S.; Khan, G.A.; Sarfraz, S.; Iqbal, J.; Batool, A.; Jwuiyad, A.; Shahida, S.; Han, C.; Wawrzkiewicz, M. The Cr(III) Exchange Mechanism of Macroporous Resins: The Effect of Functionality and Chemical Matrix, and the Statistical Verification of Ion Exchange Data. Water 2023, 15, 3655. https://doi.org/10.3390/w15203655
Shah KH, Shah NS, Khan GA, Sarfraz S, Iqbal J, Batool A, Jwuiyad A, Shahida S, Han C, Wawrzkiewicz M. The Cr(III) Exchange Mechanism of Macroporous Resins: The Effect of Functionality and Chemical Matrix, and the Statistical Verification of Ion Exchange Data. Water. 2023; 15(20):3655. https://doi.org/10.3390/w15203655
Chicago/Turabian StyleShah, Khizar Hussain, Noor S. Shah, Gul Afshan Khan, Sadaf Sarfraz, Jibran Iqbal, Aneeqa Batool, Ahmad Jwuiyad, Shabnam Shahida, Changseok Han, and Monika Wawrzkiewicz. 2023. "The Cr(III) Exchange Mechanism of Macroporous Resins: The Effect of Functionality and Chemical Matrix, and the Statistical Verification of Ion Exchange Data" Water 15, no. 20: 3655. https://doi.org/10.3390/w15203655
APA StyleShah, K. H., Shah, N. S., Khan, G. A., Sarfraz, S., Iqbal, J., Batool, A., Jwuiyad, A., Shahida, S., Han, C., & Wawrzkiewicz, M. (2023). The Cr(III) Exchange Mechanism of Macroporous Resins: The Effect of Functionality and Chemical Matrix, and the Statistical Verification of Ion Exchange Data. Water, 15(20), 3655. https://doi.org/10.3390/w15203655







