1. Introduction
Landslide-generated waves are one of the most catastrophic and frequent hazards occurring in a reservoir area and can pose great damage to structures and lives. The impact of landslide-generated impulse waves is considered one of the notable secondary hazards and is sometimes stronger than the landslide itself, especially in the reservoir area.
The largest landslide-generated wave event occurred in 1963 in Italy as 260 million cubic meters of rock fell into the reservoir of the Vajont Dam, built in 1959, producing enormous flooding due to at least 50 million cubic meters of water. The dam did not suffer any serious damage, but flooding due to the overtopping height of about 245 m above the dam crest destroyed several villages in the valley and killed almost 2000 people [
1].
Numerous reservoir areas that have suffered from landslides are in mountainous regions, where landslide-generated wave formation and propagation are greatly influenced by the river channel and opposite bank. In June 2007, a massive landslide with a volume of 3 million cubic meters occurred at the Da Yan Tang location, resulting in waves surging as high as 4 m. This event had varying impacts on three nearby townships, leading to adverse consequences such as casualties and damage in the upstream hazard zone and one downstream township. On 23 November 2008, a widespread landslide took place at the Gong Jia Fang slope in Wushan County. This event subsequently generated enormous waves. Post-event investigations revealed that the main components of the landslide consisted of limestone and marl. The total volume of the collapse reached 380,000 cubic meters, with an approximate entry width of 194 m and an entry depth of around 15 m. After sliding into the water, it was completely submerged, resulting in waves reaching a maximum height of 31.8 m, severely affecting navigation in the area. In June 2015, a landslide occurred at the mouth of the Da Ning River on the north bank in Wushan, Chongqing. Approximately 230,000 cubic meters of rock and soil rapidly slid into the river, generating massive waves nearly 6 m high. This event led to the sinking of one Coast Guard vessel and the capsizing of nine small fishing boats and seven private vessels that were moored on the opposite shore. Furthermore, the wave propagation along the opposite bank resulted in injuries and fatalities, with a total of six casualties.
In mountainous regions, bridges are among the most crucial transportation infrastructures, and their safety is of paramount concern. This concern is particularly heightened when considering the potential impact of landslide-generated waves on bridge piers. Under such circumstances, bridge piers may experience significant forces and face the risk of collapse and damage. Therefore, it is imperative to gain a comprehensive understanding of the mechanisms underlying the effects of landslide-generated waves on bridge piers, enabling the development of effective protective measures.
Previous researchers conducted numerous experiments and simulations on landslide-generated waves, yielding many landmark findings. Noda [
2] stands among the pioneering researchers who conducted experimental investigations into landslide-generated waves generated by solid blocks. Noda categorized these waves into four distinct patterns: nonlinear oscillatory, nonlinear transition, solitary-like, and dissipative transient bore. Laboratory investigations carried out by Kamphuis and Bowering [
3] regarding landslide-generated waves revealed that the characteristics of these waves primarily depend on the slide’s volume and the Froude number at the moment of impact with the water. Additionally, wave propagation speed can be approximated using solitary wave theory. Huber and Hager [
4] conducted a series of three-dimensional experiments involving granular landslides falling into a water tank. Their findings suggested a correlation between wave height and non-dimensional landslide volume values. Walder et al. [
5] studied the near-field characteristics of landslide-generated waves caused by solid blocks in a two-dimensional physical model. Their research highlighted that key factors governing near-field wave properties include non-dimensional landslide volume per unit width, non-dimensional submerged time of motion, and non-dimensional vertical impact speed. Fritz et al. [
6] conducted comprehensive two-dimensional laboratory experiments with granular materials. They presented empirical equations for predicting the patterns of LGWs based on slide properties and also introduced empirical equations for predicting energy conservation from the slide to the water. Panizzo et al. [
7] performed three-dimensional experiments and concluded that the maximum generated wave height was primarily influenced by the non-dimensional time of underwater landslide motion and the surface of the landslide front. As an illustrative example of experimental setups, Ataie-Ashtiani and Nik-Khah [
8] conducted 120 laboratory tests using both rigid and deformable slide masses. They found that the maximum wave crest amplitude was strongly affected by bed slope angle, landslide impact velocity, thickness, kinematics, deformation, and weakly by landslide shape. Mohammed and Fritz [
9] conducted physical modeling of landslide-generated waves using deformable granular landslides in a three-dimensional wave basin. Their study highlighted that the dominant control over wave characteristics lies in the landslide Froude number. They reported that 1–15% of the kinetic energy of the landslide at impact was converted into wave energy. Heller and Spinneken [
10] conducted tests to investigate the influences of the slide Froude number, relative slide thickness, and relative slide mass on the characteristics of landslide-generated waves. In a subsequent study, Heller and Spinneken [
11] explored the effects of the water body geometry on wave characteristics in both near- and far-fields, using both two- and three-dimensional physical models. They observed that, for a small slide Froude number, relative slide thickness, and relative slide mass, three-dimensional wave heights were considerably smaller both in the near- and far-field compared to those in two dimensions. Lindstrøm [
12] conducted experimental investigations into landslide-generated waves in a two-dimensional wave tank. He employed five different slide materials, including block slides and four granular slides with grain diameters ranging from 3 to 25 mm.
Table 1 summarizes some of the most important previous laboratory studies that have performed for LGWs.
Many scholars have also conducted research on the impact of mountain landslides on reservoir structures. Sainflou [
13] derived an analytical solution for nonlinear and standing waves on a vertical wall. Tadjbakhsh and Keller [
14] provided the theoretical water surface elevation as a function of the time and the spatial coordinate for periodic waves impacting a vertical wall. Landslide-generated waves can be approximated with Stokes (Dean and Dalrymple [
15]), cnoidal (Dingemans [
16]), and bore (Le Méhauté [
17]) waves (Heller and Hager [
18]; Heller et al. [
19]; Xue et al. [
20]). These different wave types result in different effects when impacting dams. Bore-like waves are typically created in the generation zone and transform into cnoidal- or solitary-like waves further offshore (Heller and Hager [
18]), or they are generated during wave breaking near the shore. Wave breaking rarely occurs at a dam as the water depth tends to increase and the wave amplitude tends to decrease towards the dam; hence, solitary-like waves represent the most extreme case in most situations (Heller et al. [
21]; Kobel et al. [
22]). A mathematical investigation of solitary waves impacting a vertical wall was conducted by Cooker et al. [
23]. The numerically deduced values of the wave force and the run-up height were successfully validated with the numerical results of Fenton and Rienecker [
24]. However, no prediction method for the pressure distribution at the wall was provided.
Landslides in these regions can directly destroy bridges and roads along their paths. Furthermore, during the secondary wave propagation process, they can also damage or wash away bridge piers. Therefore, targeted protection and monitoring of bridge piers are essential. To achieve this, it is crucial to understand the mechanisms of wave action on bridge piers, including the types and forms of pressure on piers under wave action. This understanding helps elucidate the load-bearing process on bridge piers, identify critical areas of maximum stress on bridge piers for focused protection, or serve as a reference for extreme load calculations during the initial design of bridge piers. In order to elucidate the mechanics of landslide-generated waves on bridge piers, this study conducted experimental simulations using a three-dimensional water tank. We investigated the types and origins of wave pressures on bridge piers under landslide-induced waves, analyzed the distribution patterns of different wave pressure types and their interrelationships, and ultimately provided the location of maximum pressure and a formula for calculating the maximum pressure.
2. Experimental Setup
This experiment utilized a carriage, chute, and landslide mass to simulate landslides. The carriage and chute were constructed from iron materials, with the chute’s bottom plate simulating the sliding surface. Variable baffles were positioned on both sides of the chute to control the width of the landslide body. Hinges were installed at the rear and both ends of the chute to control the angle of the landslide, as shown in
Figure 1.
The process of landslide-generated waves primarily involves the interaction between the landslide and the water body. Most landslides exhibit planar shapes, such as fan-shaped, tongue-shaped, and elongated forms. For landslides with fan-shaped and tongue-shaped planar geometries, the contact surface between the solid mass and the flowing water is effectively rectangular. In contrast, for landslides with elongated planar geometries, the contact surface is also rectangular. Therefore, in this experiment, we chose to simulate landslides with an elongated planar shape, which led us to select a rectangular flume for modeling. In reality, the sides of the landslide mass should exhibit zero friction. To replicate this condition in our experiments, we left a 1 cm space on each side when positioning the sliding block, allowing us to place a smooth 1 cm-thick cement board. During the landslide process, friction between the block and the sliding surface can generate a smooth, powdery layer. To simulate this, we applied fine clay as a base layer on the bottom plate before positioning the sliding block. This approach allowed us to model both the interaction between the sliding block and the water body and the frictional losses incurred as the block descends. To facilitate adjustments in landslide angle and height, there are pulleys both in front and behind the sliding frame.
During the downslope movement of most rockslide bodies, they may disintegrate due to the pre-existing fissures within the rock mass. As the sliding velocity increases, the degree of disintegration intensifies. Consequently, the rockslide bodies are characterized by a disintegrated structural pattern. We conducted a survey of the fracture dimensions found in the reservoir area; the size of individual blocks was determined based on the degree of fissure development and the width of the fissures. To facilitate the placement of boulders, we designed them with dimensions of length * width * height = 3:2:1. The landslide blocks were created with an average density ranging from 2.3–2.8 g/cm
3, and for this study, a density of 2.5 g/cm
3 was achieved using a mixture of mud and stones, as specified in
Table 2 for the dimensions.
Table 3 lists the mechanical properties of the test materials.
The experiments were conducted using a three-dimensional wave basin (39 m long, 8 m wide, and 1.16 m deep) at Chongqing Jiaotong University, China.
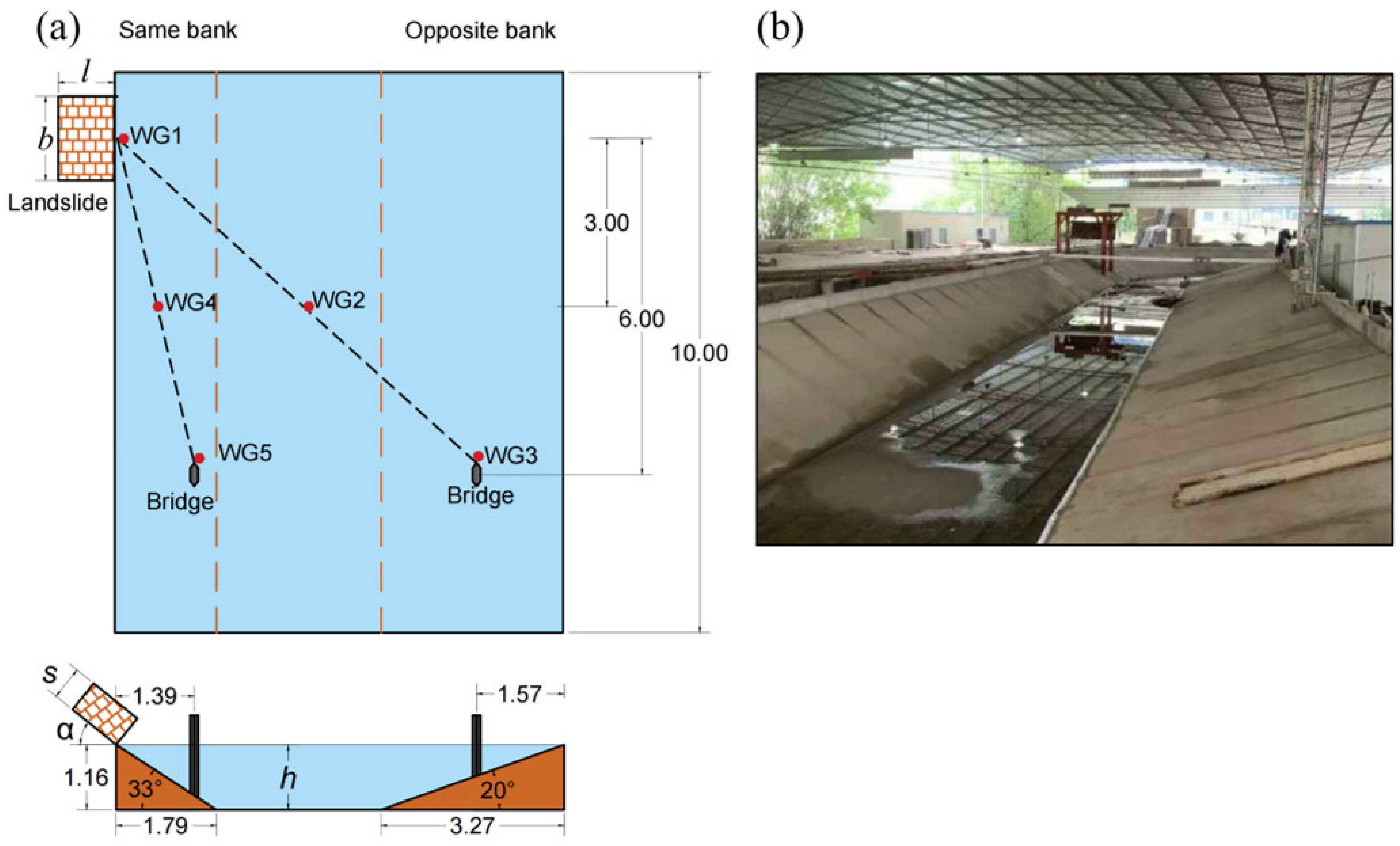
Figure 2a only shows the straight test section of the basin; the curved section, which is not part of the test section, has not been depicted. The basin was 10 m long, 8 m wide, and 1.16 m deep was used in the present study. The slopes on both sides are 20° and 33°, respectively. The experimental section was conducted in the Wanzhou section of the Three Gorges Reservoir area, where we conducted a detailed analysis of the river’s topography, measured the dimensions and angles of river cross-sections, and designed the channel dimensions to closely match those of both straight and curved sections. The channel dimensions were designed based on the dimensions of a straight channel, and after scaling down according to a scale ratio of
, the profile data statistics are presented in
Table 4. The basin was designed to simulate both the straight and curved river sections, but during the experiment, we only used the straight section. The generalized basin cross-sectional dimensions were based on the dimensions of the straight section, and the cross-sectional dimensions are consistent between the curved and straight sections.
Within a 400 m range near the landslide point, protective measures will be implemented. This study focuses on the most dangerous state of the impact of landslides on bridge piers. Therefore, the bridge piers were placed 6 m away from the landslide point at an actual engineering distance of 420 m. The bridge pier on the same bank was located on the near side of the landslide, while the bridge pier on the opposite bank was located on the far side of the landslide.
A wave gauge (WG1) was placed at the landslide point to measure the initial wave height with an accuracy of 1 mm and an acquisition frequency of 100 Hz. WG3 and WG5 were positioned 10 cm in front of the bridge piers. Placing them too close would affect the waves while placing them too far would not capture the wave height in front of the piers. WG3 measures the wave height in front of the far-side pier, while WG5 measures the wave height in front of the near-side pier. WG2 was placed at the midpoint of the line connecting the landslide and the far-side pier, and similarly, WG4 was positioned at the midpoint of the line connecting the landslide and the near-side pier. The landslide had a width
, a length
, and a thickness
, with an angle
between the landslide and the water surface. The depth of the river channel was
, as illustrated in
Figure 2.
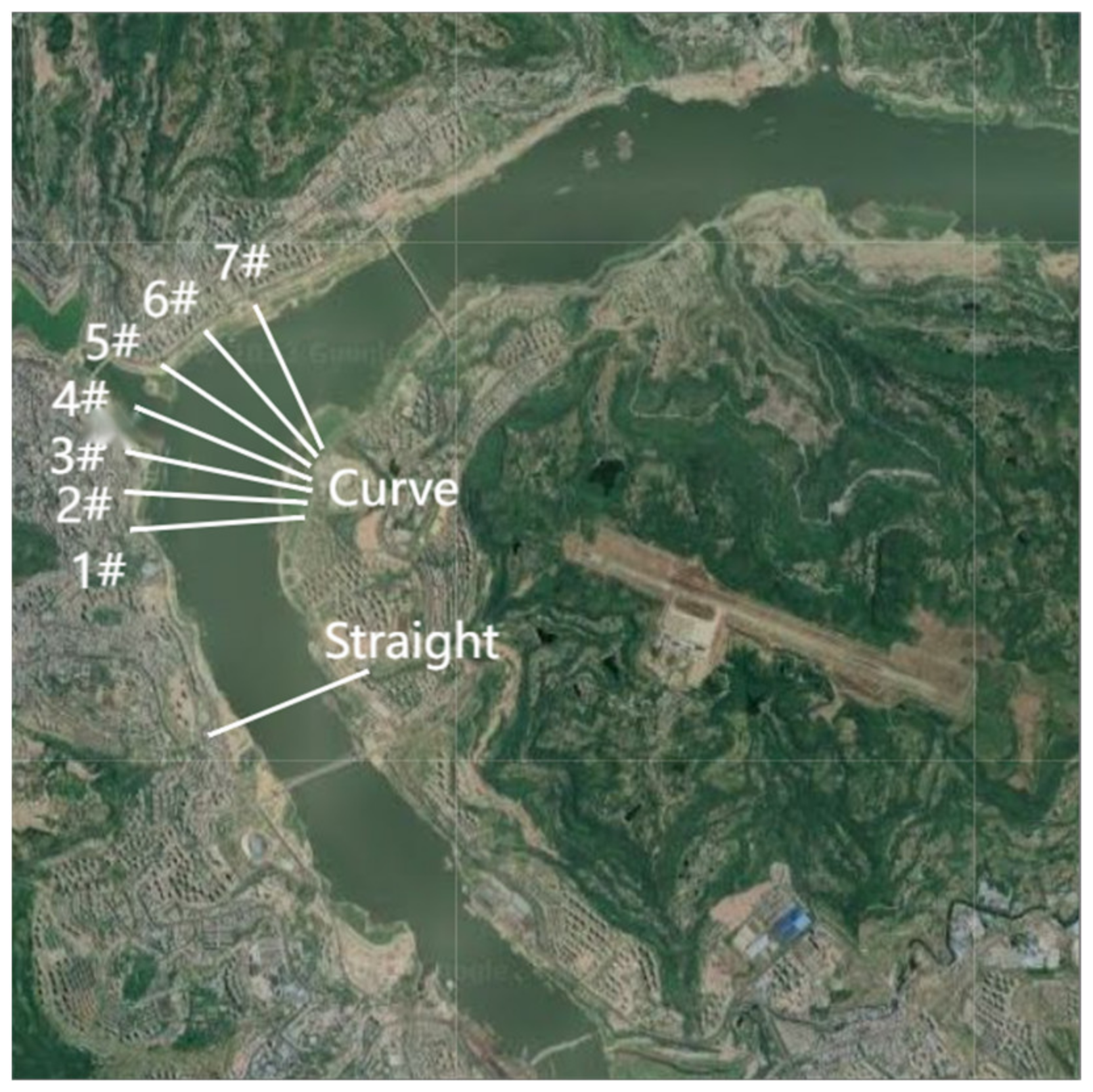
Figure 3 is a schematic diagram of the cross-sectional terrain selection for the Wanzhou river section, where ‘curve 1#’ represents cross-section 1# in the bend.
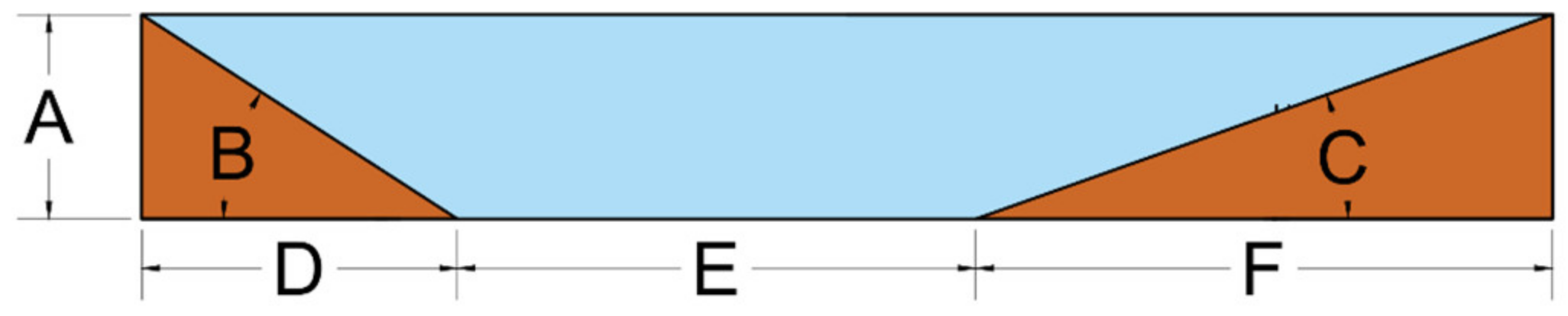
Figure 4 displays dimension labels at various positions along the cross-section, facilitating subsequent dimension statistics.
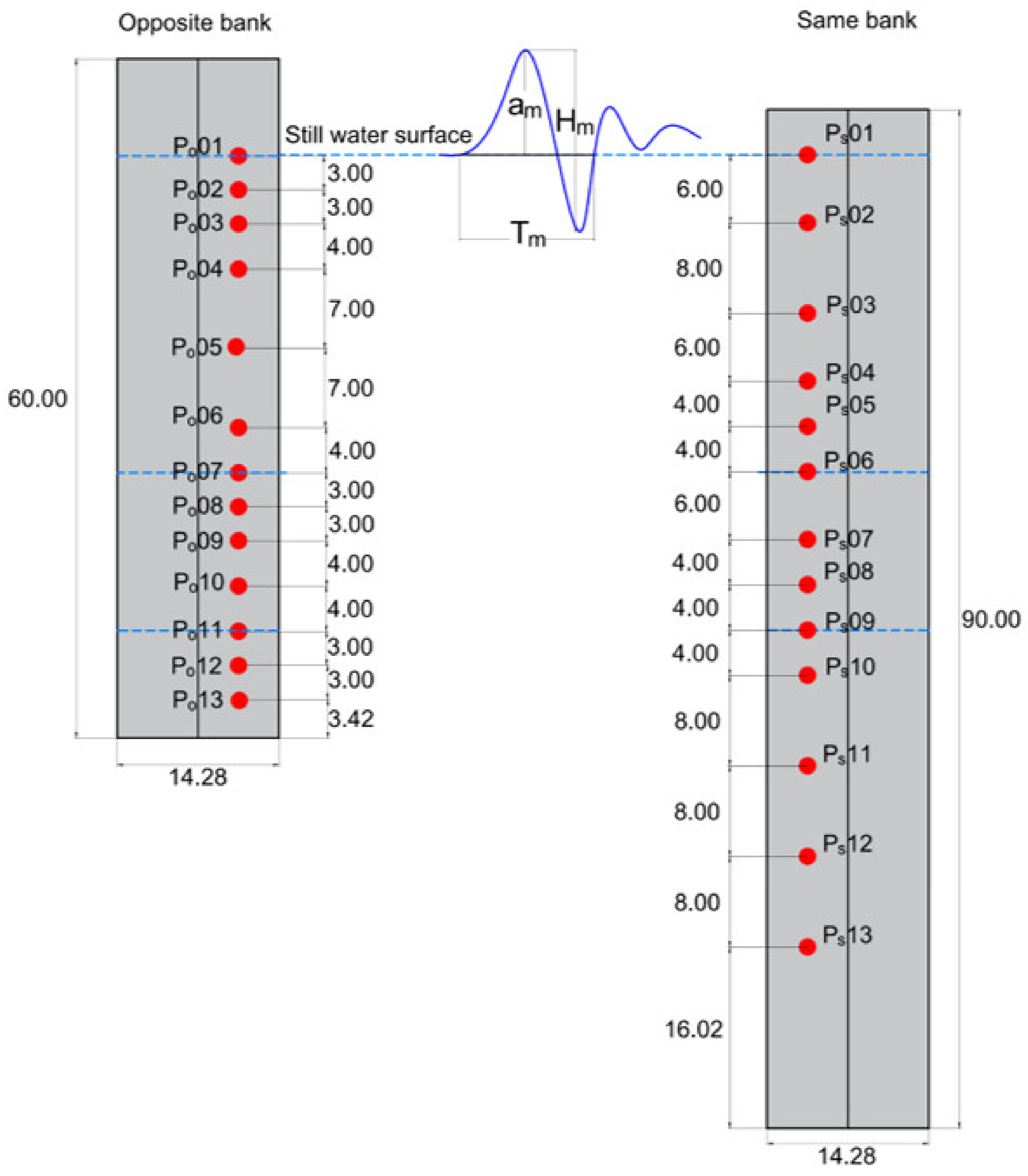
Due to the limited number of wave pressure gauges (WPGs), with a pressure acquisition frequency of 1000 Hz and a measurement accuracy of 5%, the distribution of pressure measurement points is non-uniform. Each water depth position is equipped with one pressure measurement point, with a denser arrangement of pressure measurement points near the water surface. In the longitudinal direction, a total of 13 pressure acquisition points were positioned and numbered from top to bottom as
to
on the opposite bank and
to
on the same bank (
Figure 5). When measuring with a pressure sensor, it measures the total pressure, from which is deducted the initial static pressure, so the pressure shown in this study is referred to as the hydrodynamic pressure. The first wave height is denoted as
, and the wave height upon reaching the bridge piers is denoted as
. Each experimental case was repeated three times to obtain data at all WPG positions, and the average values were subsequently analyzed to ensure the repeatability of the experiments.
The experimental water depths were chosen to be 0.74 m, 0.88 m, and 1.16 m. The portion of the landslide that exceeds the water depth contributes less during the wave generation process. Therefore, based on the water depth, this experiment used a landslide body with a length of 1 m. The widths chosen for the experiment were 0.5 m, 1.0 m, and 1.5 m, and the thicknesses selected were 0.2 m, 0.4 m, and 0.6 m. Statistical analysis revealed that the majority of unstable rock slope angles ranged from 40° to 60°. Therefore, this experiment determined landslide angles of 40° and 60°. The specific experimental conditions are outlined in
Table 5.
3. Forms and Distribution of Wave Pressure
In this paper, wave pressures can be categorized into two types: pulsating pressure (
), and resonance pressure (
) (
Figure 6).
is characterized by low frequency, with an action period consistent with the wave cycle, frequency ranging from 0.2 to 0.5 Hz. In the absence of wave reflection superposition, the first wave is the largest. The
studied in this paper refers to the difference in pressure between the first wave peak and trough.
is the pressure generated when the waves reach the bridge pier due to the resonance caused by the impact. It exhibits high-frequency and vigorous oscillations, with frequencies measured in the experiment ranging from 300 to 900 Hz. The
studied in this paper represents the maximum wave pressure obtained during the high-frequency vibration process induced by the wave impact on the bridge pier. To summarize,
results from the pressure changes caused by the variations in the water surface during the wave action process, while
arises from the resonance of the bridge pier due to the impact of the waves.
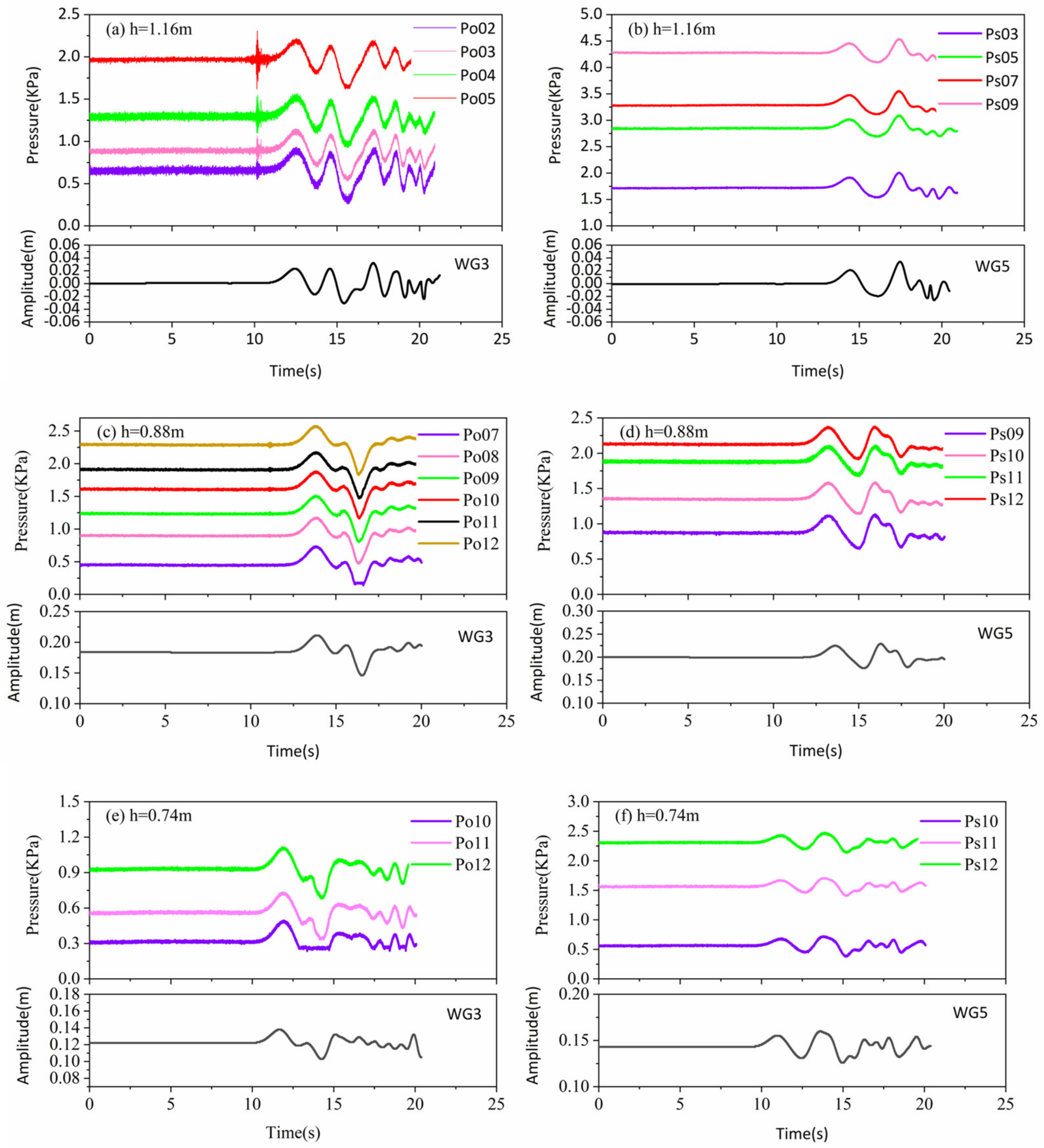
Since the dynamic wave pressures were consistently at zero before the wave arrived, for the purpose of differentiation on the graph, the initial values at each measurement point along the water depth were adjusted. When analyzing the condition of the opposite bank bridge pier at h = 1.16 m, it was found that the wave pressure time processes from
to
were entirely consistent, with identical waveforms. This consistency arises from the synchronicity of water particle motion along the water depth direction when waves approach the bridge pier. Prior to the occurrence of pulsating pressure (
), there was a common presence of resonance pressure (
) at the same time. This pressure form exhibited high-frequency oscillations, with
being both high-frequency and intense. The
had a period that was completely synchronized with the wave period. This paper focuses on the analysis of the first wave pressure, with an approximate duration of 3 s during the first wave action (
Figure 6).
It is worth noting that at the same position, using a wave pressure sampling frequency of 100 Hz did not result in . After the data were sampled at 1000 Hz and subjected to Fourier Transform Filtering (FTF), the waveform was nearly identical to the data sampled at 100 Hz, validating the high-frequency nature of . As the water depth increases, the length over which the bridge pier experiences force also increases. Consequently, the total force acting on the bridge pier increases, leading to resonance during wave impact. However, due to the height limitations of the existing water tank, further research will be conducted to provide additional evidence and insights into wave pressures under conditions of higher water levels.
The study was conducted to analyze wave pressures on bridge piers under three different operational water levels in the Three Gorges Reservoir area. The study investigates the temporal variations of wave pressure at the measurement points on the bridge piers under three different water depth conditions and compares them with the corresponding wave height variations measured by the WGs in front of the piers. Here,
represents the wave pressure at measurement points on the opposite bank bridge pier and
represents the wave pressure at measurement points on the same bank bridge pier. As shown in
Figure 7, it can be observed that under all water depth conditions during the experiment, the fluctuations in wave pressure and wave height exhibit a strong positive correlation. The variations in wave pressure along the water depth for each condition are consistent, indicating a close relationship between dynamic wave pressure on the entire bridge pier and wave height.
In various conditions, different wave profiles were generated. When comparing the wave height profiles in
Figure 7a,c,e, it can be observed that the first two waves in
Figure 7a are relatively regular, while the third wave suddenly increases in magnitude, followed by chaotic waveforms. In
Figure 7c,e, the second wave trough is larger, and subsequent waveforms are more chaotic. This variation can be attributed to the shallower water depth, which results in the bridge pier being closer to the slope, leading to shorter wave reflection and superposition times. Under the same operational condition, waveforms on the opposite side of the bridge pier (across from the slide) and on the same side of the bridge pier (along the slide) do not match, indicating significant differences in wave generation and propagation between the three-dimensional water tank and the two-dimensional flume. In the two-dimensional flume, waveforms remain consistent along the cross-sectional profile, while in the three-dimensional water tank, waveforms exhibit variations depending on the direction of generation.
Figure 7a also shows a significant high-frequency oscillation before the onset of pulsating pressure. Pre-experiments were conducted before the actual test, where the bridge pier was anchored to the slope with concrete, and the wave pressure measurement points were connected. Throughout the entire test process, there was no human intervention with the bridge pier and wave pressure measurement points. Therefore, it can be inferred that the influence of experimental equipment can be ruled out. Furthermore, this phenomenon was observed only on the bridge pier on the opposite side (across from the slide) when h = 1.16 m. Han [
25] divided the wave propagation direction into the main wave area and the secondary wave area. The main wave area extends within a 60° range from the landslide axis. The wave on the opposite side of the bridge pier falls within the main wave area, where the wave carries greater energy. In contrast, the bridge pier on the same side (along the slide) falls within the secondary wave area, where the wave carries less energy.
4. Pressure Rules on Bridge Pier
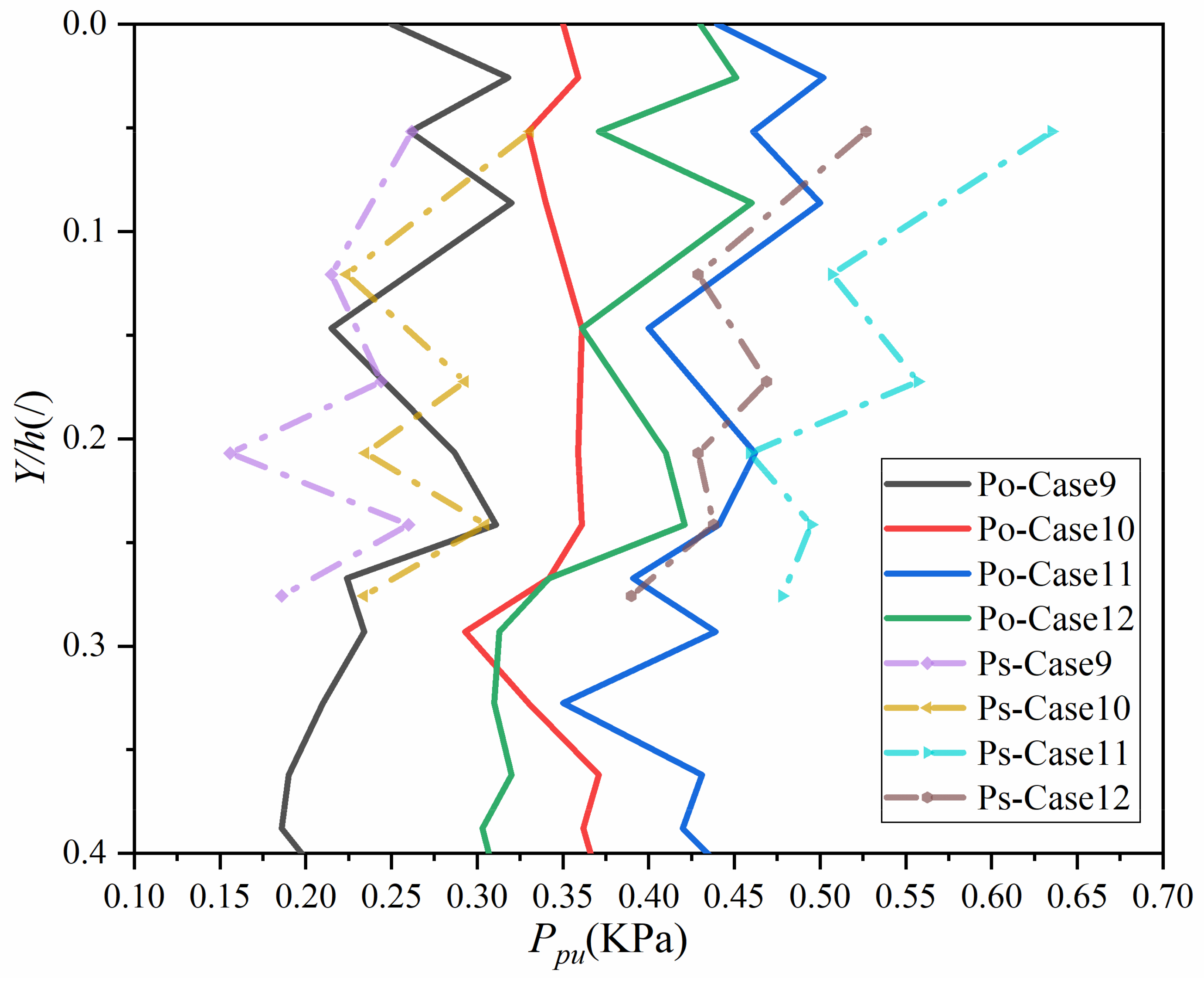
The distance from the measurement point to the water surface is
, and the water depth is
. As observed in
Figure 8, it can be seen that the distribution pattern of wave pressure along the water depth for the opposite bank bridge pier exhibits a sawtooth shape and remains relatively constant. This distribution pattern is consistent with the vertical distribution of wave pressure under the still water level, as proposed by Huang et al. [
26]. The wave pressure distribution along the water depth for the same bank bridge pier also follows a sawtooth pattern, but the point of maximum wave pressure is near the water surface. This rule is consistent with the study conducted by Tan et al. [
27]. The magnitude of wave pressure is a reflection of the energy transferred to the bridge piers by the water particles. The differences in the distribution patterns of pulsating pressure along the water depth on the opposite bank and the same bank indicate that the energy distribution along the water depth varies when landslide-generated waves propagate at different angles. It is precisely due to these differences in energy distribution that
is only present on the opposite bank bridge pier.
Comparing the same bank and opposite bank bridge piers, it can be observed that , , and . The larger the volume of the landslide, the greater the potential energy transferred to the water, resulting in larger wave heights. Due to and , so . Larger angles of the landslide result in higher effective impact velocities and, consequently, larger wave heights. It is notable that the wave pressure is highest near the still-water surface, and under all conditions, the wave pressure on the same bank near the still-water surface is greater than or equal to the wave pressure on the opposite bank. This difference is attributed to the fact that the distance from the same bank to the landslide point is shorter than the distance from the opposite bank to the landslide point.
The occurrence of
is limited to the condition of
, and an analysis was conducted for all scenarios under this water depth condition, as shown in
Figure 9. In Case 9, peaks were observed in both
and
. Case 10 and Case 11 exhibited peaks at
, while Case 12 did not show any significant peaks, with a gradual increase in a sawtooth-like pattern along the water depth. The distribution pattern of
along the water depth can be categorized into three types: single peak, multiple peaks, and no peaks. For a large volume of
,
exhibited a single peak or no peak distribution. In the case of a smaller volume of
, a double-peak distribution of
was observed. Generally, the trend along the water depth direction is an increase followed by a decrease. For all scenarios, the position with the maximum
is consistently at
, indicating that this location is the most critical.
represents the second-largest
, implying that these two positions on the bridge pier are more susceptible to damage and destruction. Therefore, enhanced protective measures should be considered in the design and maintenance of the bridge at these locations.
5. Discussion
In reference to and , The generation of is unquestionably due to wave action. However, represents a newly discovered force, and this study marks an initial exploration of . It was found that exhibits high-frequency and short-lived characteristics. Through analysis, it was hypothesized that results from the resonance of bridge piers induced by wave action, and it occurs primarily under conditions of greater water depth. Due to limitations in the experimental site, this study was unable to conduct tests under significantly greater water depths. Future research will aim to validate this hypothesis through more comprehensive experiments.
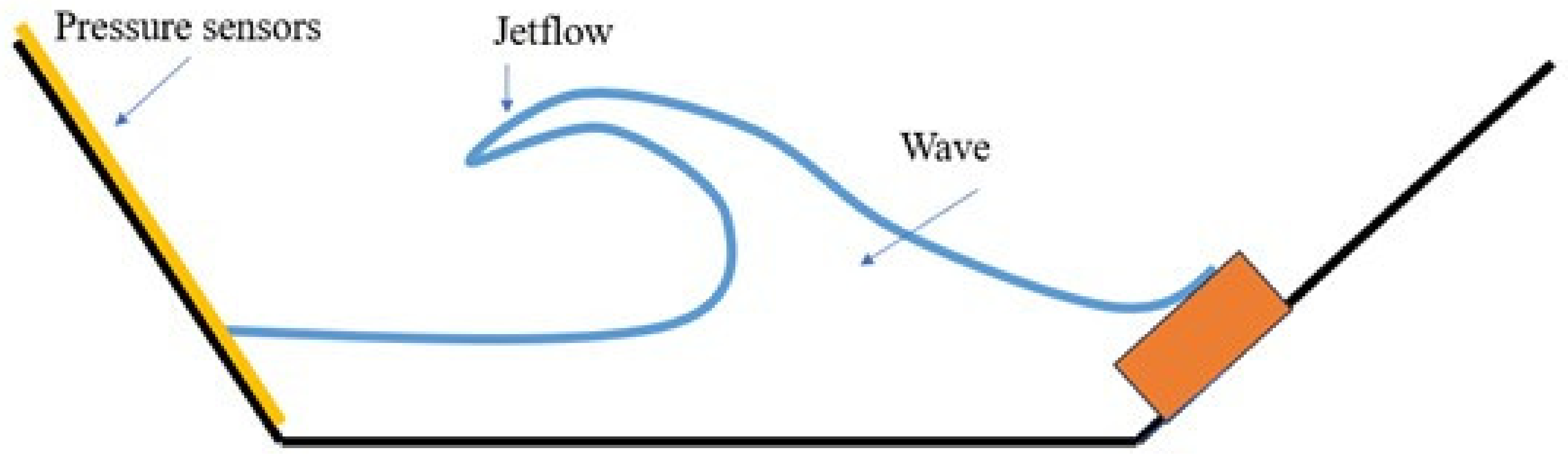
Regarding the forces exerted by waves, a recent study by TAN et al. [
27] identified impact pressure and pulsating pressure. Impact pressure was found to be distance-dependent and associated with the jet flow when it reached pressure sensors, resulting in jet flow pressure (impact pressure).
Figure 10 is a schematic diagram of jet flow and waves. Pulsating pressure was observed when waves reached the opposite side and were measured on the pressure side plates. Except for impact pressure generated by jet flow, all other pressure variations recorded in the study were classified as pulsating pressure. The pulsating pressure investigated in this paper aligns with the focus of their study. It is essential to distinguish between resonance pressure (
) and impact pressure (
) in terms of their underlying causes.
results directly from the impact of jet flow, while
is linked to the resonance of bridge piers.
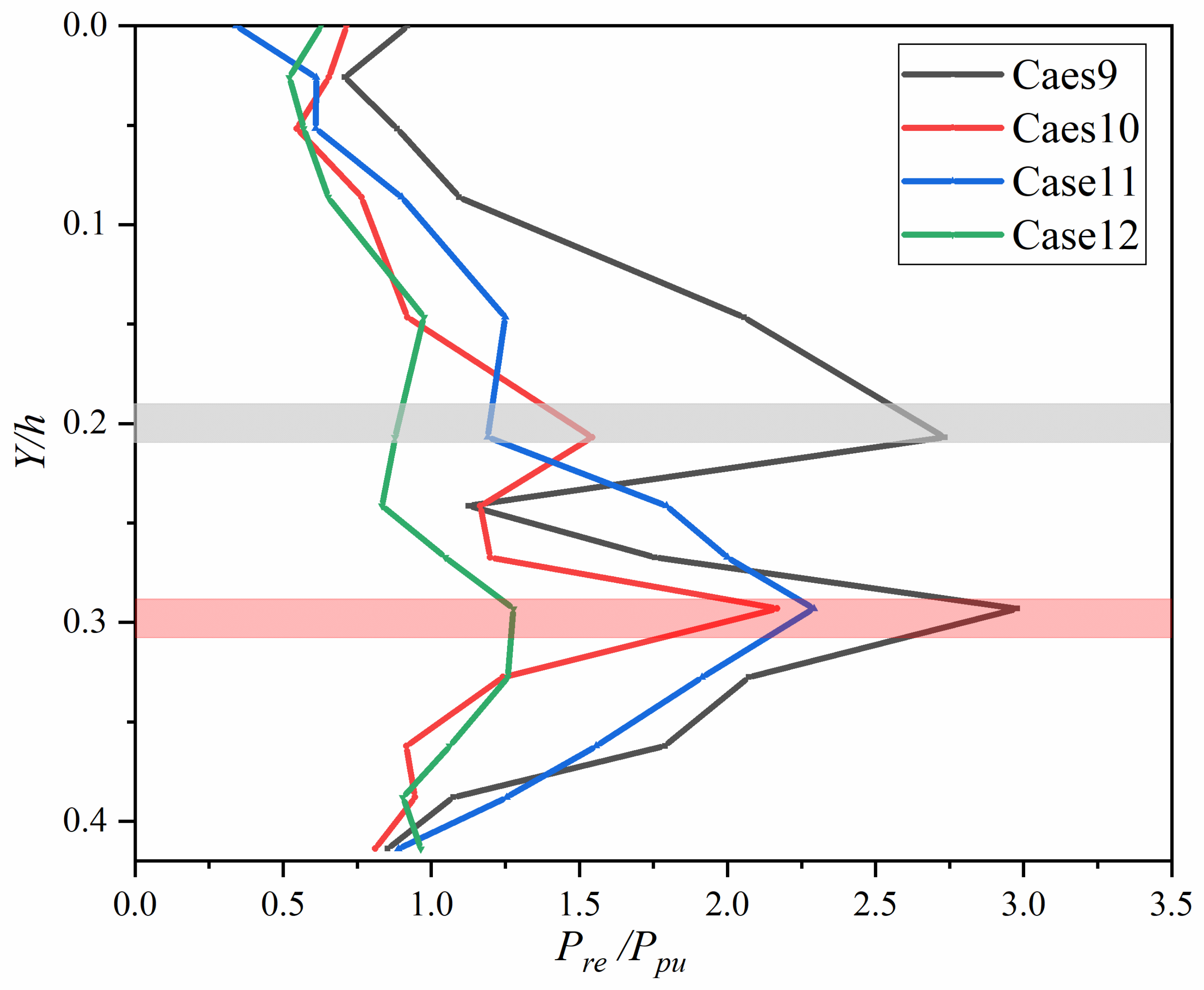
This study identified three different distribution patterns of along the water depth: no peaks, single peaks, and multiple peaks. However, due to limitations in experimental conditions and equipment, it was not possible to collect more detailed distribution data. Nevertheless, all peak distributions under various water depth conditions can be categorized within these three distribution patterns. The study also mentioned that smaller landslide volumes may result in larger peaks. This is because smaller volumes generate smaller wave heights, leading to relatively smaller values. As a result, the peaks appear larger. In the future, further research will be conducted to comprehensively investigate the impact of landslide parameters on .
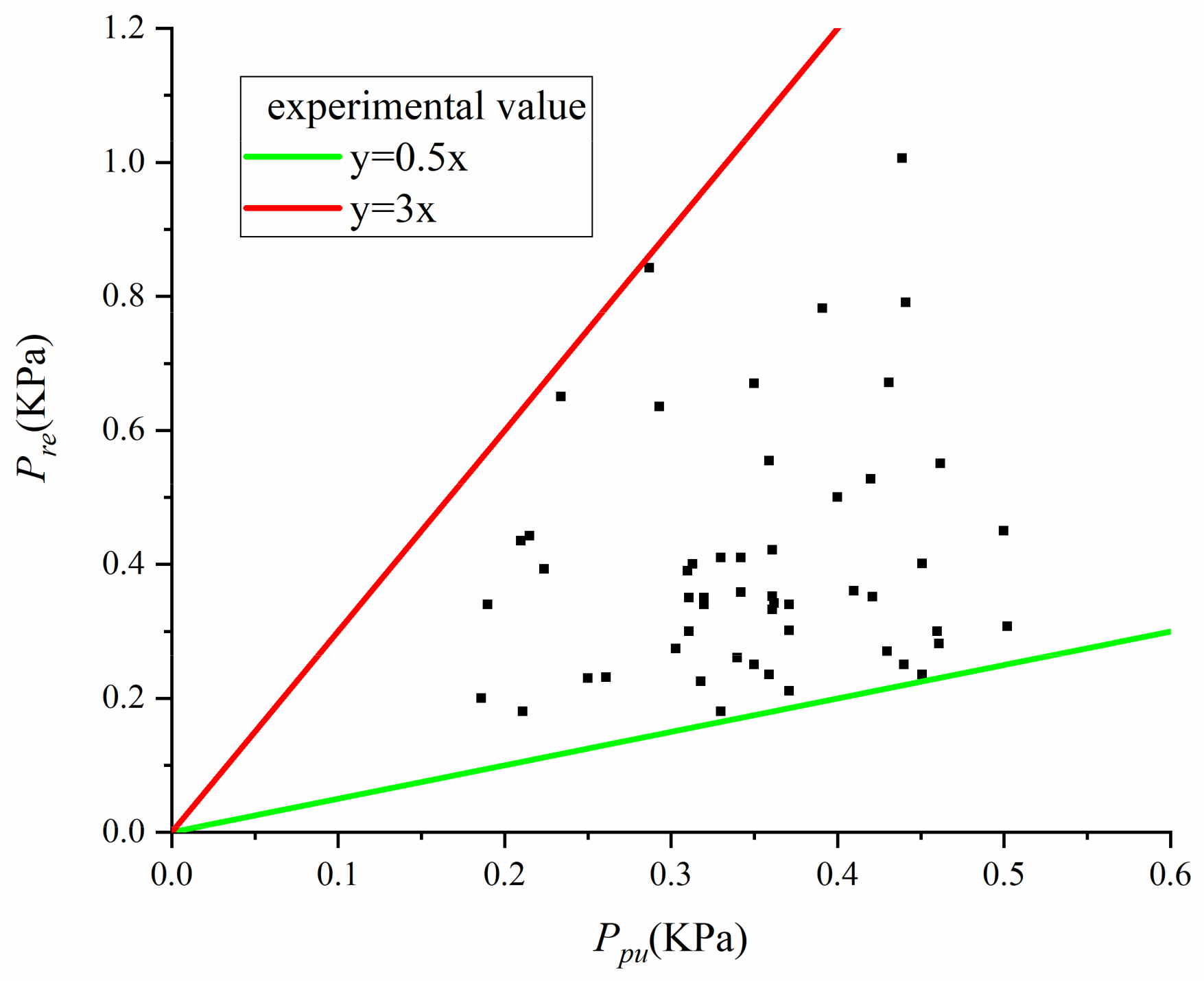
experienced by the bridge piers is a contributing factor to their damage, and it is possible that
may be more destructive than
. Therefore, this experiment examined the relationship between
and
and found that
. As discussed earlier, there is a positive correlation between
and
, as shown in
Figure 11.
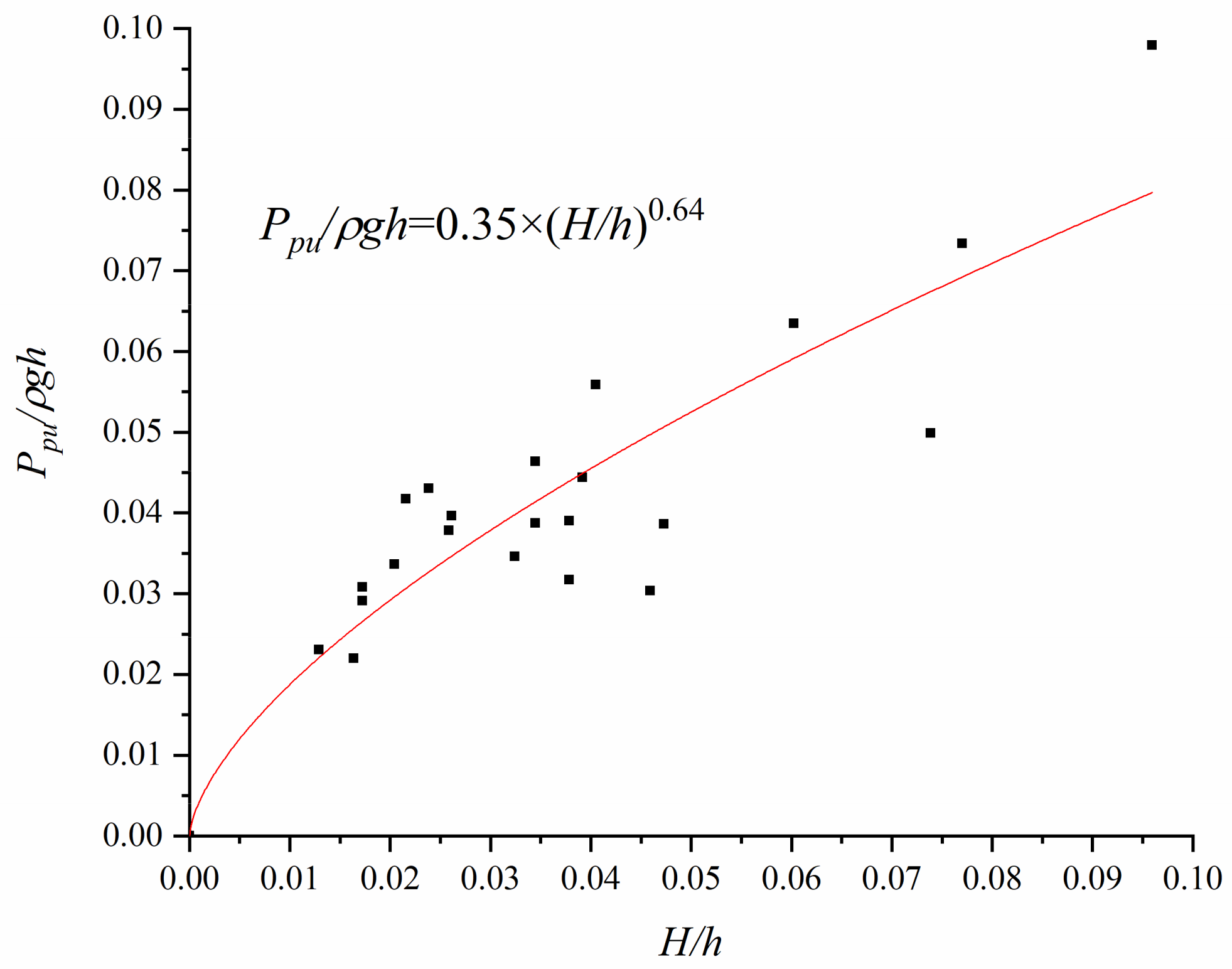
Figure 12 shows the relationship between
and
. An analysis and fitting resulted in Equation 1 with an
R2 value of 0.78. In scenarios of engineering concern, the most dangerous situations were examined, considering that
,
, leading to the formulation of Equation (4).
where
is the density of water,
is the acceleration of gravity,
is the maximum wave height in front of the pier, and
is the still water depth in the water tank.