Investigating Formation Factor–Hydraulic Conductivity Relations in Complex Geologic Environments: A Case Study in Taiwan
Abstract
:1. Introduction
2. Study Area and Data Sources
3. Methods
3.1. Data Processing and Classification
3.2. Theory of Formation Factor–Hydraulic Conductivity Relation for Clay-Free Formations
3.3. Data Clustering for Eliminating Data Containing Clay Content
- (a)
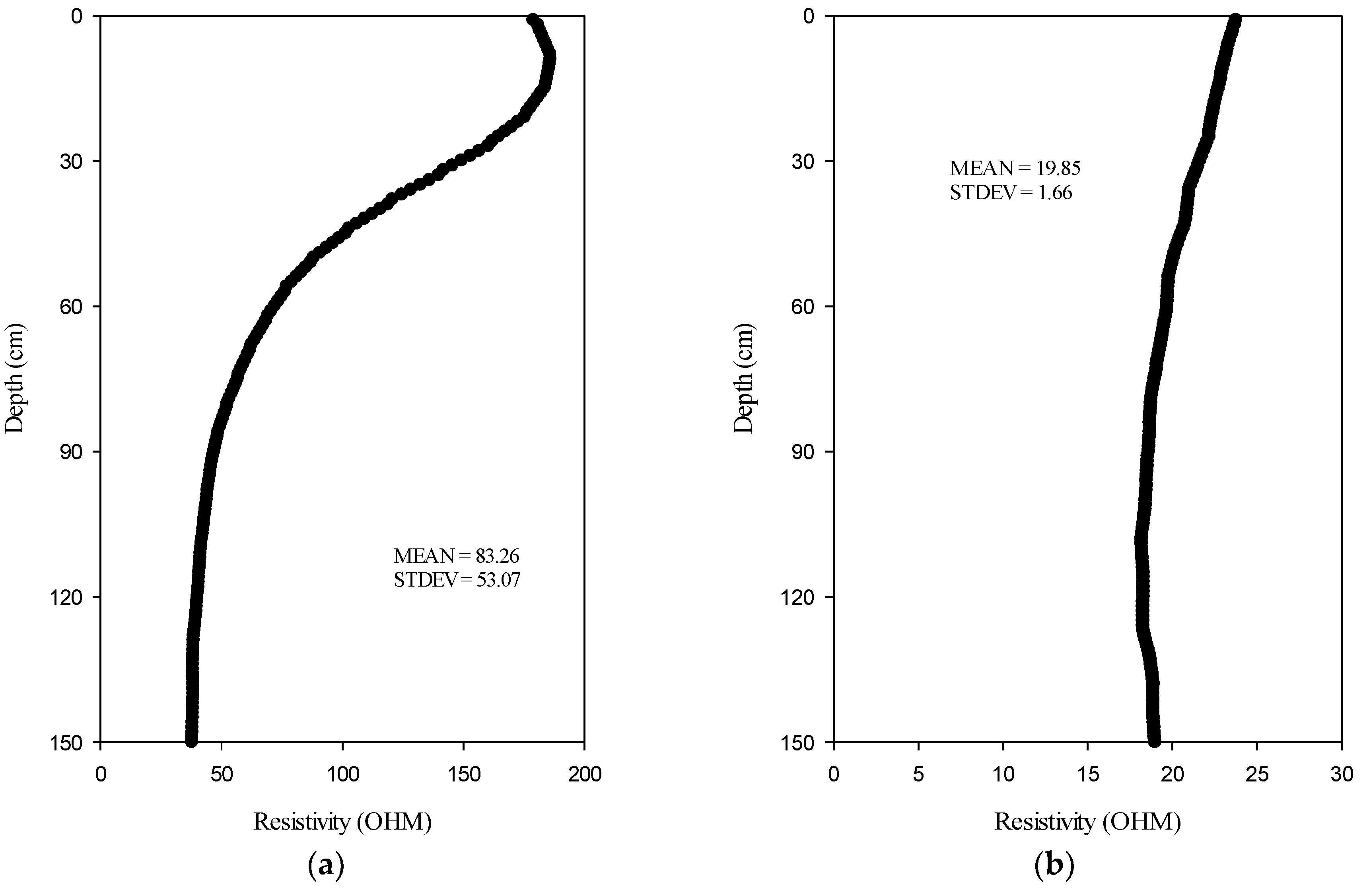
- Natural Gamma Ray Threshold
- (b)
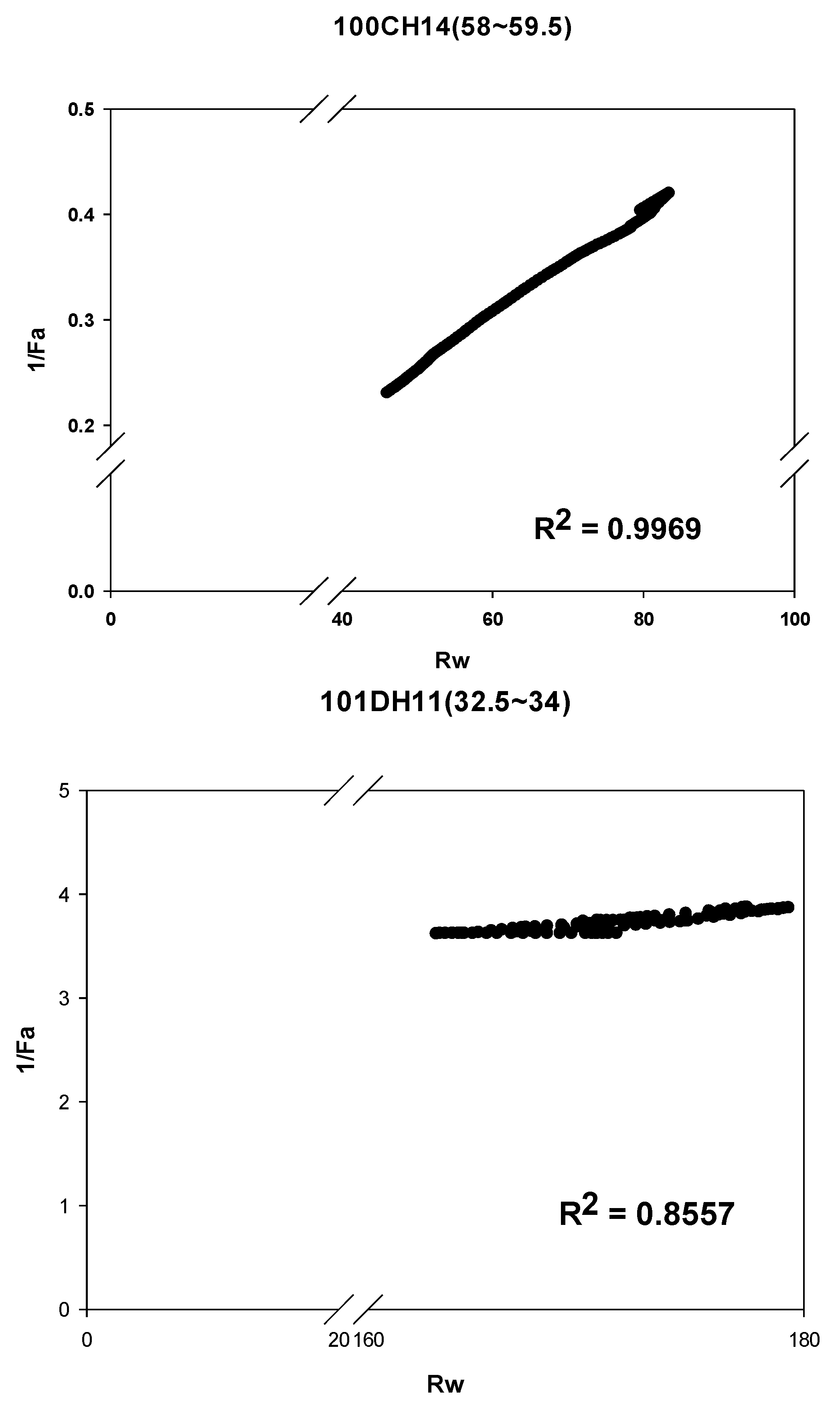
- Modified Archie’s law
4. Results and Discussion
4.1. Data Processing Result
4.2. Correlation Analysis for Various Well-logging Signals with Hydraulic Conductivity
4.3. Data Clustering Results
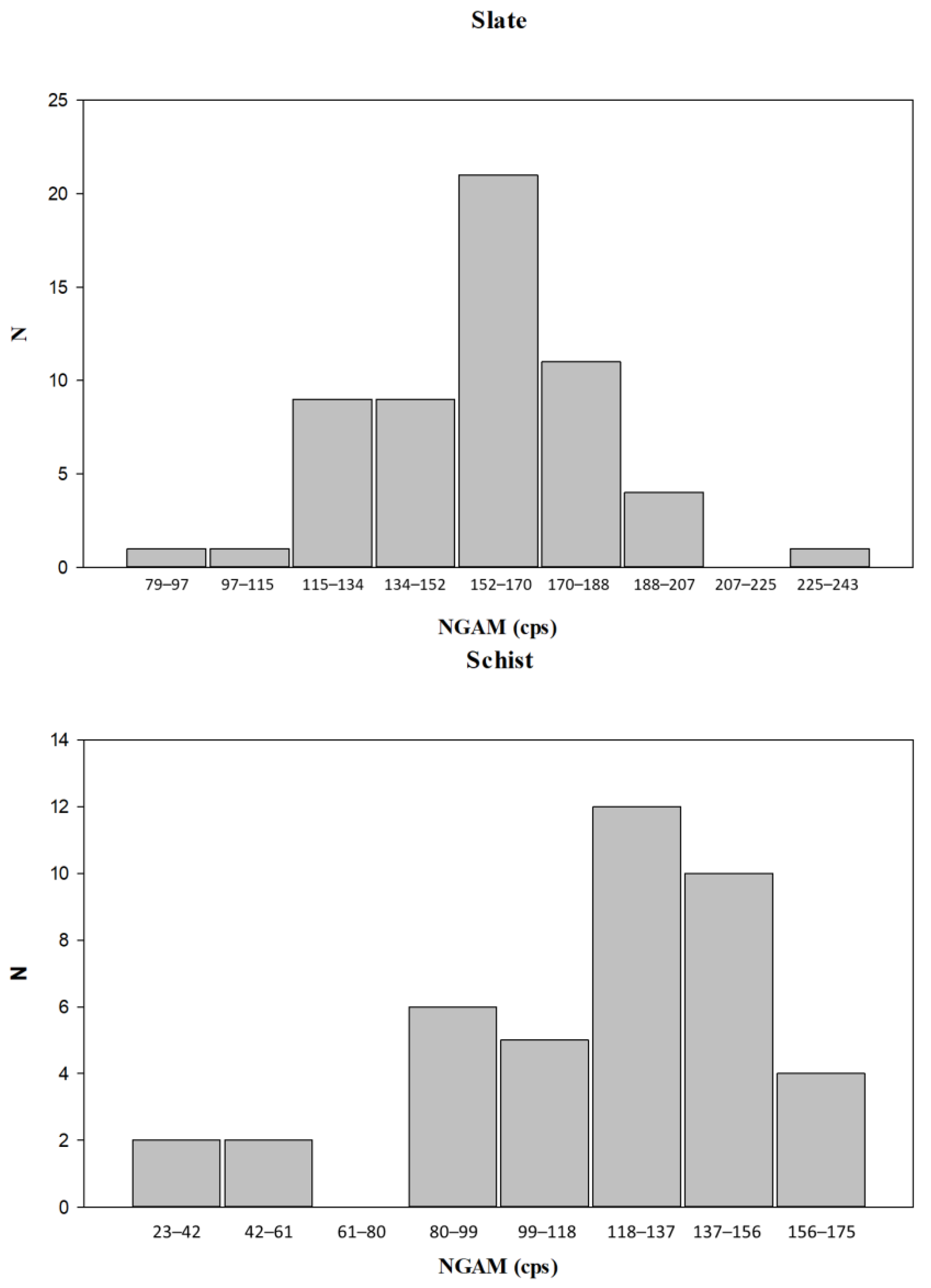
4.3.1. Outcomes from the Natural Gamma Threshold Method
4.3.2. Outcomes from the Modified Archie’s Law Method
4.4. Establishment of Hydraulic Conductivity Estimation Models
5. Conclusions
- 1.
- For results concerning data processing and classification, statistical analysis showed a high degree of geological heterogeneity in the study site has been found. While developing hydraulic conductivity estimation models, well-logging signals were suggested to be categorized by lithological types to establish effective relationships with hydraulic conductivity.
- 2.
- For results regarding correlation analysis for various single well-logging signals with hydraulic conductivity, the three types of resistivity (LON, SHN, and SPR) and fluid conductivity (COND) signals with hydraulic conductivity for most of the lithological cases had better correlation performance than SP and NGAM signals. This better performance confirmed that the resistivity and fluid conductivity parameters were required to be composed of the formation factor (F). Nevertheless, a single signal alone is insufficient for constructing a model to estimate hydraulic conductivity.
- 3.
- To improve electrical–hydraulic relationships in response to the effect of clay mineralogy, the natural gamma ray threshold clustering and modified Archie’s law clustering methods successfully play an important role in filtering clayed data. However, to satisfy Archie’s law’s theoretical requirements, many data entries for various rock types needed to be removed, indicating that Taiwan’s mountainous rock formations are complex and often contain significant clay content. Therefore, careful consideration of clay-related issues in formation layers is essential in practical engineering applications in mountainous regions.
- 4.
- With the assistance of two mud clustering techniques, this study has successfully established four permeability estimation models for three rock types (sandstone, schist, and slate). The R2 values are at least 0.6. However, the issue of limited data during model development is worth noting.
- 5.
- During the exploration of electrical well-logging data, it was found that the clay effect is present in most rock formations in Taiwan. To enhance the utilization of a mathematical model for estimating hydrogeological parameters of individual rock types using single resistivity signals, more data collection is required to ensure the reliability of the model. Furthermore, for hydrogeological parameter estimation models applicable to multiple rock types, it is recommended to consider recombining the collected signals. This approach could yield novel signal indicators, enabling the construction of new relationships between indicators and different hydrogeological parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.C.; Tsai, J.P.; Chang, L.C.; Chang, P.Y.; Lin, H. Estimating hydraulic conductivity fields in composite fan delta using vertical electrical sounding. Water 2018, 10, 1620. [Google Scholar] [CrossRef]
- Dou, Z.; Zhou, Z.; Tan, Y.; Zhou, Y. Numerical study of the influence of cavity on immiscible liquid transport in varied-wettability fractures. J. Chem. 2015, 2015, 961256. [Google Scholar] [CrossRef]
- Hsu, S.M.; Hsu, J.P.; Ke, C.C.; Lin, Y.T.; Huang, C.-C. Rock mass permeability classification schemes to facilitate groundwater availability assessment in mountainous areas: A case study in Jhuoshuei river basin of Taiwan. Geosci. J. 2019, 24, 209–224. [Google Scholar] [CrossRef]
- Zhan, S.S.; Wang, T.T.; Huang, T.H. Variations of hydraulic conductivity of fracture sets and fractured rock mass with test scale: Case study at Heshe well site in Central Taiwan. Eng. Geol. 2016, 206, 94–106. [Google Scholar] [CrossRef]
- Kaleris, V.K.; Ziogas, A.I. Using electrical resistivity logs and short duration pumping tests to estimate hydraulic conductivity profiles. J. Hydrol. 2020, 590, 125277. [Google Scholar] [CrossRef]
- Hsu, S.M. Quantifying hydraulic properties of fractured rock masses along a borehole using composite geological indices: A case study in the mid- and upper-Choshuei river basin in central Taiwan. Eng. Geol 2020, 284, 105924. [Google Scholar] [CrossRef]
- Sousa, R.L.; Einstein, H.H. Lessons from accidents during tunnel construction. Tunn. Undergr. Space Technol. 2021, 113, 103916. [Google Scholar] [CrossRef]
- Sara, M.N. Site Assessment and Remediation Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003; Volume 45, pp. 144–145. [Google Scholar]
- Kaleris, V.; Hadjitheodorou, C.; Demetracopoulos, A.C. Numerical simulation of field methods for estimating hydraulic conductivity and concentration profiles. J. Hydrol. 1995, 171, 319–353. [Google Scholar] [CrossRef]
- Lo, H.C.; Chen, P.J.; Chou, P.Y.; Hsu, S.M. The combined use of heat-pulse flowmeter logging and packer testing for transmissive fracture recognition. J. Appl. Geophys. 2014, 105, 248–258. [Google Scholar] [CrossRef]
- Molz, F.J.; Morin, R.H.; Hess, A.E.; Melville, J.G.; Güven, O. The impeller meter for measuring aquifer permeability variations: Evaluation and comparison with other tests. Water Resour. Res. 1989, 25, 1677–1683. [Google Scholar] [CrossRef]
- Asfahani, J. Porosity and hydraulic conductivity estimation of the basaltic aquifer in Southern Syria by using nuclear and electrical well logging techniques. Acta Geophys. 2017, 65, 765–775. [Google Scholar] [CrossRef]
- Kaleris, V.K.; Ziogas, A.I. Estimating hydraulic conductivity profiles using borehole resistivity logs. Procedia Environ. Sci. 2015, 25, 135–141. [Google Scholar] [CrossRef]
- Keller, C.E.; Cherry, J.A.; Parker, B.L. New method for continuous transmissivity profiling in fractured rock. Groundwater 2014, 52, 352–367. [Google Scholar] [CrossRef]
- Ren, S.; Parsekian, A.D.; Zhang, Y.; Carr, B.J. Hydraulic conductivity calibration of logging NMR in a granite aquifer, Laramie Range, Wyoming. Groundwater 2019, 57, 303–319. [Google Scholar] [CrossRef]
- Jones, P.H.; Buford, T.B. Electric logging applied to ground-water exploration. Geophysics 1951, 16, 115–139. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Huntley, D. Relations between permeability and electrical resistivity in granular aquifers. Groundwater 1986, 24, 466–474. [Google Scholar] [CrossRef]
- Worthington, P.F. Influence of matrix conduction upon hydrogeophysical relationships in arenaceous aquifers. Water Resour. Res. 1977, 13, 87–92. [Google Scholar] [CrossRef]
- Slater, L.; Lesmes, D.P. Electrical-hydraulic relationships observed for unconsolidated sediments. Water Resour. Res. 2002, 38, 31-1–31-13. [Google Scholar] [CrossRef]
- Winsauer, W.O.; Shearin Jr, H.M.; Masson, P.Y.; Williams, M. Resistivity of brine-saturated sands in relation to pore geometry. AAPG Bull. 1952, 36, 253–277. [Google Scholar]
- Khalil, M.A.; Ramalho, E.C.; Monteiro Santos, F.A. Using resistivity logs to estimate hydraulic conductivity of a Nubian sandstone aquifer in southern Egypt. Near Surf. Geophys. 2011, 9, 349–356. [Google Scholar] [CrossRef]
- Shen, B.; Wu, D.; Wang, Z. A new method for permeability estimation from conventional well logs in glutenite reservoirs. J. Geophys. Eng. 2017, 14, 1268–1274. [Google Scholar] [CrossRef]
- Waxman, M.H.; Smits, L.J.M. Electrical conductivities in oil-bearing shaly sands. Soc. Pet. Eng. J. 1968, 8, 107–122. [Google Scholar] [CrossRef]
- Central Geological Survey of Taiwan. Ground-Water Resources Investigation P\Program for Mountainous Region of Central Taiwan (1/4); Ministry of Economic Affairs: Taipei, Taiwan, 2010. [Google Scholar]
- Worthington, P.F. The uses and abuses of the Archie equations, 1: The formation factor-porosity relationship. J. Appl. Geophys. 1993, 30, 215–228. [Google Scholar] [CrossRef]
- Glover, P.W. Archie’s law–a reappraisal. Solid Earth 2016, 7, 1157–1169. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Chapuis, R.P.; Aubertin, M. On the use of the Kozeny Carman equation to predict the hydraulic conductivity of soils. Can. Geotech. J. 2003, 40, 616–628. [Google Scholar] [CrossRef]
- Khalil, M.A.; Santos, F.A.M. Hydraulic conductivity estimation from resistivity logs: A case study in Nubian sandstone aquifer. Arab. J. Geosci. 2013, 6, 205–212. [Google Scholar] [CrossRef]
- Rahman, A. A GIS based DRASTIC model for assessing groundwater vulnerability in shallow aquifer in Aligarh, India. Appl. Geogr. 2008, 28, 32–53. [Google Scholar] [CrossRef]
- Vinegar, H.J.; Waxman, M.H. Induced polarization of shaly sands. Geophysics 1984, 49, 1267–1387. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Routledge: Abingdon, UK, 2013. [Google Scholar]





| Main Lithology | Sub-Lithology | Amount |
|---|---|---|
| Sedimentary rock | Sandstone | 93 |
| Shale | 31 | |
| Sandy Shale | 3 | |
| Sandstone interbedded with Argillite | 2 | |
| Mudstone | 8 | |
| Siltstone | 14 | |
| Silty Sandstone | 20 | |
| Alternations of Sandstone and Shale | 44 | |
| Argillaceous Siltstone | 5 | |
| Quartz Sandstone | 6 | |
| Igneous rock | Andesite | 7 |
| Metamorphic rock | Volcanic Agglomerate | 6 |
| Phyllite | 6 | |
| Slate | 61 | |
| Schist | 41 | |
| Marble | 6 | |
| Gneiss | 5 | |
| Argillite | 18 | |
| Metasandstone | 3 | |
| Argillite interbedded with some Sandstone | 10 | |
| Quartzite | 7 | |
| Total | 396 |
| Signal Type | SP (V) | NGAM (cps) | COND (ohm.m) | |||||
| Category | N | μ | S.D. | μ | S.D. | μ | S.D. | |
| All lithologic types | 388 | 141.81 | 155.80 | 121.02 | 38.61 | 598.91 | 704.94 | |
| Sedimentary Rock | 230 | 127.49 | 129.31 | 114.77 | 30.93 | 634.64 | 608.68 | |
| Sandstone | 90 | 97.59 | 147.39 | 105.02 | 31.42 | 238.39 | 479.28 | |
| Shale | 30 | 147.15 | 97.09 | 129.37 | 20.23 | 810.53 | 393.21 | |
| Sandy Shale | 3 | 112.41 | 2.73 | 135.09 | 5.46 | 357.70 | 10.84 | |
| Sandstone interbedded with Argillite | 10 | 182.97 | 88.13 | 150.42 | 13.17 | 475.71 | 433.32 | |
| Mudstone | 8 | 153.16 | 12.01 | 75.20 | 43.42 | 660.81 | 177.84 | |
| Siltstone | 14 | 127.85 | 81.40 | 125.69 | 14.60 | 1430.85 | 1018.14 | |
| Silty Sandstone | 20 | 179.10 | 168.03 | 102.14 | 22.45 | 324.68 | 129.65 | |
| Alternations of Sandstone and Shale | 44 | 135.32 | 104.48 | 124.28 | 27.52 | 468.51 | 374.78 | |
| Argillaceous Siltstone | 5 | 61.72 | 6.04 | 106.40 | 7.05 | 476.60 | 10.33 | |
| Quartz Sandstone | 6 | 182.97 | 216.57 | 123.38 | 41.24 | 2100.29 | 1459.38 | |
| Igneous Rock | 13 | 238.67 | 168.08 | 43.35 | 26.55 | 359.45 | 96.49 | |
| Andesite | 7 | 124.80 | 66.79 | 59.53 | 7.32 | 329.46 | 63.19 | |
| Vocanic Agglomerate | 6 | 371.52 | 152.05 | 24.48 | 28.88 | 394.43 | 121.77 | |
| Metamorphic Rock | 145 | 155.86 | 186.87 | 137.85 | 39.11 | 563.72 | 859.02 | |
| Phyllite | 6 | 458.57 | 17.38 | 155.20 | 4.95 | 861.69 | 55.67 | |
| Slate | 57 | 133.41 | 165.13 | 157.13 | 26.16 | 782.87 | 1213.49 | |
| Schist | 41 | 155.60 | 202.61 | 119.14 | 35.60 | 375.59 | 120.84 | |
| Marble | 6 | 130.69 | 15.25 | 46.27 | 15.65 | 244.82 | 46.86 | |
| Gneiss | 5 | −55.84 | 22.01 | 143.68 | 5.69 | 269.90 | 142.64 | |
| Argillite | 18 | 203.31 | 169.42 | 157.10 | 23.74 | 277.10 | 225.91 | |
| Metasandstone | 3 | 463.68 | 4.05 | 136.56 | 34.48 | 131.96 | 12.33 | |
| Argillite interbedded with some Sandstone | 2 | 49.03 | 70.90 | 153.44 | 18.23 | 168.15 | 2.17 | |
| Quartzite | 7 | 30.03 | 127.06 | 96.60 | 42.01 | 1186.50 | 1339.26 | |
| Signal | SHN (ohm.m) | LON (ohm.m) | SPR (ohm.m) | |||||
| Category | N | μ | S.D. | μ | S.D. | Μ | S.D. | |
| All lithologic types | 388 | 288.70 | 596.58 | 243.23 | 446.49 | 182.30 | 260.95 | |
| Sedimentary Rock | 230 | 124.45 | 254.45 | 123.47 | 214.02 | 106.12 | 140.89 | |
| Sandstone | 90 | 207.92 | 366.58 | 176.30 | 289.81 | 161.32 | 193.35 | |
| Shale | 30 | 35.69 | 33.42 | 56.02 | 48.89 | 40.64 | 28.14 | |
| Sandy Shale | 3 | 30.40 | 7.35 | 38.85 | 6.28 | 58.89 | 7.84 | |
| Sandstone interbedded with Argillite | 10 | 277.11 | 228.22 | 330.14 | 247.94 | 176.69 | 100.96 | |
| Mudstone | 8 | 14.27 | 4.93 | 17.66 | 2.94 | 28.19 | 11.50 | |
| Siltstone | 14 | 27.87 | 11.44 | 47.34 | 27.40 | 31.32 | 13.51 | |
| Silty Sandstone | 20 | 60.82 | 82.72 | 104.34 | 148.53 | 73.49 | 58.88 | |
| Alternations of Sandstone and Shale | 44 | 63.51 | 79.04 | 87.46 | 135.64 | 82.45 | 69.08 | |
| Argillaceous Siltstone | 5 | 9.54 | 1.15 | 12.09 | 1.21 | 21.00 | 1.22 | |
| Quartz Sandstone | 6 | 225.83 | 222.09 | 105.54 | 85.37 | 148.34 | 173.97 | |
| Igneous Rock | 13 | 375.77 | 590.63 | 254.86 | 373.40 | 217.36 | 209.74 | |
| Andesite | 7 | 618.32 | 739.84 | 399.87 | 474.51 | 330.52 | 232.63 | |
| Volcanic Agglomerate | 6 | 92.78 | 43.96 | 85.68 | 25.45 | 85.35 | 42.46 | |
| Metamorphic Rock | 145 | 541.43 | 846.39 | 433.46 | 627.32 | 300.01 | 352.76 | |
| Phyllite | 6 | 523.33 | 120.23 | 513.80 | 79.44 | 190.98 | 42.20 | |
| Slate | 57 | 314.15 | 250.56 | 290.28 | 261.60 | 188.74 | 93.86 | |
| Schist | 41 | 379.55 | 417.83 | 289.07 | 305.18 | 238.53 | 139.27 | |
| Marble | 6 | 3973.34 | 1417.58 | 2864.96 | 1171.03 | 1606.99 | 850.91 | |
| Gneiss | 5 | 1329.79 | 327.79 | 1031.72 | 195.14 | 737.45 | 118.70 | |
| Argillite | 18 | 315.24 | 316.01 | 226.36 | 171.24 | 291.30 | 186.95 | |
| Metasandstone | 3 | 373.64 | 134.02 | 384.41 | 125.77 | 312.53 | 39.43 | |
| Argillite interbedded with Sandstone | 2 | 211.48 | 141.82 | 216.72 | 81.60 | 205.53 | 75.00 | |
| Quartzite | 7 | 598.84 | 467.85 | 491.71 | 393.95 | 270.94 | 181.78 | |
| Signal Type | All Lithologic Type | Sedimentary Rock | Igneous Rock | Metamorphic Rock | Sandstone | Slate | Schist |
|---|---|---|---|---|---|---|---|
| Sample quantity | 391 | 230 | 13 | 148 | 90 | 60 | 41 |
| SP | - | - | −0.613 | - | - | - | - |
| SHN | 0.343 | 0.575 | 0.732 | - | 0.442 | - | - |
| LON | −0.277 | 0.480 | - | - | 0.397 | - | - |
| SPR | −0.378 | 0.549 | 0.765 | 0.245 | 0.490 | - | - |
| NGAM | - | - | - | - | - | - | - |
| COND | −0.308 | −0.281 | - | −0.355 | −0.338 | - | 0.345 |
| F-Sandstone | ||||||||
|---|---|---|---|---|---|---|---|---|
| K | Data Sets | All Data | [30–187] | [30–167] | [30–148] | [30–128] | [30–109] | [30–89] |
| r | 0.180 | 0.180 | 0.213 | 0.217 | 0.254 | 0.377 | 0.554 | |
| Sig. | 0.089 | 0.094 | 0.049 | 0.050 | 0.030 | 0.006 | 0.002 | |
| N | 90 | 88 | 86 | 82 | 73 | 52 | 28 | |
| F-Slate | ||||||||
|---|---|---|---|---|---|---|---|---|
| K | Data Sets | All Data | [94–210] | [94–193] | [94–177] | [94–160] | [94–144] | [94–127] |
| r | −0.125 | −0.089 | −0.101 | −0.161 | −0.283 | −0.321 | −0.455 | |
| Sig. | 0.392 | 0.546 | 0.501 | 0.327 | 0.161 | 0.285 | 0.365 | |
| N | 49 | 48 | 47 | 39 | 26 | 13 | 6 | |
| F-Schist | |||||
|---|---|---|---|---|---|
| K | Data Sets | All Data | [23–156] | [23–137] | [23–118] |
| r | −0.102 | −0.102 | −0.461 | −0.643 | |
| Sig. | 0.526 | 0.550 | 0.015 | 0.01 | |
| N | 41 | 37 | 27 | 15 | |
| Rock Types | Sandstone | Slate | Schist | |||
|---|---|---|---|---|---|---|
| Fa/Fc | r | No. of samples | r | No. of samples | r | No. of samples |
| 0–1 | −0.1 | 41 | 0.168 | 32 | −0.085 | 16 |
| 0.2–1 | 0.003 | 21 | −0.115 | 22 | −0.297 | 10 |
| 0.4–1 | 0.245 | 12 | −0.291 | 13 | 0.353 | 6 |
| 0.6–1 | 0.406 | 10 | −0.066 | 8 | 0.936 | 3 |
| 0.8–1 | −0.800 | 4 | 3 | N.A. | 1 | |
| 0.9–1 | −1.000 | 3 | N.A. | 2 | N.A. | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, S.-M.; Liu, G.-Y.; Dong, M.-C.; Liao, Y.-F.; Li, J.-S. Investigating Formation Factor–Hydraulic Conductivity Relations in Complex Geologic Environments: A Case Study in Taiwan. Water 2023, 15, 3621. https://doi.org/10.3390/w15203621
Hsu S-M, Liu G-Y, Dong M-C, Liao Y-F, Li J-S. Investigating Formation Factor–Hydraulic Conductivity Relations in Complex Geologic Environments: A Case Study in Taiwan. Water. 2023; 15(20):3621. https://doi.org/10.3390/w15203621
Chicago/Turabian StyleHsu, Shih-Meng, Guan-Yu Liu, Ming-Chia Dong, Yi-Fan Liao, and Jia-Sheng Li. 2023. "Investigating Formation Factor–Hydraulic Conductivity Relations in Complex Geologic Environments: A Case Study in Taiwan" Water 15, no. 20: 3621. https://doi.org/10.3390/w15203621
APA StyleHsu, S.-M., Liu, G.-Y., Dong, M.-C., Liao, Y.-F., & Li, J.-S. (2023). Investigating Formation Factor–Hydraulic Conductivity Relations in Complex Geologic Environments: A Case Study in Taiwan. Water, 15(20), 3621. https://doi.org/10.3390/w15203621






