Effect of Using a Passive Rotor on the Accuracy of Flow Measurements in Sewer Pipes Using a Slug Tracer-Dilution Method
Abstract
:1. Introduction
2. Material and Method
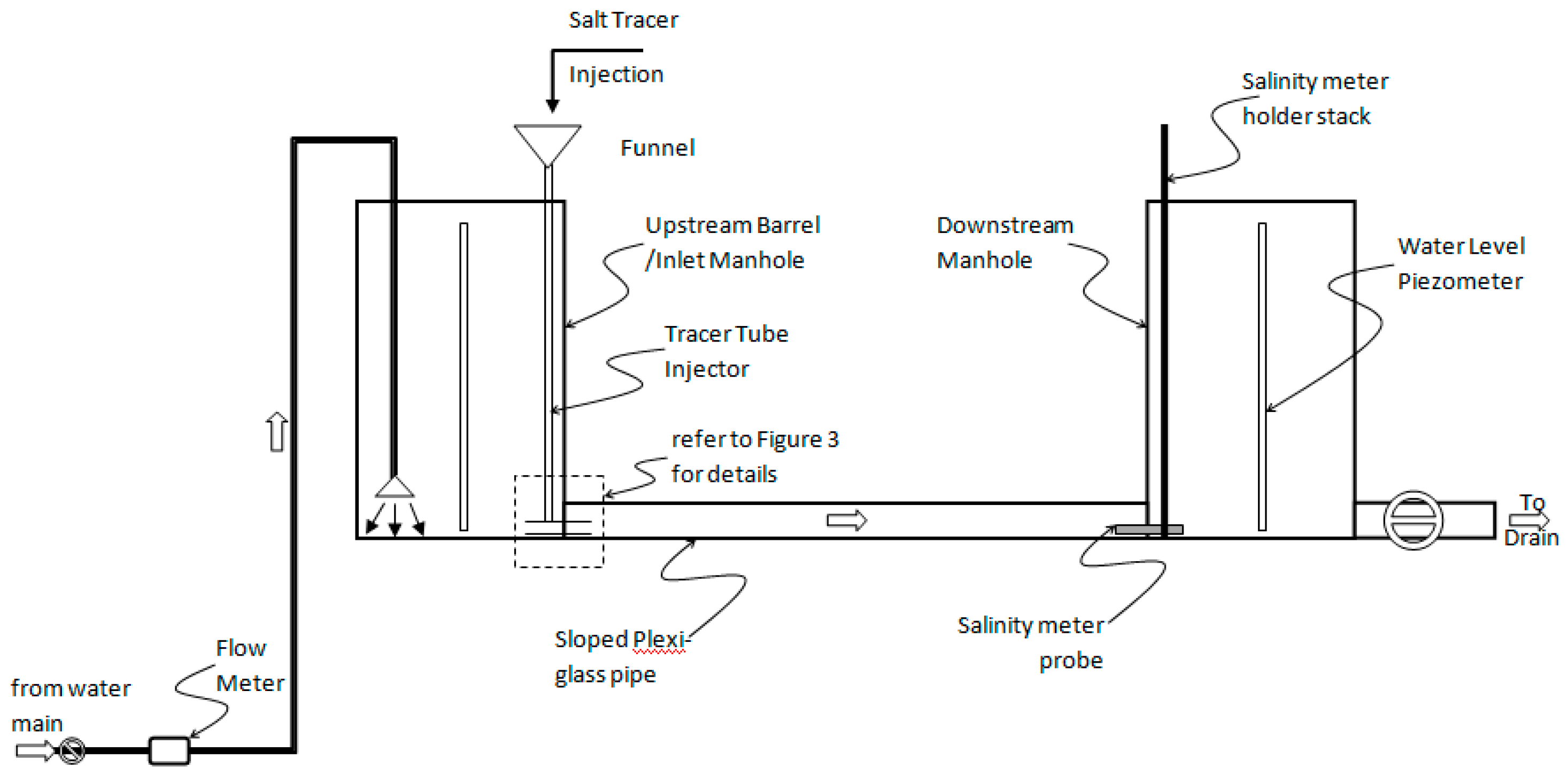
2.1. Experimental Setup
2.2. Tools and Equipment
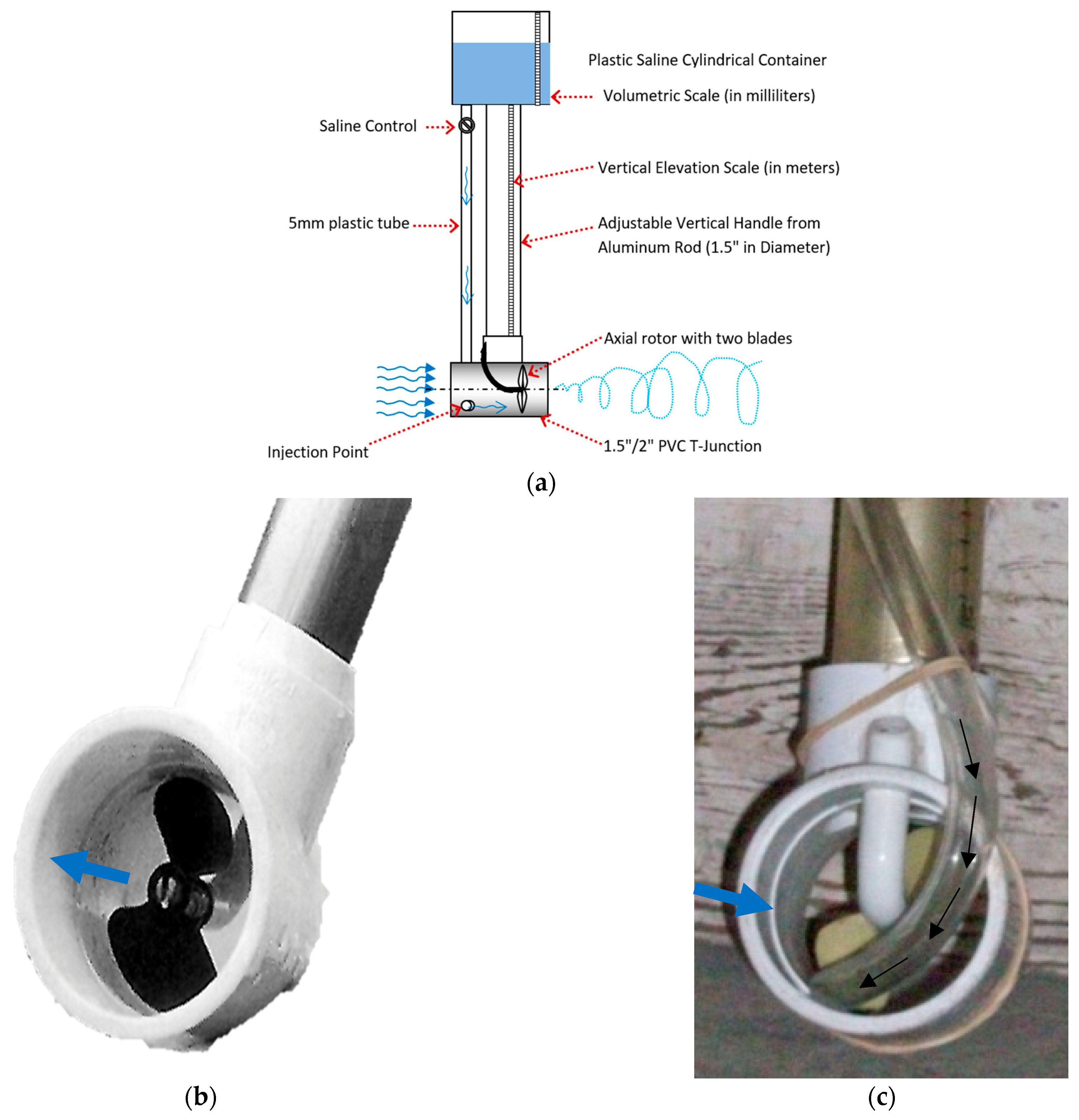
2.2.1. Salinity Injector Stick
2.2.2. Passive Fan
2.2.3. Salinity Meter
2.3. Assumptions and Simplifications
- Water flow in the sewer pipe is steady and free from debris and sludges;
- Tracers are conserved, stable, and do not react with other substances in the environment;
- The injection rate of tracer (q) was constant and very small compared to water sewer flow, this means that q/Q << 1.
2.4. Experimental Runs
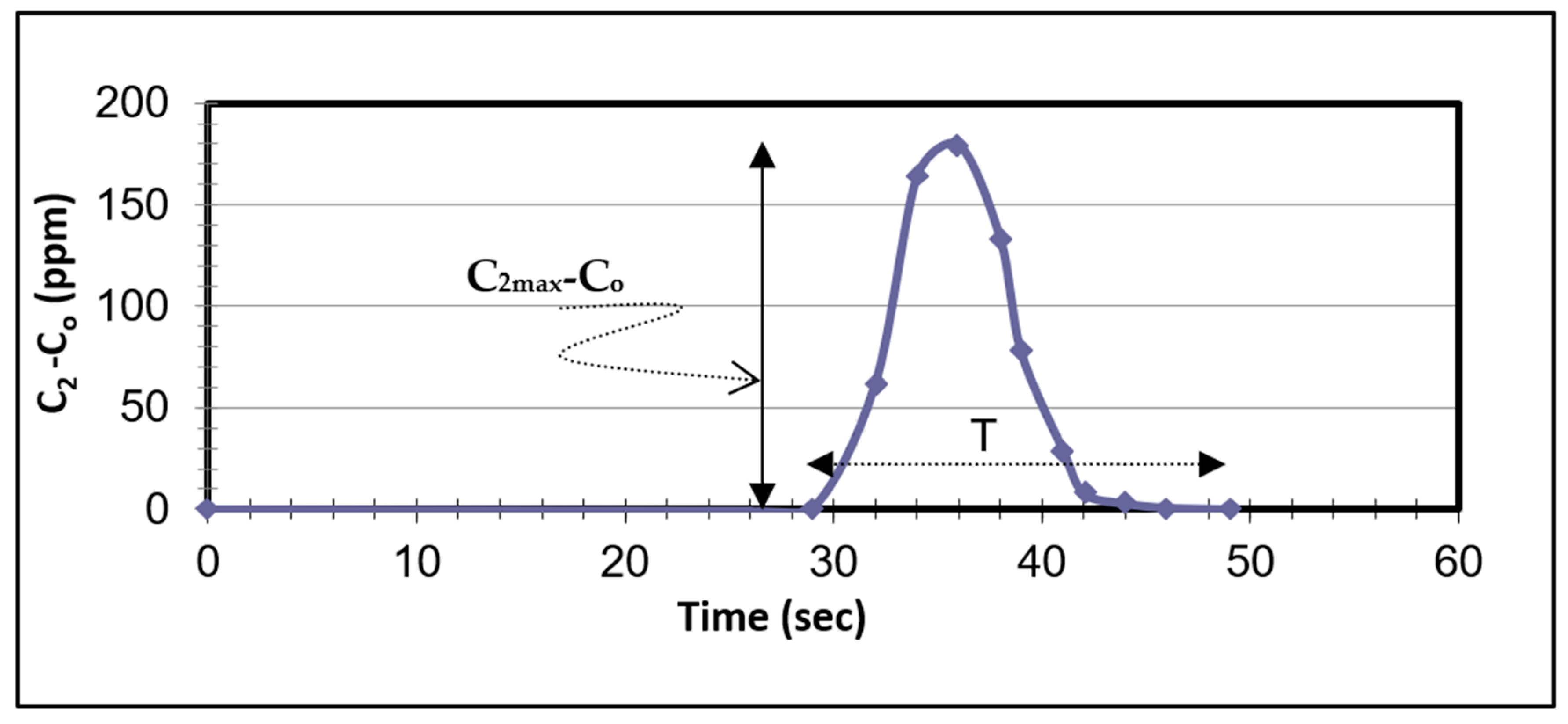
2.5. Governing Equations
3. Results and Analysis
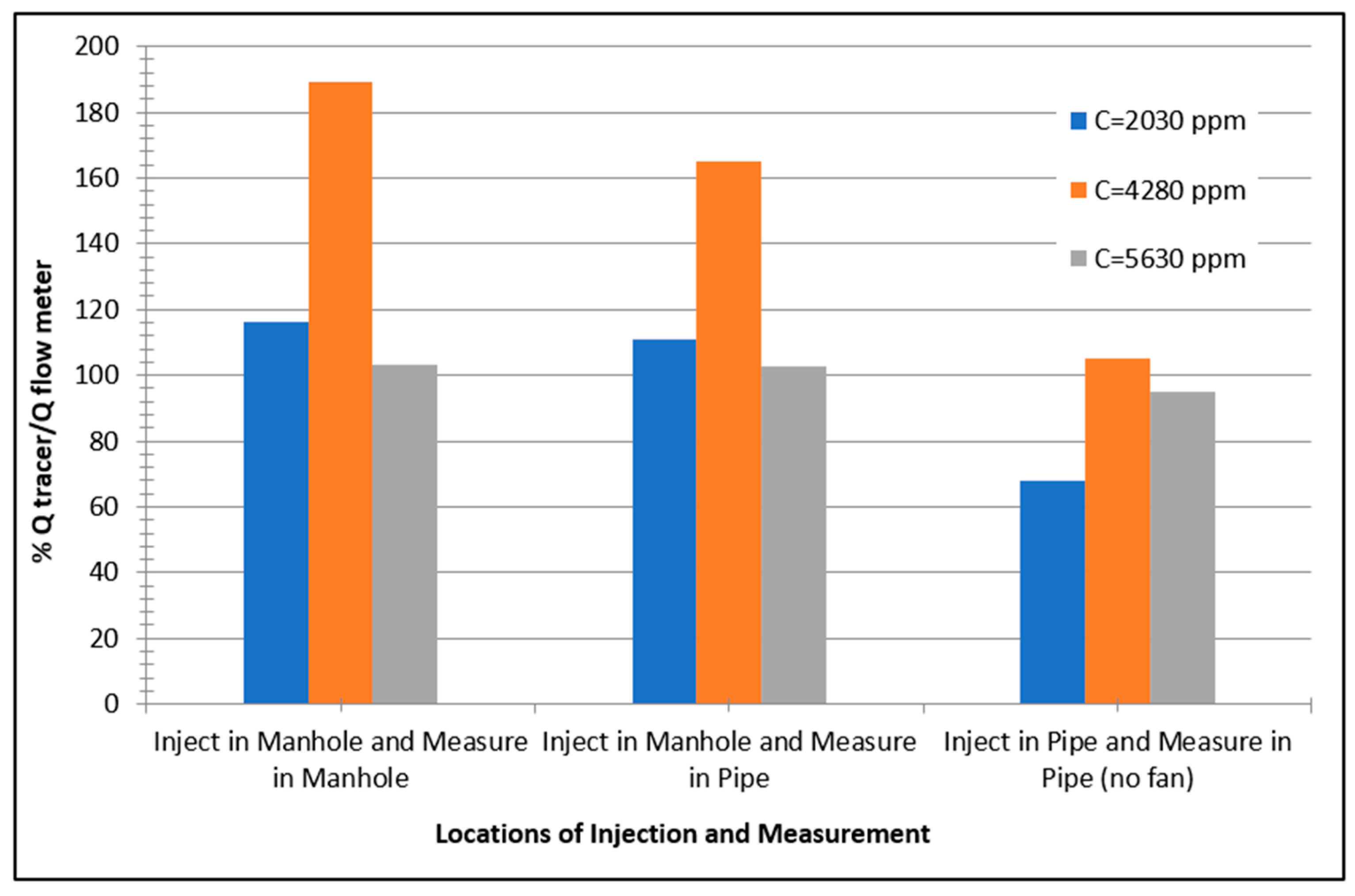
3.1. Effect of Locations of Injection and Measurement Points
- –
- Case 1: The saline injection point is inside the upstream manhole and the measuring concentration point is conducted inside the downstream manhole;
- –
- Case 2: The saline injection point is inside the upstream manhole and the measuring concentration point is conducted at the downstream end of the pipe;
- –
- Case 3: The saline injection point is at the upstream end of the pipe and the measuring concentration point is at the downstream end of the pipe.
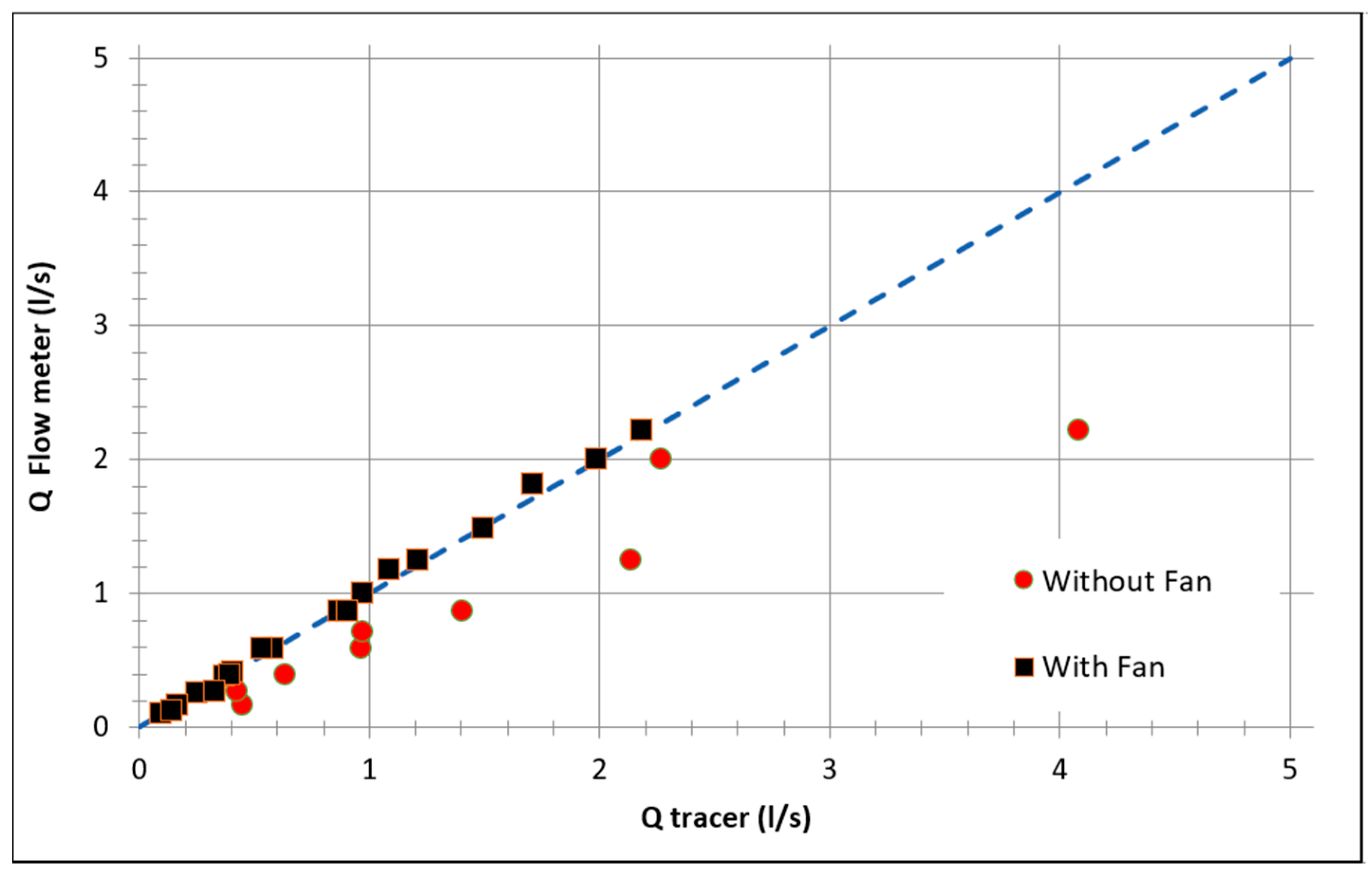
3.2. Effect of Using Passive Fan Module
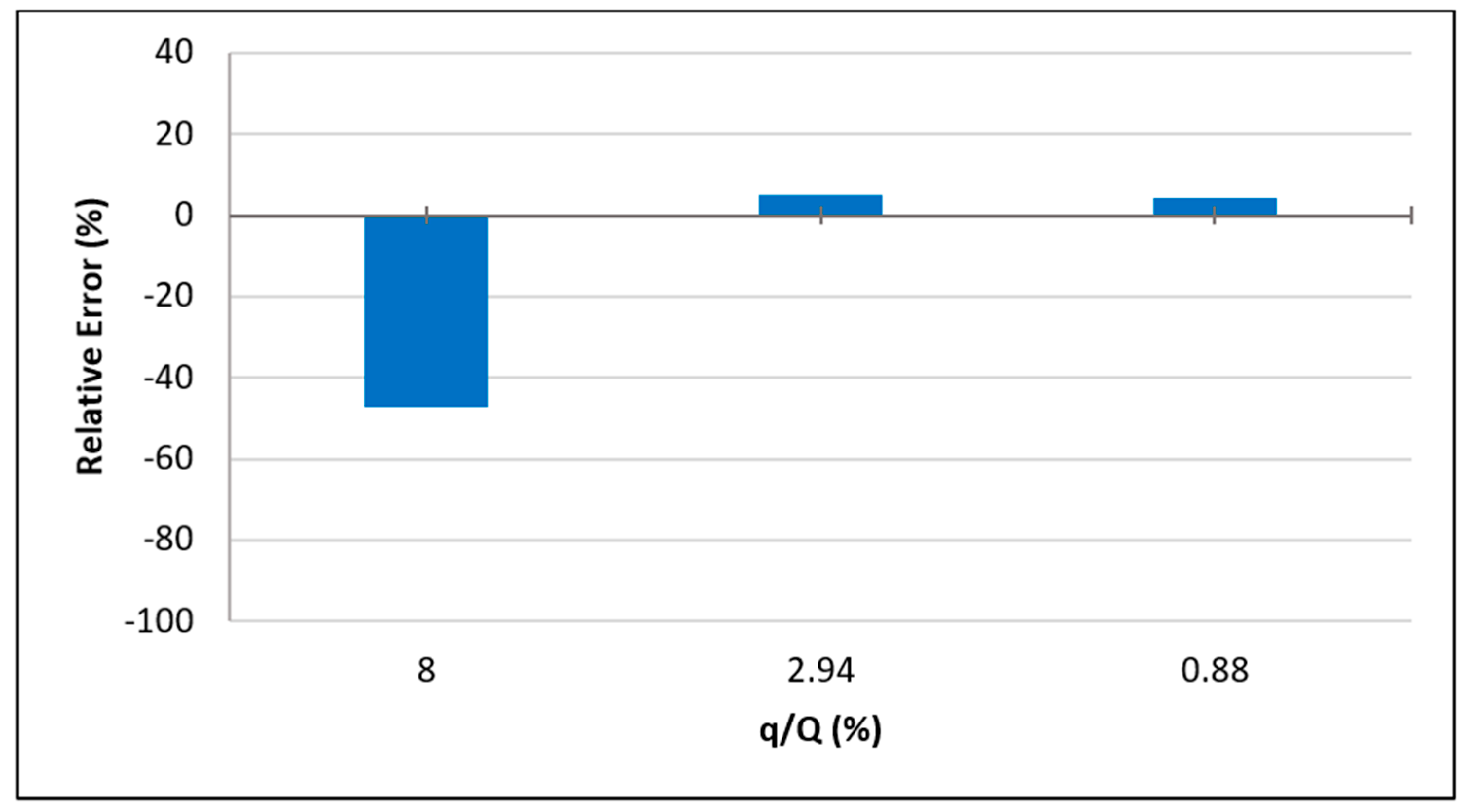
3.3. Effect of Injection Rate
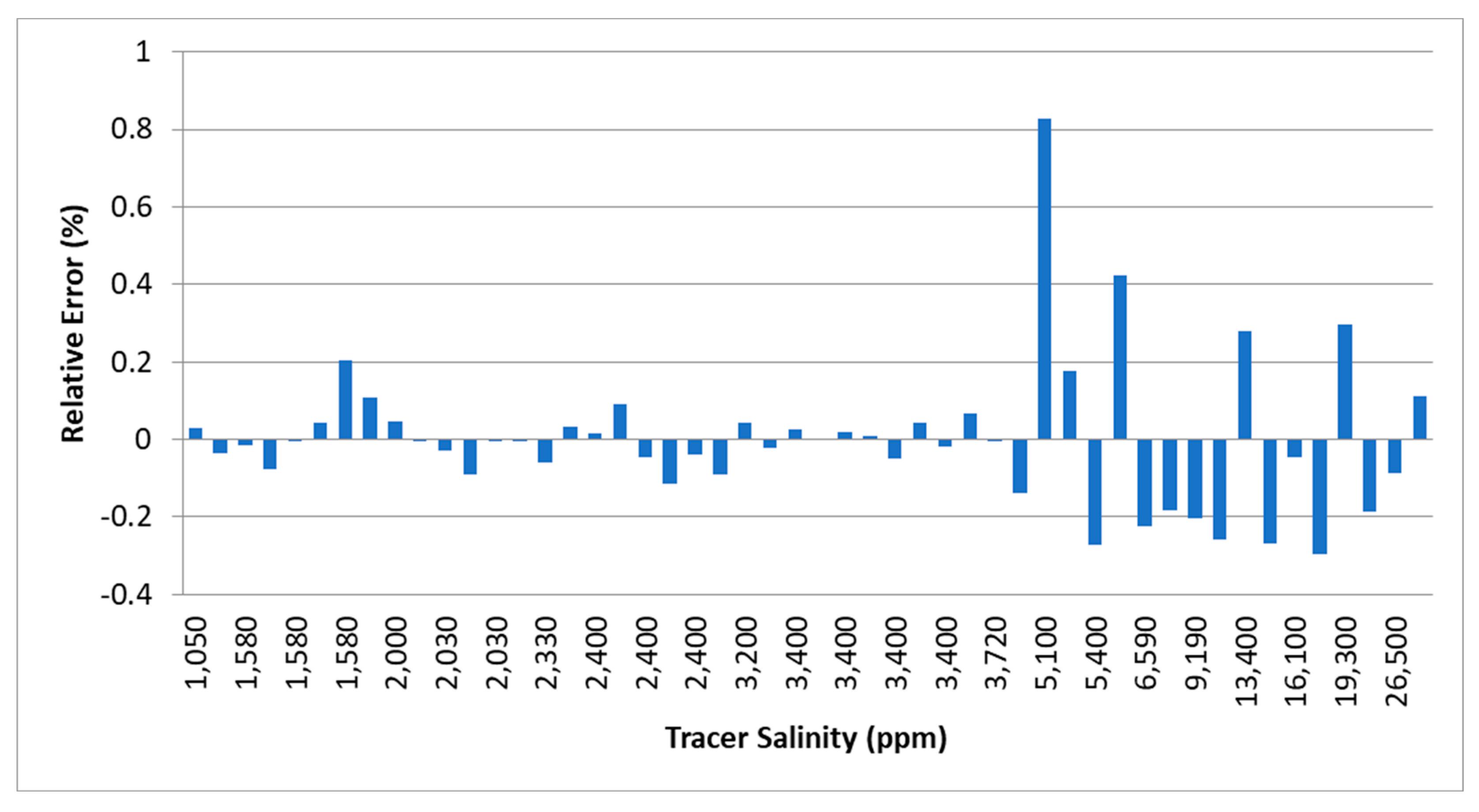
3.4. Effect of Tracer Concentration
3.5. Tracer-Based Flow Formula
3.5.1. Regression Flow Formulas based on Dimensional Analysis
3.5.2. Semi-Empirical Approach
- (1)
- The ratio of the injected tracer flux (q) to the water stream flow rate (Q) is quite small, to the extent that q/Q is negligible (i.e., q/Q << 1);
- (2)
- The salinity profile (in excess of the initial background concentration) is idealized and assumed to be triangular. Although this assumption is crude, it is used for the sake of simplicity and the correction factor will be next introduced for this regard;
- (3)
- The area under the actual measured salinity profile is equal to the area under the idealized triangular salinity profile multiplied by a correction factor F.
4. Conclusions, Challenges, and Future Work
- –
- The injected tracer rate ratio (q/Q) should be selected such that it does not exceed 3%. The recommended value is around 1%;
- –
- The recommended concentration of the injected tracer ranges from 1500 to 4500 ppm;
- –
- Two locations for tracer injection were examined. It has been noted that the most highly recommended injection point is at the upstream end of the pipe and the most highly recommended point for concentration measurement is inside the manhole close to the downstream end of the pipe and not at the manhole’s center;
- –
- A saline injector stack was developed to help inject saline at the selected injection point;
- –
- A passive axial flow fan was also proposed and could be encased in the injector stack to enhance mixing and to decrease the required minimum mixing length. It is noted that using the passive fan significantly enhanced the pulse of tracer method’s accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadoff, C.W.; Borgomeo, E.; Uhlenbrook, S. Rethinking water for SDG 6. Nat. Sustain. 2020, 3, 346–347. [Google Scholar] [CrossRef]
- Ortigara, A.R.C.; Kay, M.; Uhlenbrook, S. A review of the SDG 6 synthesis report 2018 from an education, training, and research perspective. Water 2018, 10, 1353. [Google Scholar] [CrossRef] [Green Version]
- Rao, A.S.; Marshall, S.; Gubbi, J.; Palaniswami, M.; Sinnott, R.; Pettigrovet, V. Design of low-cost autonomous water quality monitoring system. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 14–19. [Google Scholar]
- Sun, J.Y.; Jepson, W.P. Slug flow characteristics and their effect on corrosion rates in horizontal oil and gas pipelines. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4 October 1992. [Google Scholar]
- Farouk, M.; Kriaa, K.; Elgamal, M. CFD simulation of a submersible passive rotor at a pipe outlet UNDER time-varying water Jet Flux. Water 2022, 14, 2822. [Google Scholar] [CrossRef]
- Elgamal, M.; Kriaa, K.; Farouk, M. Drainage of a water tank with pipe outlet loaded by a passive rotor. Water 2021, 13, 1872. [Google Scholar] [CrossRef]
- Elgamal, M.; Abdel-Mageed, N.; Helmi, A.; Ghanem, A. Hydraulic performance of sluice gate with unloaded upstream rotor. Water SA 2017, 43, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Turkyilmazoglu, M. Eyring–Powell fluid flow through a circular pipe and heat transfer: Full solutions. Int. J. Numer. Methods Heat Fluid Flow. 2020, 30, 4765–4774. [Google Scholar]
- Spencer, E.A.; Tudhope, J.S. A Literature Survey of the Salt-Dilution Method of Flow Measurement; National Engineering Laboratory-NEL: Glasgow, UK, 1954. [Google Scholar]
- Church, M.; Kellerhals, R. Stream Gauging Techniques for Remote Areas Using Portable Equipment; Department of Energy, Mines and Resources: Ottawa, ON, Canada, 1970; pp. 55–68. [Google Scholar]
- Church, M. Electrochemical and Fluorometric Tracer Techniques for Streamflow Measurements; Technical Bulletin 12; British Geomorphological Research Group: London, UK, 1975. [Google Scholar]
- Day, T.J. On the precision of salt dilution gauging. J. Hydrol. 1976, 31, 293–306. [Google Scholar] [CrossRef]
- Day, T.J. Field procedures and evaluation of a slug dilution gauging method in mountain streams. J. Hydrol. 1977, 16, 113–133. [Google Scholar]
- Hongve, D. A revised procedure for discharge measurement by means of the salt dilution method. Hydrol. Process. 1987, 1, 267–270. [Google Scholar] [CrossRef]
- Johnstone, D.E. Some recent developments of constant-rate salt dilution gauging in rivers. J. Hydrol. 1988, 27, 128–153. [Google Scholar]
- Kite, G. Computerized stream flow measurement using slug injection. Hydrol. Process. 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Moore, R.D. Introduction to salt dilution gauging for stream flow measurement: Part 1. Streamline Watershed Manag. Bull. 2004, 7, 20–23. [Google Scholar]
- Moore, R.D. Introduction to salt dilution gauging for stream flow measurement Part II: Constant-rate injection. Streamline Watershed Manag. Bull. 2004, 8, 11–15. [Google Scholar]
- Moore, R.D. Introduction to salt dilution gauging for streamflow measurement Part III: Slug injection using salt in solution. Streamline Watershed Manag. Bull. 2005, 8, 1–6. [Google Scholar]
- Lee, S.; KMuthukumar, U.; Chandapillai, J.; Saseendran, S. Flow measurement in hydroelectric stations using tracer dilution method-case studies. In Proceedings of the IGHEM-2010, Roorkee, India, 21–23 October 2010; AHEC, IIT: Roorkee, India, 2010. [Google Scholar]
- Mastrocicco, M.; Prommer, H.; Pasti, L.; Palpacelli, S.; Colombani, N. Evaluation of saline tracer performance during electrical conductivity groundwater monitoring. J. Contam. Hydrol. 2011, 123, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hudson, R.; Fraser, J. Alternative methods of flow rating in small coastal streams. In Hydrology; Extension Note EN-014; Ministry of Forests: Nanaimo, BC, Canada, 2002; 11p. [Google Scholar]
- Hudson, R.; Fraser, J. Introduction to salt dilution gauging for streamflow measurement part IV: The mass balance (or dry injection) method. Streamline Watershed Manag. Bull. 2005, 9, 6–12. [Google Scholar]
- Sun, B.; Lu, Y.; Liu, Q.; Fang, H.; Zhang, C.; Zhang, J. Experimental and numerical analyses on mixing uniformity of water and saline in pipe flow. Water 2020, 12, 2281. [Google Scholar] [CrossRef]
- Scordo, E.B.; Moore, R.D. Transient storage processes in a steep headwater stream. J. Hydrol. Process. 2009, 23, 2671–2685. [Google Scholar] [CrossRef]
- Fabian, M.W.; Endreny Theodore, A. Seasonal variation in cascade-driven hyporheic exchange, northern Honduras. J. Hydrol. Process. 2011, 25, 1630–1646. [Google Scholar] [CrossRef]
- MacDonald, R.J.; Boon, S.; Byrne, J.M.; Silins, U. A comparison of surface and subsurface controls on summer temperature in a headwater stream. J. Hydrol. Process. 2014, 28, 2338–2347. [Google Scholar] [CrossRef]
- Zhang, J.; Kiesha, C.; Pierre, S.; Tejada-Martinez, A.E. Impacts of flow and tracer release unsteadiness on tracer analysis of Water and wastewater treatment facilities. J. Hydraul. Eng. 2019, 145, 04019004. [Google Scholar] [CrossRef]
- Thatoe Nwe Win, T.; Bogaard, T.; van de Giesen, N. A low-cost water quality monitoring system for the Ayeyarwady River in Myanmar using a participatory approach. Water 2019, 11, 1984. [Google Scholar] [CrossRef]
- Kilpatrick, F.A.; Cobb, E.D. Measurement of Discharge Using Tracer; US Geological Survey; Department of the Interior: Washington, DC, USA, 1985.





| Set of Run # | Runs Group # | Sewer Pipe Size (mm) | Concentration of Injected Tracer (ppm) | Location of | Injection Stack | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2030 | 4280 | 5630 | 6800 | 7200 | 9730 | 16,800 | Saline Injection | Concentration Measurement | ||||||
| Inside the u/s Manhole | Inside the Pipe Inlet | Inside the d/s Manhole | Inside the Pipe Outlet | Adding a Passive Rotor | ||||||||||
| 1 | 1 | 60 | √ | √ | √ | √ | √ | √ | ||||||
| 2 | √ | √ | √ | √ | √ | √ | ||||||||
| 3 | √ | √ | √ | √ | √ | √ | √ | |||||||
| 4 | √ | √ | √ | √ | √ | √ | ||||||||
| 5 | √ | √ | √ | √ | √ | √ | ||||||||
| 6 | √ | √ | √ | √ | √ | √ | √ | |||||||
| 2 | 7 | 150 | √ | √ | √ | √ | √ | √ | √ | |||||
| 8 | √ | √ | √ | √ | √ | √ | ||||||||
| 9 | √ | √ | √ | √ | √ | √ | ||||||||
| Coefficients | R2 | ||||||
|---|---|---|---|---|---|---|---|
| A | b | c | D | e | f | ||
| Regression formula #1 | 0.000139 | 1.082695 | −0.119478 | −3.541295 | 0.500887 | 0.019549 | 0.99 |
| Regression formula #2 | 0.893182 | 0 | −0.452712 | 0 | 1.403768 | −0.366871 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Mageed, N.B.; Ghanem, A.; Shaaban, I.G.; Ardakanian, A.; Ibrahem, M.M.M.; Elgamal, M. Effect of Using a Passive Rotor on the Accuracy of Flow Measurements in Sewer Pipes Using a Slug Tracer-Dilution Method. Water 2023, 15, 369. https://doi.org/10.3390/w15020369
Abdel-Mageed NB, Ghanem A, Shaaban IG, Ardakanian A, Ibrahem MMM, Elgamal M. Effect of Using a Passive Rotor on the Accuracy of Flow Measurements in Sewer Pipes Using a Slug Tracer-Dilution Method. Water. 2023; 15(2):369. https://doi.org/10.3390/w15020369
Chicago/Turabian StyleAbdel-Mageed, Neveen B., Ashraf Ghanem, Ibrahim G. Shaaban, Atiyeh Ardakanian, Mohamed M. M. Ibrahem, and Mohamed Elgamal. 2023. "Effect of Using a Passive Rotor on the Accuracy of Flow Measurements in Sewer Pipes Using a Slug Tracer-Dilution Method" Water 15, no. 2: 369. https://doi.org/10.3390/w15020369






