Theoretical Estimation of Disinfectant Mass Balance Components in Drinking Water Distribution Systems
Abstract
:1. Introduction
1.1. Water, Energy, and Water Quality Audits
1.2. Top-Down Approach for Water and Energy Audits
1.3. Proposed Estimation of Disinfectant Mass Loss Components for Top-Down Approach
2. Theoretical Analysis of Disinfectant Residual Mass Balance
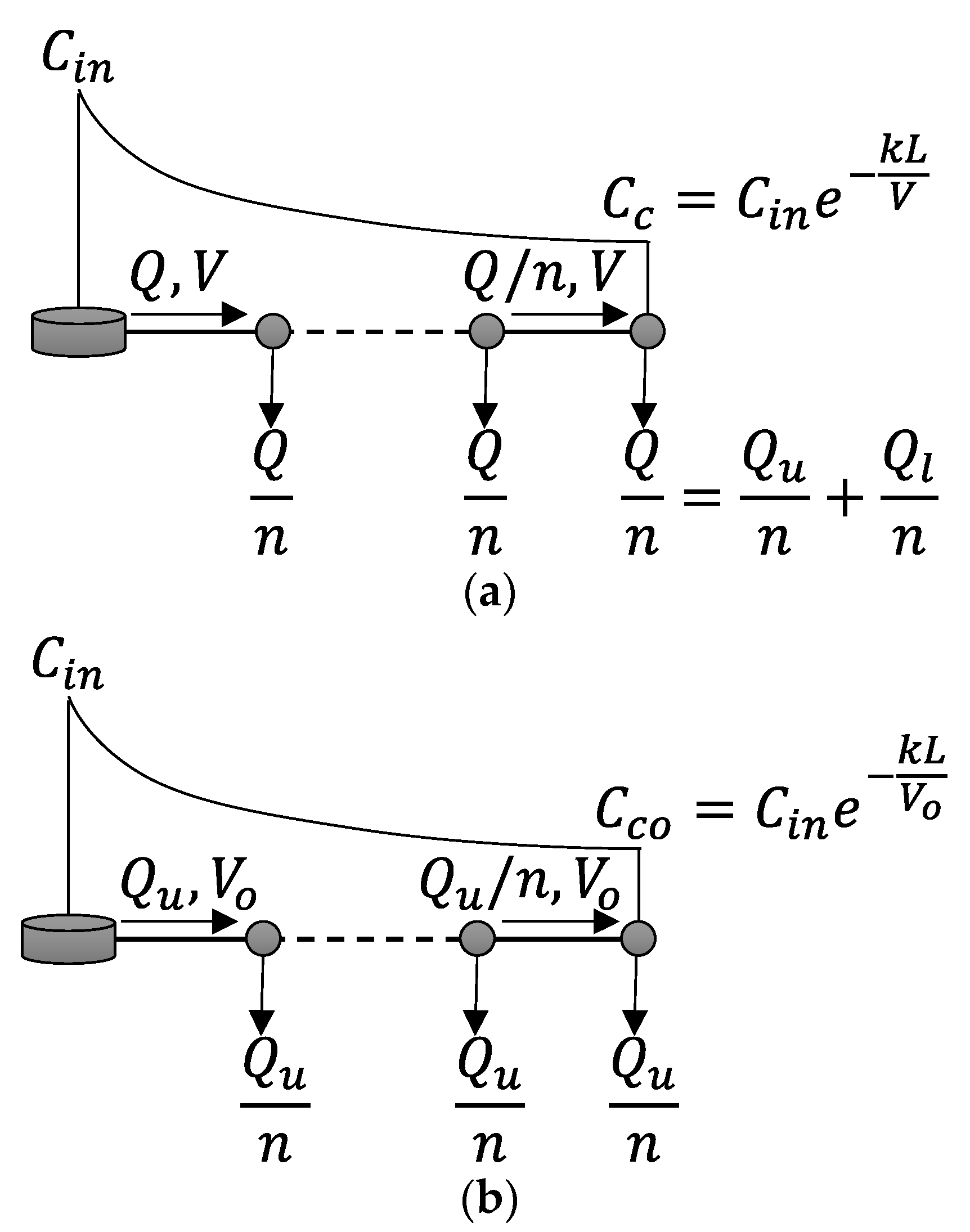
2.1. Single Pipe Network with One Demand at Pipe End
2.2. Single Pipe Network with Multiple Demands along Pipe
2.3. Branched Pipe Network
2.4. Utilization of Theory to Real Networks
3. Application to Real Water Networks
3.1. Characteristics of Water Distribution Networks
3.2. Basic Relationship for Disinfectant Mass Loss Components
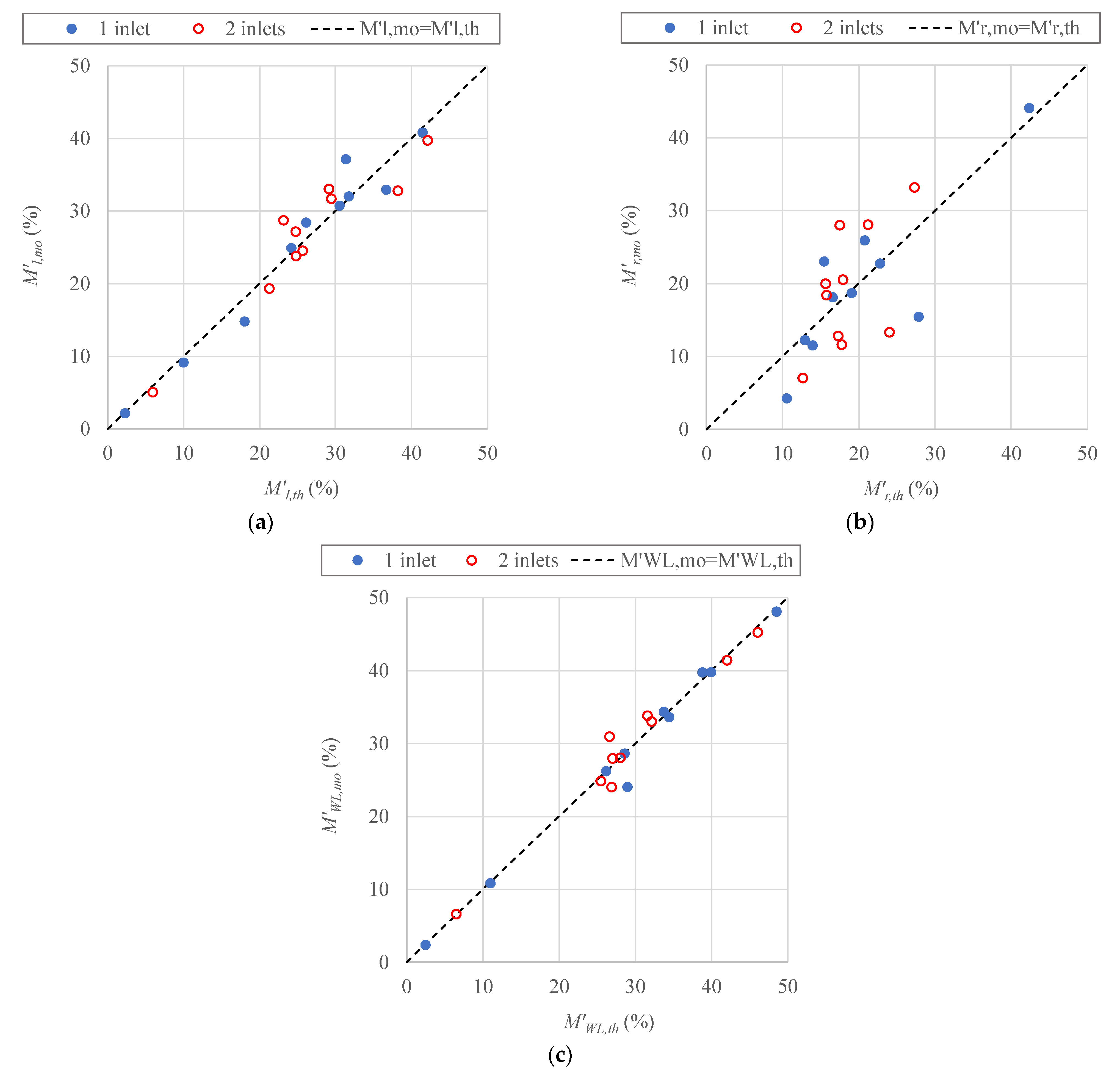
3.3. Parameter Estimation for Disinfectant Mass Loss Components
3.4. Application for Top-Down Water Quality Audit
- Choose the type of disinfectant mass balance to be complied with, as shown in Table 1.
- Collect the hydraulic data: system inflow () and flow delivered to users ()
- Compute water loss () and the ratio of water losses () by using (1) and (2), respectively.
- Collect the water quality data: input concentration () and concentration at the critical pressure point ().
- Compute the normalized time-averaged concentration at the critical pressure point () by using (56).
- Estimate the normalized values of , and in (57), (58), and (59), respectively, by using the values of the coefficients , , and and the exponents and in Table 2 for DMAs.
- Estimate the dimensional value of by using (6).
- Finally, estimate the other dimensional components (, , , and ) in Table 1 by using (12).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Coefficient in (57) | |
| Coefficient in (58) | |
| Coefficient in (59) | |
| AC | Authorized consumption |
| Exponent in (57) | |
| Exponent in (58) | |
| Normalized time-averaged critical disinfectant concentration | |
| Normalized time-averaged disinfectant concentration at critical pressure point | |
| Average disinfectant concentration | |
| Average disinfectant concentration at inlets | |
| Average disinfectant concentration without water loss | |
| Normalized critical disinfectant concentration | |
| Normalized critical disinfectant concentration for no water loss case | |
| Critical disinfectant concentration | |
| Critical disinfectant concentration at node m | |
| Critical disinfectant concentration at node m for no water loss case | |
| Critical disinfectant concentration for no water loss case | |
| Disinfectant concentration at node | |
| Input disinfectant concentration at source | |
| Disinfectant concentration at node for no water loss case | |
| CPP | Critical pressure point |
| DBP | Disinfection by-product |
| DMA | District metering area |
| DO | Dissolved oxygen |
| HAA | Halo acetic acid |
| Disinfectant decay rate | |
| Number of branching | |
| Normalized input disinfectant mass | |
| Normalized outgoing disinfectant mass through water loss | |
| Normalized outgoing disinfectant mass through water loss from models | |
| Normalized outgoing disinfectant mass through water loss from theory | |
| Normalized disinfectant mass loss by reactions | |
| Normalized disinfectant mass loss by reactions from models | |
| Normalized disinfectant mass loss by reactions from theory | |
| Normalized disinfectant mass loss by reactions for no water loss case | |
| Normalized disinfectant mass delivered to users | |
| Normalized disinfectant mass associated with water loss | |
| Normalized disinfectant mass associated with water loss from models | |
| Normalized disinfectant mass associated with water loss from theory | |
| Disinfectant mass associated with authorized consumption | |
| Input disinfectant mass | |
| Input disinfectant mass from models | |
| Outgoing disinfectant mass through water losses | |
| Disinfectant mass losses by reactions | |
| Disinfectant mass loss by chemical reactions in no water loss case | |
| Disinfectant mass delivered to users | |
| Disinfectant mass associated with water loss | |
| Number of demand nodes alone a pipe | |
| Ratio of water loss | |
| System inflow | |
| Flow due to water loss | |
| Flow delivered to users | |
| THM | Trihalomethane |
| Flow velocity | |
| Flow velocity for the no water loss case | |
| Water losses | |
| Parameter in (23) | |
| Parameter in (26) |
References
- McGuire, M.J. Eight revolutions in the history of US drinking water disinfection. Am. Water Works Assoc. J. 2006, 98, 123–149. [Google Scholar] [CrossRef]
- Singer, P.C. Control of disinfection by-products in drinking water. J. Environ. Eng. 1994, 120, 727–744. [Google Scholar] [CrossRef] [Green Version]
- Wilczak, A.; Jacangelo, J.G.; Marcinko, J.P.; Odell, L.H.; Kirmeyer, G.J. Occurrence of nitrification in chloraminated distribution systems. J. Am. Water Works Assoc. 1996, 88, 74–85. [Google Scholar] [CrossRef]
- Li, R.A.; McDonald, J.A.; Sathasivan, A.; Khan, S.J. Disinfectant residual stability leading to disinfectant decay and by-product formation in drinking water distribution systems: A systematic review. Water Res. 2019, 153, 335–348. [Google Scholar] [CrossRef] [PubMed]
- Yousefian, R.; Duchesne, S. Modeling the mixing phenomenon in water distribution networks: A state-of-the-art review. J. Water Resour. Plan. Manag. 2022, 148, 03121002. [Google Scholar] [CrossRef]
- Abdiyev, K.Z.; Maric, M.; Orynbayev, B.Y.; Toktarbay, Z.; Zhursumbaeva, M.B.; Seitkaliyeva, N.Z. Flocculating properties of 2-acrylamido-2-methyl-1-propane sulfonic acid-co-allylamine polyampholytic copolymers. Polym. Bull. 2022, 79, 10741–10756. [Google Scholar] [CrossRef]
- Azat, S.; Arkhangelsky, E.; Papathanasiou, T.; Zorpas, A.A.; Abirov, A.; Inglezakis, V.J. Synthesis of biosourced silica–Ag nanocomposites and amalgamation reaction with mercury in aqueous solutions. Comptes Rendus Chim. 2020, 23, 77–92. [Google Scholar] [CrossRef]
- Abhijith, G.R.; Kadinski, L.; Ostfeld, A. Modeling bacterial regrowth and trihalomethane formation in water distribution systems. Water 2021, 13, 463. [Google Scholar] [CrossRef]
- Abhijith, G.R.; Ostfeld, A. Contaminant fate and transport modeling in distribution systems: EPANET-C. Water 2022, 14, 1665. [Google Scholar] [CrossRef]
- Sharif, M.N.; Farahat, A.; Haider, H.; Al-Zahrani, M.A.; Rodriguez, M.J.; Sadiq, R. Risk-based framework for optimizing residual chlorine in large water distribution systems. Environ. Monit. Assess. 2017, 189, 307. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Shang, F.; Sathasivan, A. Framework for optimizing chlorine and byproduct concentrations in drinking water distribution systems. J. Am. Water Works Assoc. 2018, 110, 38–49. [Google Scholar] [CrossRef]
- Yoo, D.G.; Lee, S.M.; Lee, H.M.; Choi, Y.H.; Kim, J.H. Optimizing re-chlorination injection points for water supply networks using harmony search algorithm. Water 2018, 10, 547. [Google Scholar] [CrossRef] [Green Version]
- Abokifa, A.A.; Maheshwari, A.; Gudi, R.D.; Biswas, P. Influence of dead-end sections of drinking water distribution networks on optimization of booster chlorination systems. J. Water Resour. Plan. Manag. 2019, 145, 04019053. [Google Scholar] [CrossRef]
- Javadinejad, S.; Ostad-Ali-Askari, K.; Jafary, F. Using simulation model to determine the regulation and to optimize the quantity of chlorine injection in water distribution networks. Model Earth Syst. Environ. 2019, 5, 1015–1023. [Google Scholar] [CrossRef]
- Monteiro, L.; Carneiro, J.; Covas, D.I. Modelling chlorine wall decay in a full-scale water supply system. Urban Water J. 2020, 17, 754–762. [Google Scholar] [CrossRef]
- Li, J.; Liu, S.; Meng, F.; Wu, X.; Smith, K. An efficient constraint-based pruning method to improve chlorine dosage optimization. J. Water Resour. Plan. Manag. 2022, 148, 04022038. [Google Scholar] [CrossRef]
- Lipiwattanakarn, S.; Kaewsang, S.; Makpiboon, C.; Changklom, J.; Pornprommin, A. Water quality audit in drinking water distribution networks. J. Water Resour. Plan. Manag. 2021, 147, 04020113. [Google Scholar] [CrossRef]
- Alegre, H.; Baptista, J.M.; Cabrera, E., Jr.; Cubillo, F.; Duarte, P.; Hirner, W.; Merkel, W.; Parena, R. Performance Indicators for Water Supply Services; IWA Publishing: London, UK, 2006. [Google Scholar]
- AWWA (American Water Works Association). Manual of Water Supply Practices: M36 Water Audits and Loss Control Programs, 4th ed.; AWWA: Denver, CO, USA, 2016. [Google Scholar]
- Rupiper, A.M.; Guilliams, M.S.; Bush, M.M.; Jessoe, K.K.; Loge, F.J. Assessing data adequacy for determining utility-specific water loss reduction standards. J. Water Resour. Plan. Manag. 2021, 147, 05021011. [Google Scholar] [CrossRef]
- Cabrera, E.; Pardo, M.A.; Cobacho, R.; Cabrera Jr, E. Energy audit of water networks. J. Water Resour. Plan. Manag. 2010, 136, 669–677. [Google Scholar] [CrossRef]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. A comprehensive and well tested energy balance for water supply systems. Urban Water J. 2017, 14, 853–861. [Google Scholar] [CrossRef]
- Lenzi, C.; Bragalli, C.; Bolognesi, A.; Artina, S. From energy balance to energy efficiency indicators including water losses. Water Sci. Technol. Water Supply 2013, 13, 889–895. [Google Scholar] [CrossRef]
- Dziedzic, R.; Karney, B.W. Energy metrics for water distribution system assessment: Case study of the Toronto network. J. Water Resour. Plan. Manag. 2015, 141, 04015032. [Google Scholar] [CrossRef] [Green Version]
- Lapprasert, S.; Pornprommin, A.; Lipiwattanakarn, S.; Chittaladakorn, S. Energy balance of a trunk main network in Bangkok, Thailand. J. Am. Water Works Assoc. 2018, 110, E18–E27. [Google Scholar] [CrossRef]
- Lipiwattanakarn, S.; Kaewsang, S.; Pornprommin, A.; Wongwiset, T. Real benefits of leak repair and increasing the number of inlets to energy. Water Pract. Technol. 2019, 14, 714–725. [Google Scholar] [CrossRef]
- Jorge, C.; Almeida, M.D.; Covas, D. Energy balance in wastewater systems with energy recovery: A Portuguese case study. Infrastructures 2021, 6, 141. [Google Scholar] [CrossRef]
- Ferrante, M.; Bosco, C.; Ugarelli, R.; Magenta, L.; Eidsmo, T. Mass, energy, and cost balances in water distribution systems with PATs: The Trondheim network case study. J. Water Resour. Plan. Manag. 2020, 146, 05020005. [Google Scholar] [CrossRef]
- Loureiro, D.; Silva, C.; Cardoso, M.A.; Mamade, A.; Alegre, H.; Rosa, M.J. The development of a framework for assessing the energy efficiency in urban water systems and its demonstration in the Portuguese water sector. Water 2020, 12, 134. [Google Scholar] [CrossRef] [Green Version]
- Monteiro, L.; Cristina, R.; Covas, D. Water and energy efficiency assessment in urban green spaces. Energies 2021, 14, 5490. [Google Scholar] [CrossRef]
- Silqueira, M.G.; da Silva, F.D.; Silva, A.T.; Barbedo, M.D. A water-energy balance application with adaptations to a brazilian water supply system. Res. Soc. Dev. 2021, 10, e380101019039. [Google Scholar] [CrossRef]
- Quintiliani, C.; Di Cristo, C.; Leopardi, A. Vulnerability assessment to trihalomethane exposure in water distribution systems. Water 2018, 10, 912. [Google Scholar] [CrossRef]
- Dias, V.C.; Besner, M.C.; Prévost, M. Predicting water quality impact after district metered area implementation in a full-scale drinking water distribution system. J. Am. Water Works Assoc. 2017, 109, E363–E380. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y.J.; Shao, Y.; Neal, J.; Zhang, T. The dependence of chlorine decay and DBP formation kinetics on pipe flow properties in drinking water distribution. Water Res. 2018, 141, 32–45. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Huang, C.; Shi, X.; Dong, S.; Yuan, B.; Nguyen, T.H. Role of drinking water biofilms on residual chlorine decay and trihalomethane formation: An experimental and modeling study. Sci. Total Environ. 2018, 642, 516–525. [Google Scholar] [CrossRef]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. Top-down and bottom-up approaches for water-energy balance in Portuguese supply systems. Water 2018, 10, 577. [Google Scholar] [CrossRef] [Green Version]
- Lipiwattanakarn, S.; Kaewsang, S.; Charuwimolkul, N.; Changklom, J.; Pornprommin, A. Theoretical estimation of energy balance components in water networks for top-down approach. Water 2021, 13, 1011. [Google Scholar] [CrossRef]
- Brandt, K.; Johnson, K.M.; Elphinston, A.J. Twort’s Water Supply, 7th ed.; IWA Publishing: London, UK, 2017. [Google Scholar]
- Taha, A.F.; Wang, S.; Guo, Y.; Summers, T.H.; Gatsis, N.; Giacomoni, M.H.; Abokifa, A.A. Revisiting the water quality sensor placement problem: Optimizing network observability and state estimation metrics. J. Water Resour. Plan. Manag. 2021, 147, 04021040. [Google Scholar] [CrossRef]
- Zheng, Z.; Zheng, F.; Bi, W.; Du, J.; Duan, H.F.; Savic, D.; Kapelan, Z. Evaluating the robustness of water quality sensor placement strategies of water distribution systems considering possible sensor failures and system changes. J. Water Resour. Plan. Manag. 2022, 148, 04022050. [Google Scholar] [CrossRef]
- McKenzie, R. WRC Report No. TT 152/01: Pressure Management Program (PRESMAC); Water Research Commission: Pretoria, South Africa, 2001. [Google Scholar]
- Rossman, L.A. EPANET 2 Users Manual; Water Supply and Water Resources Division (USEPA): Cincinnati, OH, USA, 2000.
- Klise, K.; Hart, D.; Bynum, M.; Hogge, J.; Haxton, T.; Murray, R.; Burkhardt, J. Water Network Tool for Resilience (WNTR) User Manual; (No. SAND2020-9301R); Sandia National Lab (SNL-NM): Albuquerque, NM, USA, 2020.





| DMA ID | No. of Inlets | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (%) | (mg/L) | (%) | (%) | (g/day) | (%) | (%) | (%) | ||
| 1 | 1 | 37.1 | 1.03 | 83.3 | 38.7 | 5074 | 32.0 | 12.3 | 33.6 |
| 2 | 1 | 28.6 | 0.73 | 79.8 | 25.8 | 3939 | 24.9 | 11.5 | 26.2 |
| 3 | 1 | 44.6 | 0.52 | 41.8 | 31.1 | 3735 | 37.1 | 15.5 | 39.8 |
| 4 | 1 | 38.5 | 0.78 | 63.7 | 18.9 | 5091 | 30.7 | 18.7 | 34.4 |
| 5 | 1 | 44.2 | 0.63 | 74.8 | 29.8 | 5555 | 32.9 | 23.0 | 39.8 |
| 6 | 1 | 54.9 | 0.67 | 53.6 | 22.1 | 8347 | 40.8 | 22.8 | 48.1 |
| 7 | 1 | 32.4 | 0.77 | 18.4 | 14.4 | 4727 | 14.8 | 44.1 | 24.0 |
| 8 | 1 | 12.9 | 0.73 | 58.9 | 7.8 | 4841 | 9.1 | 25.9 | 10.8 |
| 9 | 1 | 29.7 | 0.85 | 91.9 | 5.3 | 5227 | 28.4 | 4.3 | 28.6 |
| 10 | 1 | 2.8 | 0.61 | 71.2 | 50.1 | 3251 | 2.2 | 18.1 | 2.4 |
| 11 | 2 | 30.0 | 0.81 | 73.8 | 35.3 | 6257 | 23.8 | 18.4 | 24.0 |
| 12 | 2 | 50.9 | 0.65 | 74.1 | 46.9 | 3212 | 39.7 | 20.0 | 45.2 |
| 13 | 2 | 31.9 | 0.75 | 67.1 | 43.9 | 4867 | 24.5 | 20.6 | 28.1 |
| 14 | 2 | 33.9 | 0.41 | 84.4 | 65.9 | 3808 | 33.0 | 7.1 | 33.8 |
| 15 | 2 | 7.7 | 0.72 | 57.7 | 26.9 | 6480 | 5.1 | 28.1 | 6.6 |
| 16 | 2 | 36.3 | 0.60 | 69.0 | 6.4 | 5805 | 31.7 | 12.8 | 33.0 |
| 17 | 2 | 30.7 | 0.57 | 67.6 | 10.9 | 7404 | 27.2 | 11.6 | 28.0 |
| 18 | 2 | 30.0 | 0.72 | 43.0 | 0.3 | 6821 | 19.3 | 33.2 | 24.9 |
| 19 | 2 | 31.2 | 0.68 | 50.5 | 20.0 | 4774 | 28.7 | 13.3 | 31.0 |
| 20 | 2 | 47.2 | 0.65 | 68.4 | 15.9 | 7691 | 32.8 | 28.0 | 41.4 |
| Avg. | 1.5 | 32.8 | 0.69 | 64.7 | 25.8 | 5345 | 25.9 | 19.5 | 29.2 |
| Component | Equation | ||||
|---|---|---|---|---|---|
| (57) | 0.9106 | 0.2844 | 0.963 | 2.86 | |
| (58) | 0.9151 | 0.2726 | 0.755 | 5.99 | |
| (59) | 0.4962 | - | 0.989 | 1.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wongpeerak, K.; Charuwimolkul, N.; Changklom, J.; Lipiwattanakarn, S.; Pornprommin, A. Theoretical Estimation of Disinfectant Mass Balance Components in Drinking Water Distribution Systems. Water 2023, 15, 368. https://doi.org/10.3390/w15020368
Wongpeerak K, Charuwimolkul N, Changklom J, Lipiwattanakarn S, Pornprommin A. Theoretical Estimation of Disinfectant Mass Balance Components in Drinking Water Distribution Systems. Water. 2023; 15(2):368. https://doi.org/10.3390/w15020368
Chicago/Turabian StyleWongpeerak, Kittikun, Natchapol Charuwimolkul, Jiramate Changklom, Surachai Lipiwattanakarn, and Adichai Pornprommin. 2023. "Theoretical Estimation of Disinfectant Mass Balance Components in Drinking Water Distribution Systems" Water 15, no. 2: 368. https://doi.org/10.3390/w15020368






