Investigation on Water Levels for Cascaded Hydropower Reservoirs to Drawdown at the End of Dry Seasons
Abstract
:1. Introduction
2. Problem Formulation
3. Solution Strategy
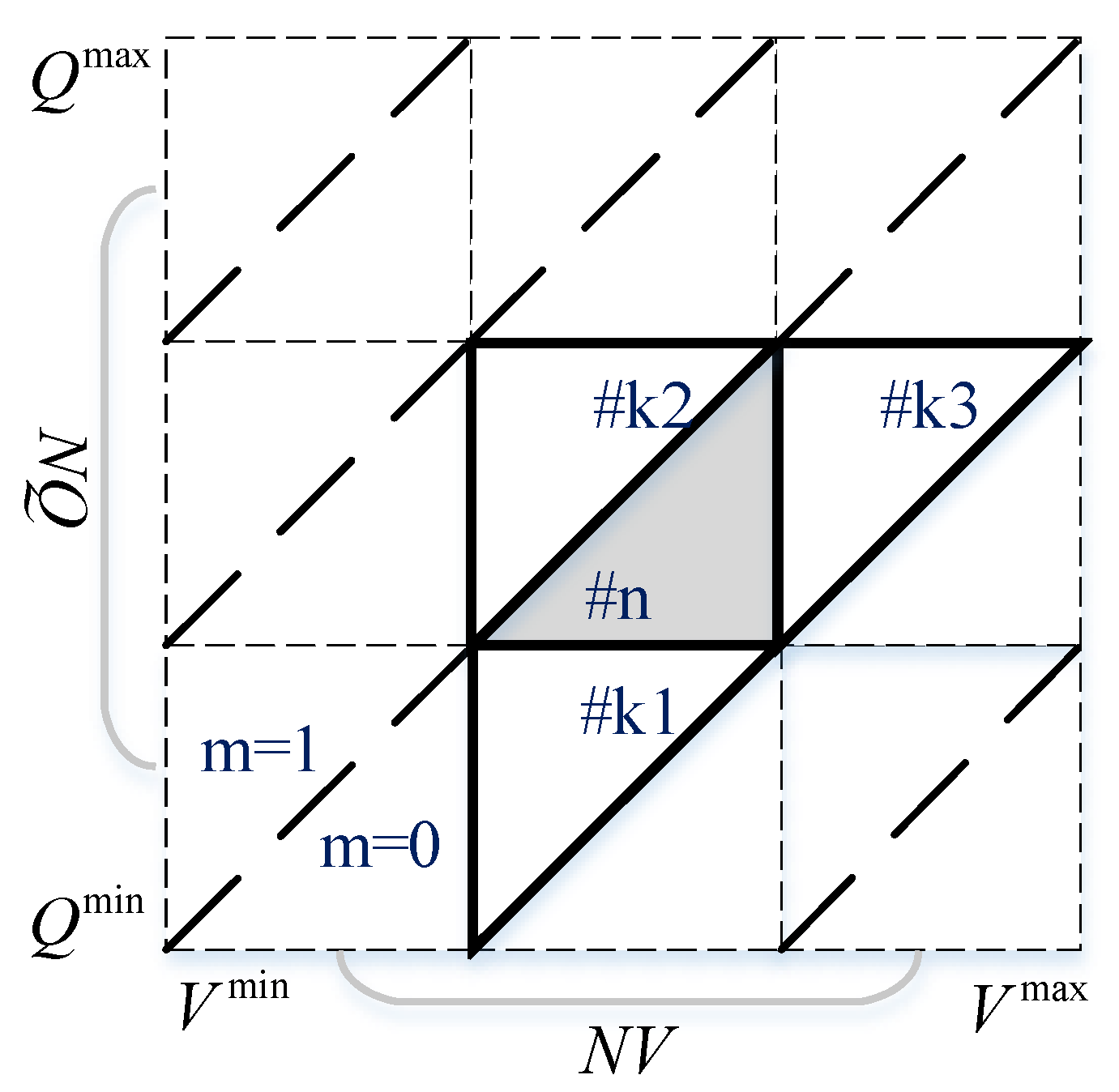
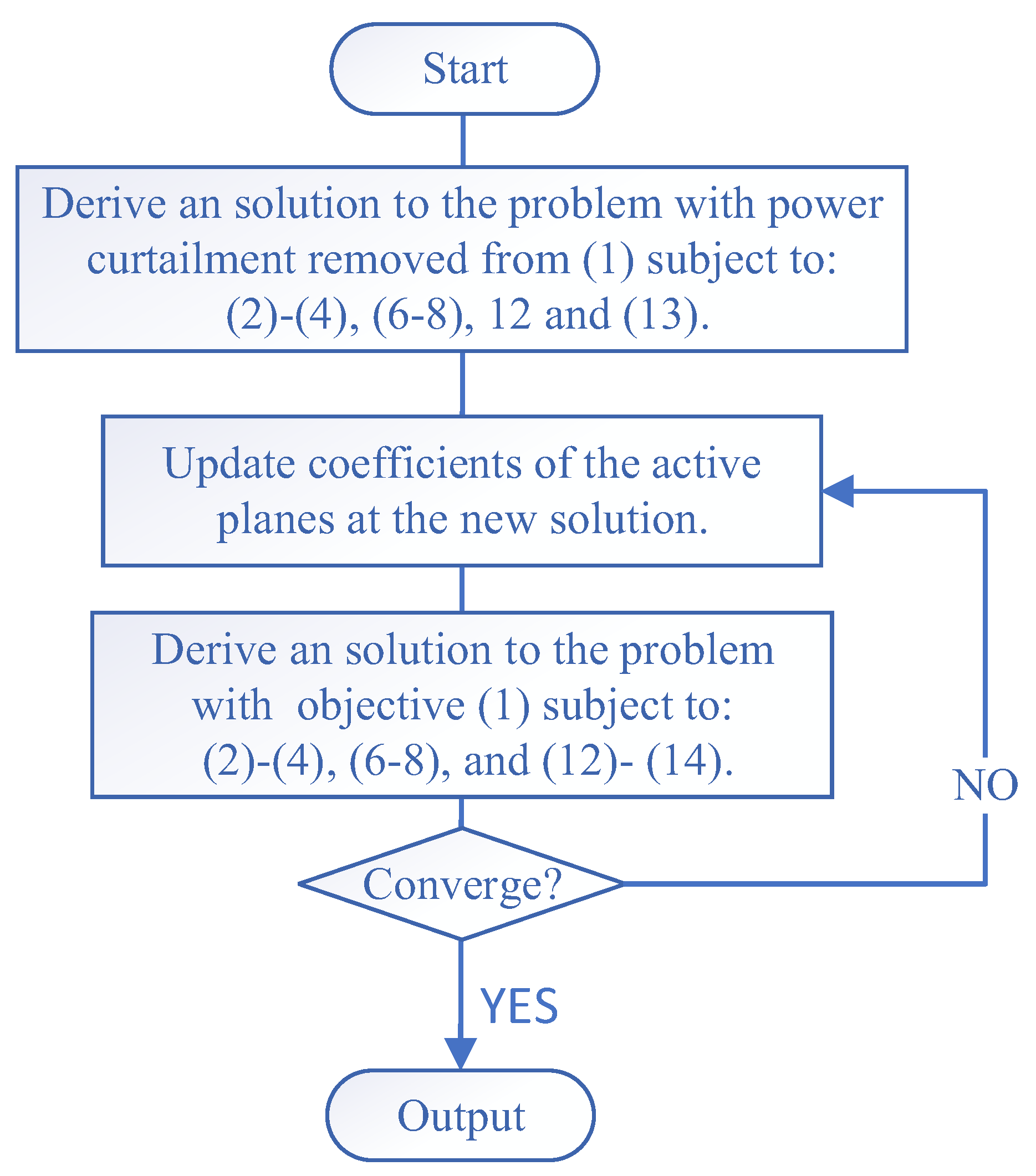
3.1. Solution Method
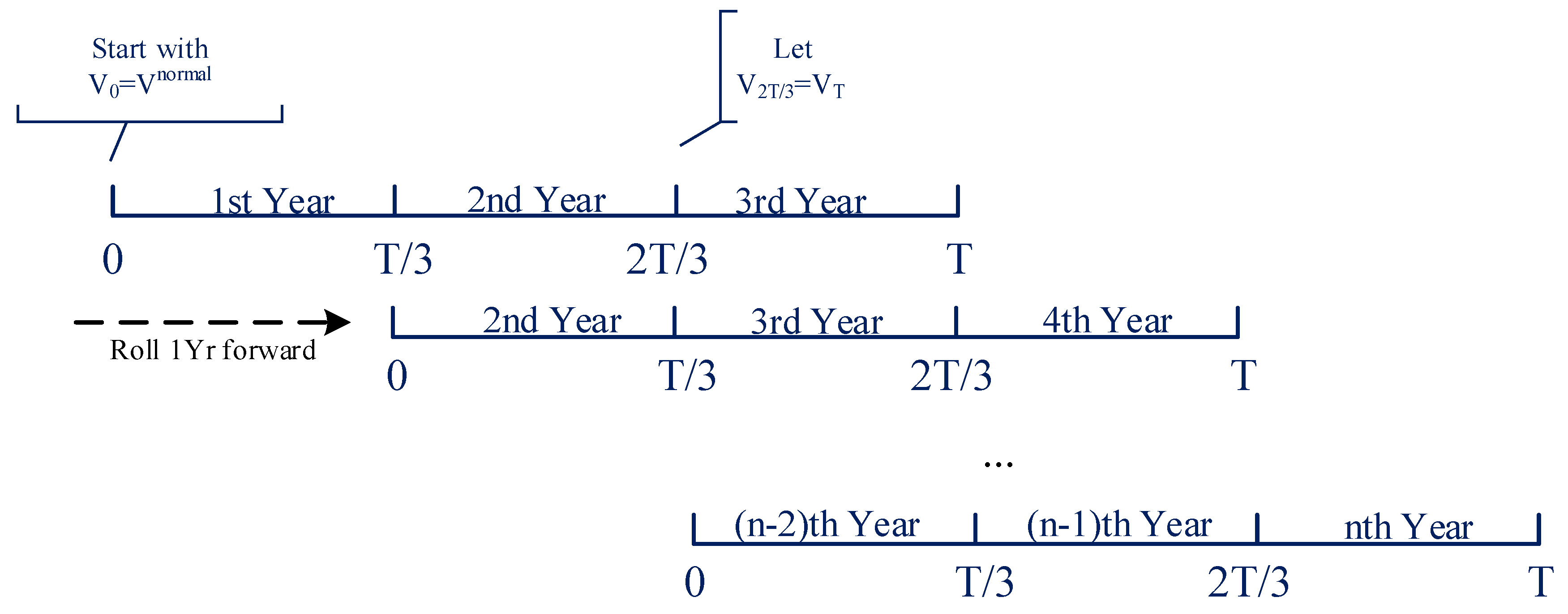
3.2. Simulation Strategy
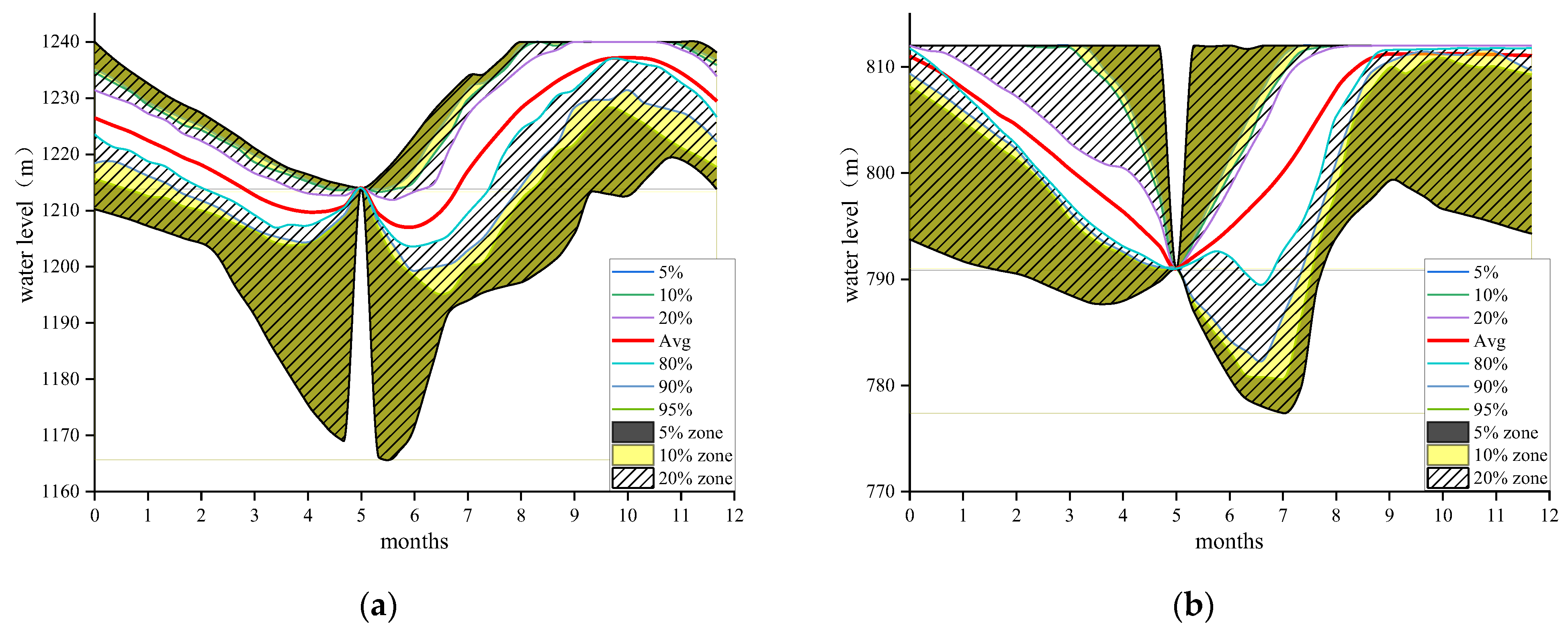
4. Case Studies
4.1. Engineering Background
4.2. Assessment of Optional Drawdown Levels
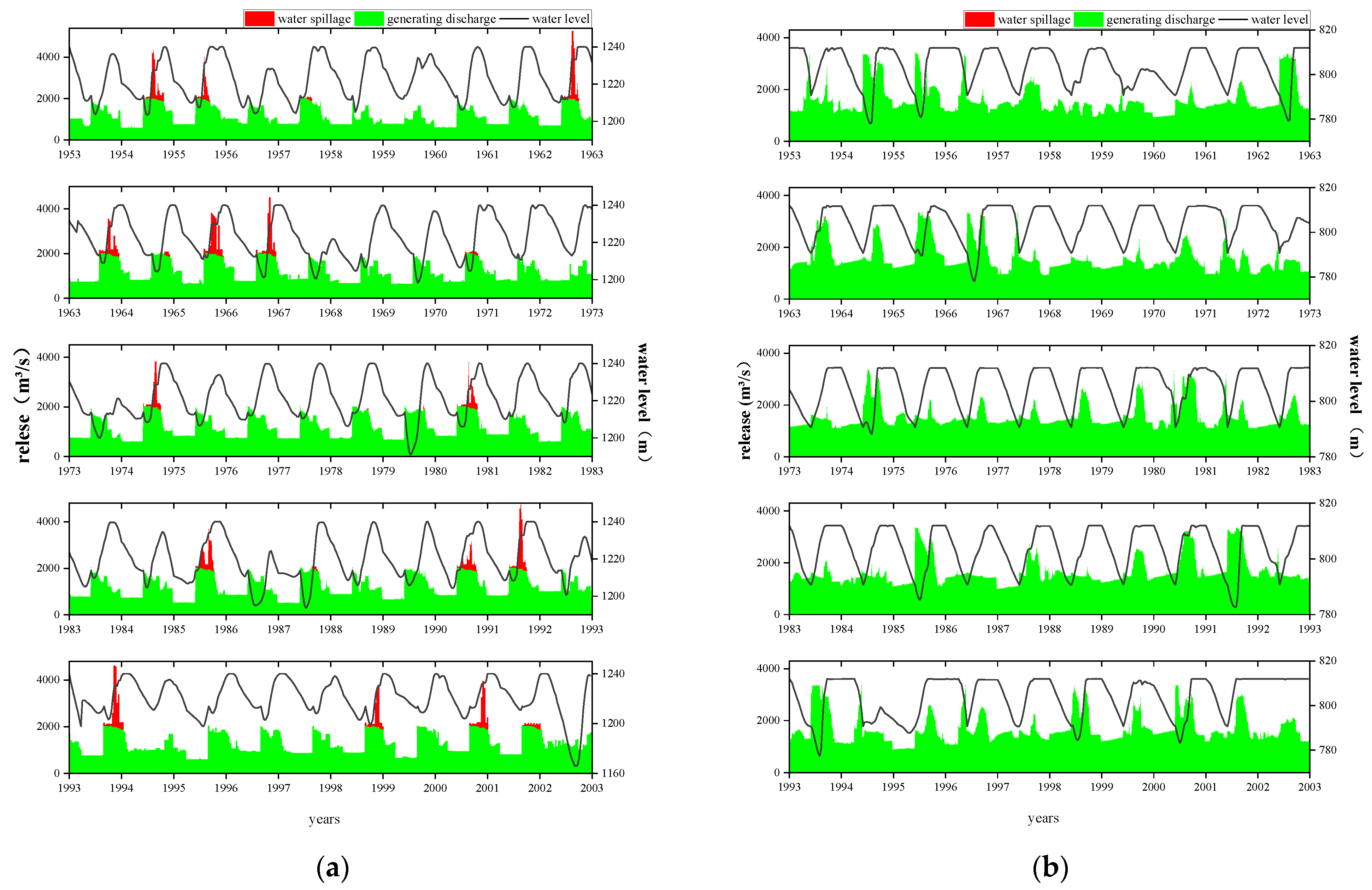
4.3. Simulation Results of the 7th Option
5. Conclusions
- (1)
- The preferential drawdown water levels should be between 1185–1214 m for the OY07 and 774–791 m for OY10 as it is in favor of both the total hydropower production and the firm third-monthly hydropower output.
- (2)
- Targeting higher drawdown levels of the OY07 and OY10 will lead to more hydropower production during the flood season, mainly attributable to higher water heads that contribute to higher generation efficiency.
- (3)
- The hydropower productions during dry season will be less when targeting higher drawdown levels. The hydropower production during the year, as well as the firm hydropower output, goes up first and then down when elevating the drawdown water levels of the over-year reservoirs, with the maximums in total hydropower production and firm hydropower output achieved by drawing the OY07 and OY10’s water levels down to (774 m, 791 m) and (1185 m, 1214 m), respectively.
- (4)
- Targeting higher drawdown water levels at the end of dry seasons has, if any, minimal impact on the upstream reservoirs of the OY07 in the hydropower curtailment due to the generating capacity, but will result in a more significant curtailment in the downstream hydro-plants due to a smaller storage capacity available to reduce spillages.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Algarvio, H. The Role of Local Citizen Energy Communities in the Road to Carbon-Neutral Power Systems: Outcomes from a Case Study in Portugal. Smart Cities 2021, 4, 840–863. [Google Scholar] [CrossRef]
- Zou, C.; Xiong, B.; Xue, H.; Zheng, D.; Ge, Z.; Wang, Y.; Jiang, L.; Pan, S.; Wu, S. The role of new energy in carbon neutral. Pet. Explor. Dev. 2021, 48, 480–491. [Google Scholar] [CrossRef]
- Bamisile, O.; Wang, X.; Adun, H.; Ejiyi, C.J.; Obiora, S.; Huang, Q.; Hu, W. A 2030 and 2050 feasible/sustainable decarbonization perusal for China’s Sichuan Province: A deep carbon neutrality analysis and Energy PLAN. Energy Convers. Manag. 2022, 261, 115605. [Google Scholar] [CrossRef]
- Bilgili, M.; Bilirgen, H.; Ozbek, A.; Ekinci, F.; Demirdelen, T. The role of hydropower installations for sustainable energy development in Turkey and the world. Renew. Energy 2018, 126, 755–764. [Google Scholar] [CrossRef]
- De Souza Dias, V.; Pereira da Luz, M.; Medero, G.M.; Tarley Ferreira Nascimento, D. An Overview of Hydropower Reservoirs in Brazil: Current Situation, Future Perspectives and Impacts of Climate Change. Water 2018, 10, 592. [Google Scholar] [CrossRef] [Green Version]
- Wagner, B.; Hauer, C.; Habersack, H. Current hydropower developments in Europe. Curr. Opin. Environ. Sustain. 2019, 37, 41–49. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Fan, X.; Cheng, Z. Hydropower development situation and prospects in China. Renew. Sustain. Energy Rev. 2018, 82, 232–239. [Google Scholar] [CrossRef]
- Dogmus, Ö.C.; Nielsen, J.Ø. Is the hydropower boom actually taking place? A case study of a South East European country, Bosnia and Herzegovina. Renew. Sustain. Energy Rev. 2019, 110, 278–289. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, J.; Leduc, S.; Mesfun, S.; Kraxner, F.; Mao, G.; Qi, W.; Wang, Z. Hydropower production benefits more from 1.5 °C than 2 °C climate scenario. Water Resour. Res. 2020, 56, e2019WR025519. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R. Modeling California’s high-elevation hydropower systems in energy units. Water Resour. Res. 2009, 45, W09413. [Google Scholar] [CrossRef]
- Lu, S.; Shang, Y.; Li, W.; Peng, Y.; Wu, X. Economic benefit analysis of joint operation of cascaded reservoirs. J. Clean. Prod. 2018, 179, 731–737. [Google Scholar] [CrossRef]
- Berga, L. The role of hydropower in climate change mitigation and adaptation: A review. Engineering 2016, 2, 313–318. [Google Scholar] [CrossRef] [Green Version]
- Oven-Thompson, K.; Alercon, L.; Marks, D.H. Agricultural vs. hydropower tradeoffs in the operation of the High Aswan Dam. Water Resour. Res. 1982, 18, 1605–1613. [Google Scholar] [CrossRef]
- Farfan, J.; Breyer, C. Combining floating solar photovoltaic power plants and hydropower reservoirs: A virtual battery of great global potential. Energy Procedia 2018, 155, 403–411. [Google Scholar] [CrossRef]
- Hirth, L. The benefits of flexibility: The value of wind energy with hydropower. Appl. Energy 2016, 181, 210–223. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Ma, G.; Wang, Y. Determining the optimal year-end water level of a multi-year regulating storage reservoir: A case study. Water Sci. Technol. Water Supply 2016, 16, 284–294. [Google Scholar] [CrossRef]
- Jiang, Z.; Song, P.; Liao, X. Optimization of Year-End Water Level of Multi-Year Regulating Reservoir in Cascade Hydropower System Considering the Inflow Frequency Difference. Energies 2020, 13, 5345. [Google Scholar] [CrossRef]
- Liu, J.; Huang, C.H.; Zeng, G.Z. Comparative analysis of year-end water level determining methods for cascade carryover storage reservoirs. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Zvenigorod, Russia, 4–7 September 2017; IOP Publishing: Qingdao, China, 2017; Volume 82, p. 012060. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zhang, S.; Geng, S.; Jiang, Y.; Li, H.; Zhang, D. Application of decision trees to the determination of the year-end level of a carryover storage reservoir based on the iterative dichotomizer 3. Int. J. Electr. Power Energy Syst. 2015, 64, 375–383. [Google Scholar] [CrossRef]
- Celeste, A.B.; Billib, M. Evaluation of stochastic reservoir operation optimization models. Adv. Water Resour. 2009, 32, 1429–1443. [Google Scholar] [CrossRef]
- De Souza Zambelli, M.; Martins, L.S.; Soares Filho, S. Advantages of deterministic optimization in long-term hydrothermal scheduling of large-scale power systems. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; IEEE: New York, NY, USA, 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Allen, R.B.; Bridgeman, S.G. Dynamic programming in hydropower scheduling. J. Water Resour. Plan. Manag. 1986, 112, 339–353. [Google Scholar] [CrossRef]
- Zambelli, M.S.; Soares, S.; da Silva, D. Deterministic versus stochastic dynamic programming for long term hydropower scheduling. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; IEEE: New York, NY, USA, 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Kang, C.; Guo, M.; Wang, J. Short-term hydrothermal scheduling using a two-stage linear programming with special ordered sets method. Water Resour. Manag. 2017, 31, 3329–3341. [Google Scholar] [CrossRef]
- Zheng, H.; Feng, S.; Chen, C.; Wang, J. A new three-triangle based method to linearly concave hydropower output in long-term reservoir operation. Energy 2022, 250, 123784. [Google Scholar] [CrossRef]

| Number | Name | Annual Inflow (m3/s) | Installed Capacity (MW) | Dead Water Level (m) | Normal Water Level (m) | Operability |
|---|---|---|---|---|---|---|
| 1 | D01 | 744 | 990 | 1901 | 1906 | Daily |
| 2 | D02 | 758 | 420 | 1814 | 1818 | Daily |
| 3 | S03 | 902 | 1900 | 1586 | 1619 | Seasonal |
| 4 | D04 | 923 | 920 | 1472 | 1477 | Daily |
| 5 | W05 | 960 | 1400 | 1398 | 1408 | Weekly |
| 6 | D06 | 1010 | 900 | 1303 | 1307 | Daily |
| 7 | OY07 | 1210 | 4200 | 1166 | 1240 | Over-year |
| 8 | S08 | 1230 | 1670 | 988 | 994 | Seasonal |
| 9 | S09 | 1330 | 1350 | 887 | 899 | Seasonal |
| 10 | OY10 | 1740 | 5850 | 765 | 812 | Over-year |
| 11 | W11 | 1810 | 1750 | 591 | 602 | Weekly |
| Option | Water Level (m) | Hydropower Production (TW) | Curtailment (TW) | Full-Refilling Rate | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| OY07 | OY10 | Annu. | Dry | Flood | Firm | Up | Down | OY07 | OY10 | |
| 1 | 1166 | 765 | 102.17 | 48.63 | 53.54 | 1.54 | 4.86 | 0.76 | 38% | 54% |
| 2 | 1176 | 770 | 102.9 | 48.23 | 54.67 | 1.56 | 4.85 | 0.87 | 40% | 64% |
| 3 | 1185 | 774 | 103.54 | 47.51 | 56.03 | 1.56 | 4.85 | 1.06 | 46% | 76% |
| 4 | 1193 | 779 | 104.06 | 46.87 | 57.19 | 1.54 | 4.85 | 1.30 | 52% | 90% |
| 5 | 1201 | 783 | 104.47 | 46.23 | 58.24 | 1.52 | 4.85 | 1.54 | 64% | 92% |
| 6 | 1207 | 787 | 104.75 | 45.43 | 59.33 | 1.50 | 4.85 | 1.80 | 64% | 98% |
| 7 | 1214 | 791 | 104.82 | 44.09 | 60.73 | 1.45 | 4.85 | 2.12 | 78% | 100% |
| 8 | 1219 | 794 | 104.64 | 42.53 | 62.12 | 1.38 | 4.85 | 2.59 | 82% | 100% |
| 9 | 1225 | 798 | 104.32 | 40.88 | 63.45 | 1.31 | 4.85 | 2.59 | 88% | 100% |
| 10 | 1231 | 801 | 103.74 | 39.09 | 64.65 | 1.22 | 4.85 | 3.86 | 94% | 100% |
| 11 | 1236 | 804 | 103.24 | 37.39 | 65.84 | 1.14 | 4.85 | 4.56 | 100% | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Luo, X.; Zheng, H.; Zhang, C.; Wang, Y.; Chen, K.; Wang, J. Investigation on Water Levels for Cascaded Hydropower Reservoirs to Drawdown at the End of Dry Seasons. Water 2023, 15, 362. https://doi.org/10.3390/w15020362
Liu S, Luo X, Zheng H, Zhang C, Wang Y, Chen K, Wang J. Investigation on Water Levels for Cascaded Hydropower Reservoirs to Drawdown at the End of Dry Seasons. Water. 2023; 15(2):362. https://doi.org/10.3390/w15020362
Chicago/Turabian StyleLiu, Shuangquan, Xuhan Luo, Hao Zheng, Congtong Zhang, Youxiang Wang, Kai Chen, and Jinwen Wang. 2023. "Investigation on Water Levels for Cascaded Hydropower Reservoirs to Drawdown at the End of Dry Seasons" Water 15, no. 2: 362. https://doi.org/10.3390/w15020362
APA StyleLiu, S., Luo, X., Zheng, H., Zhang, C., Wang, Y., Chen, K., & Wang, J. (2023). Investigation on Water Levels for Cascaded Hydropower Reservoirs to Drawdown at the End of Dry Seasons. Water, 15(2), 362. https://doi.org/10.3390/w15020362






