Prediction of the Periglacial Debris Flow in Southeast Tibet Based on Imbalanced Small Sample Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Method
2.2.1. Borderline SMOTE
2.2.2. Random Forest (RF)
2.2.3. Support Vector Machine (SVM)
2.3. Data and Indicators
2.3.1. Data Sources
2.3.2. Basic Indicators
- -
- Meteorology
- -
- Topography
- -
- Geology
- -
- Underlying surface
3. Results and Discussion
3.1. Selection of Prediction Indicators
3.2. Modeling and Comparative Analysis
3.2.1. Training and Validation
3.2.2. Testing
3.2.3. Comparison
I-D Model and I-D-A Model
Resampling Model and Non-Resampling Model
SMOTE Model and Borderline SMOTE Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Decaulne, A.; Saemundsson, P.; Petursson, O. Debris flow triggered by rapid snowmelt: A case study in the glei.arhjalli area, northwestern Iceland. Geogr. Ann. Ser. A Phys. Geogr. 2005, 87, 487–500. [Google Scholar] [CrossRef]
- Legg, N.T.; Meigs, A.J.; Grant, G.E.; Kennard, P. Debris flow initiation in proglacial gullies on Mount Rainier, Washington. Geomorphology 2014, 226, 249–260. [Google Scholar] [CrossRef]
- Wei, R.; Zeng, Q.; Davies, T.; Yuan, G.; Wang, K.; Xue, X.; Yin, Q. Geohazard cascade and mechanism of large debris flows in Tianmo gully, SE Tibetan Plateau and implications to hazard monitoring. Eng. Geol. 2018, 233, 172–182. [Google Scholar] [CrossRef]
- Kumar, A.; Bhambri, R.; Tiwari, S.K.; Verma, A.; Gupta, A.K.; Kawishwar, P. Evolution of debris flow and moraine failure in the Gangotri Glacier region, Garhwal Himalaya: Hydro-geomorphological aspects. Geomorphology 2019, 333, 152–166. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. 2015, 20, 1729–1742. [Google Scholar] [CrossRef]
- Yu, G.-A.; Yao, W.; Huang, H.Q.; Liu, Z. Debris flows originating in the mountain cryosphere under a changing climate: A review. Prog. Phys. Geogr. Earth Environ. 2020, 45, 339–374. [Google Scholar] [CrossRef]
- Deng, M.; Chen, N.; Ding, H. Rainfall characteristics and thresholds for periglacial debris flows in the Parlung Zangbo Basin, southeast Tibetan Plateau. J. Earth Syst. Sci. 2018, 127, 11. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, J.J.; Wang, J.C.; Chen, L.; Yang, D.X. Formation mechanism and disaster characteristics of debris flow in the Tianmo gully in Tibet. Hydrogeol. Eng. Geol. 2019, 46, 144–153. [Google Scholar]
- Gruber, S.; Haeberli, W. Permafrost in steep bedrock slopes and its temperature-related destabilization following climate change. J. Geophys. Res. Atmos. 2007, 112, F2. [Google Scholar] [CrossRef]
- Krautblatter, M.; Funk, D.; Günzel, F.K. Why permafrost rocks become unstable: A rock-ice-mechanical model in time and space. Earth Surf. Process. Landforms 2013, 38, 876–887. [Google Scholar] [CrossRef]
- Harris, C.; Davies, M.C.R.; Etzelmüller, B. The assessment of potential geotechnical hazards associated with mountain permafrost in a warming global climate. Permafr. Periglac. Process. 2001, 12, 145–156. [Google Scholar] [CrossRef]
- Iverson, R.; Vallance, J. New views of granular mass flows. Geology 2001, 29, 115–118. [Google Scholar] [CrossRef]
- Liang, W.-J.; Zhuang, D.-F.; Jiang, D.; Pan, J.-J.; Ren, H.-Y. Assessment of debris flow hazards using a Bayesian Network. Geomorphology 2012, 171–172, 94–100. [Google Scholar] [CrossRef]
- Staley, D.M.; Negri, J.A.; Kean, J.W.; Laber, J.L.; Tillery, A.C.; Youberg, A.M. Prediction of spatially explicit rainfall intensity–duration thresholds for post-fire debris-flow generation in the western United States. Geomorphology 2017, 278, 149–162. [Google Scholar] [CrossRef]
- Addison, P.; Oommen, T.; Sha, Q. Assessment of post-wildfire debris flow occurrence using classifier tree. Geomat. Nat. Hazards Risk 2019, 10, 505–518. [Google Scholar] [CrossRef]
- Walter, F.; Amann, F.; Kos, A.; Kenner, R.; Phillips, M.; de Preux, A.; Huss, M.; Tognacca, C.; Clinton, J.; Diehl, T.; et al. Direct observations of a three million cubic meter rock-slope collapse with almost immediate initiation of ensuing debris flows. Geomorphology 2020, 351, 106933. [Google Scholar] [CrossRef]
- Michie, D.; Spiegelhalter, D.J.; Taylor, C.C. Machine Learning, Neural and Statistical Classification; Citeseer: Princeton, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Costache, R. Flash-Flood Potential assessment in the upper and middle sector of Prahova river catchment (Romania). A comparative approach between four hybrid models. Sci. Total. Environ. 2018, 659, 1115–1134. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Cui, Y.; Cheng, D.; Chan, D. Investigation of Post-Fire Debris Flows in Montecito. ISPRS Int. J. Geo-Inf. 2018, 8, 5. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Zhang, Y.; Chen, C.P. A SVM controller for the stable walking of biped robots based on small sample sizes. Appl. Soft Comput. 2016, 38, 738–753. [Google Scholar] [CrossRef]
- Squarcina, L.; Villa, F.M.; Nobile, M.; Grisan, E.; Brambilla, P. Deep learning for the prediction of treatment response in depression. J. Affect. Disord. 2020, 281, 618–622. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Schlögl, M.; Stuetz, R.; Laaha, G.; Melcher, M. A comparison of statistical learning methods for deriving determining factors of accident occurrence from an imbalanced high resolution dataset. Accid. Anal. Prev. 2019, 127, 134–149. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Wang, J.; Wei, X.; Gong, Y. Training mixture of weighted SVM for object detection using EM algorithm. Neurocomputing 2015, 149, 473–482. [Google Scholar] [CrossRef]
- Cheng, Z.L.; Liang, S.; Liu, J.K.; Liu, D.X. Distribution and change of glacier lakes in the upper Palongzangbu River. Bull. Soil Water Conserv. 2012, 32, 8–12. [Google Scholar]
- Liu, J.; Yao, X.J.; Gao, Y.P.; Qi, M.M.; Duan, H.; Zhang, D. Glacial Lake variation and hazard assessment of glacial lakes outburst in the Parlung Zangbo River Basin. J. Lake Sci. 2019, 31, 244–255. [Google Scholar]
- Lv, R.R.; Tang, B.X.; Zhu, P.Y. Debris Flow and Environment in Tibet; Press of Chengdu Science and Technology: Chengdu, China, 1999. [Google Scholar]
- Jia, Y. The Impact Mechanism of Climate Warming on Mountain Hazards in the Southeast Tibet. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2018; pp. 118–143. [Google Scholar]
- Zeng, X.Y.; Zhang, J.J.; Yang, D.X.; Wang, J.C.; Gao, B.; Li, Y. Characteristics and Geneses of Low Frequency Debris Flow along Parlongzangbo River Zone: Take Chaobulongba Gully as an Example. Sci. Technol. Eng. 2019, 19, 103–107. [Google Scholar]
- Li, Y.L.; Wang, J.C.; Chen, L.; Liu, J.; Yang, D.; Zhang, J. Characteristics and geneses of the group-occurring debris flows along Parlung Zangbo River zone in 2016. Res. Soil. Water Conserv. 2018, 25, 401–406. [Google Scholar]
- Dong, L.-J.; Li, X.-B.; Peng, K. Prediction of rockburst classification using Random Forest. Trans. Nonferrous Met. Soc. China 2013, 23, 472–477. [Google Scholar] [CrossRef]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Hui, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3644, pp. 878–887. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Quinlan, J.R. Introduction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill: Boston, MA, USA, 1997. [Google Scholar]
- Dimitriadis, S.I.; Liparas, D.; Dni, A. How random is the random forest? Random forest algorithm on the service of structural imaging biomarkers for Alzheimer’s disease: From Alzheimer’s disease neuroimaging initiative (ADNI) database. Neural Regen. Res. 2018, 13, 962–970. [Google Scholar] [CrossRef]
- Ming, D.; Zhou, T.; Wang, M.; Tan, T. Land cover classification using random forest with genetic algorithm-based parameter optimization. J. Appl. Remote. Sens. 2016, 10, 035021. [Google Scholar] [CrossRef]
- Zhou, T.N.; Ming, D.P.; Zhao, R. Land cover classification based on algorithm of parameter optimization random forests. Sci. Surv. Mapp. 2017, 42, 88–94. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Rebetez, M.; Lugon, R.; Baeriswyl, P.A. Climatic change and debris flows in high mountain regions: The case study of the Ritigraben Torrent (Swiss Alps). In Climatic Change at High Elevation Sites; Diaz, H.F., Beniston, M., Bradley, R.S., Eds.; Springer: Dordrecht, The Netherlands, 1997; pp. 139–157. [Google Scholar]
- Chleborad, A.F. Use of Air Temperature Data to Anticipate the Onset of Snowmelt-Season Landslides (USGS Open-File Report 98-0124); US Geological Survey: Reston, VA, USA, 1998. [Google Scholar]
- Deng, M.; Chen, N.; Liu, M. Meteorological factors driving glacial till variation and the associated periglacial debris flows in Tianmo Valley, south-eastern Tibetan Plateau. Nat. Hazards Earth Syst. Sci. 2017, 17, 345–356. [Google Scholar] [CrossRef]
- Chen, N.S.; Wang, Z.; Tian, S.F.; Zhu, Y.H. Study on debris flow process induced by moraine soil mass failure. Quat. Sci. 2019, 39, 1235–1245. [Google Scholar]
- Greenway, D. Vegetation and Slope Stability. In Slope Stability: Geotechnical Engineering and Geomorphology; Anderson, M.G., Richards, K.S., Eds.; John Wiley and Sons Ltd: Hoboken, NJ, USA, 1987. [Google Scholar]
- Wilkinson, P.L.; Anderson, M.G.; Lloyd, D.M. An integrated hydrological model for rain-induced landslide prediction. Earth Surf. Process. Landforms 2002, 27, 1285–1297. [Google Scholar] [CrossRef]
- Coppin, N.J.; Richards, I.G. Use of Vegetation in Civil Engineering; Construction Industry Research and Information Association (CIRIA): London, UK, 1990. [Google Scholar]
- Emadi-Tafti, M.; Ataie-Ashtiani, B.; Hosseini, S.M. Integrated impacts of vegetation and soil type on slope stability: A case study of Kheyrud Forest, Iran. Ecol. Model. 2021, 446, 109498. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flow Mechanics, Prediction and Countermeasures; Taylor and Francis Group: London, UK, 2007; p. 108. [Google Scholar]
- Du, J.; Fan, Z.-J.; Xu, W.-T.; Dong, L.-Y. Research Progress of Initial Mechanism on Debris Flow and Related Discrimination Methods: A Review. Front. Earth Sci. 2021, 9, 629567. [Google Scholar] [CrossRef]
- Bradley, P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recogn. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef]
- Lee, T.; Kim, M.; Kim, S.-P. Improvement of P300-Based Brain–Computer Interfaces for Home Appliances Control by Data Balancing Techniques. Sensors 2020, 20, 5576. [Google Scholar] [CrossRef]
- Lei, C.; Deng, J.; Cao, K.; Xiao, Y.; Ma, L.; Wang, W.; Ma, T.; Shu, C. A comparison of random forest and support vector machine approaches to predict coal spontaneous combustion in gob. Fuel 2019, 239, 297–311. [Google Scholar] [CrossRef]
- Tang, Z.; Mei, Z.; Liu, W.; Xia, Y. Identification of the key factors affecting Chinese carbon intensity and their historical trends using random forest algorithm. J. Geogr. Sci. 2020, 30, 743–756. [Google Scholar] [CrossRef]
- Caine, N. The Rainfall Intensity—Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar] [CrossRef]
- Abancó, C.; Hürlimann, M.; Moya, J.; Berenguer, M. Critical rainfall conditions for the initiation of torrential flows. Results from the Rebaixader catchment (Central Pyrenees). J. Hydrol. 2016, 541, 218–229. [Google Scholar] [CrossRef]
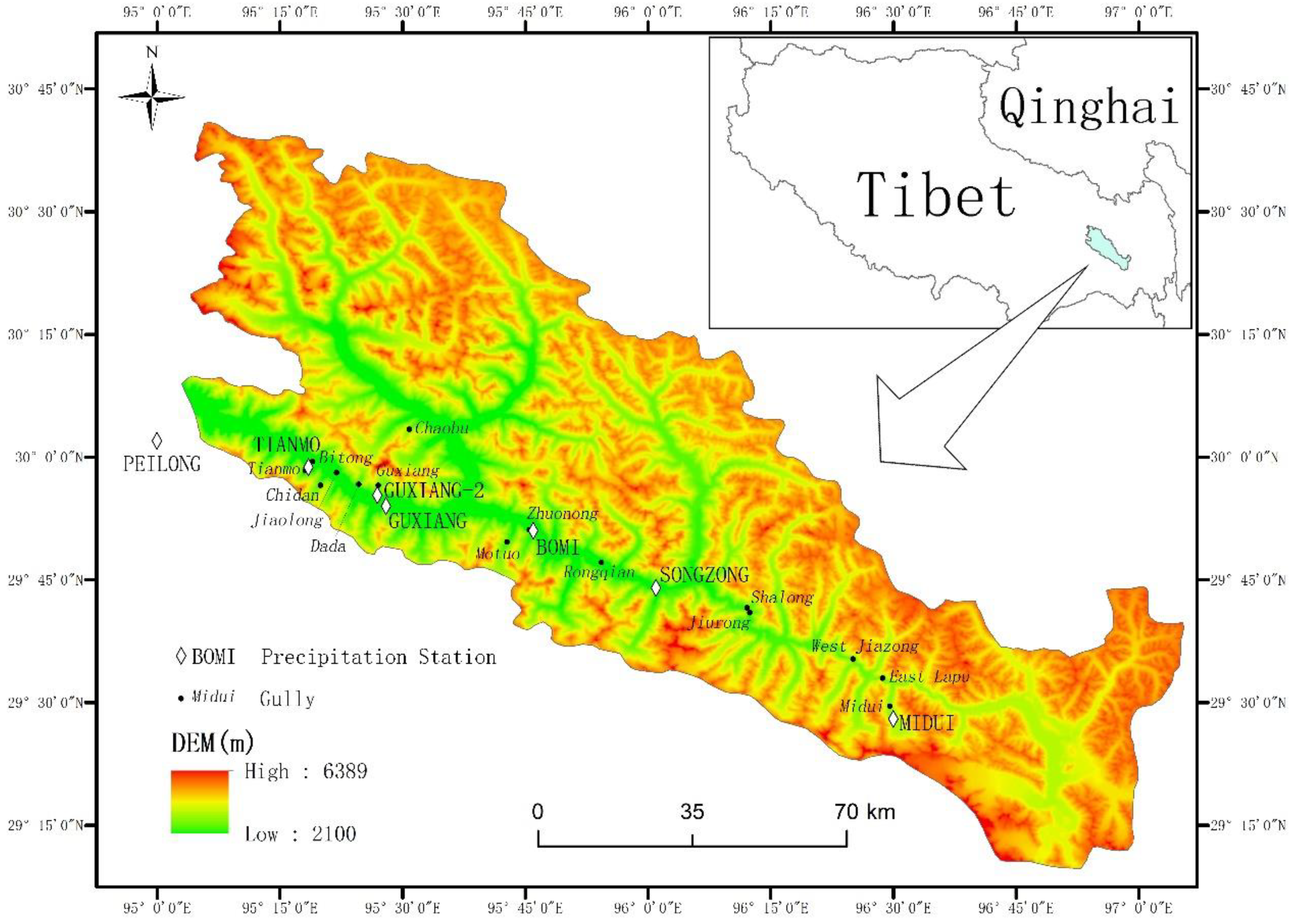

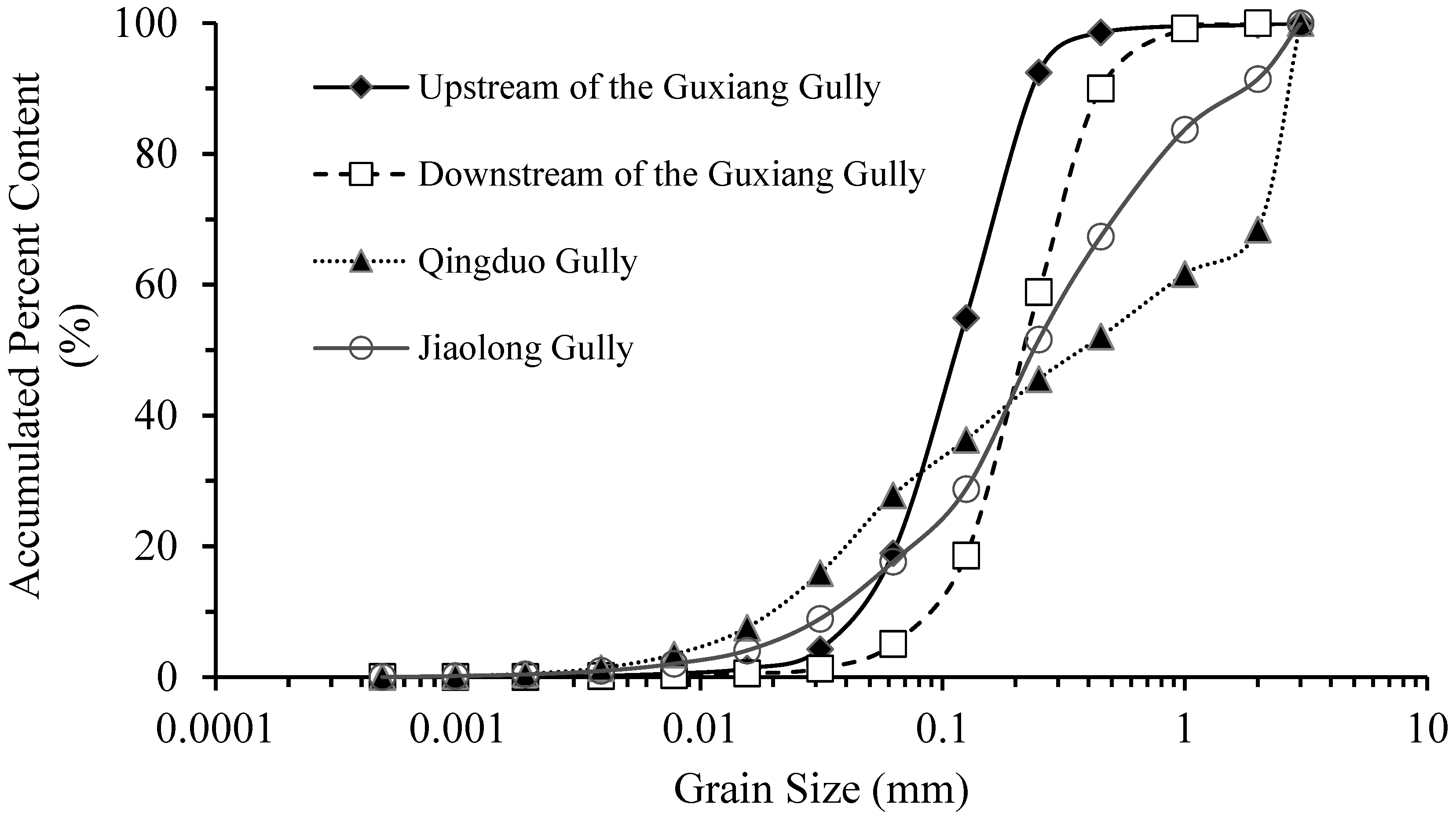
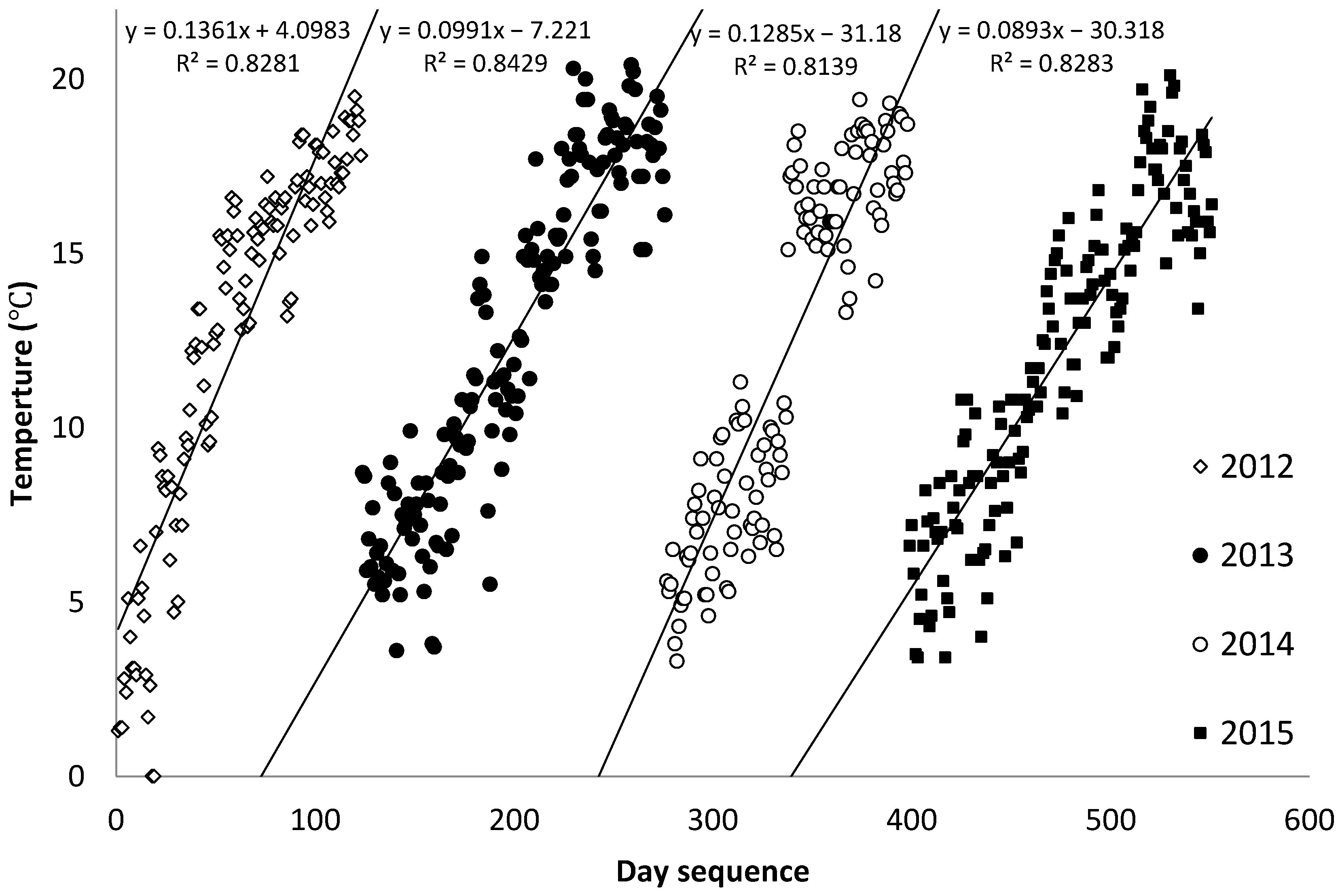

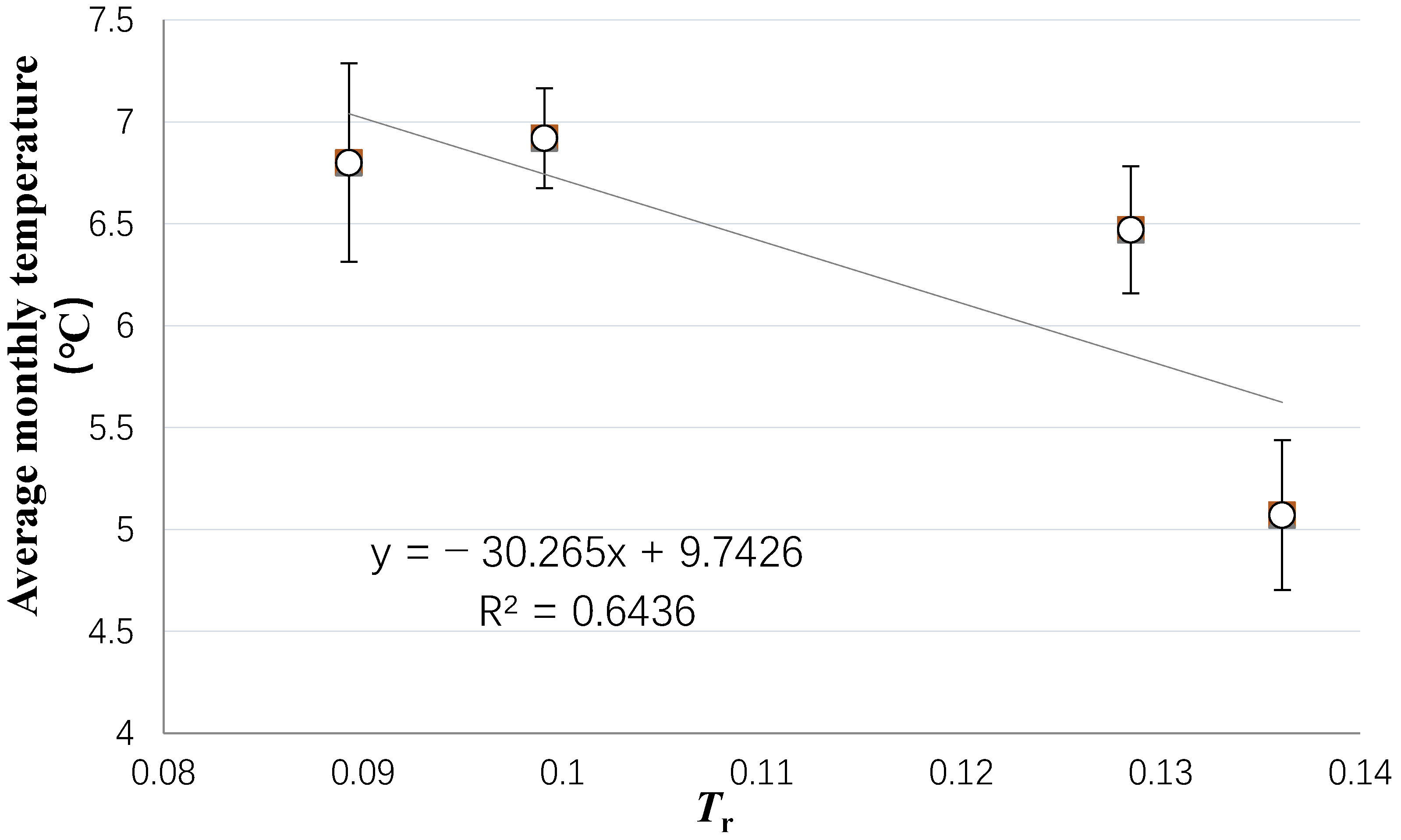
|
Gully No. | Gully |
Area (km2) |
Event No. | Date | Time |
Possible Causes |
Monitoring Station |
|---|---|---|---|---|---|---|---|
| 1 | Bitong | 24 | DF1 | 2016-09-05 | 06:30 | Snowmelt, Precipitation | PEILONG |
| DF2 | 2018-07-11 | 03:00 | Snowmelt, Precipitation | GUXIANG | |||
| 2 | Chaobu | 16 | DF3 | 2017-08-03 | 17:00 | Ice and Snow melt | GUXIANG |
| 3 | Chidan | 28 | DF4 | 2016-09-05 | 11:00 | Snowmelt, Precipitation | PEILONG |
| 4 | Dada | 3 | DF5 | 2020-07-10 | 16:10 | Snowmelt, Precipitation | TIANMO |
| 5 | East Lapu | 4 | DF6 * | 2013-07-05 | 21:00 | Snowmelt, Precipitation | MIDUI/ SONGZONG |
| DF7 * | 2014-07-24 | 20:00 | Snowmelt, Precipitation | ||||
| DF8 | 2018-05-22 | 17:00 | Snowmelt, Precipitation | ||||
| 6 | Guxiang | 25 | DF9 | 2020-07-09 | 21:00 | Ice and Snow melt | GUXIANG-2 |
| 7 | Jiaolong | 22 | DF10 | 2016-09-05 | —— | Snowmelt, Precipitation | PEILONG |
| 8 | Jiurong | 7 | DF11 * | 2014-08.18 | 23:00 | Snowmelt, Precipitation | SONGZONG |
| DF12 * | 2014-08-23 | 02:00 | Snowmelt, Precipitation | ||||
| DF13 * | 2015-08-04 | 22:30 | Snowmelt, Precipitation | ||||
| DF14 * | 2015-08-20 | 07:40 | Snowmelt, Precipitation | ||||
| 9 | Midui | 1 | DF15 * | 2015-08-19 | 23:30 | Snowmelt, Precipitation | MIDUI/ SONGZONG |
| 10 | Motuo | 3 | DF16 * | 2015-08-19 | 22:30 | Snowmelt, Precipitation | BOMI/ SONGZONG |
| 11 | Rongqian | 5 | DF17 * | 2015-08-19 | 18:30 | Snowmelt, Precipitation | BOMI/ SONGZONG |
| 12 | Shalong | 15 | DF18 * | 2015-08-19 | 21:00 | Snowmelt, Precipitation | SONGZONG |
| 13 | Tianmo | 18 | DF19 | 2018-07-11 | 03:00 | Snowmelt, Precipitation | GUXIANG |
| 14 | West Jiazong | 2 | DF20 * | 2012-09-22 | 09:00 | Snowmelt, Precipitation | MIDUI |
| DF21 * | 2013-07-05 | 21:00 | Snowmelt, Precipitation | ||||
| DF22 * | 2013-07-31 | 18:00 | Snowmelt, Precipitation | ||||
| 15 | Zhuonong | 5 | DF23 * | 2015-08-19 | 19:20 | Snowmelt, Precipitation | BOMI/ SONGZONG |
| Type | Content | Sources |
|---|---|---|
| Precipitation | Hourly data of the stations of PEIlONG, BOMI, GUXIANG, SONGZONG, MIDUI on the day and the adjacent days of debris flow events in 2012–2018, and daily data of the 10 days before the event day; hourly data of GUXIANG-2 and TIANMO stations on the day and the adjacent days of debris flow events in 2020, and daily data of the 7 days before the event day | Data from 2012 to 2018 collected from the Bomi Geologic Hazard Observation Station of the Institute of Mountain Hazards and Environment, CAS; data of 2020 sourced from the field observation |
| Temperature | Daily maximum, minimum, and average data of Bomi station in 2012–2020 and Tianmo station in 2020 on the event day and the 15 days before the event day | Data of the Bomi station collected from the China Meteorological Data Service Centre; data of the Tianmo station sourced from the field observation |
| Landform | DEM of the Parlong Zangbo Basin | SRTM 90 m DEM and ASTER 30 m GDEMv2 |
| Geology | National 1:2.5 million geological map of China | National Geological Archives Data Center, China |
| Vegetation Cover | NDVI of the study area in typical months from 2012 to 2020 | MODIS 500 m monthly synthetic product |
| Snow Cover | Snow cover products from 2012 to 2015 | Maximum_Snow_Extent MOD_Grid_Snow_500 m products of MOD10A2 |
| No. |
Precipitation Station | Year | Date |
Event No. * | D (h) |
I
a (mm/h) |
I
m
(mm/h) |
A
3 (mm) |
A
5 (mm) |
A
10 (mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | BOMI | 2012 | 09-21 | 1 | 2 | 0.8 | 1.0 | 10.0 | 14.2 | 21.3 |
| 2 | 2012 | 09-22 | 1 | 1 | 1.0 | 1.0 | 5.8 | 9.4 | 16.2 | |
| 3 | 2012 | 09-22 | 2 | 3 | 2.0 | 5.0 | 5.8 | 9.4 | 16.2 | |
| 4 | 2012 | 09-22 | 3 | 13 | 1.4 | 4.0 | 5.8 | 9.4 | 16.2 | |
| 5 | 2013 | 07-05 | 1 | 2 | 0.8 | 1.0 | 0.1 | 0.3 | 2.8 | |
| 6 | 2013 | 07-05 | 2 | 9 | 2.1 | 4.5 | 0.1 | 0.3 | 2.8 | |
| 7 | 2014 | 07-23 | 1 | 4 | 1.9 | 4.5 | 2.9 | 3.7 | 6.9 | |
| 8 | 2014 | 07-24 | 1 | 1 | 1.5 | 1.5 | 5.7 | 7.2 | 10.7 | |
| 9 | 2014 | 07-24 | 2 | 4 | 1.0 | 2.0 | 5.7 | 7.2 | 10.7 | |
| 10 | 2014 | 07-24 | 3 | 4 | 1.8 | 3.5 | 5.7 | 7.2 | 10.7 | |
| 11 | 2014 | 07-25 | 1 | 3 | 0.8 | 1.5 | 6.5 | 8.8 | 12.6 | |
| 12 | 2014 | 08-18 | 1 | 1 | 1.0 | 1.0 | 4.4 | 8.5 | 14.7 | |
| 13 | 2014 | 08-22 | 1 | 3 | 0.8 | 1.0 | 4.5 | 5.8 | 10.4 | |
| 14 | 2014 | 08-22 | 2 | 1 | 1.0 | 1.0 | 4.5 | 5.8 | 10.4 | |
| 15 | 2014 | 08-22 | 3 | 3 | 0.7 | 1.0 | 4.5 | 5.8 | 10.4 | |
| 16 | 2014 | 08-22 | 4 | 2 | 1.3 | 1.5 | 4.5 | 5.8 | 10.4 | |
| 17 | 2014 | 08-22 | 5 | 2 | 1.8 | 2.0 | 4.5 | 5.8 | 10.4 | |
| 18 | 2014 | 08-23 | 1 | 14 | 1.0 | 3.5 | 7.3 | 9.4 | 14.1 | |
| 19 | SONGZONG | 2012 | 09-21 | 1 | 3 | 1.2 | 1.5 | 10.8 | 15.5 | 22.5 |
| 20 | 2012 | 09-21 | 2 | 4 | 1.9 | 2.5 | 10.8 | 15.5 | 22.5 | |
| 21 | 2012 | 09-22 | 1 | 11 | 2.9 | 7.0 | 12.5 | 17.7 | 25.8 | |
| 22 | 2012 | 09-23 | 1 | 10 | 1.6 | 2.5 | 28.4 | 36.7 | 49.0 | |
| 23 | 2013 | 07-05 | 1 | 5 | 1.3 | 3.0 | 0.8 | 0.9 | 2.8 | |
| 24 | 2013 | 07-05 | 2 | 1 | 1.5 | 1.5 | 0.8 | 0.9 | 2.8 | |
| 25 | 2013 | 07-06 | 1 | 4 | 1.8 | 3.0 | 6.4 | 7.7 | 10.3 | |
| 26 | 2014 | 07-23 | 1 | 1 | 1.5 | 1.5 | 0.4 | 0.6 | 2.4 | |
| 27 | 2014 | 07-24 | 1 | 3 | 1.0 | 1.5 | 0.9 | 1.2 | 2.7 | |
| 28 | 2014 | 07-24 | 2 | 2 | 3.0 | 2.5 | 0.9 | 1.2 | 2.7 | |
| 29 | 2014 | 08-18 | 1 | 2 | 5.0 | 2.5 | 2.7 | 6.4 | 11.7 | |
| 30 | 2014 | 08-22 | 1 | 4 | 0.6 | 2.5 | 3.9 | 5.3 | 9.4 | |
| 31 | 2014 | 08-23 | 1 | 9 | 2.4 | 5.0 | 8.6 | 11.5 | 16.2 | |
| 32 | 2015 | 08-03 | 1 | 2 | 4.0 | 2.5 | 0.0 | 0.0 | 0.2 | |
| 33 | 2015 | 08-04 | 1 | 3 | 3.2 | 6.0 | 6.5 | 7.8 | 9.1 | |
| 34 | 2015 | 08-04 | 2 | 2 | 3.8 | 5.0 | 6.5 | 7.8 | 9.1 | |
| 35 | 2015 | 08-17 | 1 | 2 | 1.0 | 1.0 | 1.0 | 1.3 | 2.1 | |
| 36 | 2015 | 08-17 | 2 | 3 | 1.2 | 1.5 | 1.0 | 1.3 | 2.1 | |
| 37 | 2015 | 08-17 | 3 | 4 | 0.6 | 1.0 | 1.0 | 1.3 | 2.1 | |
| 38 | 2015 | 08-18 | 1 | 1 | 1.0 | 1.0 | 7.0 | 8.6 | 10.3 | |
| 39 | 2015 | 08-19 | 1 | 9 | 1.1 | 2.0 | 11.4 | 14.7 | 18.3 | |
| 40 | 2015 | 08-19 | 2 | 10 | 2.5 | 6.0 | 11.4 | 14.7 | 18.3 | |
| 41 | MIDUI | 2012 | 09-22 | 1 | 17 | 1.3 | 3.0 | 3.9 | 5.9 | 10.3 |
| 42 | 2012 | 09-22 | 2 | 13 | 1.2 | 3.0 | 3.9 | 5.9 | 10.3 | |
| 43 | 2012 | 09-23 | 1 | 1 | 1.5 | 1.5 | 15.6 | 19.9 | 26.3 | |
| 44 | 2012 | 09-23 | 2 | 9 | 1.5 | 5.5 | 15.6 | 19.9 | 26.3 | |
| 45 | 2013 | 07-04 | 1 | 4 | 1.8 | 2.5 | 0.0 | 0.0 | 1.4 | |
| 46 | 2013 | 07-05 | 1 | 2 | 1.5 | 1.5 | 2.8 | 3.3 | 4.8 | |
| 47 | 2014 | 07-23 | 1 | 1 | 1.0 | 1.0 | 1.6 | 2.3 | 3.7 | |
| 48 | 2014 | 07-23 | 2 | 2 | 1.0 | 1.0 | 1.6 | 2.3 | 3.7 | |
| 49 | 2014 | 07-23 | 3 | 2 | 1.3 | 1.5 | 1.6 | 2.3 | 3.7 | |
| 50 | 2014 | 07-24 | 1 | 6 | 2.1 | 3.5 | 3.4 | 4.7 | 6.4 | |
| 51 | 2014 | 08-22 | 1 | 4 | 0.8 | 1.0 | 0.9 | 2.1 | 5.4 | |
| 52 | 2014 | 08-23 | 1 | 9 | 1.7 | 2.5 | 3.1 | 4.5 | 7.3 | |
| 53 | 2014 | 08-24 | 1 | 8 | 1.6 | 3.5 | 8.6 | 11.2 | 15.1 |
| Year | Date | C v 5 | C v 10 | C v 15 | T 5 | T 10 | T 15 | T a |
|---|---|---|---|---|---|---|---|---|
| 2012 | 09-22 | 0.29 | 0.37 | 0.37 | 14.1 | 13.7 | 14.4 | 43.3 |
| 2012 | 09-21 | 0.30 | 0.38 | 0.38 | 13.8 | 13.8 | 14.6 | 44.0 |
| 2012 | 09-23 | 0.40 | 0.44 | 0.41 | 13.9 | 13.4 | 14.1 | 39.6 |
| 2013 | 07-06 | 0.11 | 0.26 | 0.29 | 18.7 | 17.5 | 17.5 | 56.8 |
| 2013 | 07-04 | 0.14 | 0.33 | 0.30 | 17.9 | 16.8 | 17.5 | 55.8 |
| 2013 | 07-05 | 0.11 | 0.29 | 0.30 | 18.5 | 17.2 | 17.6 | 56.4 |
| 2013 | 07-31 | 0.26 | 0.30 | 0.33 | 18.5 | 18.0 | 17.8 | 54.3 |
| 2014 | 07-23 | 0.23 | 0.34 | 0.29 | 18.1 | 17.2 | 17.6 | 56.6 |
| 2014 | 07-25 | 0.23 | 0.24 | 0.30 | 18.2 | 17.2 | 17.4 | 53.6 |
| 2014 | 07-24 | 0.20 | 0.36 | 0.30 | 18.4 | 17.1 | 17.5 | 55.1 |
| 2014 | 08-18 | 0.55 | 0.39 | 0.32 | 14.6 | 16.3 | 17.2 | 42.0 |
| 2014 | 08-22 | 0.26 | 0.42 | 0.35 | 16.3 | 15.6 | 16.5 | 48.9 |
| 2014 | 08-23 | 0.30 | 0.41 | 0.35 | 16.0 | 15.3 | 16.2 | 45.8 |
| 2014 | 08-24 | 0.35 | 0.42 | 0.36 | 15.6 | 15.0 | 16.0 | 44.2 |
| 2015 | 08-04 | 0.15 | 0.19 | 0.25 | 17.3 | 17.2 | 16.6 | 54.6 |
| 2015 | 08-03 | 0.14 | 0.19 | 0.25 | 17.0 | 16.8 | 16.5 | 53.4 |
| 2015 | 08-17 | 0.31 | 0.37 | 0.31 | 18.8 | 17.9 | 17.9 | 54.2 |
| 2015 | 08-18 | 0.46 | 0.41 | 0.38 | 18.0 | 18.0 | 17.7 | 50.6 |
| 2015 | 08-19 | 0.46 | 0.49 | 0.43 | 17.0 | 17.9 | 17.6 | 47.8 |
| 2015 | 08-20 | 0.38 | 0.53 | 0.48 | 15.9 | 17.5 | 17.3 | 44.4 |
| Gully | Hd (m) | Sa (°) | Gg (°) | As | P (%) | F | L |
|---|---|---|---|---|---|---|---|
| Zhuonong | 1832.62 | 32 | 11.4 | East–Northwest | −65.5 | 0.33 | Extremely hard |
| West Jiazong | 1858.96 | 37 | 34.0 | South–Southwest | −12.6 | 0.00 | Extremely hard |
| Shalong | 1508.94 | 32 | 13.4 | Southwest–West | −3.8 | 0.31 | Secondary hard |
| Rongqian | 1993.82 | 32 | 29.4 | South–Southwest | −4.9 | 0.10 | Extremely hard |
| Motuo | 1510.14 | 27 | 28.6 | East–Southeast | −2.2 | 0.25 | Extremely hard |
| Midui | 1262.14 | 34 | 31.8 | East–Northeast | 4.2 | 0.33 | Secondary hard |
| Jiurong | 1751.91 | 36 | 23.5 | West–Northwest | −28.0 | 0.21 | Secondary hard |
| East Lapu | 1563.89 | 36 | 30.1 | South–Southwest | 3.1 | 0.10 | Extremely hard |
| Gully | NDVI | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Training/Validation Phase | Testing Phase | ||||||||
| 2012-08 | 2013-06 | 2014-07 | 2015-07 | 2016-08 | 2017-07 | 2018-04 | 2018-06 | 2020-07 | |
| Tianmo | 0.12 | 0.18 | 0.20 | 0.70 | 0.40 | 0.51 | |||
| Chidan | 0.23 | 0.37 | 0.31 | 0.75 | 0.69 | ||||
| Jiaolong | 0.12 | 0.16 | 0.17 | 0.51 | 0.37 | ||||
| Chaobu | 0.13 | 0.20 | 0.52 | 0.83 | 0.64 | ||||
| Bitong | 0.12 | 0.18 | 0.20 | 0.51 | 0.44 | 0.29 | 0.39 | ||
| Dada | 0.16 | 0.19 | 0.43 | 0.61 | 0.39 | ||||
| Guxiang | 0.12 | 0.17 | 0.19 | 0.42 | 0.30 | 0.28 | |||
| Zhuonong | 0.24 | 0.48 | 0.31 | 0.69 | |||||
| West Jiazong | 0.16 | 0.42 | 0.28 | 0.43 | |||||
| Shalong | 0.18 | 0.27 | 0.23 | 0.38 | |||||
| Rongqian | 0.24 | 0.34 | 0.22 | 0.51 | |||||
| Motuo | 0.29 | 0.47 | 0.38 | 0.62 | |||||
| Midui | 0.06 | 0.11 | 0.08 | 0.16 | |||||
| Jiurong | 0.34 | 0.41 | 0.42 | 0.57 | 0.22 | ||||
| East Lapu | 0.26 | 0.30 | 0.23 | 0.32 | 0.04 | ||||
| Gully | ASCd | MSCa | |||
|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2015 | ||
| Zhuonong | 89.2 | 93.6 | 86.0 | 93.0 | 86.5 |
| West Jiazong | 84.3 | 91.6 | 100.0 | 80.0 | 98.5 |
| Shalong | 43.8 | 100.0 | 80.1 | 94.5 | 93.1 |
| Rongqian | 93.7 | 100.0 | 83.9 | 79.5 | 77.5 |
| Motuo | 90.9 | 100.0 | 86.3 | 100.0 | 100.0 |
| Midui | 80.0 | 90.0 | 80.0 | 100.0 | 100.0 |
| Jiurong | 100.0 | 100.0 | 82.3 | 100.0 | 92.4 |
| East Lapu | 91.4 | 91.4 | 100.0 | 96.0 | 90.9 |
| Rank | Correlation Analysis | SVM-RFE | GainRatio | |||
|---|---|---|---|---|---|---|
| Coefficient | Indicator | Average Merit | Indicator | Score | Indicator | |
| 1 | 0.42 ** | NDVIt | 23 ± 2.7 | D | 0.47 | Cv10 |
| 2 | −0.36 ** | Tr | 22.5 ± 3.0 | T10 | 0.47 | Cv15 |
| 3 | 0.34 ** | D | 21.4 ± 2.6 | A5 | 0.26 | Cv5 |
| 4 | 0.30 ** | Cv15 | 21.2 ± 1.5 | T15 | 0.24 | A3 |
| 5 | 0.27 ** | T10 | 20.3 ± 4.1 | Cv15 | 0.24 | Im |
| 6 | 0.26 ** | Im | 20.3 ± 1.1 | A10 | 0.16 | NDVIt |
| 7 | 0.25 ** | A3 | 19.8 ± 1.9 | Im | 0.11 | T10 |
| 8 | 0.24 ** | Cv5 | 19.3 ± 2.1 | Cv10 | 0.11 | T15 |
| 9 | 0.24 ** | Cv10 | 18.4 ± 1.4 | NDVIt | 0.11 | D |
| 10 | 0.23 ** | A5 | 16.9 ± 5.2 | Ia | 0.06 | Ia |
| 11 | 0.22 ** | Ia | 15.1 ± 2.7 | A3 | 0 | A10 |
| 12 | 0.21 ** | T15 | 14.1 ± 0.3 | Sa | 0 | T5 |
| 13 | 0.19 * | A10 | 12.4 ± 1.0 | Hd | 0 | A5 |
| 14 | 0.11 | Sa | 8.8 ± 3.2 | ASCd | 0 | MSCa |
| 15 | 0.08 | T5 | 8.8 ± 4.3 | Cv5 | 0 | ASCd |
| 16 | 0.06 | ASCd | 8.3 ± 2.8 | T5 | 0 | F |
| 17 | −0.06 | L | 8.1 ± 4.7 | MSCa | 0 | P |
| 18 | 0.039 | A | 6.8 ± 3.6 | Gg | 0 | As |
| 19 | 0.03 | As | 6.7 ± 1.9 | As | 0 | NDVIs |
| 20 | −0.03 | F | 6.4 ± 2.65 | P | 0 | Gg |
| 21 | −0.02 | Ta | 6.3 ± 3.55 | NDVIs | 0 | A |
| 22 | −0.02 | Hd | 6.2 ± 3.25 | Ta | 0 | Hd |
| 23 | 0.02 | P | 5.7 ± 3.44 | L | 0 | L |
| 24 | 0.01 | MSCa | 4.1 ± 2.74 | F | 0 | Sa |
| 25 | 0.01 | Gg | 4.1 ± 3.05 | A | 0 | Ta |
| 26 | 0.01 | NDVIs | ||||
| True Class | Predicted Class | |
|---|---|---|
| + | − | |
| + | TP | FN |
| – | FP | TN |
| Phase | Model | Class | TPR | FPR | Precision | F-Measure | MCC | AUC |
|---|---|---|---|---|---|---|---|---|
|
Training and Validation | RF | No | 0.966 | 0.013 | 0.986 | 0.976 | 0.953 | 0.997 |
| Yes | 0.987 | 0.034 | 0.967 | 0.977 | ||||
| WA | 0.977 | 0.023 | 0.977 | 0.977 | ||||
| SVM | No | 0.886 | 0.034 | 0.964 | 0.923 | 0.855 | 0.926 | |
| Yes | 0.966 | 0.114 | 0.894 | 0.929 | ||||
| WA | 0.926 | 0.074 | 0.929 | 0.926 | ||||
| LSVM | No | 0.765 | 0.342 | 0.691 | 0.726 | 0.425 | 0.711 | |
| Yes | 0.658 | 0.235 | 0.737 | 0.695 | ||||
| WA | 0.711 | 0.289 | 0.714 | 0.711 | ||||
| Testing | RF | No | 0.750 | 0.222 | 0.750 | 0.750 | 0.528 | 0.778 |
| Yes | 0.778 | 0.250 | 0.778 | 0.778 | ||||
| WA | 0.765 | 0.237 | 0.765 | 0.765 | ||||
| SVM | No | 0.500 | 0.222 | 0.667 | 0.571 | 0.290 | 0.639 | |
| Yes | 0.778 | 0.500 | 0.636 | 0.700 | ||||
| WA | 0.647 | 0.369 | 0.651 | 0.639 | ||||
| LSVM | No | 0.375 | 0.111 | 0.750 | 0.500 | 0.311 | 0.632 | |
| Yes | 0.889 | 0.625 | 0.615 | 0.727 | ||||
| WA | 0.647 | 0.383 | 0.679 | 0.620 |
| Phase | Model | RF | SVM | LSVM | |||
|---|---|---|---|---|---|---|---|
| Class | No | Yes | No | Yes | No | Yes | |
|
Training and Validation | No | 144 | 5 | 132 | 17 | 114 | 35 |
| Yes | 2 | 147 | 5 | 144 | 51 | 98 | |
| Testing | No | 6 | 2 | 4 | 4 | 3 | 5 |
| Yes | 2 | 7 | 2 | 7 | 1 | 8 | |
| No. | Gully | Date | Station | A 3 | D | I m | NDVI t | S a | C v 15 | T 10 | Debris Flow | RF | SVM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Chidan | 2016-09-05 | PEILONG | 21.75 | 15.00 | 4.70 | 0.69 | 30.70 | 0.43 | 16.80 | Yes | √ | √ |
| 2 | Jiaolong | 2016-09-05 | PEILONG | 21.75 | 15.00 | 4.70 | 0.37 | 36.20 | 0.43 | 16.80 | Yes | √ | √ |
| 3 | Bitong | 2016-09-05 | PEILONG | 21.75 | 15.00 | 4.70 | 0.44 | 34.50 | 0.43 | 16.80 | Yes | √ | √ |
| 4 | Chaobu | 2017-08-03 | GUXIANG | 3.10 | 1.00 | 0.20 | 0.64 | 35.00 | 0.17 | 18.30 | Yes | √ | × |
| 5 | Chaobu | 2017-08-02 | GUXIANG | 0.09 | 6.00 | 1.60 | 0.64 | 35.00 | 0.17 | 18.40 | No | √ | √ |
| 6 | Guxiang | 2017-08-03 | GUXIANG | 3.10 | 1.00 | 0.20 | 0.30 | 35.60 | 0.17 | 18.30 | No | √ | √ |
| 7 | East Lapu | 2018-05-22 | SONGZONG | 0.00 | 0.00 | 0.00 | 0.04 | 36.00 | 0.21 | 14.00 | Yes | × | × |
| 8 | East Lapu | 2018-05-21 | SONGZONG | 0.00 | 0.00 | 0.00 | 0.01 | 36.00 | 0.21 | 13.10 | No | √ | √ |
| 9 | Jiurong | 2018-05-22 | SONGZONG | 0.00 | 0.00 | 0.00 | 0.22 | 36.00 | 0.21 | 14.00 | No | √ | √ |
| 10 | Tianmo | 2018-07-11 | GUXIANG | 12.94 | 10.00 | 3.10 | 0.40 | 37.70 | 0.24 | 18.20 | Yes | √ | √ |
| 11 | Bitong | 2018-07-11 | GUXIANG | 12.94 | 10.00 | 3.10 | 0.29 | 34.50 | 0.24 | 18.20 | Yes | √ | √ |
| 12 | Guxiang | 2018-07-11 | GUXIANG | 12.94 | 10.00 | 3.10 | 0.28 | 35.60 | 0.24 | 18.20 | No | × | × |
| 13 | Dada | 2020-07-09 | TIANMO | 0.65 | 2.35 | 6.00 | 0.39 | 33.00 | 0.37 | 16.26 | No | √ | × |
| 14 | Dada | 2020-07-10 | TIANMO | 6.50 | 3.00 | 7.60 | 0.39 | 33.00 | 0.35 | 16.19 | Yes | √ | √ |
| 15 | Tianmo | 2020-07-10 | TIANMO | 6.50 | 3.00 | 7.60 | 0.51 | 37.70 | 0.35 | 16.19 | No | × | × |
| 16 | Guxiang | 2020-07-08 | GUXIANG-2 | 0.20 | 0.00 | 0.00 | 0.39 | 35.60 | 0.37 | 15.98 | No | √ | × |
| 17 | Guxiang | 2020-07-09 | GUXIANG-2 | 0.35 | 3.80 | 2.33 | 0.39 | 35.60 | 0.37 | 16.26 | Yes | × | √ |
| Dependent Variable | Independent Variable | Standardized Coefficients | t-Value | p-Value | F-Value | Adjusted R2 |
|---|---|---|---|---|---|---|
| RF outputs | A3 | 0.790 | 4.986 | 0.000 | 24.862 | 0.599 |
| SVM outputs | Cv15 | 0.818 | 5.891 | 0.000 | 19.167 | 0.694 |
| T10 | 0.338 | 2.433 | 0.029 |
| Phase | Model | Class | TPR | FPR | MCC | ROC |
|---|---|---|---|---|---|---|
|
Training and Validation | Original | No | 0.966 | 0.013 | 0.953 | 0.997 |
| Yes | 0.987 | 0.034 | ||||
| WA | 0.977 | 0.023 | ||||
| Without A3 | No | 0.946 | 0.020 | 0.927 | 0.995 | |
| Yes | 0.980 | 0.054 | ||||
| WA | 0.963 | 0.037 | ||||
| Non-resample | No | 0.980 | 0.375 | 0.664 | 0.947 | |
| Yes | 0.625 | 0.020 | ||||
| WA | 0.945 | 0.341 | ||||
| SMOTE | No | 0.966 | 0.028 | 0.939 | 0.995 | |
| Yes | 0.972 | 0.034 | ||||
| WA | 0.969 | 0.031 | ||||
| Testing | Original | No | 0.750 | 0.222 | 0.528 | 0.778 |
| Yes | 0.778 | 0.250 | ||||
| WA | 0.765 | 0.237 | ||||
| Without A3 | No | 0.500 | 0.333 | 0.169 | 0.736 | |
| Yes | 0.667 | 0.500 | ||||
| WA | 0.588 | 0.422 | ||||
| Non-resample | No | 0.750 | 0.667 | 0.091 | 0.729 | |
| Yes | 0.333 | 0.250 | ||||
| WA | 0.529 | 0.446 | ||||
| SMOTE | No | 0.750 | 0.556 | 0.203 | 0.750 | |
| Yes | 0.444 | 0.250 | ||||
| WA | 0.588 | 0.394 |
| Model | Phase | Training & Validation | Testing | ||
|---|---|---|---|---|---|
| Class | No | Yes | No | Yes | |
| Original | No | 144 | 5 | 6 | 2 |
| Yes | 2 | 147 | 2 | 7 | |
| Without A3 | No | 141 | 8 | 4 | 4 |
| Yes | 3 | 146 | 3 | 6 | |
| Non-resample | No | 146 | 3 | 6 | 2 |
| Yes | 6 | 10 | 6 | 3 | |
| SMOTE | No | 144 | 5 | 6 | 2 |
| Yes | 4 | 140 | 5 | 4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Zhang, H.-y.; Hu, K.-h.; Wang, L.; Dong, L.-y. Prediction of the Periglacial Debris Flow in Southeast Tibet Based on Imbalanced Small Sample Data. Water 2023, 15, 310. https://doi.org/10.3390/w15020310
Du J, Zhang H-y, Hu K-h, Wang L, Dong L-y. Prediction of the Periglacial Debris Flow in Southeast Tibet Based on Imbalanced Small Sample Data. Water. 2023; 15(2):310. https://doi.org/10.3390/w15020310
Chicago/Turabian StyleDu, Jun, Hong-ya Zhang, Kai-heng Hu, Lin Wang, and Lin-yao Dong. 2023. "Prediction of the Periglacial Debris Flow in Southeast Tibet Based on Imbalanced Small Sample Data" Water 15, no. 2: 310. https://doi.org/10.3390/w15020310
APA StyleDu, J., Zhang, H.-y., Hu, K.-h., Wang, L., & Dong, L.-y. (2023). Prediction of the Periglacial Debris Flow in Southeast Tibet Based on Imbalanced Small Sample Data. Water, 15(2), 310. https://doi.org/10.3390/w15020310







