Study on Pore Structure Evolution Characteristics of Weakly Cemented Sandstone under Freeze–Thaw Based on NMR
Abstract
:1. Introduction
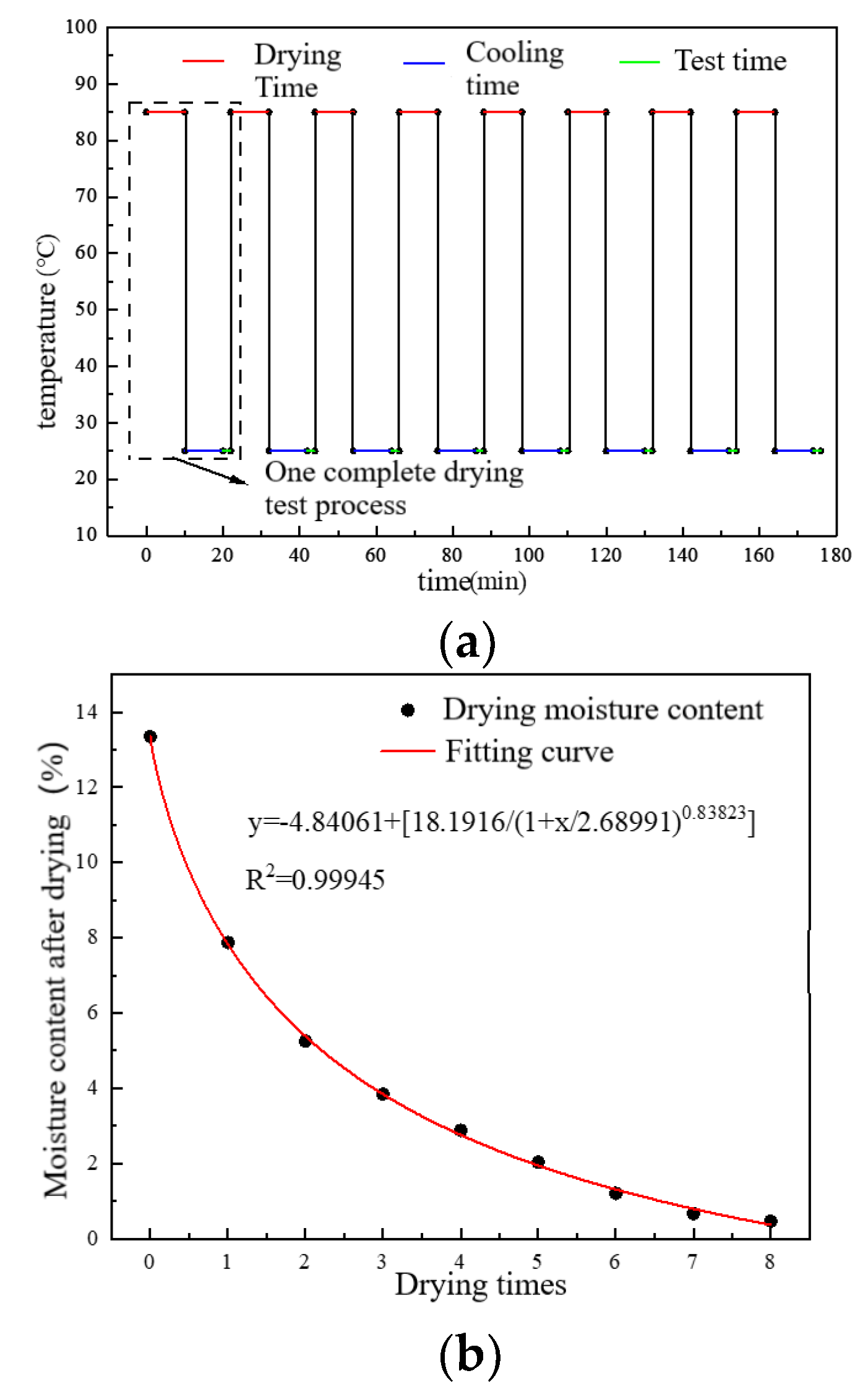
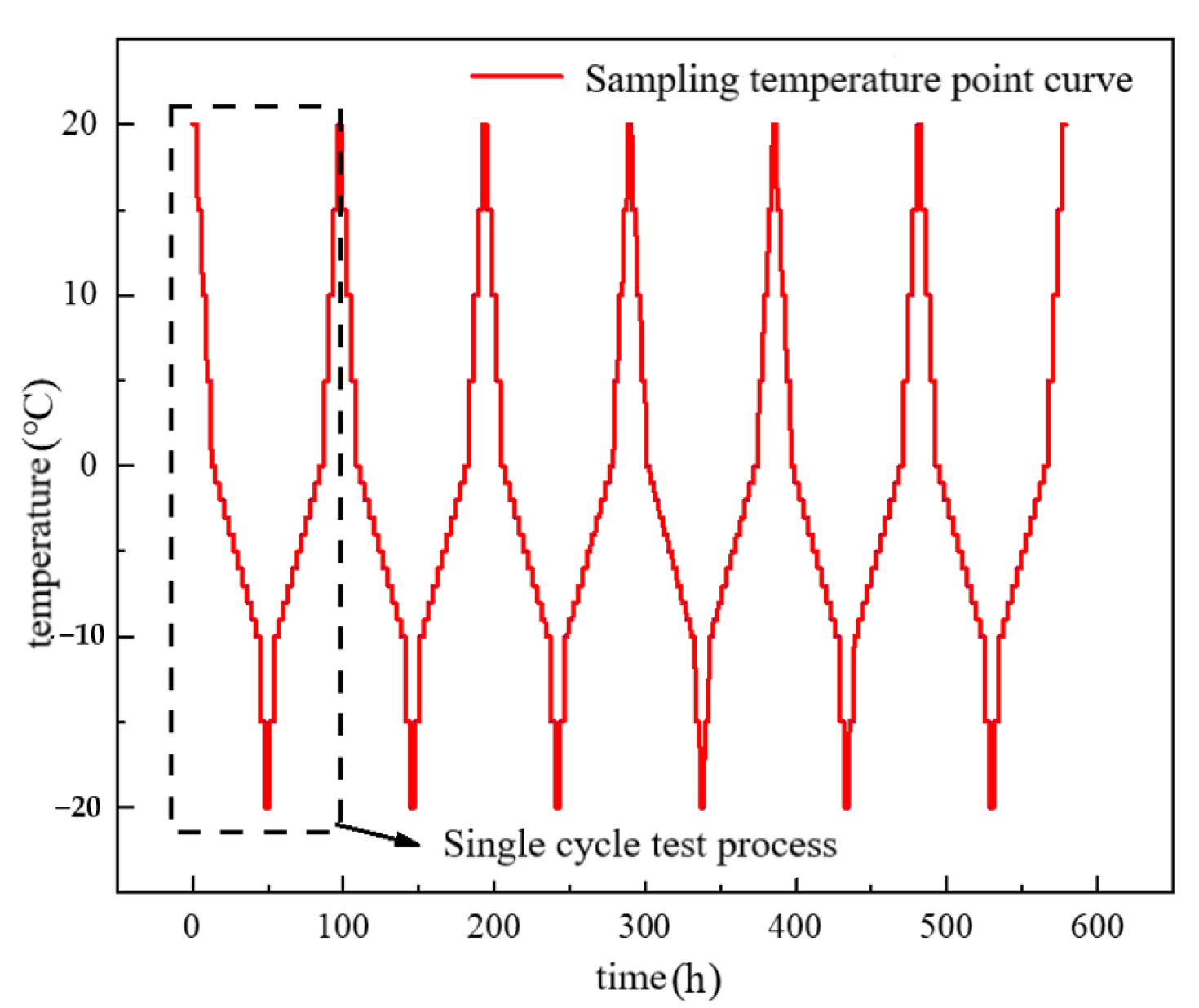
2. Test Materials and Methods
3. Analysis of Pore Structure of Rock under Freeze–Thaw Cycles
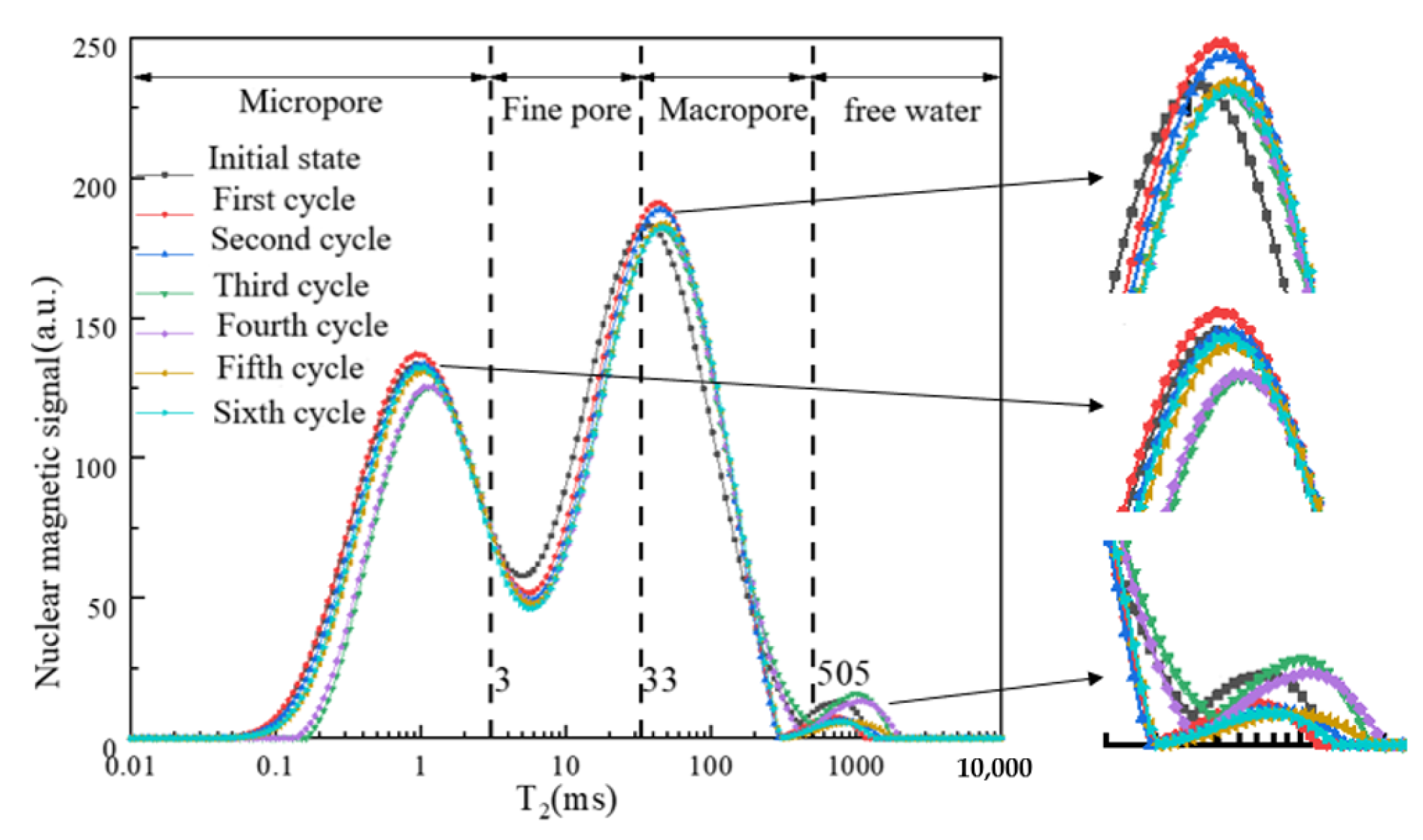
3.1. Variation Rule of Pores at Different Scales
3.2. Change Rule of Bound and Free Pores
4. Fractal Characteristics of T2 under Freeze–Thaw Cycles
4.1. T2 Fractal Theory of NMR
4.2. Analysis of Pore Fractal Characteristics
5. Characteristics of T2 Peak Splitting under Freeze–Thaw Cycles
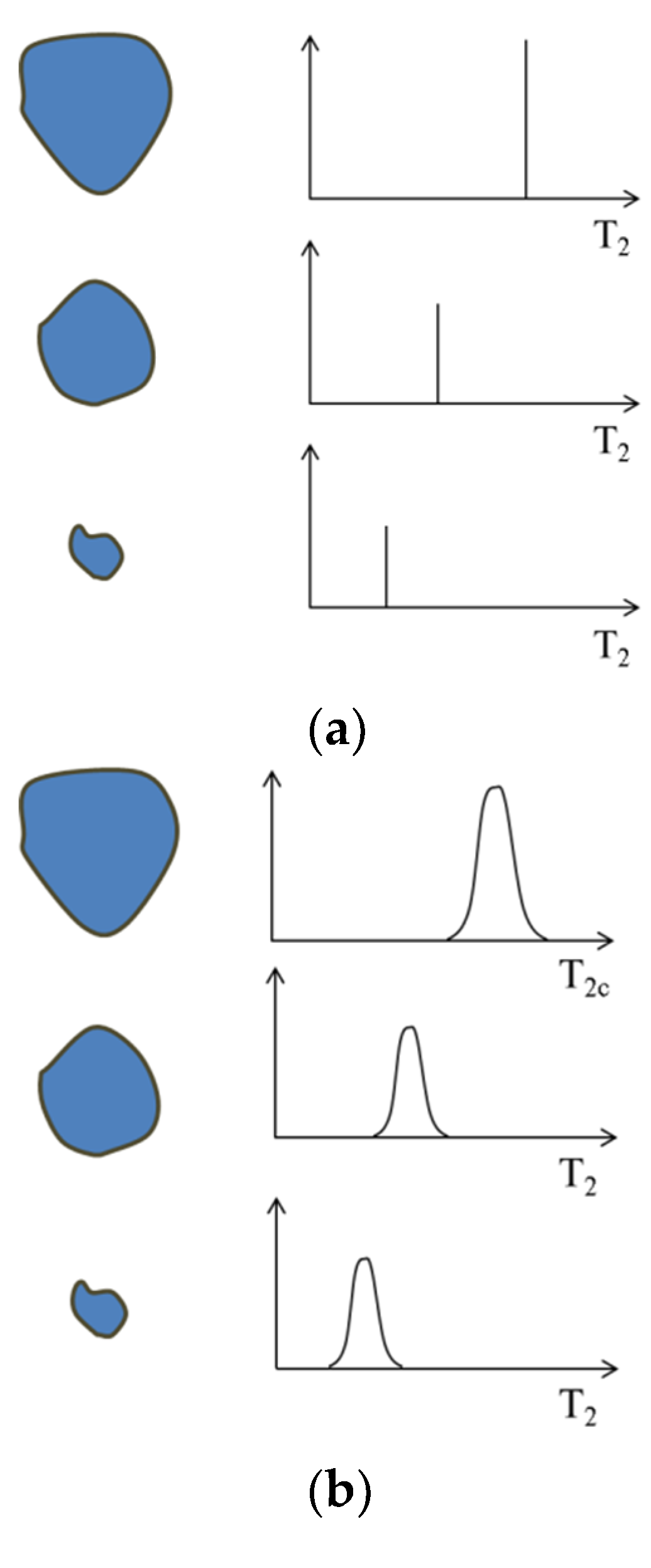
5.1. NMR Pore Size Division and Processing Method
5.1.1. NMR Pore Size Division
5.1.2. Processing Method of Peak Splitting
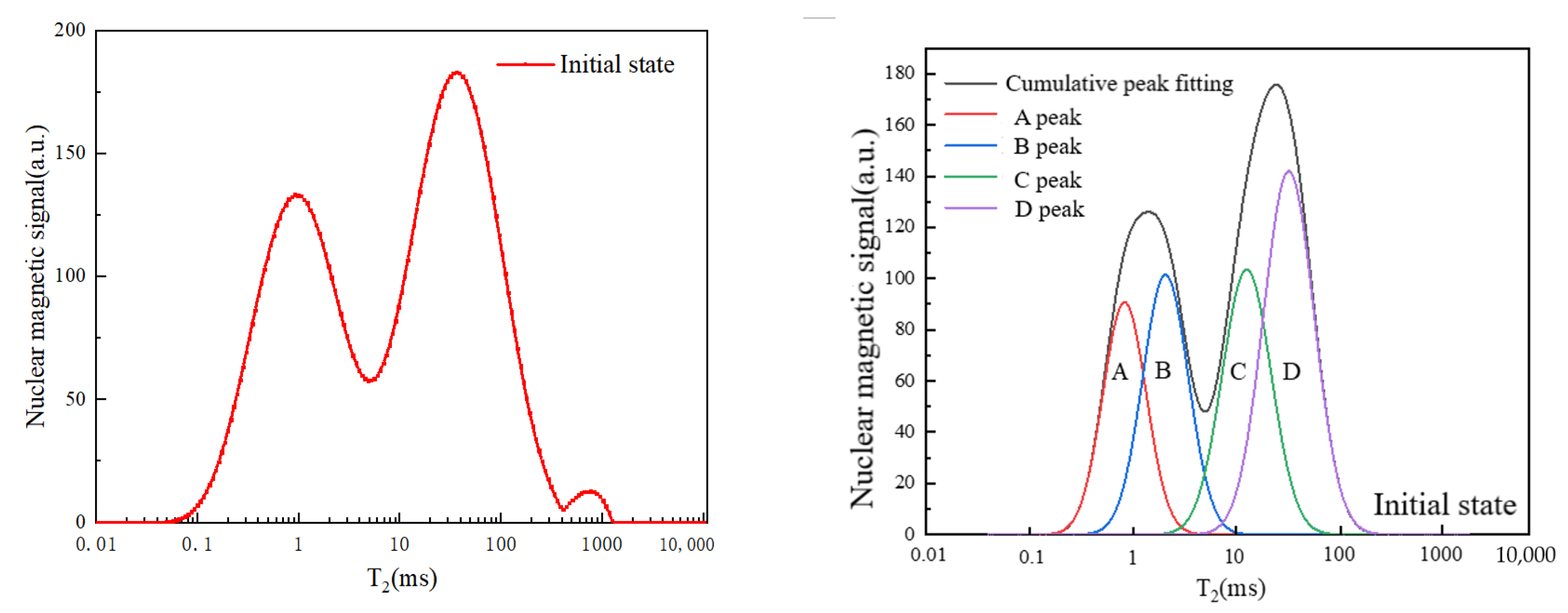
5.2. Peak Splitting Analysis of Pore
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Fan, X. A review on pore structure characterization in tight sandstones. Earth-Sci. Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G.; Cao, J.; Xiao, C.; Wang, S.; Pang, X.; Qin, Z. Investigation of pore structure and petrophysical property in tight sandstones. Mar. Pet. Geol. 2018, 91, 179–189. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, G.; Liu, B.; Ai, Y.; Cai, D.; Yang, S.; Chen, K. Pore structure evaluation in ultra-deep tight sandstones using NMR measurements and fractal analysis. J. Pet. Sci. Eng. 2022, 211, 110180. [Google Scholar] [CrossRef]
- Behroozmand, A.A.; Keating, K.; Auken, E. A Review of the Principles and Applications of the NMR Technique for Near-Surface Characterization. Surv. Geophys. 2015, 36, 27–85. [Google Scholar] [CrossRef]
- Meyer, M.; Buchmann, C.; Schaumann, G.E. Determination of quantitative pore-size distribution of soils with 1H NMR relaxometry. Eur. J. Soil Sci. 2018, 69, 393–406. [Google Scholar] [CrossRef]
- Benson, P.; Meredith, P.; Platzman, E.; White, R. Pore fabric shape anisotropy in porous sandstones and its relation to elastic wave velocity and permeability anisotropy under hydrostatic pressure. Int. J. Rock Mech. Min. Sci. 2005, 42, 890–899. [Google Scholar] [CrossRef]
- Ye, D.; Liu, G.; Luo, N.; Gao, F.; Zhu, X.; Yue, F. Quantitative Analysis of the Topological Structure of Rock Pore Network. Geofluids 2021, 2021, 3554563. [Google Scholar] [CrossRef]
- Dou, W.; Liu, L.; Jia, L.; Xu, Z.; Wang, M.; Du, C. Pore structure, fractal characteristics and permeability prediction of tight sandstones: A case study from Yanchang Formation, Ordos Basin, China. Mar. Pet. Geol. 2021, 123, 104737. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, W.; Liu, Z.; Wang, Y.; Zhao, D.; Wang, W. Fractal characteristics of effective seepage channel structure of water infusion coal based on NMR experiment. Rock Soil Mech. 2020, 41, 1279–1286. (In Chinese) [Google Scholar]
- Ding, Z.W.; Li, X.F.; Tang, Q.B.; Jia, J.D. Study on correlation between fractal characteristics of pore distribution and strength of sandstone particles. Chin. J. Rock Mech. Eng. 2020, 39, 1787–1796. (In Chinese) [Google Scholar]
- Jia, P.; Mao, S.; Qian, Y.; Wang, Q.; Lu, J. The Dynamic Compressive Properties and Energy Dissipation Law of Sandstone Subjected to Freeze–Thaw Damage. Water 2022, 14, 3632. [Google Scholar] [CrossRef]
- Huang, S.; Yu, S.; Ye, Y.; Ye, Z.; Cheng, A. Pore structure change and physico-mechanical properties deterioration of sandstone suffering freeze-thaw actions. Constr. Build. Mater. 2022, 330, 127200. [Google Scholar] [CrossRef]
- Niu, C.; Zhu, Z.; Zhou, L.; Li, X.; Ying, P.; Dong, Y.; Deng, S. Study on the microscopic damage evolution and dynamic fracture properties of sandstone under freeze-thaw cycles. Cold Reg. Sci. Technol. 2021, 191, 103328. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.Y.; Liu, S.; Wang, H.Y.; Liu, S.H. Static and dynamic mechanical properties of sedimentary rock after freeze-thaw or thermal shock weathering. Eng. Geol. 2016, 210, 148–157. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Yang, G.; Yun, Y.; Lin, J.; Ye, W.; Zhang, H.; Zhang, Y. Investigation of Sandstone Mesostructure Damage Caused by Freeze-Thaw Cycles via CT Image Enhancement Technology. Adv. Civ.Eng. 2020, 2020, 8875814. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, S.; Li, Z.; Zhu, R.; Xie, S.; Jing, C.; Lei, L. Multifractal study of three-dimensional pore structure of sand-conglomerate reservoir based on CT images. Energy Fuels 2018, 32, 4797–4807. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Y.; Wang, Y.; Ma, Z.; Huang, X. Quantitative study on coal and shale pore structure and surface roughness based on atomic force microscopy and image processing. Fuel 2019, 244, 78–90. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Y.; Wang, Y.; Ma, Z.; Huang, X. Characterization of multi-type pore structure and fractal characteristics of the Dalong Formation marine shale in northern Sichuan Basin. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 42, 2764–2777. [Google Scholar]
- Liu, S.; Xu, J.; Liu, S.; Wang, P. Fractal study on the dynamic fracture of red sandstone after F-T cycles. Environ. Earth Sci. 2022, 81, 152. [Google Scholar] [CrossRef]
- Abdolghanizadeh, K.; Hosseini, M.; Saghafiyazdi, M. Effect of freezing temperature and number of freeze–thaw cycles on mode I and mode II fracture toughness of sandstone. Theor. Appl. Fract. Mech. 2019, 105, 102428. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, S. Qualitative and quantitative characterization of shale microscopic pore characteristics based on image analysis technology. Adv. Earth Sci. 2016, 31, 751–763. (In Chinese) [Google Scholar]
- Sun, Y.; Guo, S. Characteristics of microscopic pores of shale from Upper Sinian Doushantuo Formation in the western of Hunan and Hubei, China and the main controlling factors. J. Earth Sci.Environ. 2017, 39, 114–125. [Google Scholar]
- Jia, H.; Ding, S.; Zi, F.; Dong, Y.; Shen, Y. Evolution in sandstone pore structures with freeze-thaw cycling and interpretation of damage mechanisms in saturated porous rocks. Catena 2020, 195, 104915. [Google Scholar] [CrossRef]
- Li, J.; Kaunda, R.B.; Zhou, K. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Reg. Sci. Technol. 2018, 154, 133–141. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, C.; Cao, P.; Zhou, K. Freeze–thaw damage evolution of fractured rock mass using nuclear magnetic resonance technology. Cold Reg. Sci. Technol. 2020, 170, 102951. [Google Scholar] [CrossRef]
- Hou, C.; Jin, X.; He, J. Investigation on the Microscopic Deterioration Characteristics of Anhydrite Rock Exposed to Freeze-Thaw Cycles. Int. J. Geomech. 2022, 22, 04022013. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, Y.; Chen, X. Study on the Evolution of Pore Structure of Anthracite Coal under Liquid-Nitrogen Freeze-Thaw Cycles. ACS Omega 2022, 7, 4648–4654. [Google Scholar] [CrossRef] [PubMed]
- Park, C.J.; Synn, H.; Shin, D.S. Experimental study on the thermal characteristics of rock at low temperatures. Int. J. Rock Mech. Min. Sci. 2004, 4, 81–86. [Google Scholar] [CrossRef]
- Jia, H.L.; Liu, Q.B.; Xiang, W.; Zhang, W.; Lang, L. Damage evolution model of saturated sandstone under freeze-thaw cycles. Chin. J. Rock Mech. Eng. 2013, 32, 3049–3055. (In Chinese) [Google Scholar]
- Jia, H.L.; Xiang, W.; Tan, L.; Zhang, W.L.; Zeng, W.; Cao, S.; Cheng, C.J. Theoretical analysis and experimental verification of freeze-thaw damage mechanism of sandstone. Chin. J. Rock Mech. Eng. 2016, 35, 879–895. (In Chinese) [Google Scholar]
- Jia, H.; Xiang, W. Direct observation of the pore structure of sandstone after repeated frost action. Electron. Geotech. Eng. 2015, 20, 11. [Google Scholar]
- Jia, H.; Xiang, W.; Krautblatter, M. Quantifying Rock Fatigue and Decreasing Compressive and Tensile Strength after Repeated Freeze-Thaw Cycles. Permafr. Periglac. Process. 2015, 26, 368–377. [Google Scholar] [CrossRef]
- Jia, H.; Ding, S.; Wang, Y.; Zi, F.; Sun, Q.; Yang, G. An NMR-based investigation of pore water freezing process in sandstone. Cold Reg. Sci. Technol. 2019, 168, 102893. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Ma, Y.; Yang, K.; Tang, M. Dynamic Response and Fractal Characteristics of a Pore-Fracture System in Ultralow Permeability Sandstone Based on Low-Field NMR. Energy Fuels 2020, 35, 397–407. [Google Scholar] [CrossRef]
- Chen, S.; Tang, D.; Tao, S.; Ji, X.; Xu, H. Fractal analysis of the dynamic variation in pore-fracture systems under the action of stress using a low-field NMR relaxation method: An experimental study of coals from western Guizhou in China. J. Pet. Sci. Eng. 2019, 173, 617–629. [Google Scholar] [CrossRef]
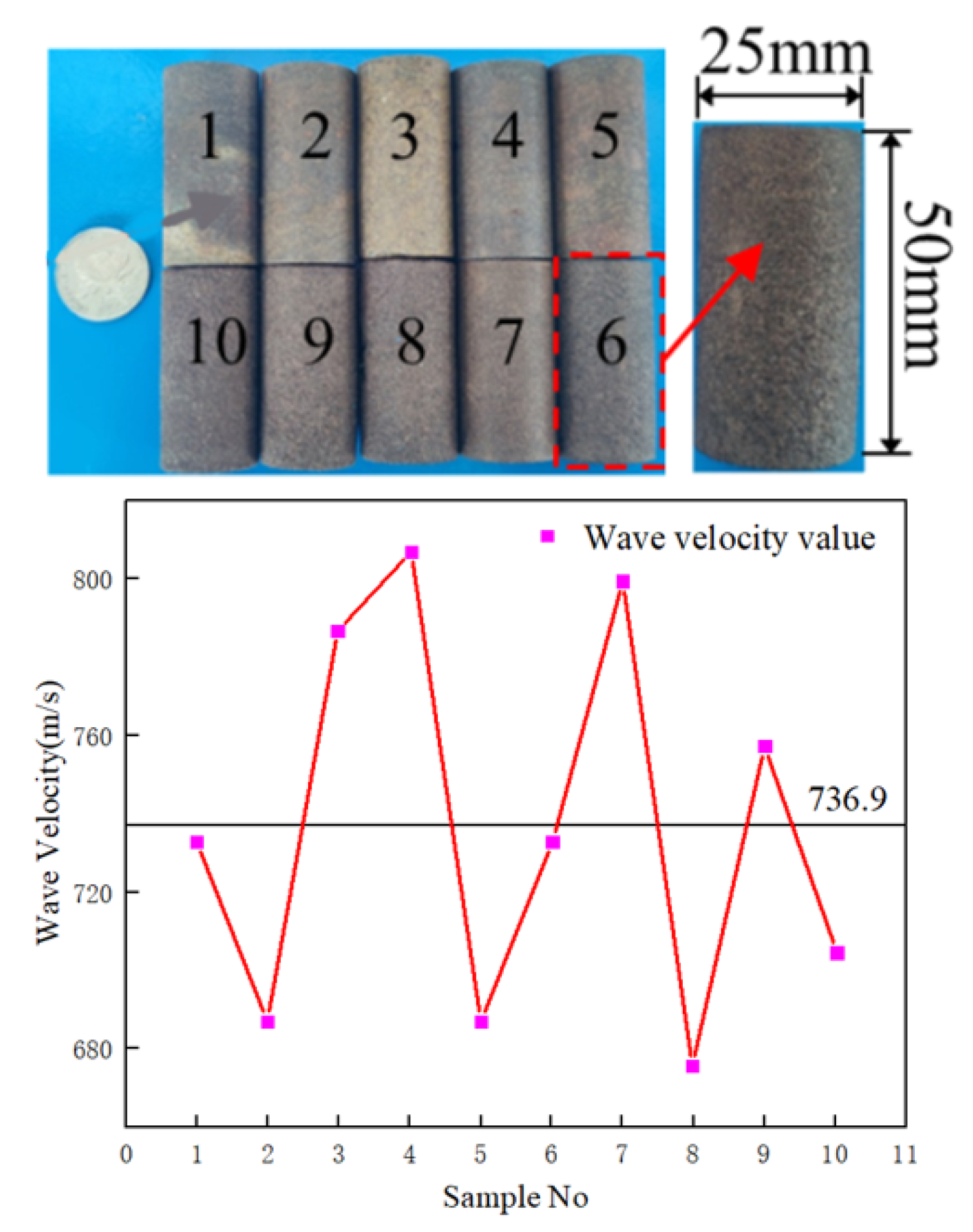

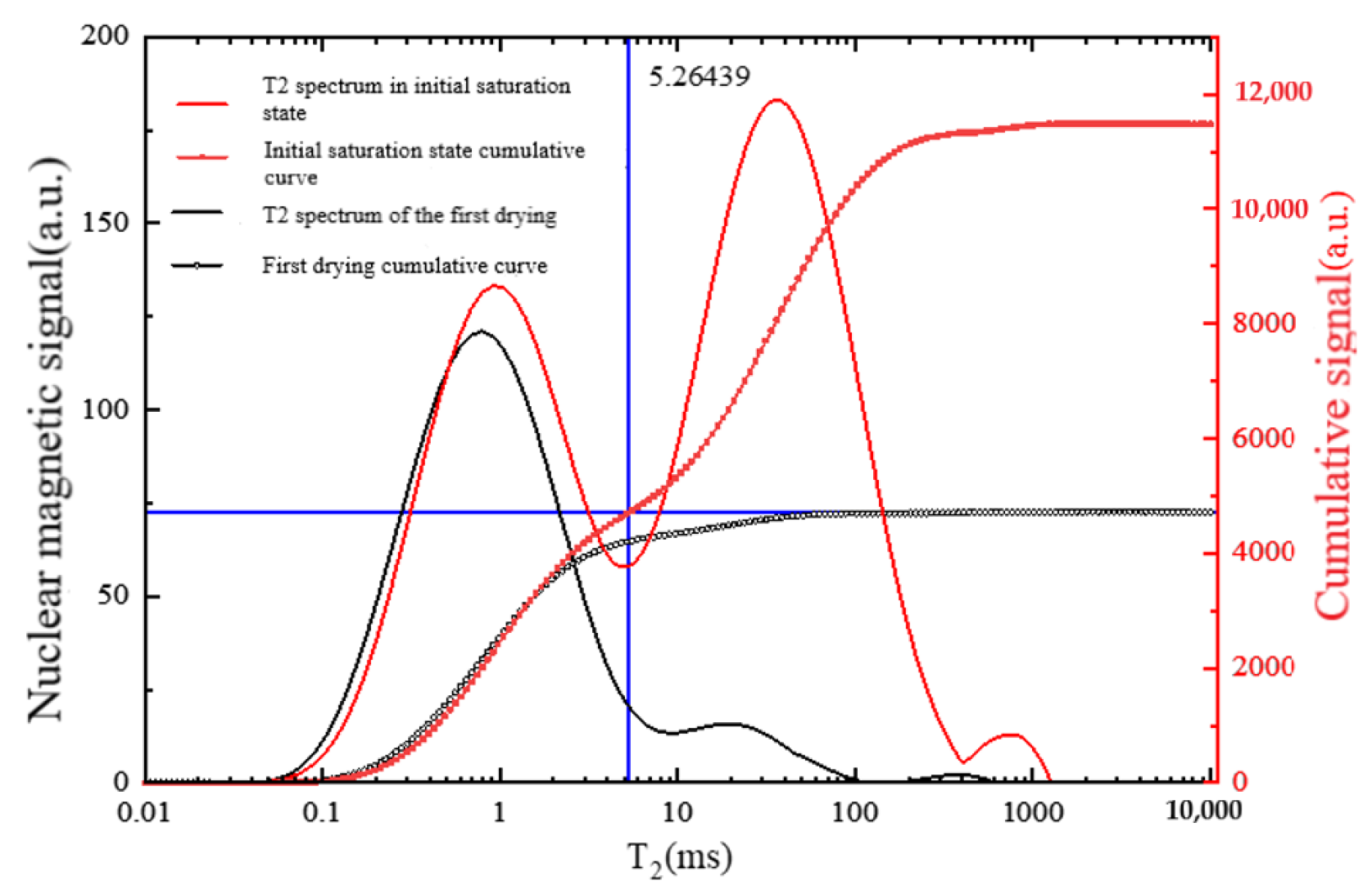
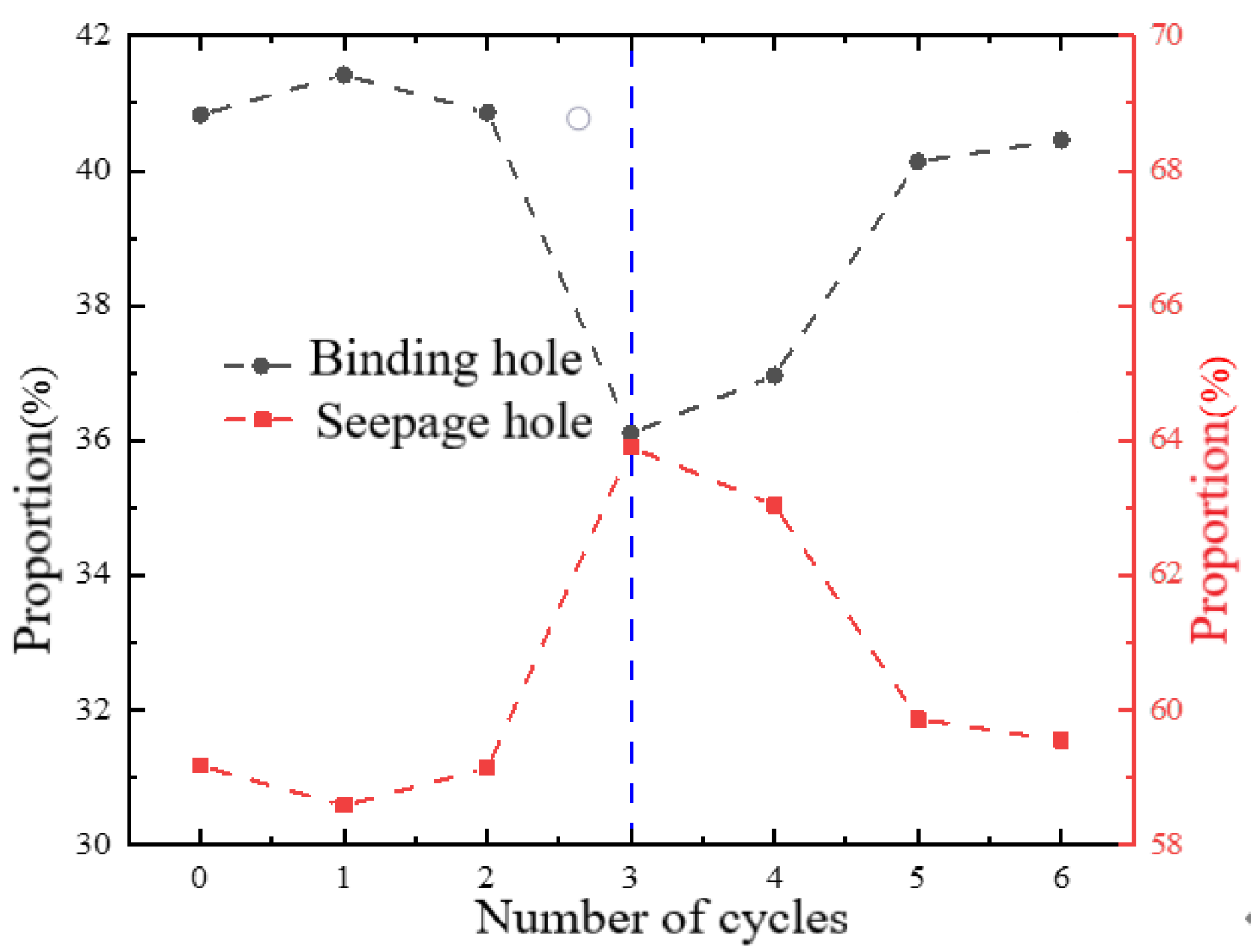
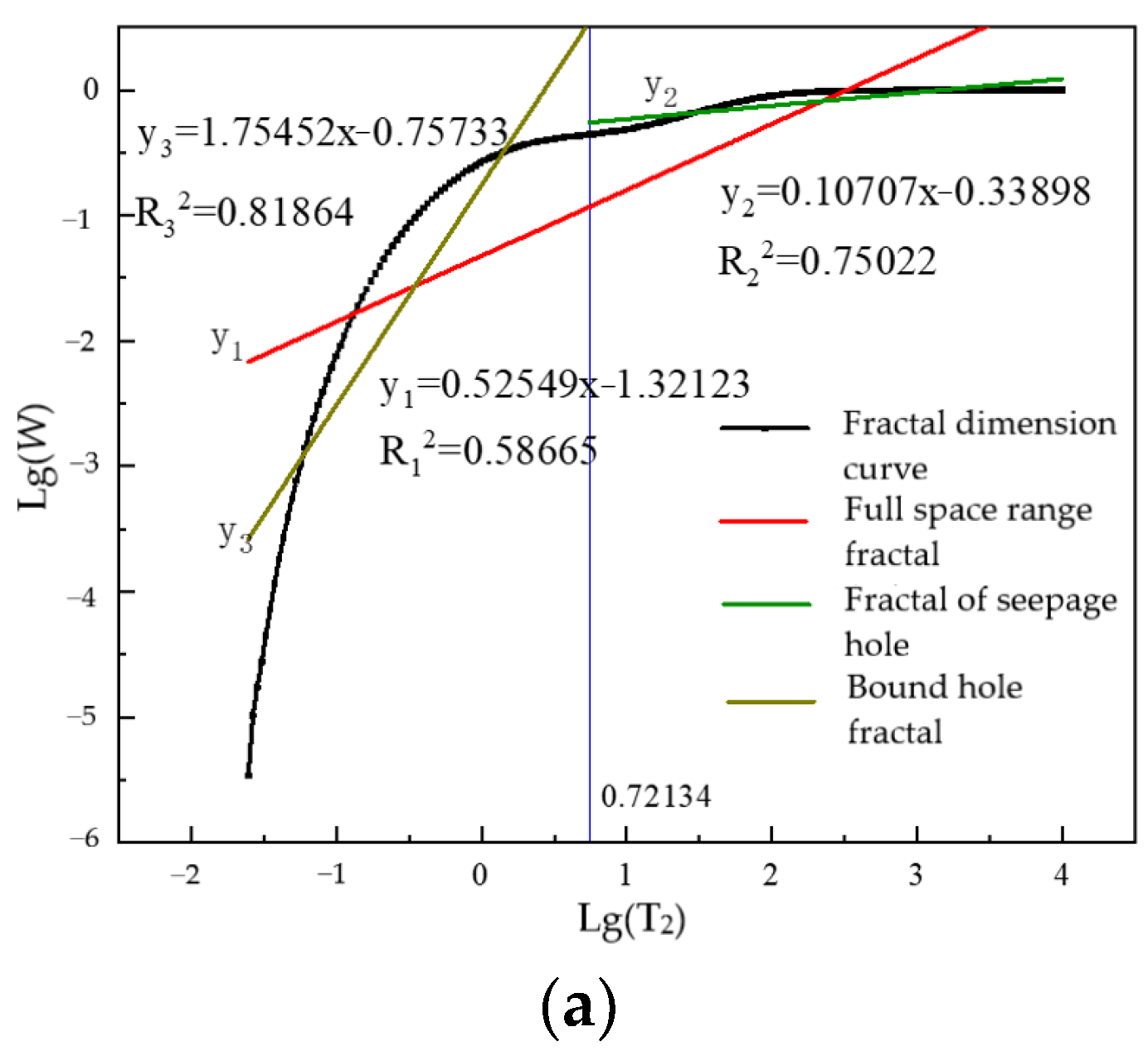
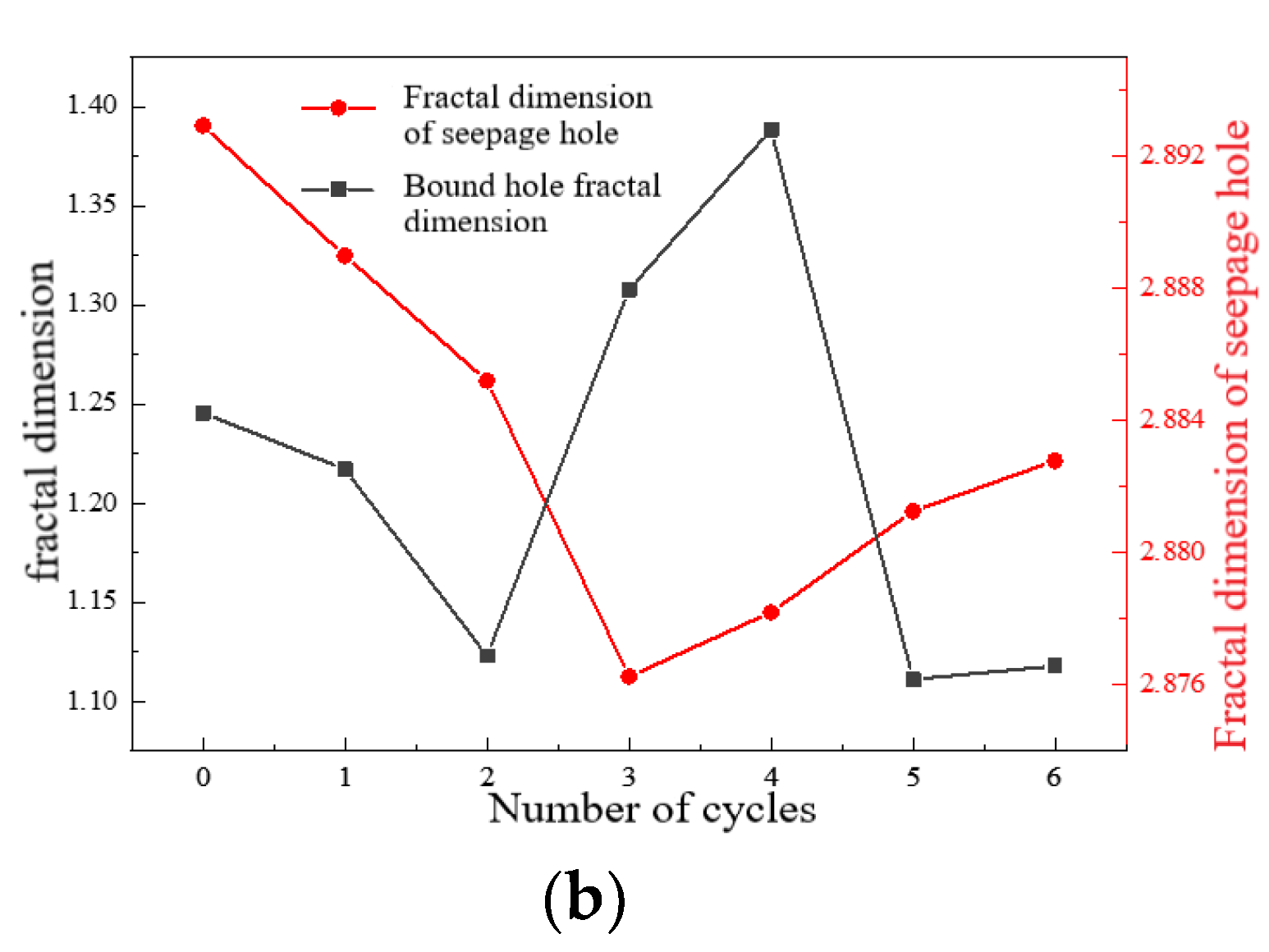

| Wave Velocity (m/s) | Saturation Density (g/cm3) | Dry Density (g/cm3) | Saturated Volume Water Content (%) |
|---|---|---|---|
| 736.9 | 2.23 | 2.13 | 13.35 |
| Peak | Peak Center (ms) | Half-Peak Width (ms) |
|---|---|---|
| 1 | 0.488 | 0.384 |
| 2 | 1.589 | 1.244 |
| 3 | 15.703 | 12.522 |
| 4 | 54.789 | 44.436 |
| Number of Cycles | A Crest | B Crest | C Crest | D Crest | Degree of Fit (%) | |
|---|---|---|---|---|---|---|
| Peak height | 0 | 90.784 | 101.479 | 103.548 | 141.959 | 99.765 |
| 1 | 92.749 | 108.714 | 90.065 | 167.824 | 99.670 | |
| 2 | 88.429 | 105.401 | 84.361 | 168.092 | 99.685 | |
| 3 | 92.971 | 72.600 | 96.993 | 138.538 | 99.929 | |
| 4 | 93.125 | 78.784 | 93.756 | 147.266 | 99.902 | |
| 5 | 88.665 | 98.723 | 85.167 | 162.382 | 99.720 | |
| 6 | 89.577 | 98.239 | 85.081 | 161.522 | 99.703 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Yang, Y.; Yin, J.; Liu, Y.; Li, X. Study on Pore Structure Evolution Characteristics of Weakly Cemented Sandstone under Freeze–Thaw Based on NMR. Water 2023, 15, 281. https://doi.org/10.3390/w15020281
Lin J, Yang Y, Yin J, Liu Y, Li X. Study on Pore Structure Evolution Characteristics of Weakly Cemented Sandstone under Freeze–Thaw Based on NMR. Water. 2023; 15(2):281. https://doi.org/10.3390/w15020281
Chicago/Turabian StyleLin, Jian, Yi Yang, Jianchao Yin, Yang Liu, and Xiangwei Li. 2023. "Study on Pore Structure Evolution Characteristics of Weakly Cemented Sandstone under Freeze–Thaw Based on NMR" Water 15, no. 2: 281. https://doi.org/10.3390/w15020281
APA StyleLin, J., Yang, Y., Yin, J., Liu, Y., & Li, X. (2023). Study on Pore Structure Evolution Characteristics of Weakly Cemented Sandstone under Freeze–Thaw Based on NMR. Water, 15(2), 281. https://doi.org/10.3390/w15020281






