Regionalizing Streamflow Regime Function through Integrations of Geographical Controls in Mountainous Basins
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Flow Duration Curve Method
2.3. Independent Variables Selection
2.4. Regionalization Approach
2.5. Leave-One Cross-Validation Method
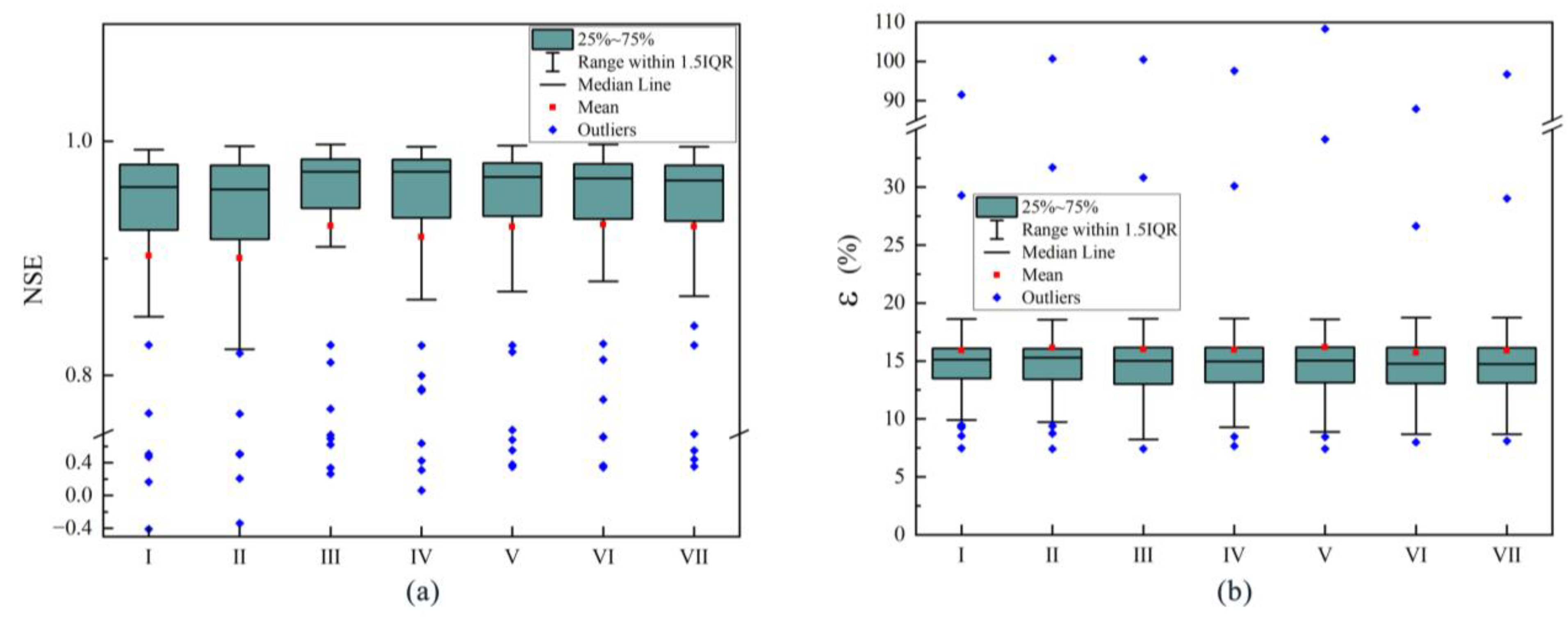
3. Results
3.1. The Selection of Functional Models
3.2. Controlling Descriptors Adopted as Independent Variables
3.3. Assessments of Regionalization Models
4. Discussions
4.1. Applicability of the Model
4.2. Future Research Questions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ID | Station | P (mm) | Max 1d (mm) | Max 3d (mm) | Max 7d (mm) | RR (mm/d) | FR (mm/d) |
|---|---|---|---|---|---|---|---|
| 1 | Ziluoshan | 760 | 65.24 | 37.31 | 20.68 | 5.26 | −5.12 |
| 2 | Zhongtang | 806 | 104.40 | 54.79 | 30.55 | 7.38 | −7.17 |
| 3 | Jizhong | 820 | 132.20 | 60.55 | 33.04 | 8.81 | −8.41 |
| 4 | Xiagushan | 764 | 85.67 | 44.26 | 25.01 | 7.00 | −6.74 |
| 5 | Gaocheng | 670 | 61.94 | 30.81 | 18.19 | 5.84 | −5.79 |
| 6 | Lixin | 930 | 100.90 | 50.07 | 25.87 | 8.78 | −8.65 |
| 7 | Guanzhai | 814 | 79.77 | 38.71 | 20.72 | 5.92 | −5.78 |
| 8 | Dapoling | 1097 | 84.07 | 41.38 | 21.39 | 6.20 | −5.87 |
| 9 | Luzhuang | 1016 | 106.70 | 53.84 | 26.48 | 7.97 | −7.44 |
| 10 | Tanjiahe | 1366 | 107.40 | 46.12 | 25.96 | 8.27 | −8.28 |
| 11 | Zhumadian | 985 | 109.40 | 53.30 | 26.29 | 8.85 | −8.35 |
| 12 | Nanlidian | 1251 | 111.90 | 55.71 | 29.71 | 9.48 | −8.74 |
| 13 | Peihe | 1346 | 104.00 | 48.61 | 28.34 | 11.27 | −10.80 |
| 14 | Baiqueyuan | 1287 | 106.40 | 49.94 | 27.59 | 9.49 | −9.09 |
| 15 | Huangnizhuang | 1332 | 108.30 | 60.22 | 32.40 | 9.62 | −9.29 |
| 16 | Qilin | 1347 | 116.70 | 60.11 | 33.13 | 10.80 | −10.13 |
| 17 | Zhangchong | 1407 | 108.70 | 58.07 | 32.25 | 9.95 | −9.53 |
| 18 | Bailianya | 1457 | 105.50 | 54.09 | 30.21 | 9.72 | −9.10 |
| 19 | Huanghewei | 1518 | 119.00 | 59.97 | 34.42 | 10.15 | −9.79 |
| 20 | Xiaotian | 1457 | 98.64 | 52.05 | 30.17 | 8.53 | −7.84 |
| 21 | Taoxi | 1215 | 76.17 | 39.15 | 21.55 | 6.65 | −5.99 |
| 22 | Liukou | 1788 | 136.60 | 69.43 | 41.23 | 13.17 | −13.18 |
| 23 | Dahekou | 1803 | 121.20 | 63.83 | 35.66 | 9.80 | −9.57 |
| 24 | Yuetan | 1778 | 110.90 | 59.23 | 36.41 | 9.87 | −9.53 |
| 25 | Shancha | 1973 | 88.73 | 48.99 | 29.69 | 10.63 | −10.27 |
| 26 | Wananba | 1798 | 87.51 | 45.14 | 24.30 | 9.60 | −9.69 |
| 27 | Sankouzhen | 1862 | 107.30 | 60.74 | 34.70 | 10.17 | −9.77 |
| 28 | Tunxi | 1770 | 104.40 | 57.38 | 34.78 | 8.77 | −8.29 |
| 29 | Yuxi | 1684 | 98.98 | 56.68 | 33.60 | 8.94 | −8.50 |
| 30 | Linxi | 1599 | 93.23 | 44.77 | 27.52 | 9.57 | −9.41 |
| 31 | Hulesi | 1574 | 85.89 | 46.88 | 26.48 | 8.33 | −7.92 |
| 32 | Misai | 1778 | 134.00 | 80.46 | 47.71 | 9.42 | −8.62 |
| 33 | Zhongzhou | 1788 | 94.34 | 52.50 | 30.79 | 10.61 | −10.30 |
| 34 | Yancun | 1602 | 86.07 | 55.76 | 32.44 | 8.83 | −8.30 |
| 35 | Baikuoban | 1527 | 93.20 | 50.29 | 30.63 | 9.80 | −9.61 |
| 36 | Shangzouban | 1509 | 81.18 | 43.62 | 28.67 | 10.46 | −10.40 |
| 37 | Yuankou | 1519 | 85.61 | 47.91 | 28.43 | 8.56 | −8.08 |
| 38 | Qingshandian | 1558 | 84.53 | 43.16 | 25.75 | 8.16 | −7.65 |
| 39 | Fenshui | 1582 | 89.13 | 45.35 | 28.03 | 8.27 | −7.50 |
| 40 | Shanjiao | 1499 | 70.17 | 35.72 | 23.71 | 8.87 | −8.68 |
| 41 | Laoshikan | 1687 | 93.08 | 41.70 | 22.24 | 6.56 | −5.92 |
| 42 | Qianyu | 1578 | 69.46 | 38.04 | 22.86 | 7.29 | −6.71 |
| 43 | Shangbao | 1579 | 83.24 | 44.34 | 27.01 | 8.19 | −7.79 |
| 44 | Qiaodongcun | 1631 | 89.97 | 47.31 | 27.18 | 8.41 | −7.90 |
| 45 | Hengtangcun | 1568 | 93.98 | 50.36 | 27.67 | 7.66 | −7.39 |
| 46 | Yubujie | 1466 | 96.25 | 45.18 | 25.32 | 8.97 | −8.43 |
| 47 | Shangxiantan | 1473 | 74.72 | 39.00 | 24.20 | 7.22 | −6.91 |
| 48 | Jiangwan | 1483 | 94.24 | 49.94 | 28.40 | 9.45 | −9.00 |
| 49 | Liantangkou | 1484 | 69.03 | 37.40 | 23.43 | 7.23 | −6.68 |
| 50 | Daixi | 1429 | 80.95 | 42.65 | 23.65 | 8.08 | −7.73 |
| 51 | Yiwufotang | 1477 | 67.59 | 38.28 | 23.87 | 5.52 | −4.83 |
| 52 | Dongyangyanxia | 1485 | 82.86 | 42.56 | 25.51 | 7.48 | −7.00 |
| 53 | Daitou | 1847 | 167.50 | 82.15 | 43.80 | 10.44 | −10.21 |
| 54 | Qiulu | 1707 | 147.20 | 73.22 | 37.67 | 8.72 | −8.55 |
| 55 | Caodian | 1492 | 93.49 | 47.53 | 26.82 | 8.28 | −7.93 |
| 56 | Shuangjiangxi | 1449 | 87.23 | 41.37 | 23.25 | 7.78 | −7.28 |
| 57 | Xixi | 1528 | 93.10 | 45.36 | 24.66 | 7.84 | −7.22 |
| 58 | Huangze | 1518 | 113.90 | 55.65 | 29.01 | 8.46 | −7.78 |
| 59 | Yutan | 1717 | 85.78 | 46.60 | 29.03 | 8.41 | −8.31 |
| 60 | Jianning(Xikou) | 1722 | 90.85 | 51.71 | 31.49 | 8.02 | −7.58 |
| 61 | Hongtian | 1610 | 85.31 | 45.96 | 26.61 | 7.71 | −7.46 |
| 62 | Chongan(Wuyishan) | 1918 | 103.10 | 59.27 | 36.48 | 8.34 | −8.13 |
| 63 | Fengyang | 1749 | 100.00 | 55.46 | 31.19 | 9.03 | −8.77 |
| 64 | Taipingkou | 1482 | 107.40 | 54.20 | 29.30 | 7.87 | −7.62 |
| ID | Station | A (km2) | H (m) | β (°) | CC | CP | TI | HI | AS | RC | RF | D | NDVI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Ziluoshan | 1800 | 822 | 19.37 | −4.12 × 10−5 | −1.33 × 10−4 | 6.37 | 0.29 | 0.47 | 0.21 | 0.34 | 1.10 | 0.90 |
| 2 | Zhongtang | 485 | 677 | 19.80 | −6.44 × 10−5 | −1.18 × 10−4 | 6.35 | 0.25 | 0.47 | 0.27 | 0.53 | 1.12 | 0.91 |
| 3 | Jizhong | 46 | 393 | 12.61 | −1.83 × 10−4 | −1.33 × 10−4 | 6.93 | 0.27 | 0.50 | 0.33 | 0.90 | 1.28 | 0.90 |
| 4 | Xiagushan | 354 | 468 | 15.15 | −7.48 × 10−5 | −1.38 × 10−4 | 6.69 | 0.25 | 0.45 | 0.26 | 0.62 | 1.12 | 0.87 |
| 5 | Gaocheng | 620 | 489 | 11.18 | −5.26 × 10−5 | −5.34 × 10−5 | 7.19 | 0.21 | 0.31 | 0.24 | 0.54 | 1.11 | 0.84 |
| 6 | Lixin | 77.8 | 172 | 6.62 | −8.28 × 10−5 | −1.70 × 10−4 | 7.71 | 0.18 | 0.26 | 0.16 | 0.46 | 1.19 | 0.83 |
| 7 | Guanzhai | 1124 | 173 | 8.29 | −3.03 × 10−5 | −2.21 × 10−5 | 7.60 | 0.16 | 0.20 | 0.26 | 0.86 | 1.09 | 0.87 |
| 8 | Dapoling | 1640 | 231 | 9.57 | −2.86 × 10−5 | −1.18 × 10−4 | 7.34 | 0.14 | 0.24 | 0.23 | 0.80 | 1.08 | 0.89 |
| 9 | Luzhuang | 396 | 212 | 8.46 | −4.91 × 10−5 | −1.18 × 10−4 | 7.49 | 0.17 | 0.27 | 0.29 | 0.68 | 1.15 | 0.88 |
| 10 | Tanjiahe | 152 | 281 | 15.36 | −1.09 × 10−5 | −1.32 × 10−4 | 6.67 | 0.25 | 0.53 | 0.29 | 0.56 | 1.19 | 0.91 |
| 11 | Zhumadian | 121 | 100 | 4.27 | −4.52 × 10−5 | −8.54 × 10−5 | 8.33 | 0.10 | 0.08 | 0.23 | 0.65 | 1.23 | 0.85 |
| 12 | Nanlidian | 1500 | 170 | 11.71 | −3.68 × 10−5 | −9.62 × 10−5 | 7.09 | 0.23 | 0.34 | 0.15 | 0.42 | 1.08 | 0.90 |
| 13 | Peihe | 17.9 | 435 | 21.69 | −2.31 × 10−5 | −1.38 × 10−4 | 6.12 | 0.50 | 0.74 | 0.31 | 0.54 | 1.28 | 0.93 |
| 14 | Baiqueyuan | 284 | 225 | 12.24 | −6.38 × 10−5 | −1.15 × 10−4 | 6.99 | 0.22 | 0.42 | 0.26 | 0.67 | 1.12 | 0.90 |
| 15 | Huangnizhuang | 805 | 487 | 18.04 | −5.64 × 10−5 | −1.11 × 10−4 | 6.48 | 0.27 | 0.40 | 0.19 | 0.58 | 1.09 | 0.93 |
| 16 | Qilin | 185 | 532 | 18.22 | −1.10 × 10−5 | −1.22 × 10−4 | 6.44 | 0.28 | 0.53 | 0.23 | 0.34 | 1.16 | 0.93 |
| 17 | Zhangchong | 493 | 671 | 19.02 | −9.63 × 10−5 | −1.29 × 10−4 | 6.37 | 0.34 | 0.45 | 0.17 | 0.28 | 1.12 | 0.93 |
| 18 | Bailianya | 745 | 667 | 19.25 | −5.97 × 10−5 | −1.38 × 10−4 | 6.31 | 0.34 | 0.48 | 0.21 | 0.51 | 1.11 | 0.93 |
| 19 | Huanghewei | 270 | 829 | 20.92 | −9.66 × 10−5 | −1.38 × 10−4 | 6.22 | 0.41 | 0.51 | 0.26 | 0.41 | 1.12 | 0.92 |
| 20 | Xiaotian | 372 | 595 | 20.89 | −7.99 × 10−5 | −1.26 × 10−4 | 6.26 | 0.27 | 0.39 | 0.21 | 0.44 | 1.12 | 0.93 |
| 21 | Taoxi | 1510 | 55 | 5.83 | −2.07 × 10−5 | −7.39 × 10−5 | 7.95 | 0.16 | 0.14 | 0.16 | 0.61 | 1.08 | 0.89 |
| 22 | Liukou | 101 | 562 | 24.37 | −1.87 × 10−4 | −9.34 × 10−5 | 6.13 | 0.28 | 0.43 | 0.26 | 0.43 | 1.14 | 0.94 |
| 23 | Dahekou | 409 | 432 | 22.58 | −1.06 × 10−4 | −1.11 × 10−4 | 6.23 | 0.32 | 0.44 | 0.23 | 0.53 | 1.12 | 0.94 |
| 24 | Yuetan | 954 | 428 | 21.22 | −6.28 × 10−5 | −9.31 × 10−5 | 6.38 | 0.22 | 0.22 | 0.21 | 0.40 | 1.09 | 0.94 |
| 25 | Shancha | 57.8 | 841 | 27.13 | −2.01 × 10−4 | −1.36 × 10−4 | 5.94 | 0.37 | 0.71 | 0.31 | 0.89 | 1.17 | 0.91 |
| 26 | Wananba | 869 | 363 | 17.96 | −5.88 × 10−5 | −1.22 × 10−4 | 6.88 | 0.20 | 0.39 | 0.23 | 0.51 | 1.09 | 0.92 |
| 27 | Sankouzhen | 259 | 604 | 23.53 | −1.10 × 10−4 | −1.51 × 10−4 | 6.17 | 0.28 | 0.61 | 0.28 | 0.53 | 1.14 | 0.93 |
| 28 | Tunxi | 2670 | 381 | 18.81 | −4.39 × 10−5 | −1.05 × 10−4 | 6.65 | 0.19 | 0.38 | 0.19 | 0.59 | 1.07 | 0.92 |
| 29 | Yuxi | 1599 | 383 | 17.99 | −4.78 × 10−5 | −1.37 × 10−4 | 6.57 | 0.19 | 0.40 | 0.18 | 0.60 | 1.09 | 0.91 |
| 30 | Linxi | 585 | 391 | 18.41 | −7.10 × 10−5 | −8.65 × 10−5 | 6.50 | 0.23 | 0.45 | 0.19 | 0.45 | 1.11 | 0.91 |
| 31 | Hulesi | 492 | 436 | 21.53 | −7.28 × 10−5 | −1.58 × 10−4 | 6.30 | 0.28 | 0.41 | 0.28 | 0.81 | 1.11 | 0.93 |
| 32 | Misai | 793 | 450 | 22.10 | −6.59 × 10−5 | −1.41 × 10−4 | 6.26 | 0.30 | 0.55 | 0.21 | 0.53 | 1.09 | 0.92 |
| 33 | Zhongzhou | 257 | 599 | 25.43 | −9.58 × 10−5 | −8.94 × 10−5 | 6.01 | 0.38 | 0.60 | 0.30 | 0.61 | 1.12 | 0.93 |
| 34 | Yancun | 180 | 546 | 24.75 | −1.49 × 10−4 | −1.65 × 10−4 | 6.11 | 0.34 | 0.61 | 0.23 | 0.48 | 1.17 | 0.91 |
| 35 | Baikuoban | 180 | 493 | 26.09 | −1.56 × 10−4 | −1.57 × 10−4 | 5.94 | 0.29 | 1.04 | 0.28 | 0.32 | 1.17 | 0.91 |
| 36 | Shangzouban | 42.9 | 381 | 23.18 | −2.88 × 10−4 | −2.09 × 10−4 | 6.15 | 0.33 | 0.64 | 0.36 | 0.66 | 1.23 | 0.92 |
| 37 | Yuankou | 687 | 270 | 18.72 | −8.58 × 10−5 | −1.87 × 10−4 | 6.52 | 0.23 | 0.43 | 0.21 | 0.50 | 1.11 | 0.91 |
| 38 | Qingshandian | 1429 | 587 | 22.95 | −5.23 × 10−5 | −1.54 × 10−4 | 6.24 | 0.32 | 0.57 | 0.22 | 0.48 | 1.10 | 0.92 |
| 39 | Fenshui | 2640 | 476 | 21.64 | −4.20 × 10−5 | −1.67 × 10−4 | 6.24 | 0.27 | 0.51 | 0.17 | 0.54 | 1.07 | 0.92 |
| 40 | Shanjiao | 189 | 658 | 26.32 | −1.29 × 10−4 | −1.40 × 10−4 | 5.93 | 0.45 | 0.62 | 0.24 | 0.26 | 1.15 | 0.94 |
| 41 | Laoshikan | 241 | 541 | 21.91 | −8.32 × 10−5 | −1.53 × 10−4 | 6.24 | 0.31 | 0.69 | 0.24 | 0.46 | 1.15 | 0.93 |
| 42 | Qianyu | 333 | 264 | 18.46 | −9.66 × 10−5 | −1.92 × 10−4 | 6.66 | 0.28 | 0.47 | 0.24 | 0.45 | 1.13 | 0.92 |
| 43 | Shangbao | 516 | 668 | 25.67 | −9.85 × 10−5 | −1.31 × 10−4 | 5.95 | 0.42 | 0.54 | 0.22 | 0.38 | 1.09 | 0.92 |
| 44 | Qiaodongcun | 233 | 437 | 19.70 | −9.01 × 10−5 | −1.77 × 10−4 | 6.37 | 0.26 | 0.69 | 0.29 | 0.50 | 1.17 | 0.92 |
| 45 | Hengtangcun | 1316 | 277 | 16.91 | −5.27 × 10−5 | −1.77 × 10−4 | 6.69 | 0.17 | 0.37 | 0.18 | 0.55 | 1.09 | 0.91 |
| 46 | Yubujie | 289 | 81 | 8.73 | −2.72 × 10−5 | −1.36 × 10−4 | 7.73 | 0.12 | 0.32 | 0.25 | 0.47 | 1.21 | 0.89 |
| 47 | Shangxiantan | 806 | 489 | 21.92 | −5.58 × 10−5 | −1.70 × 10−4 | 6.17 | 0.29 | 0.51 | 0.24 | 0.46 | 1.11 | 0.92 |
| 48 | Jiangwan | 20.9 | 306 | 20.09 | −2.64 × 10−5 | −2.29 × 10−4 | 6.20 | 0.45 | 0.56 | 0.24 | 0.29 | 1.18 | 0.94 |
| 49 | Liantangkou | 1341 | 232 | 14.24 | −3.59 × 10−5 | −1.84 × 10−4 | 6.94 | 0.21 | 0.43 | 0.26 | 0.81 | 1.09 | 0.88 |
| 50 | Daixi | 162 | 203 | 16.50 | −1.32 × 10−5 | −2.31 × 10−4 | 6.55 | 0.28 | 0.62 | 0.21 | 0.51 | 1.16 | 0.92 |
| 51 | Yiwufotang | 2341 | 285 | 15.55 | −3.77 × 10−5 | −1.60 × 10−4 | 6.84 | 0.25 | 0.46 | 0.14 | 0.56 | 1.07 | 0.88 |
| 52 | Dongyangyanxia | 830 | 305 | 16.74 | −5.90 × 10−5 | −1.99 × 10−4 | 6.66 | 0.22 | 0.42 | 0.17 | 0.49 | 1.07 | 0.89 |
| 53 | Daitou | 343 | 456 | 21.71 | −8.10 × 10−5 | −1.20 × 10−4 | 6.30 | 0.38 | 0.78 | 0.27 | 0.64 | 1.11 | 0.91 |
| 54 | Qiulu | 269 | 491 | 23.28 | −7.91 × 10−5 | −1.12 × 10−4 | 6.16 | 0.38 | 0.65 | 0.23 | 0.51 | 1.12 | 0.92 |
| 55 | Caodian | 253 | 602 | 24.33 | −7.86 × 10−5 | −1.47 × 10−4 | 6.08 | 0.37 | 0.57 | 0.29 | 0.50 | 1.13 | 0.92 |
| 56 | Shuangjiangxi | 356 | 297 | 19.72 | −9.91 × 10−5 | −1.93 × 10−4 | 6.32 | 0.37 | 0.61 | 0.21 | 0.55 | 1.12 | 0.92 |
| 57 | Xixi | 300 | 498 | 17.54 | −9.03 × 10−5 | −1.76 × 10−4 | 6.52 | 0.50 | 0.37 | 0.23 | 0.33 | 1.13 | 0.90 |
| 58 | Huangze | 542 | 310 | 17.21 | −6.76 × 10−5 | −1.50 × 10−4 | 6.56 | 0.29 | 0.58 | 0.17 | 0.36 | 1.10 | 0.91 |
| 59 | Yutan | 621 | 525 | 16.10 | −7.64 × 10−5 | −1.11 × 10−4 | 6.77 | 0.34 | 0.38 | 0.18 | 0.48 | 1.09 | 0.92 |
| 60 | Jianning (Xikou) | 1354 | 556 | 16.69 | −4.72 × 10−5 | −1.06 × 10−4 | 6.72 | 0.20 | 0.25 | 0.20 | 0.62 | 1.06 | 0.92 |
| 61 | Hongtian | 1074 | 722 | 20.39 | −5.11 × 10−5 | −1.03 × 10−4 | 6.36 | 0.38 | 0.51 | 0.24 | 0.43 | 1.09 | 0.93 |
| 62 | Chongan (Wuyishan) | 1078 | 723 | 21.62 | −5.51 × 10−5 | −1.06 × 10−4 | 6.28 | 0.27 | 0.46 | 0.21 | 0.66 | 1.10 | 0.93 |
| 63 | Fengyang | 271 | 824 | 17.88 | −9.07 × 10−5 | −1.46 × 10−4 | 6.46 | 0.29 | 0.46 | 0.19 | 0.53 | 1.14 | 0.88 |
| 64 | Taipingkou | 244 | 527 | 18.39 | −8.80 × 10−5 | −1.77 × 10−4 | 6.41 | 0.44 | 0.65 | 0.19 | 0.56 | 1.13 | 0.91 |
| ID | Station | AW | SHC (cm/s) | MBD (g/cm3) | IR (%) | FLD (km/km2) |
|---|---|---|---|---|---|---|
| 1 | Ziluoshan | 104.96 | 3.46 × 10−4 | 1.55 | 0.84 | 0.04 |
| 2 | Zhongtang | 110.79 | 2.05 × 10−4 | 1.55 | 0.95 | 0.06 |
| 3 | Jizhong | 102.46 | 2.54 × 10−4 | 1.55 | 0.95 | 0.00 |
| 4 | Xiagushan | 116.62 | 3.60 × 10−4 | 1.55 | 0.48 | 0.07 |
| 5 | Gaocheng | 103.29 | 3.46 × 10−4 | 1.56 | 0.10 | 0.07 |
| 6 | Lixin | 118.29 | 5.65 × 10−5 | 1.47 | 1.00 | 0.03 |
| 7 | Guanzhai | 116.62 | 8.47 × 10−5 | 1.49 | 0.33 | 0.06 |
| 8 | Dapoling | 120.79 | 2.47 × 10−4 | 1.53 | 0.26 | 0.12 |
| 9 | Luzhuang | 114.12 | 8.47 × 10−5 | 1.49 | 0.51 | 0.08 |
| 10 | Tanjiahe | 102.46 | 2.12 × 10−4 | 1.54 | 0.91 | 0.11 |
| 11 | Zhumadian | 116.62 | 4.24 × 10−5 | 1.46 | 0.00 | 0.03 |
| 12 | Nanlidian | 118.29 | 1.91 × 10−4 | 1.52 | 0.32 | 0.13 |
| 13 | Peihe | 114.12 | 1.77 × 10−4 | 1.53 | 1.00 | 0.00 |
| 14 | Baiqueyuan | 125.78 | 2.61 × 10−4 | 1.50 | 0.72 | 0.06 |
| 15 | Huangnizhuang | 119.12 | 2.47 × 10−4 | 1.46 | 0.65 | 0.11 |
| 16 | Qilin | 122.45 | 2.26 × 10−4 | 1.46 | 0.28 | 0.16 |
| 17 | Zhangchong | 125.78 | 2.19 × 10−4 | 1.46 | 0.26 | 0.00 |
| 18 | Bailianya | 124.12 | 2.61 × 10−4 | 1.43 | 0.40 | 0.04 |
| 19 | Huanghewei | 120.79 | 2.19 × 10−4 | 1.46 | 0.48 | 0.03 |
| 20 | Xiaotian | 123.28 | 2.40 × 10−4 | 1.46 | 0.71 | 0.07 |
| 21 | Taoxi | 121.62 | 1.98 × 10−4 | 1.46 | 0.04 | 0.02 |
| 22 | Liukou | 114.95 | 4.24 × 10−5 | 1.39 | 0.00 | 0.00 |
| 23 | Dahekou | 114.12 | 3.53 × 10−5 | 1.35 | 0.02 | 0.05 |
| 24 | Yuetan | 115.79 | 4.24 × 10−5 | 1.39 | 0.01 | 0.04 |
| 25 | Shancha | 136.61 | 1.06 × 10−4 | 1.38 | 0.43 | 0.12 |
| 26 | Wananba | 115.79 | 9.18 × 10−5 | 1.43 | 0.17 | 0.05 |
| 27 | Sankouzhen | 131.61 | 9.18 × 10−5 | 1.37 | 0.26 | 0.03 |
| 28 | Tunxi | 115.79 | 7.06 × 10−5 | 1.42 | 0.10 | 0.06 |
| 29 | Yuxi | 113.29 | 7.77 × 10−5 | 1.44 | 0.18 | 0.07 |
| 30 | Linxi | 115.79 | 4.94 × 10−5 | 1.39 | 0.25 | 0.11 |
| 31 | Hulesi | 117.45 | 4.94 × 10−5 | 1.40 | 0.24 | 0.13 |
| 32 | Misai | 112.46 | 3.53 × 10−5 | 1.40 | 0.40 | 0.09 |
| 33 | Zhongzhou | 99.96 | 2.68 × 10−4 | 1.48 | 0.27 | 0.00 |
| 34 | Yancun | 109.12 | 7.77 × 10−5 | 1.47 | 0.07 | 0.09 |
| 35 | Baikuoban | 118.29 | 2.12 × 10−5 | 1.35 | 0.00 | 0.05 |
| 36 | Shangzouban | 98.29 | 9.18 × 10−5 | 1.46 | 0.12 | 0.00 |
| 37 | Yuankou | 112.46 | 7.77 × 10−5 | 1.44 | 0.52 | 0.07 |
| 38 | Qingshandian | 109.96 | 3.53 × 10−5 | 1.39 | 0.38 | 0.07 |
| 39 | Fenshui | 113.29 | 2.82 × 10−5 | 1.38 | 0.27 | 0.06 |
| 40 | Shanjiao | 114.95 | 3.53 × 10−5 | 1.38 | 0.95 | 0.00 |
| 41 | Laoshikan | 114.95 | 4.24 × 10−5 | 1.39 | 0.63 | 0.10 |
| 42 | Qianyu | 110.79 | 2.12 × 10−5 | 1.36 | 0.25 | 0.02 |
| 43 | Shangbao | 116.62 | 2.82 × 10−5 | 1.36 | 0.78 | 0.09 |
| 44 | Qiaodongcun | 116.62 | 3.53 × 10−5 | 1.36 | 0.50 | 0.00 |
| 45 | Hengtangcun | 114.95 | 6.35 × 10−5 | 1.42 | 0.39 | 0.06 |
| 46 | Yubujie | 119.12 | 2.19 × 10−4 | 1.47 | 0.09 | 0.00 |
| 47 | Shangxiantan | 117.45 | 4.24 × 10−5 | 1.39 | 0.75 | 0.13 |
| 48 | Jiangwan | 106.62 | 1.13 × 10−4 | 1.48 | 1.00 | 0.00 |
| 49 | Liantangkou | 108.29 | 1.55 × 10−4 | 1.47 | 0.58 | 0.06 |
| 50 | Daixi | 111.62 | 7.06 × 10−5 | 1.48 | 0.82 | 0.02 |
| 51 | Yiwufotang | 111.62 | 9.18 × 10−5 | 1.45 | 0.63 | 0.09 |
| 52 | Dongyangyanxia | 112.46 | 7.06 × 10−5 | 1.44 | 0.73 | 0.13 |
| 53 | Daitou | 118.29 | 3.53 × 10−5 | 1.41 | 0.26 | 0.00 |
| 54 | Qiulu | 114.95 | 2.82 × 10−5 | 1.37 | 1.00 | 0.00 |
| 55 | Caodian | 114.95 | 3.53 × 10−5 | 1.43 | 0.77 | 0.09 |
| 56 | Shuangjiangxi | 107.46 | 5.65 × 10−5 | 1.43 | 0.86 | 0.15 |
| 57 | Xixi | 120.79 | 7.06 × 10−5 | 1.42 | 0.94 | 0.00 |
| 58 | Huangze | 114.95 | 4.94 × 10−5 | 1.40 | 0.86 | 0.04 |
| 59 | Yutan | 119.12 | 4.24 × 10−5 | 1.40 | 0.44 | 0.13 |
| 60 | Jianning(Xikou) | 120.79 | 4.94 × 10−5 | 1.41 | 0.34 | 0.11 |
| 61 | Hongtian | 114.95 | 4.24 × 10−5 | 1.42 | 0.66 | 0.06 |
| 62 | Chongan(Wuyishan) | 117.45 | 5.65 × 10−5 | 1.41 | 0.75 | 0.04 |
| 63 | Fengyang | 119.12 | 8.47 × 10−5 | 1.42 | 0.90 | 0.02 |
| 64 | Taipingkou | 119.12 | 3.53 × 10−5 | 1.39 | 0.93 | 0.08 |
| ID | Station | NSE | ε (%) | ID | Station | NSE | ε (%) |
|---|---|---|---|---|---|---|---|
| 1 | Ziluoshan | 0.26 | 18.16 | 33 | Zhongzhou | 0.97 | 16.16 |
| 2 | Zhongtang | 0.77 | 16.42 | 34 | Yancun | 0.93 | 14.41 |
| 3 | Jizhong | 0.99 | 12.07 | 35 | Baikuoban | 0.99 | 13.72 |
| 4 | Xiagushan | 0.74 | 15.20 | 36 | Shangzouban | 0.96 | 12.87 |
| 5 | Gaocheng | 0.34 | 100.50 | 37 | Yuankou | 0.98 | 15.67 |
| 6 | Lixin | 0.81 | 13.60 | 38 | Qingshandian | 0.98 | 13.78 |
| 7 | Guanzhai | 0.91 | 11.90 | 39 | Fenshui | 0.98 | 14.41 |
| 8 | Dapoling | 1.00 | 13.92 | 40 | Shanjiao | 0.93 | 13.13 |
| 9 | Luzhuang | 0.96 | 16.95 | 41 | Laoshikan | 0.62 | 15.80 |
| 10 | Tanjiahe | 0.93 | 18.01 | 42 | Qianyu | 0.95 | 18.44 |
| 11 | Zhumadian | 0.99 | 18.63 | 43 | Shangbao | 0.99 | 14.30 |
| 12 | Nanlidian | 0.99 | 15.30 | 44 | Qiaodongcun | 0.96 | 15.76 |
| 13 | Peihe | 0.97 | 18.09 | 45 | Hengtangcun | 0.83 | 11.35 |
| 14 | Baiqueyuan | 0.94 | 14.53 | 46 | Yubujie | 0.96 | 15.58 |
| 15 | Huangnizhuang | 0.99 | 14.30 | 47 | Shangxiantan | 0.96 | 16.10 |
| 16 | Qilin | 0.94 | 11.70 | 48 | Jiangwan | 0.98 | 17.86 |
| 17 | Zhangchong | 1.00 | 11.39 | 49 | Liantangkou | 0.98 | 15.95 |
| 18 | Bailianya | 0.98 | 11.44 | 50 | Daixi | 0.98 | 17.79 |
| 19 | Huanghewei | 0.98 | 8.24 | 51 | Yiwufotang | 0.98 | 14.52 |
| 20 | Xiaotian | 0.96 | 13.53 | 52 | Dongyangyanxia | 0.98 | 16.79 |
| 21 | Taoxi | 0.92 | 30.82 | 53 | Daitou | 0.99 | 12.74 |
| 22 | Liukou | 0.96 | 14.30 | 54 | Qiulu | 0.99 | 11.69 |
| 23 | Dahekou | 0.99 | 15.79 | 55 | Caodian | 0.97 | 16.19 |
| 24 | Yuetan | 0.99 | 14.31 | 56 | Shuangjiangxi | 0.98 | 18.03 |
| 25 | Shancha | 0.95 | 16.72 | 57 | Xixi | 0.97 | 15.45 |
| 26 | Wananba | 0.95 | 16.37 | 58 | Huangze | 0.91 | 15.74 |
| 27 | Sankouzhen | 0.98 | 13.73 | 59 | Yutan | 0.98 | 10.14 |
| 28 | Tunxi | 0.98 | 14.97 | 60 | Jianning | 0.97 | 7.42 |
| 29 | Yuxi | 0.99 | 15.33 | 61 | Hongtian | 0.69 | 9.62 |
| 30 | Linxi | 0.97 | 15.41 | 62 | Chongan | 0.99 | 11.77 |
| 31 | Hulesi | 0.99 | 15.25 | 63 | Fengyang | 0.97 | 9.53 |
| 32 | Misai | 0.99 | 15.06 | 64 | Taipingkou | 0.98 | 9.46 |
References
- Razavi, T.; Coulibaly, P. Streamflow Prediction in Ungauged Basins: Review of Regionalization Methods. Am. Soc. Civ. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Nruthya, K.; Srinivas, V.V. Evaluating Methods to Predict Streamflow at Ungauged Sites Using Regional Flow Duration Curves: A Case Study. Aquat. Procedia 2015, 4, 641–648. [Google Scholar] [CrossRef]
- Betterle, A.; Schirmer, M.; Botter, G. Flow dynamics at the continental scale: Streamflow correlation and hydrological similarity. Hydrol. Process. 2019, 33, 627–646. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Ganora, D.; Claps, P.; Laio, F.; Viglione, A. An approach to estimate nonparametric flow duration curves in ungauged basins. Water Resour. Res. 2009, 45, W10418. [Google Scholar] [CrossRef]
- Oudin, L.; Kay, A.; Andréassian, V.; Perrin, C. Are seemingly physically similar catchments truly hydrologically similar? Water Resour. Res. 2010, 46, W11558. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. FLOW DURATION CURVES II: A REVIEW OF APPLICATIONS IN WATER RESOURCES PLANNING. J. Am. Water Resour. 1995, 31, 1029–1039. [Google Scholar] [CrossRef]
- Pugliese, A.; Castellarin, A.; Brath, A. Geostatistical prediction of flow–duration curves in an index-flow framework. Hydrol. Earth Syst. Sci. 2014, 18, 3801–3816. [Google Scholar] [CrossRef] [Green Version]
- Gaviria, C.; Carvajal-Serna, F. Regionalization of flow duration curves in Colombia. Hydrol. Res. 2022, 53, 1075–1089. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q.; Zhang, L.; Chiew, F.H.S. A new regionalization approach and its application to predict flow duration curve in ungauged basins. J. Hydrol. 2010, 389, 137–145. [Google Scholar] [CrossRef]
- Ye, S.; Yaeger, M.; Coopersmith, E.; Cheng, L.; Sivapalan, M. Exploring the physical controls of regional patterns of flow duration curves—Part 2: Role of seasonality, the regime curve, and associated process controls. Hydrol. Earth Syst. Sci. 2012, 16, 4447–4465. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Liu, J.; Srivastava, P.; Liu, H.; Li, X.; Shen, X.; Tan, H. The Dominant Control of Relief on Soil Water Content Distribution During Wet--Dry Transitions in Headwaters. Water Resour. Res. 2021, 57, e2021WR029587. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Han, X.; Shen, X.; Liang, Z.; Wang, S. Variable storage behavior controlled by rainfall intensity and profile structure upon saturation excess overland flow generation. J. Hydrol. 2022, 610, 127860. [Google Scholar] [CrossRef]
- Castellarin, A.; Galeati, G.; Brandimarte, L.; Montanari, A.; Brath, A. Regional flow-duration curves: Reliability for ungauged basins. Adv. Water Resour. 2004, 27, 953–965. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Improved methods for daily streamflow estimates at ungauged sites. Water Resour. Res. 2012, 48, 2523. [Google Scholar] [CrossRef] [Green Version]
- Ridolfi, E.; Kumar, H.; Bárdossy, A. A methodology to estimate flow duration curves at partially ungauged basins. Hydrol. Earth Syst. Sci. 2020, 24, 2043–2060. [Google Scholar] [CrossRef] [Green Version]
- LeBoutillier, D.; Waylen, P. A Stochastic Model of Flow Duration Curves. Water Resour. Res. 1993, 29, 3535–3541. [Google Scholar] [CrossRef]
- Cheng, L.; Yaeger, M.; Viglione, A.; Coopersmith, E.; Ye, S.; Sivapalan, M. Exploring the physical controls of regional patterns of flow duration curves—Part 1: Insights from statistical analyses. Hydrol. Earth Syst. Sci. 2012, 16, 4435–4446. [Google Scholar] [CrossRef] [Green Version]
- Quimpo, R.; Alejandrino, A.; McNally, T. Regionalized Flow Duration Curves for Philippines. J. Water Resour. Plan. Manag. 1983, 109, 320–330. [Google Scholar] [CrossRef]
- Mimikou, M.; Kaemaki, S. Regionalization of flow duration characteristics. J. Hydrol. 1985, 82, 77–91. [Google Scholar] [CrossRef]
- Viola, F.; Noto, L.V.; Cannarozzo, M.; La Loggia, G. Regional flow duration curves for ungauged sites in Sicily. Hydrol. Earth Syst. Sci. 2011, 15, 323–331. [Google Scholar] [CrossRef] [Green Version]
- Fouad, G.; Loáiciga, H.A. Independent variable selection for regression modeling of the flow duration curve for ungauged basins in the United States. J. Hydrol. 2020, 587, 124975. [Google Scholar] [CrossRef]
- Silva, R.d.S.e.; Blanco, C.J.C.; Pessoa, F.C.L. Alternative for the regionalization of flow duration curves. J. Appl. Water Eng. Res. 2019, 7, 198–206. [Google Scholar] [CrossRef]
- Pessoa, F.C.L.; Blanco, C.J.C.; Gomes, E.P. Regionalization of flow duration curves in the Amazon with the definition of homogeneous regions via fuzzy C-means. Acad. Bras. Cienc. 2021, 93, e20190747. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z.; Askari, M. Assessment of Flow Duration Curve fitting equations. In Stochastic Hydrological Modelling in water Management, 1st ed.; Universiti TeknologiMalaysia, UTM Press: Skudai, Malaysia, 2015; pp. 29–52. [Google Scholar]
- Otache, M.Y.; Tyabo, M.A.; Animashaun, I.M.; Ezekiel, L.P. Application of Parametric-Based Framework for Regionalisation of Flow Duration Curves. J. Geosci. Environ. Prot. 2016, 04, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Cooke, C.D.; Buttle, J.M. Assessing basin storage: Comparison of hydrometric-- and tracer--based indices of dynamic and total storage. Hydrol. Process. 2020, 34, 2012–2031. [Google Scholar] [CrossRef]
- Chengmei, L.; Zhongmin, L.; Shaopeng, Q.I.U.; Yupeng, F.U.; Yanping, C.U.I. Application of SC-Nash runoff model in small watershed of hilly area. S.—N. Water Transf. Water Sci. Technol. 2021, 19, 246–254. [Google Scholar]
- Mohamoud, Y. Prediction of Daily Flow Duration Curves and Streamflow for Ungauged Catchments Using Regional Flow Duration Curves. Hydrol. Sci. J. 2008, 53, 706–724. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, Z.; Zhang, L. Changes in streamflow regime following vegetation changes from paired catchments. Hydrol. Process. 2012, 26, 1561–1573. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Liu, C.-W. A regional model of low flow for southern Taiwan. Hydrol. Process. 2002, 16, 2017–2034. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Yang, S.; He, R. Understanding the hierarchical controls of geographical features on hydrological responses in humid mountainous areas through a stepwise clustering scheme. Stoch. Environ. Res. Risk Assess. 2021, 36, 1521–1540. [Google Scholar] [CrossRef]
- Smakhtin, V.Y.; Hughes, D.A.; Creuse-Naudin, E. Regionalization of daily flow characteristics in part of the Eastern Cape, South Africa. Hydrol. Sci. J. 1997, 42, 919–936. [Google Scholar] [CrossRef] [Green Version]
- Ward, R.C.a.R.M. Principles of Hydrology, 3rd ed.; McGraw-Hill: Berkshire, UK, 1990. [Google Scholar]
- Kroll, C.N.; Song, P. Impact of multicollinearity on small sample hydrologic regression models. Water Resour. Res. 2013, 49, 3756–3769. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, J.; Lin, L.; Wang, A. Exploring hydrologically similar catchments in terms of the physical characteristics of upstream regions. Hydrol. Res. 2017, 49, 1467–1483. [Google Scholar] [CrossRef]
- Panthi, J.; Talchabhadel, R.; Ghimire, G.R.; Sharma, S.; Dahal, P.; Baniya, R.; Boving, T.; Pradhanang, S.M.; Parajuli, B. Hydrologic Regionalization under Data Scarcity: Implications for Streamflow Prediction. J. Hydrol. Eng. 2021, 26, 05021022. [Google Scholar] [CrossRef]
- Hocking, R.R. The Analysis and Selection of Variables in Linear Regression. Biometrics 1976, 32, 1–49. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Boscarello, L.; Ravazzani, G.; Cislaghi, A.; Mancini, M. Regionalization of Flow-Duration Curves through Catchment Classification with Streamflow Signatures and Physiographic-Climate Indices. J. Hydrol. Eng. 2016, 21, 05015027. [Google Scholar] [CrossRef]
- Mendicino, G.; Senatore, A. Evaluation of parametric and statistical approaches for the regionalization of flow duration curves in intermittent regimes. J. Hydrol. 2013, 480, 19–32. [Google Scholar] [CrossRef]
- Castellarin, A.; Camorani, G.; Brath, A. Predicting annual and long-term flow-duration curves in ungauged basins. Adv. Water Resour. 2007, 30, 937–953. [Google Scholar] [CrossRef]
- Mazvimavi, D. Estimation of Flow Characteristics of Ungauged Catchments: Case Study in Zimbabwe. 188 f. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2003. [Google Scholar]
- Yu, P.-S.; Yang, T.-C.; Wang, Y.-C. Uncertainty Analysis of Regional Flow Duration Curves. J. Water Resour. Plan. Manag. 2002, 128, 424–430. [Google Scholar] [CrossRef]
- Swain, J.B.; Patra, K.C. Streamflow Estimation in Ungauged Catchments Using Regional Flow Duration Curve: Comparative Study. J. Hydrol. Eng. 2017, 22, 04017010. [Google Scholar] [CrossRef]
- Acreman, M.C.; Sinclair, C.D. Classification of drainage basins according to their physical characteristics; an application for flood frequency analysis in Scotland. J. Hydrol. 1986, 84, 365–380. [Google Scholar] [CrossRef]
- Boscarello, L.; Ravazzani, G.; Mancini, M. Catchment Multisite Discharge Measurements for Hydrological Model Calibration. Procedia Environ. Sci. 2013, 19, 158–167. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Xu, S.; Han, X.; Chen, X.; He, R. A Multi-Dimensional Hydro-Climatic Similarity and Classification Framework Based on Budyko Theory for Continental-Scale Applications in China. Water 2019, 11, 319. [Google Scholar] [CrossRef] [Green Version]
- Razavi, T.; Coulibaly, P. An evaluation of regionalization and watershed classification schemes for continuous daily streamflow prediction in ungauged watersheds. Can. Water Resour. J. Rev. Can. Des. Ressour. Hydr. 2016, 42, 2–20. [Google Scholar] [CrossRef]
- Choubin, B.; Solaimani, K.; Rezanezhad, F.; Habibnejad Roshan, M.; Malekian, A.; Shamshirband, S. Streamflow regionalization using a similarity approach in ungauged basins: Application of the geo-environmental signatures in the Karkheh River Basin, Iran. Catena 2019, 182, 104128. [Google Scholar] [CrossRef]




| Abbreviation | Description | Unit | |
|---|---|---|---|
| Rainfall | P | Average annual rainfall | mm |
| Max 1d | Maximum 1 d of annual rainfall | mm | |
| Max 3d | Maximum 3 d of annual rainfall | mm | |
| Max 7d | Maximum 7 d of annual rainfall | mm | |
| RR | Rate of increase in daily rainfall a | mm/d | |
| FR | Rate of decline in daily rainfall b | mm/d | |
| Topography | A | Basin area | km2 |
| H | Average elevation | m | |
| β | Average gradient | ° | |
| CC | Average plan curvature c | - | |
| CP | Average profile curvature d | - | |
| TI | Average topographic index | - | |
| HI | Integral of area–altitude curve | - | |
| AS | Gradient of integral of area–altitude curve | - | |
| RC | Circularity ratio | - | |
| RF | Form factor | - | |
| D | Fractal dimension of river network | - | |
| NDVI | Normalized difference vegetation index | - | |
| Soil and geology | AW | Available moisture content e | mm/m |
| SHC | Saturated hydraulic conductivity | cm/s | |
| MBD | Matric bulk density | g/cm3 | |
| IR | Proportion of impermeable rock formation (igneous rock) area | % | |
| FLD | Line density of cracks or faults | km/km2 |
| ID | Station | a | b | NSE | ε (%) | ID | Station | a | b | NSE | ε (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Ziluoshan | 0.0016 | 0.9202 | 1.00 | 0.10 | 33 | Zhongzhou | 0.0126 | 0.7578 | 0.99 | 1.18 |
| 2 | Zhongtang | 0.0023 | 0.9659 | 1.00 | 0.23 | 34 | Yancun | 0.0143 | 0.7543 | 0.99 | 1.34 |
| 3 | Jizhong | 0.0036 | 0.9263 | 1.00 | 0.33 | 35 | Baikuoban | 0.0104 | 0.7582 | 0.99 | 0.88 |
| 4 | Xiagushan | 0.0013 | 1.0352 | 1.00 | 0.07 | 36 | Shangzouban | 0.0123 | 0.6882 | 0.98 | 1.11 |
| 5 | Gaocheng | 0.0066 | 0.8471 | 1.00 | 0.34 | 37 | Yuankou | 0.0107 | 0.7387 | 0.99 | 1.06 |
| 6 | Lixin | 0.0010 | 1.2433 | 1.00 | 0.05 | 38 | Qingshandian | 0.0127 | 0.6941 | 0.98 | 1.11 |
| 7 | Guanzhai | 0.0011 | 1.0302 | 1.00 | 0.06 | 39 | Fenshui | 0.0110 | 0.7129 | 0.98 | 0.99 |
| 8 | Dapoling | 0.0025 | 0.9074 | 1.00 | 0.19 | 40 | Shanjiao | 0.0172 | 0.6387 | 0.97 | 1.50 |
| 9 | Luzhuang | 0.0011 | 1.0941 | 1.00 | 0.09 | 41 | Laoshikan | 0.0109 | 0.6184 | 0.97 | 0.87 |
| 10 | Tanjiahe | 0.0036 | 0.9749 | 1.00 | 0.35 | 42 | Qianyu | 0.0076 | 0.7491 | 0.99 | 0.75 |
| 11 | Zhumadian | 0.0003 | 1.3868 | 1.00 | 0.04 | 43 | Shangbao | 0.0117 | 0.7194 | 0.99 | 1.02 |
| 12 | Nanlidian | 0.0030 | 0.9483 | 1.00 | 0.26 | 44 | Qiaodongcun | 0.0087 | 0.7359 | 0.99 | 0.70 |
| 13 | Peihe | 0.0050 | 0.9219 | 1.00 | 0.57 | 45 | Hengtangcun | 0.0096 | 0.6685 | 0.99 | 0.57 |
| 14 | Baiqueyuan | 0.0047 | 0.9019 | 1.00 | 0.40 | 46 | Yubujie | 0.0079 | 0.7217 | 0.98 | 0.81 |
| 15 | Huangnizhuang | 0.0052 | 0.8705 | 1.00 | 0.36 | 47 | Shangxiantan | 0.0100 | 0.7494 | 0.99 | 1.00 |
| 16 | Qilin | 0.0075 | 0.8524 | 1.00 | 0.54 | 48 | Jiangwan | 0.0091 | 0.7549 | 0.98 | 1.11 |
| 17 | Zhangchong | 0.0076 | 0.7999 | 1.00 | 0.46 | 49 | Liantangkou | 0.0085 | 0.7229 | 0.98 | 0.82 |
| 18 | Bailianya | 0.0076 | 0.8118 | 1.00 | 0.50 | 50 | Daixi | 0.0071 | 0.7569 | 0.98 | 0.79 |
| 19 | Huanghewei | 0.0129 | 0.7189 | 1.00 | 0.60 | 51 | Yiwufotang | 0.0078 | 0.7232 | 0.99 | 0.61 |
| 20 | Xiaotian | 0.0096 | 0.7869 | 0.99 | 0.79 | 52 | Dongyangyanxia | 0.0068 | 0.7666 | 0.99 | 0.62 |
| 21 | Taoxi | 0.0055 | 0.7771 | 0.99 | 0.59 | 53 | Daitou | 0.0140 | 0.7616 | 0.99 | 1.03 |
| 22 | Liukou | 0.0163 | 0.7470 | 0.99 | 1.33 | 54 | Qiulu | 0.0125 | 0.7516 | 0.99 | 0.85 |
| 23 | Dahekou | 0.0114 | 0.7862 | 0.99 | 1.01 | 55 | Caodian | 0.0110 | 0.7451 | 0.99 | 1.11 |
| 24 | Yuetan | 0.0145 | 0.7214 | 0.99 | 1.21 | 56 | Shuangjiangxi | 0.0084 | 0.7574 | 0.98 | 0.99 |
| 25 | Shancha | 0.0167 | 0.7178 | 0.98 | 1.66 | 57 | Xixi | 0.0095 | 0.7320 | 0.99 | 0.79 |
| 26 | Wananba | 0.0114 | 0.7245 | 0.99 | 0.91 | 58 | Huangze | 0.0064 | 0.7766 | 0.99 | 0.50 |
| 27 | Sankouzhen | 0.0164 | 0.6811 | 0.98 | 1.47 | 59 | Yutan | 0.0132 | 0.6616 | 0.99 | 0.93 |
| 28 | Tunxi | 0.0139 | 0.7177 | 0.99 | 1.26 | 60 | Jianning | 0.0147 | 0.6319 | 0.99 | 0.81 |
| 29 | Yuxi | 0.0089 | 0.7803 | 0.99 | 0.72 | 61 | Hongtian | 0.0151 | 0.5558 | 0.97 | 0.89 |
| 30 | Linxi | 0.0077 | 0.7625 | 0.99 | 0.64 | 62 | Chongan | 0.0148 | 0.6985 | 0.99 | 0.85 |
| 31 | Hulesi | 0.0097 | 0.7491 | 0.99 | 0.85 | 63 | Fengyang | 0.0169 | 0.6194 | 0.98 | 1.08 |
| 32 | Misai | 0.0135 | 0.7834 | 0.99 | 1.21 | 64 | Taipingkou | 0.0108 | 0.6970 | 0.99 | 0.73 |
| Combination | Independent Variables | Regionalization Models |
|---|---|---|
| Ⅰ | P, H, β, TI | |
| Ⅱ | P, H, β, TI, NDVI | |
| Ⅲ | P, H, β, TI, Max7d | |
| Ⅳ | P, H, β, TI, Max3d | |
| Ⅴ | P, H, β, TI, NDV I, Max7d | |
| Ⅵ | P, H, β, TI, Max7d, Max3d | |
| Ⅶ | P, H, β, TI, NDVI, Max7d, Max3d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Gao, M.; Liu, J.; Wu, P.; Yang, Y. Regionalizing Streamflow Regime Function through Integrations of Geographical Controls in Mountainous Basins. Water 2023, 15, 280. https://doi.org/10.3390/w15020280
Yang S, Gao M, Liu J, Wu P, Yang Y. Regionalizing Streamflow Regime Function through Integrations of Geographical Controls in Mountainous Basins. Water. 2023; 15(2):280. https://doi.org/10.3390/w15020280
Chicago/Turabian StyleYang, Shuang, Mengzhu Gao, Jintao Liu, Pengfei Wu, and Yaqian Yang. 2023. "Regionalizing Streamflow Regime Function through Integrations of Geographical Controls in Mountainous Basins" Water 15, no. 2: 280. https://doi.org/10.3390/w15020280
APA StyleYang, S., Gao, M., Liu, J., Wu, P., & Yang, Y. (2023). Regionalizing Streamflow Regime Function through Integrations of Geographical Controls in Mountainous Basins. Water, 15(2), 280. https://doi.org/10.3390/w15020280







