Abstract
Considering the wide applicability of two-parameter distributions in the frequency analysis of extreme events, this article presents new elements regarding the use of thirteen two-parameter probability distributions, using three parameter estimation methods. All the necessary elements for the application of these distributions are presented using the method of ordinary moments (MOM), the method of linear moments (L-moments) and the method of high order linear moments (LH-moments). Only these three methods are analyzed, because they are usually applied in the analysis regarding the regionalization of extreme events. As a case study, the frequency analysis of the maximum annual flows on the Siret River, Lungoci station, Romania, was made. For the recommended methods (L- and LH-moments), from the thirteen analyzed distributions, the log-normal distribution had the best results, with the theoretical values L-coefficient of variation and L-kurtosis (0.297, 0.192, 0.323, 0.185, 0.336, and 0.185) best approximating the corresponding values of the recorded data (0.339, 0.185, 0.233, 0.199, 0.198, and 0.205).
1. Introduction
Frequency analysis represents a direct method of determining extreme events in hydrology that may be expected to occur for a given period.
The analysis involves the use of probability distributions to estimate the quantiles related to rare events with certain return periods, corresponding to small exceeding probabilities, where, in most cases, there are no recorded data.
In general, the analysis uses distributions of at least three parameters, in order to calibrate the high-order moments as much as possible. However, there are also situations in which the use of two-parameter probability distributions is preferred, such as the determination of maximum flow, maximum precipitation, and maximum volumes, or to use probability distribution functions such as synthetic unit hydrograph (SUH).
Considering that many researchers still use two-parameter distributions in performing frequency analyzes of extreme events in hydrology, the article aims to provide guidelines for a proper use of these types of statistical distributions. It also presents new elements and relations for a significant number of distributions with applicability in frequency analysis, which presents certain advantages compared to the usual two-parameter distributions in hydrology (such as Gumbel, log-logistic, exponential), as well as greater flexibility with the possibility of modeling the different forms of heavy tail curves, an advantage mainly due to the fact that these distributions are characterized by various values of higher order moments (coefficient of variation, skewness, kurtosis), aspects that do not characterize distributions such as Gumbel, log-logistic, or exponential.
Thus, this manuscript presents some of the most used two-parameter distributions, i.e., Gumbel (G), gamma (Γ2), log-normal (LN2), logistic (L2), log-logistic (LL2), Weibull (W2), Fréchet (F2), the shifted exponential (E2), and generalized exponential (GE), but also some less analyzed distributions, with applicability in these types of analyses, i.e., Rayleigh (R2), Pearson V (PV2), chi (CH2), and inverse chi (ICH2) distributions. The limited applicability by researchers of these last distributions is due to the complexity of the equations needed to estimate the parameters, as well as the lack of closed forms of the inverse function. It should be mentioned from the beginning that the manuscript does not exclude the possibility of using other distributions and methods in the frequency analysis of extreme events in hydrology, but only expands the possibility for researchers to use a larger number of distributions, this aspect being only beneficial to a corresponding holistic analysis from a statistical and hydrological point of view.
Why is the presentation of these distributions important? It is important because, considering the still widespread use of two-parameter distributions in FFA, based on the diagrams and variation relations of L-skewness and L-kurtosis, a pre-selection of distributions that can be successfully applied using the L- and LH-moments method can be used, respecting the performance criteria specific to these methods. Thus, the analysis is simplified and greatly reduces the calculation time, being able to replace the use of distributions with a larger number of parameters. For this purpose, the case study includes a four-parameter distribution, namely, the Burr distribution, which calibrates exactly all the linear moments, being thus characterized, from a statistical point of view, by a high degree of confidence, but for which the estimation of the parameters requires difficult calculations requiring the solution of a system of four non-linear equations.
The proposed distributions covers a wide variety of extreme events analyzed in hydrology: the Gumbel distribution is usually used to obtain the intensity–duration–frequency curves of rainfall intensity [1,2,3,4,5,6], to determine the maximum flows [7,8,9,10,11], and to determine the minimum flows [12,13,14,15,15]; the gamma distribution is often used for SUH design [16,17,18,19,20,21], as well as for the analysis of maximum flows [22,23,24]; the log-logistic distribution is applied to determine the maximum precipitation [25,26,27,28] and to determine the maximum flows [25,29,30]; HUSSAIN [28] applied the Fréchet distribution to determine the maximum precipitation; Ahilan et al. [31,32] analyzed the Fréchet distribution to determine the maximum flow rates; Bhunya et al. [19,20,21] used the two-parameter Weibull distribution for SUH design.
In the case of distributions W2, F2, PV2, using the MOM and the L-moments method, the new contributions were presented in previous materials [33].
In this article, only the new elements regarding these thirteen distributions and their applicability are presented, such as the relations for parameter estimation using the first and second order LH-moments. Moreover, new elements are presented regarding the parameter estimation with MOM and L-moments, for the distributions Rayleigh, chi, and inverse chi, and also improved estimation relations, compared to existing approximate relations in the literature, for the gamma distribution being introduced for the first time in FFA. All these new elements are centralized in Table 1.

Table 1.
New elements of the distributions presented in the manuscript.
Considering the diverse use of two-parameter distributions in frequency analysis in hydrology, the main purpose of the article is the presentation of exact and approximate parameter estimation relationships for these probability distributions, as well as the presentation of the relationships and diagrams necessary to choose the best distribution using the L-moments method and the LH-moments method. For these methods and distributions, the necessary relationships for parameter estimation and rigorous criteria for selecting the best model have not been presented so far, with this being the first time they appeared in science.
In general, the main disadvantage of using these two-parameter distributions is the fact that, regardless of the parameter estimation method, they cannot calibrate the higher-order moments (skewness, ; kurtosis, ; L-skewness, ; L-kurtosis, ; LH-skewness, ; LH-kurtosis, ). This aspect makes it extremely difficult to choose the best distribution. Another disadvantage is the fact that many two-parameter distributions have constant values of these statistical indicators, such as Gumbel, exponential shifted, normal, uniform, Weibull, Fréchet, etc. [22,34]. This disadvantage is greatly reduced in the case of Γ2, LN2, CH2, and ICH2 distributions, where the higher order statistical indicators (, , , , , ) have distinct values depending on the second order statistical indicator (, , ). Thus, the presentation of the variation diagrams of these statistical indicators, using the L- and LH-moments methods, represents another element of novelty constituting the main criterion for selecting the best distribution. Using these two parameter estimation methods, the criterion for selecting the best distribution is for the difference to be as low as possible, between the theoretical values of the L-, LH-skewness and L-, LH-kurtosis indicators from those corresponding to the analyzed data set, especially in the case of small (n < 25) and medium (n < 50) series of observed data, preferably L-, LH-kurtosis, because, in general, it gives the heavy tail tendency [34]. In the case of large data sets (n > 80), additional criteria can be applied, namely the use of indicators and performance tests (relative mean error, relative absolute error, Kolmogorov–Smirnov, Anderson–Darling, etc.).
In the case of parameter estimation with MOM, although it is possible to create theoretical diagrams of skewness and kurtosis variation depending on the coefficient of variation (), the big disadvantage is the fact that the method is much less stable and robust to the variability of the length of the recorded data sets, with the skewness and kurtosis requiring important corrections, an aspect that very often cannot be fulfilled. Therefore, in the case of this method, for short and medium data sets, the selection criterion of the best distribution is not a rigorous one, involving subjective aspects that should not be found in such an analysis.
Another important element of the frequency analysis is the need to present the relative errors depending on the variability of the length of the observed data, knowing that this variability implies uncertainties on three levels, namely, in the estimation of statistical indicators, in the estimation of distribution parameters, and in the estimation of quantiles [25].
The manuscript presents as a case study the determination of the maximum flows on the Siret river, Romania, but the main purpose is to present the mathematical foundation of these distributions and parameter estimation methods, presenting for the first time explicit relations (exact and approximate) of parameter estimation using these methods. A comparative analysis is made regarding the advantages and disadvantages of the different parameter estimation methods. Rigorous criteria for choosing the best distribution and methods are provided.
Considering that the vast majority of the distributions presented (using these methods) are not included in dedicated programs, it is imperative to present the equations necessary for the use of these distributions, for the verification and reproduction of the analysis, but most importantly for facilitating the use of these distributions by researchers. These represent aspects of particular importance in a research that must be transparent and objective.
Only these parameter estimation methods are analyzed because they are used in the processes of regionalization of extreme events. Statistical regionalization is usually carried out by identifying homogeneous regions (HRs), where some theoretical moments are assumed as constant, while others can be expressed as functions of specific geomorphic covariates [35]. HRs are often identified by adopting: (1) geographical or administrative criteria; (2) cluster analysis [36,37,38,39]; or (3) artificial intelligence techniques [40]. Moreover, approaches that do not define fixed-boundary regions [41,42,43,44] are receiving increasing attention [45,46,47].
Taking into account that the existing regulations in Romania [48] also recommend the use of two-parameter distributions in determining the maximum flow rates, it is important that their application is performed appropriately and with mathematical rigor.
This research is part of a much larger and more complex research in the development of normative proposals regarding the frequency analysis of extreme events, by identifying methods and probability distributions characterized by mathematical and hydrological rigor.
The manuscript brings new contributions regarding the frequency analysis of maximum flows using two-parameter distributions, such as parameter estimation relations for MOM, L-, and LH-moments methods, rigorous criteria regarding the choice of the best distribution, and diagrams and relationships of – and –.
2. Methods
The methods for estimating the parameters of these probability distributions are the ordinary method of moments, the linear method of moments, and the high-order linear method of moments.
They are only analyzed because these methods can be used in the regionalization analysis of extreme events in hydrology, because they are based on statistical indicators that can be determined regionally [22,34,49].
In the case of other parameter estimation methods, such as the maximum likelihood method, the least squares method, the Bayesian method, etc., these are methods that can only be used at-site.
Among the three methods analyzed in this manuscript, the recommended methods are the L-moments method and the LH-moments method, because they are less subject to bias, more robust, and present objective criteria for selecting the best distributions [22,34,50,51]. The MOM method is presented comparatively, but it has the big disadvantage that there are no rigorous criteria for choosing the best fit distribution, the method involving corrections on high-order moments, which implies real difficulties, even in the case of using distributions with high numbers of parameters [34,49].
2.1. Density, Cumulative, and Inverse Functions
In this section, the density functions, , the cumulative functions, , and the inverse functions of the analyzed distributions are presented [22,23,25,34,52,53]. Table 2 shows all those elements.

Table 2.
The density, cumulative, and quantile functions.
All predefined functions presented are explained in previous materials [33] and in the nomenclature section.
2.2. Relation between Parameters and Constraints for the Analyzed Methods
In this section, only the new elements added to the thirteen analyzed distributions are presented, regarding the parameter estimation. For the LH-moments method, all relationships are new. Only the relationships related to the first level LH-moments are presented. The relationships corresponding to the second level LH-moments are presented in Appendix A.
In general, the LH-moments can be applied to linear moments up to the fourth order [54], but in this paper only the moments of the first and second level are analyzed, because they can represent an alternative to the frequency analysis of extreme events using partial series (POT or AES), both having the same purpose, namely, giving a lower importance to small extreme values from the series of annual maximum values.
2.2.1. Pearson V Distribution (PV2)
The relationships for the exact and approximate estimation of the PV2 distribution parameters, using MOM and L-moments, were presented in previous materials [33].
For the first level LH-moments, parameter can be approximated with the following exponential function with a logarithmic argument:
With the parameter known, the parameter can be estimated with the following relation:
where and . It can be seen that the integral depends only on the parameter , thus, it can be approximated with the following exponential function:
where and represent the first two LH-moments, and represents the LH-variation coefficient [54].
2.2.2. Chi Distribution (CH2)
Considering that the relations for estimating the parameters of this two-parameter distribution have not been presented before, this section presents the exact and approximate relations for estimating them using all three estimation methods.
The exact estimation of the parameters with the L-moments and LH-moments method is performed numerically (definite integrals) based on the equations using the quantile function.
To estimate the parameters with MOM, it is necessary to solve the following system of equations:
where and represent the arithmetic mean and variance.
Parameter can be obtained approximately using an exponential function depending on the coefficient of variation ():
With the parameter determined, the parameter is calculated :
For L-moments, the parameter can be obtained approximately depending on the L-coefficient of variation ():
if , the shape parameter can be approximated with the following exponential function:
if , the shape parameter can be approximated with the following exponential function:
if , the shape parameter can be approximated with the following exponential function:
With the parameter determined, the parameter is calculated:
where represent the first two L-moments and represents the L-coefficient of variation [34].
For the first level LH-moments, the equations are the following:
if , the shape parameter can be approximated with an exponential function with 8 terms:
if , the shape parameter can be approximated with an exponential function with 8 terms:
Results:
where , which can be approximated with an exponential function with 10 terms:
2.2.3. Inverse Chi Distribution (ICH2)
To estimate the parameters with MOM, it is necessary to solve the following system of equations:
Parameter can be obtained approximately with the following exponential function with 5 terms depending on the logarithmic coefficient of variation:
For L-moments, parameter can be obtained approximately depending on , with the following exponential function consisting of 9 terms:
For the first level LH-moments, the shape parameter can be determined using an exponential function with 7 terms:
where and , simplified with the help of an exponential function with 10 terms:
2.2.4. Gamma Distribution (Γ2)
The parameters with MOM are determined based on the equations presented in [22,23]. Considering that the inverse function does not have a close form, it can be calculated using Chow’s relation and the Cornish–Fisher and Kite frequency factors [22].
For the L-moments method, the shape parameter can be approximately calculated using the relation presented by Hosking [34].
For the first level LH-moments, the shape parameter can be approximated as follows:
if , the approximation uses an exponential function with 5 terms:
if , a rational function is used:
where , which can be simplified with a rational function:
2.2.5. Log-Normal Distribution (LN2)
The parameters with MOM are determined based on the equations presented in [22,23,55]. For the L-moments method, the scale parameter can be approximately calculated with the following new polynomial relation:
For first level LH-moments, the approximate relations of the scale parameter are:
if , a polynomial relation of 5 terms is used:
if , the approximation to be made with the help of an exponential relation of 7 terms:
where , which can be simplified with the following exponential function:
2.2.6. Gumbel (G)
The parameters with MOM and L-moments are determined based on the equations presented in [22,23,55,56,57].
For first level LH-moments, the relationships are as follows:
where represents the Euler constant.
2.2.7. Logistic (L2)
The parameters with MOM and L-moments are determined based on the equations presented in [22,23,57].
For first level LH-moments, the relationships are as follows:
2.2.8. Log-Logistic (LL2)
The parameters with MOM and L-moments are determined based on the equations presented in [57,58].
In the case of MOM estimation, the shape parameter can be approximated according to the coefficient of variation, with the following new exponential relationship:
For first level LH-moments, the relationships are as follows:
2.2.9. Exponential Shifted Distribution (E2)
The parameters with MOM and L-moments are determined based on the equations presented in [58].
For first level LH-moments, the relationships are as follows:
2.2.10. Rayleigh Distribution (R2)
The parameters with MOM are determined with the following expressions:
The equations, for the estimation with L-moments, are the following:
For first level LH-moments, the relationships are as follows:
2.2.11. Weibull Distribution (W2)
The parameters with MOM and L-moments are determined based on the equations presented in [22,23,33,55,57,58].
For first level LH-moments, the relationships are as follows:
The shape parameter can be approximated with the following relations:
if , an exponential function of 5 terms is used:
if , an exponential function of 5 terms is used:
With the known shape parameter, the scale parameter is determined with the following relation:
2.2.12. Fréchet Distribution (F2)
The parameters with MOM and L-moments are determined based on the equations presented in [22,23,33,55,57,58].
For first level LH-moments, the relationships are as follows:
The shape parameter can be approximated with the following exponential relation ():
2.2.13. Generalized Exponential Distribution (EG)
The parameters with MOM and L-moments are determined based on the equations presented in [33,52].
For first level LH-moments, the shape parameter can be approximated with the following relations:
if , the approximation relation is an exponential function with 5 terms:
if , the approximation function is an exponential one with 7 terms:
where, , simplified using the following exponential function with 7 terms:
The frequency analysis of the maximum flows is carried out according to the stages shown in Figure 1.
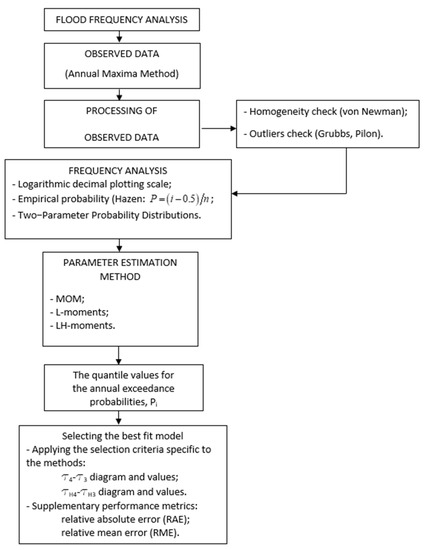
Figure 1.
Stages in the development of flood frequency analysis.
The data used represent the series of maximum flows characteristic of each year of analysis, thus, ensuring the independence of the data. Additionally, the verification was carried out using the Cunnane criterion and the USWRC 1976.
Regarding the homogeneity of the data, this condition was checked with the von Newman test, the data being homogeneous.
The analyzed series does not contain extreme values, the condition being checked with the help of the Grubbs–Beck and Pilon tests. Additional data regarding the results of these tests can be found in Section 4.1.
For the graphic representation of the observed data, the Hazen empirical probability was used. The logarithmic decimal plotting scale was chosen because it represents a more optimal method for highlighting the maximum flows related to the low annual exceedance probabilities.
The selection criteria of the best distribution related to each method is made with their specific criteria, with the mention that the L- and LH-moments methods are defined by rigorous selection criteria.
3. Study Area and Data
This study analyzes the Siret river, by performing a frequency analysis of the maximum annual flows, using the methods and probability distributions presented.
The Siret River (cadastral code XII) is located in the north-eastern part of Romania, being the left tributary of the Danube River.
The dependent Siret river system is 647 km long, originating from the territory of Ukraine, from the woody Carpathians [59,60,61].
Of the total length, 559 km (middle and lower Siret) are on the territory of Romania. It has the largest hydrographic basin on the territory of Romania, namely, 42,890 km2, representing approximately 18.1% of the country’s surface.
The river has an average slope of 1.7‰, a sinuosity coefficient of 1.86, an average altitude of 515 m, and a forestation coefficient of 0.37 [61]. Figure 2 shows the hydrographic basin of the Siret river [60].
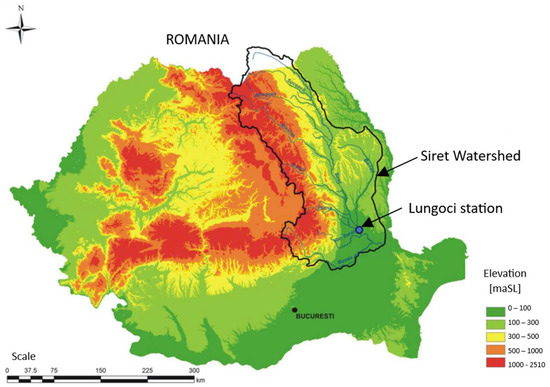
Figure 2.
Location of the hydrographic basin of the Siret River, Romania.
The maximum flows characteristic of this river are the result of snow melting superimposed with the fall of precipitation, usually occurring in the spring–summer months [62].
The river has a modified regime, with various retention works that influence the maximum annual values. In the Siret hydrographic watershed there are more than 100 multi-use reservoirs, and their contribution to flood mitigation is relatively low, because mitigation volumes are reduced compared to flood volumes, which have a peak flow greater than the flow with a 10% exceedance probability.
Table 3 shows the chronological series of the maximum annual flows recorded at the Lungoci hydrometric station, in the period 1970–2008, according to the Romanian Normative NP 129 [48]. The recorded series has a length of 39 maximum flows characteristic of each year. The maximum flow rates of the analyzed series vary between 275 m3/s and 4650 m3/s.

Table 3.
The annual maximum series for Siret River, Romania.
Figure 3 shows the observed data, on the Siret River, Romania, for the entire analysis period.
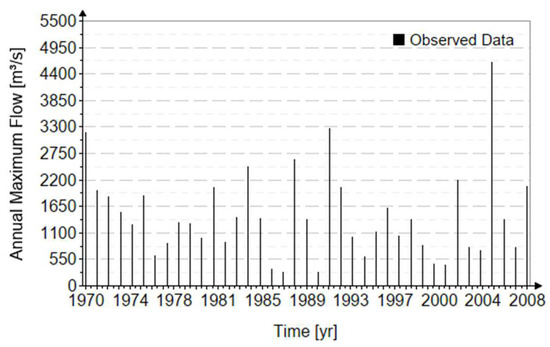
Figure 3.
The graph of data recorded at the hydrometric station on the Siret River.
From a statistical point of view, the three parameter estimation methods require the determination of some characteristic statistical indicators, such as the arithmetic mean (), mean square deviation (), the coefficient of variation (), the skewness (), the kurtosis (), L- and LH-coefficient of variation (, ), L- and LH-skewness (, ), and the L- and LH-kurtosis (, ). The values of these indicators, related to the analyzed data set, are presented in Table 4.

Table 4.
The statistical indicators for the Siret River (1970–2008), Romania.
The values of and confirm a low variation in maximum annual flows. The value of , which often requires certain corrections, confirms the fact that the skewness is to the right. In the case of the LH-moments methods, substantial changes in the indicators can be observed due to the attribution, in the analysis, of a lower importance to the lower extreme values.
4. Results and Discussion
The purpose of the analysis is to verify the performances of the described methods and distributions, in order to forecast the values of the quantiles corresponding to extremely rare events.
4.1. Verification of Independence, Stationarity, and Homogeneity
In a first stage, the criteria regarding the independence, stationarity, and homogeneity of the analyzed data were checked.
The independence of the data is ensured by the selection criterion, the data representing the maximum value corresponding to each year. However, there is the possibility that two maximum values characterize different years, but still come from the same flood, especially if the flood is multimodal. Thus, data independence was verified with the Cunnane criterion and the USWRC 1976 criterion [63,64].
The analyzed data are homogeneous, the value of the von Newman test [65] being greater than 2, namely, 2.026.
Regarding the stationarity, it was checked with t-test [66], for 5% level of significance. The calculated value of the test is 0.277. The critical value of the test is 2.03. It should be mentioned that climate change leads to a possible loss of this stationarity.
4.2. Quantile Estimation
Taking into account that two-parameter distributions still have an extended applicability in these types of analyses, for the case study of the Siret river, different two-parameter distributions from different families, with different particularities, are applied.
The obtained results differ depending on the characteristics of the distributions and on the estimation methods of the parameters, but also on the influence of the variability of the lengths of the data sets recorded in the estimation of the statistical indicators, parameters, and estimated quantiles.
Compared to other parameter estimation methods, these three analyzed methods are based on the determination of some statistical indicators related to each method, representing a real advantage in the regionalization process.
Figure 4a–d graphically presents the comparison of the results obtained for the Siret river. The empirical probability used for the graphic representation of the recorded values is the Hazen probability [22,55], based on the considerations presented in Section 4.3. The decimal logarithmic scale on the horizontal axis was used, because we wanted to highlight the heavy tail (the domain of rare events).
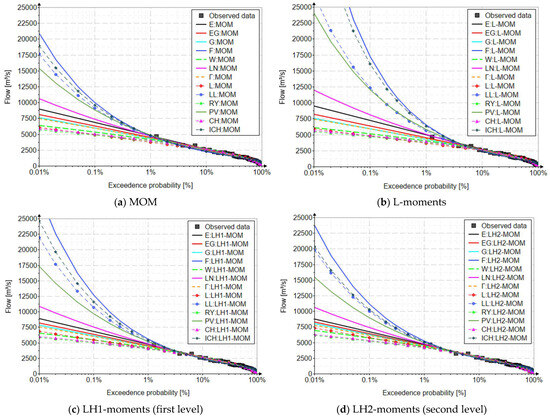
Figure 4.
Graphic presentation of the maximum annual flows recorded in the period 1970–2008 adjustments to probability distributions for Siret River, Romania.
Following the presented results, it can be observed that the quantile values differ substantially depending on the distribution and the parameter estimation method. Some distributions are characterized by a heavy tail overestimating the values (Fréchet distribution), while other distributions underestimate the values (Rayleigh distribution).
The analysis was made especially for the estimation of the quantiles related to the range of exceedance probabilities between 0.01–1%. The analysis of the resulting values must always be performed separately depending on the estimation method. For all three parameter estimation methods, the extreme curves (upper and lower) are those defined by the Fréchet and Rayleigh distributions.
In the case of MOM, the maximum values obtained (p = 0.01%) are 20,886 m3/s for the Fréchet distribution and 5687 m3/s for the Rayleigh distribution. For L-moments methods, the values of the amounts of the two distributions are 45,446 m3/s, and 5494 m3/s. In the case of the two methods of LH-moments, the values of the quantiles of the distributions are 28,814 m3/s and 5859 m3/s for the first level of LH-moments, and 23,709 m3/s and 6156 m3/s for the second level LH-moments.
Analyzing the data obtained with first and second level LH-moments, one can observe the effect of separating the maximum flow rates, assigning greater importance to the values that actually represent floods.
4.3. Performance Criterion
Considering the varied range of results obtained, a crucial stage in such frequency analyzes is the choice of the best probability distribution.
In general, for the selection of the best distribution, certain statistical tests are applied (Kolmogorov–Smirnov, Anderson–Darling, chi-square test, Lilliefors test, Cramér–von Mises, Shapiro–Wilk, etc.) [65] or performance indicators (relative mean error, mean absolute error, Kling–Gupta, Nash–Sutcliffe, root mean square error, etc.) [23,34,65,66], but these are relevant only when the data series are long enough (considered to be n > 80).
In the case of MOM estimation (as in the case of the maximum likelihood method), the big disadvantage of this method is that in the case of small and medium data sets there are no rigorous selection criteria, and in general the analysis is characterized by a high degree of subjectivity, involving only a graphic visual choice [67].
Regarding the L- and LH-methods, they currently have more rigorous selection criteria. The selection of the best distribution is made exclusively on the basis of the calibration of the statistical indicators of the data series, which are less sensitive to the variability of data lengths [22,34,64]. The selection criterion is the calibration of indicators of order three (L-skewness) and four (L-kurtosis), and the methods assume the calibration of all these ratios of linear moments [33,68,69].
In the case of two-parameter distributions, they properly calibrate only the L-coefficient of variation (the ratio between the moment of second order and the first moment of order). Regarding moments of order three and four, many two-parameter distributions have these constant values (Gumbel, normal, exponential shifted, etc.), which presents a big disadvantage. Thus, this article presents distributions that have the advantage of the fact that these indicators do not have constant values, but show a variation depending on the L-coefficient of variation. It is also presents, as the main criterion for selecting the best distribution, the relationships and variation graphs of the L-coefficient of variation and L-skewness and the L-coefficient of variation and L-kurtosis, thus, substantially facilitating the rigor of the selection (Appendix B and Appendix C). It is mentioned that the choice of the best distribution is performed using the fourth-order linear moment criterion.
The importance of presenting these criteria in the selection of the best two-parameter distribution using L- and LH-moments estimation is the fact that, mathematically, the vast majority of two- and three-parameter probability distributions are defined by the same variation curves of L-skewness−L-kurtosis (Appendix F shows as example, the log-normal distribution of two and three parameters).
Thus, Table 5 presents the values of the theoretical statistical indicators of the distributions obtained based on the analyzed series, as well as the values of two performance indicators (relative mean error and mean absolute error).

Table 5.
Performance criterion for probability distributions adjustment ranking.
The statistical and theoretical values of the indicators L and LH and the coefficient of variation are not presented, because all the analyzed distributions calibrate this indicator accordingly.
Considering the relatively short length of the analyzed series (n = 39), it is not possible to establish a performance criterion using the resulting values of the two performance indicators.
Where the relative mean error (RME) and the relative absolute error (RAE) have the following expressions:
in which represent the sample size, the observed value, and the estimated value for a given probability.
From the point of view of the obtained results, the LN2 distribution has the best results, with the values of the L-kurtosis indicators (0.192 for the L-moments method, 0.185 for the first level LH-moments method, and 0.185 for the second level LH-moments method) being the closest to those of the analyzed series. The graphic confirmation can be found in Figure A1, Figure A2, Figure A3 and Figure A4 from Appendix B, Appendix C, Appendix D and Appendix E.
For MOM, as previously mentioned, it is difficult to choose the best distribution based on statistical tests and performance indicators, especially in the case of short and medium data sets. Based on the graphical analysis of the obtained results, for the Siret river, the best two-parameter distribution, using MOM, is also selected using the LN2 distribution.
A correct use of two-parameter distributions (using the L- and LH-moments method) can replace a more laborious analysis that requires the use of at least four-parameter distributions for the calibration of all linear moments characteristic of the L and LH-moments methods. Thus, Figure 5 compares the results of the LN2 distribution (the best model result) with those obtained with the four-parameter Burr distribution that fulfills all four conditions imposed by the method of linear moments.
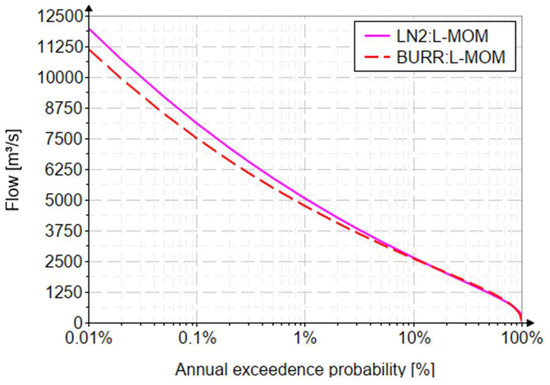
Figure 5.
Graphic representation of LN2 and Burr distribution curves.
It can be easily observed that the two curves are very close, the resulting values being characterized by very small differences. For the flow with the probability of exceeding or being equal to 0.01%, the values generated by the two distributions are 11,972 m3/s for LN2, and 11,128 m3/s for the Burr distribution, representing a relative error of 7.6%, more than acceptable for the forecast of these very rare events.
4.4. The Influence of the Variability of the Length of the Recorded Series
Any analysis is characterized by certain errors. In the case of the frequency analysis, it is mandatory to present the relative errors specific to the distribution chosen as the best model. Thus, regardless of the parameter estimation methods, it is necessary to present the relative errors in the estimation of statistical indicators, parameters, and quantiles, the latter being the most important. Thus, for exemplification, three cases are presented, for the three distributions chosen as the best models, for the three methods.
Thus, taking into account the results obtained, both for MOM and L-moments, the recorded values are assumed to come from an LN2 distribution.
Starting from the theoretical values of the statistical indicators (characteristic of a large number of values, 1000 < n < 5000), the relative errors corresponding to some samples of 80, 50, 25, and 39 values are determined as in the case of the Siret river.
In the case of MOM, two usual values of the coefficient of variation are chosen, namely, 1 and 2, and 0.634, corresponding to that of the analyzed data.
In the analysis with L-moments, the values of the L-coefficient of variation () were chosen 0.3, 0.5, 0.75, and 0.339 related to the analyzed series. In both methods, for simplification, the arithmetic mean () is chosen as 1. The theoretical values of the L-skewness indicators () and L-kurtosis () is determined, depending on the L-coefficient of variation (), with the following new relationships:
The values of the statistical indicators, the estimated parameters, and the resulting amounts, characteristic of the sampling, are presented in Table 6, Table 7 and Table 8.

Table 6.
The relative errors using MOM.

Table 7.
The relative errors using L-moments.

Table 8.
The relative errors using MOM and L-moments for Siret River.
Considering that in the frequency analysis the main element is the estimation of the quantiles, according to the exceedance probabilities of interest (0.01, 0.1, 0.5, 1%), the errors corresponding to the analyzed series have values of 7.59, 614, 4.96, and 438% using MOM, and 0.54, 0.47, 0.43, and 0.4% using L-moments. It can be seen that the L-moments method is much more stable and robust to the variability of the data series lengths. This method also shows stability regarding the existence of outliers [34].
4.5. Confidence Interval
Considering all these uncertainties regarding the estimation of the quantile values, it is necessary to determine and graphically represent the confidence interval of the inverse function.
It will be represented only for the distribution chosen as the best model for the flow series of the Siret river, namely, the LN2 distribution.
For MOM, the confidence interval is determined based on the relationships presented in the literature [22] specific to this method, as well as the use of Chow’s relationship on a Gaussian assumption [22,55,64,68,69], being an element accessible to everyone, an important aspect in the development of a standard regarding maximum flows. For the L-moments and LH-moments method, the confidence interval is determined based on Chow’s relationship but using the frequency factor with the parameters estimated with these two methods, for a significance level of 10%. Figure 6 shows the confidence intervals for the chosen model (LN2) and for all the methods used.
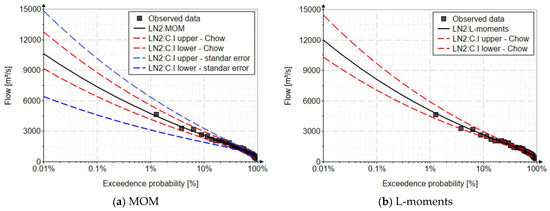
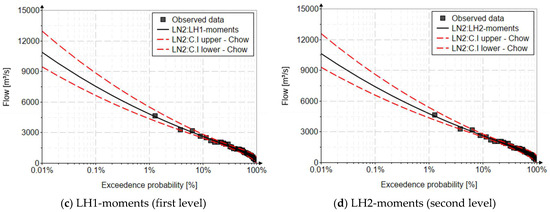
Figure 6.
Confidence interval for the LN2 distribution, using MOM, L-, and LH-moments.
There are other methods for determining the confidence interval, such as the standard bootstrap technique or parametric Monte Carlo simulations, but which require a more complex analysis, inaccessible to everyone and still characterized by certain limitations [70,71,72].
5. Conclusions
The article presents a significant number of two-parameter distributions, from different families. New relationships are presented regarding the estimation of their parameters with three methods often used in frequency analysis. The need for research is the high applicability of two-parameter distributions in frequency analysis of extreme events [73,74,75]. This is also emphasized by the lack of inclusion of these distributions, for these methods, in programs dedicated to these types of analyses.
An exhaustive analysis regarding the choice of the best model, characteristic of each method, is also presented, as well as a comprehensive analysis regarding the determination of the relative errors, influenced by the variability of the lengths of the data sets. Establishing the priority criterion for the selection of the best distribution is the L-coefficient of variation and L-kurtosis, because it gives the heavy tail tendency in a more pronounced way than the criterion of the L-coefficient of variation and L-skewness. This avoids the choice of two-parameter distributions that underestimate the values of rare events (low excess probabilities).
For the Siret River, following the analysis and results obtained for the registered data, the LN2 distribution gives the best results, with the important observation that the choice in the case of MOM always involves, in the case of short and medium data sets, some subjective aspects, as there are no sufficiently rigorous criteria. For the recommended methods (L- and LH-moments), from the thirteen analyzed distributions, the log-normal distribution had the best results, with the theoretical values of the L-coefficient of variation and L-kurtosis best approximating the corresponding values of the recorded data.
Taking into account all the elements presented and the analysis performed, especially the comparative analysis with the four-parameter Burr distribution, it can be concluded that the best method for using two-parameter distributions in FFA is the method of linear moments, because there are more rigorous criteria of choosing the best model.
All this information related to frequency analysis, using these methods and two-parameter distributions, will help researchers to perform a well-founded and rigorous analysis. In general, the methods and criteria are also valid in the case of frequency analysis using distributions of three or more parameters.
6. Future Directions
All this research is part of a holistic research carried out at the Faculty of Hydrotechnics regarding the identification of probability distributions and optimal estimation methods for the proposal to develop some regulations regarding the regionalization analysis of extreme events specific to Romania, because the existing regulation NP129/2011 [48] is not applied and has Soviet approaches, which are outdated and has some non-technical interpretations such as the interval of uncertainty [76].
All these new elements presented in the manuscript will be included in dedicated, open-source programs, facilitating the application of these methods, in FFA.
Author Contributions
Conceptualization, C.G.A., S.C.S. and C.I.; methodology, C.G.A., S.C.S. and C.I.; software, C.G.A., S.C.S. and C.I.; vali-dation, C.G.A., S.C.S. and C.I.; formal analysis, C.G.A., S.C.S. and C.I.; investigation, C.G.A., S.C.S. and C.I.; resources, C.G.A., S.C.S. and C.I.; data curation, C.G.A., S.C.S. and C.I.; writing—original draft preparation C.G.A. and C.I.; writing—review and editing, C.G.A., S.C.S. and C.I.; visualization, C.G.A., S.C.S. and C.I.; supervision, C.I. and C.G.A.; project administration, C.G.A., S.C.S. and C.I.; funding acquisition, C.G.A., S.C.S. and C.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| MOM | The method of ordinary moments |
| L-moments | The method of linear moments |
| LH-moments | The method of higher order linear moments |
| LH-skewness | |
| coefficient of LH variation | |
| LH-kurtosis | |
| Expected value; arithmetic mean | |
| Standard deviation | |
| Variance | |
| Coefficient of variation | |
| Coefficient of skewness; skewness | |
| Coefficient of kurtosis; kurtosis | |
| Linear moments | |
| Coefficient of variation based on the L-moments method | |
| Coefficient of skewness based on the L-moments method | |
| Coefficient of kurtosis based on the L-moments method | |
| SUH | Synthetic unit hydrograph |
| FFA | Flood frequency analysis |
| Distr. | Distributions |
| AMS | Annual maximum series |
| AES | Annual exceedance series |
| POT | Peaks over threshold |
| RME | Relative mean error |
| RAE | Relative absolute error |
| n | Observed values length |
| , returns the value of the Euler gamma function of | |
| , returns the value of the incomplete gamma function of x with parameter | |
| Returns the cumulative probability distribution for value x, for gamma distribution | |
| Returns the inverse cumulative probability distribution for probability p, for gamma distribution | |
| Returns the cumulative probability distribution for value x, for log-normal distribution | |
| Returns the inverse cumulative probability distribution for probability p, for normal distribution |
Appendix A. The Equations Needed to Estimate the Parameters of the Distributions Analyzed with the Second Level LH-Moments Method
Pearson V distribution (PV2)
For the second level LH-moments:
and
where and , simplified by the next function:
where represent the first two second level LH-moments.
Chi distribution (CH2)
For the second level LH-moments:
if
if
where , simplified by the next function:
Inverse Chi distribution (ICH2)
For the second level LH-moments:
where and , simplified by:
Gamma distribution (Γ2)
For the second level LH-moments:
if
if
where , simplified by:
Log-normal distribution (LN2)
For the second level LH-moments ():
where , simplified by:
Gumbel distribution (G)
For second level LH-moments, the relations are as follows:
where , representing the Euler constant.
Logistic distribution (L)
For second level LH-moments, the relations are as follows:
Log-logistic distribution (LL)
For second level LH-moments, the relations are as follows:
Exponential shifted distribution (E)
For second level LH-moments, the relations are as follows:
Rayleigh distribution (RY)
For second level LH-moments, the relations are as follows:
Weibull distribution (W2)
For second level LH-moments, the relations are as follows:
The shape parameter can be approximated with the following relation:
if
if
Fréchet distribution (F2)
For second level LH-moments, the relations are as follows:
The shape parameter can be approximated with the following relation ():
Generalized exponential distribution (EG)
For second level LH-moments, the shape parameter can be approximated with the following relation:
if
if
where , simplified by:
Appendix B. The Variation of the L-Coefficient of Variation and L-Skewness Indicators
Figure A1 shows the variation diagram of L-coefficient of variation and that of L-skewness, for the distributions of two analyzed parameters.
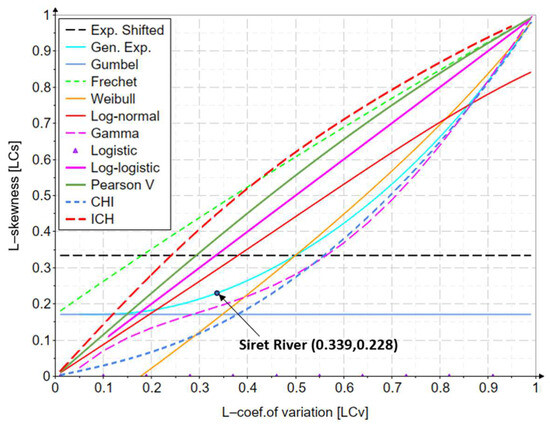
Figure A1.
The variation of the L-coefficient of variation and L-skewness indicators.
The coefficients of the polynomial relations of the curves are presented in Table A1.

Table A1.
The coefficients of the polynomial relations L-coef. of variation—L-skewness.
Table A1.
The coefficients of the polynomial relations L-coef. of variation—L-skewness.
| Distri. | a | b | c | d | e | F | g | h |
|---|---|---|---|---|---|---|---|---|
| PV2 | −0.0001917 | 1.1529202 | 0.0294715 | −0.2631688 | 0.0726675 | 0.0082297 | − | − |
| CH2 | 0.0004323 | 0.2807334 | −0.0430794 | 1.8541968 | −1.7156534 | 0.6229576 | − | − |
| ICH2 | −0.0002993 | 1.4436764 | 0.1135055 | −1.9275226 | 2.1920275 | −0.8234554 | − | − |
| Γ2 | −0.0391816 | 1.4110631 | −3.7802846 | 5.5291654 | −2.1095786 | − | − | − |
| LN2 | −0.0002591 | 0.8729448 | −0.0501133 | 0.2295347 | −0.1775573 | −0.0274784 | − | − |
| G | 0.17 | − | − | − | − | − | − | − |
| L2 | 0 | − | − | − | − | − | − | − |
| LL2 | −0.0006562 | 1.0079457 | −0.0329979 | 0.0623802 | −0.055145 | 0.0185172 | − | − |
| E2 | 0.333 | − | − | − | − | − | − | − |
| W2 | −0.1703052 | 0.9398552 | 0.018723 | 0.4181828 | −0.5281551 | 0.316262 | − | − |
| F2 | 0.1699209 | 0.9282028 | −0.1346628 | 0.059188 | −0.0323458 | 0.0097365 | − | − |
| EG | 0.1718596 | −0.0186894 | −0.5142945 | 6.6116454 | −15.2797982 | 18.9061827 | −11.9625983 | 3.086354 |
Appendix C. The Variation of the L-Coefficient of Variation and L-Kurtosis Indicators
Figure A2 shows the variation diagram of the L-coefficient of variation and that of the L-kurtosis, for the two-parameter distributions analyzed.
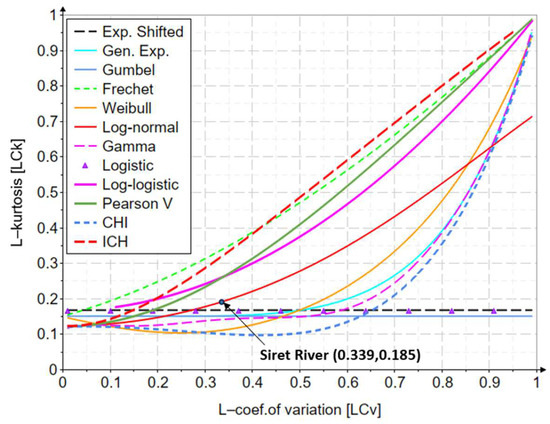
Figure A2.
The variation of the L-coefficient of variation and L-kurtosis indicators.
The coefficients of the polynomial relations of the curves are presented in Table A2.

Table A2.
The coefficients of the polynomial relations L-coef. of variation—L-kurtosis.
Table A2.
The coefficients of the polynomial relations L-coef. of variation—L-kurtosis.
| Distri. | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| PV2 | 0.121657 | 0.0071769 | 1.2560619 | 0.0771191 | −0.7944921 | 0.3328855 | − | − |
| CH2 | 0.1213293 | 0.0404724 | −0.477597 | 0.4377973 | −0.0125957 | 0.8787673 | − | − |
| ICH2 | 0.1240545 | −0.0820187 | 3.1385337 | −4.3958185 | 3.1511425 | −0.9360638 | − | − |
| Γ2 | 0.111265 | 0.6051105 | −8.7842189 | 54.0170023 | −158.5178178 | 236.7611686 | −172.8904655 | 49.7065434 |
| LN2 | 0.1225154 | −0.0050638 | 0.645454 | −0.2319042 | 0.5976604 | −0.4065955 | − | − |
| G | 0.15 | − | − | − | − | − | − | − |
| L2 | 0.167 | − | − | − | − | − | − | − |
| LL2 | 0.1661175 | 0.0030562 | 0.8327474 | −0.0194309 | 0.0337421 | −0.0164053 | − | − |
| E2 | 0.167 | − | − | − | − | − | − | − |
| W2 | 0.1483271 | −0.2980059 | 0.0732036 | 2.1491468 | −2.7095195 | 1.6098771 | − | − |
| F2 | 0.1502186 | 0.3664572 | 0.6287946 | −0.1909754 | 0.0527471 | −0.0072194 | − | − |
| EG | 0.1497942 | 0.0160813 | −0.1661789 | 0.8261955 | −2.9101087 | 6.2913235 | −5.449721 | 2.2420203 |
Appendix D. The Variation of the LH1-Coefficient of Variation and LH1-Kurtosis Indicators
Figure A3 shows the variation diagram of LH-coefficient of variation and that of LH-kurtosis level 1, for the distributions of two analyzed parameters.
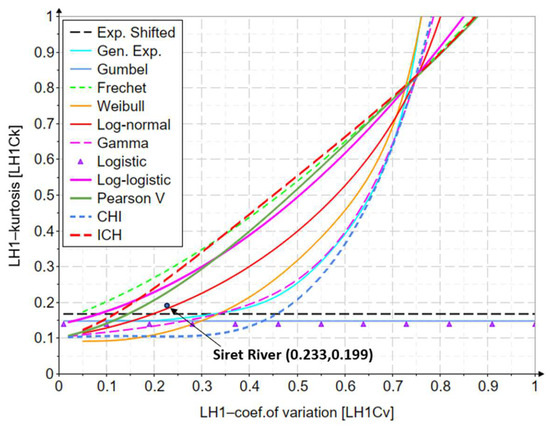
Figure A3.
The variation of the LH1-coefficient of variation and LH1-kurtosis indicators.
The coefficients of the polynomial relations of the curves are presented in Table A3.

Table A3.
The coefficients of the polynomial relations LH1-coef. of variation—LH1-kurtosis.
Table A3.
The coefficients of the polynomial relations LH1-coef. of variation—LH1-kurtosis.
| Distri. | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| PV2 | 0.1004997 | 0.292656 | 1.0008339 | 2.0588671 | −7.7323389 | 12.1937321 | −10.6476016 | 3.9436365 |
| CH2 | 0.1010727 | 0.0922381 | −0.5050765 | 1.1759753 | −6.6011686 | 28.3506375 | −36.2598981 | 17.0000729 |
| ICH2 | 0.1022551 | 0.3034118 | 2.5332548 | −2.6261401 | −4.418888 | 14.6204376 | −14.5656434 | 5.3004996 |
| Γ2 | 0.1004253 | 0.1903975 | −0.8069067 | 6.0228661 | −18.8551149 | 31.3886981 | −21.5847741 | 6.3951538 |
| LN2 | 0.0988166 | 0.3076349 | −0.9595792 | 11.0149111 | −38.709332 | 76.4660396 | −77.9330237 | 32.6604631 |
| G | 0.147 | − | − | − | − | − | − | − |
| L2 | 0.139 | − | − | − | − | − | − | − |
| LL2 | 0.1388953 | 0.2775671 | 0.8667413 | −0.0149542 | 0.047448 | −0.0829821 | 0.0752559 | −0.0276298 |
| E2 | 1/6 | − | − | − | − | − | − | − |
| W2 | 0.0844016 | 0.3029746 | −5.5886575 | 48.1205437 | −188.6420239 | 405.4808188 | −443.9531166 | 194.2511079 |
| F2 | 0.146923 | 0.4817256 | 0.6511338 | −0.136756 | 0.096521 | −0.0887558 | 0.0489938 | −0.0119077 |
| EG | −0.0366576 | 5.3965209 | −61.4345945 | 353.7629361 | −1121.4563457 | 1985.0062856 | −1826.9074675 | 682.8051867 |
Appendix E. The Variation of the LH2-Coefficient of Variation and LH2-Kurtosis Indicators
Figure A4 shows the variation diagram of LH-coefficient of variation and that of LH-kurtosis level 2, for the distributions of two analyzed parameters.
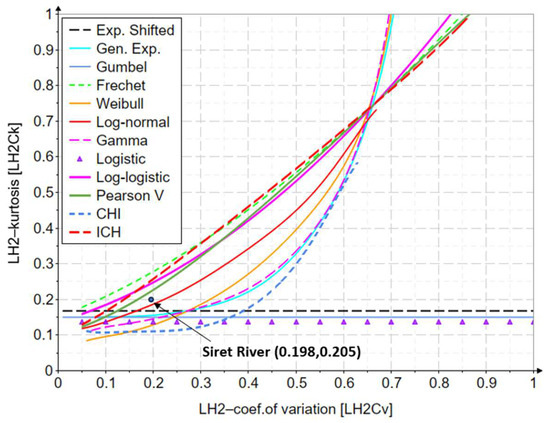
Figure A4.
The variation of the LH2-coefficient of variation and LH2-kurtosis indicators.
The coefficients of the polynomial relations of the curves are presented in Table A4.

Table A4.
The coefficients of the polynomial relations LH2-coef. of variation—LH2-kurtosis.
Table A4.
The coefficients of the polynomial relations LH2-coef. of variation—LH2-kurtosis.
| Distri. | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| PV2 | 0.1019966 | 0.3458635 | 1.6934638 | −2.0716386 | 3.9406792 | −7.7061967 | 7.940556 | −3.1142546 |
| CH2 | 0.1788641 | −2.4675698 | 32.9743564 | −221.3367071 | 816.6808185 | −1673.2210574 | 1809.2068515 | −799.5794934 |
| ICH2 | 0.10269 | 0.405204 | 3.1244053 | −8.8334769 | 14.4272457 | −12.2679676 | 4.1467925 | 0.1336807 |
| Γ2 | 0.0224198 | 2.655331 | −30.3474827 | 192.6112105 | −677.4308143 | 1339.6273577 | −1380.3785736 | 580.9917308 |
| LN2 | 0.1215363 | −0.5897867 | 14.258069 | −102.3363839 | 411.1762845 | −889.5213195 | 977.47264 | −425.6337204 |
| G | 0.149 | − | − | − | − | − | − | − |
| L2 | 0.137 | − | − | − | − | − | − | − |
| LL2 | 0.1375002 | 0.393745 | 0.7875544 | − 0.0002881 | 0.0007848 | − 0.0010697 | 0.0006184 | − 0.0000684 |
| E2 | 1/6 | − | − | − | − | − | − | − |
| W2 | 0.0313158 | 1.6564735 | −19.6694972 | 134.0362792 | −484.408682 | 988.4336673 | −1058.0966681 | 462.9493577 |
| F2 | 0.1493018 | 0.519344 | 0.6106182 | −0.0654596 | 0.0023034 | 0.0418728 | −0.056094 | 0.0245651 |
| EG | 0.0686757 | 2.4784372 | −29.9302087 | 184.6220035 | −626.7790598 | 1197.7383131 | −1190.6470888 | 482.7517552 |
Appendix F. A Comparative Analysis of the Log-Normal Distribution
The log-normal distributions of two and three parameters (LN2, LN3) have the same variation curve, but for each data set analyzed they are defined by different points on this curve. This is due to the fact that these higher order indicators are characterized only by the scale parameter. The difference lies in the fact that for the two-parameter distribution, it only calibrates the L-coefficient of variation (the generated L-skewness and L-kurtosis values being the theoretical ones of the distribution), while the three-parameter distribution calibrates including the L-skewness (the L-kurtosis value being the theoretical one of the distribution). Both statistical indicators are considered in module, defined between 0–1, and always have distinct values. The same phenomenon also happens in the case of other distributions, such as gamma and Pearson III (gamma of three parameters), Weibull of two and three parameters, log-logistic of two and three parameters, etc.
Figure A5 shows these differences between LN2 and LN3, based on the analyzed data series of the Siret River.
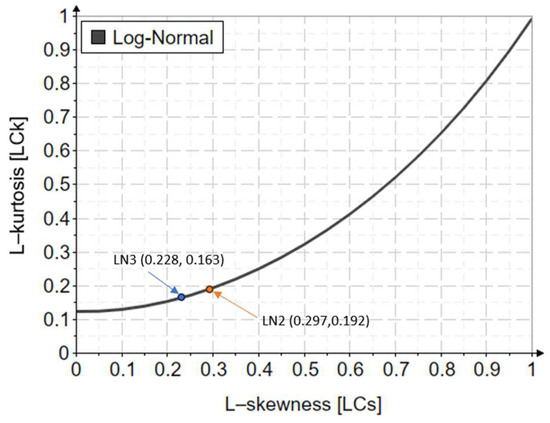
Figure A5.
Variation diagram of the theoretical indicators for the log-normal distribution.
For the LN3 distribution, the value 0.228 is the calibrated L-skewness (it is that of the analyzed data), and the value 0.163 represents the theoretical L-kurtosis value of the distribution.
In the case of the LN2 distribution, the values 0.297 and 0.192 are the theoretical values of the distribution, obtained according to the L-variation coefficient calibrated on the data series.
References
- Elsebaie, I. Developing rainfall intensity–duration–frequency relationship for two regions in Saudi Arabia. J. King Saud Univ.-Eng. Sci. 2012, 24, 131–140. [Google Scholar] [CrossRef]
- Ewea, H.A.; Elfeki, A.M.; Al-Amri, N.S. Al-Amri Development of intensity–duration–frequency curves for the Kingdom of Saudi Arabia. Geomat. Nat. Hazards Risk 2017, 8, 570–584. [Google Scholar] [CrossRef]
- Agarwal, S.; Kumar, S.; Singh, U.K. Intensity Duration Frequency Curve Generation using Historical and Future Downscaled Rainfall Data. Indian J. Ecol. 2021, 48, 275–280. [Google Scholar]
- Palaka, R.; Prajwala, G.; Navyasri, K.V.S.N.; Anish, I. Development of intensity duration frequency curves for narsapur mandal, telangana state, India. Int. J. Res. Eng. Technol. 2016, 5, 109–113. [Google Scholar]
- Kawara, A.Q.; Elsebaie, I.H. Development of Rainfall Intensity, Duration and Frequency Relationship on a Daily and Sub-Daily Basis (Case Study: Yalamlam Area, Saudi Arabia). Water 2022, 14, 897. [Google Scholar] [CrossRef]
- Markiewicz, I. Depth–Duration–Frequency Relationship Model of Extreme Precipitation in Flood Risk Assessment in the Upper Vistula Basin. Water 2021, 13, 3439. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistical theory of floods and droughts. J. Inst. Water Eng. 1958, 12, 157–184. [Google Scholar]
- Subah, Z.; Bala, S.K.; Ryu, J.H. Assessing Urban Flooding Extent of the Baunia Khal Watershed in Dhaka, Bangladesh. Water 2023, 15, 1183. [Google Scholar] [CrossRef]
- Vangelis, H.; Zotou, I.; Kourtis, I.M.; Bellos, V.; Tsihrintzis, V.A. Relationship of Rainfall and Flood Return Periods through Hydrologic and Hydraulic Modeling. Water 2022, 14, 3618. [Google Scholar] [CrossRef]
- Hydrology Subcommittee; Interagency Advisory Committee on Water Data; U.S. Department of the Interior; U.S. Geological Survey; Office of Water Data Coordination. Bulletin 17B Guidelines for Determining Flood Flow Frequency; Hydrology Subcommittee, Interagency Advisory Committee on Water Data, U.S. Department of the Interior, U.S. Geological Survey, Office of Water Data Coordination: Reston, VA, USA, 1981.
- U.S. Department of the Interior; U.S. Geological Survey. Bulletin 17C Guidelines for Determining Flood Flow Frequency; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2017.
- Dhakal, S.; Bhattarai, U.; Marahatta, S.; Devkota, P. Impact of climate change on the full spectrum of future low flows of Budhigandaki River Basin in Nepal using Gumbel distribution. Int. J. Energy Water Res. 2023, 7, 191–203. [Google Scholar] [CrossRef]
- Langat, P.K.; Kumar, L.; Koech, R. Identification of the Most Suitable Probability Distribution Models for Maximum, Minimum, and Mean Streamflow. Water 2019, 11, 734. [Google Scholar] [CrossRef]
- Balacco, G.; Carbonara, A.; Gioia, A.; Iacobellis, V.; Piccinni, A.F. Evaluation of Peak Water Demand Factors in Puglia (Southern Italy). Water 2017, 9, 96. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, Q.; Yao, R.; Singh, V.P.; Song, C. Low Flow Regimes of the Tarim River Basin, China: Probabilistic Behavior, Causes and Implications. Water 2018, 10, 470. [Google Scholar] [CrossRef]
- Gray, D.M. Synthetic hydrographs for small drainage areas. J. Hydraul. Div. ASCE 1961, 87 HY4, 33–54. [Google Scholar] [CrossRef]
- Haktanir, T.; Nurullah, S. Suitability of two-parameter gamma distribution and three-parameter beta distribution as synthetic hydrographs in Anatolia. Hydrol. Sci. J. 1990, 35, 167–184. [Google Scholar] [CrossRef]
- Croley, T.E. Gamma synthetic hydrographs. J. Amst. Hydrol. 1980, 47, 41–52. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Berndtsson, R.; Ojha, C.S.P.; Mishra, S.K. Suitability of Gamma, Chi-square, Weibull and Beta distributions as synthetic unit hydrographs. J. Hydrol. 2007, 334, 28–38. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Berndtsson, R.; Singh, P.K.; Hubert, P. Comparison between Weibull and gamma distributions to derive synthetic unit hydrograph using Horton ratios. Water Resour. 2008, 44, WR006031. [Google Scholar] [CrossRef]
- Bhunya, P. Synthetic Unit Hydrograph Methods: A Critical Review. Open Hydrol. J. 2011, 5, 1–8. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press LLC.: Boca Raton, FL, USA, 2000. [Google Scholar]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- World Meteorological Organization. (WMO-No.718) 1989 Statistical Distributions for Flood Frequency Analysis; Operational Hydrology Report no. 33; WHO: Geneva, Switzerland, 1989. [Google Scholar]
- Singh, V.P.; Guo, H. Parameter estimation for 2-parameter log-logistic distribution (LLD2) by maximum entropy. Civ. Eng. Syst. 1995, 12, 343–357. [Google Scholar] [CrossRef]
- Shoukri, M.M.; Mian, I.U.H.; Tracy, D.S. Sampling properties of estimators of the log-logistic distribution with application to Canadian precipitation data. Can. J. Stat. Rev. Can. Stat. 1988, 16, 223–236. [Google Scholar] [CrossRef]
- Fitzgerald, D.L. Analysis of extreme rainfall using the log logistic distribution. Stoch. Environ. Res. Risk Assess. 2005, 19, 249–257. [Google Scholar] [CrossRef]
- Hussain, Z. Rainfall frequency analysis using frechet and log-logistic distributions of sites of azad jammu and kashmir, pakistan. Appl. Ecol. Environ. Res. 2019, 17, 13607–13623. [Google Scholar] [CrossRef]
- Ahmad, M.I.; Sinclair, C.D.; Werritti, A. Log-logistic flood frequency analysis. J. Hydrol. 1988, 98, 205–224. [Google Scholar] [CrossRef]
- Haktanir, T. Statistical modeling of annual maximum flows in Turkish rivers. Hydrol. Sci. J. 1991, 36, 367–389. [Google Scholar] [CrossRef]
- Ahilan, S.; Bruen, M.; O’Sullivan, J.J. Influences on flood frequency distributions in Irish river catchments. Hydrol. Earth Syst. Sci. 2012, 16, 1137–1150. [Google Scholar] [CrossRef]
- Tegegne, G.; Melesse, A.M.; Asfaw, D.H.; Worqlul, A.W. Flood Frequency Analyses over Different Basin Scales in the Blue Nile River Basin, Ethiopia. Hydrology 2020, 7, 44. [Google Scholar] [CrossRef]
- Anghel, C.G.; Ilinca, C. Parameter Estimation for Some Probability Distributions Used in Hydrology. Appl. Sci. 2022, 12, 12588. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L–Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- De Luca, D.L.; Napolitano, F. A user-friendly software for modelling extreme values: EXTRASTAR (extremes abacus for statistical regionalization). Environ. Model. Softw. 2023, 161, 105622. [Google Scholar] [CrossRef]
- Alem, A.M.; Tilahun, S.A.; Moges, M.A.; Melesse, A.M. A Regional Hourly Maximum Rainfall Extraction Method for Part of Upper Blue Nile Basin, Ethiopia; Elsevier Inc.: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. Identification of Homogeneous Regions for Regional Frequency Analysis Using the Self-Organizing Map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Rao, A.R.; Srinivas, V.V. Introduction. In Regionalization of Watersheds: An Approach Based on Cluster Analysis; Rao, A.R., Srinivas, V.V., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 1–16. [Google Scholar]
- Yin, Y.; Chen, H.; Xu, C.Y.; Xu, W.; Chen, C.; Sun, S. Spatio-Temporal Characteristics of the Extreme Precipitation by L-Moment-Based Index-Flood Method in the Yangtze River Delta Region. China Theor. Appl. Climatol. 2016, 124, 1005–1022. [Google Scholar] [CrossRef]
- Cassalho, F.; Beskow, S.; de Mello, C.R.; de Moura, M.M.; de Oliveira, L.F.; de Aguiar, M.S. Artificial intelligence for identifying hydrologically homogeneous regions: A state-of-the-art regional flood frequency analysis. Hydrol. Process. 2019, 33, 1101–1116. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Tasker, G.D. Regional hydrologic analysis: 1. Ordinary, weighted, and generalized least squares compared. Water Resour. Res. 1985, 21, 1421–1432. [Google Scholar] [CrossRef]
- Griffis, V.W.; Stedinger, J.R. The use of GLS regression in regional hydrologic analyses. J. Hydrol. 2007, 344, 82–95. [Google Scholar] [CrossRef]
- Borga, M.; Vezzani, C.; Fontana, G.D. Regional Rainfall Depth–Duration–Frequency Equations for an Alpine Region. Nat. Hazards 2005, 36, 221–235. [Google Scholar] [CrossRef]
- Libertino, A.; Allamano, P.; Laio, F.; Claps, P. Regional-scale analysis of extreme precipitation from short and fragmented records. Adv. Water Resour. 2018, 112, 147–159. [Google Scholar] [CrossRef]
- Chokmani, K.; Ouarda, T.B.M.J. Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour. Res. 2004, 40, W1251. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.M.J. Depth and homogeneity in regional flood frequency analysis. Water Resour. Res. 2008, 44, W11422. [Google Scholar] [CrossRef]
- Skoien, J.; Merz, R.; Bloschl, G. Top-kriging—Geostatistics on stream networks. Hydrol. Earth Syst. Sci. 2006, 10, 277–287. [Google Scholar] [CrossRef]
- Ministry of Regional Development and Tourism. The Regulations Regarding the Establishment of Maximum Flows and Volumes for the Calculation of Hydrotechnical Retention Constructions; Indicative NP 129–2011; Ministry of Regional Development and Tourism: Bucharest, Romania, 2012.
- Diacon, C.; Serban, P. Hydrological Syntheses and Regionalizations; Technical Publishing House: Bucharest, Romania, 1994. [Google Scholar]
- Houghton, C. Birth of a Parent: The Wakeby Distribution for Modeling Flood Flows; Working Paper no. MIT-EL77–033WP; Water Resources Research: Tucson, AZ, USA, 1978; Volume 14. [Google Scholar]
- Murshed, S.; Park, B.-J.; Jeong, B.-Y.; Park, J.-S. LH-Moments of Some Distributions Useful in Hydrology. Commun. Stat. Appl. Methods 2009, 16, 647–658. [Google Scholar] [CrossRef]
- Rameshwar, D.G.; Kundu, D. Generalized exponential distribution: Different method of estimations. J. Stat. Comput. Simul. 2001, 69, 315–337. [Google Scholar]
- Crooks, G.E. Field Guide to Continuous Probability Distributions; Berkeley Institute for Theoretical Science: Berkeley, CA, USA, 2019. [Google Scholar]
- Wang, Q.J. LH moments for statistical analysis of extreme events. Water Resour. Res. 1997, 33, 2841–2848. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill, Inc.: New York, NY, USA, 1988; ISBN 007-010810-2. [Google Scholar]
- World Meteorological Organization. (WMO-No.233) Estimation of Maximum Floods; Technical Note no. 98; WHO: Geneva, Switzerland, 1969. [Google Scholar]
- Grimaldi, S.; Kao, S.-C.; Castellarin, A.; Papalexiou, S.-M.; Viglione, A.; Laio, F.; Aksoy, H.; Gedikli, A. Statistical Hydrology. In Treatise on Water Science; Elsevier: Oxford, UK, 2011; Volume 2, pp. 479–517. [Google Scholar]
- Department of the Army; U.S. Army Corps of Engineers. EM 1110–2-1415 Hydrologic Frequency Analysis, Engineering and Design; Department of the Army, U.S. Army Corps of Engineers: Washington, DC, USA, 1993.
- Ministry of the Environment. The Romanian Water Classification Atlas, Part I—Morpho-Hydrographic Data on the Surface Hydrographic Network; Ministry of the Environment: Bucharest, Romania, 1992.
- Obreja, F. The Study of Sediment Yield in the Siret River Basin. Ph.D. Thesis, Stefan the Great University, Suceava, Romania, 2013. [Google Scholar]
- Vanmaercke, M.; Obreja, F.; Poesen, J. Seismic controls on contemporary sediment export in the Siret river catchment, Romania. Geomorphology 2014, 216, 247–262. [Google Scholar] [CrossRef]
- Zavoianu, I. Hydrology; Romania de Maine Publishing House: Bucharest, Romania, 2006. [Google Scholar]
- Lang, M.; Ouarda, T.B.; Bobée, B. Towards operational guidelines for over-threshold modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- Anghel, C.G.; Ilinca, C. Evaluation of Various Generalized Pareto Probability Distributions for Flood Frequency Analysis. Water 2023, 15, 1557. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K. Stochastic Modelling of Time Series. In Hydrologic Time Series Analysis: Theory and Practice; Machiwal, D., Jha, M.K., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 85–95. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kochanek, K.; Bogdanowicz, E. Flood frequency analysis supported by the largest historical flood. Nat. Hazards Earth Syst. Sci. 2014, 14, 1543–1551. [Google Scholar] [CrossRef]
- Benaini, M.; Achite, M.; Amin, M.G.M.; Singh, V.P. Frequency analysis of annual maximum daily precipitation in northeastern Algeria: Mapping and implications under climate variability. Theor. Appl. Climatol. 2023, 153, 1411–1424. [Google Scholar] [CrossRef]
- Anghel, C.G.; Ilinca, C. Predicting Flood Frequency with the LH-Moments Method: A Case Study of Prigor River, Romania. Water 2023, 15, 2077. [Google Scholar] [CrossRef]
- Ilinca, C.; Anghel, C.G. Frequency Analysis of Extreme Events Using the Univariate Beta Family Probability Distributions. Appl. Sci. 2023, 13, 4640. [Google Scholar] [CrossRef]
- Rao, G.S.; Albassam, M.; Aslam, M. Evaluation of Bootstrap Confidence Intervals Using a New Non-Normal Process Capability Index. Symmetry 2019, 11, 484. [Google Scholar] [CrossRef]
- Beaumont, J.-F.; Émond, N. A Bootstrap Variance Estimation Method for Multistage Sampling and Two-Phase Sampling When Poisson Sampling Is Used at the Second Phase. Stats 2022, 5, 339–357. [Google Scholar] [CrossRef]
- Bochniak, A.; Kluza, P.A.; Kuna-Broniowska, I.; Koszel, M. Application of Non-Parametric Bootstrap Confidence Intervals for Evaluation of the Expected Value of the Droplet Stain Diameter Following the Spraying Process. Sustainability 2019, 11, 7037. [Google Scholar] [CrossRef]
- Markiewicz, I.; Bogdanowicz, E.; Kochanek, K. On the Uncertainty and Changeability of the Estimates of Seasonal Maximum Flows. Water 2020, 12, 704. [Google Scholar] [CrossRef]
- Markiewicz, I.; Bogdanowicz, E.; Kochanek, K. Quantile Mixture and Probability Mixture Models in a Multi-Model Approach to Flood Frequency Analysis. Water 2020, 12, 2851. [Google Scholar] [CrossRef]
- Kochanek, K.; Strupczewski, W.G.; Bogdanowicz, E.; Markiewicz, I. The bias of the maximum likelihood estimates of flood quantiles based solely on the largest historical records. J. Hydrol. 2020, 584, 124740. [Google Scholar] [CrossRef]
- Drobot, R.; Draghia, A.F.; Chendes, V.; Sirbu, N.; Dinu, C. Consideratii privind viiturile sintetice pe Dunare. Hidrotehnica 2023, 68. (In Romanian) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).