An Evaluation of the Humanitarian Supply Chains in the Event of Flash Flooding
Abstract
:1. Introduction
- To add the perspective of service quality to construct an evaluation index system that is more complete and comprehensive;
- To integrate the fuzzy theory into the evaluation method to make the evaluation results closer to the real-life situation;
- To evaluate the performance of humanitarian supply chains using an ensemble ANP-PFs-VIKOR method.
2. Literature Review
2.1. Definition of Indicators
2.2. Review of Humanitarian Supply Chain Assessment Methods
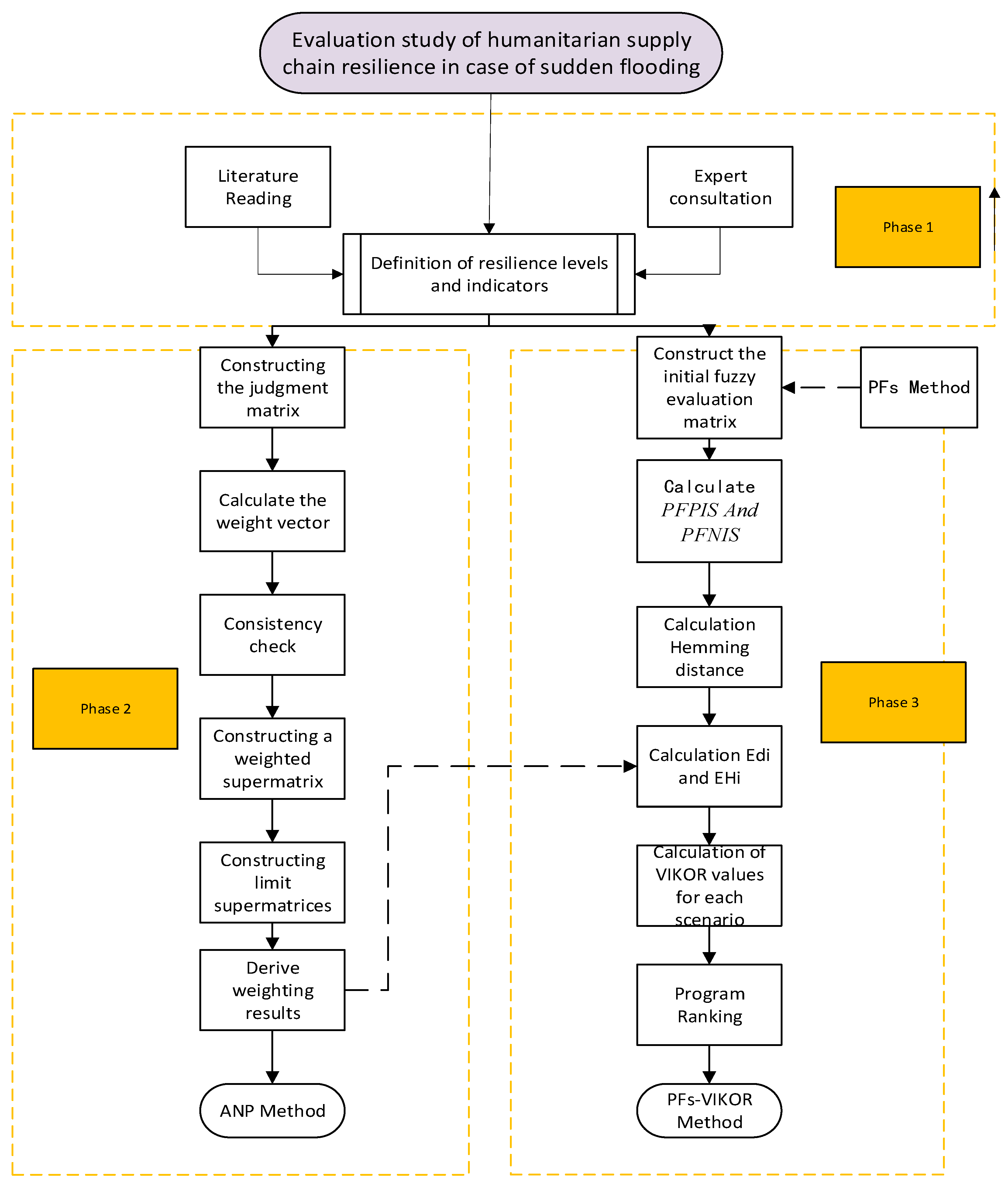
3. Methods
3.1. ANP Method
- Construct the judgment matrix [64]
- 2.
- Calculate the weight vector [64]
- (1)
- Element normalization process. =, (i,j = 1, 2, …, n)
- (2)
- Summing the normalized matrices by rows: =
- (3)
- For =, normalized, ,(i,j = 1, 2, …, n)
- Calculate the maximum eigenvalue
- 2.
- Calculate the consistency index CI
- 3.
- Calculate consistency ratio
3.2. Pythagoras (PFs) Fuzzy Theory
3.2.1. Pythagorean Fuzzy Set Definition [65]
3.2.2. Pythagorean Fuzzy Set Arithmetic Rule [65]
3.2.3. Comparison of Fuzzy Numbers and the Hemming Distance [65]
- If , then
- If , then
- If , then
3.2.4. Pythagorean Fuzzy Weighted Averaging [65]
3.2.5. Fuzzy Semantic Transformation [65]
3.3. PFs-VIKOR Steps
4. Case Study
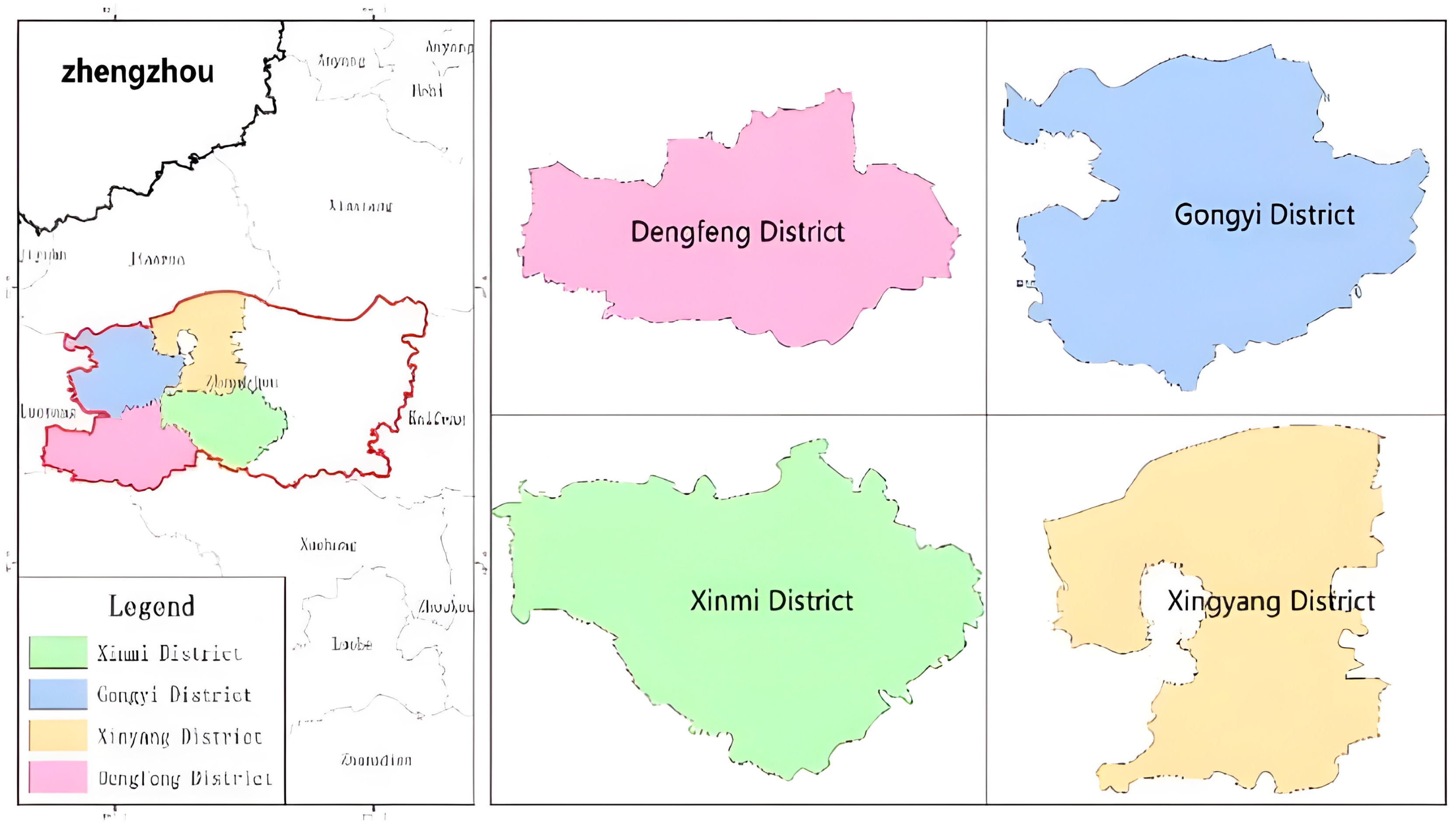
4.1. Study Areas
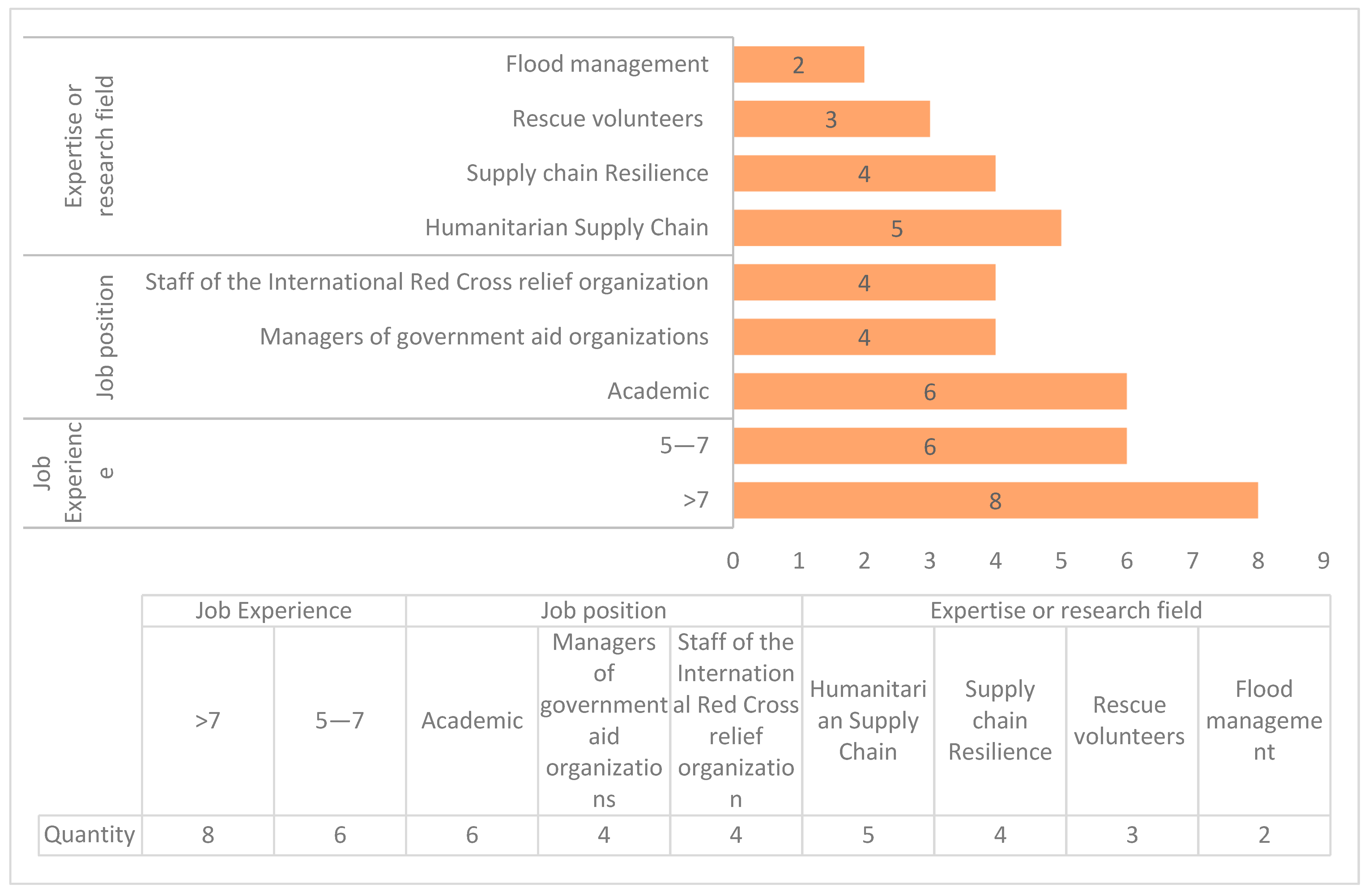
4.2. Data Collection
4.3. Modeling Based on the ANP-PFs-VIKOR Approach
5. Discussion
5.1. ANP Discussion
5.2. PFs-VIKOR Discussion
6. Conclusions and Recommendations
- (1)
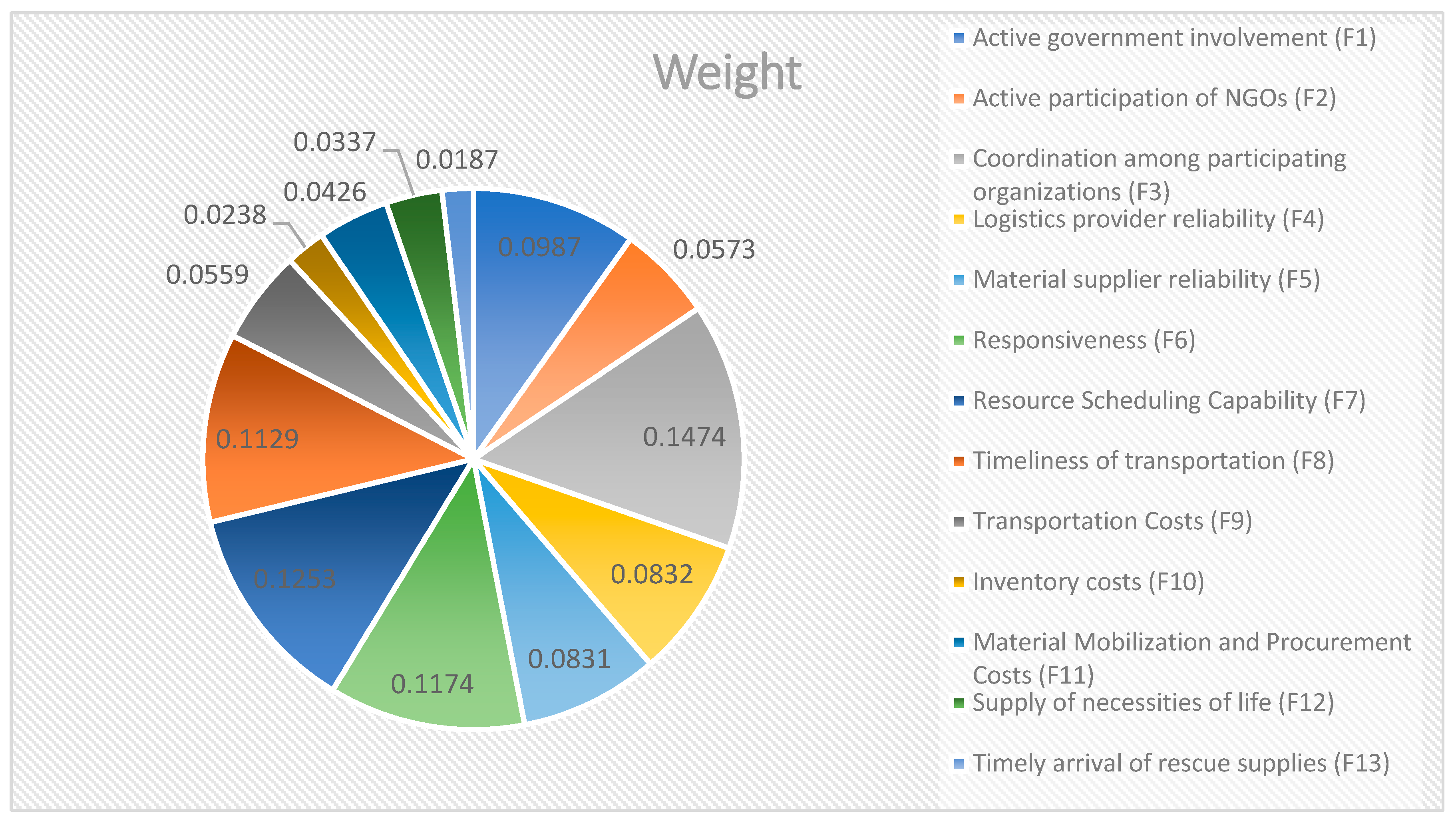
- Improving the coordination of participating organizations in humanitarian relief. The analysis of the ANP results shows that the coordination of participating organizations is the most important factor affecting the resilience of the humanitarian supply chain. John et al. argue that the introduction of coordination mechanisms in humanitarian supply chains significantly increases the efficiency of the entire supply chain and contributes to its resilience level [49]. Therefore, in the process of emergency and humanitarian relief, a coordination mechanism should be introduced to enable close cooperation between the participating organizations.
- (2)
- Improving resource mobilization capacity and response of humanitarian supply chains. It is concluded that resource scheduling capacity (F7) and responsiveness (F6) are important influences on the resilience of humanitarian supply chains. Therefore, all parties in the humanitarian supply chain should pay close attention to this indicator, improve response capacity and response speed, and improve resource scheduling capacity, so as to make the humanitarian supply chain more resilient.
- (3)
- Improving service quality in humanitarian supply chains. In recent years, Ali Anjomshoae et al. (2022) proposed that the service quality of the rescued should be considered in the humanitarian supply chain [7]. Hence, service quality should be included in the evaluation of resilience of humanitarian supply chains, and this can help improve the performance of the system while also making the results more accurate and valid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Active Government Involvement (F1) | Active Participation of NGOs (F2) | Coordination among Participating Organizations (F3) | Logistics Provider Reliability (F4) | Supply of Necessities of Life (F12) | Distribution of Relief Supplies (F13) | ||
|---|---|---|---|---|---|---|---|
| Organizational involvement A | Active government involvement (F1) | 0 | |||||
| Active participation of NGOs (F2) | 0 | ||||||
| Coordination among participating organizations (F3) | 0 | ||||||
| Reliability B | Logistics provider reliability (F4) | ||||||
| Material supplier reliability (F5) | |||||||
| Agility C | Responsiveness (F6) | ||||||
| Resource scheduling capability (F7) | |||||||
| Timeliness of transportation (F8) | |||||||
| Cost factor D | Transportation costs (F9) | ||||||
| Inventory costs (F10) | |||||||
| Material mobilization and procurement costs (F11) | |||||||
| Quality of service E | Supply of necessities of life (F12) | 0 | |||||
| Distribution of relief supplies (F13) | 0 |
Appendix B
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 |
| F2 | 0.27 | 0.11 | 0.25 | 0.27 | 0.11 | 0.27 | 0.21 | 0.17 | 0.27 | 0.27 | 0.27 | 0.26 | 0.26 |
| F3 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 |
| F4 | 0.41 | 0.42 | 0.42 | 0.41 | 0.42 | 0.41 | 0.42 | 0.42 | 0.42 | 0.42 | 0.47 | 0.42 | 0.42 |
| F5 | 0.43 | 0.43 | 0.43 | 0.41 | 0.42 | 0.41 | 0.42 | 0.43 | 0.48 | 0.42 | 0.42 | 0.44 | 0.43 |
| F6 | 0.61 | 0.62 | 0.61 | 0.61 | 0.51 | 0.61 | 0.64 | 0.61 | 0.64 | 0.63 | 0.62 | 0.54 | 0.61 |
| F7 | 0.83 | 0.83 | 0.84 | 0.80 | 0.82 | 0.81 | 0.82 | 0.83 | 0.84 | 0.84 | 0.82 | 0.79 | 0.83 |
| F8 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 |
| F9 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.12 | 0.11 |
| F10 | 0.11 | 0.12 | 0.13 | 0.11 | 0.12 | 0.11 | 0.12 | 0.12 | 0.12 | 0.14 | 0.11 | 0.12 | 0.12 |
| F11 | 0.22 | 0.24 | 0.24 | 0.22 | 0.21 | 0.22 | 0.23 | 0.23 | 0.22 | 0.24 | 0.22 | 0.23 | 0.29 |
| F12 | 0.11 | 0.12 | 0.13 | 0.11 | 0.12 | 0.11 | 0.12 | 0.12 | 0.12 | 0.14 | 0.11 | 0.12 | 0.12 |
| F13 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 |
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 5 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 | 0.09 |
| F2 8 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.07 |
| F3 2 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 |
| F4 6 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 |
| F5 7 | 0.08 | 0.07 | 0.07 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.07 | 0.07 | 0.08 |
| F6 3 | 0.12 | 0.12 | 0.12 | 0.11 | 0.11 | 0.11 | 0.14 | 0.11 | 0.14 | 0.11 | 0.10 | 0.09 | 0.11 |
| F7 1 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 |
| F8 4 | 0.11 | 0.10 | 0.11 | 0.10 | 0.10 | 0.11 | 0.10 | 0.10 | 0.09 | 0.09 | 0.11 | 0.09 | 0.10 |
| F9 9 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.05 | 0.06 | 0.05 | 0.05 |
| F10 12 | 0.02 | 0.02 | 0.03 | 0.01 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| F11 10 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.02 | 0.03 | 0.03 | 0.04 | 0.04 | 0.03 | 0.04 | 0.04 |
| F12 11 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | 0.03 | 0.02 | 0.02 | 0.03 | 0.04 | 0.03 | 0.03 | 0.02 |
| F13 13 | 0.01 | 0.01 | 0.01 | 0.02 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 0.10 | 0.09 | 0.09 | 0.11 | 0.08 | 0.10 | 0.11 | 0.09 | 0.08 | 0.09 | 0.09 | 0.09 | 0.09 |
| F2 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.07 |
| F3 | 0.13 | 0.12 | 0.12 | 0.11 | 0.12 | 0.12 | 0.11 | 0.13 | 0.11 | 0.12 | 0.11 | 0.12 | 0.12 |
| F4 | 0.09 | 0.08 | 0.08 | 0.09 | 0.08 | 0.08 | 0.08 | 0.08 | 0.09 | 0.08 | 0.07 | 0.08 | 0.08 |
| F5 | 0.08 | 0.07 | 0.07 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.07 | 0.09 | 0.08 |
| F6 | 0.11 | 0.11 | 0.10 | 0.11 | 0.11 | 0.10 | 0.12 | 0.09 | 0.11 | 0.12 | 0.10 | 0.09 | 0.11 |
| F7 | 0.15 | 0.16 | 0.17 | 0.16 | 0.16 | 0.15 | 0.17 | 0.16 | 0.16 | 0.17 | 0.15 | 0.16 | 0.15 |
| F8 | 0.11 | 0.10 | 0.08 | 0.10 | 0.09 | 0.09 | 0.10 | 0.10 | 0.09 | 0.09 | 0.11 | 0.09 | 0.10 |
| F9 | 0.04 | 0.04 | 0.04 | 0.04 | 0.05 | 0.04 | 0.05 | 0.05 | 0.06 | 0.04 | 0.04 | 0.04 | 0.05 |
| F10 | 0.02 | 0.01 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 |
| F11 | 0.03 | 0.04 | 0.04 | 0.03 | 0.03 | 0.02 | 0.03 | 0.03 | 0.04 | 0.04 | 0.03 | 0.04 | 0.04 |
| F12 | 0.03 | 0.03 | 0.02 | 0.03 | 0.02 | 0.03 | 0.02 | 0.01 | 0.03 | 0.01 | 0.03 | 0.03 | 0.02 |
| F13 | 0.01 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
Appendix C
| F1 | 0.7500 | 0.0625 | 0.5500 | 0.2025 |
| F2 | 0.6982 | 0.0917 | 0.5110 | 0.2406 |
| F3 | 0.6500 | 0.1225 | 0.3973 | 0.3660 |
| F4 | 0.7500 | 0.0625 | 0.4500 | 0.3025 |
| F5 | 0.7500 | 0.0625 | 0.4500 | 0.3025 |
| F6 | 0.6500 | 0.1225 | 0.3973 | 0.3660 |
| F7 | 0.7500 | 0.0625 | 0.3973 | 0.3660 |
| F8 | 0.6500 | 0.1225 | 0.5500 | 0.2025 |
| F9 | 0.5500 | 0.2025 | 0.7500 | 0.0625 |
| F10 | 0.4500 | 0.3025 | 0.6500 | 0.1225 |
| F11 | 0.4500 | 0.3025 | 0.6500 | 0.1225 |
| F12 | 0.6982 | 0.0917 | 0.4500 | 0.3025 |
| F13 | 0.7500 | 0.0625 | 0.4500 | 0.3025 |
| Xingyang | Gongyi | Dengfeng | Xinmi | ||
|---|---|---|---|---|---|
| F1 | 0.0848 | 0.1115 | 0.0000 | 0.0848 | 0.1115 |
| F2 | 0.0884 | 0.0762 | 0.0000 | 0.0562 | 0.0884 |
| F3 | 0.0729 | 0.0628 | 0.0000 | 0.0470 | 0.0729 |
| F4 | 0.1362 | 0.1237 | 0.0000 | 0.0848 | 0.1362 |
| F5 | 0.1362 | 0.1272 | 0.0000 | 0.0848 | 0.1362 |
| F6 | 0.0729 | 0.0718 | 0.0000 | 0.0592 | 0.0729 |
| F7 | 0.1373 | 0.1377 | 0.0000 | 0.0848 | 0.1373 |
| F8 | 0.0470 | 0.0000 | 0.0470 | 0.0000 | 0.0470 |
| F9 | 0.0200 | 0.0000 | 0.1115 | 0.0000 | 0.1115 |
| F10 | 0.0000 | 0.0248 | 0.0718 | 0.0125 | 0.0718 |
| F11 | 0.0718 | 0.0718 | 0.0000 | 0.0718 | 0.0718 |
| F12 | 0.1009 | 0.1009 | 0.0000 | 0.0762 | 0.1009 |
| F13 | 0.1115 | 0.1362 | 0.0000 | 0.0848 | 0.1362 |
| Xingyang | Gongyi | Dengfeng | Xinmi | |
|---|---|---|---|---|
| F1 | 0.7610 | 1.0000 | 0.0000 | 0.7610 |
| F2 | 0.9998 | 0.8615 | 0.0000 | 0.6354 |
| F3 | 1.0003 | 0.8618 | 0.0000 | 0.6451 |
| F4 | 1.0000 | 0.9081 | 0.0000 | 0.6227 |
| F5 | 1.0000 | 0.9342 | 0.0000 | 0.6227 |
| F6 | 1.0003 | 0.9849 | 0.0000 | 0.8130 |
| F7 | 1.0001 | 1.0029 | 0.0000 | 0.6177 |
| F8 | 1.0000 | 0.0000 | 1.0000 | 0.0000 |
| F9 | 0.1794 | 0.0000 | 1.0000 | 0.0000 |
| F10 | 0.0000 | 0.3449 | 1.0000 | 0.1745 |
| F11 | 1.0000 | 1.0000 | 0.0000 | 1.0000 |
| F12 | 1.0000 | 1.0000 | 0.0000 | 0.7548 |
| F13 | 0.8183 | 1.0000 | 0.0000 | 0.6227 |
References
- Diakakis, M.; Deligiannakis, G. Vehicle-related flood fatalities in Greece. Environ. Hazards 2013, 12, 278–290. [Google Scholar] [CrossRef]
- National Disaster Reduction Center of the Ministry of Water Resources and the Ministry of Emergency Management. Available online: http://cdr.iwhr.com/fhkhjzzx/index.htm (accessed on 13 June 2023).
- The Centre for Research on the Epidemiology of Disasters (CREDS). Available online: https://www.cred.be (accessed on 13 June 2023).
- Shan, J. New field of GS1:Humanitarian relief logistics. Barcode Inf. Syst. 2017, 1, 28. (In Chinese) [Google Scholar]
- Lei, Z. Research on humanitarian supply chain for post-disaster relief. Jiangsu Bus. Theory 2012, 8, 147–149. (In Chinese) [Google Scholar]
- Yang, J.; Xiao, L. Comparative analysis of humanitarian logistics and commercial logistics. Port Econ. 2009, 7, 45–47. (In Chinese) [Google Scholar]
- Anjomshoae, A.; Banomyong, R.; Mohammed, F.; Kunz, N. A systematic review of humanitarian supply chains performance measurement literature from 2007 to 2021. Int. J. Disaster Risk Reduct. 2022, 72, 102852. [Google Scholar] [CrossRef]
- Peng, M.; Peng, Y.; Chen, H. Post-seismic supply chain risk management: A system dynamics disruption analysis approach for inventory and logistics planning. Comput. Oper. Res. 2014, 42, 14–24. [Google Scholar] [CrossRef]
- Sharma, S.K.; Routroy, S.; Singh, R.K.; Nag, U. Analysis of supply chain vulnerability factors in manufacturing enterprises: A fuzzy DEMATEL approach. Int. J. Logist. Res. Appl. 2022, 1–28. [Google Scholar] [CrossRef]
- Dubey, R.; Bryde, D.J.; Foropon, C.; Graham, G.; Giannakis, M.; Mishra, D.B. Agility in humanitarian supply chain: An organizational information processing perspective and relational view. Ann. Oper. Res. 2020, 319, 559–579. [Google Scholar] [CrossRef]
- Agarwal, S.; Kant, R.; Shankar, R. Evaluating solutions to overcome humanitarian supply chain management barriers: A hybrid fuzzy SWARA—Fuzzy WASPAS approach. Int. J. Disaster Risk Reduct. 2020, 51, 101838. [Google Scholar] [CrossRef]
- Jin, D.; Xu, Y. A study of supply chain performance in humanitarian relief—Perspectives on authoritative governance, market competition and partner cooperation. Econ. Manag. 2013, 35, 171–178. (In Chinese) [Google Scholar]
- Cao, K.; Long, J.; Yang, Y. An empirical study on the relationship between organizational trust, knowledge sharing and organizational performance. Beijing Res. Manag. 2008, 5. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, W.; Hara, C. A study on the relationship between firms’ ability to influence government/industry and new product performance. Sci. Res. 2011, 29, 906–913. (In Chinese) [Google Scholar]
- Yang, K. A preliminary study on the international humanitarian relief coordination mechanism under the framework of the United Nations. Shanghai Int. Outlook 2010, 3. (In Chinese) [Google Scholar] [CrossRef]
- Roh, S.; Lin, H.H.; Jang, H. Performance indicators for humanitarian relief logistics in Taiwan. Asian J. Shipp. Logist. 2022, 38, 173–180. [Google Scholar] [CrossRef]
- Lu, Q.; Goh, M.; De Souza, R. A SCOR framework to measure logistics performance of humanitarian organizations. J. Humanit. Logist. Supply Chain Manag. 2016, 6, 222–239. [Google Scholar] [CrossRef]
- Wang, W.; Huang, L.; Liang, X. On the simulation-based reliability of complex emergency logistics networks in post-accident rescues. Int. J. Environ. Res. Public Health 2018, 15, 79. [Google Scholar] [CrossRef]
- Jia, D. From Epidemic Shock: Supply Chain Resilience is the Key to Recovery—An Interview with Mr. Jia Dian’an of Baker & McKenzie Beijing. China Money Mark. 2020, 5, 68–72. (In Chinese) [Google Scholar]
- Larrea, O. Key performance indicators in humanitarian logistics in Colombia. IFAC Proc. Vol. 2013, 46, 211–216. [Google Scholar] [CrossRef]
- Maharjan, R.; Hanaoka, S. Warehouse location determination for humanitarian relief distribution in Nepal. Transp. Res. Procedia 2017, 25, 1151–1163. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J. Agent-based evaluation of humanitarian relief goods supply capability. Int. J. Disaster Risk Reduct. 2019, 36, 101105. [Google Scholar] [CrossRef]
- Oloruntoba, R.; Kovács, G. A commentary on agility in humanitarian aid supply chains. Supply Chain Manag. 2015, 20, 708–716. [Google Scholar] [CrossRef]
- Haavisto, I.; Goentzel, J. Measuring humanitarian supply chain performance in a multi-goal context. J. Humanit. Logist. Supply Chain Manag. 2015, 5, 300–324. [Google Scholar] [CrossRef]
- Yusuf, Y.; Menhat, M.S.; Abubakar, T.; Ogbuke, N.J. Agile capabilities as necessary conditions for maximising sustainable supply chain performance: An empirical investigation. Int. J. Prod. Econ. 2020, 222, 107501. [Google Scholar]
- Chern, J.-H. An Empirical Study on the Performance Evaluation of Indicators for the Nonprofit Organizations—An Example of 300 Major Foundations in Taiwan; Nation Defense University: Taiwan, China, 2002. [Google Scholar]
- Kazancoglu, I.; Ozbiltekin-Pala, M.; Mangla, S.K.; Kazancoglu, Y.; Jabeen, F. Role of flexibility, agility and responsiveness for sustainable supply chain resilience during COVID-19. J. Clean. Prod. 2022, 362, 132431. [Google Scholar] [CrossRef]
- Ahn, S.; Rhim, H.; Seog, S.H. Response time and vendor–assembler relationship in a supply chain. Eur. J. Oper. Res. 2008, 184, 652–666. [Google Scholar] [CrossRef]
- Wang, F. Research on Supply Chain Decision Making and Monitoring Based on Response Time; Huazhong University of Science and Technology: Wuhan, China, 2006. (In Chinese) [Google Scholar]
- Sahebjamnia, N.; Torabi, S.A.; Mansouri, S.A. A hybrid decision support system for managing humanitarian relief chain. Decis. Support Syst. 2017, 95, 12–26. [Google Scholar] [CrossRef]
- Shingne, H.; Shriram, R. Heuristic deep learning scheduling in cloud for resource-intensive internet of things systems. Comput. Electr. Eng. 2023, 108, 108652. [Google Scholar] [CrossRef]
- Mathur, S.; Chaba, Y.; Noliya, A. Performance Analysis of Support Vector Machine Learning Based Carrier Aggregation Resource scheduling in 5G Mobile Communication. Procedia Comput. Sci. 2023, 218, 2776–2785. [Google Scholar] [CrossRef]
- Ghorbani, M.; Ramezanian, R. Integration of carrier selection and supplier selection problem in humanitarian logistics. Comput. Ind. Eng. 2020, 144, 106473. [Google Scholar] [CrossRef]
- Darvishan, A.; Lim, G.J. Dynamic network flow optimization for real-time evacuation reroute planning under multiple road disruptions. Reliab. Eng. Syst. Saf. 2021, 214, 107644. [Google Scholar] [CrossRef]
- Qiao, S. Research on the Effectiveness of Supply Chain Cost Control of Suning.com Based on Entropy Value Method; Hunan Institute of Technology: Yueyang, China, 2022. [Google Scholar] [CrossRef]
- Whybark, D.C. Issues in managing disaster relief inventories. Int. J. Prod. Econ. 2007, 108, 228–235. [Google Scholar] [CrossRef]
- Das, R.; Hanaoka, S. Relief inventory modelling with stochastic lead-time and demand. Eur. J. Oper. Res. 2014, 235, 616–623. [Google Scholar] [CrossRef]
- Balcik, B.; Beamon, B.M. Facility location in humanitarian relief. Int. J. Logist. 2008, 11, 101–121. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Pérez, N.; Jaller, M.; Van Wassenhove, L.N.; Aros-Vera, F. On the appropriate objective function for post-disaster humanitarian logistics models. J. Oper. Manag. 2013, 31, 262–280. [Google Scholar] [CrossRef]
- Chen, D.; Fang, X.; Li, Y.; Ni, S.; Zhang, Q.; Sang, C.K. Three-level multimodal transportation network for cross-regional emergency resources dispatch under demand and route reliability. Reliab. Eng. Syst. Saf. 2022, 222, 108461. [Google Scholar] [CrossRef]
- Beamon, B.M.; Balcik, B. Performance measurement in humanitarian relief chains. Int. J. Public Sect. Manag. 2008, 21, 4–25. [Google Scholar] [CrossRef]
- Ye, F.; Xu, X. Cost allocation model for optimizing supply chain inventory with controllable lead time. Comput. Ind. Eng. 2010, 59, 93–99. [Google Scholar] [CrossRef]
- Fontainha, T.C.; Leiras, A.; Bandeira, R.A.D.M.; Scavarda, L.F. Stakeholder satisfaction in complex relationships during the disaster response: A structured review and a case study perspective. Prod. Plan. Control 2022, 33, 517–528. [Google Scholar] [CrossRef]
- Merckx, G.; Chaturvedi, A. Short vs. long-term procurement contracts when supplier can invest in cost reduction. Int. J. Prod. Econ. 2020, 227, 107652. [Google Scholar] [CrossRef]
- Ghavamifar, A.; Torabi, S.A.; Moshtari, M. A hybrid relief procurement contract for humanitarian logistics. Transp. Res. Part E Logist. Transp. Rev. 2022, 167, 102916. [Google Scholar] [CrossRef]
- Wang, Y. Research on Realization Mechanism and Management Strategy of Supply Chain Low Carbon Innovation Considering Consumer Preference; Shandong University of Science and Technology: Qingdao, China, 2020. (In Chinese) [Google Scholar]
- Huo, J.; Zhang, J.; Xu, S. Analysis of strategic stockpiling and rotational storage of emergency medical supplies—Taking masks as an example. Shanghai Manag. Sci. 2023, 45, 43–49. (In Chinese) [Google Scholar]
- Chatzichristaki, C.; Stefanidis, S.; Stefanidis, P.; Stathis, D. Analysis of the flash flood in Rhodes Island (South Greece) on 22 November 2013. Silva 2015, 16, 76–86. [Google Scholar]
- John, L.; Gurumurthy, A.; Soni, G.; Jain, V. Modelling the inter-relationship between factors affecting coordination in a humanitarian supply chain: A case of Chennai flood relief. Ann. Oper. Res. 2019, 283, 1227–1258. [Google Scholar] [CrossRef]
- Steurer, J. The Delphi method: An efficient procedure to generate knowledge. Skeletal. Radiol. 2011, 40, 959–961. [Google Scholar] [CrossRef] [PubMed]
- Belton, I.; MacDonald, A.; Wright, G.; Hamlin, I. Improving the practical application of the Delphi method in group-based judgment: A six-step prescription for a well-founded and defensible process. Technol. Forecast. Soc. Chang. 2019, 147, 72–82. [Google Scholar] [CrossRef]
- Yang, X.; Xu, Z.; Xu, J. Large-scale group Delphi method with heterogeneous decision information and dynamic weights. Expert Syst. Appl. 2023, 213, 09574174. [Google Scholar] [CrossRef]
- Shafiee, M.; Zare-Mehrjerdi, Y.; Govindan, K.; Dastgoshade, S. A causality analysis of risks to perishable product supply chain networks during the COVID-19 outbreak era: An extended DEMATEL method under Pythagorean fuzzy environment. Transp. Res. Part E Logist. Transp. Rev. 2022, 163, 102759. [Google Scholar] [CrossRef]
- Sharifyazdi, M.; Navangul, K.A.; Gharehgozli, A.; Jahre, M. On- and offshore prepositioning and delivery mechanism for humanitarian relief operations. Int. J. Prod. Res. 2018, 56, 6164–6182. [Google Scholar] [CrossRef]
- Altay, N.; Gunasekaran, A.; Dubey, R.; Childe, S.J. Agility and resilience as antecedents of supply chain performance under moderating effects of organizational culture within the humanitariansetting: A dynamic capability view. Prod. Plan. Control 2018, 29, 1158–1174. [Google Scholar] [CrossRef]
- Singh, R.K.; Gupta, A.; Gunasekaran, A. Analysing the interaction of factors for resilient humanitarian supply chain. Int. J. Prod. Res. 2018, 56, 6809–6827. [Google Scholar] [CrossRef]
- Nezhadroshan, A.M.; Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M. A scenario-based possibilistic-stochastic programming approach to address resilient humanitarian logistics considering travel time and resilience levels of facilities. Int. J. Syst. Sci.-Oper. Logist. 2021, 8, 321–347. [Google Scholar] [CrossRef]
- Rakesh, N.; Sonal, C. Operational excellence in humanitarian logistics and supply chain management through leagile framework: A case study from a non-mature economy. Prod. Plan. Control 2022, 33, 606–621. [Google Scholar]
- Rahman, M.M.; Tasnim, F.; Mukta, M.Z.; Abedin, A.; Aryal, K.R. Assessing Barriers in Humanitarian Supply Chains for Cyclone in Coastal Areas of Bangladesh: An Interpretive Structural Modeling (ISM) Approach. Sustainability 2022, 14, 9724. [Google Scholar] [CrossRef]
- Giedelmann-L, N.; Guerrero, W.J.; Solano-Charris, E.L. System dynamics approach for food inventory policy assessment in a humanitarian supply chain. Int. J. Disaster Risk Reduct. 2022, 81, 103286. [Google Scholar] [CrossRef]
- Bag, S.; Gupta, S.; Wood, L. Big data analytics in sustainable humanitarian supply chain: Barriers and their interactions. Ann. Oper. Res. 2020, 319, 721–760. [Google Scholar] [CrossRef]
- Li, H.; Murat, A.; Huang, W. Selection of contract suppliers under price and demand uncertainty in a dynamic market. Eur. J. Oper. Res. 2009, 198, 830–847. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Wan, C.; Qu, Y.; Cornélissen, G.; Halberg, F. In vitro circadian ANP secretion by gene transferring cells encapsulated in polycaprolactone tubes: Gene chronotherapy. Peptides 2004, 25, 1259–1267. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Gao, M.; Liang, K. Identification of factors affecting the synergy of multiple subjects in the development and utilization of “urban minerals” based on ANP-BPNN. Manag. Rev. 2023, 35, 16–27. (In Chinese) [Google Scholar]
- Yang, W.; Liu, C. A hesitant Pythagorean fuzzy multi-attribute decision-making method based on DEMATEL and VIKOR. J. Eng. Math. 2021, 38, 797–808. (In Chinese) [Google Scholar]
- Zhang, X.; Xu, Z. Extension of TOPSIS to Multiple Criteria Decision Making with Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Ding, X.-F.; Liu, H.-C. A 2-dimension uncertain linguistic DEMATEL method for identifying critical success factors in emergency management. Appl. Soft Comput. 2018, 71, 386–395. [Google Scholar] [CrossRef]
- Investigation Report on the “20 July” Exceptionally Heavy Rainstorm Disaster in Zhengzhou. Available online: https://www.mem.gov.cn/gk/sgcc/tbzdsgdcbg/202201/P020220121639049697767.pdf (accessed on 20 June 2023).
| Standard | Indicator | Main Contents |
|---|---|---|
| Organizational involvement A | Active government involvement (F1) | Government plays a major role in the humanitarian supply chain [11,12,13] |
| Active participation of NGOs (F2) | NGOs are gaining ground in the humanitarian supply chain [14] | |
| Coordination among participating organizations (F3) | Coordination among supply chain members is important for humanitarian supply chain resilience [15,16] | |
| Reliability B | Logistics provider reliability (F4) | Logistics providers can accelerate the relief process and improve the resilience of the humanitarian supply chain [17,18,19] |
| Agility C | Material supplier reliability (F5) | Timely supply of materials helps to speed up the rescue process and enhance rescue efficiency [20,21,22] |
| Responsiveness (F6) | Rapid supply chain response enhances supply chain agility [23,24,25] | |
| Resource scheduling capability (F7) | Having the ability to quickly dispatch resources makes the humanitarian supply chain more resilient [26,27] | |
| Cost factor D | Timeliness of transportation (F8) | Timely transportation allows for smooth relief efforts and further improves supply chain resilience performance [28,29] |
| Transportation costs (F9) | Lower transportation costs can lead to increased supply chain revenue and increased supply chain operability [30,31] | |
| Inventory costs (F10) | Reducing inventory costs contributes to a sustainable supply chain, thereby increasing its resilience [32,33] | |
| Material mobilization and procurement costs (F11) | Lower material raising and procurement costs allow for more material to be raised on the same budget, and increased material availability helps improve supply chain performance [34,35] | |
| Quality of service E | Supply of necessities of life (F12) | The main function of the humanitarian supply chain is to provide the necessities of life to the relief workers [36,37,38] |
| Distribution of relief supplies (F13) | Distribution of relief supplies can protect the lives and livelihoods of those waiting for help [39,40,41] |
| References | Description | Method |
|---|---|---|
| [54] | A combination of pre-positioning relief items in the mainland and anticipating them onboard ships and at terminals is proposed to help improve the efficiency of disaster relief operations as well as the resilience of the supply chain | Goal planning |
| [55] | The impact of supply chain agility (SCAG) and supply chain resilience (SCRES) on performance, mediated by organizational culture, was investigated | DCV |
| [56] | Fuzzy MICMAC methodology was used to identify and analyze the factors that develop resilience in humanitarian supply chains | Fuzzy-MICMAC |
| [59] | Interpretive structural modeling (ISM) was used to assess the barriers in the humanitarian supply chain in coastal Bangladesh under the influence of cyclones | ISM |
| [60] | A dynamic systems model approach was used to compare centralized and decentralized supply chain configurations and apply them to humanitarian supply chains | Dynamic systems model |
| [61] | Weighting of humanitarian supply chain barriers in a big-data-driven context assessed by fuzzy full explanatory structural model (F-T-ISM) | F-T-ISM |
| Proposed method | Thirteen representative indicators were selected to evaluate humanitarian supply chain resilience factors, and the VIKOR evaluation method was used to rank the resilience of humanitarian supply chains in five typical disaster areas | PFs-ANP-VIKOR |
| Fuzzy Natural Semantics | The Pythagorean Fuzzy Set ) |
|---|---|
| Very low (VL) | (0.15, 0.85) |
| Low (L) | (0.25, 0.75) |
| Moderately low (ML) | (0.35, 0.65) |
| Medium (M) | (0.55, 0.45) |
| Moderately high (MH) | (0.65, 0.35) |
| High (H) | (0.75, 0.25) |
| Very high (VH) | (0.85, 0.15) |
| Standard | Weight | Indicator | Weight | Rank |
|---|---|---|---|---|
| Organizational involvement A | 0.2813 | Active government involvement (F1) | 0.0987 | 5 |
| Active participation of NGOs (F2) | 0.0573 | 8 | ||
| Coordination among participating organizations (F3) | 0.1474 | 1 | ||
| Reliability B | 0.1663 | Logistics provider reliability (F4) | 0.0832 | 6 |
| Material supplier reliability (F5) | 0.0831 | 7 | ||
| Responsiveness (F6) | 0.1174 | 3 | ||
| Agility C | 0.3777 | Resource scheduling capability (F7) | 0.1253 | 2 |
| Timeliness of transportation (F8) | 0.1129 | 4 | ||
| Cost factor D | 0.1223 | Transportation costs (F9) | 0.0559 | 9 |
| Inventory costs (F10) | 0.0238 | 12 | ||
| Material mobilization and procurement costs (F11) | 0.0426 | 10 | ||
| Quality of service E | 0.0524 | Supply of necessities of life (F12) | 0.0337 | 11 |
| Distribution of relief supplies (F13) | 0.0187 | 13 |
| Xingyang | Gongyi | Dengfeng | Xinmi | |||||
|---|---|---|---|---|---|---|---|---|
| F1 | 0.6113 | 0.1521 | 0.5500 | 0.2025 | 0.7500 | 0.0625 | 0.6113 | 0.1521 |
| F2 | 0.5110 | 0.2406 | 0.5500 | 0.2025 | 0.6982 | 0.0917 | 0.5974 | 0.1631 |
| F3 | 0.3973 | 0.3660 | 0.4971 | 0.2546 | 0.6500 | 0.1225 | 0.5500 | 0.2025 |
| F4 | 0.4500 | 0.3025 | 0.5110 | 0.2406 | 0.7500 | 0.0625 | 0.6113 | 0.1521 |
| F5 | 0.4500 | 0.3025 | 0.4971 | 0.2546 | 0.7500 | 0.0625 | 0.6113 | 0.1521 |
| F6 | 0.3973 | 0.3660 | 0.4500 | 0.3025 | 0.6500 | 0.1225 | 0.5110 | 0.2406 |
| F7 | 0.3973 | 0.3660 | 0.4111 | 0.3492 | 0.7500 | 0.0625 | 0.6113 | 0.1521 |
| F8 | 0.5500 | 0.2025 | 0.6500 | 0.1225 | 0.5500 | 0.2025 | 0.6500 | 0.1225 |
| F9 | 0.5974 | 0.1631 | 0.5500 | 0.2025 | 0.7500 | 0.0625 | 0.5500 | 0.2025 |
| F10 | 0.4500 | 0.3025 | 0.5500 | 0.2025 | 0.6500 | 0.1225 | 0.5110 | 0.2406 |
| F11 | 0.6500 | 0.1225 | 0.6500 | 0.1225 | 0.4500 | 0.3025 | 0.6500 | 0.1225 |
| F12 | 0.4500 | 0.3025 | 0.4500 | 0.3025 | 0.6982 | 0.0917 | 0.5500 | 0.2025 |
| F13 | 0.5500 | 0.2025 | 0.4500 | 0.3025 | 0.7500 | 0.0625 | 0.6113 | 0.1521 |
| Rank | Rank | Rank | ||||
|---|---|---|---|---|---|---|
| Xingyang | 0.4986 | 4 | 0.1018 | 4 | 0.5221 | 4 |
| Gongyi | 0.3739 | 3 | 0.0930 | 3 | 0.4365 | 3 |
| Xinmi | 0.2859 | 2 | 0.0811 | 2 | 0.4279 | 2 |
| Dengfeng | 0.2701 | 1 | 0.0605 | 1 | 0.4008 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Li, W.; Proverbs, D.; Chen, W. An Evaluation of the Humanitarian Supply Chains in the Event of Flash Flooding. Water 2023, 15, 3323. https://doi.org/10.3390/w15183323
Xu W, Li W, Proverbs D, Chen W. An Evaluation of the Humanitarian Supply Chains in the Event of Flash Flooding. Water. 2023; 15(18):3323. https://doi.org/10.3390/w15183323
Chicago/Turabian StyleXu, Wenping, Wenzhuo Li, David Proverbs, and Wenbo Chen. 2023. "An Evaluation of the Humanitarian Supply Chains in the Event of Flash Flooding" Water 15, no. 18: 3323. https://doi.org/10.3390/w15183323







