Residual Saturation Effects on CO2 Migration and Caprock Sealing: A Study of Permeability and Capillary Pressure Models
Abstract
:1. Introduction
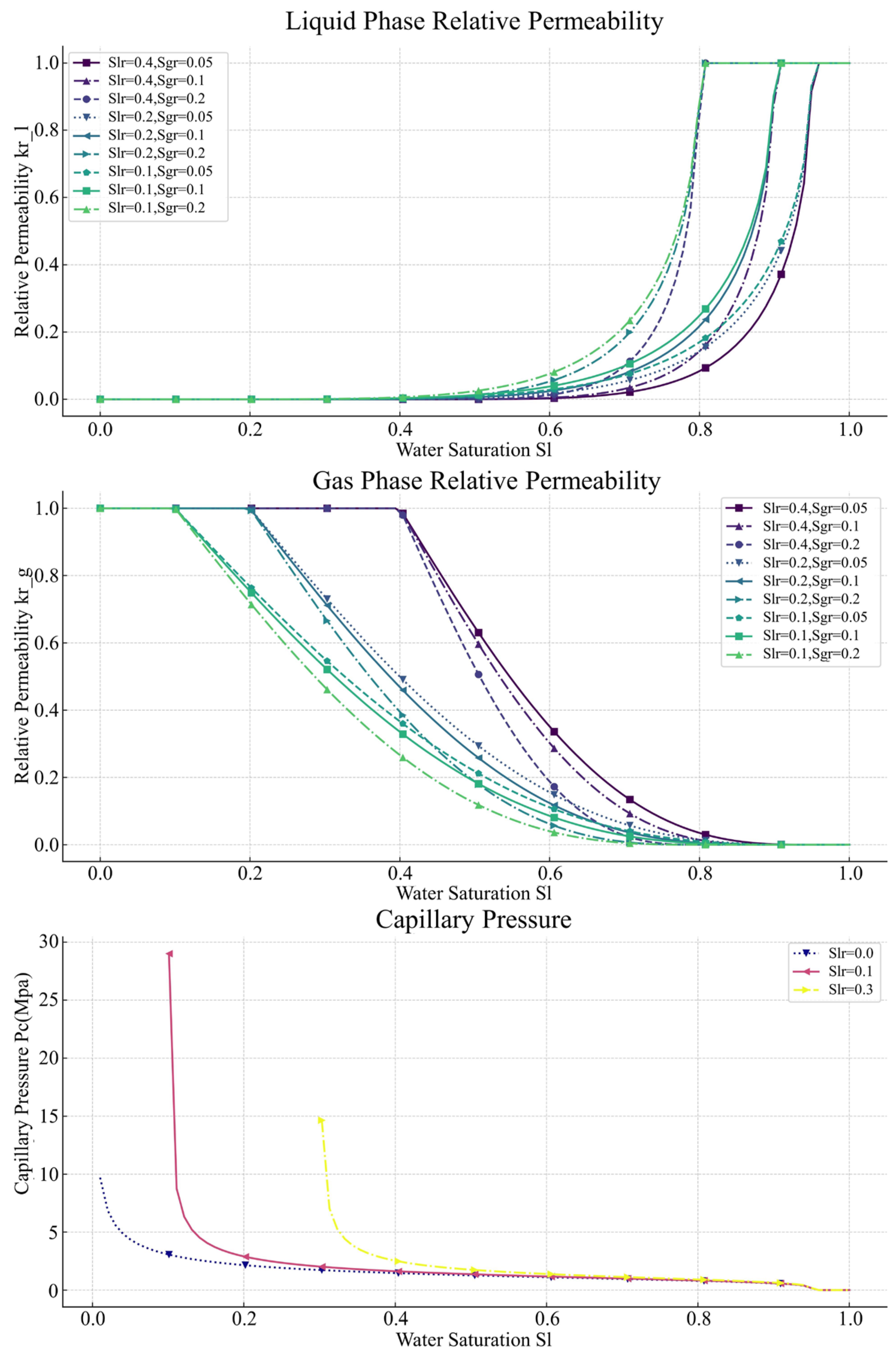
2. The Relative Permeability and Capillary Pressure Models
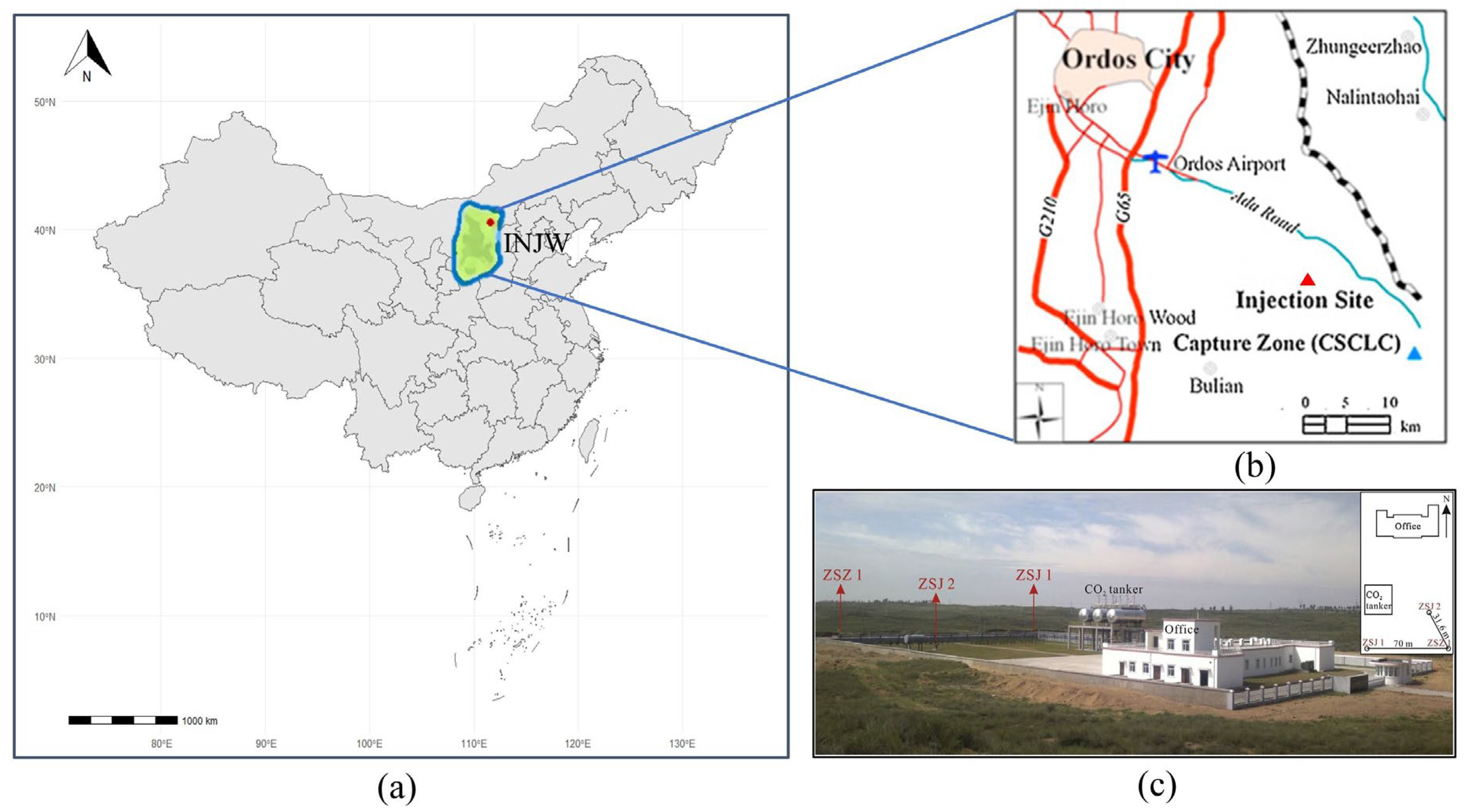
3. Project Overview
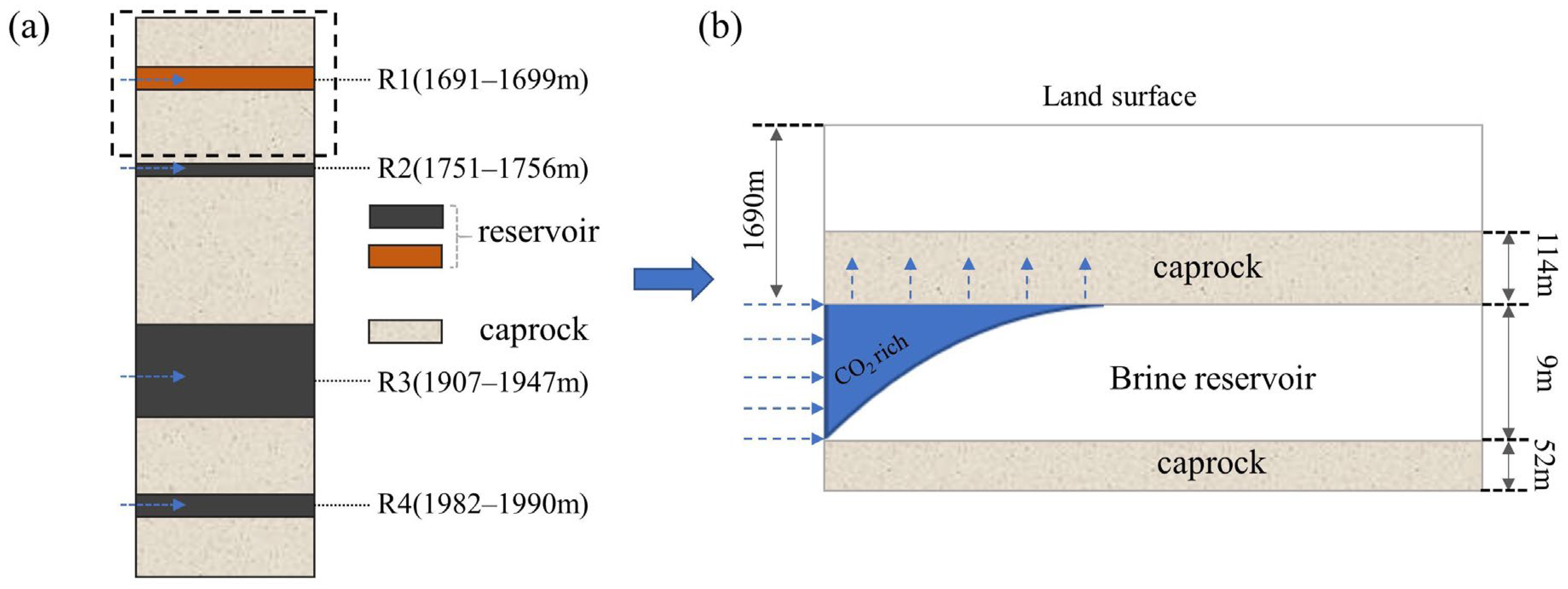
4. Model Establishment
4.1. Modeling Approach and Modeling Tools
4.2. Spatial Discretization and Model Parameters
4.3. Initial Conditions and Boundary Conditions
5. Results and Discussions
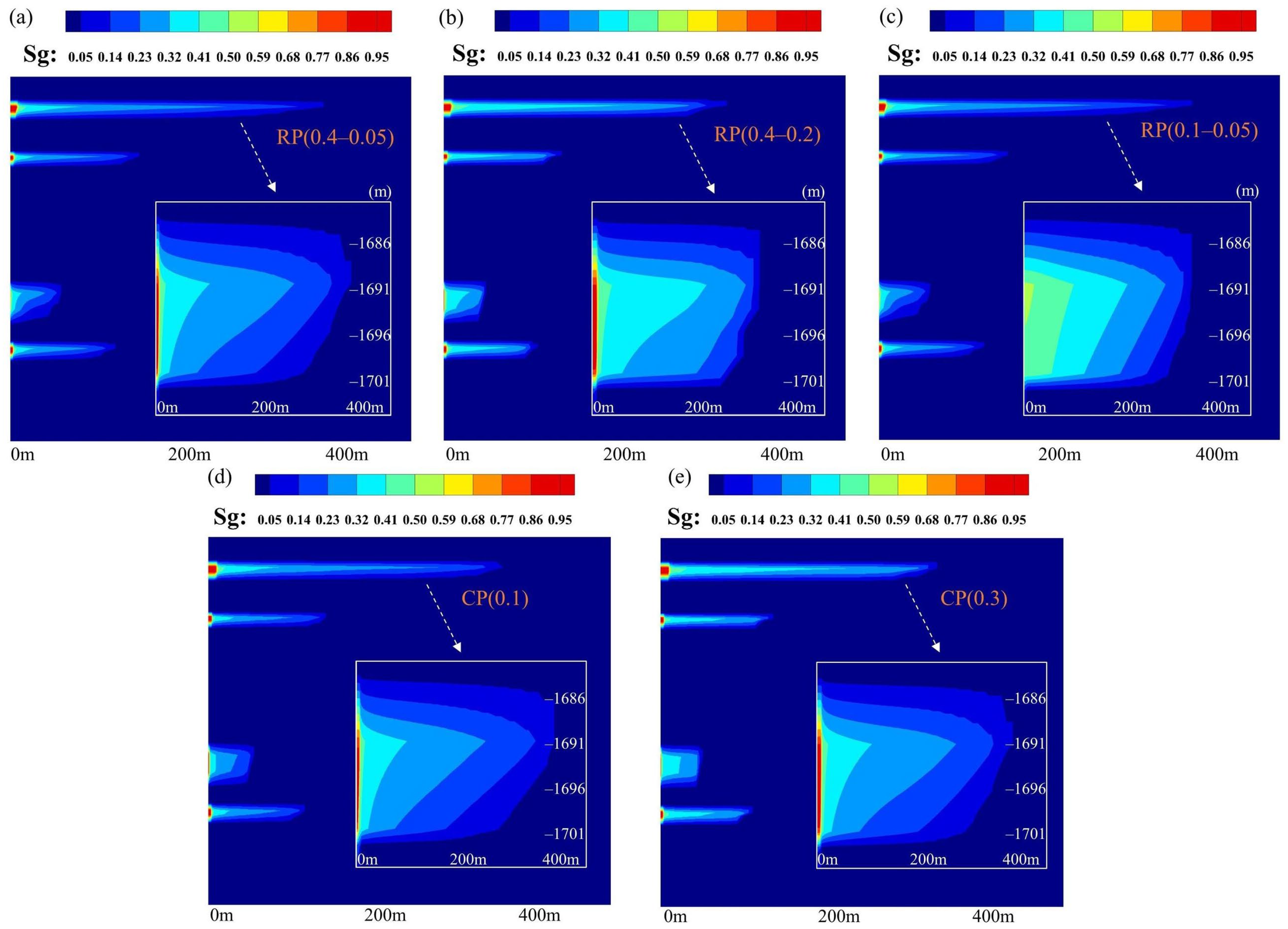
5.1. Distribution and Migration Behavior of CO2 in the Reservoir–Caprock System
5.2. Assessment of the Sealing Efficacy of the Caprock
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| mass or heat flux of component | |
| apparent friction coefficient | |
| specific enthalpy of phase | |
| absolute permeability | |
| relative permeability of phase | |
| mass or energy per volume of component | |
| pressure | |
| fluid pressure in phase | |
| sinks and sources of component | |
| closed boundary surface of | |
| grain density of the rock | |
| porosity | |
| specific heat of the rock | |
| saturation of phase | |
| time | |
| temperature | |
| mixture velocity (velocity of mass center) | |
| or | velocity of phase |
| specific internal energy of phase | |
| subdomain of the flow system | |
| mass fraction of component present in phase | |
| thermal conductivity | |
| density of phase | |
| gorg | gravitational acceleration |
References
- He, H.; Lian, J.; Chen, C.; Xiong, Q.; Li, C.C.; Zhang, M. Enabling Multi-Chemisorption Sites on Carbon Nanofibers Cathodes by an In-situ Exfoliation Strategy for High-Performance Zn–Ion Hybrid Capacitors. Nano-Micro. Lett. 2022, 14, 106. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Setzler, B.P.; Wang, J.; Nash, J.; Wang, T.; Xu, B.; Yan, Y. An Efficient Direct Ammonia Fuel Cell for Affordable Carbon-Neutral Transportation. Joule 2019, 3, 2472–2484. [Google Scholar] [CrossRef]
- Aminu, M.D.; Nabavi, S.A.; Rochelle, C.A.; Manovic, V. A review of developments in carbon dioxide storage. Appl. Energy 2017, 208, 1389–1419. [Google Scholar] [CrossRef]
- Ajayi, T.; Gomes, J.S.; Bera, A. A review of CO2 storage in geological formations emphasizing modeling, monitoring and capacity estimation approaches. Pet. Sci. 2019, 16, 1028–1063. [Google Scholar] [CrossRef]
- Zhou, N.; Lu, S.; Wang, M.; Liu, W.; Guan, Y.; Tan, H.; Wang, Z. Applicability of fractal capillary pressure models to sandstones. J. Pet. Sci. Eng. 2020, 185, 106626. [Google Scholar] [CrossRef]
- Kalam, S.; Olayiwola, T.; Al-Rubaii, M.M.; Amaechi, B.I.; Jamal, M.S.; Awotunde, A.A. Carbon dioxide sequestration in underground formations: Review of experimental, modeling, and field studies. J. Pet. Explor. Prod. Technol. 2021, 11, 303–325. [Google Scholar] [CrossRef]
- Khudaida, K.J.; Das, D.B. A numerical study of capillary pressure–saturation relationship for supercritical carbon dioxide (CO2) injection in deep saline aquifer. Chem. Eng. Res. Des. 2014, 92, 3017–3030. [Google Scholar] [CrossRef]
- Song, J.; Zhang, D. Comprehensive Review of Caprock-Sealing Mechanisms for Geologic Carbon Sequestration. Environ. Sci. Technol. 2013, 47, 9–22. [Google Scholar] [CrossRef]
- Jiao, Z.; Pawar, R.; Duguid, A.; Bourcier, W.; Haussmann, C.; Coddington, K.; Harp, D.; Ganshin, Y.; Quillinan, S.; McLaughlin, F.; et al. A Field Demonstration of an Active Reservoir Pressure Management through Fluid Injection and Displaced Fluid Extraction at the Rock Springs Uplift a Priority Geologic CO2 Storage Site for Wyoming. Energy Procedia 2017, 114, 2799–2811. [Google Scholar] [CrossRef]
- Das, D.B.; Mirzaei, M.; Widdows, N. Non-uniqueness in capillary pressure–saturation–relative permeability relationships for two-phase flow in porous media: Interplay between intensity and distribution of random micro-heterogeneities. Chem. Eng. Sci. 2006, 61, 6786–6803. [Google Scholar] [CrossRef]
- Celia, M.A.; Bachu, S.; Nordbotten, J.M.; Bandilla, K.W. Status of CO2 storage in deep saline aquifers with emphasis on modeling approaches and practical simulations. Water Resour. Res. 2015, 51, 6846–6892. [Google Scholar] [CrossRef]
- Bachu, S. Screening and ranking of sedimentary basins for sequestration of CO2 in geological media in response to climate change. Environ. Geol. 2003, 44, 277–289. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, K.; Sung, W.; Yoo, I. Analysis of the Leakage Possibility of Injected CO2 in a Saline Aquifer. 2010. Available online: https://pubs.acs.org/doi/pdf/10.1021/ef100073m (accessed on 7 February 2023).
- Yang, D.; Wang, S.; Zhang, Y. Analysis of CO2 Migration during Nanofluid-Based Supercritical CO2 Geological Storage in Saline Aquifers. Aerosol Air Qual. Res. 2014, 14, 1411–1417. [Google Scholar] [CrossRef]
- Zhang, K.; Xie, J.; Li, C.; Hu, L.; Wu, X.; Wang, Y. A full chain CCS demonstration project in northeast Ordos Basin, China: Operational experience and challenges. Int. J. Greenh. Gas Control 2016, 50, 218–230. [Google Scholar] [CrossRef]
- Fawad, M.; Mondol, N.H. Monitoring geological storage of CO2: A new approach. Sci. Rep. 2021, 11, 5942. [Google Scholar] [CrossRef] [PubMed]
- Fawad, M.; Mondol, N.H. Monitoring geological storage of CO2 using a new rock physics model. Sci. Rep. 2022, 12, 297. [Google Scholar] [CrossRef]
- Jia, W.; McPherson, B. Multiphase Flow Associated with Geological CO2 Storage. In Science of Carbon Storage in Deep Saline Formations; Elsevier: Amsterdam, The Netherlands, 2019; pp. 117–143. [Google Scholar] [CrossRef]
- Juanes, R.; Spiteri, E.J.; Orr, F.M., Jr.; Blunt, M.J. Impact of relative permeability hysteresis on geological CO2 storage. Water Resour. Res. 2006, 42, W12418. [Google Scholar] [CrossRef]
- Yang, D.; Gu, Y. Permeability change during CO2 injection in coal: An experimental study. Int. J. Coal Geol. 2004, 59, 245–261. [Google Scholar]
- Pruess, K.; García, J. Multiphase flow dynamics during CO2 injection into saline aquifers. Environ. Geol. 2002, 42, 282–295. [Google Scholar] [CrossRef]
- Li, Z.; Dong, M.; Li, S.; Huang, S. CO2 storage in the Permian saline aquifers in the Ordos Basin, China. Int. J. Greenh. Gas Control 2013, 13, 155–168. [Google Scholar] [CrossRef]
- Deng, H.; Stauffer, P.H.; Dai, Z.; Jiao, Z.; Surdam, R.C. Simulation of industrial-scale CO2 storage: Multi-scale heterogeneity and its impacts on storage capacity, injectivity and leakage. Int. J. Greenh. Gas Control 2012, 10, 397–418. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide Version 2.0; Lawrence Berkeley National Laboratory Report LBNL-43134; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 1999.
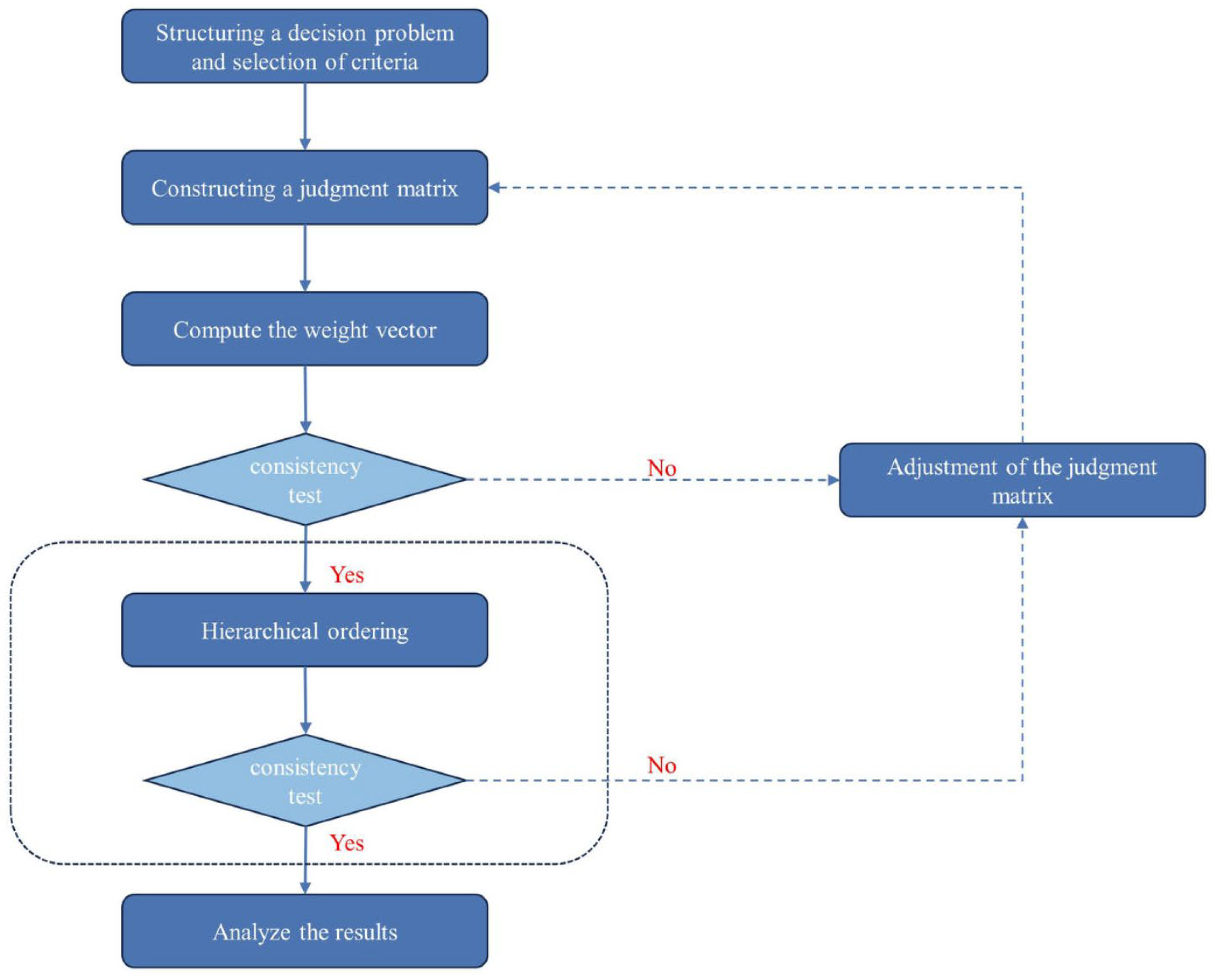
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Corey, A.T. The interrelation between gas and oil relative permeabilities. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
- Li, C.; Zhang, K.; Wang, Y.; Guo, C.; Maggi, F. Experimental and numerical analysis of reservoir performance for geological CO2 storage in the Ordos Basin in China. Int. J. Greenh. Gas Control 2016, 45, 216–232. [Google Scholar] [CrossRef]
- Li, Q.; Liu, G.Z.; Liu, X.H.; Li, X.C. Application of a health, safety, and environmental screening and ranking framework to the Shenhua CCS project. Int. J. Greenh. Gas Control 2013, 17, 504–514. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, K.; Hu, L.; Wang, Y.; Chen, M. Understanding the carbon dioxide sequestration in low-permeability saline aquifers in the Ordos Basin with numerical simulations, Greenhouse Gases: Science and Technology. Greenh. Gases Sci. Technol. 2015, 5, 558–576. [Google Scholar] [CrossRef]
- Pruess, K. ECO2N: A TOUGH2 Fluid Property Module for Mixtures of Water, NaCl, and CO2; Lawrence Berkeley National Laboratory Report LBNL-57952; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2005.
- Pruess, K.; Spycher, N. ECO2N—A fluid property module for the TOUGH2 code for studies of CO2 storage in saline aquifers. Energy Convers. Manag. 2007, 48, 1761–1767. [Google Scholar] [CrossRef]
- Yang, F.; Bai, B.; Tang, D.; Shari, D.; David, W. Characteristics of CO2 sequestration in saline aquifers. Fuel 2018, 216, 391–401. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Hesse, M.A.; Orr, F.M.; Tchelepi, H.A. Gravity currents with residual trapping. J. Fluid Mech. 2008, 611, 35–60. [Google Scholar] [CrossRef]
- Krevor, S.; Blunt, M.J.; Benson, S.M.; Pentland, C.H.; Reynolds, C.; Al-Menhali, A.; Niu, B. Capillary trapping for geologic carbon dioxide storage—From pore scale physics to field scale implications. Int. J. Greenh. Gas Control 2015, 40, 221–237. [Google Scholar] [CrossRef]
- Zhao, B.; MacMinn, C.W.; Juanes, R. Residual trapping, solubility trapping and capillary pinning complement each other to limit CO2 migration in deep saline aquifers. Energy Procedia 2014, 63, 3833–3839. [Google Scholar] [CrossRef]
- Whittaker, S.; Rostron, B.; Hawkes, C.; Gardner, C.; White, D.; Johnson, J.; Chalaturnyk, R.; Seeburger, D. A decade of CO2 injection into depleting oil fields: Monitoring and research activities of the IEA GHG Weyburn-Midale CO2 Monitoring and Storage Project. Energy Procedia 2011, 4, 6069–6076. [Google Scholar] [CrossRef]
- Raza, A.; Gholami, R.; Rezaee, R.; Bing, C.H.; Nagarajan, R.; Hamid, M.A. CO2 storage in depleted gas reservoirs: A study on the effect of residual gas saturation. Petroleum 2018, 4, 95–107. [Google Scholar] [CrossRef]
- Li, Y.; Ranjith, P.G.; Perera, M.S.A.; Yu, Q. Residual water formation during the CO2 storage process in deep saline aquifers and factors influencing it: A review. J. CO2 Util. 2017, 20, 253–262. [Google Scholar] [CrossRef]
- Ali, M.; Jha, N.K.; Pal, N.; Keshavarz, A.; Hoteit, H.; Sarmadivaleh, M. Recent advances in carbon dioxide geological storage, experimental procedures, influencing parameters, and future outlook. Earth-Sci. Rev. 2022, 225, 103895. [Google Scholar] [CrossRef]
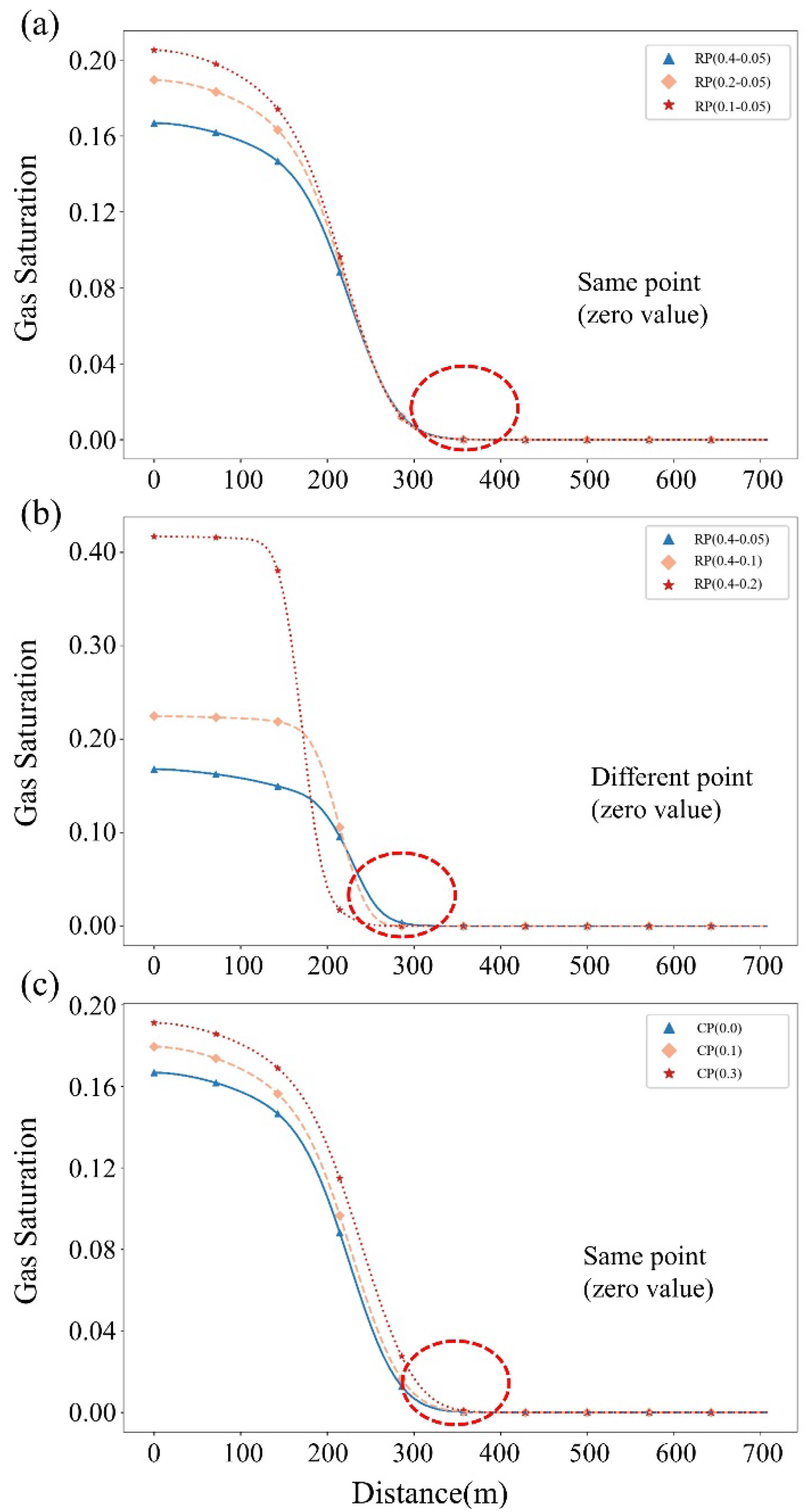
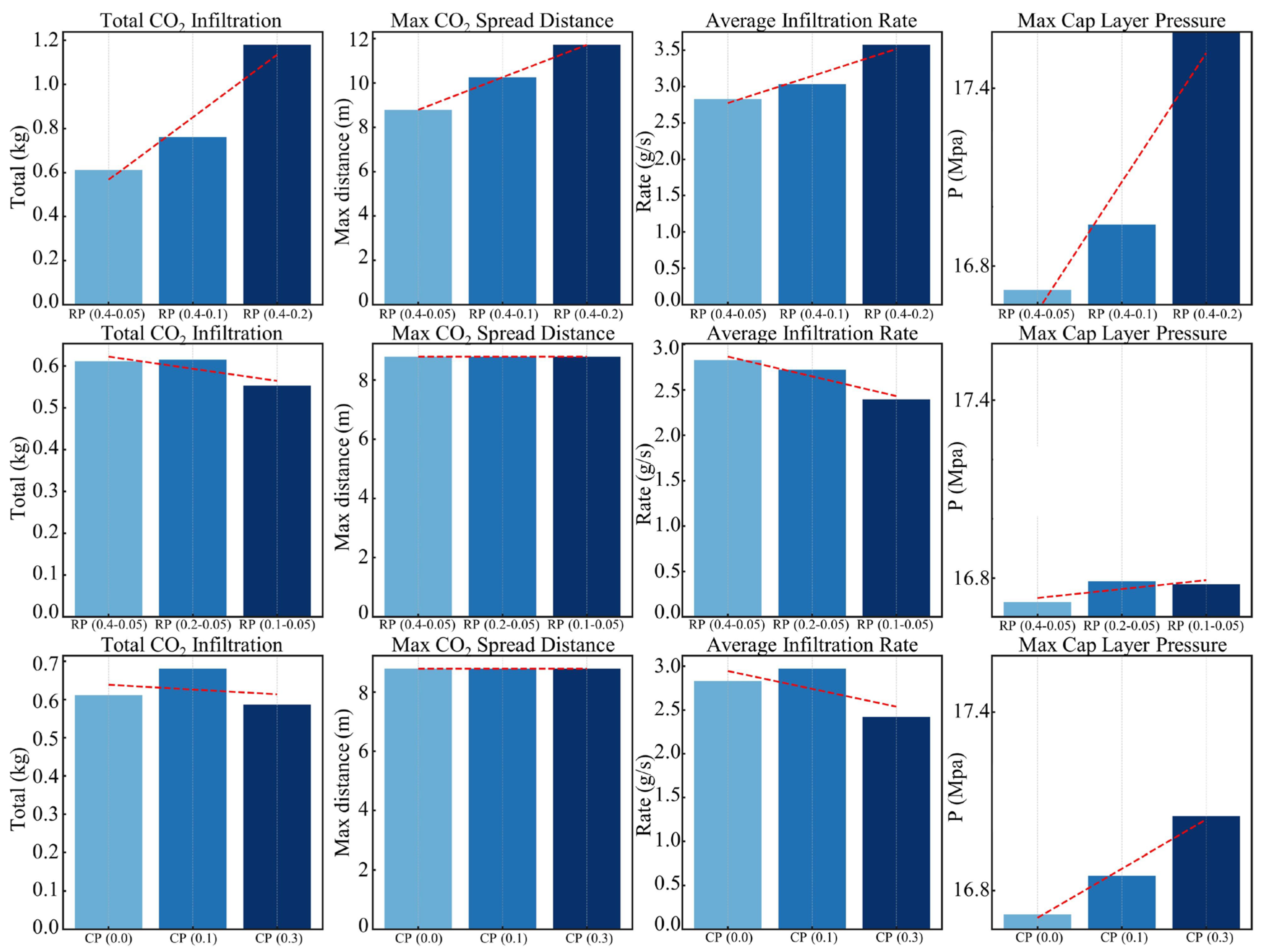

| Description | Equation |
|---|---|
| Mass and Energy Conservation | |
| For Mass | |
| For Energy | |
| Darcy’s law |
| Formation | Reservoir Thickness (m) | Cap Thickness (m) | m2) | Porosity (%) | Fracturing Pressure (MPa) | Formation Pressure (MPa) |
|---|---|---|---|---|---|---|
| R1 | 9 | 1699 | 2.81 | 10.6 | 35.29 | 17.45 |
| R2 | 5 | 57 | 5.47 | 12.4 | 37.53 | 17.89 |
| R3 | 40 | 191 | 1.431 | 9.7 | 38.95 | 20.15 |
| R4 | 8 | 43 | 6.58 | 12.9 | 42.60 | 21.43 |
| Caprock | - | - | - | 4.3 | - | - |
| Parameters | Values |
|---|---|
| Porosity | 0.05–0.13 |
| Permeability | |
| Rock grain density | |
| Specific heat of the rock grain | |
| Thermal conductivity | |
| Initial temperature distribution | |
| Initial pressure distribution | |
| Relative permeability model | |
| Capillary pressure model |
| Classification | Model Classification | ||
|---|---|---|---|
| RP (0.4–0.05) | 0.4 | 0.05 | Relative permeability model |
| RP (0.4–0.1) | 0.4 | 0.1 | Relative permeability model |
| RP (0.4–0.2) | 0.4 | 0.2 | Relative permeability model |
| RP (0.2–0.05) | 0.2 | 0.05 | Relative permeability model |
| RP (0.1–0.05) | 0.1 | 0.05 | Relative permeability model |
| CP (0.0) | 0.0 | -- | capillary pressure model |
| CP (0.1) | 0.1 | -- | capillary pressure model |
| CP (0.3) | 0.3 | -- | capillary pressure model |
| Caprock Pressure | Maximum Ingress Distance | Total Amount of CO2 Ingress | Ingress Rate | Weights | |
|---|---|---|---|---|---|
| Caprock pressure | 1 | 5 | 5 | 5 | 0.537 |
| Maximum ingress distance | 0.2 | 1 | 4 | 5 | 0.279 |
| Total amount of CO2 ingress | 0.2 | 0.25 | 1 | 3 | 0.121 |
| Ingress rate | 0.2 | 0.2 | 0.33 | 1 | 0.063 |
| Caprock Pressure | Maximum Ingress Distance | Total Amount of CO2 Ingress | Ingress Rate | Comprehensive Weight | Comprehensive Weight | |
|---|---|---|---|---|---|---|
| Weights | 0.537 | 0.279 | 0.121 | 0.063 | - | - |
| RP (0.4–0.05) | 0.154 | 0.111 | 0.125 | 0.146 | 0.138 | 3 |
| RP (0.4–0.1) | 0.205 | 0.167 | 0.167 | 0.167 | 0.187 | 2 |
| RP (0.4–0.2) | 0.256 | 0.278 | 0.208 | 0.208 | 0.254 | 1 |
| RP (0.2–0.05) | 0.077 | 0.111 | 0.104 | 0.104 | 0.091 | 7 |
| RP (0.1–0.05) | 0.128 | 0.111 | 0.104 | 0.104 | 0.119 | 4 |
| CP (0.0) | 0.154 | 0.111 | 0.125 | 0.146 | 0.138 | 3 |
| CP (0.1) | 0.103 | 0.111 | 0.167 | 0.167 | 0.117 | 5 |
| CP (0.3) | 0.077 | 0.111 | 0.125 | 0.104 | 0.094 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, B.; Feng, G.; Zhang, Y.; Qi, S.; Li, P.; Huang, T. Residual Saturation Effects on CO2 Migration and Caprock Sealing: A Study of Permeability and Capillary Pressure Models. Water 2023, 15, 3316. https://doi.org/10.3390/w15183316
Chu B, Feng G, Zhang Y, Qi S, Li P, Huang T. Residual Saturation Effects on CO2 Migration and Caprock Sealing: A Study of Permeability and Capillary Pressure Models. Water. 2023; 15(18):3316. https://doi.org/10.3390/w15183316
Chicago/Turabian StyleChu, Bingfei, Guanhong Feng, Yan Zhang, Shengwen Qi, Pushuang Li, and Tianming Huang. 2023. "Residual Saturation Effects on CO2 Migration and Caprock Sealing: A Study of Permeability and Capillary Pressure Models" Water 15, no. 18: 3316. https://doi.org/10.3390/w15183316
APA StyleChu, B., Feng, G., Zhang, Y., Qi, S., Li, P., & Huang, T. (2023). Residual Saturation Effects on CO2 Migration and Caprock Sealing: A Study of Permeability and Capillary Pressure Models. Water, 15(18), 3316. https://doi.org/10.3390/w15183316









