3.1. POD of Snapshots Collections Describing Falling Time
For the first time, we focused our analysis on POD decompositions obtained for snapshot collection limited to the convective sediment cloud descent. Thus, M~Tf/0.1 was chosen as equal to 15 for Dp1 (which corresponds to time Tf = 1.5 s) and 13 for Dp2 (Tf = 1.3 s).
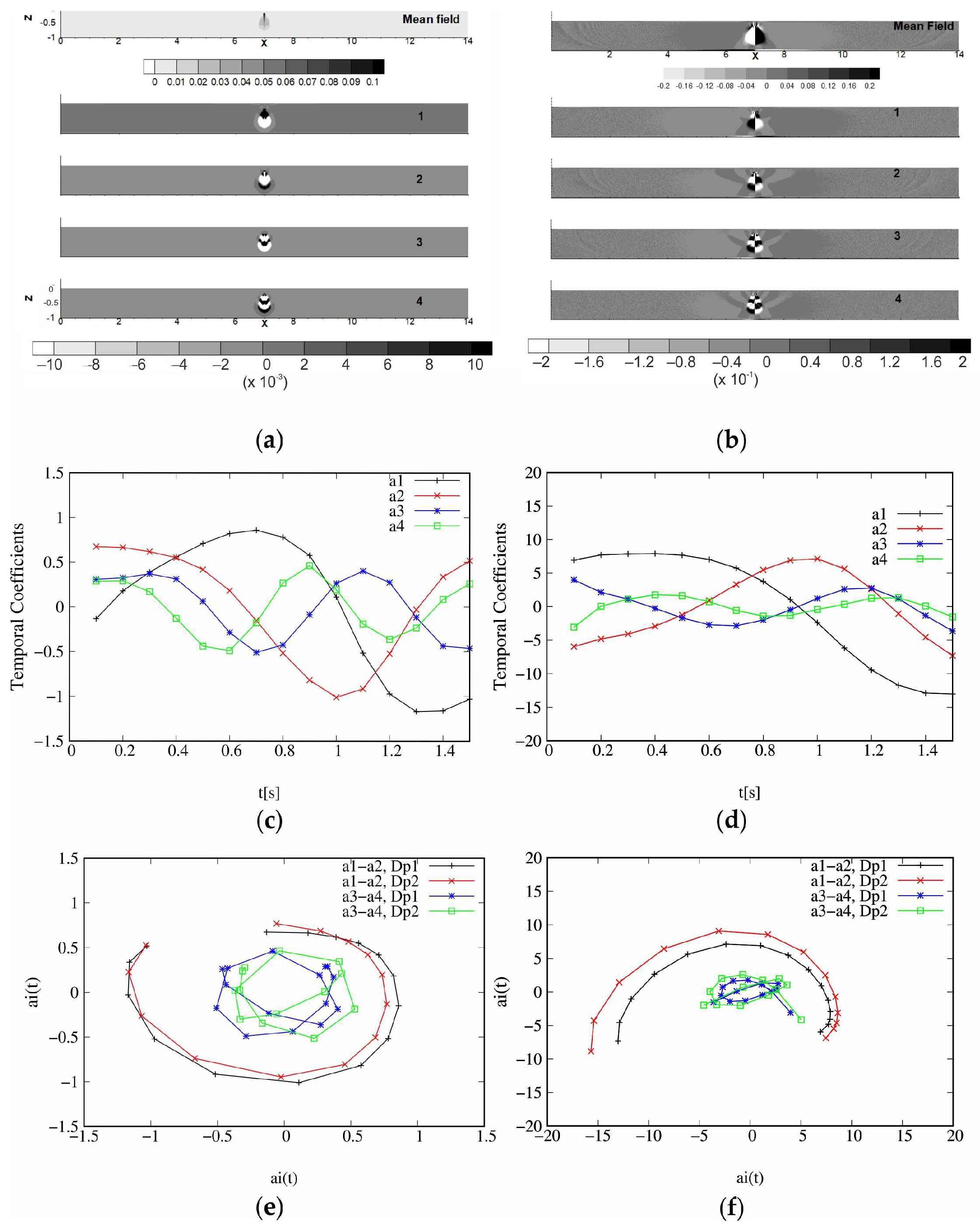
Figure 4a (i.e.,
Figure 4b) shows the mean solid volume fraction field (i.e., mean solid phase velocity field) for
Dp1 and POD
1C (i.e., for
Dp1 and POD
2C) and also the first spatial eigenfunctions extracted from the difference compared to the mean field, in other words the eigenfunctions linked to the most energetic eigenvalues.
The spatial dimensionless eigenfunctions extracted by POD
2C (cf.
Figure 4b) present strong and compact couples of counter-rotating structures or POD modes associated to the appearance and growing of symmetrical vortices during the falling of the water–sediment mixture. The number of the POD modes observed in an eigenfunction
increases with the index
k. Similarly, the eigenfunctions obtained from the POD
1C decompositions exhibit aligned and piled POD modes (cf.
Figure 4a). This arrangement is, obviously, strictly associated to the convective descent of sediment. The eigenfunctions extracted for the
Dp2 case are not shown here. The spatio-temporal modes extracted from this snapshot collections have broadly similar characteristics to the
Dp1 case. However, the increase in
Dp, leading to the enhancement of the particles’ weight, implies the elongation in the form of the POD modes.
As observed in
Figure 4c (i.e.,
Figure 4d), the four first
temporal coefficients extracted from the decomposition POD1C of the difference compared to the mean solid volume fraction
(i.e., POD2C of the difference compared to the mean solid volume velocities
) show oscillations. For
and
, the oscillations are twice as short as for
and
. The phase space projections
and
illustrate the correlation between the temporal coefficients of the most energetical eigenfunctions and their relative frequency (cf.
Figure 4e,f) (the two first eigenvalues have an energy contribution greater than 20% and for the two next ones, the individual contribution is lower than 10%. The choice was, therefore, made to verify the phasing of the dynamics between eigenmodes whose energy contributions are of the same order). The harmonious shape of curves indicates a strong correlation between the two temporal coefficients shown in the projection. For the POD
1C applied to a snapshot collection corresponding to the falling time,
has a circular shape, while
seems to have a temporal pattern close to
Tf/2.
Note that in the POD2C case, the characteristic time of the phase space projections seem to be a slightly longer that in the POD1C case. It can be inferred that the dynamics of the phenomenon have a small difference for the solid volume fraction and the solid volume velocities behaviors.
Moreover, these phase space projections reveal a similar phasing during the falling time, despite the modification of the sediment particle diameter. In other words, the dynamics of the most energetics eigenfunctions extracted from the difference compared to the mean solid volume fraction and the difference compared to the mean solid volume velocities stay unchanged.
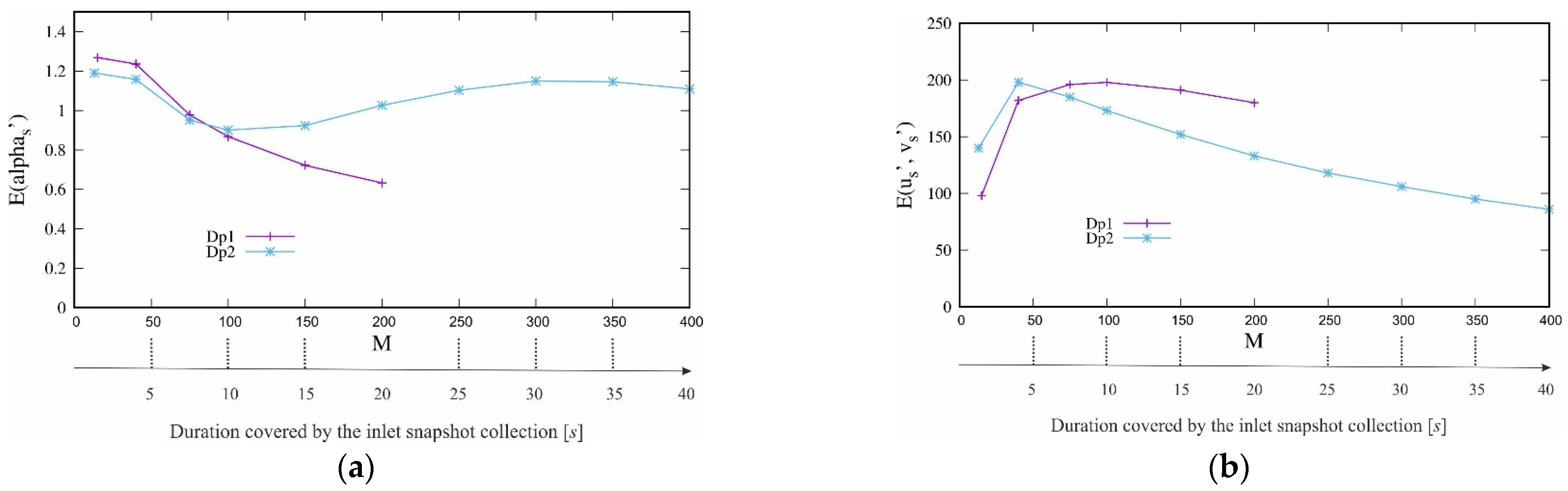
From the energetic point of view, it can be observed that (cf.
Table 3), as expected, the total kinetic energy values
and
are mainly accumulated in the first eigenvalue. The contribution
is close to ~65%, and
is close of ~42% for both POD
1C and POD
2C.
Moreover, note that only three modes are necessary to reach more than 95% of the kinetic energy and contain the dynamics of the difference compared to the mean solid volume fraction flow. The behaviour of the difference compared to the mean solid volume fraction seems to be more complex; indeed, more spatio-temporal modes are necessary to contain the same percentage of equal to 80%.
Dp has an impact on the amount of total energy extracted (cf.
Table 3). On the one hand (POD
1C), the
Dp impact on the dynamics of the volume fraction is slight (a reduction of 7%), and on the other hand (POD
2C), its impact on the velocity field reaches 30% of augmentation. Moreover, note that the distribution of the contributions of the first four values remains, with very slight differences, the same for the two particle diameters. This confirms that the dynamics of these phenomena are weakly impacted by the modification of the diameter of the particles. Thus, the particle size and its weight seem to have a modest impact on the solid volume fraction distributions during the sediment descent stage; however, this impact is most marked on the level of agitation of the solid phase velocities.
3.2. POD for Snapshot Collection Describing All the Release Phenomenon
In the following, we will focus our analysis on decompositions obtained for snapshot collections with a size
M growing from 15 (13) for the case
Dp1 (
Dp2) until 200, with
dt = 0.1 s; in other words, from a short duration of 1.5 s (1.3 s) to a duration of 20 s, describing the three steps of the release phenomenon. For
Dp2, complementary decompositions have been made for values of
M until from
M = 400 (a duration of 40 s).
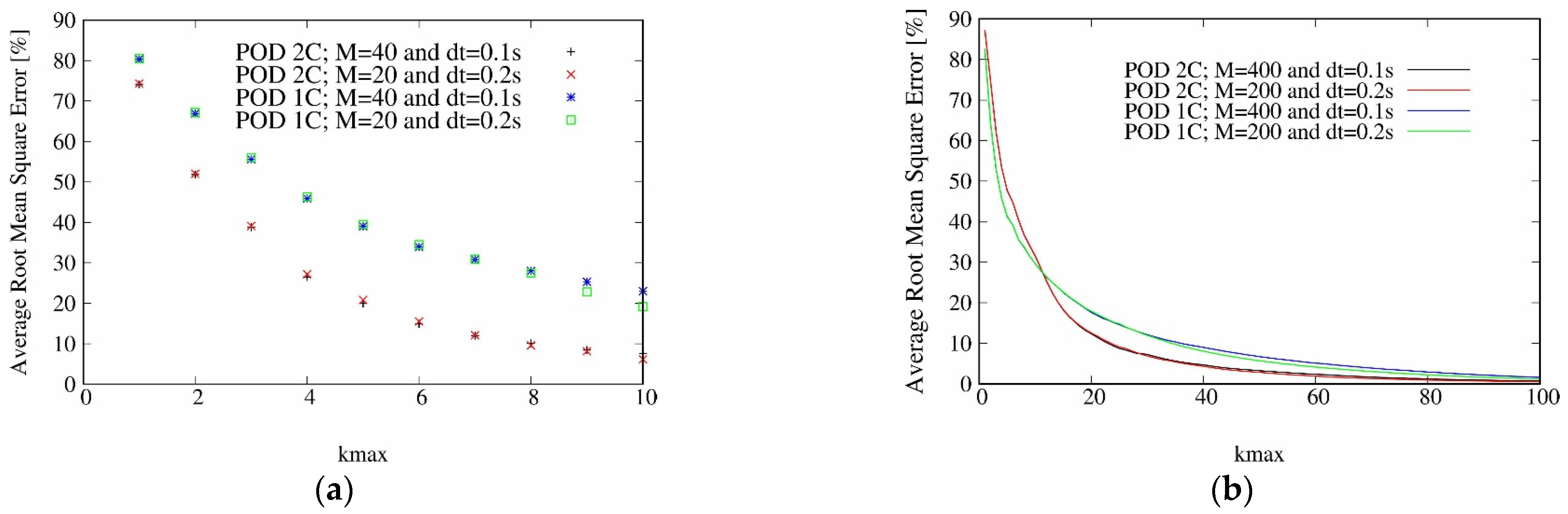
Figure 5 shows the evolution of the total energy (E) captured by POD decompositions according to the number of snapshots
M decomposed for
and for
for
Dp1 and
Dp2.
The energetic aspect has been completed by information dealing with the spatial dimensionless eigenfunctions extracted by POD
1C and POD
2C applied on snapshot collections obtained for
Dp1 and
M = 200 and a duration of 20 s (cf.
Figure 6 and
Figure 7 for
Dp1).
The contribution of the three most energetic eigenvalues to the total energies
and
are presented in the
Table 4. Note that, with the increase in the particle diameter,
stays close to ~62%, while
passes from
(for
Dp1) to 63% (for
Dp2). Thus, the particle’s size and its weight seem to have an impact on the complexity of the behavior compared to the mean solid volume fraction.
In the same way as seen in the previous paragraph, for decompositions limited to the falling time snapshot collections, a small number of spatio-temporal modes is enough to extract 95% of the total energy. In the case relative to the solid volume fraction velocities, there were 10 modes (compared to the 200 modes extracted) in the POD2C decomposition based on the parameter and 15–18 in the POD1C decomposition based on . It is clear that, for this specific set-up, it would be possible to obtain a reduced-order model covering the different steps of the sediment release.
For POD
2C applied to
and the
Dp1 case, the total kinetic energy contained by the two initial counter-rotating vortices increases until a maximum value of 198 reached
M = 100, corresponding to a total collection time of ~10 s (cf.
Figure 5b). This growth observed during (and just beyond) beyond the falling time implies an enhancement in the level of agitation of the solid phase velocities linked to the sediment descent. For snapshot collections with a size
M > 100,
slowly decreases with
M values, to reach 180 at 20 s. This implies that the level of agitation of the flow during the entire event, and more particularly during the formation of a turbidity current, become weaker. It is be reasonable to associate it with the mixing and dilution of the sediment. Thus, it is not surprising to observe (cf.
Figure 5a) for POD
1C applied to
that the energy curve decreases for
Dp1 from 1.19 to 0.86 (for a duration of 10 s) and 0.63 (for 20 s).
What is the impact of
Dp on the evolution of
according to the size (
M) of the decomposed snapshot collection? Additional decompositions resulted in
Dp2 and
M growing up to 400. Note that for
M > 200 the snapshot collections contain a lot of data relative to the turbidity current step. The slight decrease observed for
Dp1 is most drastic and earliest for the largest particle diameter case
Dp2: in this case
decreases from 198 (for a duration of 5 s) to 133 (for 20 s) and 86 (for 40 s). It seems that, as observed for the vertical descent phase of the release, the marked influence of the particle size and weight is also present during the passive transport of the sediment leading to a resistance opposed to the motion of the solid phase. In an opposite way, for the
curves (cf.
Figure 6a) the trend observed for
Dp1 and
Dp2 becomes different at around
M = 100. Indeed, while
continues to decrease for
Dp1, for the largest particle diameter case
Dp2 we observe an augmentation until ~1.1 for 20 s, and then a stabilization until 40 s. This trend is observed for POD
2C applied to inlet snapshot collections including the third step of the release phenomenon, characterized by a long and complete collapse of sediment, concentrated at the bottom (cf.
Figure 2b). Indeed, as observed by Nguyen et al. [
5], the radius of the particle bed grows and reaches nearly 4 m for a total time of 20 s in both
Dp cases. However, the collapsing of the sediment mixture differs until time
t > 15 s.
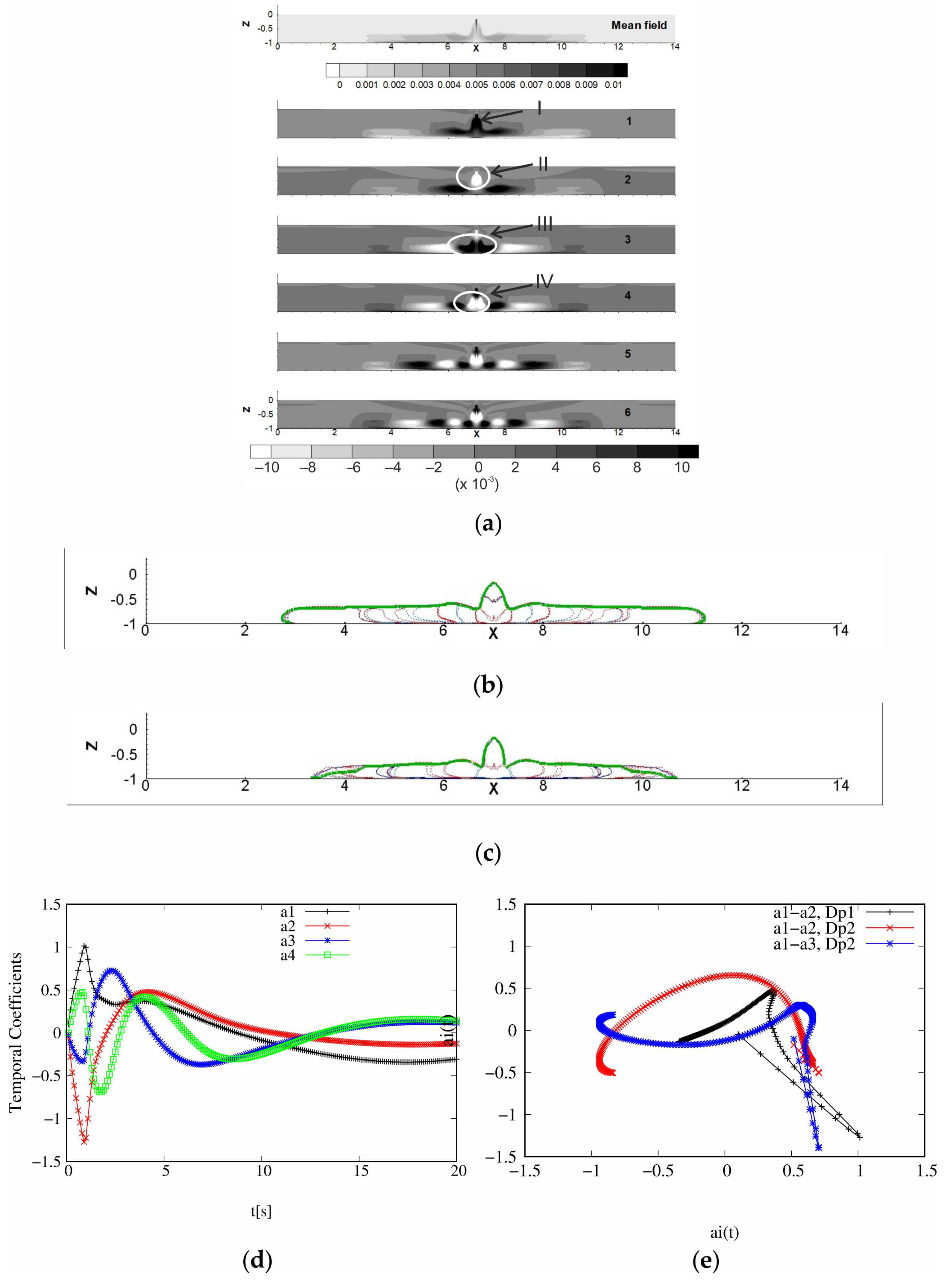
Eigenfunctions extracted for the
Dp1 case for POD
2C applied on the difference compared to the mean solid volume velocities snapshots (cf.
Figure 7a) reveal well-defined POD modes, which also support the existence of a low complexity of the dynamics. In the same way, the temporal coefficient reveals a marked temporal organization (cf.
Figure 7d,e). The marked oscillations observed during the first seconds are smoothed after the falling time. The phase space projection
present a harmonious shape. For
Dp1, the footprint of falling and collapse of the water–sediment mixture is present on the four most energetic POD
2C eigenfunctions. They put to the fore strong counter-rotating structures associated to the appearance of the initial counter-rotating vortices due to sediment falling and water–sediment mixture collapse. All these eigenfunctions present POD modes stretched on the bottom. Indeed, the opposition of the quiet water to the motion implies their stretched shape. For
k ≥ 3 other compact, counter-rotating, and symmetrical POD modes of
evolve parallel to the bottom, above the flat POD modes previously described. Their size decreases with the increasing index.
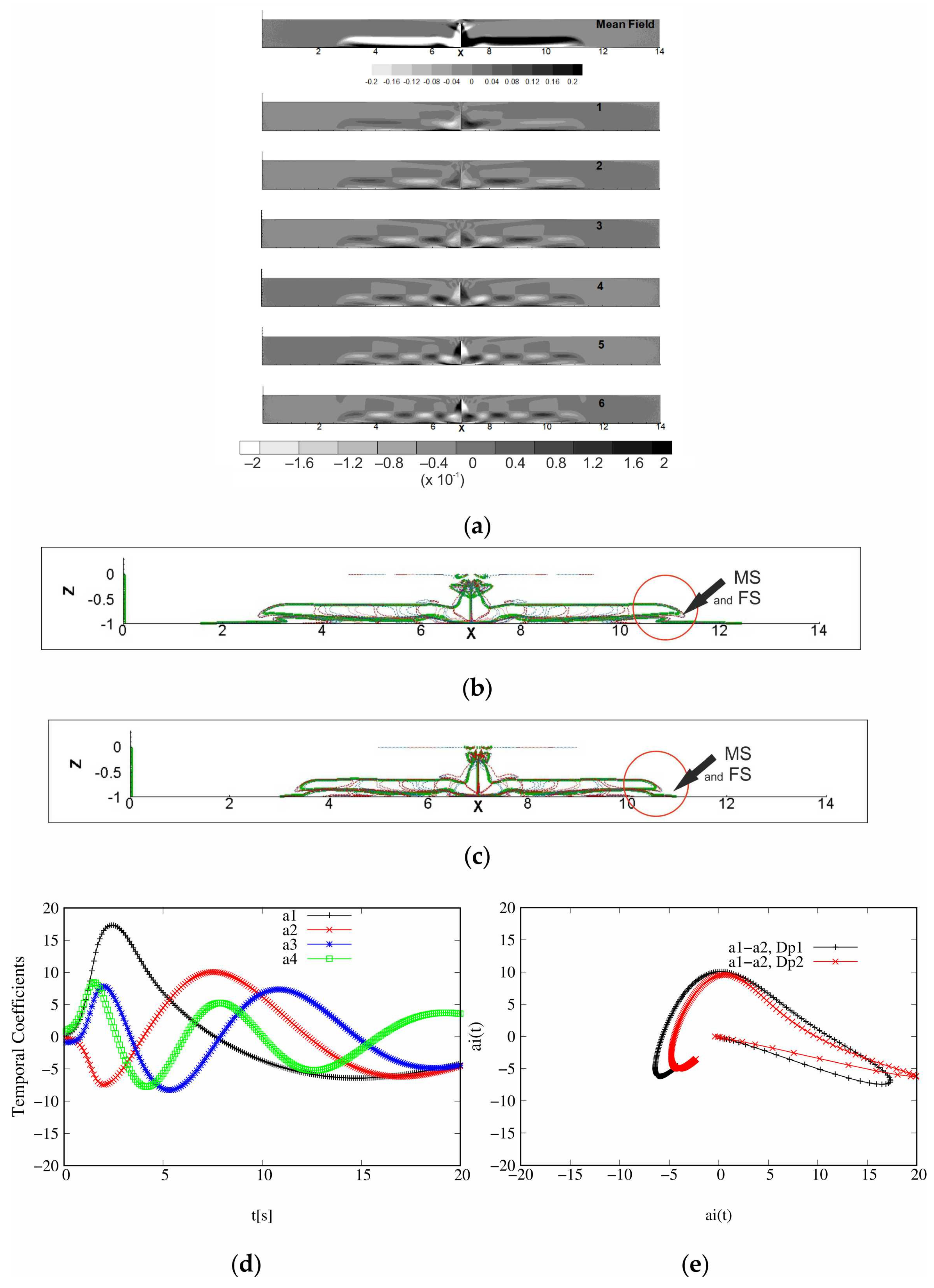
Eigenfunction sets extracted within POD
1C also reveal well-defined compact and strong POD modes. Temporal coefficient also reveals a marked temporal organization (cf.
Figure 6d,e) (as will be noticed in the following, for the snapshot collection describing all the release phenomenon, the contribution of the first eigenvalues is less marked than in the falling time snapshot collection case. The three, or even the first four, eigenvalues can have contributions of the same order. Also, drawing other curves
, … may be relevant. As can be observed (cf.
Figure 6e), the phase space projection
for the two particle diameters studied in this work have different shapes. However, it can be observed that there is a similarity between
—
Dp1 and
—
Dp2.). Note that the oscillations fade faster to reach constant values, thus, the dynamics of the solid volume fraction seem to reach a stability ahead of the dynamics of the solid volume velocity. In the
Dp1 case (cf.
Figure 6a), the two most energetic eigenfunctions, namely
and
show central POD modes (labelled I and II) strongly linked to the water–sediment mixture falling; they also present a symmetrical couple of modes dealing with the deposit of the water–sediment mixture after its collapse and the transport of the particle cloud.
seems to be also marked by collapse and the deposit of water–sediment mixture. POD modes labelled III and IV (cf.
Figure 6a) are linked to the sediment collapse, while the other ones are linked to the density current. For
Dp1, one layer of strong symmetrical POD modes on the bottom, linked to the progressive passive transport of density, appears for
with
k ≥ 5 and
k ≥ 6 for
Dp2. In the case of
Dp1, the POD modes have regular contours, while for
Dp2 they seem to be weaker and less regular. For
Dp2, the presence of a larger particle diameter
Dp implies that the POD modes (I and II) linked to the deposit of the water–sediment mixture are also present in the third eigenfunction.
To define the outline for the solid volume fraction velocities, we identified the places where there is no motion of the solid volume during all the mixture release.
Figure 7b,c show outlines superimposed on the four first eigenfunctions, respectively, for
Dp1 and
Dp2. The mean field presents two main counter-rotating and symmetrical structures (MS). The interaction with the surface leads to the appearance of flat structures (FS) along the bottom. The MS structure on the right turns in the clockwise sense (as observed in the mean solid volume fraction velocity field, cf.
Figure 7a), inducing the mixing of the flow and, thus, a water–sediment mixture resuspension. The right flat structure (FS) turns in the anti-clockwise sense and induces the retention of the water–sediment mixture. All of the most energetic eigenfunctions present the two layers of POD modes previously identified. For
Dp1, the main structures (MS) overcome and overtake the coherent creeping structures (FS) (cf.
Figure 7b). As a result, the cloud outline does not show any crushing (cf.
Figure 6b). Note that the particle cloud was identified as the place where the solid volume fraction becomes different to 0 during the mixture release. The cloud outline is the front of the particle cloud. In the opposite way, for
Dp2, the lower layer extends almost as far as the upper one (cf.
Figure 6c) and the density front of the particle cloud outlines a crushing in its extremity. Thus, it is not surprising to observe the external POD modes collapsing due to the resistance of the bottom to transport of sediments (more difficult density transport). This slump is due to the slowdown in the front density observed in the turbidity snapshots (cf.
Figure 2b). Thus, the influence of the size and the weight of the particles due to a larger
Dp induces to POD modes more marked by the settling of the water–sediment mixture after the sediment collapse.
To retrieve the settling information by the way of the POD
1C, we associate the base parameter
to the duration covered by the inlet snapshots collection, which needs to be sufficient to clearly observe the settling in the concentration field (cf.
Figure 2). POD
2C is associated with the two-dimensional base parameter
, and it presents the advantage of revealing the trends based on shorter snapshots collections than in the POD
1C because the inlet data contains the settling velocity data.
3.3. Impact of the Ambient Current
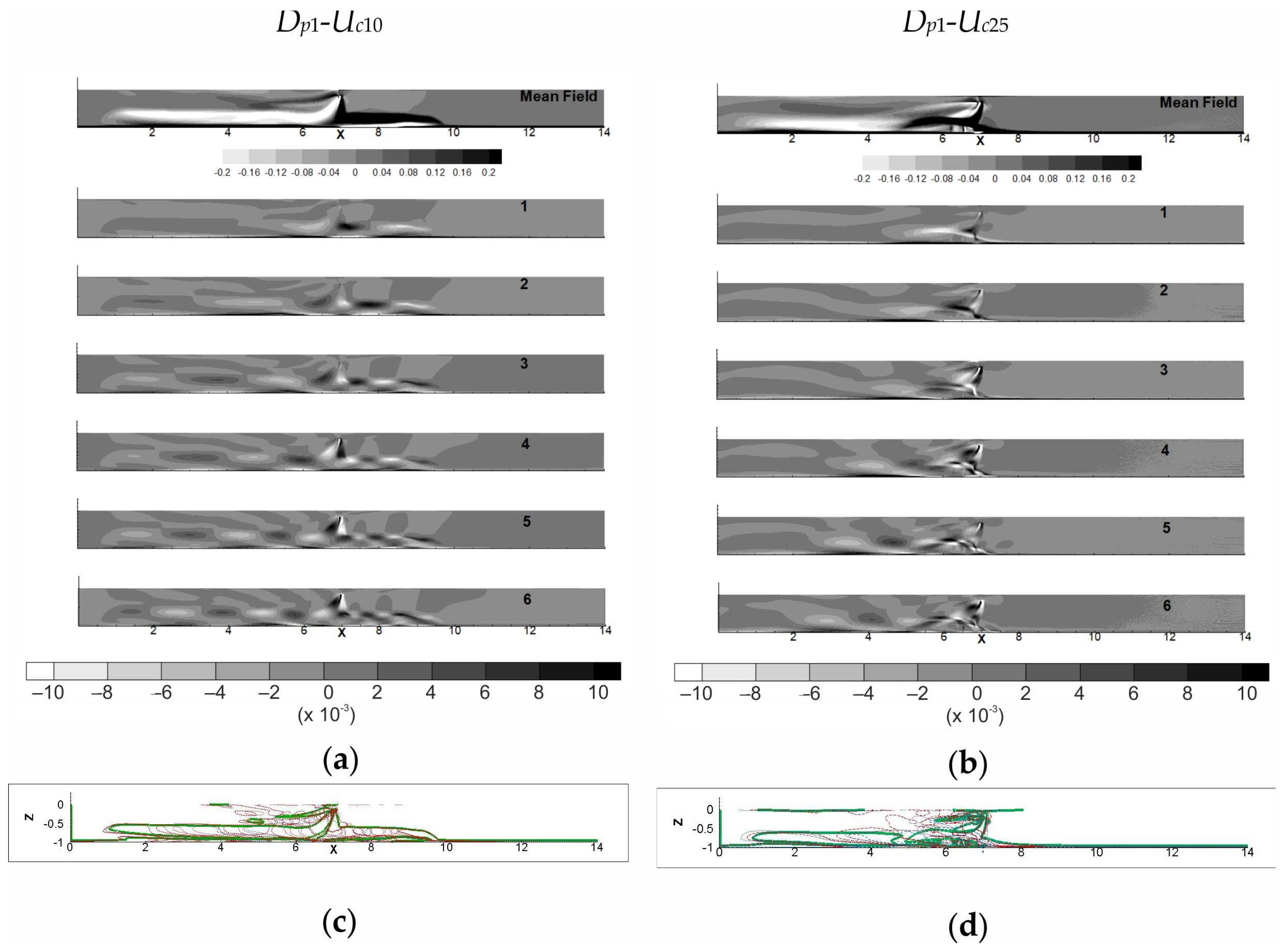
In the following section, the impact of the ambient current on the water–sediment mixture release for Dp1 will be studied. POD1C and POD2C will be applied to determine the differences between the mean solid volume fraction fields and the mean solid phase velocities fields for cases within an ambient current going from Uc = 10 cm/s to Uc = 25 cm/s (Dp1-Uc10, Dp1-Uc15, Dp1-Uc20, Dp1-Uc25).
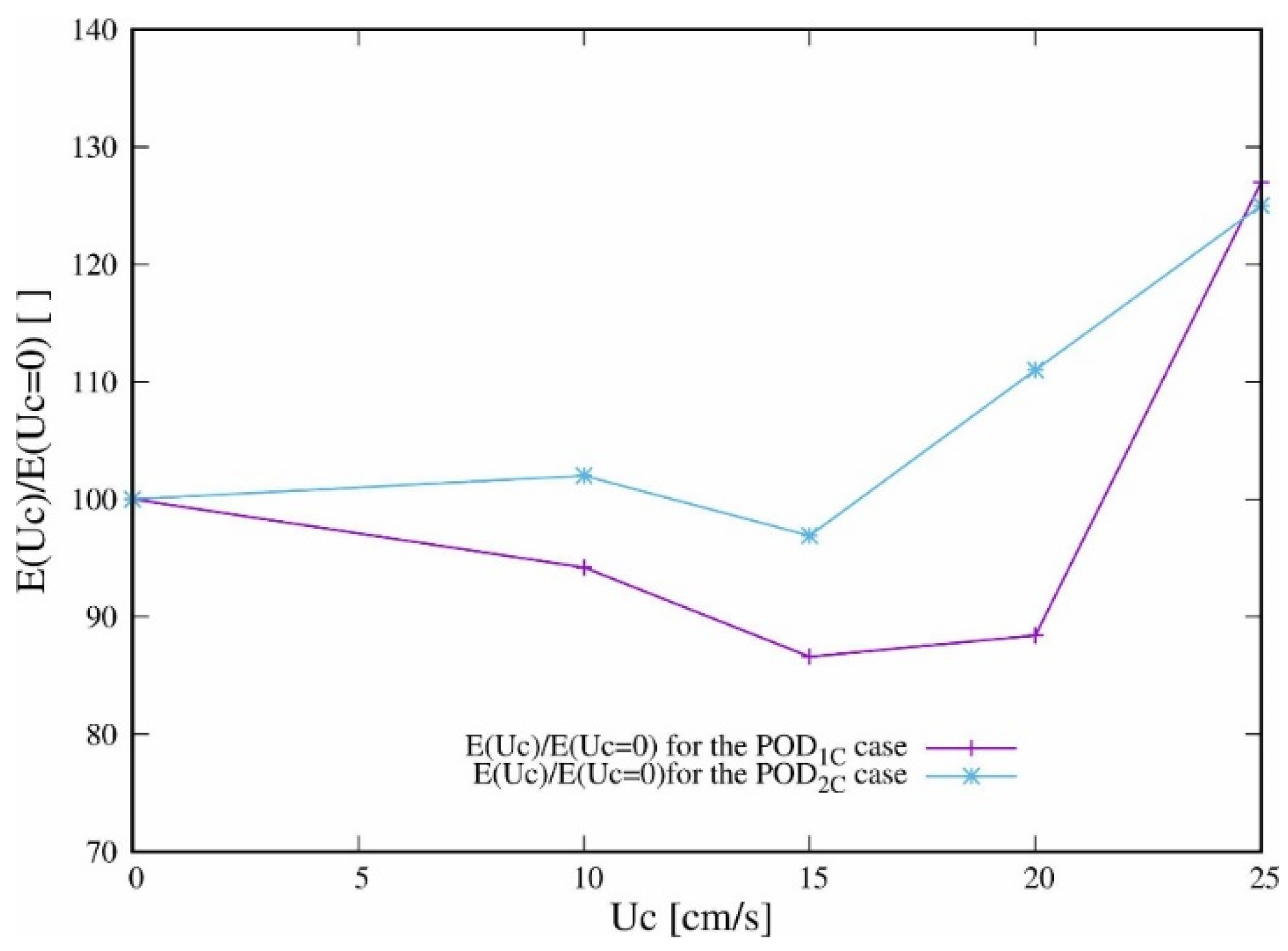
Figure 8 shows the impact of
Uc on the total energy extracted by both decompositions applied in this work for sand 1.
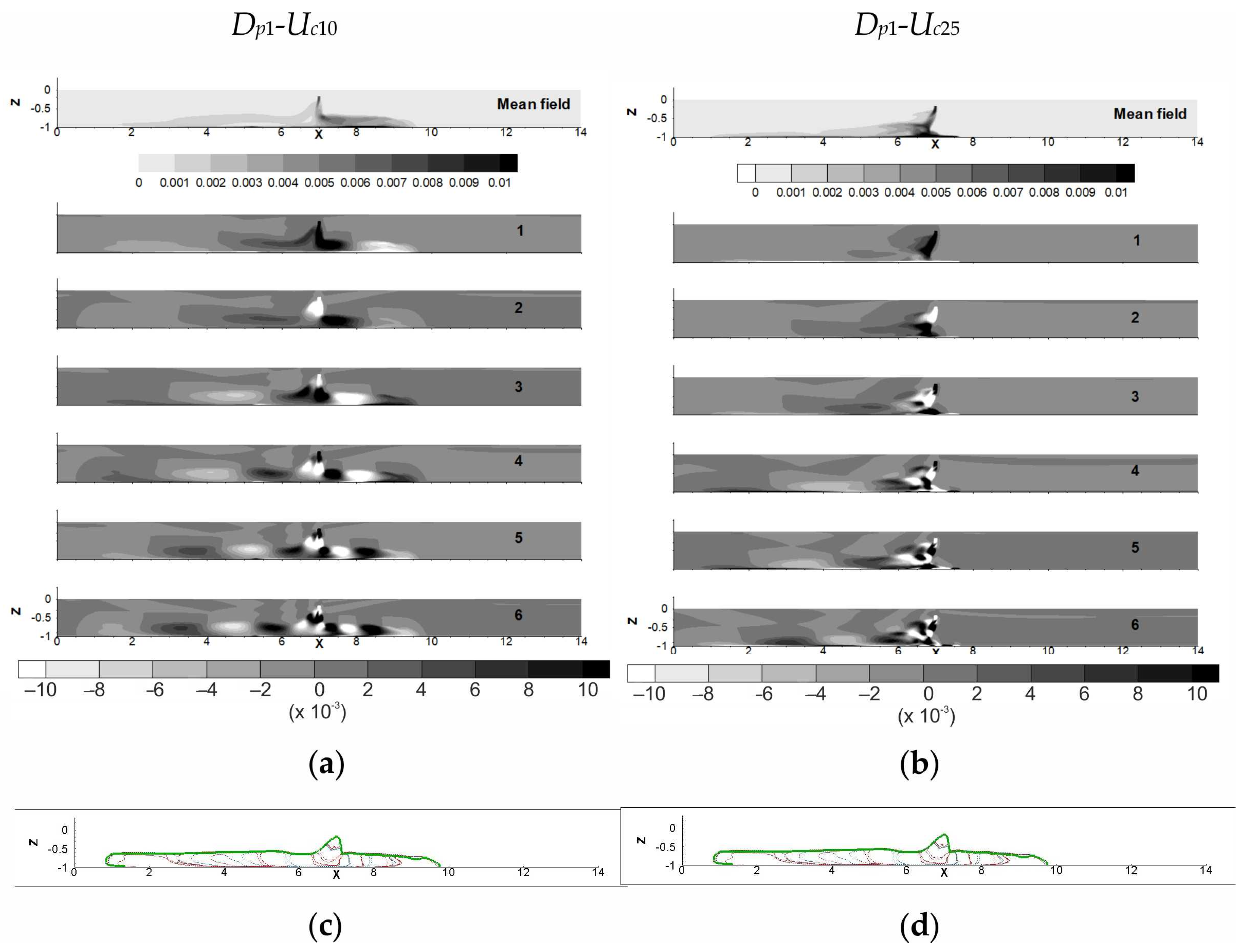
Figure 9 and
Figure 10, respectively, present eigenfunctions obtained from the
and
snapshot decompositions for the cases
Dp1-
Uc10 and
Dp1-
Uc25.
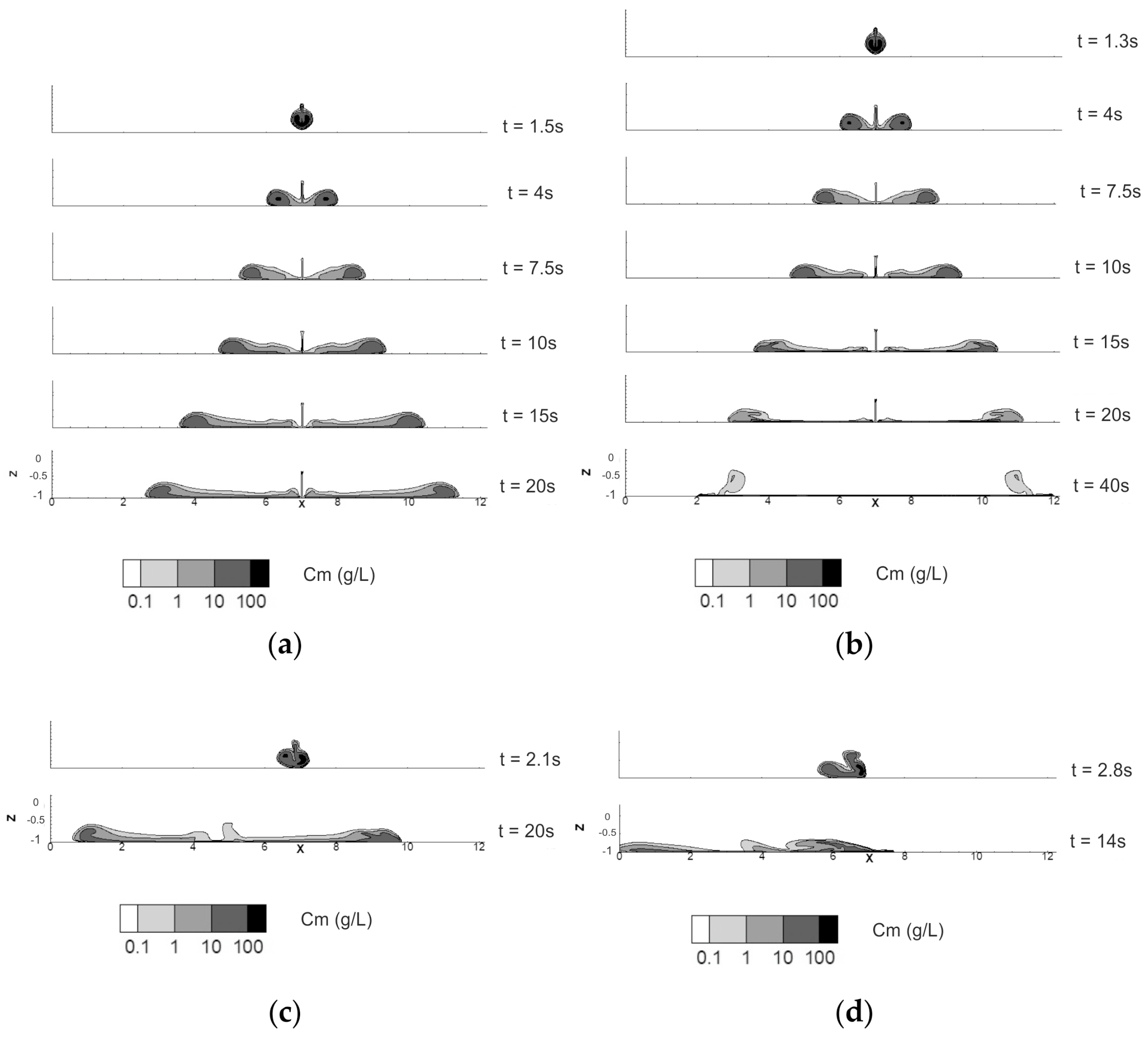
As noticed by Nguyen et al. [
4], ambient current (Uc) breaks the symmetry of the turbidity distribution during the water–sediment mixture release (cf.
Figure 2c,d). The water–sediment mixture occupation zone is shifted to the upstream direction. Thus, during 20 s after water–sediment mixture release, the downstream radius linearly increases from 4 m (for
Uc = 0 cm/s) to 10 m for (
Uc = 25 cm/s). The upstream radius linearly decreases from 4 m to nearly 0 because the propagation velocity of the front of the density current on the bottom decreases with
Uc. Thus, for the cases with ambient velocity, the number of calculation steps (
Ns) necessary to observe that the sediment cloud is out of the computation domain, but goes down with increasing ambient velocity (cf.
Table 1). To analyze and compare the water–sediment mixture release phenomenon, the size
M of the collection of decomposed snapshots is chosen to be equal to
Ns.
and
are presented in
Table 5 for different values of
Uc. As previously noticed, for
Uc = 0 cm/s and POD
2C decomposition is based on the parameter
and 10 modes (compared to the
M = 200 modes extracted), in other words 5% of
M. This ratio evolves until it reaches 7.9% with the increasing
Uc. The presence of the ambient current leads to a modest increment in the number of eigenvalues necessary to reach 95% of the total energy extracted. A similar trend is observed for results extracted by POD
1C (cf.
Table 5).
As shown in
Figure 8, the ambient current seems to have a modest impact on the amount of
extracted for
Uc values less than
Uc = 15 cm/s. Then, for strong ambient currents, we observe a modification in the evolution, as
reaches a marked augmentation of nearly 124%. The level agitation of the solid volume phase velocities suddenly increases beyond a threshold placed between 15 and 20 cm/s. It can be inferred that, below this threshold, the resistance opposed to the strength of Uc limits the development of the agitation. Note that the evolution of
shows more marked differences. Before the threshold we observe a clear decrease, then a similar augmentation of ~124% is also reached for
Uc = 20 cm/s.
Moreover, this observation completes the values of falling time (
Tf) and the water–sediment mixture release diameter when the collapse occurs, as measured by Nguyen [
4] for sand 1 and the different values of
Uc studied in this work. This author noticed an augmentation of both values with the increase in
Uc; however, this augmentation is clearly less marked when the ambient current reaches 20 cm/s.
As can be seen in
Figure 9 and
Figure 10, it appears that the ambient current presence breaks the symmetry of the POD modes in all the eigenfunctions for both POD decompositions. For
Dp1-
Uc10, the stretching of upstream POD modes of the eigenfunctions extracted by POD
2C stays slight (
Figure 10a). The increase in the
Uc value leads to a decrease in the size of the POD modes, their gradual stretching and distortion and their displacement in the left direction. In other words, as shown in
Figure 10, according to the strength of the ambient current the dynamics of the solid volume fraction can exhibit: a regime within a marked spatial organization and POD modes placed on both sides of the water–sediment mixture injection point (
Dp1-
Uc10), or a regime showing a heavy loss of the spatial organization of the eigenfunctions and all the POD modes placed on the left of water–sediment mixture injection point (
Dp1-
Uc25). The eigenfunctions extracted by POD
2C for different values of
Uc, and not presented here, highlight that the transition between the two regimes occurs at a value between 15 and 20 cm/s. Obviously, this shape of the POD modes reflects the presence of shear observed on turbidity snapshots (cf.
Figure 2c,d). Note that at the early steps of time, turbidity isocontours have regular shapes; later, when sediments evolve on the bottom, turbidity presents irregular contours. With the increase in the
Uc value, the shearing and the irregularity of the turbidity contours appears at an earlier time after the sediment injection. A similar impact of an ambient current can be also observed on the eigenfunctions obtained from POD
1C decomposition of the difference compared to the mean solid volume fraction snapshots. Indeed, for
Dp1-
Uc10 (cf.
Figure 9), POD modes of density transport placed downstream the point of injection of the water–sediment mixture are slightly distorted, and the deformation is more marked for upstream POD modes. These collapses and distortions are due to the resistance of the bottom to the density transport against the direction of the ambient current. It can be also shown that the POD modes placed upstream have more important intensities compared to the downstream ones. Obviously, this intensity distribution reflects that sediment is pushed by the ambient current to the left. Changes from
Uc = 10 cm/s to
Uc = 25 cm/s imply an amplification of the loss of the spatial organization of the solid phase volume fraction, in other words the destruction of the coherency of the particle’s clouds.
Figure 9c and
Figure 10c (i.e.,
Figure 9d and
Figure 10d) show the POD mode outlines (solid line) superimposed to the four first eigenfunctions for
Dp1-
Uc10 (i.e.,
Dp1-
Uc25). As previously noticed, in all the eigenfunctions, the POD modes have been displaced to the left, pushed by the ambient current. For
Uc = 25 cm/s, the higher value of ambient current studied in this paper, all the POD modes observed in both sets of eigenfunctions are strictly placed on the left of the water–sediment mixture injection point.
In spite of the displacement towards the left, the front of the density cloud and POD mode outlines observed for
Dp1-
Uc10 (cf.
Figure 9c and
Figure 10c) have strong similarities with the features found without the ambient current. A different behavior is noted for
Uc = 25 cm/s, similar to the one previously shown for the
Dp2-
Uc0 case. A lower layer of flat creeping structures (FS) extends almost as far as the main and upper structures (MS) (cf.
Figure 10d). Thus, the downstream front of the particle cloud outline shows a crushing linked to the resistance of the bottom against the sediment transport. Note that the sediment plume observed in
Figure 2d (
t = 14 s) has a very low concentration.