A Novel Intelligent Model for Monthly Streamflow Prediction Using Similarity-Derived Method
Abstract
:1. Introduction
2. Problem Formulation and Solution Techniques
2.1. Data Processing
2.2. Similarity Parameters
- 1.
- The base magnitude assigned to streamflow, being no more than 1.0:
- 2.
- Zero-weights assigned to streamflow unknown in the forecast period:
- 3.
- Zero-weights assigned to rainfalls unavailable in the forecast period:
2.3. Similarity Derivation Model
2.4. Brief Introduction of the Methods for Comparison
3. Case Studies
3.1. Research Domain and Data
3.2. Parameters in Calibration
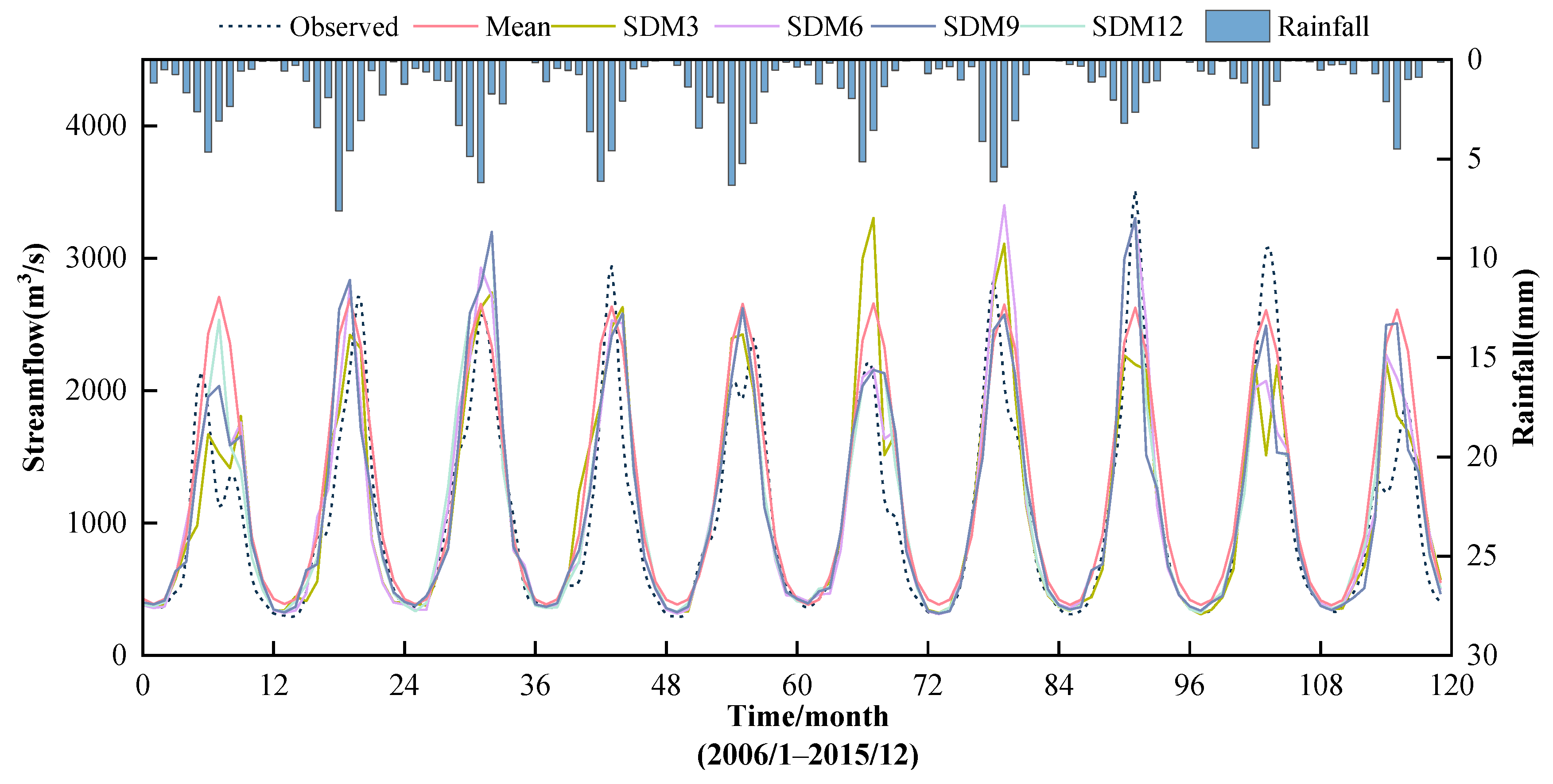
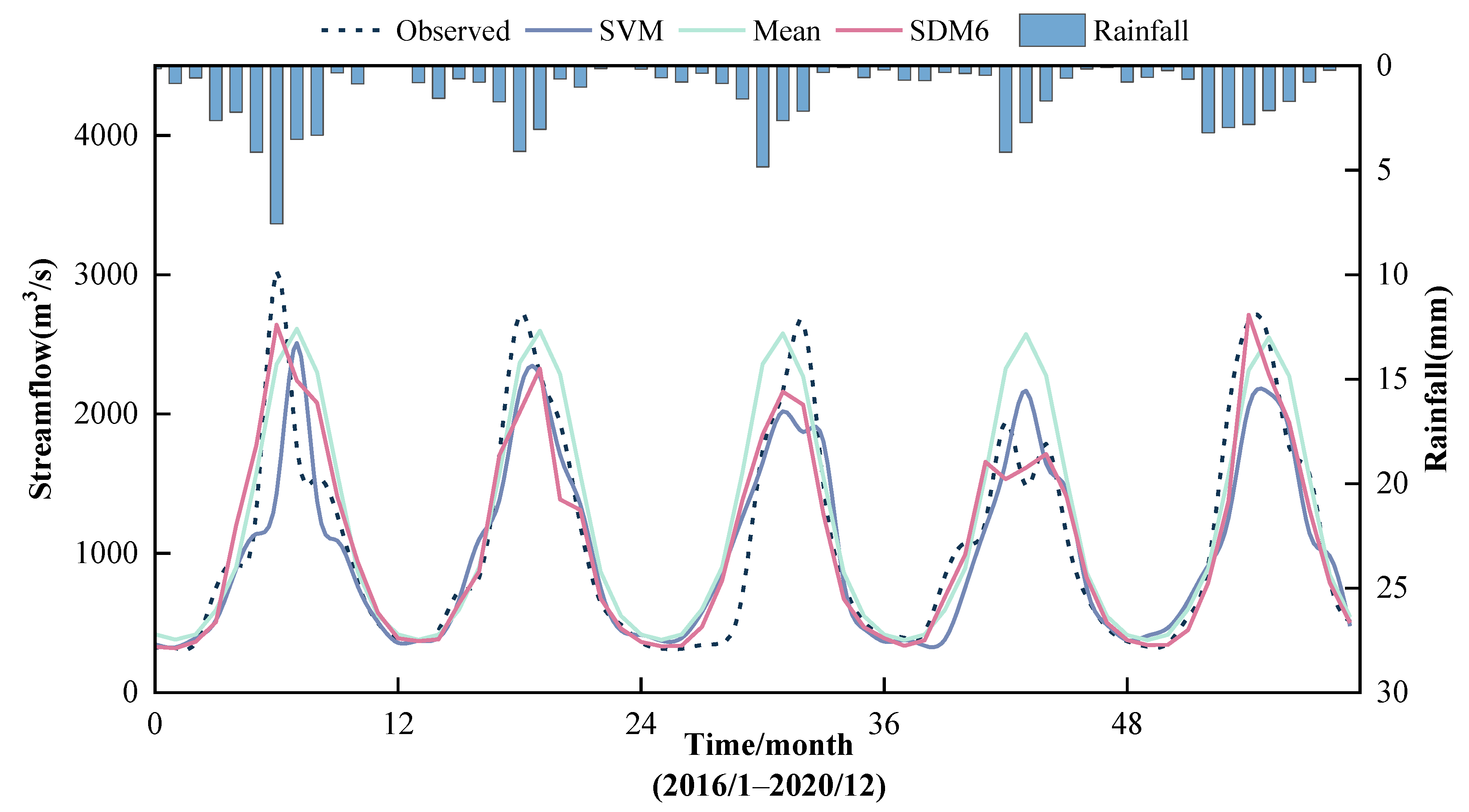
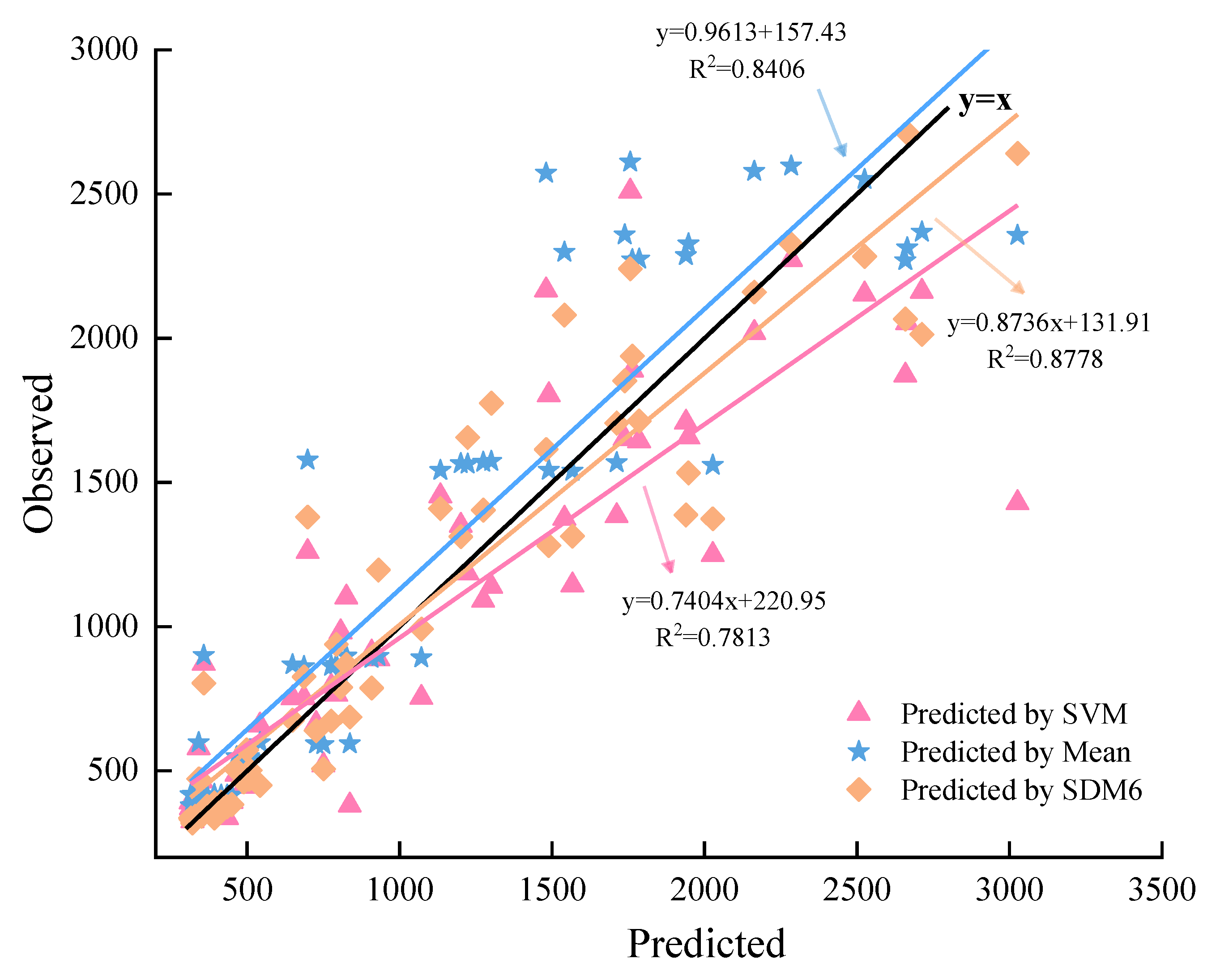
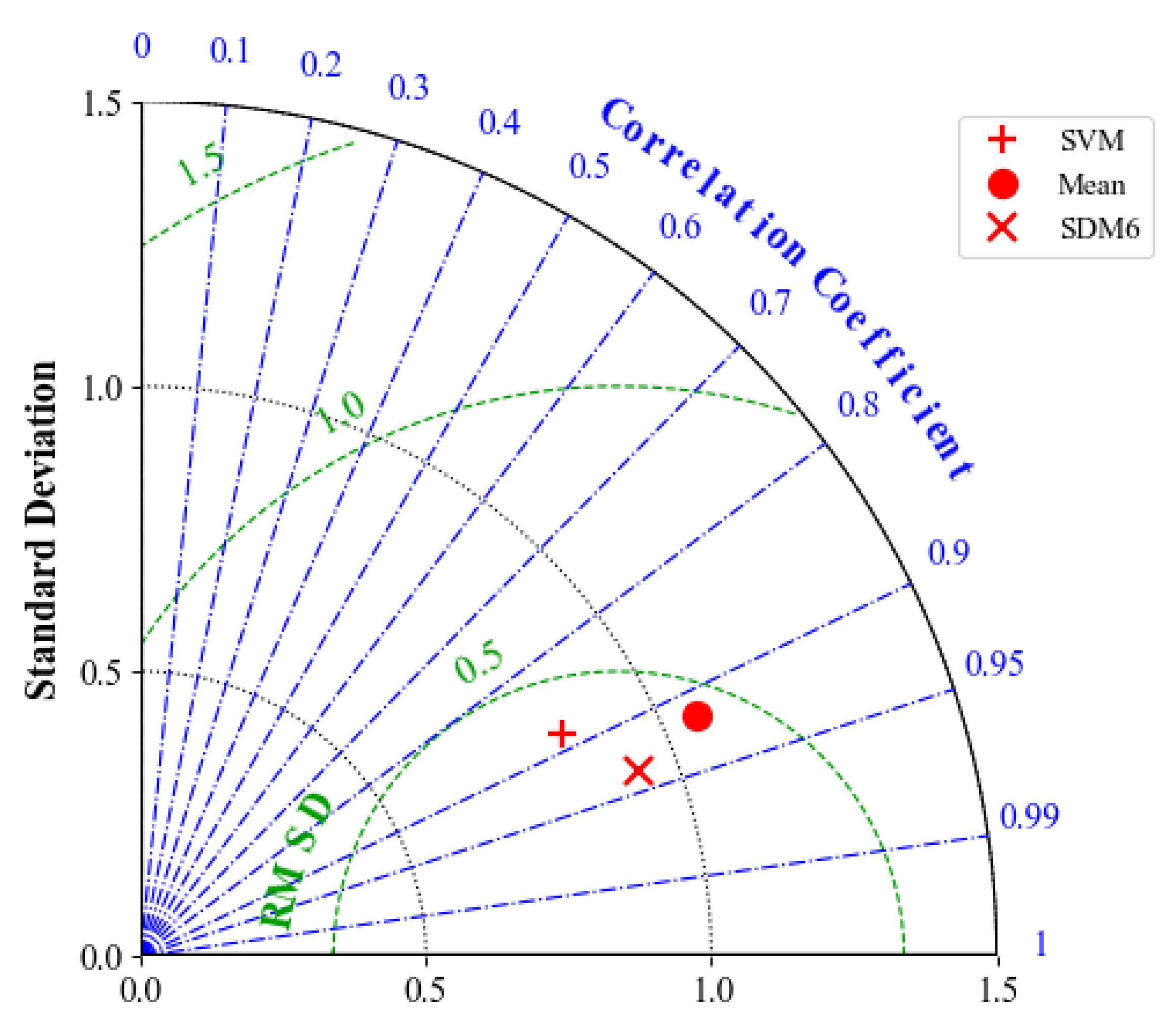
3.3. Results in Verification
3.4. Results in Validation
4. Conclusions
- The assessment during a verification period on different reference periods (3, 6, 9, and 12) reveals that SDM6 with a reference period of six months demonstrates the best performance.
- SDM6 during a validation period achieves 261.97 m3/s in RMSE, 16.01% in MAPE, and 87.74% in NSE, improving the Mean model by 79.9 m3/s in RMSE, 6.07% in MAPE, and 8.62% in NSE, and the SVM by 53.65 m3/s, 0.24%, and 5.53%, respectively.
- (1)
- The model requires relatively long historical runoff data, making it unsuitable for basins with short or discontinuous data records.
- (2)
- The model’s solving process requires multiple calls to the solver, leading to slower computation speed.
- (1)
- Future work can explore optimizing additional variables, including the number of similar years and forecast months, to further investigate the model’s performance.
- (2)
- Further investigation is warranted to understand the influence of historical rainfall on identifying the similar years used to derive the forecast streamflow.
- (3)
- The model and procedures may also be extended to encompass daily, weekly, and annual streamflow predictions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Napolitano, G.; Serinaldi, F.; See, L. Impact of EMD decomposition and random initialisation of weights in ANN hindcasting of daily stream flow series: An empirical examination. J. Hydrol. 2011, 406, 199–214. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, J.; Qin, H.; Zou, Q.; Li, Q. Monthly streamflow forecasting based on improved support vector machine model. Expert Syst. Appl. 2011, 38, 13073–13081. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Cheng, C.T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Wang, X.; Engel, B.; Yuan, X.; Yuan, P. Variation Analysis of Streamflows from 1956 to 2016 Along the Yellow River, China. Water 2018, 10, 1231. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Wang, Y.; Chen, Y. The study on the runoff change based on the heuristic segmentation algorithm and approximate entropy. Zhongshan Daxue Xuebao/Acta Sci. Natralium Univ. Sunyatseni 2014, 53, 154–160. [Google Scholar]
- Wang, W.C.; Xu, D.M.; Chau, K.W.; Chen, S. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Chow, F.K.; Kollet, S.J. The groundwater-land-surface-atmosphere connection: Soil moisture effects on the atmospheric boundary layer in fully-coupled simulations. Adv. Water Resour. 2007, 30, 2447–2466. [Google Scholar] [CrossRef]
- Yetemen, O.; Istanbulluoglu, E.; Flores-Cervantes, J.H.; Vivoni, E.R.; Bras, R.L. Ecohydrologic role of solar radiation on landscape evolution. Water Resour. Res. 2015, 51, 1127–1157. [Google Scholar] [CrossRef]
- Sulis, M.; Paniconi, C.; Marrocu, M.; Huard, D.; Chaumont, D. Hydrologic response to multimodel climate output using a physically based model of groundwater/surface water interactions. Water Resour. Res. 2012, 48, W12510. [Google Scholar] [CrossRef]
- Ebel, B.A.; Mirus, B.B. Disturbance hydrology: Challenges and opportunities. Hydrol. Process. 2014, 28, 5140–5148. [Google Scholar] [CrossRef]
- Van Roosmalen, L.; Sonnenborg, T.O.; Jensen, K.H. Impact of climate and land use change on the hydrology of a large-scale agricultural catchment. Water Resour. Res. 2009, 45, W00A15. [Google Scholar] [CrossRef]
- Pierini, N.A.; Vivoni, E.R.; Robles-Morua, A.; Scott, R.L.; Nearing, M.A. Using observations and a distributed hydrologic model to explore runoff thresholds linked with mesquite encroachment in the Sonoran Desert. Water Resour. Res. 2014, 50, 8191–8215. [Google Scholar] [CrossRef]
- Partington, D.; Brunner, P.; Simmons, C.T.; Werner, A.D.; Therrien, R.; Maier, H.R.; Dandy, G.C. Evaluation of outputs from automated baseflow separation methods against simulated baseflow from a physically based, surface water-groundwater flow model. J. Hydrol. 2012, 458–459, 28–39. [Google Scholar] [CrossRef]
- Bathurst, J.C.; O’Connell, P.E. Future of distributed modelling: The Systeme Hydrologique Europeen. Hydrol. Process. 1992, 6, 265–277. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, M.K.; Chatterjee, C.; Mishra, A. Reservoir Inflow Forecasting Using Ensemble Models Based on Neural Networks, Wavelet Analysis and Bootstrap Method. Water Resour. Manag. 2015, 29, 4863–4883. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Yin, Z.; Yang, L.; Singh, V.P. Two-phase extreme learning machines integrated with the complete ensemble empirical mode decomposition with adaptive noise algorithm for multi-scale runoff prediction problems. J. Hydrol. 2019, 570, 167–184. [Google Scholar] [CrossRef]
- Raman, H.; Sunilkumar, N. Multivariate modelling of water resources time series using artificial neural networks. Hydrol. Sci. J. 1995, 40, 145–163. [Google Scholar] [CrossRef]
- Afan, H.A.; El-Shafie, A.; Yaseen, Z.M.; Hameed, M.M.; Wan Mohtar, W.H.M.; Hussain, A. ANN Based Sediment Prediction Model Utilizing Different Input Scenarios. Water Resour. Manag. 2015, 29, 1231–1245. [Google Scholar] [CrossRef]
- Moreido, V.; Gartsman, B.; Solomatine, D.P.; Suchilina, Z. How Well Can Machine Learning Models Perform without Hydrologists? Application of Rational Feature Selection to Improve Hydrological Forecasting. Water 2021, 13, 1696. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, Y.C. A counterpropagation fuzzy-neural network modeling approach to real time streamflow prediction. J. Hydrol. 2001, 245, 153–164. [Google Scholar] [CrossRef]
- Ni, Q.; Wang, L.; Ye, R.; Yang, F.; Sivakumar, M. Evolutionary modeling for streamflow forecasting with minimal datasets: A case study in the West Malian River, China. Environ. Eng. Sci. 2010, 27, 377–385. [Google Scholar] [CrossRef]
- Zhan, X.; Qin, H.; Liu, Y.; Yao, L.; Xie, W.; Liu, G.; Zhou, J. Variational Bayesian Neural Network for Ensemble Flood Forecasting. Water 2020, 12, 2740. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, X.; Xu, Y.; Xi, D.; Zhang, Y.; Zheng, X. An EMD-Based Chaotic Least Squares Support Vector Machine Hybrid Model for Annual Runoff Forecasting. Water 2017, 9, 153. [Google Scholar] [CrossRef]
- Coulibaly, P.; Baldwin, C.K. Nonstationary hydrological time series forecasting using nonlinear dynamic methods. J. Hydrol. 2005, 307, 164–174. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Wu, W.; Jiang, Y.; Chu, Q.; Meng, X. A classification-based deep belief networks model framework for daily streamflow forecasting. J. Hydrol. 2021, 595, 125967. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Kahya, E. A Pareto-optimal moving average multigene genetic programming model for daily streamflow prediction. J. Hydrol. 2017, 549, 603–615. [Google Scholar] [CrossRef]
- Maass, A.; Hufschmidt, M.M.; Dorfman, R.; Thomas Jr, H.A.; Marglin, S.A.; Fair, G.M. 12. Mathematical Synthesis of Streamflow Sequences for the Analysis of River Basins by Simulation. In Design of Water-Resource Systems: New Techniques for Relating Economic Objectives, Engineering Analysis, and Governmental Planning; Harvard University Press: Cambridge, MA, USA, 1962. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rojo, J.D.; Carvajal, L.F.; Velasquez, J.D. Streamflow Prediction using a Forecast Combining System. IEEE Lat. Am. Trans. 2015, 13, 1035–1040. [Google Scholar] [CrossRef]
- Fan, H.; He, D.M.; Wang, H.L. Environmental consequences of damming the mainstream Lancang-Mekong River: A review. Earth Sci. Rev. 2015, 146, 77–91. [Google Scholar] [CrossRef]
- Liu, J.G.; Chen, D.L.; Mao, G.Q.; Irannezhad, M.; Pokhrel, Y. Past and Future Changes in Climate and Water Resources in the Lancang-Mekong River Basin: Current Understanding and Future Research Directions. Engineering 2022, 13, 144–152. [Google Scholar] [CrossRef]

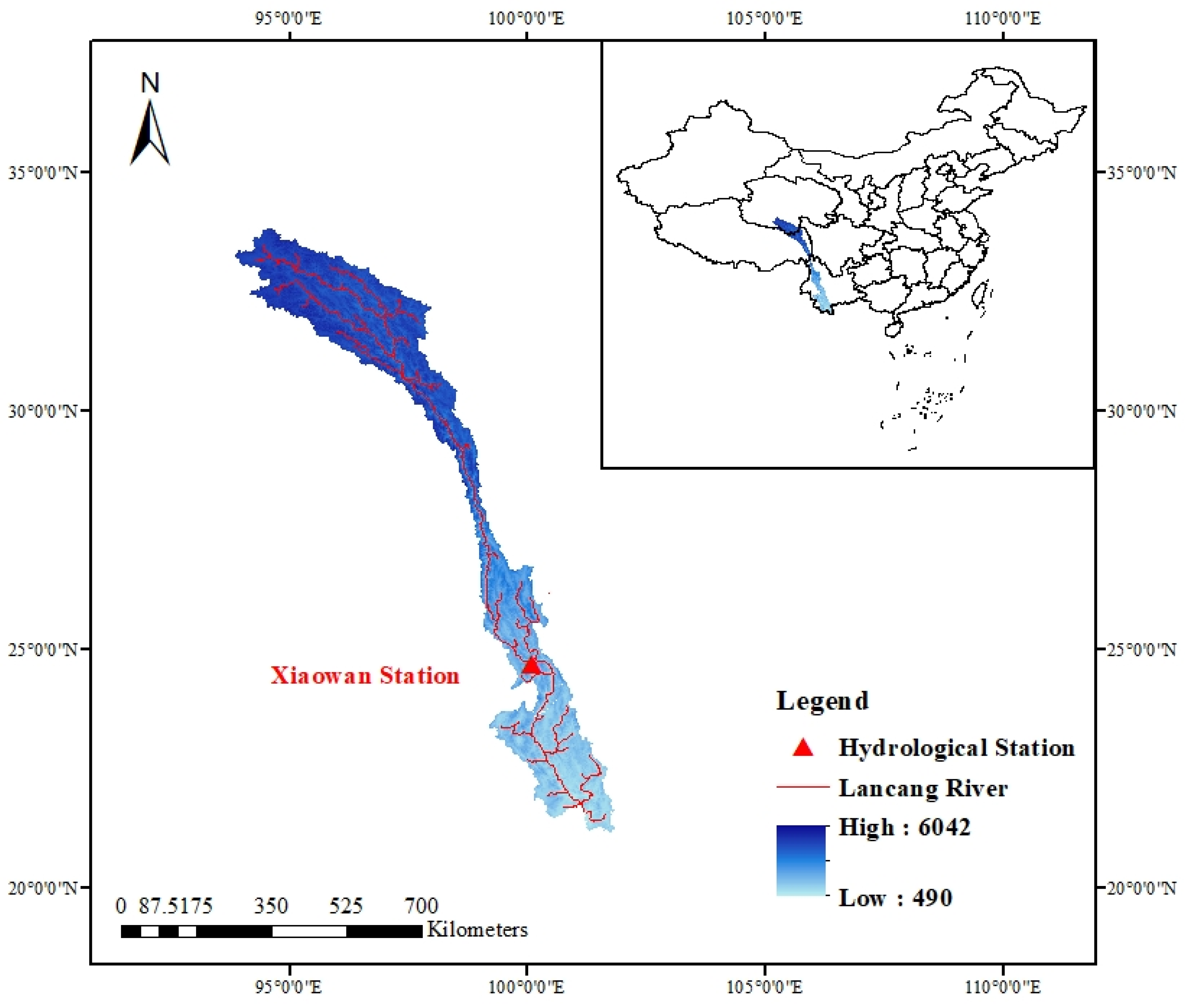
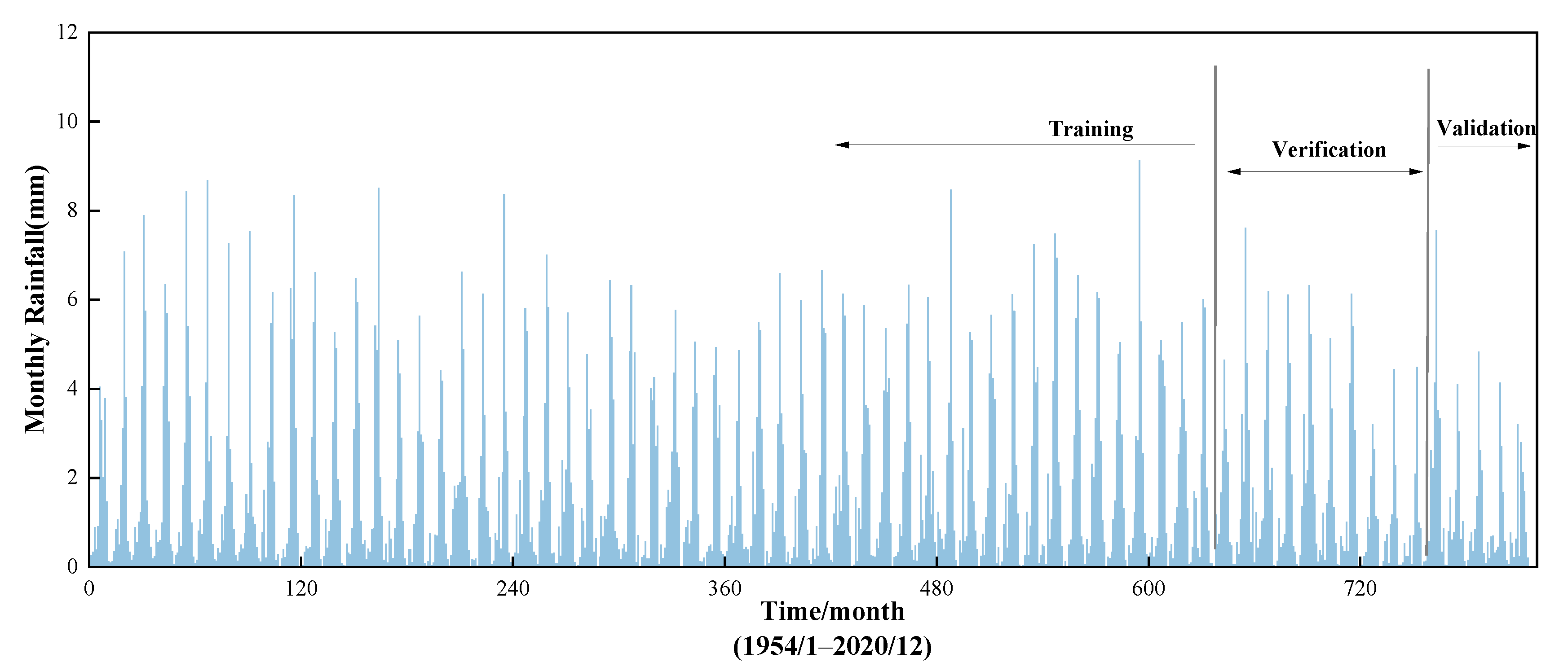
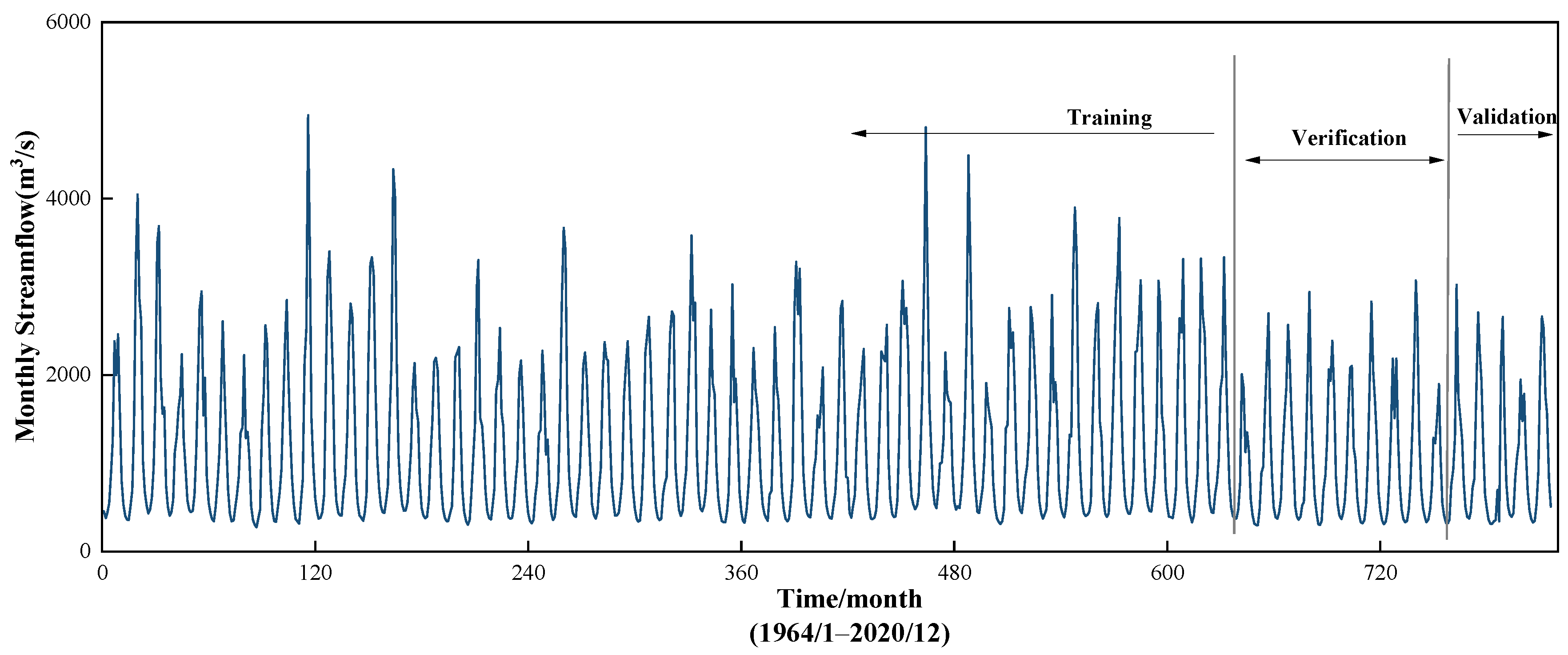
| Station | Period | Max (m3/s) | Min (m3/s) | Mean (m3/s) | Cv | Cs |
|---|---|---|---|---|---|---|
| Xiaowan | 1954–2020 | 4948.0 | 275.0 | 1201.55 | 0.73 | 1.15 |
| Ref (t) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Jan | Apr | Jul | Oct | Jan | Apr | Jul | Oct | |
| m-6 | 0 | 0 | 0 | 0 | 0.7 | 3296.6 | 5954 | 0 |
| m-5 | 1.10 × 10−5 | 2.90 × 10−3 | 7.60 × 10−1 | 0 | 0.4 | 0 | 0 | 0 |
| m-4 | 1.60 × 10−5 | 0 | 0 | 7.50 × 10−4 | 1.4 | 0 | 0 | 0 |
| m-3 | 8.80 × 10−5 | 0 | 0 | 1.20 × 10−2 | 0 | 0 | 0 | 0 |
| m-2 | 0 | 0 | 0 | 4.50 × 10−4 | 0 | 0 | 0 | 26.8 |
| m-1 | 4.10 × 10−3 | 3.30 × 10−1 | 7.60 × 10−3 | 9.40 × 10−4 | 51.1 | 772.1 | 1401.9 | 97.4 |
| Ref (t) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Jan | Apr | Jul | Oct | Jan | Apr | Jul | Oct | |
| m-9 | 1.80 × 10−3 | 0 | 0 | 0 | 0 | 0 | 0 | 1491.6 |
| m-8 | 1.00 × 10−3 | 0 | 0 | 9.90 × 10−2 | 17.2 | 0 | 0 | 1505.1 |
| m-7 | 0 | 3.60 × 10−5 | 0 | 0 | 0 | 34.5 | 60,073.3 | 559 |
| m-6 | 0 | 0 | 0 | 0 | 3.6 | 337.9 | 11,402.2 | 0 |
| m-5 | 8.10 × 10−5 | 4.10 × 10−1 | 9.40 × 10−1 | 0 | 1.7 | 0 | 0 | 0 |
| m-4 | 1.60 × 10−4 | 0 | 0 | 2.70 × 10−3 | 11.7 | 0 | 0 | 0 |
| m-3 | 5.50 × 10−4 | 0 | 0 | 3.20 × 10−3 | 0 | 0 | 0 | 0 |
| m-2 | 0 | 0 | 0 | 1.30 × 10−3 | 0 | 0 | 0 | 31.5 |
| m-1 | 2.40 × 10−2 | 3.10 × 10−2 | 9.90 × 10−3 | 3.00 × 10−3 | 156.7 | 69 | 1804.5 | 330.9 |
| Indicators | MEAN | SDM3 | SDM6 | SDM9 | SDM12 |
|---|---|---|---|---|---|
| RMSE (m3/s) | 374.47 | 371.31 | 359.22 | 370.57 | 373.14 |
| MAPE (%) | 23.82 | 18.59 | 18.46 | 18.39 | 18.3 |
| NSE (%) | 75.13 | 75.55 | 77.12 | 75.65 | 75.31 |
| Indicators | Mean | SVM | SDM6 |
|---|---|---|---|
| RMSE (m3/s) | 341.87 | 315.62 | 261.97 |
| MAPE (%) | 22.98 | 16.25 | 16.01 |
| NSE (%) | 79.12 | 82.21 | 87.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Cheng, M.; Zhang, H.; Xia, W.; Luo, X.; Wang, J. A Novel Intelligent Model for Monthly Streamflow Prediction Using Similarity-Derived Method. Water 2023, 15, 3270. https://doi.org/10.3390/w15183270
Xu Z, Cheng M, Zhang H, Xia W, Luo X, Wang J. A Novel Intelligent Model for Monthly Streamflow Prediction Using Similarity-Derived Method. Water. 2023; 15(18):3270. https://doi.org/10.3390/w15183270
Chicago/Turabian StyleXu, Zifan, Meng Cheng, Hong Zhang, Wang Xia, Xuhan Luo, and Jinwen Wang. 2023. "A Novel Intelligent Model for Monthly Streamflow Prediction Using Similarity-Derived Method" Water 15, no. 18: 3270. https://doi.org/10.3390/w15183270






