Stormwater Uptake in Sponge-Like Porous Bodies Surrounded by a Pond: A Fluid Mechanics Analysis
Abstract
:1. Introduction
2. Mathematical Modelling of the Water Uptake of the Surrounding Pond for Different Conditions
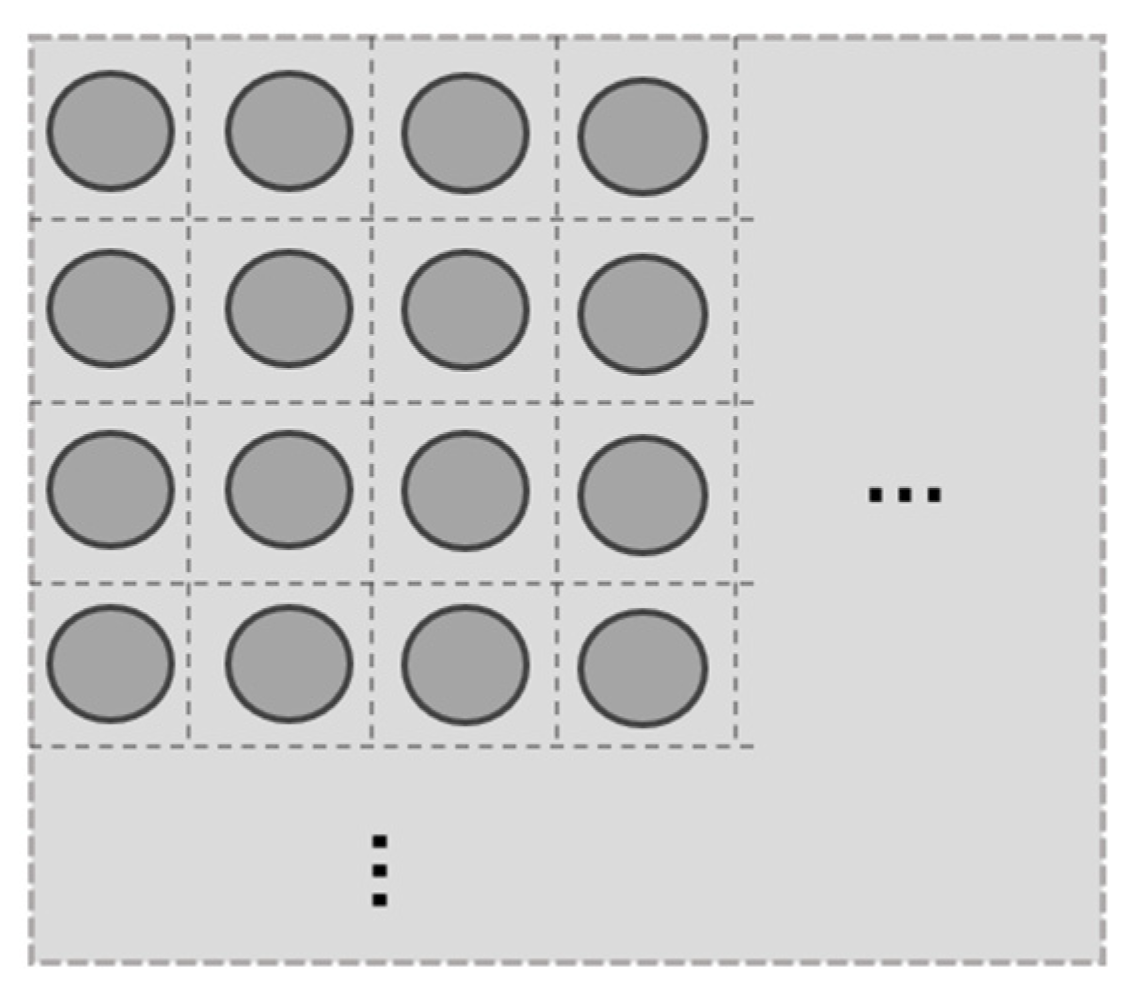
2.1. The Up-Flow SPB Storage Concept
2.2. Governing Equations
2.2.1. Mathematical Modelling for Case 1
2.2.2. Mathematical Modelling for Case 2
2.2.3. Mathematical Modelling for Case 3
2.2.4. Mathematical Modelling for Case 4
2.3. Parametric Study
3. Results
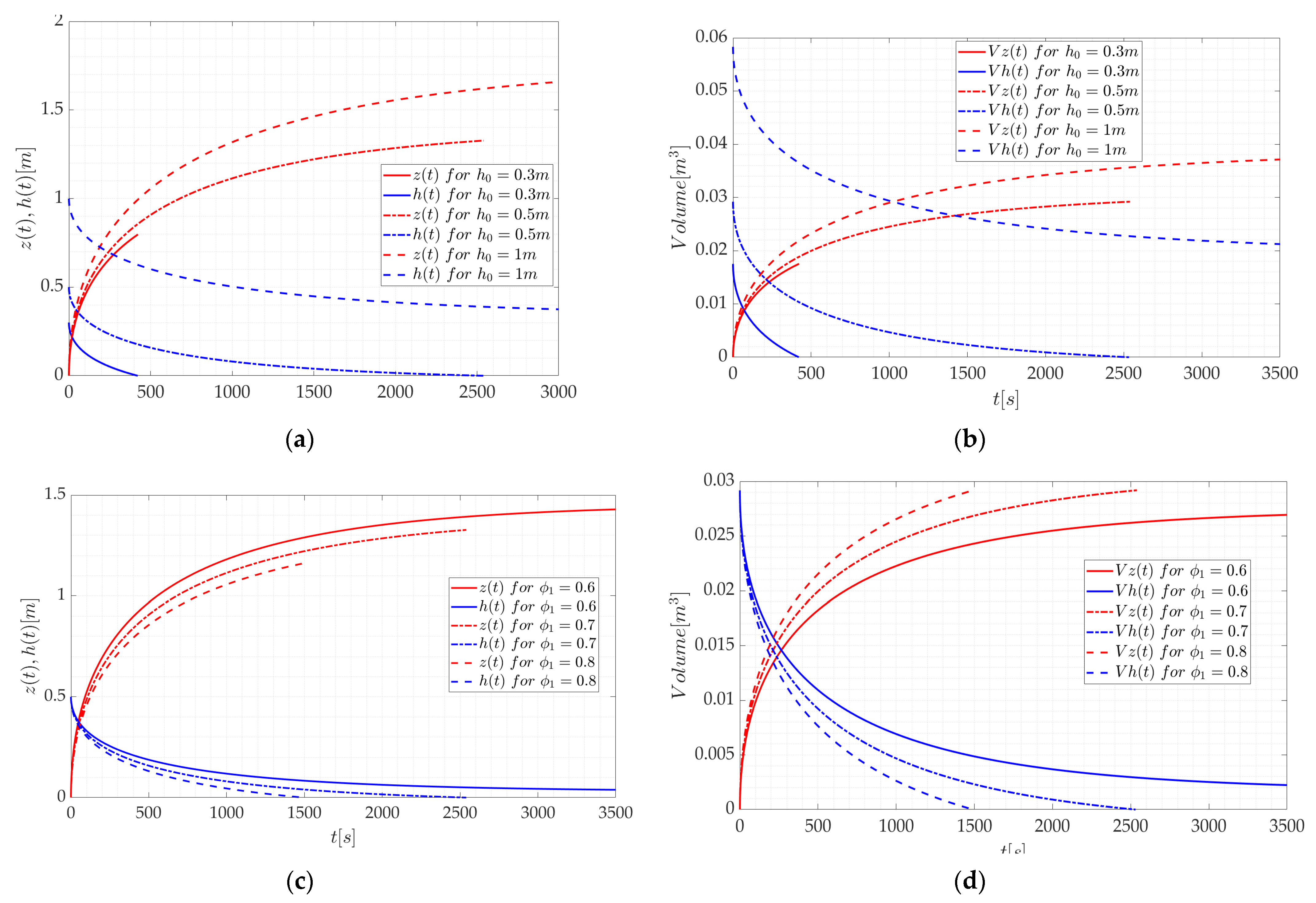
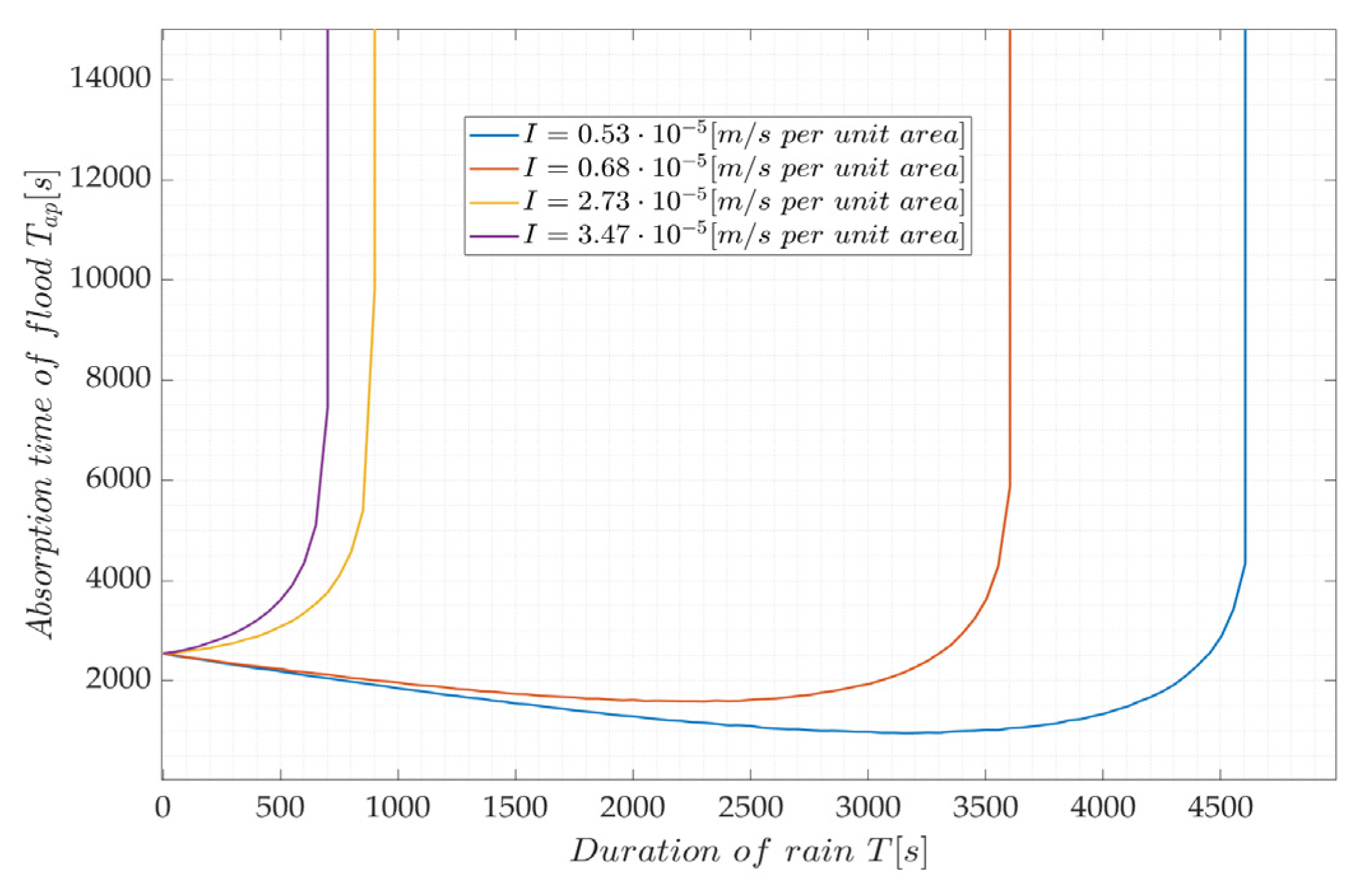
3.1. Case 1
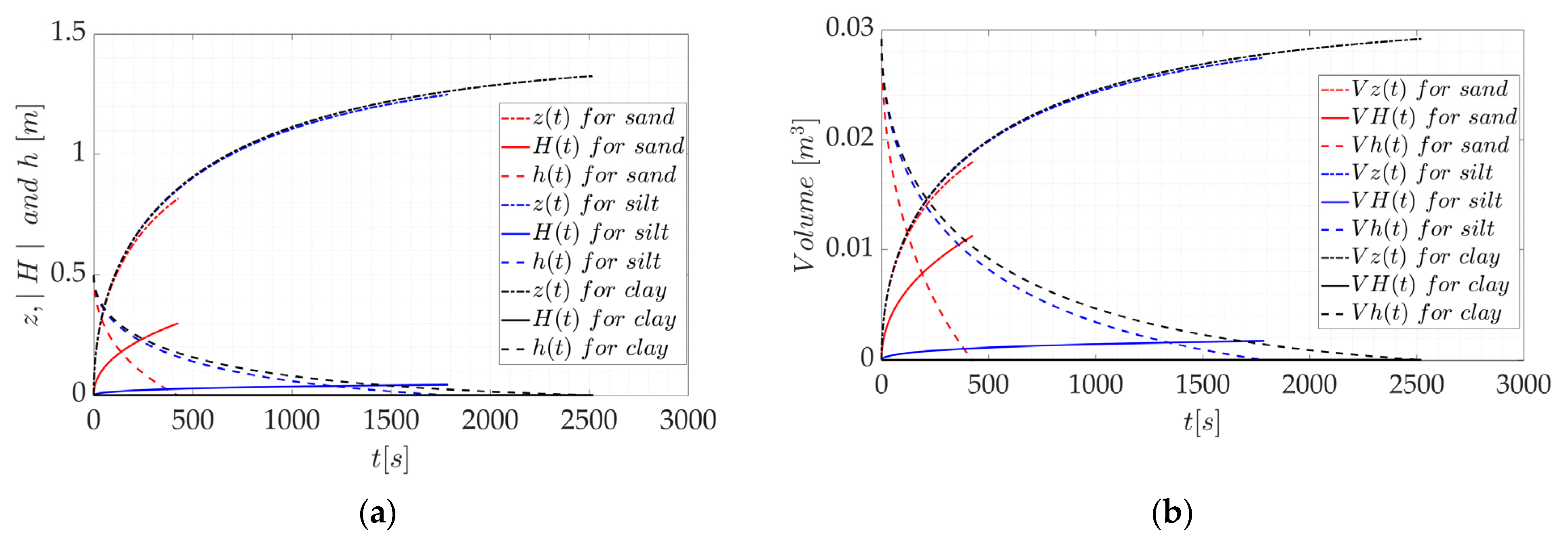
3.2. Case 2
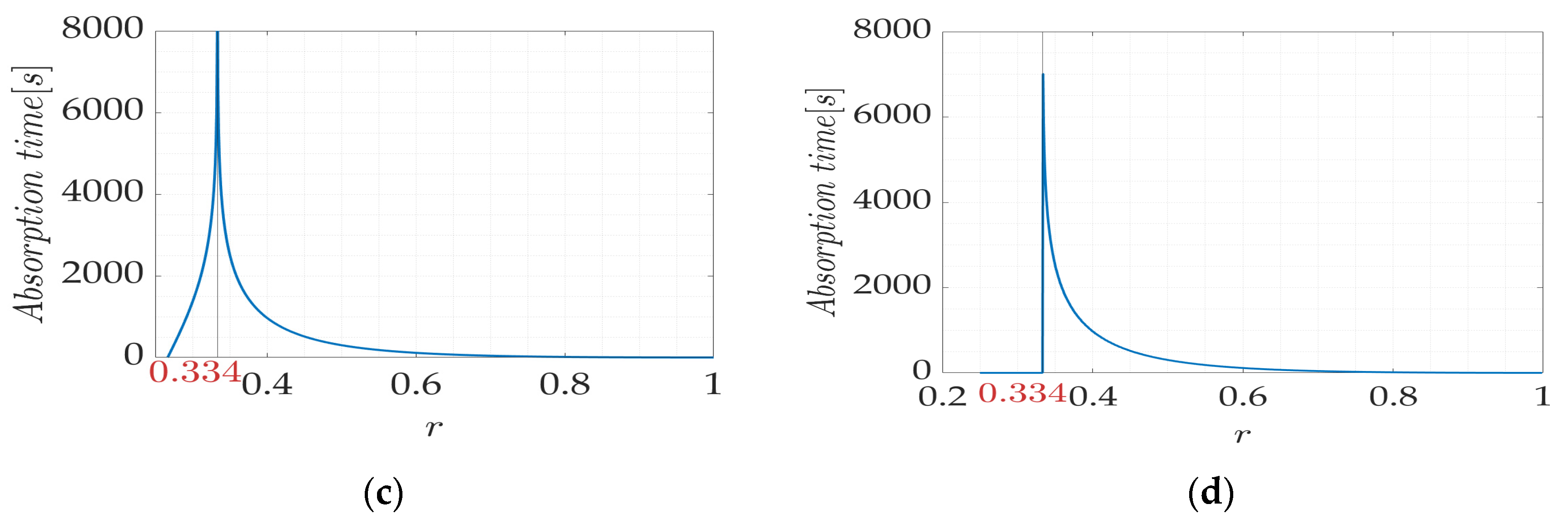
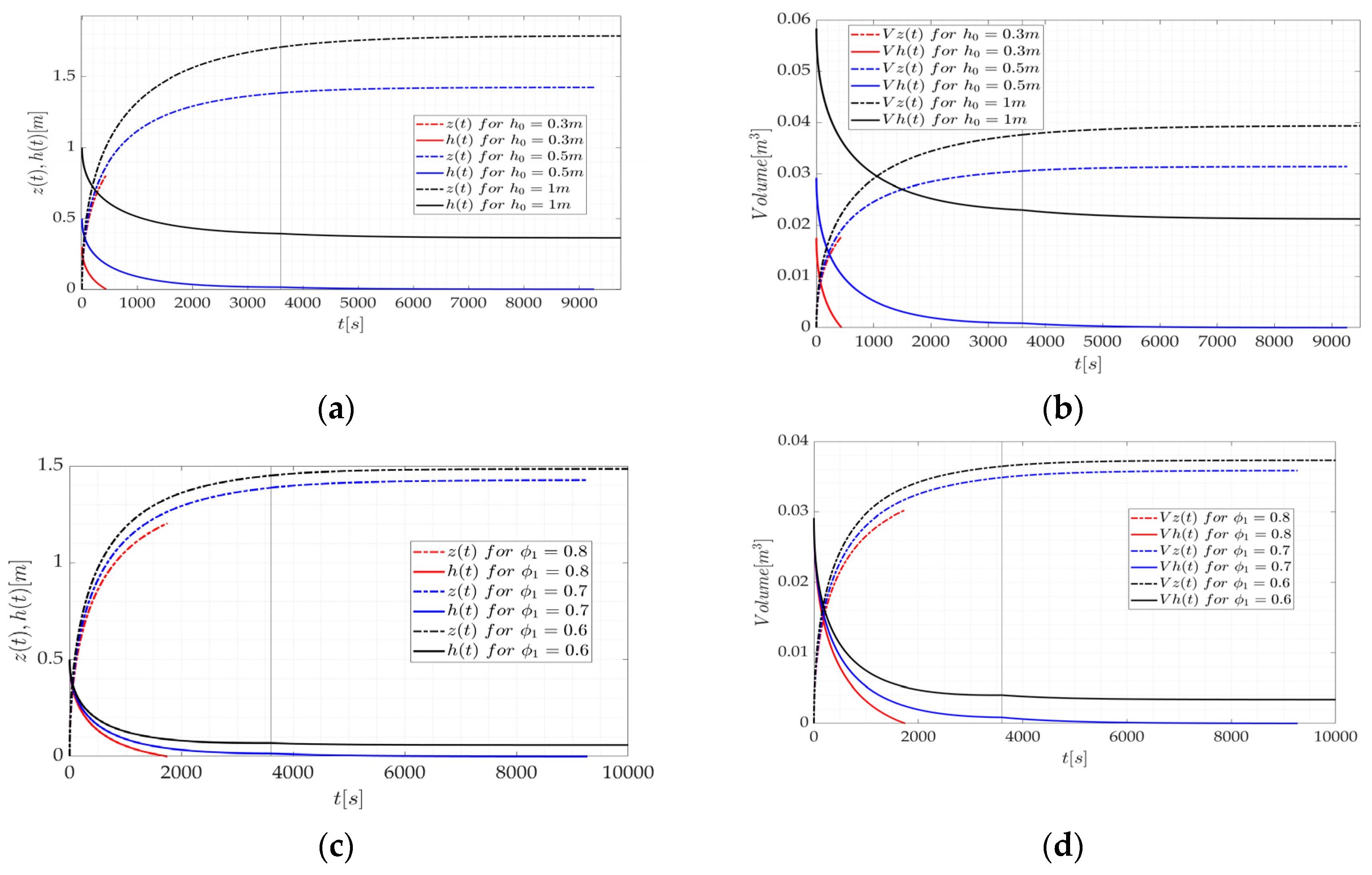
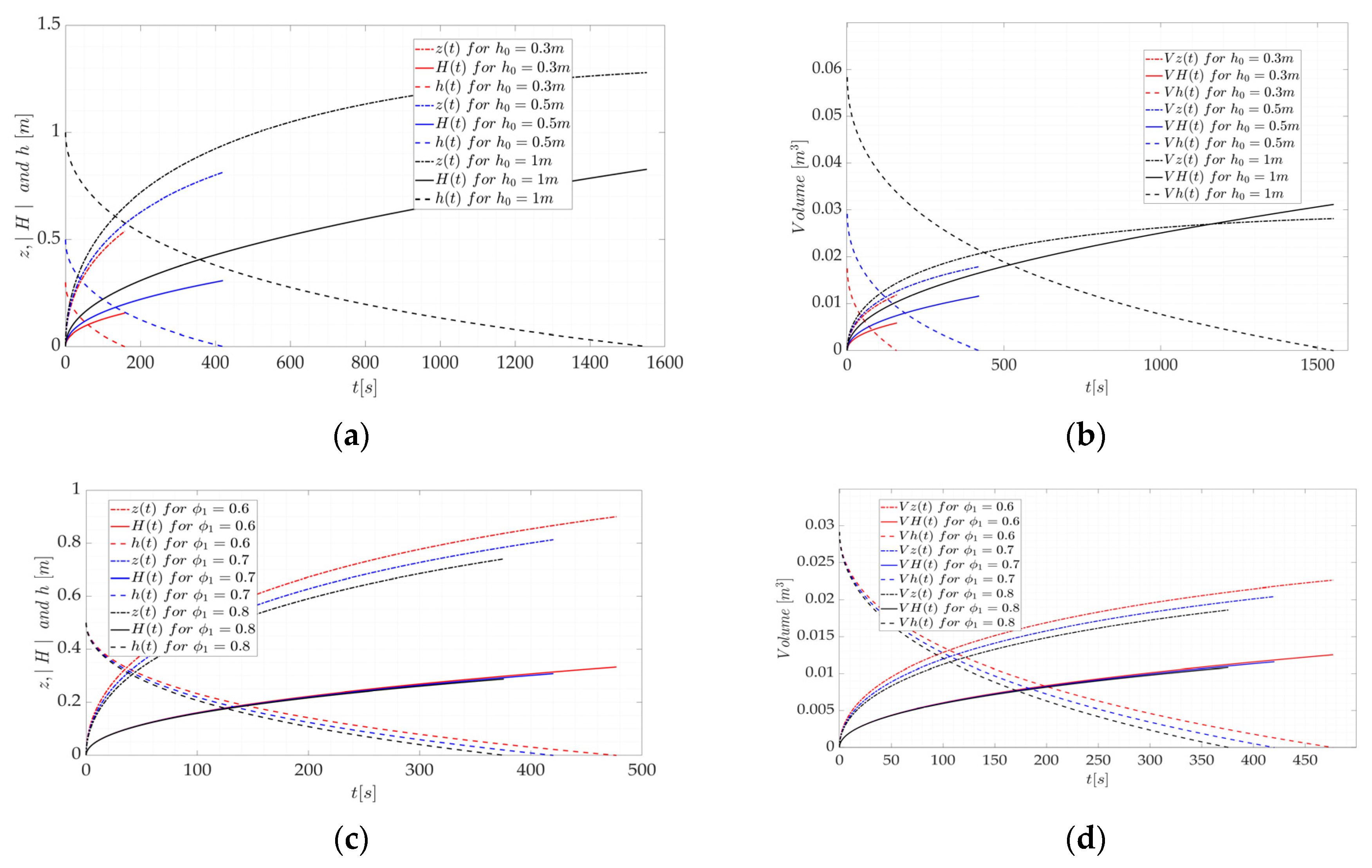
3.3. Case 3 and Case 4
3.4. Summary
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Case 1
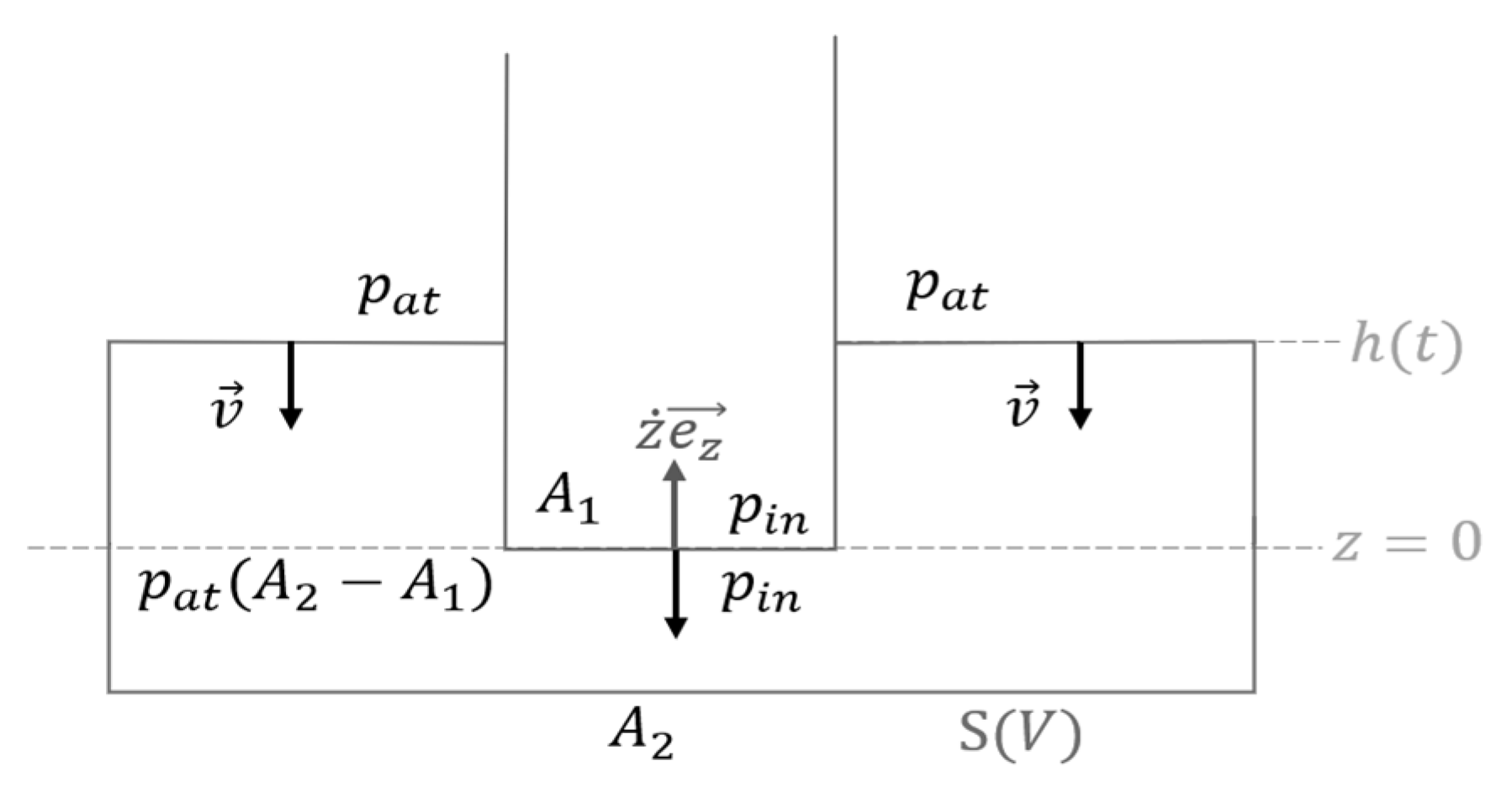
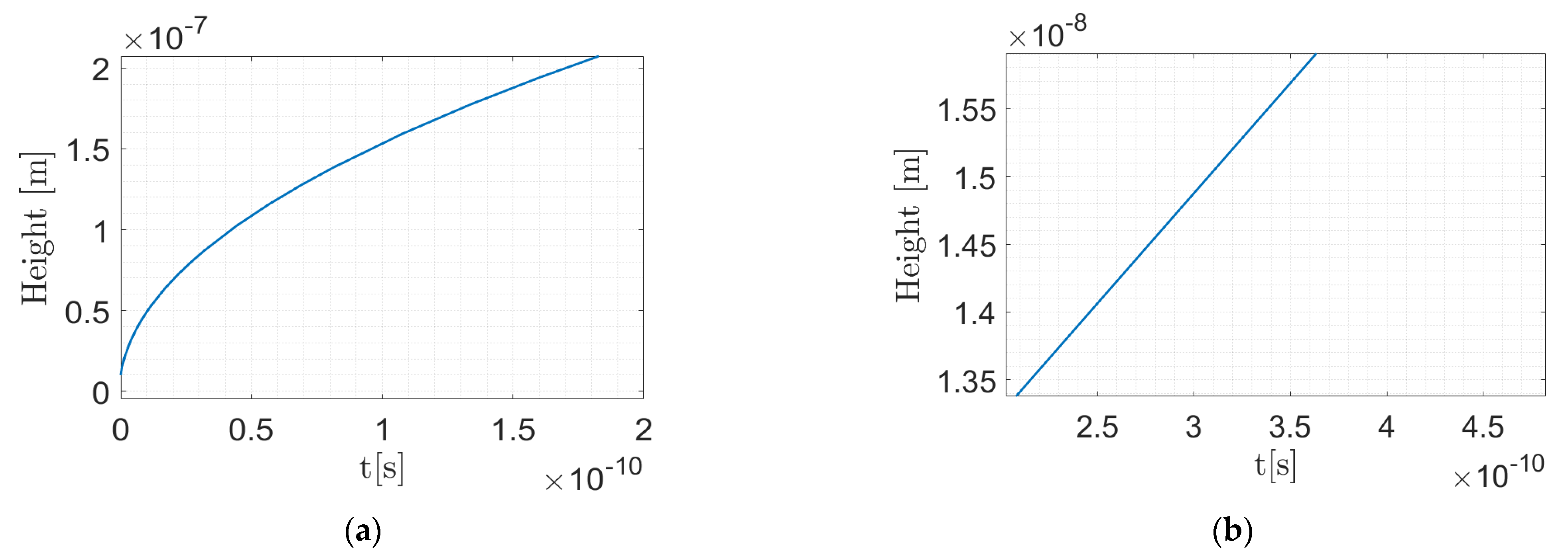
Appendix A.2. Case 2
Appendix A.3. Case 3
Appendix A.4. Case 4
Appendix B

Appendix C
References
- Lundström, T.S.; Åkerstedt, H.O.; Larsson, I.A.S.; Marsalek, J.; Viklander, M. Dynamic Distributed Storage of Stormwater in Sponge-Like Porous Bodies: Modelling Water Uptake. Water 2020, 12, 2080. [Google Scholar] [CrossRef]
- Marsalek, J.; Schreier, H. Innovation in Stormwater Management in Canada: The Way Forward. Water Qual. Res. J. 2009, 44, v–x. [Google Scholar] [CrossRef]
- Toronto Region Conservation Authority. Evaluation of Residential Lot Level Stormwater Practices; Toronto Region Conservation Authority (TRCA): Toronto, ON, Canada, 2013. [Google Scholar]
- Åkerstedt, H.O.; Lundström, T.S.; Larsson, I.A.S.; Marsalek, J.; Viklander, M. Modeling the Swelling of Hydrogels with Application to Storage of Stormwater. Water 2021, 13, 34. [Google Scholar] [CrossRef]
- Zarandi, M.A.F.; Pillai, K.M.; Kimmel, A.S. Spontaneous Imbibition of Liquids in Glass-Fiber Wicks. Part I: Usefulness of a Sharp-Front Approach. AIChE J. 2018, 64, 294–305. [Google Scholar] [CrossRef]
- Faghihi Zarandi, M.A.; Pillai, K. Spontaneous Imbibition of Liquid in Glass Fiber Wicks, Part II: Validation of a Diffuse-Front Model. AIChE J. 2017, 64, 306–315. [Google Scholar] [CrossRef]
- Vo, H.N.; Pucci, M.F.; Corn, S.; Le Moigne, N.; Garat, W.; Drapier, S.; Liotier, P.J. Capillary Wicking in Bio-Based Reinforcements Undergoing Swelling—Dual Scale Consideration of Porous Medium. Compos. Part A Appl. Sci. Manuf. 2020, 134, 105893. [Google Scholar] [CrossRef]
- Foudazi, R.; Zowada, R.; Manas-Zloczower, I.; Feke, D.L. Porous Hydrogels: Present Challenges and Future Opportunities. Langmuir 2023, 39, 2092–2111. [Google Scholar] [CrossRef]
- Khayamyan, S.; Lundström, T.S.; Hellström, J.G.I.; Gren, P.; Lycksam, H. Measurements of Transitional and Turbulent Flow in a Randomly Packed Bed of Spheres with Particle Image Velocimetry. Transp. Porous Media 2017, 116, 413–431. [Google Scholar] [CrossRef]
- Alastal, K.; Ababou, R. Moving Multi-Front (MMF): A Generalized Green-Ampt Approach for Vertical Unsaturated Flows. J. Hydrol. 2019, 579, 124184. [Google Scholar] [CrossRef]
- Caputo, J.-G.; Stepanyants, Y.A. Front Solutions of Richards’ Equation. Transp. Porous Media 2008, 74, 1–20. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Bear, J. 7.6 Direct Integration in One-Dimensional Problems. In Dynamics of Fluids in Porous Media; Environmental Science Series; American Elsevier: New York, NY, USA, 1972; ISBN 978-0-444-00114-6. [Google Scholar]
- Bear, J. 9.4 Unsaturated Flow. In Dynamics of Fluids in Porous Media; Environmental Science Series; American Elsevier: New York, NY, USA, 1972; ISBN 978-0-444-00114-6. [Google Scholar]
- Kuraz, M.; Holub, J.; Jerabek, J. Numerical Solution of the Richards Equation Based Catchment Runoff Model with Dd-Adaptivity Algorithm and Boussinesq Equation Estimator. Pollack Period. 2017, 12, 29–44. [Google Scholar] [CrossRef]
- Piikki, K.; Söderström, M. Digital Soil Mapping of Arable Land in Sweden—Validation of Performance at Multiple Scales. Geoderma 2019, 352, 342–350. [Google Scholar] [CrossRef]
- Detmann, B. Linear Elastic Wave Propagation in Unsaturated Sands, Silts, Loams and Clays. Transp. Porous Media 2011, 86, 537–557. [Google Scholar] [CrossRef]
- Haghighatafshar, S.; Nordlöf, B.; Roldin, M.; Gustafsson, L.-G.; la Cour Jansen, J.; Jönsson, K. Efficiency of Blue-Green Stormwater Retrofits for Flood Mitigation—Conclusions Drawn from a Case Study in Malmö, Sweden. J. Environ. Manag. 2018, 207, 60–69. [Google Scholar] [CrossRef]
- MSE-MyWebPages Melbourne School of Engineering. Available online: https://people.eng.unimelb.edu.au/stsy/geomechanics_text/Ch5_Flow.pdf (accessed on 11 March 2023).
- Woessner, W.W.; Eileen, P.P. Hydrogeologic Properties of Earth Materials and Principles of Groundwater Flow; The Groundwater Project: Guelph, ON, Canada, 2020. [Google Scholar]
- Yu, C.; Cheng, J.J.; Jones, L.G.; Wang, Y.Y.; Faillace, E.; Loureiro, C.; Chia, Y.P. Data Collection Handbook to Support Modeling the Impacts of Radioactive Material in Soil; USA, 1993; p. 152. Available online: https://resrad.evs.anl.gov/docs/data_collection_1993.pdf (accessed on 5 April 2023).
- Olsson, J.; Södling, J.; Berg, P.; Wern, L.; Eronn, A. Short-duration rainfall extremes in Sweden: A regional analysis. Hydrol. Res. 2019, 50, 945–960. [Google Scholar] [CrossRef]
- Berggren, K. Urban Stormwater Systems in Future Climates—Assessment and Management of Hydraulic Overloading. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2014. [Google Scholar]
- Zhao, G.; Wan, Y.; Lei, Z.; Liang, R.; Li, K.; Pu, X. Effect of Urban Underlying Surface Change on Stormwater Runoff Process Based on the SWMM and Green-Ampt Infiltration Model. Water Supply 2021, 21, 4301–4315. [Google Scholar] [CrossRef]
- Vodák, R.; Fürst, T.; Šír, M.; Kmec, J. The Difference between Semi-Continuum Model and Richards’ Equation for Unsaturated Porous Media Flow. Sci. Rep. 2022, 12, 7650. [Google Scholar] [CrossRef]
- Chali, A.K.N.; Hashemi, S.R.; Akbarpour, A. Numerical Solution of the Richards Equation in Unsaturated Soil Using the Meshless Petrov–Galerkin Method. Appl. Water Sci. 2023, 13, 119. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhu, Y. Study of the Water Vertical Infiltration Path in Unsaturated Soil Based on a Variational Method: Application of Power Function Distribution of D (θ). Hydrol. Sci. J. 2022, 67, 2254–2261. [Google Scholar] [CrossRef]
- Wei, L.; Yang, M.; Li, Z.; Shao, J.; Li, L.; Chen, P.; Li, S.; Zhao, R. Experimental Investigation of Relationship between Infiltration Rate and Soil Moisture under Rainfall Conditions. Water 2022, 14, 1347. [Google Scholar] [CrossRef]
- Timsina, R.C.; Khanal, H.; Ludu, A.; Uprety, K.N. Numerical Solution of Water Flow in Unsaturated Soil with Evapotraspiration. Nepali Math. Sci. Rep. 2021, 38, 35–45. [Google Scholar] [CrossRef]
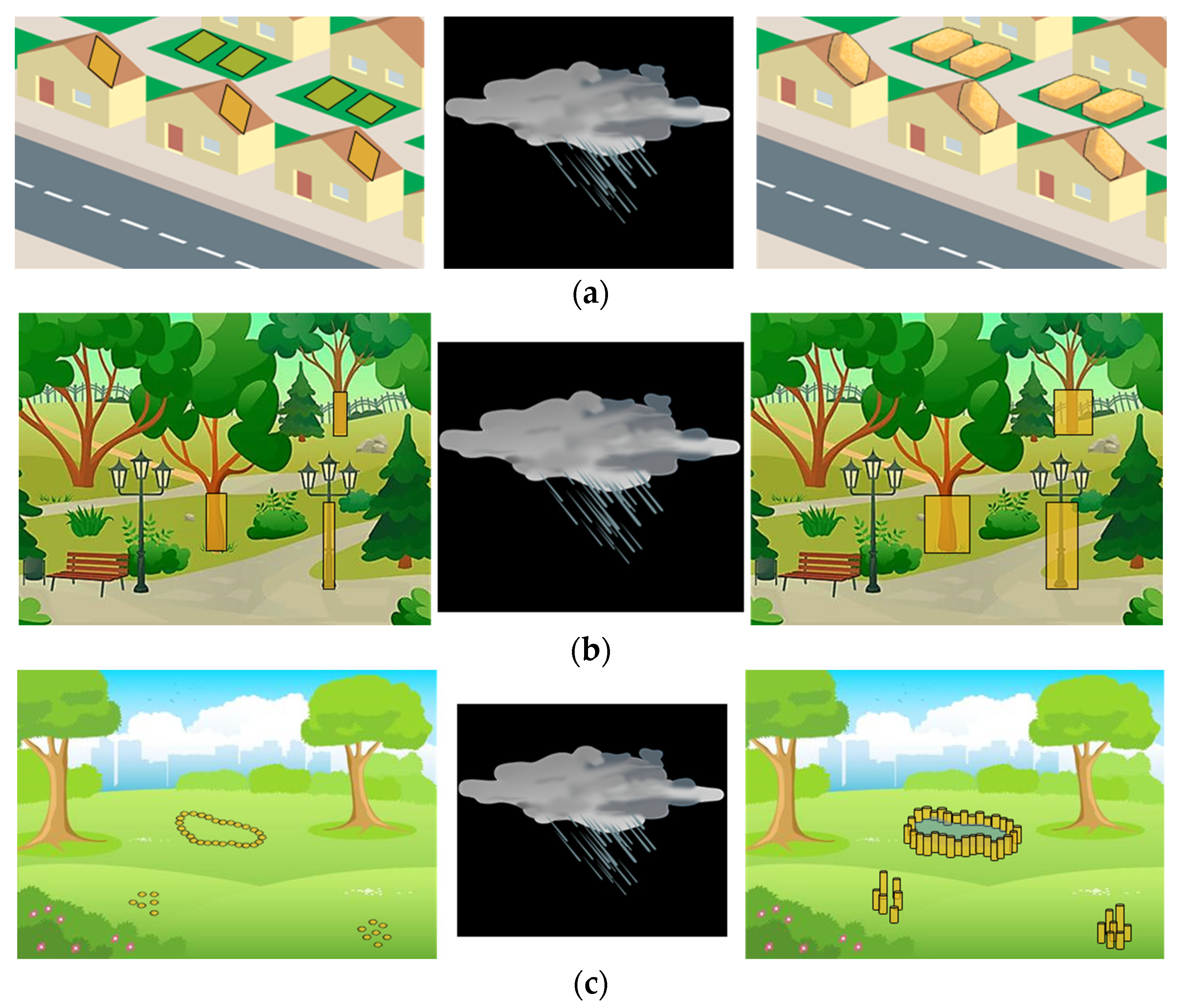
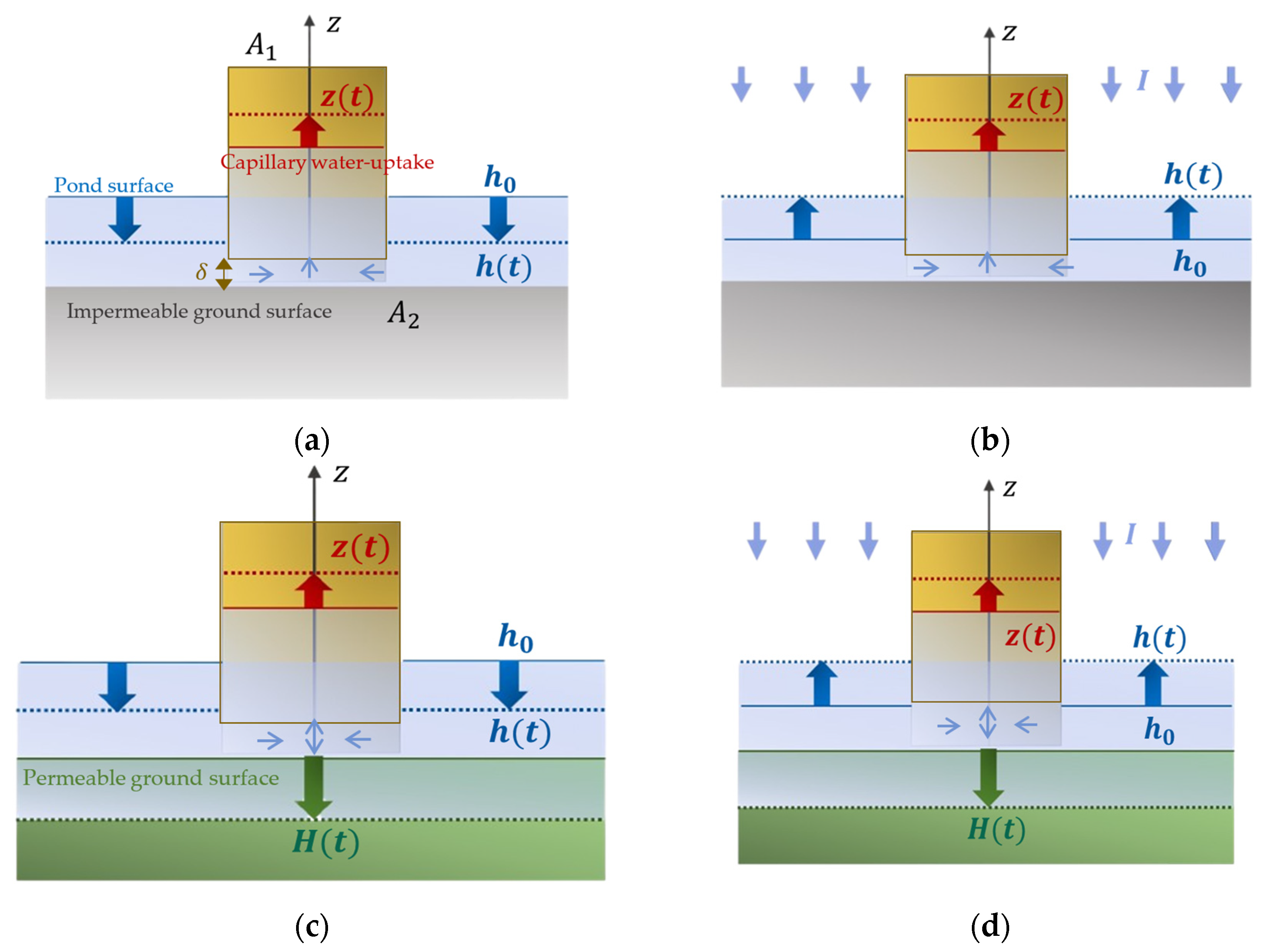





| Soil Type | (%) | |
|---|---|---|
| Sand | ||
| Silty | ||
| Clay |
| Event | ||
|---|---|---|
| Southwest (SW) | North (N) | |
| Uniform intensity 60 min duration, with return period 1:10 years | ||
| 60 min duration event with a high-intensity burst of 5 min, return period 1:10 years, Berggren [23] | Preceding rainfall (during the first 27.5 min) = 7 mm | Preceding rainfall (during the first 27.5 min) = 5.4 mm |
| [m] | (%) |
|---|---|
per Unit Area | per Unit Area | per Unit Area | |||||||
|---|---|---|---|---|---|---|---|---|---|
| for case 1 | indefinite | 2523 | 1458 | 407 | 2522 | indefinite | no rain | no rain | no rain |
| for case 2 | indefinite | 9221 | 1649 | 423 | 9220 | indefinite | 4630 | 9221 | indefinite |
| for case 3 | 461 | 410 | 366 | 148 | 410 | 1481 | no rain | no rain | no rain |
| for case 4 | 472 | 420 | 370 | 153 | 420 | 1540 | 417 | 419 | 458 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barcot, A.; Åkerstedt, H.O.; Larsson, I.A.S.; Lundström, T.S. Stormwater Uptake in Sponge-Like Porous Bodies Surrounded by a Pond: A Fluid Mechanics Analysis. Water 2023, 15, 3209. https://doi.org/10.3390/w15183209
Barcot A, Åkerstedt HO, Larsson IAS, Lundström TS. Stormwater Uptake in Sponge-Like Porous Bodies Surrounded by a Pond: A Fluid Mechanics Analysis. Water. 2023; 15(18):3209. https://doi.org/10.3390/w15183209
Chicago/Turabian StyleBarcot, Ana, Hans O. Åkerstedt, I. A. Sofia Larsson, and T. Staffan Lundström. 2023. "Stormwater Uptake in Sponge-Like Porous Bodies Surrounded by a Pond: A Fluid Mechanics Analysis" Water 15, no. 18: 3209. https://doi.org/10.3390/w15183209







