Runoff Prediction in the Xijiang River Basin Based on Long Short-Term Memory with Variant Models and Its Interpretable Analysis
Abstract
:1. Introduction
2. Study Area and Data Processing
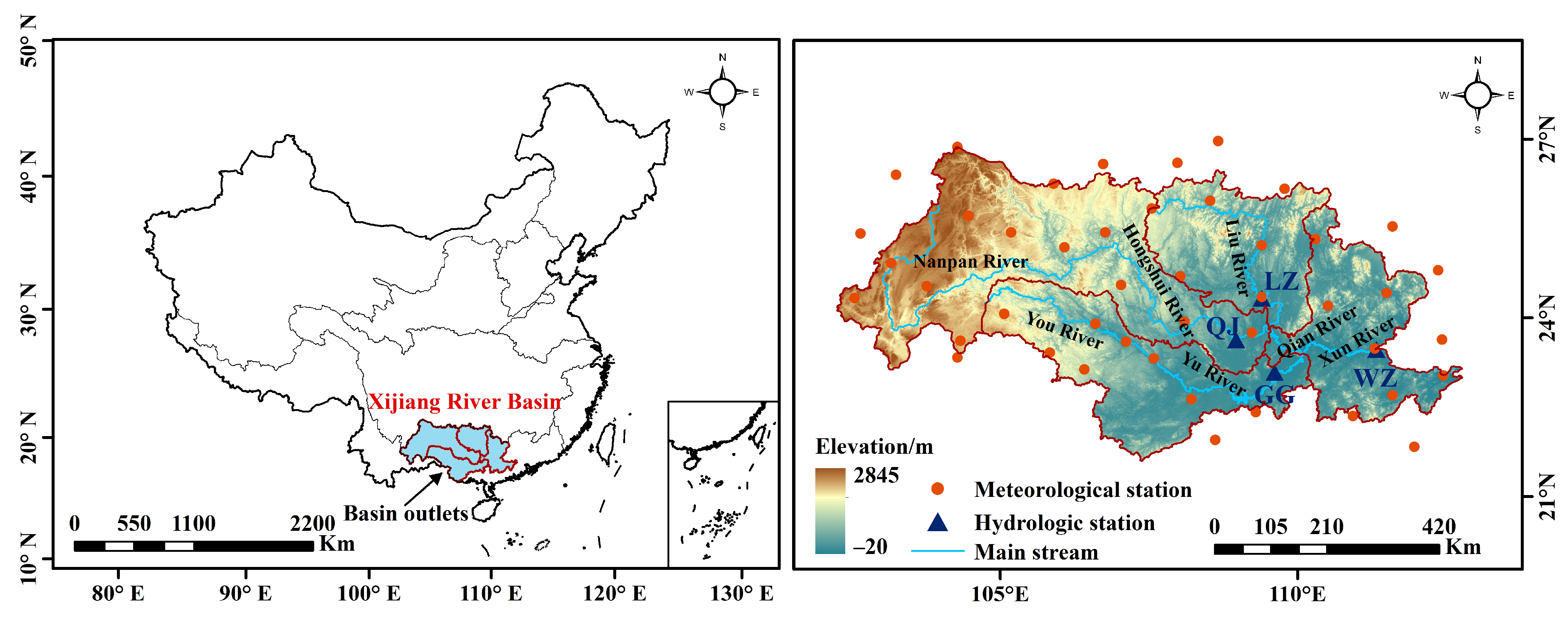
2.1. Study Area
2.2. Data Processing
3. Methodology
3.1. Model Introduction
3.2. Wavelet Analysis
3.3. Evaluation Indicators
3.4. Interpretable Machine Learning Method
4. Results
4.1. Feature Selection
4.1.1. Selection of Atmospheric Circulation Factors
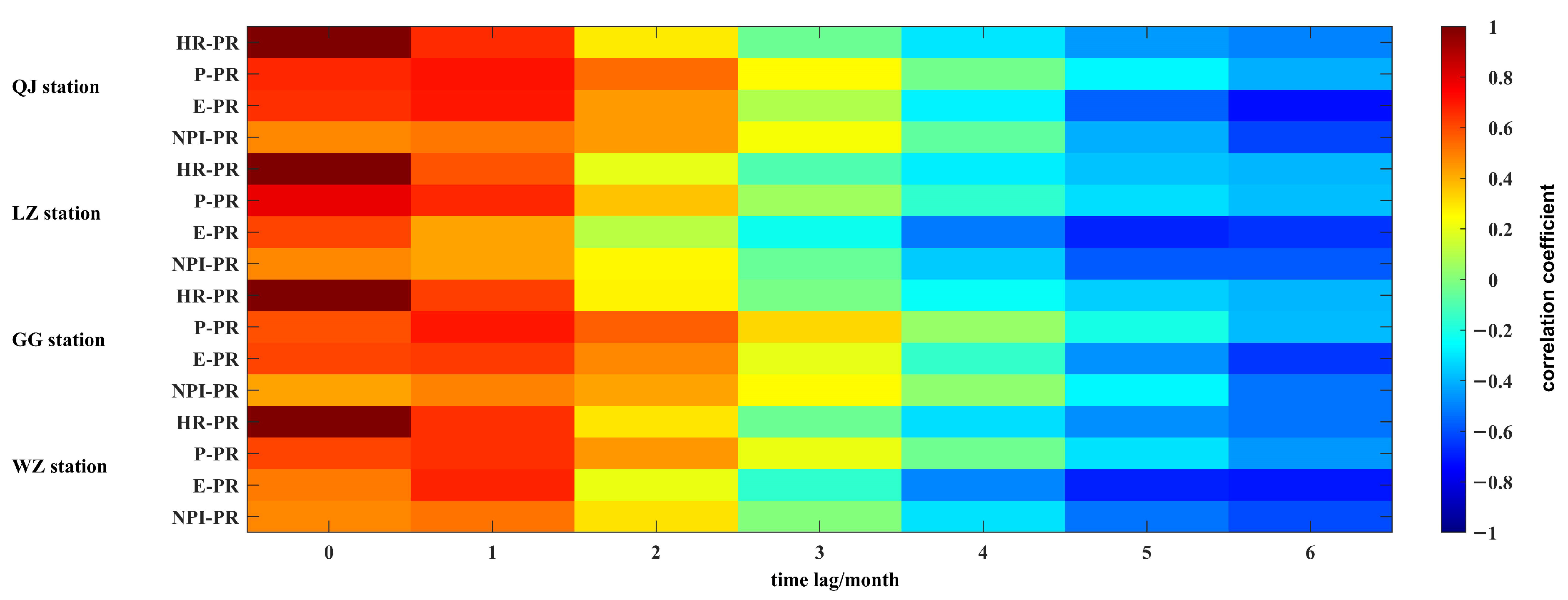
4.1.2. Delayed Effect Analysis
4.2. Driving Effect of Atmospheric Circulation Factors on Runoff Change
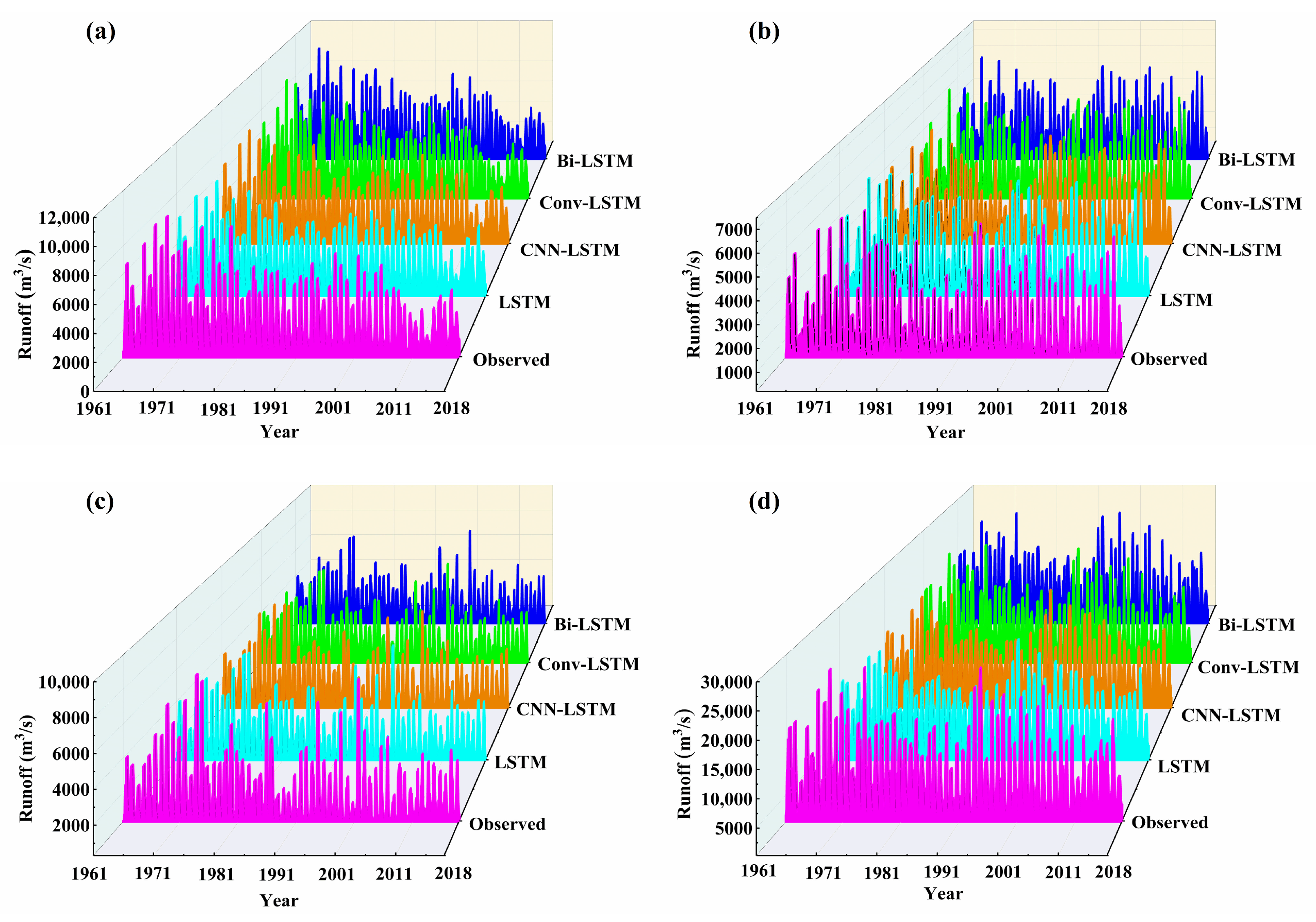
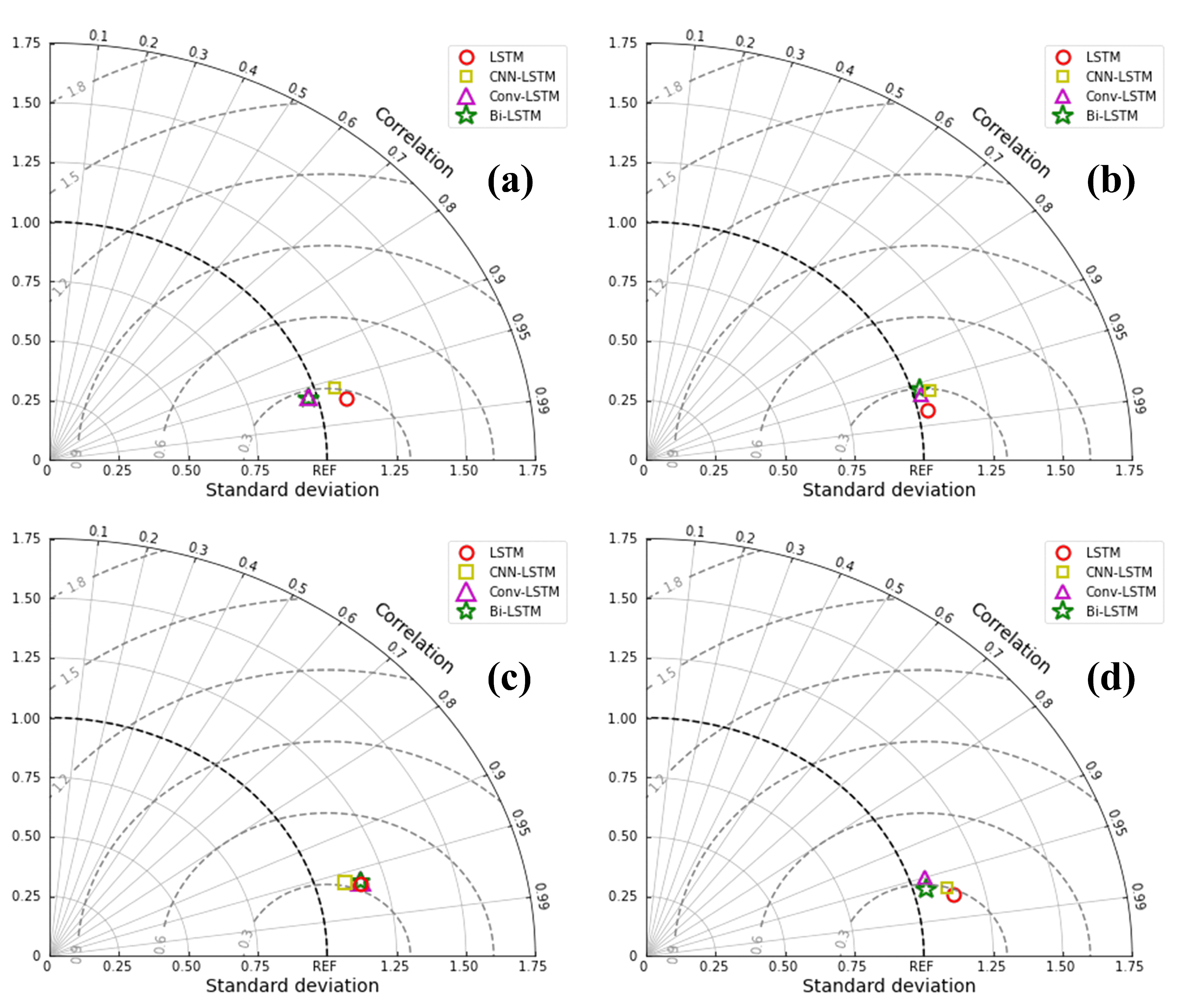
4.3. Comparative Analysis of Model Prediction Performance
4.3.1. Prediction Performance of Different Models in the Same Forecast Period
4.3.2. Prediction Performance of Optimal Model under Different Foresight Periods
4.4. Interpretability Analysis of LSTM Model
5. Discussion
5.1. Reasons for Differences in Model Prediction Accuracy
5.2. Uncertainty
5.3. Advantages and Limitations
6. Conclusions
- (1)
- The NPI is the most influential atmospheric circulation factor affecting the runoff in the XJB.
- (2)
- When comparing different models with the same forecast period, the LSTM model had higher NSE results in the QJ, LZ, GG, and WZ, with values of 0.950, 0.960, 0.954, and 0.955, respectively. These values were higher than those in the other three models tested at the same stations. Therefore, it can be concluded that the LSTM model is the optimal choice among the four models used in this study.
- (3)
- With the optimal model, the LSTM model, its prediction results decreased as the foresight period increased. Specifically, the NSE decreased by 4.7% when the foresight period increased from one month to two months, and it decreased by 3.9% when the foresight period increased from two months to three months. This suggested that although the decrease in the NSE was slow as the foresight period increased, there was a converging trend of a declining NSE with a longer foresight period.
- (4)
- Based on SHAP values, an interpretability analysis was conducted on the LSTM model. The results showed that in the XJB, historical runoff had the greatest impact on runoff prediction results, followed by precipitation, evaporation, and the NPI. Evaporation was negatively correlated with runoff, while historical runoff, precipitation, and the NPI were positively correlated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Sepehri, A.; Sarrafzadeh, M.H. Effect of nitrifiers community on fouling mitigation and nitrification efficiency in a membrane bioreactor. Chem. Eng. Process. 2018, 128, 10–18. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, J.; Gu, L. Overall uncertainty of climate change impacts on watershed hydrology in China. Int. J. Climatol. 2022, 42, 507–520. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.Z.; Ye, L.; Meng, C.Q. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Amiri, E. Forecasting daily river flows using nonlinear time series models. J. Hydrol. 2015, 527, 1054–1072. [Google Scholar] [CrossRef]
- Speight, L.J.; Cranston, M.D.; White, C.J.; Kelly, L. Operational and emerging capabilities for surface water flood forecasting. Wires Water 2021, 8, e1517. [Google Scholar] [CrossRef]
- Kalra, A.; Miller, W.P.; Lamb, K.W.; Ahmad, S.; Piechota, T. Using large-scale climatic patterns for improving long lead time streamffow forecasts for Gunnison and San Juan River Basins. Hydrol. Process. 2013, 27, 1543–1559. [Google Scholar] [CrossRef]
- Lin, G.F.; Chou, Y.C.; Wu, M.C. Typhoon flood forecasting using integrated two-stage Support Vector Machine approach. J. Hydrol. 2013, 486, 334–342. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Faghih, M.; Mirzaei, M.; Adamowski, J.; Lee, J.; El-Shaffe, A. Uncertainty estimation in ffood inundation mapping: An application of non-parametric bootstrapping: Uncertainty in ffood inundation mapping. River Res. Appl. 2017, 33, 611–619. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall–runoff modelling. J. Hydroinformatics 2020, 22, 541–561. [Google Scholar] [CrossRef]
- Dou, Y.; Ye, L.; Gupta, H.V.; Zhang, H.; Behrangi, A.; Zhou, H. Improved flood forecasting in basins with no precipitation stations: Constrained runoff correction using multiple satellite precipitation products. Water Resour. Res. 2021, 57, e2021WR029682. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Mirzaei, M.; Yu, H.; Dehghani, A.; Galavi, H.; Shokri, V. A novel stacked long short-term memory approach of deep learning for streamflow simulation. Sustainability 2021, 13, 13384. [Google Scholar] [CrossRef]
- Kim, T.; Yang, T.T.; Gao, S.; Zhang, L.J.; Ding, Z.Y.; Wen, X.; Gourley, J.J.; Hong, Y. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Rahmani, F.; Lawson, K.; Ouyang, W.; Appling, A.; Oliver, S.; Shen, C. Exploring the exceptional performance of a deep learning stream temperature model and the value of streamflow data. Environ. Res. Lett. 2021, 16, 024025. [Google Scholar] [CrossRef]
- Jiang, S.J.; Zheng, Y.; Solomatine, D. Improving AI system awareness of geoscience knowledge: Symbiotic integration of physical approaches and deep learning. Geophys. Res. Lett. 2020, 47, e2020GL088229. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Chai, H.K.; Mirzaei, M. Improved SVR machine learning models for agricultural drought prediction at downstream of Langat River Basin, Malaysia. J. Water Clim. Chang. 2020, 11, 1383–1398. [Google Scholar] [CrossRef]
- Fan, C.; Song, C.; Liu, K.; Ke, L.; Xue, B.; Chen, T.; Fu, C.; Cheng, J. Century-scale reconstruction of water storage changes of the largest lake in the inner mongolia plateau using a machine learning approach. Water Resour. Res. 2021, 57, e2020WR028831. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Mishra, A.K. Multi-layer high-resolution soil moisture estimation using machine learning over the United States. Remote Sens. Environ. 2021, 266, 112706. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Wang, J.; Sangaiah, A.; Xie, Y.; Yin, X.C. Analysis and prediction of water quality using LSTM deep neural networks in IoT environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.F.; Zhang, S.; Han, J.C.; Wang, G.Q.; Zhang, M.X.; Lin, Q.A. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nering, G.; Lin, J.; Hochreiter, S. Rainfall-runoff prediction at multiple timescales with a single Long Short-Term Memory network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Yuan, X.H.; Chen, C.; Lei, X.H.; Yuan, Y.B.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of long short-term memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.L.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yan, H. A long short-term components neural network model with data augmentation for daily runoff forecasting. J. Hydrol. 2023, 617, 128853. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A deep cnn-lstm model for particulate matter (PM2.5) forecasting in smart cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN-LSTM deep learning mode. Stoch. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Moishin, M.; Deo, R.C.; Prasad, R.; Raj, N.; Abdulla, S. Designing deep-based learning flood forecast model with ConvLSTM hybrid algorithm. IEEE Access 2021, 9, 50982–50993. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Coupling a hybrid CNN-LSTM deep learning model with a boundary corrected maximal overlap discrete wavelet transform for multiscale Lake water level forecasting. J. Hydrol. 2021, 598, 126196. [Google Scholar] [CrossRef]
- Jaseena, K.U.; Kovoor, B.C. Decomposition-based hybrid wind speed forecasting model using deep bidirectional LSTM networks. Energ. Convers. Manag. 2021, 234, 113944. [Google Scholar] [CrossRef]
- Ha, S.; Liu, D.; Mu, L. Prediction of Yangtze River streamflow based on deep learning neural network with El Niño-Southern Oscillation. Sci. Rep. 2021, 11, 11738. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- McGovern, A.; Ryan, L.; Gagne, D.J.; Jergensen, G.E.; Elmore, K.L.; Homeyer, C.R.; Smith, T. Making the black box more transparent: Understanding the physical implications of machine learning. Bull. Am. Meteorol. Soc. 2019, 100, 2175–2199. [Google Scholar] [CrossRef]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What role does hydrological science play in the age of machine learning? Water Resour. Res. 2020, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Lee, Y.G.; Oh, J.Y.; Kim, D.; Kim, G. Shap value-based feature importance analysis for short-term load forecasting. J. Electr. Eng. Technol. 2023, 18, 579–588. [Google Scholar] [CrossRef]
- Kitani, R.; Iwata, S. Verification of Interpretability of Phase-Resolved Partial Discharge Using a CNN With SHAP. IEEE Access 2023, 11, 4752–4762. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Xia, Q.; He, J.; He, B.; Chu, Y.; Li, W.; Sun, J.; Wen, D. Effect and genesis of soil nitrogen loading and hydrogeological conditions on the distribution of shallow groundwater nitrogen pollution in the North China Plain. Water Res. 2023, 243, 120346. [Google Scholar] [CrossRef] [PubMed]
- Molnar, C. Interpretable Machine Learning; Lulu Press: Morrisville, NC, USA, 2020. [Google Scholar]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Lama, L.; Wilhelmsson, O.; Norlander, E.; Gustafsson, L.; Lager, A.; Tynelius, P.; Ẅarvik, L.; Östenson, C.G. Machine learning for prediction of diabetes risk in middle-aged Swedish people. Heliyon 2021, 7, e07419. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Xie, Y.; Wu, L.; Jiang, L. Quantifying and comparing the effects of key risk factors on various types of roadway segment crashes with LightGBM and SHAP. Accid. Anal. Prev. 2021, 159, 106261. [Google Scholar] [CrossRef]
- Mangalathu, S.; Hwang, S.H.; Jeon, J.S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Wang, R.Z.; Kim, J.H.; Li, M.H. Predicting stream water quality under different urban development pattern scenarios with an interpretable machine learning approach. Sci. Total Environ. 2021, 761, 144057. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H.; Liang, S. Prediction of estuarine water quality using interpretable machine learning approach. J. Hydrol. 2022, 605, 127320. [Google Scholar] [CrossRef]
- Huang, S.Z.; Li, P.; Huang, Q.; Leng, G.Y.; Hou, B.B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Liu, S.Y.; Huang, S.Z.; Huang, Q.; Xie, Y.Y.; Leng, G.Y.; Luan, J.K.; Song, X.Y.; Wei, X.; Li, X.Y. Identification of the non-stationarity of extreme precipitation events and correlations with large-scale ocean-atmospheric circulation patterns: A case study in the Wei River Basin, China. J. Hydrol. 2017, 548, 184–195. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wang, H.; Leng, G.; Wang, L.; Liang, H. A hybrid VMD-SVM model for practical streamflow prediction using an innovative input selection framework. Water Resour. Manag. 2021, 35, 1321–1337. [Google Scholar] [CrossRef]
- Song, P.; Liu, W.; Sun, J.; Wang, C.; Kong, L.; Nong, Z.; Lei, X.; Wang, H. Annual runoff forecasting based on multi-model information fusion and residual error correction in the Ganjiang River Basin. Water 2020, 12, 2086. [Google Scholar] [CrossRef]
- Yan, X.G.; Wu, L.N.; Zhou, Y.; Song, J.L.; Deng, S.X. On the association of Co-kriging interpolation method research based on GlS: A case study in Karst area of Guizhou Province. J. Yunnan Univ. 2017, 39, 432–439. (In Chinese) [Google Scholar]
- Khan, M.; Almazah, M.M.; EIlahi, A.; Niaz, R.; Al-Rezami, A.Y.; Zaman, B. Spatial interpolation of water quality index based on Ordinary kriging and Universal kriging. Geomat. Nat. Hazards Risk 2023, 14, 2190853. [Google Scholar] [CrossRef]
- Wu, H.C.; Yang, Q.L.; Liu, J.M.; Wang, G.Q. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep learning for precipitation nowcasting: A benchmark and a new model. Adv. Neural Inf. Process. Syst. 2017, 30, 144–146. [Google Scholar]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the northern hemisphere winter. Bull. Am. Meteorol. Soc. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Ng, E.K.W.; Chan, J.C.L. Geophysical applications of partial wavelet coherence and multiple wavelet coherence. J. Atmos. Ocean. Technol. 2012, 29, 1845–1853. [Google Scholar] [CrossRef]
- Hu, W.; Si, B.C. Technical Note: Multiple wavelet coherence for untangling scale specific and localized multivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 2016, 20, 3183–3191. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Biswas, A.; Gharabaghi, B.; Hu, W. A multiscale and multivariate analysis of precipitation and streamflow variability in relation to ENSO, NAO and PDO. J. Hydrol. 2019, 574, 288–307. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Yu, D.Y.; Zhu, W.J.; Pan, Y.Z. The role of atmospheric circulation system playing in coupling relationship between spring NPP and precipitation in East Asia area. Environ. Monit. Assess. 2008, 145, 135–143. [Google Scholar]
- Sangrody, H.; Zhou, N.; Salih, T.; Khorramdel, B.; Motalleb, M.; Sareiloo, M. Long term forecasting using machine learning methods. In Proceedings of the IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 22–23 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Yue, Z.X.; Ai, P.; Xiong, C.S.; Hong, M.; Song, Y.H. Mid- to long-term runoff prediction by combining the deep belief network and partial least-squares regression. J. Hydroinformatics 2020, 22, 1283–1305. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of flow based on a CNN-LSTM combined deep learning approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Wu, J.H.; Wang, Z.C.; Hu, Y.; Tao, S.; Dong, J.H.; Tsakiris, G. Runoff forecasting using convolutional neural networks and optimized Bi-directional long short-term memory. Water Resour. Manag. 2023, 37, 937–953. [Google Scholar] [CrossRef]
- Gamboa, J.C.B. Deep Learning for time-series analysis. Comput. Sci. 2017, 1701, 01887. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Wang, S.Z.; Cao, J.N.; Yu, P. Deep Learning for spatio-temporal data mining: A survey. IEEE Trans. Knowl. Data Eng. 2022, 34, 3681–3700. [Google Scholar] [CrossRef]
- Sivakumar, B.; Berndtsson, R. Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting; World Scientific: Singapore, 2010. [Google Scholar]
- Bai, Y.; Bezak, N.; Zeng, B.; Li, C.; Zhang, J. Daily runoff forecasting using a cascade long short-term memory model that considers different variables. Water Resour. Manag. 2021, 35, 1167–1181. [Google Scholar] [CrossRef]
- Zeng, M.; Li, J.Q.; Ming, Y.W.; Yang, S.S.; Li, J. Analysis on the influence of reservoir group on the runoff of Datong station in dry season. IOP Conf. Ser. Earth Environ. Sci. 2021, 768, 012047. [Google Scholar] [CrossRef]
- Guo, W.X.; Hu, J.W.; Wang, H.X. Analysis of runoff variation characteristics and influencing factors in the Wujiang River basin in the past 30 years. Int. J. Environ. Res. Public Health 2021, 19, 372. [Google Scholar] [CrossRef] [PubMed]
- Jong, S.I.; Om, K.C.; Pak, Y.I. Influences of atmospheric circulation patterns on interannual variability of winter precipitation over the northern part of the Korean Peninsula. Clim. Res. 2021, 85, 35–50. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Singh, V.P.; Li, J. Regionalization and spatial changing properties of droughts across the Pearl River basin, China. J. Hydrol. 2012, 472, 355–366. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, S.; Xia, J.; Zhan, C.; Wang, W.; Luo, X.; Chen, N.; Li, J. Analysis of drought and flood alternation and its driving factors in the Yangtze River basin under climate change. Atmos. Res. 2022, 270, 106087. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. Comput. Sci. 2014, 9, 1556. [Google Scholar]






| Evaluation Indicators | Formula | Optimal Value |
|---|---|---|
| RMSE | 0 | |
| MAE | 0 | |
| NSE | 1 |
| Hydrological Station | ENSO | PDO | NAO | AO | AMO | DMI | NPI | PNA | SSI |
|---|---|---|---|---|---|---|---|---|---|
| QJ | 0.026 | 0.013 | −0.029 | 0.073 | −0.032 | −0.015 | 0.512 ** | −0.052 | 0.018 |
| LZ | 0.072 | 0.055 | −0.049 | 0.087 * | 0.026 | 0.024 | 0.452 ** | −0.088 * | 0.034 |
| GG | −0.021 | −0.063 | −0.042 | 0.064 | −0.028 | −0.026 | 0.487 ** | −0.056 | 0.008 |
| WZ | 0.040 | 0.024 | −0.001 | 0.098 ** | −0.031 | 0.006 | 0.517 ** | −0.087 * | 0.021 |
| Station | Model | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| NSE | RMSE (103 m3/s) | MAE (103 m3/s) | NSE | RMSE (103 m3/s) | MAE (103 m3/s) | ||
| QJ | LSTM | 0.944 | 0.456 | 0.274 | 0.950 | 0.249 | 0.203 |
| CNN-LSTM | 0.921 | 0.529 | 0.308 | 0.920 | 0.305 | 0.244 | |
| Conv-LSTM | 0.920 | 0.535 | 0.312 | 0.939 | 0.275 | 0.218 | |
| Bi-LSTM | 0.927 | 0.526 | 0.296 | 0.942 | 0.269 | 0.212 | |
| LZ | LSTM | 0.959 | 0.252 | 0.137 | 0.960 | 0.241 | 0.210 |
| CNN-LSTM | 0.925 | 0.338 | 0.163 | 0.926 | 0.343 | 0.282 | |
| Conv-LSTM | 0.929 | 0.337 | 0.231 | 0.925 | 0.363 | 0.326 | |
| Bi-LSTM | 0.916 | 0.362 | 0.251 | 0.926 | 0.340 | 0.269 | |
| GG | LSTM | 0.933 | 0.405 | 0.237 | 0.954 | 0.221 | 0.195 |
| CNN-LSTM | 0.922 | 0.416 | 0.248 | 0.923 | 0.286 | 0.242 | |
| Conv-LSTM | 0.927 | 0.415 | 0.246 | 0.919 | 0.296 | 0.249 | |
| Bi-LSTM | 0.928 | 0.412 | 0.242 | 0.922 | 0.288 | 0.245 | |
| WZ | LSTM | 0.950 | 1.318 | 0.869 | 0.955 | 0.833 | 0.698 |
| CNN-LSTM | 0.934 | 1.439 | 0.901 | 0.923 | 1.060 | 0.818 | |
| Conv-LSTM | 0.900 | 1.695 | 0.928 | 0.906 | 1.197 | 0.922 | |
| Bi-LSTM | 0.920 | 1.460 | 0.916 | 0.911 | 1.153 | 0.867 | |
| Forecast Period | Error Indicator | QJ | LZ | GG | WZ |
|---|---|---|---|---|---|
| 1 month | NSE | 0.950 | 0.960 | 0.954 | 0.955 |
| RMSE (103 m3/s) | 0.249 | 0.241 | 0.221 | 0.833 | |
| MAE (103 m3/s) | 0.203 | 0.210 | 0.195 | 0.698 | |
| 2 month | NSE | 0.897 | 0.901 | 0.889 | 0.893 |
| RMSE (103 m3/s) | 0.295 | 0.274 | 0.243 | 1.310 | |
| MAE (103 m3/s) | 0.266 | 0.280 | 0.244 | 0.832 | |
| 3 month | NSE | 0.858 | 0.863 | 0.859 | 0.849 |
| RMSE (103 m3/s) | 0.312 | 0.290 | 0.269 | 1.664 | |
| MAE (103 m3/s) | 0.297 | 0.321 | 0.276 | 0.920 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Gao, H.; Tian, Y.; Jiang, Y.; Li, Z.; Guo, L. Runoff Prediction in the Xijiang River Basin Based on Long Short-Term Memory with Variant Models and Its Interpretable Analysis. Water 2023, 15, 3184. https://doi.org/10.3390/w15183184
Tian Q, Gao H, Tian Y, Jiang Y, Li Z, Guo L. Runoff Prediction in the Xijiang River Basin Based on Long Short-Term Memory with Variant Models and Its Interpretable Analysis. Water. 2023; 15(18):3184. https://doi.org/10.3390/w15183184
Chicago/Turabian StyleTian, Qingqing, Hang Gao, Yu Tian, Yunzhong Jiang, Zexuan Li, and Lei Guo. 2023. "Runoff Prediction in the Xijiang River Basin Based on Long Short-Term Memory with Variant Models and Its Interpretable Analysis" Water 15, no. 18: 3184. https://doi.org/10.3390/w15183184
APA StyleTian, Q., Gao, H., Tian, Y., Jiang, Y., Li, Z., & Guo, L. (2023). Runoff Prediction in the Xijiang River Basin Based on Long Short-Term Memory with Variant Models and Its Interpretable Analysis. Water, 15(18), 3184. https://doi.org/10.3390/w15183184





