Characteristics of Hydrological and Meteorological Drought Based on Intensity-Duration-Frequency (IDF) Curves
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. Standardized Drought Indices
2.2.1. Standard Precipitation Index (SPI)
2.2.2. Standard Precipitation Evapotranspiration Index (SPEI)
2.2.3. Standardized Streamflow Index (SSI)
3. Methodology and Basic Concepts
3.1. Basic Concepts
3.2. Methodology
- ∗
- The proposed methodology calculates the DI with any drought index. In this research, there are three ways, two of which are meteorological drought indices SPI and SPEI, and the other is the hydrological drought index SSI.
- ∗
- Determination of whether the month is dry or wet based on the drought definition using DI according to run and SPI theories. This point provides added value to this research because it is based on a comprehensive definition of drought characteristics.
- ∗
- Determination of the specific drought duration (SD).
- ∗
- Calculation of the maximum consecutive severity (MCS) and critical intensity (CI) for each specific duration (SD). CISD is assigned to the last month and year of the drought duration. (See Figure 2).

- ∗
- Finding the years with CI value and those without drought events.
- ∗
- Frequency analysis includes the return period (T) determination, which can be 2-year, 10-year, or 500-year. The probability for each return period P(T) is calculated using Equation (4); the probability of years without any critical intensity P(0) by Equation (5); the probability of drought years P(d) or non-zero years by Equation (6).
- ∗
- The probability cumulative distribution function (CDF) of the drought years (non-zero values) at zero level is calculable in Equation (8). This probability will predict the critical intensity (CI) for each drought duration and return period.
4. Results and Discussion
5. Conclusions
- To comprehensively understand and analyze drought characteristics, there is a need to divide a drought event into many specific drought duration intervals. Consequently, the severity and intensity of each specific drought duration should be evaluated.
- Drought characteristics are different based on drought definition. Both SPI and run theory must then be carried out to obtain the extreme drought characteristics.
- The normal probability distribution function was the dominant and suitable PDF for critical intensity values.
- Developed IDF drought curves should be used directly by designers and decision-makers for design and risk assessment purposes because of their simplicity and ease of interpretation, precise quantification, and practical application.
- Based on the dry years for both the run and SPI theories, the specific drought duration remained between 9 and 14 months. Data were insufficient for a specific drought duration longer than 14 months for deriving a suitable PDF.
- For 2 years return period, the IDF drought curve was calculated up to 4 months of specific drought duration. The CI for a longer specific drought duration cannot be calculated.
- Compared to the conventional risk analysis methods which depend on the drought events, the new concepts and framework provide us with a comprehensive understanding and range of choices regarding drought duration and return period.
- One of the major outcomes of our research is to provide water managers and suppliers with a new tool and approach to making decisions on appropriate management actions regarding drought frequency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sai, M.; Murthy, C.; Chandrasekar, K.; Jeyaseelan, A.; Diwakar, P.; Dadhwal, V. Agricultural drought: Assessment & monitoring. Mausam 2016, 67, 131–142. [Google Scholar]
- Du, C.; Chen, J.; Nie, T. Spatial–temporal changes in meteorological and agricultural droughts in Northeast China: Change patterns, response relationships and causes. Nat. Hazards 2021, 110, 155–173. [Google Scholar] [CrossRef]
- Caloiero, T.; Veltri, S.; Caloiero, P.; Frustaci, F. Drought Analysis in Europe and in the Mediterranean Basin Using the Standardized Precipitation Index. Water 2018, 10, 1043. [Google Scholar] [CrossRef]
- Stathi, E.; Kastridis, A.; Myronidis, D. Analysis of Hydrometeorological Characteristics and Water Demand in Semi-Arid Mediterranean Catchments under Water Deficit Conditions. Climate 2023, 11, 137. [Google Scholar] [CrossRef]
- UNESCO; UN-Water. United Nations World Water Development Report 2020: Water and Climate Change; UNESCO: Paris, France, 2020. [Google Scholar]
- Wilhite, D.A. Drought as a Natural Hazard: Concepts and Definitions. In Drought: A Global Assessment; Routledge: London, UK, 2000; pp. 3–18. [Google Scholar]
- Yang, J. Comprehensive drought characteristics analysis based on a nonlinear multivariate drought index. J. Hydrol. 2017, 557, 651–667. [Google Scholar] [CrossRef]
- Stathi, E.; Kastridis, A.; Myronidis, D. Analysis of Hydrometeorological Trends and Drought Severity in Water-Demanding Mediterranean Islands under Climate Change Conditions. Climate 2023, 11, 106. [Google Scholar] [CrossRef]
- Ghebreyesus, D.T.; Sharif, H.O. Development and Assessment of High-Resolution Radar-Based Precipitation Intensity-Duration-Curve (IDF) Curves for the State of Texas. Remote Sens. 2021, 13, 2890. [Google Scholar] [CrossRef]
- Danandeh, M.A.; Vaheddoost, B. Identification of the trends associated with the SPI and SPEI indices across Ankara, Turkey. Theor. Appl. Climatol. 2020, 139, 1531–1542. [Google Scholar] [CrossRef]
- Moccia, B.; Mineo, C.; Ridolfi, E.; Russo, F.; Napolitano, F. SPI-Based Drought Classification in Italy: Influence of Different Probability Distribution Functions. Water 2022, 14, 3668. [Google Scholar] [CrossRef]
- Şen, Z.; Şişman, E.; Dabanli, I. Wet and dry spell feature charts for practical uses. Nat. Hazards 2020, 104, 1975–1986. [Google Scholar] [CrossRef]
- Wilhite, D.A. Managing drought risk in a changing climate. Clim. Res. 2016, 70, 99–102. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Ogunrinde, A.T.; Olasehinde, D.A.; Olotu, Y. Assessing the sensitivity of standardized precipitation evapotranspiration index to three potential evapotranspiration models in Nigeria. Sci. Afr. 2020, 8, e00431. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.Y.; Kleist, Y. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, 2. [Google Scholar] [CrossRef]
- Yevjevich, V.M. Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1967. [Google Scholar]
- Şen, Z. Run-sums of annual flow series. J. Hydrol. 2009, 35, 311–324. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Multivariate real-time assessment of droughts via copula-based multi-site Hazard Trajectories and Fans. J. Hydrol. 2015, 526, 101–115. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Mersin, D.; Tayfur, G.; Vaheddoost, B.; Safari, M.J.S. Historical Trends Associated with Annual Temperature and Precipitation in Aegean Turkey, Where Are We Heading? Sustainability 2022, 14, 13380. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Eslamian, S.; Ostad-Ali-Askari, K.; Singh, V.P.; Dalezios, N.R.; Ghane, M.; Yihdego, Y.; Matouq, M. A review of drought indices. Int. J. Constr. Res. Civ. Eng. 2017, 3, 48–66. [Google Scholar]
- Dalezios, N.R.; Loukas, A.; Vasiliades, L.; Liakopoulos, E. Severity-durationfrequency analysis of droughts and wet periods in Greece. Hydrol. Sci. J. 2001, 45, 751–769. [Google Scholar] [CrossRef]
- Shiau, J.T.; Modarres, R. Copula-based drought severity-duration-frequency analysis in Iran. Meteorol. Appl. 2009, 16, 481–489. [Google Scholar] [CrossRef]
- Halwatura, D.; Lechner, A.M.; Arnold, S. Drought severity–duration–fre quency curves: A foundation for risk assessment and planning tool for ecosystem establishment in post-mining landscapes. Hydrol. Earth Syst. Sci. 2015, 19, 1069–1091. [Google Scholar] [CrossRef]
- Heidari, H.; Arabi, M.; Ghanbari, M.; Warziniack, T. A Probabilistic Approach for Characterization of Sub-Annual Socioeconomic Drought Intensity-Duration-Frequency (IDF) Relationships in a Changing Environment. Water 2020, 12, 1522. [Google Scholar] [CrossRef]
- Ma, M.; Zang, H.; Wang, W.; Cui, H.; Sun, Y.; Cheng, Y. Copula-Based Severity–Duration–Frequency (SDF) Analysis of Streamflow Drought in the Source Area of the Yellow River, China. Water 2023, 15, 2741. [Google Scholar] [CrossRef]
- Jafari, S.M.; Nikoo, M.R.; Sadegh, M.; Chen, M.; Gandomi, A.H. Non-parametric severity-duration-frequency analysis of drought based on satellite-based product and model fusion techniques. Environ. Sci. Pollut. Res. 2023, 30, 42087–42107. [Google Scholar] [CrossRef] [PubMed]
- Won, J.; Kim, S. Future drought analysis using SPI and EDDI to consider climate change in South Korea. Water Supply 2020, 20, 3266–3280. [Google Scholar] [CrossRef]
- Cavus, Y.; Aksoy, H. Critical drought severity/intensity-duration-frequency curves based on precipitation deficit. J. Hydrol. 2020, 584, 124312. [Google Scholar] [CrossRef]
- Pandya, P.; Gontia, N.K. Development of drought severity–duration–frequency curves for identifying drought proneness in semi-arid regions. J. Water Clim. Change 2023, 14, 824–842. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Chen, Z.; Ren, Z. Assessment of candidate distributions for SPI/SPEI and sensitivity of drought to climatic variables in China. Int. J. Climatol. 2019, 39, 4392–4412. [Google Scholar] [CrossRef]
- Stephens, M.A. Use of the Kolmogorov–Smirnov, Cramér–Von Mises and related statistics without extensive tables. J. R. Stat. Soc. 1970, 32B, 115–122. [Google Scholar] [CrossRef]
- Şen, Z.; Almazroui, M. Actual Precipitation Index (API) for Drought classification. Earth Syst. Environ. 2021, 5, 59–70. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop evapotranspiration. In FAO Irrigation and Drainage; FAO: Rome, Italy, 1998; Paper 56. [Google Scholar]
- Abramowitz, M.; Irene, A.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series 5; US Government Printing Office: Washington, DC, USA, 1968; Volume 55.
- Abu Arra, A.; Şişman, E. Investigation of the main difference between the run and SPI theories regarding drought characteristics. AHI EVRAN 3rd Int. Conf. Sci. Res. 2023, 2, 124–134. [Google Scholar]
- Chebbi, A.; Bargaoui, Z.K.; da Conceição Cunha, M. Development of a method of robust rain gauge network optimization based on intensity-duration-frequency results. Hydrol. Earth Syst. Sci. 2013, 17, 4259–4268. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Thorolfsson, S.T.; Alfredsen, K. Regional frequency analysis of extreme precipitation with consideration of uncertainties to update IDF curves for the city of Trondheim. J. Hydrol. 2013, 498, 305–318. [Google Scholar] [CrossRef]
- Elsebaie, I.H.; El Alfy, M.; Kawara, A.Q. Spatiotemporal Variability of Intensity–Duration–Frequency (IDF) Curves in Arid Areas: Wadi AL-Lith, Saudi Arabia as a Case Study. Hydrology 2022, 9, 6. [Google Scholar] [CrossRef]




| Station’s Name | Lat (N) | Long (W) | Monthly Precipitation (P)—mm | Standard Deviation (mm) | Monthly Temperature (T)—°C | Standard Deviation °C |
|---|---|---|---|---|---|---|
| Durham University Station | 54.77 | 1.59 | 54.37 | 31.74 | 8.6 | 4.46 |
| Station’s Name | Lat (N) | Long (E) | Monthly Stream flow (Q)—m3/s | Standard Deviation (m3/s) | - | - |
| Lüleburgaz station | 41.35 | 27.35 | 9.57 | 13.2 | - | - |
| Specific drought duration | SD |
| Total number of years | N |
| Number of drought years | ND |
| Number of years without any drought | N0 = N – ND |
| The probability of years without any drought event | |
| The probability of drought years | |
| Return period | T |
| The probability of each return period | |
| The cumulative probability distribution function of the drought years |
| SD (Month) | |||||
|---|---|---|---|---|---|
| T (Year) | 1 | 2 | 3 | 4 | |
| 2 | 0.5 | ||||
| 5 | 0.2 | ||||
| 10 | 0.1 | ||||
| 25 | 0.04 | ||||
| 50 | 0.02 | ||||
| 100 | 0.01 | ||||
| 200 | 0.005 | ||||
| 500 | 0.002 | ||||
| D (month) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Total Years | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 |
| Years with drought | 81 | 79 | 75 | 65 | 63 | 61 | 55 | 51 | 47 | 43 | 37 | 34 |
| Years without drought | 73 | 75 | 79 | 89 | 91 | 93 | 99 | 103 | 107 | 111 | 117 | 120 |
| P(0) | 0.47 | 0.49 | 0.51 | 0.58 | 0.59 | 0.60 | 0.64 | 0.67 | 0.69 | 0.72 | 0.76 | 0.78 |
| P(d) | 0.53 | 0.51 | 0.49 | 0.42 | 0.41 | 0.40 | 0.36 | 0.33 | 0.31 | 0.28 | 0.24 | 0.22 |
| Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | Nor. | |
| −1.5 | −1.39 | −1.34 | −1.35 | −1.35 | −1.33 | −1.35 | −1.34 | −1.28 | −1.29 | −1.14 | −1 | |
| 0.57 | 0.59 | 0.58 | 0.59 | 0.59 | 0.59 | 0.58 | 0.57 | 0.55 | 0.54 | 0.49 | 0.44 | |
| T (Year) | Critical Intensity (CI) for 12 months | |||||||||||
| 5 | −1.67 | −1.55 | −1.47 | −1.39 | −1.36 | −1.32 | −1.26 | −1.15 | −1.06 | −0.98 | −0.67 | −0.42 |
| 10 | −2.00 | −1.90 | −1.82 | −1.77 | −1.76 | −1.72 | −1.69 | −1.60 | −1.52 | −1.49 | −1.24 | −1.05 |
| 25 | −2.31 | −2.23 | −2.15 | −2.12 | −2.11 | −2.08 | −2.06 | −1.96 | −1.90 | −1.87 | −1.62 | −1.40 |
| 50 | −2.51 | −2.43 | −2.35 | −2.33 | −2.32 | −2.30 | −2.27 | −2.19 | −2.11 | −2.08 | −1.82 | −1.59 |
| 100 | −2.68 | −2.61 | −2.52 | −2.51 | −2.51 | −2.48 | −2.46 | −2.37 | −2.29 | −2.26 | −2.00 | −1.75 |
| 200 | −2.83 | −2.76 | −2.69 | −2.68 | −2.68 | −2.64 | −2.62 | −2.54 | −2.46 | −2.42 | −2.14 | −1.88 |
| 500 | −3.02 | −2.95 | −2.88 | −2.87 | −2.87 | −2.85 | −2.81 | −2.73 | −2.63 | −2.61 | −2.32 | −2.04 |
| Timescale = 3 Months | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
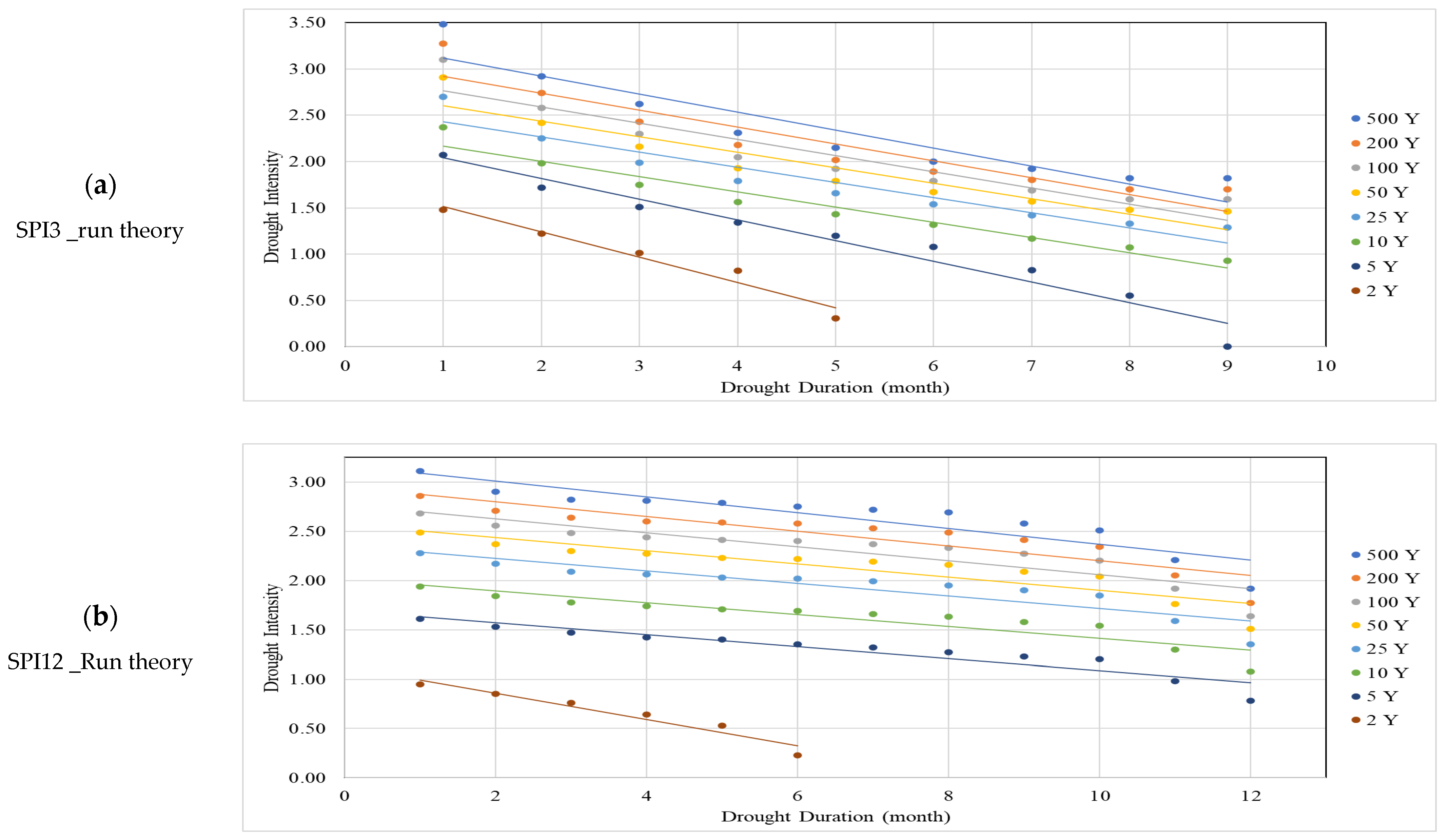
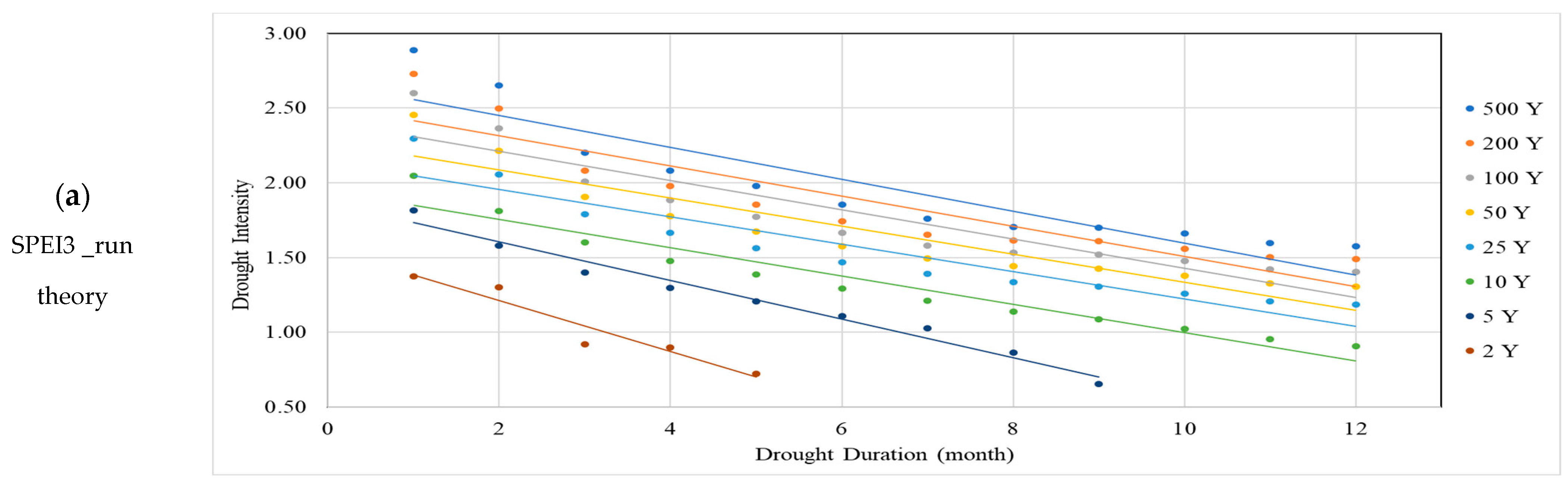
| SPI_Run Theory | SPI_SPI Theory | SPEI_Run Theory | SPEI_SPI Theory | |||||||||
| T (Year) | Max. D | Max. I | Slope | Max. D | Max. I | Slope | Max. D | Max. I | Slope | Max. D | Max. I | Slope |
| 2 | 6.5 | 1.79 | 0.274 | 4.4 | 2.06 | 0.495 | 9.1 | 1.55 | 0.171 | 6.3 | 1.73 | 0.276 |
| 5 | 11.0 | 2.17 | 0.197 | 9.0 | 2.31 | 0.257 | 14.4 | 1.86 | 0.129 | 11.4 | 1.97 | 0.173 |
| 10 | 14.1 | 2.33 | 0.165 | 10.5 | 2.53 | 0.24 | 20.4 | 1.94 | 0.095 | 13.3 | 2.13 | 0.16 |
| 25 | 15.9 | 2.59 | 0.163 | 14.6 | 2.63 | 0.18 | 23.5 | 2.14 | 0.091 | 18.1 | 2.21 | 0.122 |
| 50 | 16.5 | 2.77 | 0.168 | 16.3 | 2.77 | 0.17 | 24.1 | 2.27 | 0.094 | 20.1 | 2.31 | 0.115 |
| 100 | 16.8 | 2.94 | 0.175 | 16.8 | 2.92 | 0.174 | 24.6 | 2.41 | 0.098 | 21.6 | 2.4 | 0.111 |
| 200 | 16.9 | 3.1 | 0.183 | 17.3 | 3.05 | 0.176 | 25.0 | 2.52 | 0.101 | 22.1 | 2.48 | 0.112 |
| 500 | 17.1 | 3.31 | 0.1942 | 17.9 | 3.2 | 0.179 | 25.0 | 2.67 | 0.107 | 24.1 | 2.58 | 0.107 |
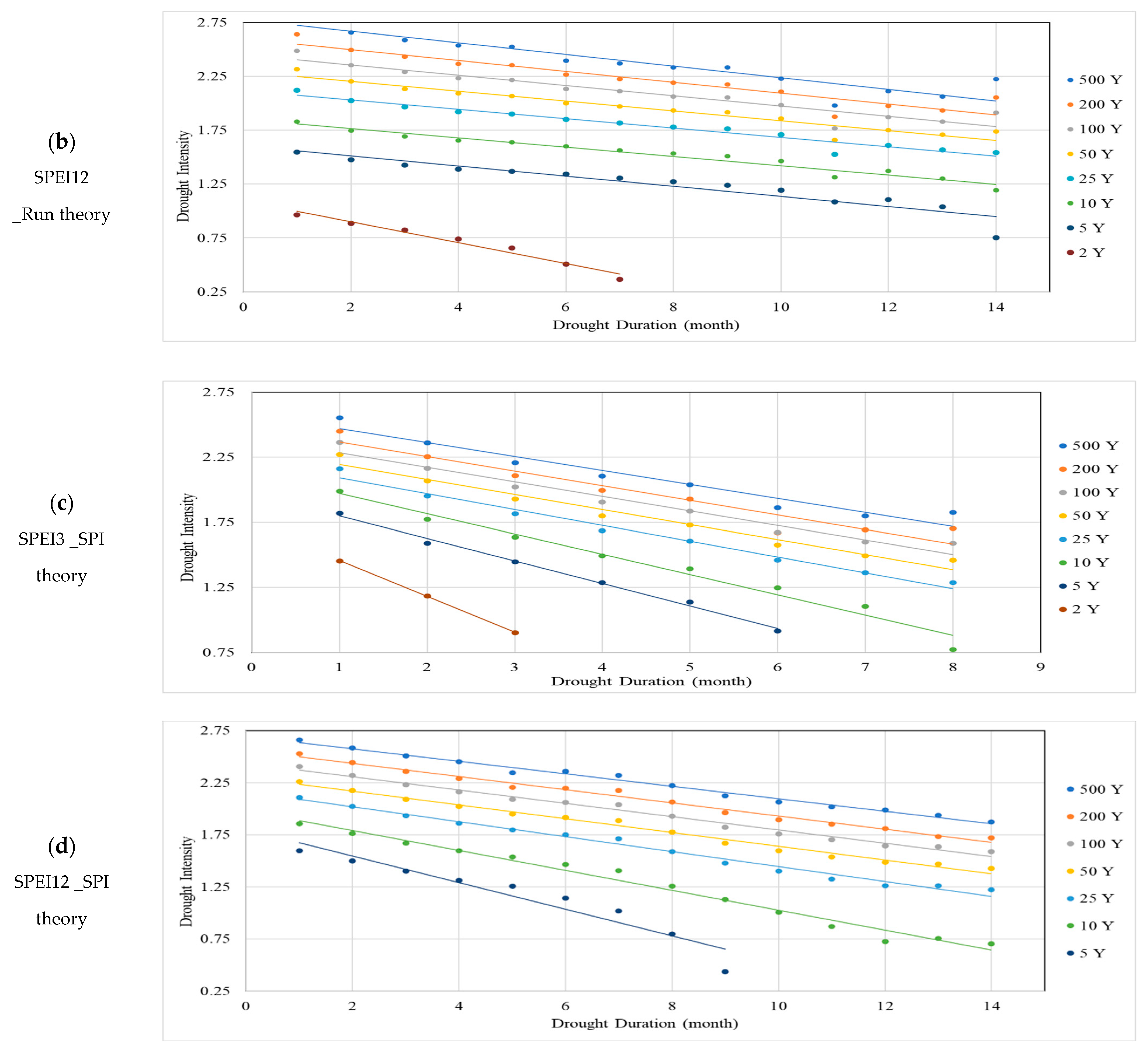
| Timescale = 12 Months | ||||||||||||
| SPI_Run Theory | SPI_SPI Theory | SPEI_Run Theory | SPEI_SPI Theory | |||||||||
| T (Year) | Max. D | Max. I | Slope | Max. D | Max. I | Slope | Max. D | Max. I | Slope | Max. D | Max. I | Slope |
| 2 | 9.6 | 1.28 | 0.134 | - | - | - | 11.2 | 1.1 | 0.098 | - | - | - |
| 5 | 27.9 | 1.7 | 0.061 | 19.0 | 1.82 | 0.096 | 34.3 | 1.61 | 0.047 | 13.8 | 1.8 | 0.13 |
| 10 | 33.5 | 2.01 | 0.06 | 29.2 | 2.1 | 0.072 | 43.0 | 1.85 | 0.043 | 20.6 | 1.98 | 0.096 |
| 25 | 36.7 | 2.35 | 0.064 | 36.1 | 2.42 | 0.067 | 48.2 | 2.12 | 0.044 | 30.0 | 2.16 | 0.072 |
| 50 | 38.4 | 2.57 | 0.067 | 39.1 | 2.62 | 0.067 | 50.0 | 2.3 | 0.046 | 34.8 | 2.3 | 0.066 |
| 100 | 39.0 | 2.77 | 0.071 | 41.8 | 2.8 | 0.067 | 51.0 | 2.45 | 0.048 | 38.1 | 2.44 | 0.064 |
| 200 | 39.3 | 2.95 | 0.075 | 43.7 | 2.97 | 0.068 | 52.0 | 2.6 | 0.05 | 40.6 | 2.56 | 0.063 |
| 500 | 39.6 | 3.17 | 0.08 | 45.3 | 3.17 | 0.07 | 51.5 | 2.78 | 0.054 | 45.0 | 2.7 | 0.06 |
| Timescale = 3 Months | Timescale = 12 Months | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSI_Run Theory | SSI_SPI Theory | SSI_Run Theory | SSI_SPI Theory | |||||||||
| T (Year) | Max. D | Max. I | Slope | Max. D | Max. I | Slope | Max. D | Max. I | Slope | Max. D | Max. I | Slope |
| 2 | 9.30 | 1.06 | 0.114 | - | - | - | 9.1 | 0.48 | 0.053 | - | - | - |
| 5 | 35.00 | 1.4 | 0.04 | 32.4 | 1.46 | 0.045 | 46.2 | 1.34 | 0.029 | 46.5 | 1.44 | 0.031 |
| 10 | 42.37 | 1.61 | 0.038 | 38.9 | 1.71 | 0.044 | 43.9 | 1.67 | 0.038 | 42.9 | 1.76 | 0.041 |
| 25 | 52.57 | 1.84 | 0.035 | 37.9 | 1.97 | 0.052 | 42.9 | 2 | 0.0466 | 39.8 | 2.07 | 0.052 |
| 50 | 43.91 | 2.02 | 0.046 | 36.6 | 2.12 | 0.058 | 42.3 | 2.2 | 0.052 | 37.5 | 2.25 | 0.06 |
| 100 | 43.20 | 2.16 | 0.05 | 35.3 | 2.26 | 0.064 | 41.8 | 2.38 | 0.057 | 37.1 | 2.41 | 0.065 |
| 200 | 42.59 | 2.3 | 0.054 | 34.5 | 2.38 | 0.069 | 41.0 | 2.54 | 0.062 | 36.1 | 2.56 | 0.071 |
| 500 | 41.17 | 2.47 | 0.06 | 33.4 | 2.54 | 0.076 | 39.7 | 2.74 | 0.069 | 35.7 | 2.71 | 0.076 |
| SPI12 Using Conventional Method | SPI12 Using IDF Drought Curves | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| T (Years) | |||||||||
| Duration (m) | Average | Maximum | 5 | 10 | 25 | 50 | 100 | 200 | 500 |
| 2 | −0.82 | −1.28 | −1.55 | −1.9 | −2.23 | −2.43 | −2.61 | −2.76 | −2.95 |
| 3 | −1.36 | −0.94 | −1.47 | −1.82 | −2.15 | −2.35 | −2.52 | −2.69 | −2.88 |
| 4 | - (*) | - | −1.39 | −1.77 | −2.12 | −2.33 | −2.51 | −2.68 | −2.87 |
| 5 | - | - | −1.36 | −1.76 | −2.11 | −2.32 | −2.51 | −2.68 | −2.87 |
| 6 | −0.87 | −1.11 | −1.32 | −1.72 | −2.08 | −2.3 | −2.48 | −2.64 | −2.85 |
| 7 | −0.75 | −1.25 | −1.26 | −1.69 | −2.06 | −2.27 | −2.46 | −2.62 | −2.81 |
| 8 | −1.19 | −2.02 | −1.15 | −1.6 | −1.96 | −2.19 | −2.37 | −2.54 | −2.73 |
| 9 | −0.65 | −1.01 | −1.06 | −1.52 | −1.9 | −2.11 | −2.29 | −2.46 | −2.63 |
| 10 | −1.1 | −1.6 | −0.98 | −1.49 | −1.87 | −2.08 | −2.26 | −2.42 | −2.61 |
| 11 | −0.53 | −1.22 | −0.67 | −1.24 | −1.62 | −1.82 | −2 | −2.14 | −2.32 |
| 12 | - | - | −0.42 | −1.05 | −1.4 | −1.59 | −1.75 | −1.88 | −2.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu Arra, A.; Şişman, E. Characteristics of Hydrological and Meteorological Drought Based on Intensity-Duration-Frequency (IDF) Curves. Water 2023, 15, 3142. https://doi.org/10.3390/w15173142
Abu Arra A, Şişman E. Characteristics of Hydrological and Meteorological Drought Based on Intensity-Duration-Frequency (IDF) Curves. Water. 2023; 15(17):3142. https://doi.org/10.3390/w15173142
Chicago/Turabian StyleAbu Arra, Ahmad, and Eyüp Şişman. 2023. "Characteristics of Hydrological and Meteorological Drought Based on Intensity-Duration-Frequency (IDF) Curves" Water 15, no. 17: 3142. https://doi.org/10.3390/w15173142






