Non-Equilibrium Bedload Transport Model Applied to Erosive Overtopping Dambreach
Abstract
:1. Introduction
2. Mathematical Modelling of 2D Generalized Bedload Transport
3. Numerical Scheme for the 2D Bedload Transport Model
3.1. Transport Layer Updating with Capacity and Non-Capacity Approaches
- Equilibrium hypothesis: The new transport layer thickness is directly computed as:where is the Shields excess (7) at the i cell computed from the updated conservative variables .
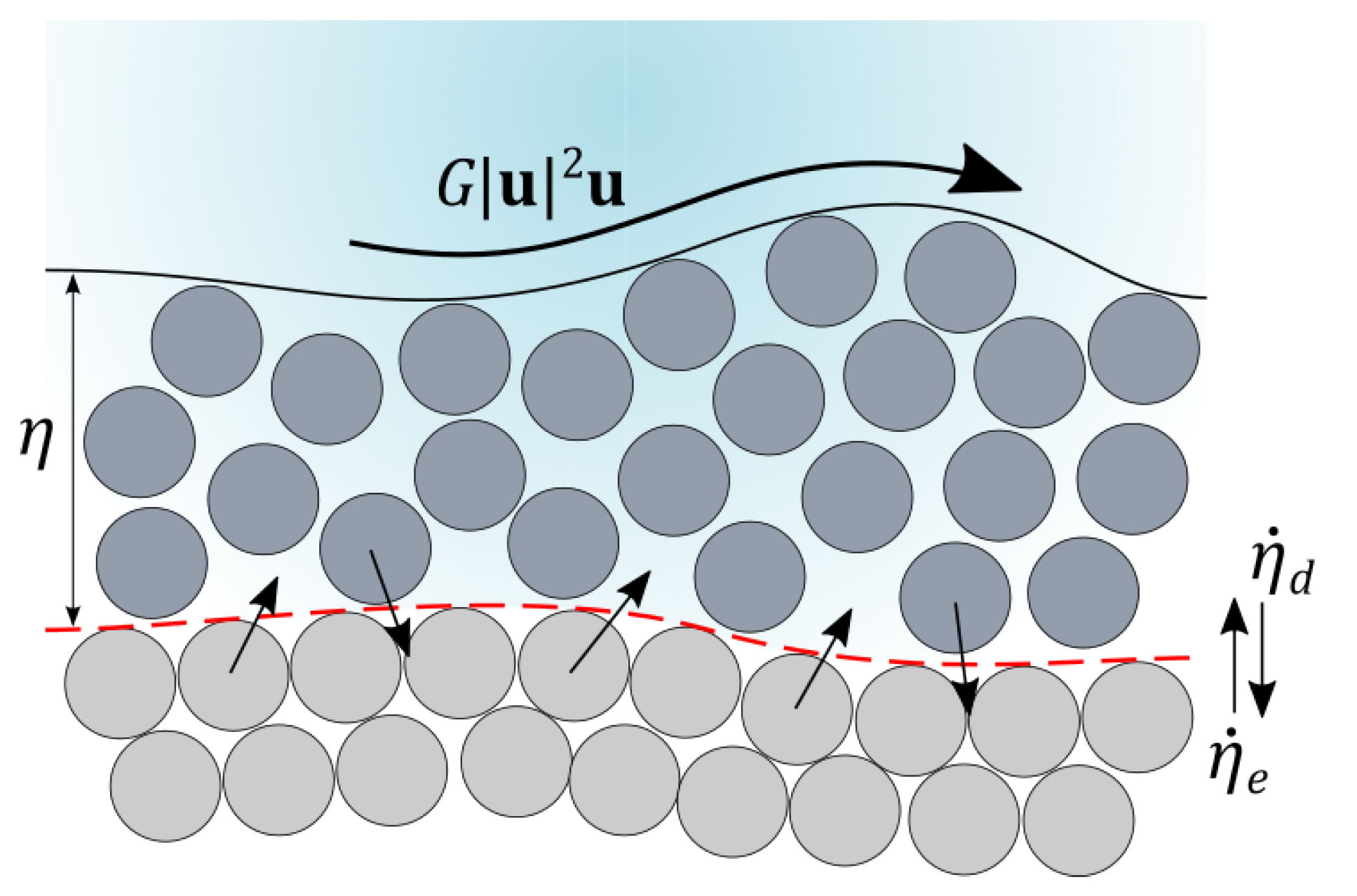
- Non-capacity approach: This leads to the necessity of solving Equation (9) each time step. The updating formula for the transport layer thickness is expressed as:being the numerical normal flux at the kth intercell edge for the transport layer equation and and the values of the entrainment and deposition rates for the i cell at time n, respectively. To compute the numerical flux , the bedload transport layer Equation (9) is projected along the normal direction to the edge and approximated by the local scalar Riemann problem:where the virtual bedload wave celerity is defined as:being and , and the bedload numerical flux is computed as:The cell-centered exchange rates and between the underlying static stratum and the transport layer are computed as:
3.2. Morphological Collapse Mechanism
- Positive bed slope if
- Negative bed slope if
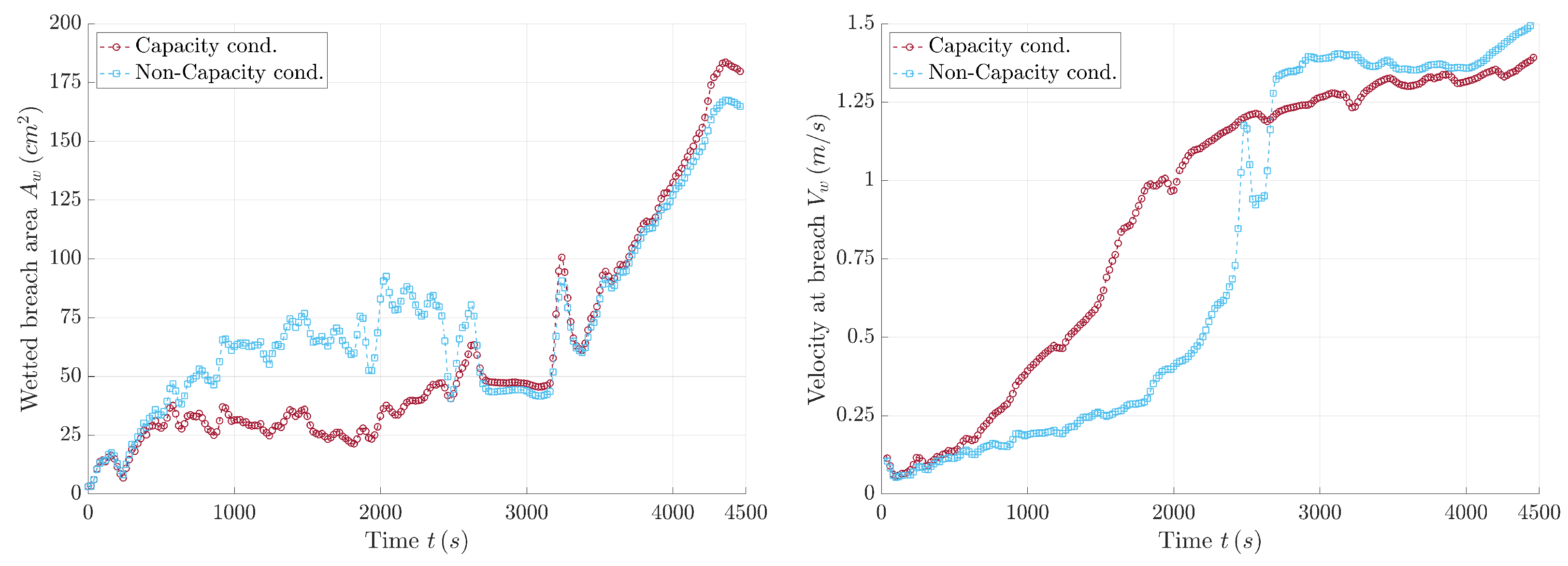
4. Numerical Results and Discussion
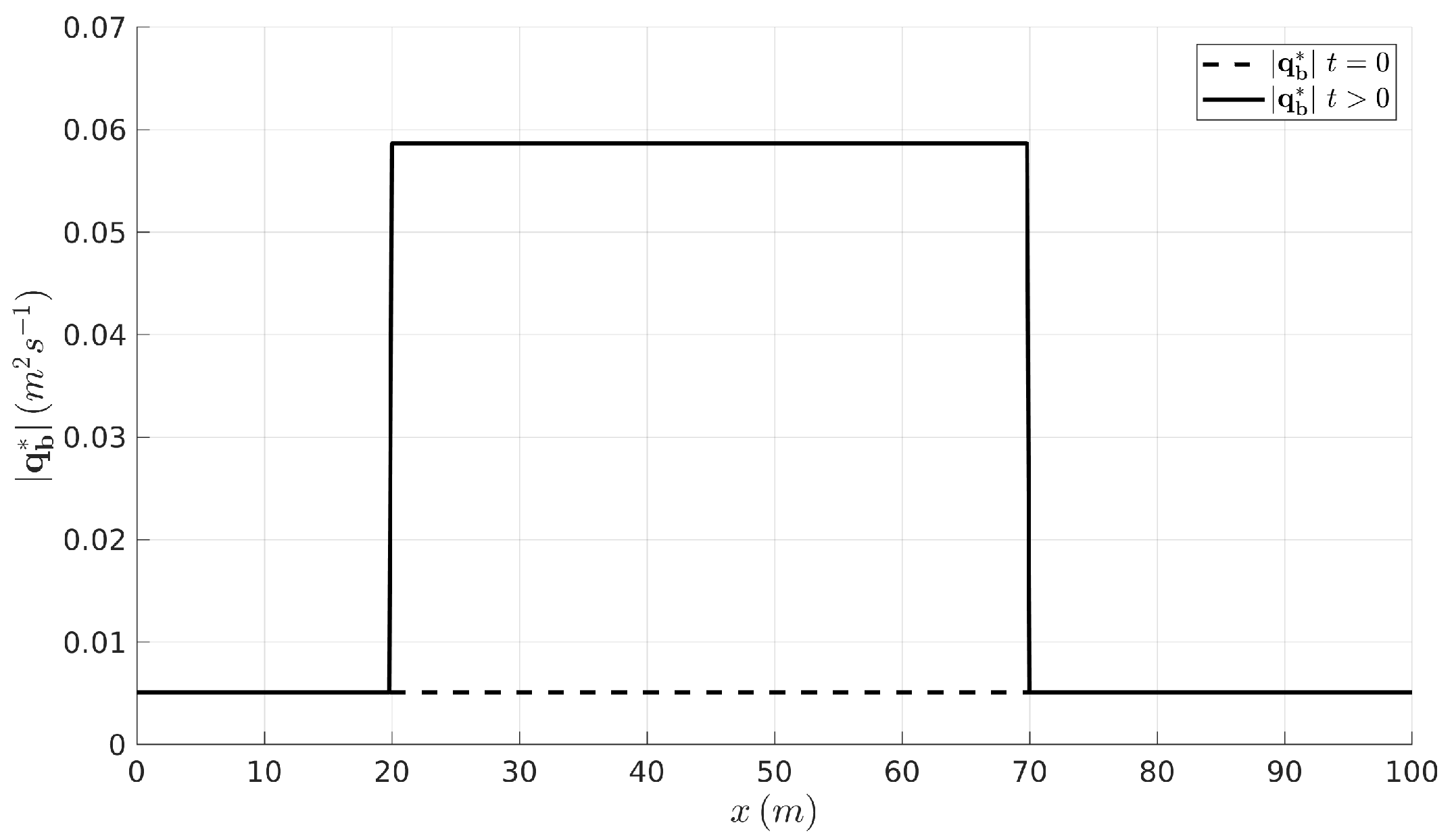
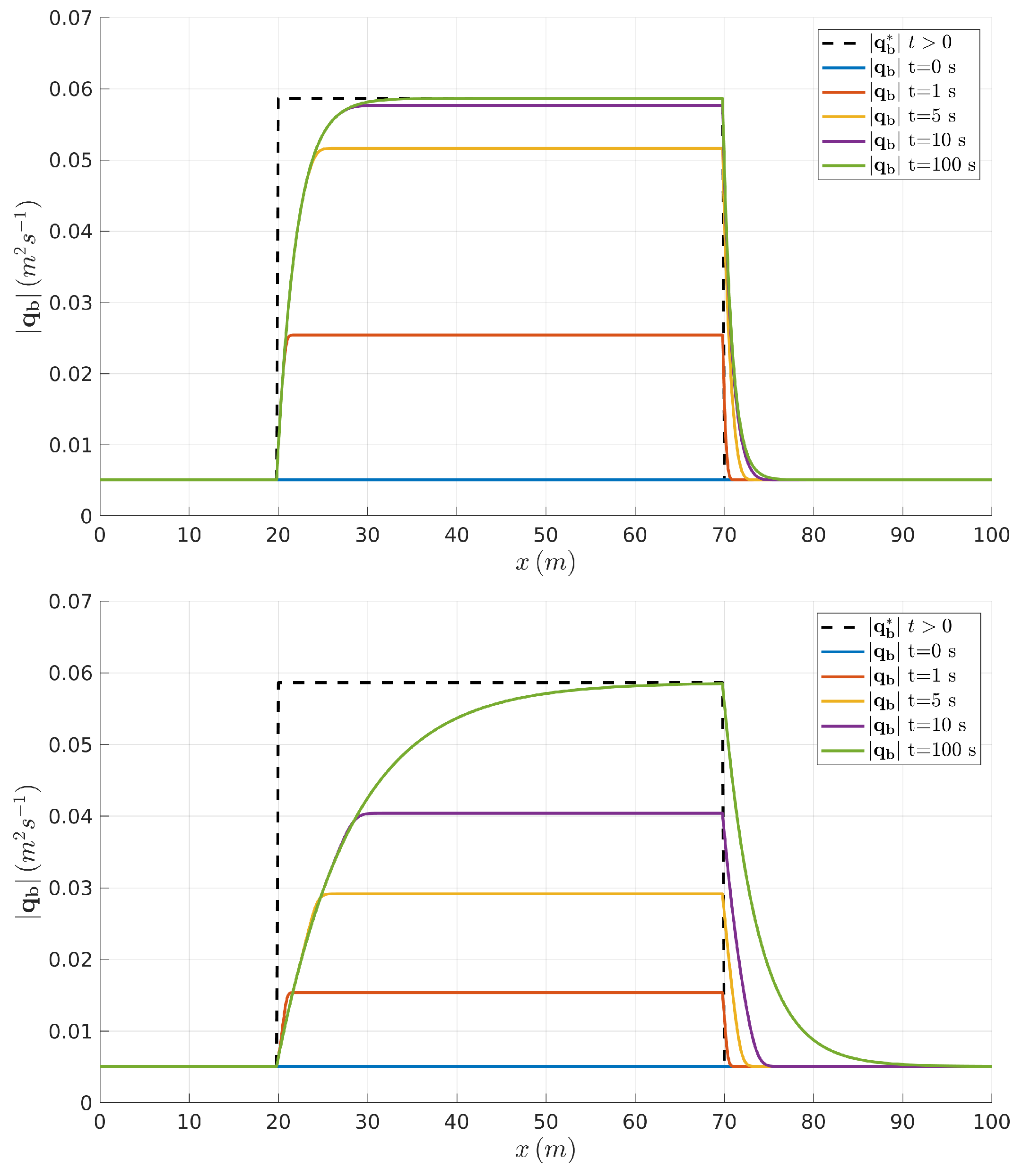
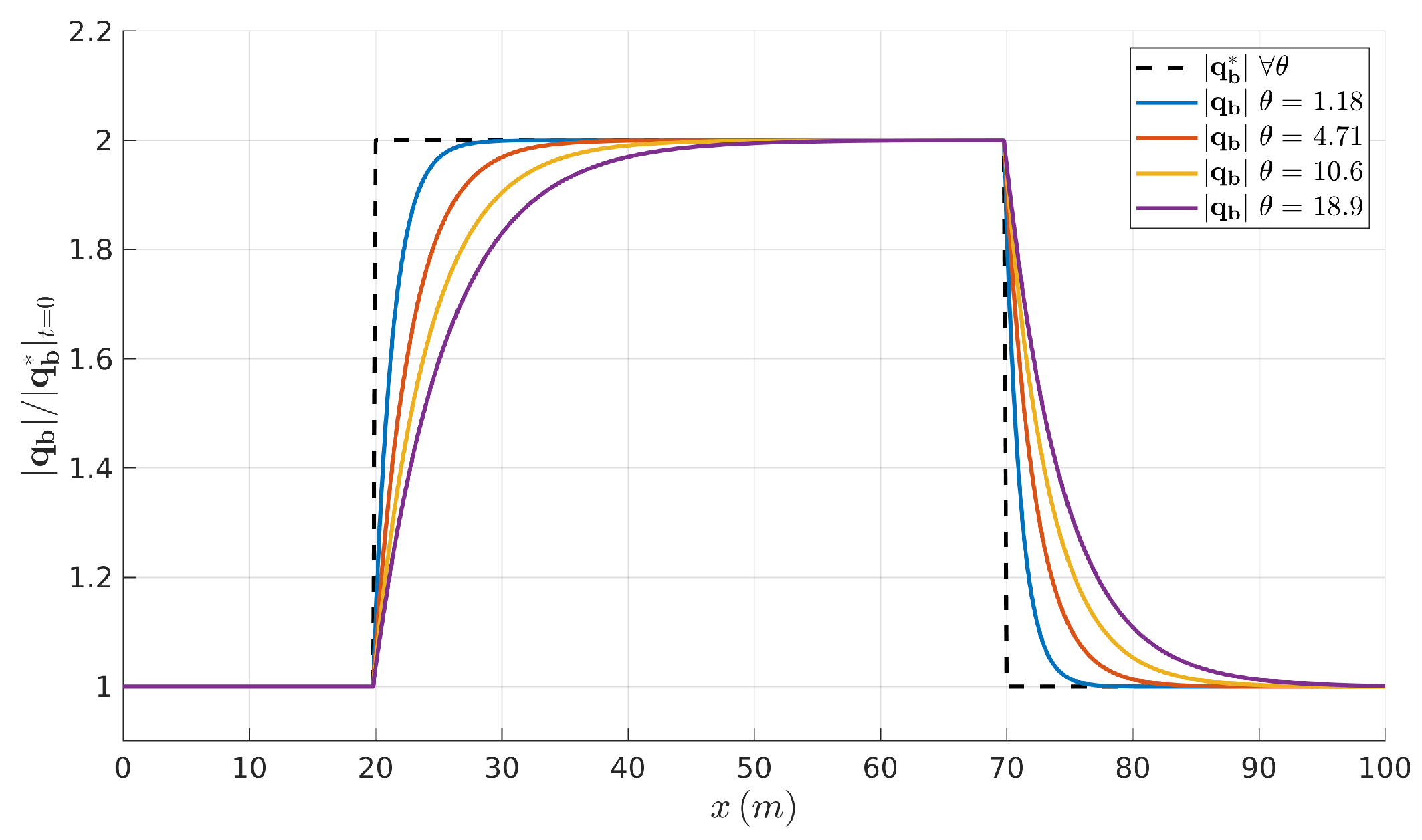
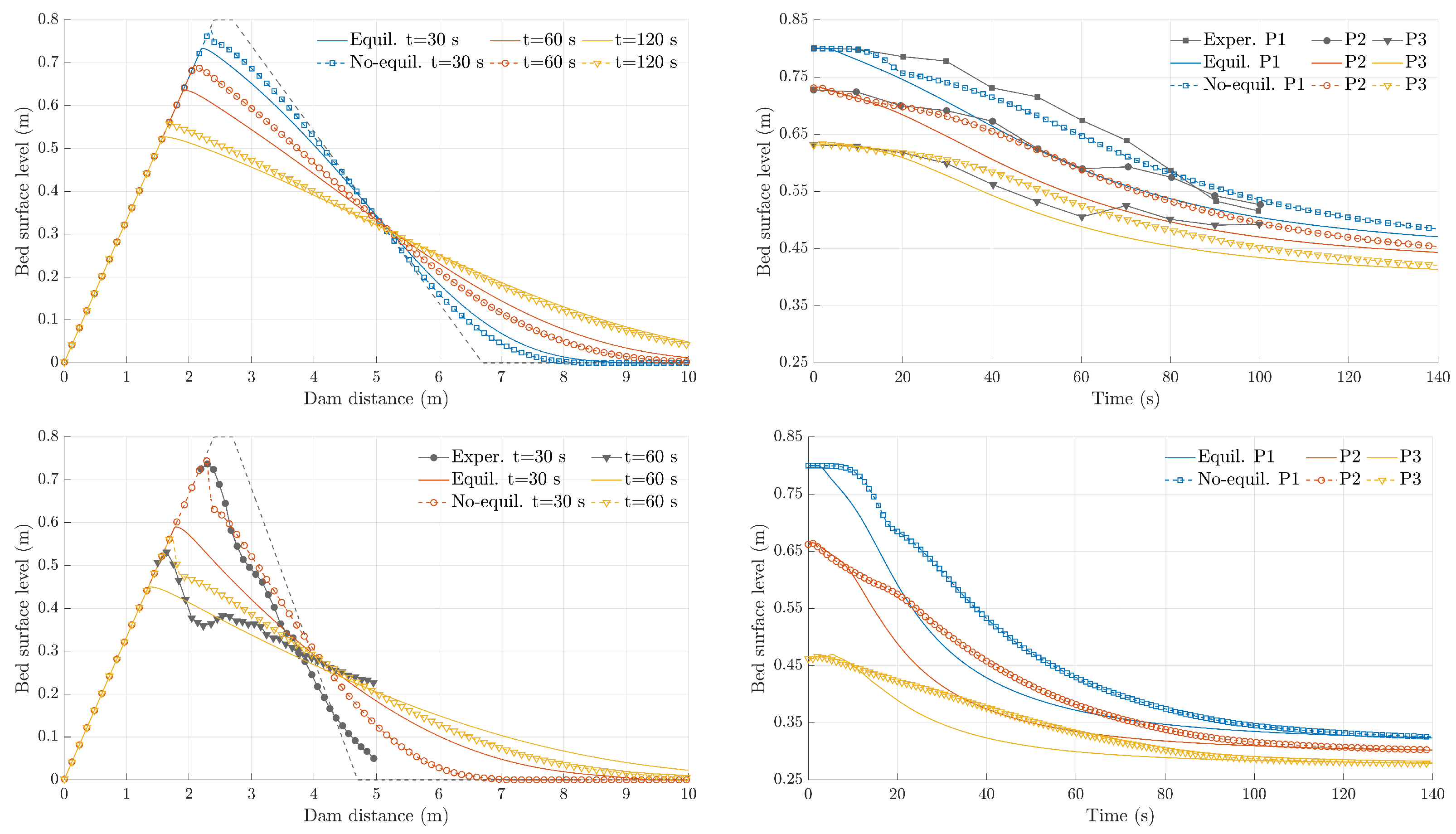
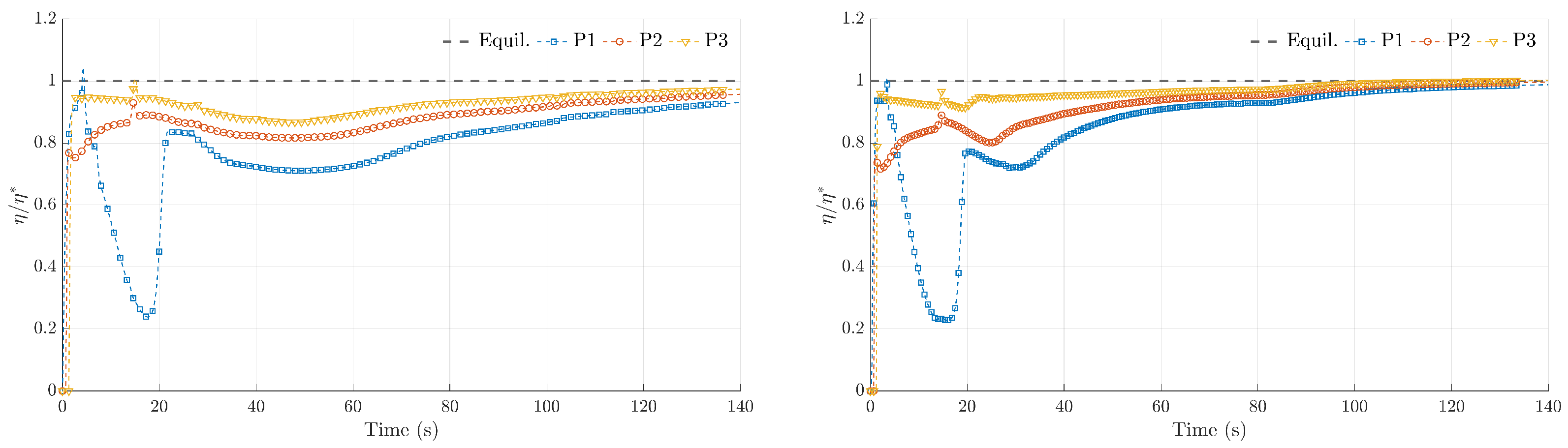
4.1. Adaptation of the Non-Equilibrium Bedload Rate to Equilibrium States
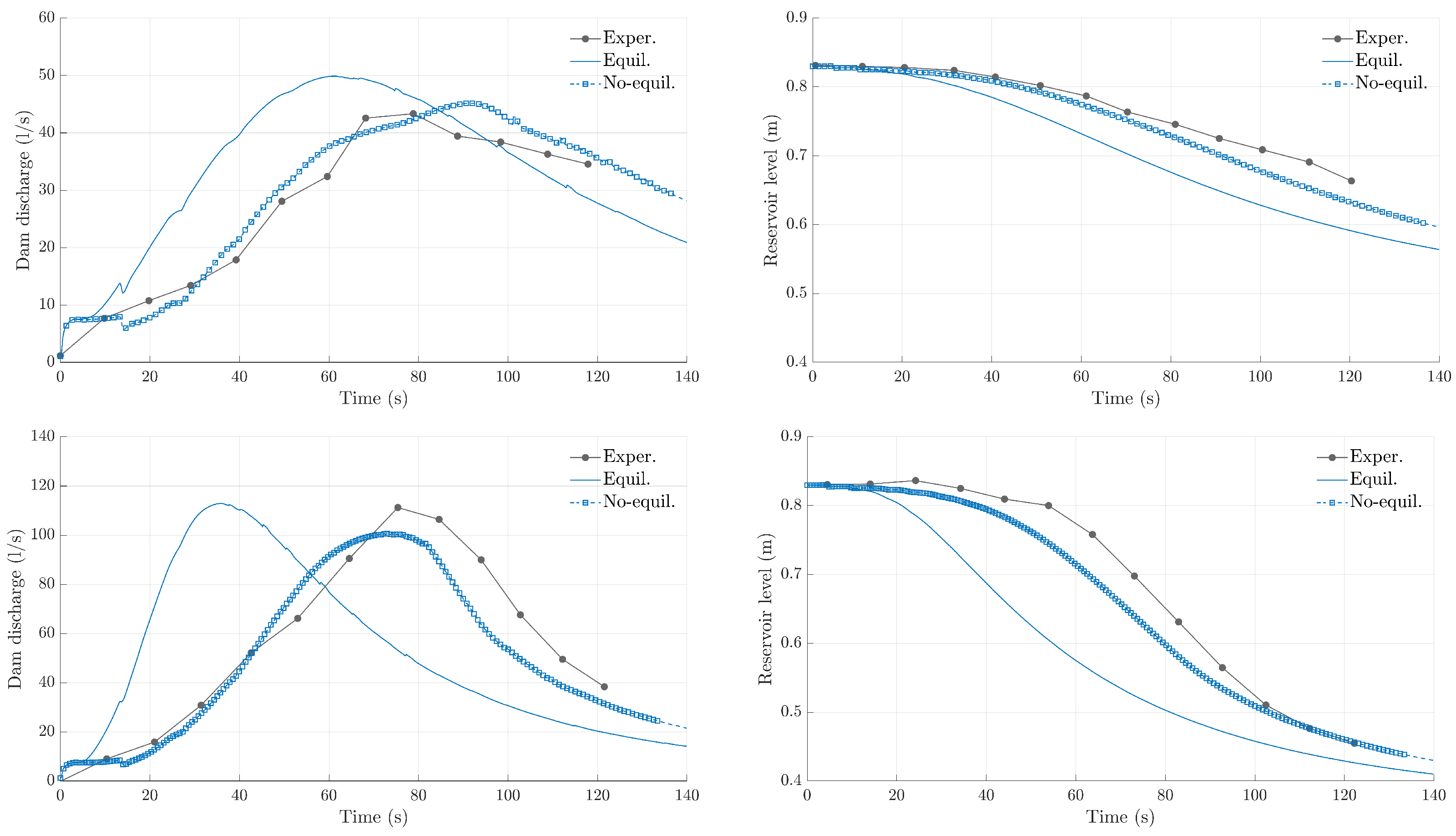
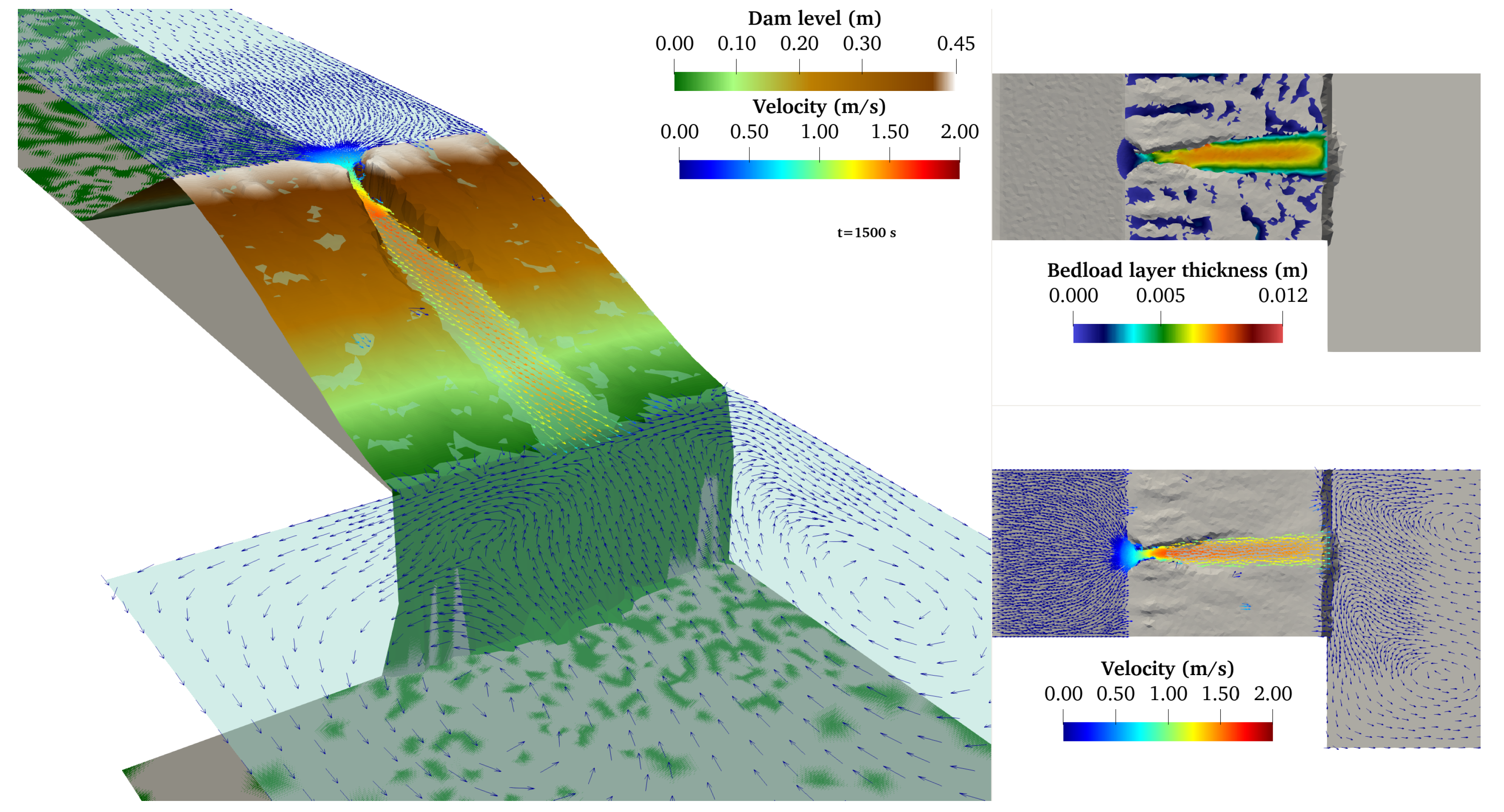
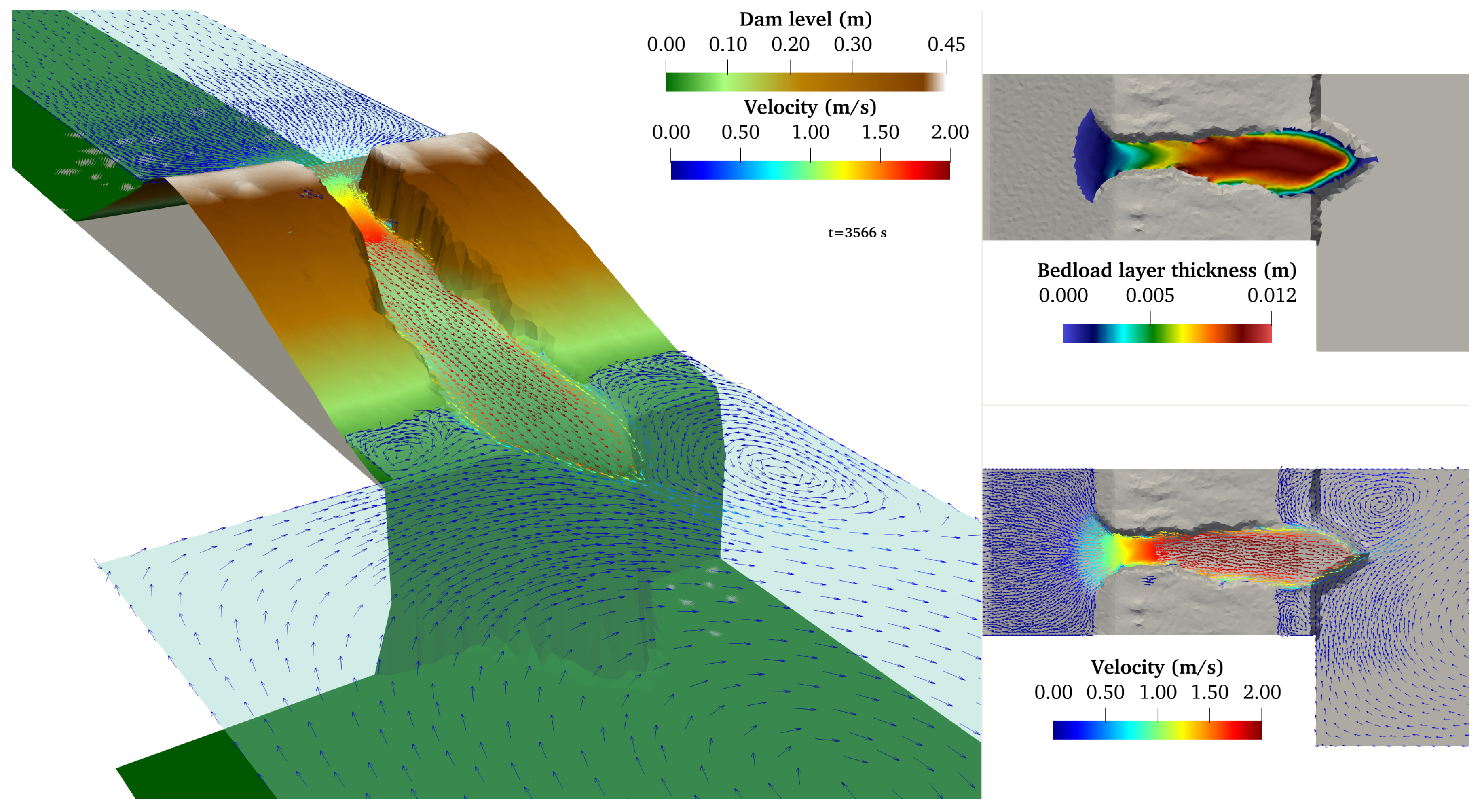
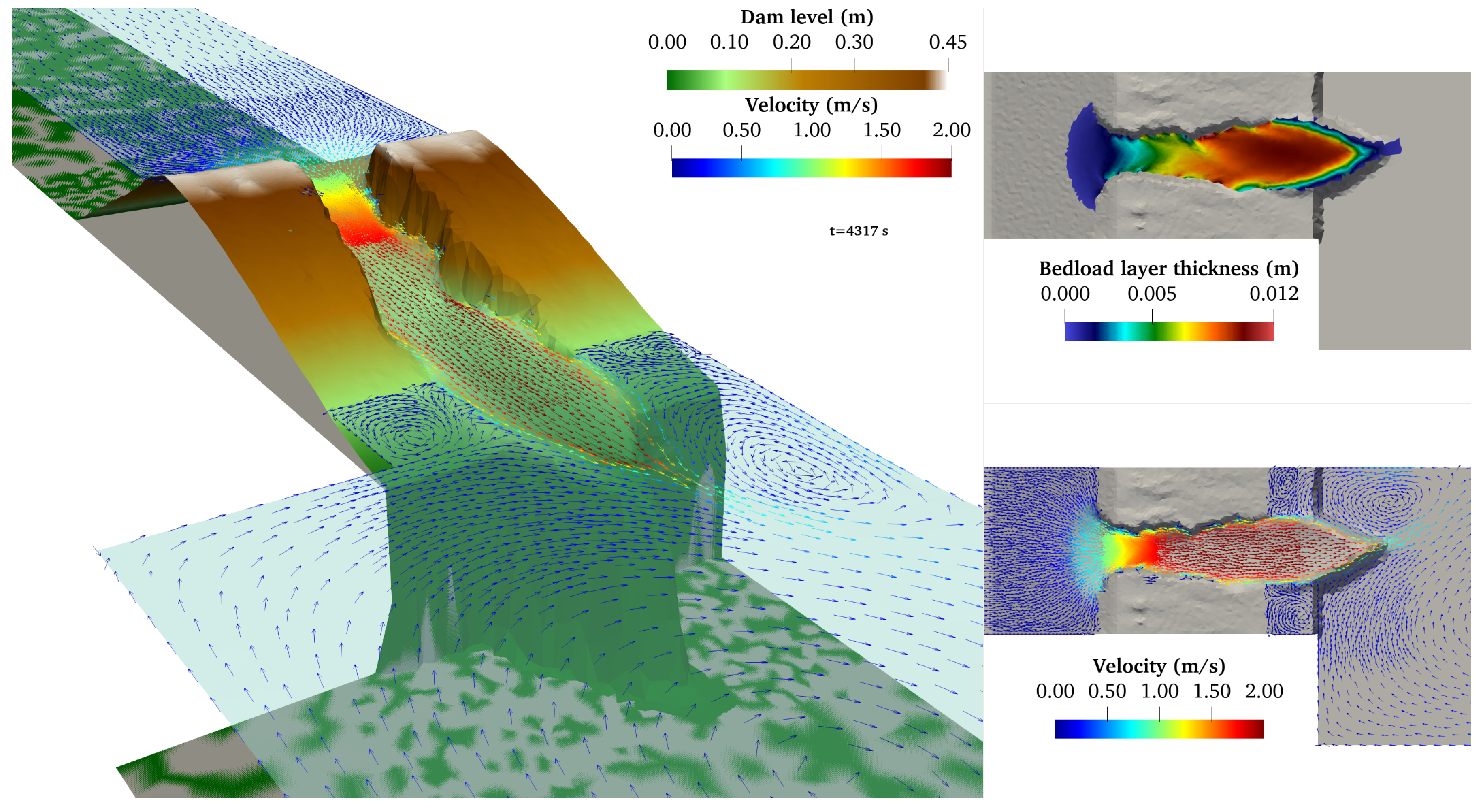
4.2. Dike Breaking by Overtopping Flow Erosion
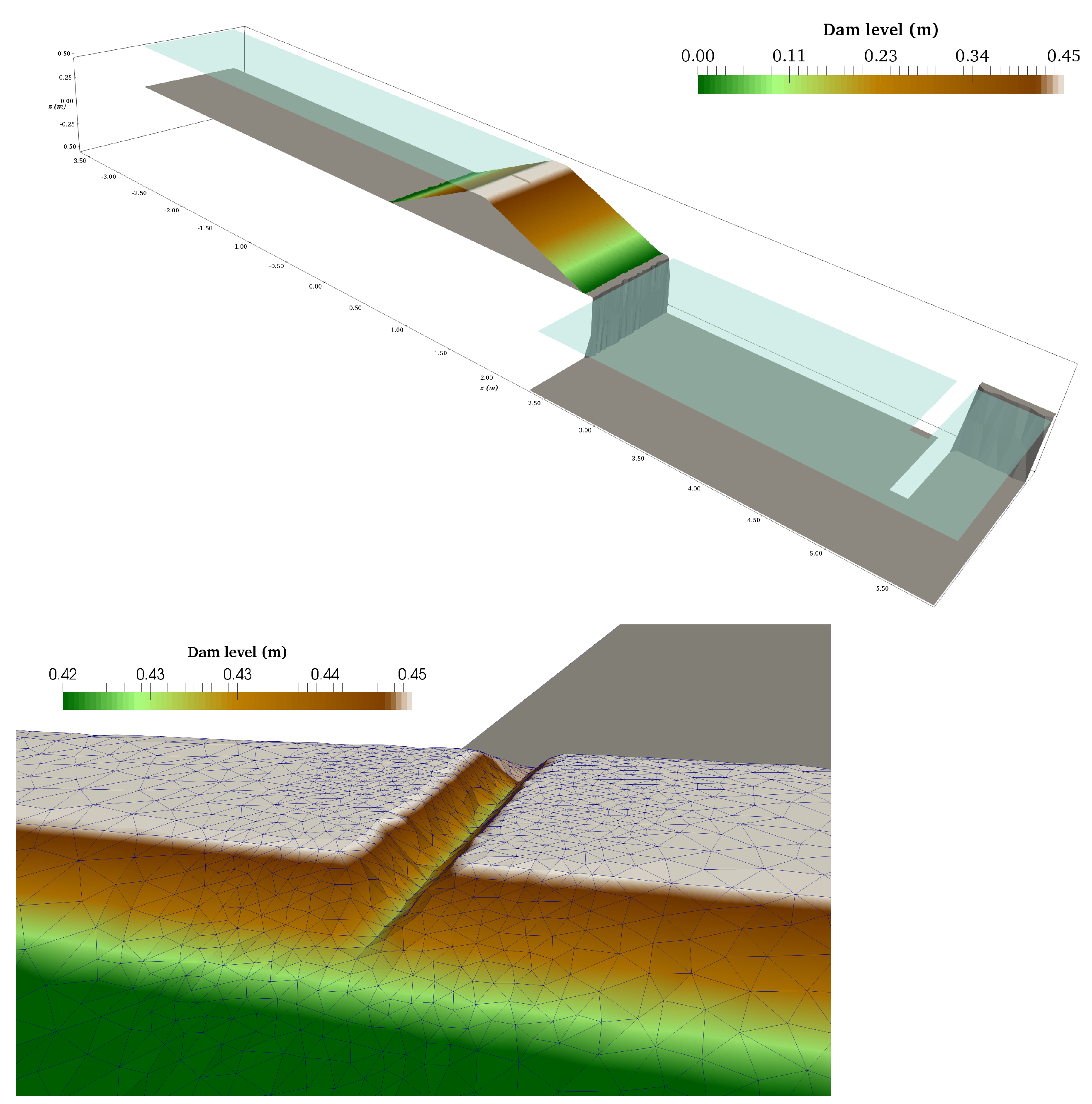
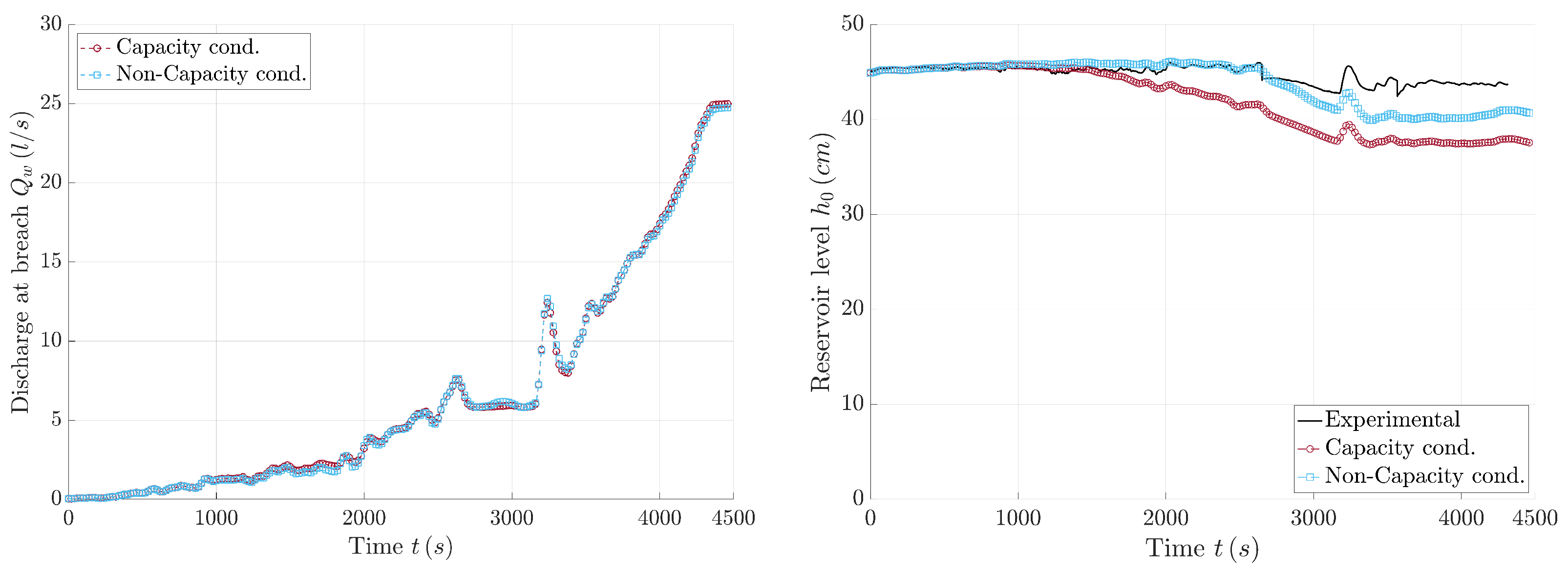
4.3. Breach Opening in Homogeneous Dam
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FV | Finite Volume |
| RMSE | Root Mean Square Error |
References
- Yang, C. Sediment Transport: Theory and Practice; McGraw-Hill Inc.: New York, NY, USA, 1996. [Google Scholar]
- Juez, C.; Murillo, J.; Garcia-Navarro, P. Numerical assessment of bed-load discharge formulations for transient flow in 1D and 2D situations. J. Hydroinform. 2013, 15, 1234–1257. [Google Scholar] [CrossRef]
- Tingsanchali, T.; Chinnarasri, C. Numerical modelling of dam failure due to flow overtopping. Hydrol. Sci. J. 2001, 46, 113–130. [Google Scholar] [CrossRef]
- Cao, Z.; Day, R.; Egashira, S. Coupled and Decoupled Numerical Modeling of Flow and Morphological Evolution in Alluvial Rivers. J. Hydraul. Eng. 2002, 128, 306–321. [Google Scholar] [CrossRef]
- Hudson, J.; Sweby, P.K. Formulations for Numerically Approximating Hyperbolic Systems Governing Sediment Transport. J. Sci. Comput. 2003, 19, 225–252. [Google Scholar] [CrossRef]
- Goutière, L.; Soares-Frazão, S.; Savary, C.; Laraichi, T.; Zech, Y. One-Dimensional Model for Transient Flows Involving Bed-Load Sediment Transport and Changes in Flow Regimes. J. Hydraul. Eng. 2008, 134, 726–735. [Google Scholar] [CrossRef]
- Castro-Díaz, M.; Fernández-Nieto, E.; Ferreiro, A. Sediment transport models in Shallow Water equations and numerical approach by high order finite volume methods. Comput. Fluids 2008, 37, 299–316. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]
- Juez, C.; Murillo, J.; García-Navarro, P. A 2D weakly-coupled and efficient numerical model for transient shallow flow and movable bed. Adv. Water Resour. 2014, 71, 93–109. [Google Scholar] [CrossRef]
- Martínez-Aranda, S.; Murillo, J.; García-Navarro, P. A 1D numerical model for the simulation of unsteady and highly erosive flows in rivers. Comput. Fluids 2019, 181, 8–34. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S. One-Dimensional Modeling of Dam-Break Flow over Movable Beds. J. Hydraul. Eng. 2007, 133, 48–58. [Google Scholar] [CrossRef]
- El Kadi Abderrezzak, K.; Paquier, A. One-dimensional numerical modeling of sediment transport and bed deformation in open channels. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Cao, Z.; Li, Z.; Pender, G.; Hu, P. Non-capacity or capacity model for fluvial sediment transport. Proc. Inst. Civil Eng. Water Manag. 2012, 165, 193–211. [Google Scholar] [CrossRef]
- Fernández-Nieto, E.; Lucas, C.; Morales-de Luna, T.; Cordier, S. On the influence of the thickness of the sediment moving layer in the definition of the bedload transport formula in Exner systems. Comput. Fluids 2014, 91, 87–106. [Google Scholar] [CrossRef]
- Bohorquez, P.; Ancey, C. Particle diffusion in non-equilibrium bedload transport simulations. Appl. Math. Model. 2016, 40, 7474–7492. [Google Scholar] [CrossRef]
- Van-Rijn, L. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993; Chapter 10, Bed Material Transport, Erosion and Deposition in Non-Steady and Non-Uniform Flow. [Google Scholar]
- Cao, Z.; Hu, P.; Pender, G. Multiple Time Scales of Fluvial Processes with Bed Load Sediment and Implications for Mathematical Modeling. J. Hydraul. Eng. 2011, 137, 267–276. [Google Scholar] [CrossRef]
- El Kadi Abderrezzak, K.; Paquier, A.; Gay, B. One-dimensional numerical modelling of dam-break waves over movable beds: Application to experimental and field cases. Environ. Fluid Mech. 2008, 8, 169–198. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, J. 1D finite volume model of unsteady flow over mobile bed. J. Hydrol. 2011, 405, 57–68. [Google Scholar] [CrossRef]
- Soliman, M.R.; Ushijima, S. Equilibrium and Non-equilibrium Sediment Transport Modeling Based On Parallel MACS Algorithm. J. Jpn. Soc. Civil Eng. 2013, 69, 79–86. [Google Scholar] [CrossRef]
- van Rijn, L. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Lee, H.; Hsu, I. Investigation of Saltating Particle Motions. J. Hydraul. Eng. 1994, 120, 831–845. [Google Scholar] [CrossRef]
- Ferreira, R.M.L.; Franca, M.J.; Leal, J.G.A.B.; Cardoso, A.H. Mathematical modelling of shallow flows: Closure models drawn from grain-scale mechanics of sediment transport and flow hydrodynamics. Can. J. Civil Eng. 2009, 36, 1605–1621. [Google Scholar] [CrossRef]
- Charru, F. Selection of the ripple length on a granular bed sheared by a liquid flow. Phys. Fluids 2006, 18, 121508. [Google Scholar] [CrossRef]
- Zech, Y.; Soares-Frazão, S.; Spinewine, B.; Grelle, N.L. Dam-break induced sediment movement: Experimental approaches and numerical modelling. J. Hydraul. Res. 2008, 46, 176–190. [Google Scholar] [CrossRef]
- Fernández-Nieto, E.D.; Luna, T.M.d.; Narbona-Reina, G.; Zabsonré, J.d.D. Formal deduction of the Saint-Venant-Exner model including arbitrarily sloping sediment beds and associated energy. Math. Model. Numer. Anal. 2017, 51, 115–145. [Google Scholar] [CrossRef]
- Singh, U.; Ahmad, Z. Transport rate and bed profile computations for clay–silt–gravel mixture. Environ. Earth Sci. 2019, 78, 432. [Google Scholar] [CrossRef]
- Singh, U.K.; Jamei, M.; Karbasi, M.; Malik, A.; Pandey, M. Application of a modern multi-level ensemble approach for the estimation of critical shear stress in cohesive sediment mixture. J. Hydrol. 2022, 607, 127549. [Google Scholar] [CrossRef]
- Martínez-Aranda, S.; Murillo, J.; García-Navarro, P. A comparative analysis of capacity and non-capacity formulations for the simulation of unsteady flows over finite-depth erodible beds. Adv. Water Resour. 2019. in print. [Google Scholar] [CrossRef]
- Martínez-Aranda, S.; Meurice, R.; Soares-Frazão, S.; García-Navarro, P. Comparative analysis of HLLC- and Roe-based Models for the simulation of a dam-break flow in an erodible channel with a 90º bend. Water 2021, 13, 1840. [Google Scholar] [CrossRef]
- Grass, A. Sediments Transport by Waves and Currents; Department of Civil Engineering, University College: London, UK, 1981. [Google Scholar]
- Murillo, J.; García-Navarro, P. An Exner-based coupled model for two-dimensional transient flow over erodible bed. J. Comput. Phys. 2010, 229, 8704–8732. [Google Scholar] [CrossRef]
- Godlewski, E.; Raviart, P.A. Numerical Approximation of Hyperbolic Systems of Conservation Laws; Springer: New York, NY, USA, 1996. [Google Scholar]
- Martínez-Aranda, S.; Murillo, J.; García-Navarro, P. Comparison of new efficient 2D models for the simulation of bedload transport using the augmented Roe approach. Adv. Water Resour. 2021, 153, 103931. [Google Scholar] [CrossRef]
- Wu, W.; Vieira, D.; Wang, S. One-Dimensional Numerical Model for Nonuniform Sediment Transport under Unsteady Flows in Channel Networks. J. Hydraul. Eng. 2004, 130, 914–923. [Google Scholar] [CrossRef]
- Wu, W. Computational River Dynamics; CRC Press: London, UK, 2007. [Google Scholar]

| Formulation | ||||
|---|---|---|---|---|
| MPM | 0.047 | |||
| Nielsen | 0.047 | |||
| Fernandez-Luque | 0.037 | |||
| Wong | 0.0495 | |||
| Smart | 0.047 | |||
| Wu | 0.030 |
| Case | (L/s) | ||||
|---|---|---|---|---|---|
| C1 | 1V:3H | 1V:5H | 1.05 | 0.24 | 0.012 |
| C2 | 1V:3H | 1V:3H | 1.23 | 0.34 | 0.017 |
| Data Series | Equil. | No-Equil. |
|---|---|---|
| C1—Bed level in P1 | 0.057 m | 0.023 m |
| C1—Bed level in P2 | 0.053 m | 0.022 m |
| C1—Bed level in P3 | 0.033 m | 0.020 m |
| C2—Bed level profile at s | 0.112 m | 0.061 m |
| C2—Bed level profile at s | 0.029 m | 0.039 m |
| Data Series | Equil. | No-Equil. |
|---|---|---|
| C1—Dam discharge | 10.94 L/s | 3.10 L/s |
| C1—Reservoir level | 0.055 m | 0.019 m |
| C2—Dam discharge | 45.02 L/s | 11.76 L/s |
| C2—Reservoir level | 0.116 m | 0.034 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Aranda, S.; Fernández-Pato, J.; García-Navarro, P. Non-Equilibrium Bedload Transport Model Applied to Erosive Overtopping Dambreach. Water 2023, 15, 3094. https://doi.org/10.3390/w15173094
Martínez-Aranda S, Fernández-Pato J, García-Navarro P. Non-Equilibrium Bedload Transport Model Applied to Erosive Overtopping Dambreach. Water. 2023; 15(17):3094. https://doi.org/10.3390/w15173094
Chicago/Turabian StyleMartínez-Aranda, Sergio, Javier Fernández-Pato, and Pilar García-Navarro. 2023. "Non-Equilibrium Bedload Transport Model Applied to Erosive Overtopping Dambreach" Water 15, no. 17: 3094. https://doi.org/10.3390/w15173094





