Longitudinal Mixing in Flows with Submerged Rigid Aquatic Canopies
Abstract
:1. Introduction
2. Previous Work
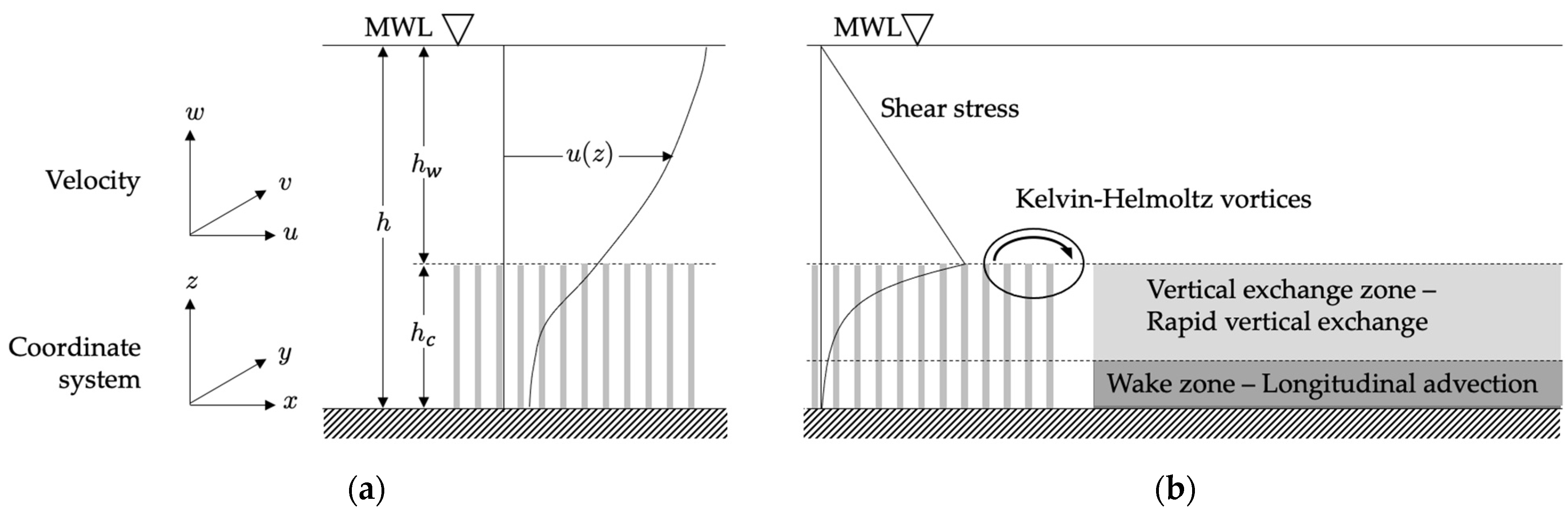
2.1. Flow Velocity in the Presence of Submerged Vegetation
2.2. Longitudinal Dispersion in the Presence of Submerged Vegetation
3. Methodology
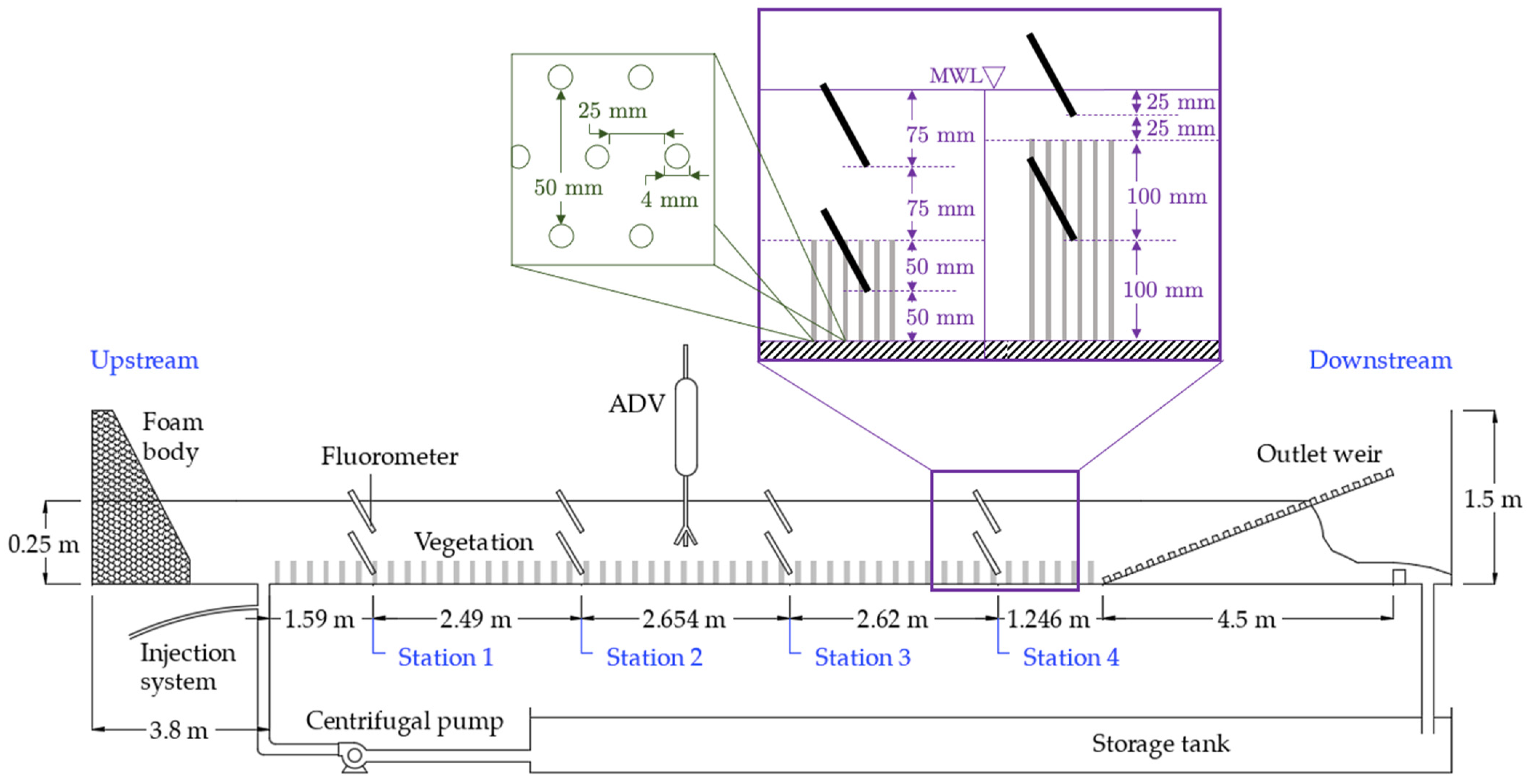
3.1. Velocity Measurements
3.2. Longitudinal Mixing Measurements
3.3. Calculation of the Coefficient of Longitudinal Dispersion from the N-Zone Model
3.3.1. Calculating the Shear Stresses
3.3.2. Calculating Diffusivity
3.3.3. Calculating the Coefficient of Longitudinal Dispersion
4. Results
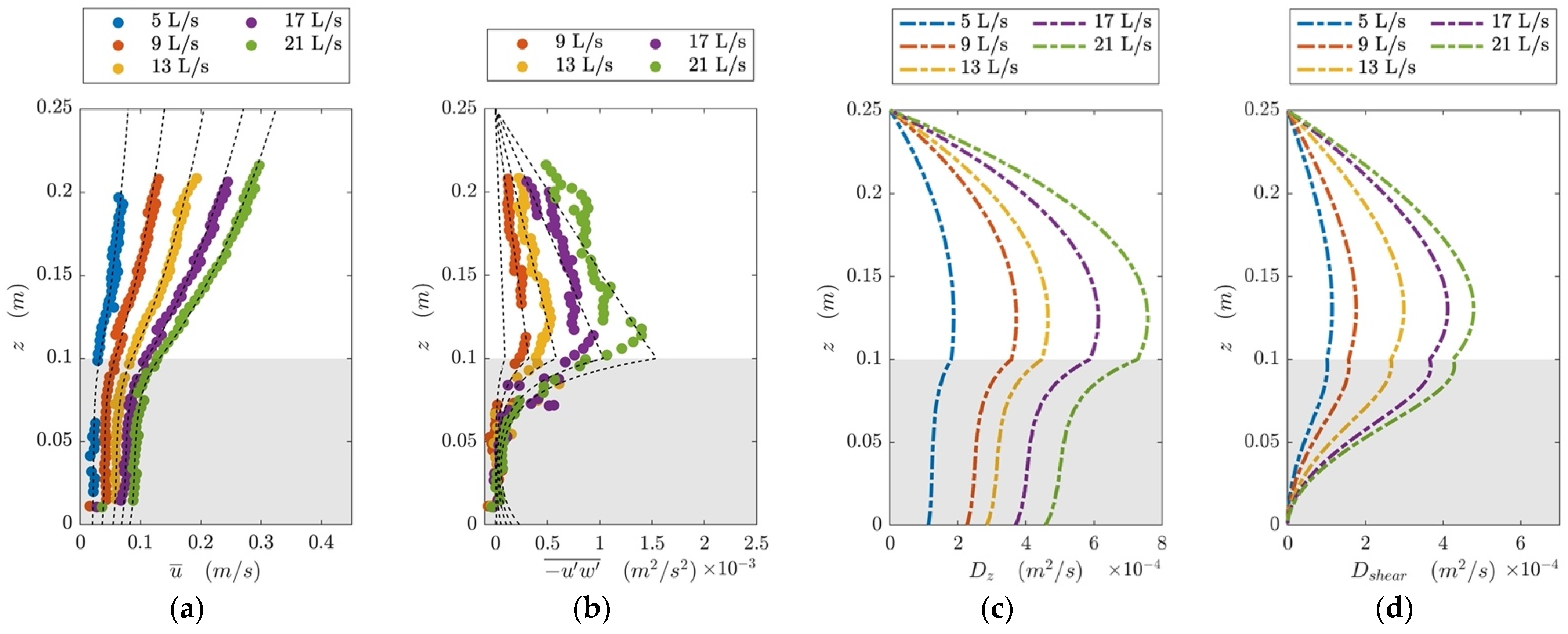
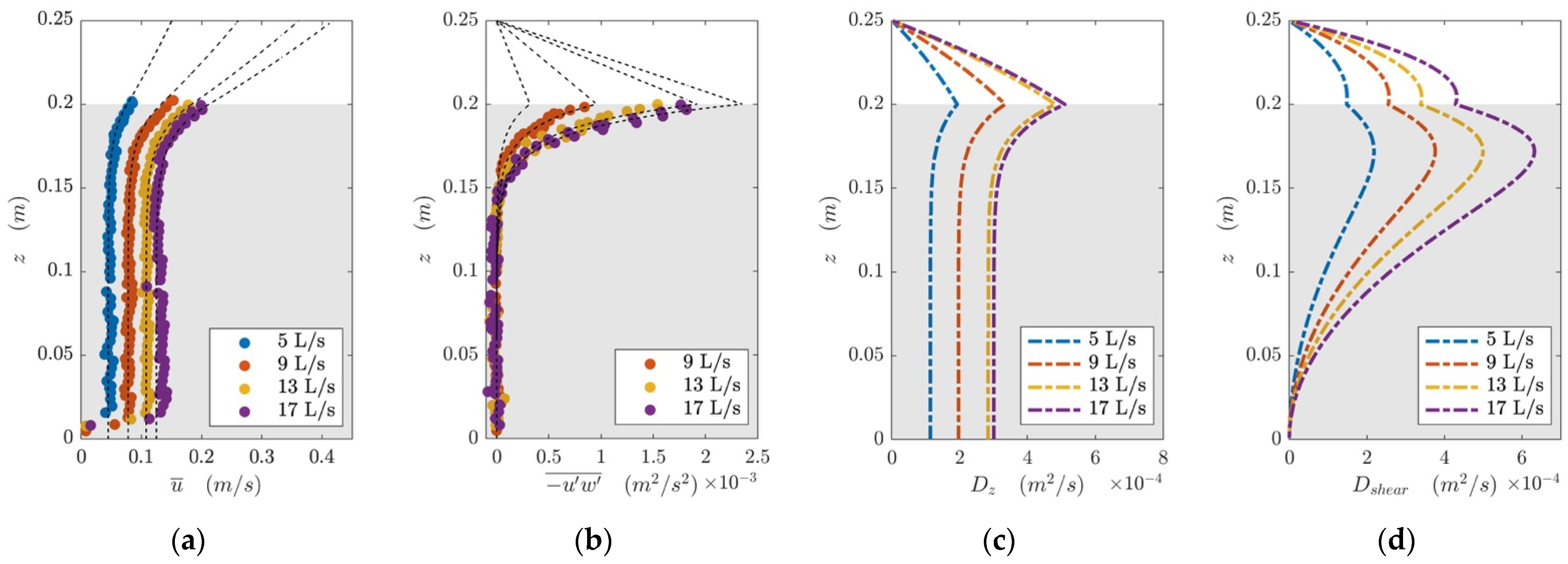
4.1. Velocity Profile
4.2. Shear Stress Profile
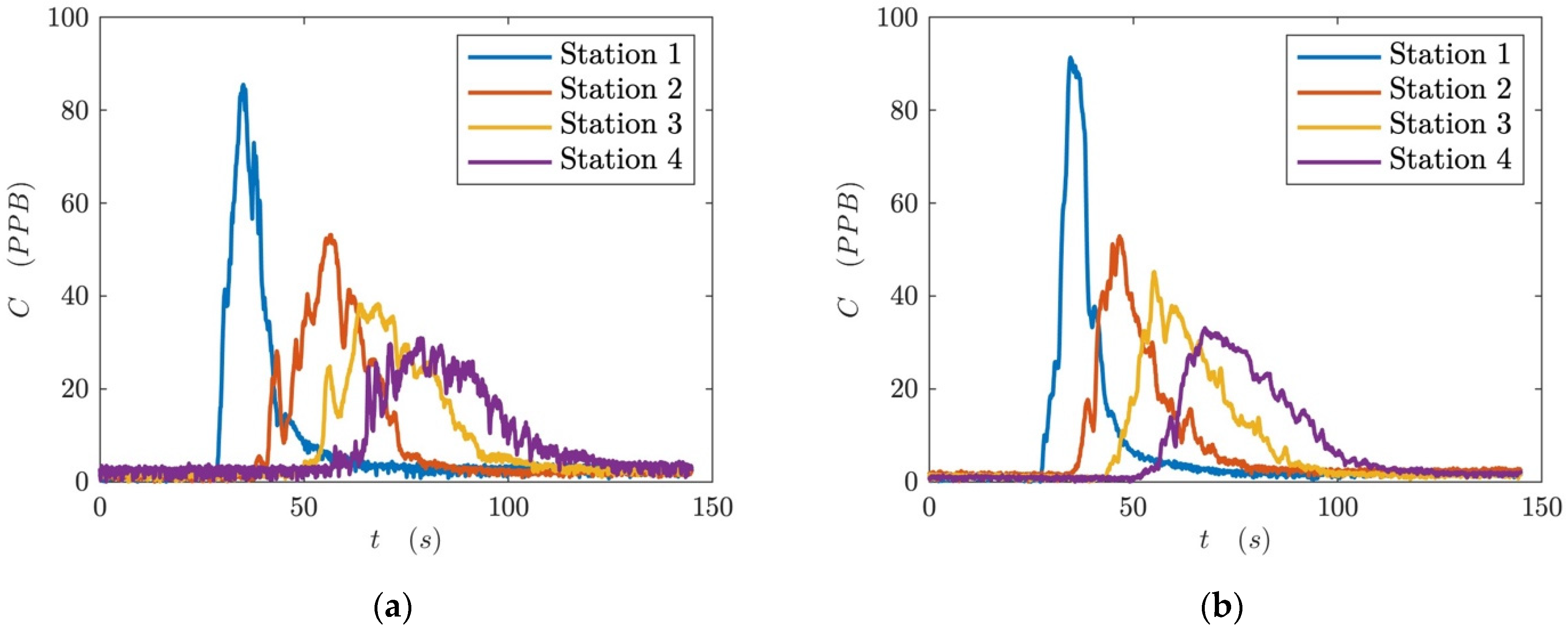
4.3. Longitudinal Dispersion Measurements
4.4. Application of the N-Zone Model
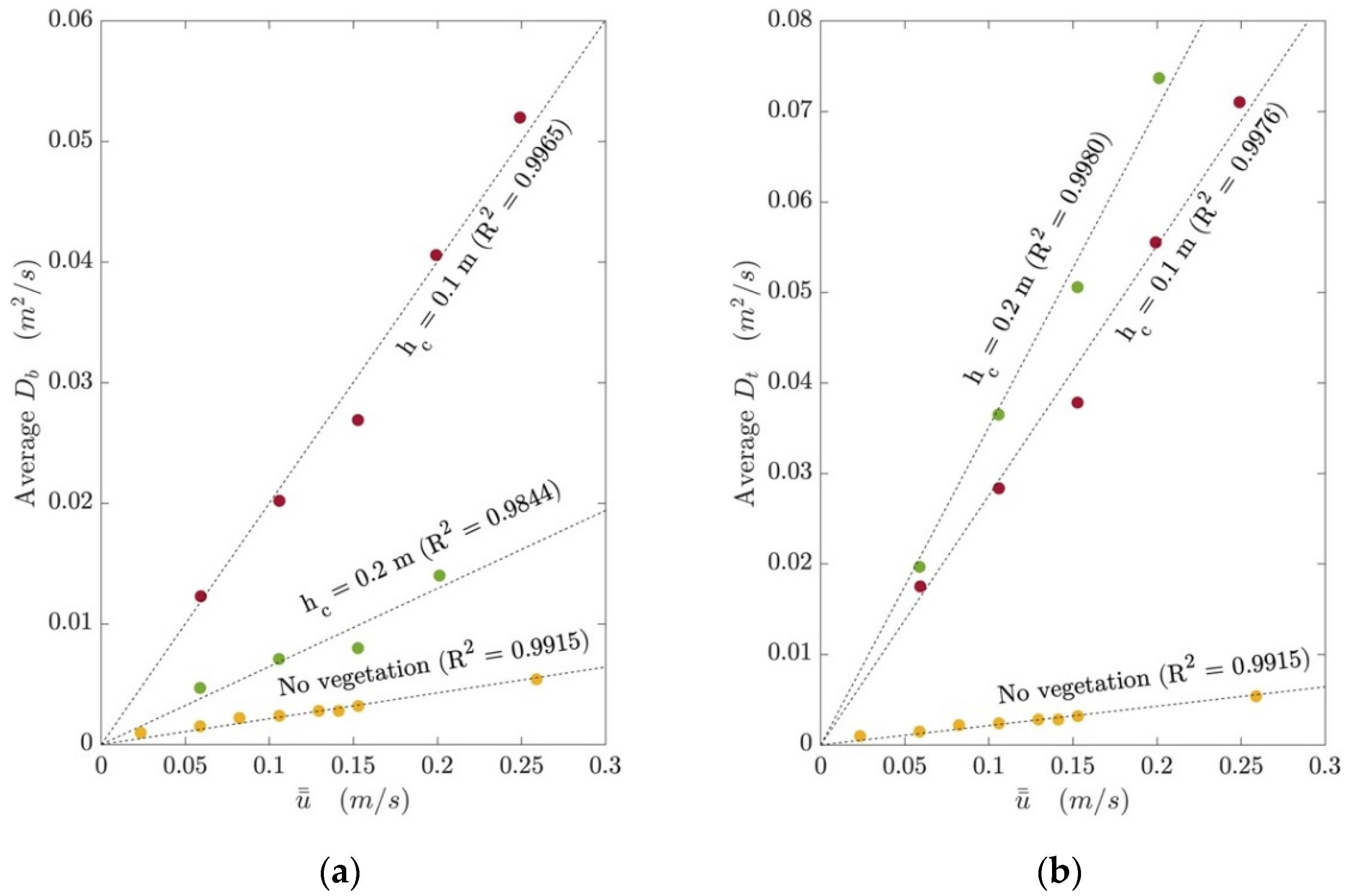
4.4.1. Obtaining Horizontal and Vertical Diffusivity Profiles
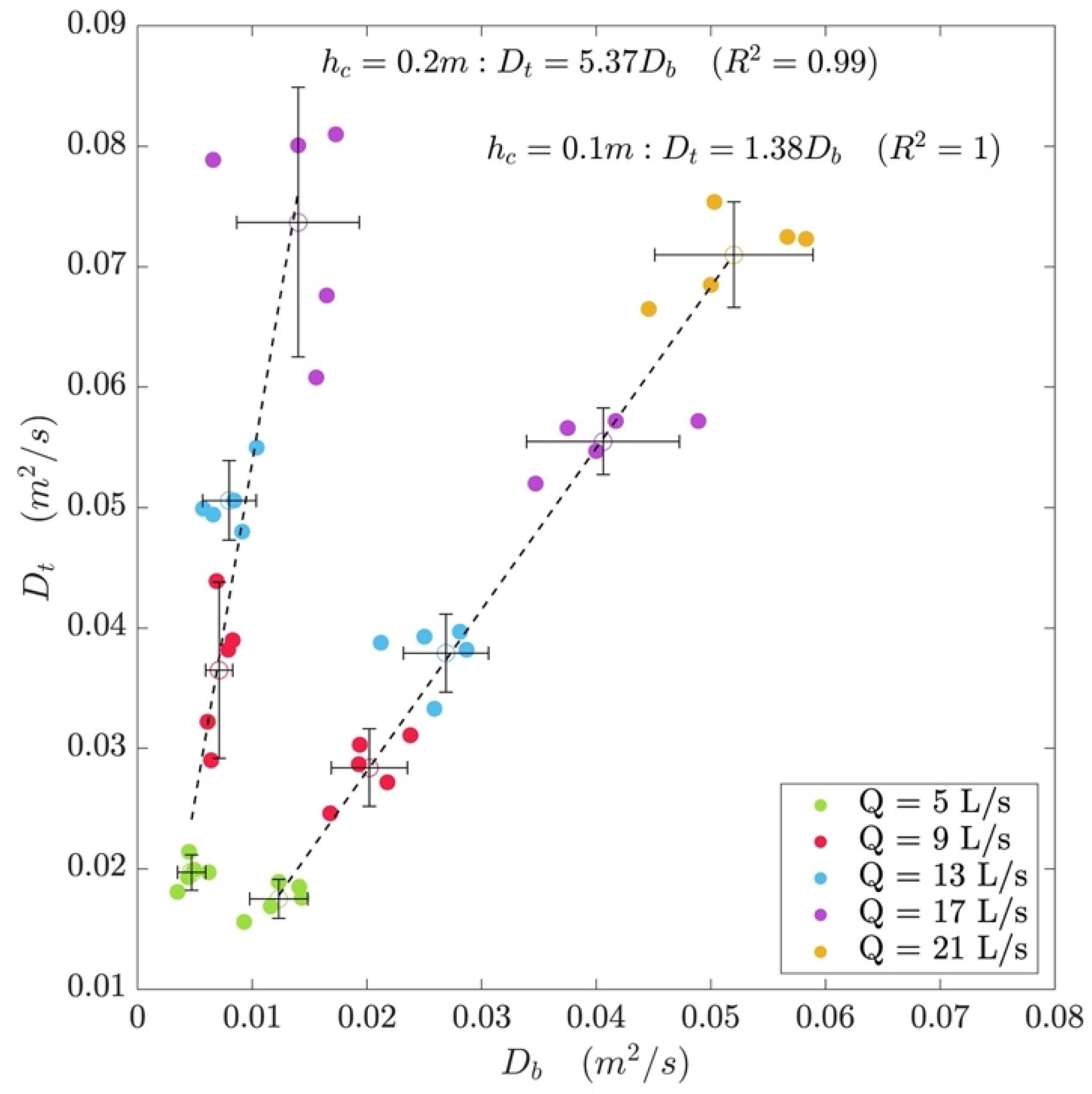
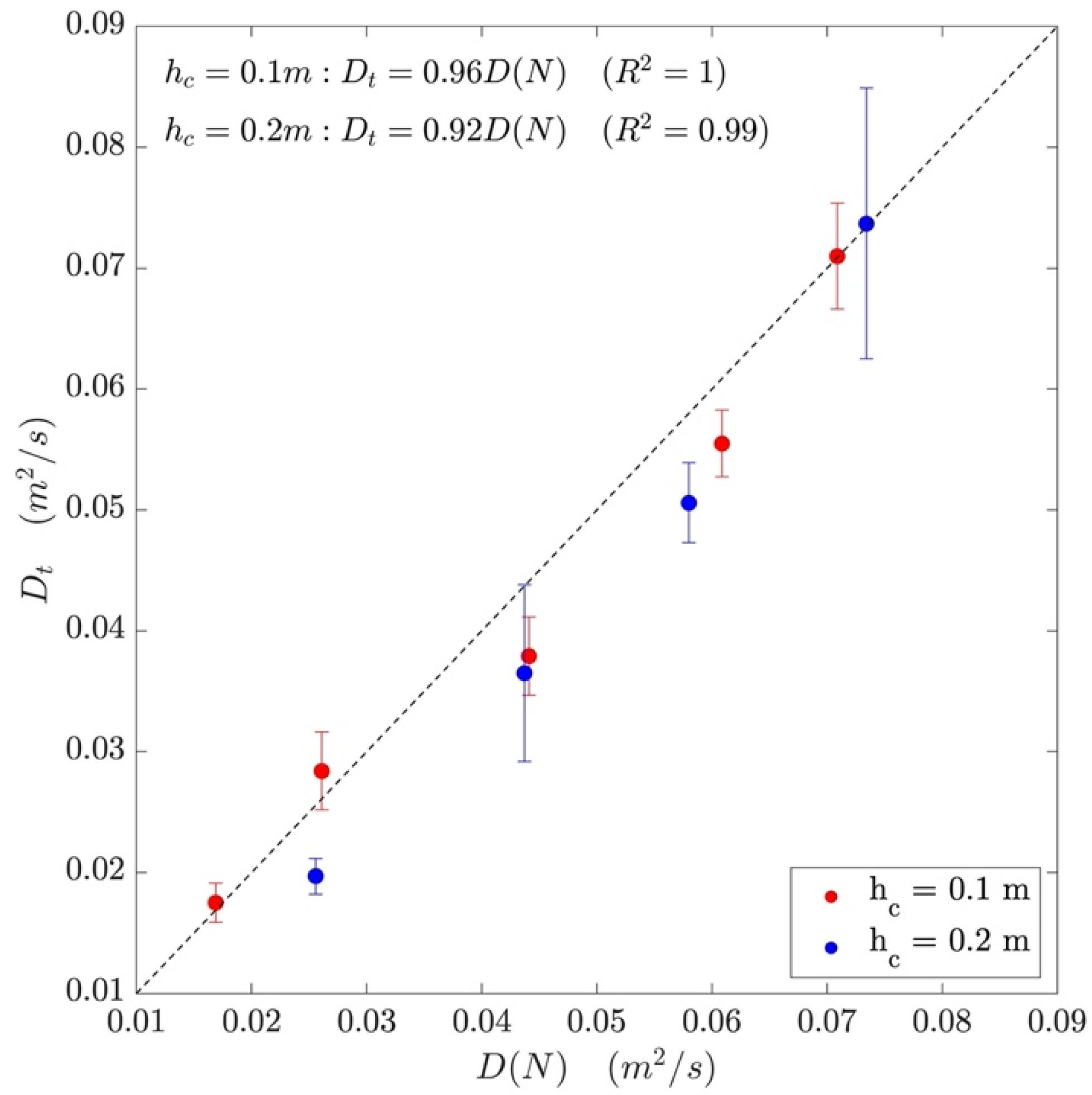
4.4.2. Calculating the Coefficient of Longitudinal Dispersion
5. Discussion
5.1. Vertical Mixing in the Presence of Submerged Canopies
5.2. Longitudinal Dispersion in the Presence of Submerged Canopies
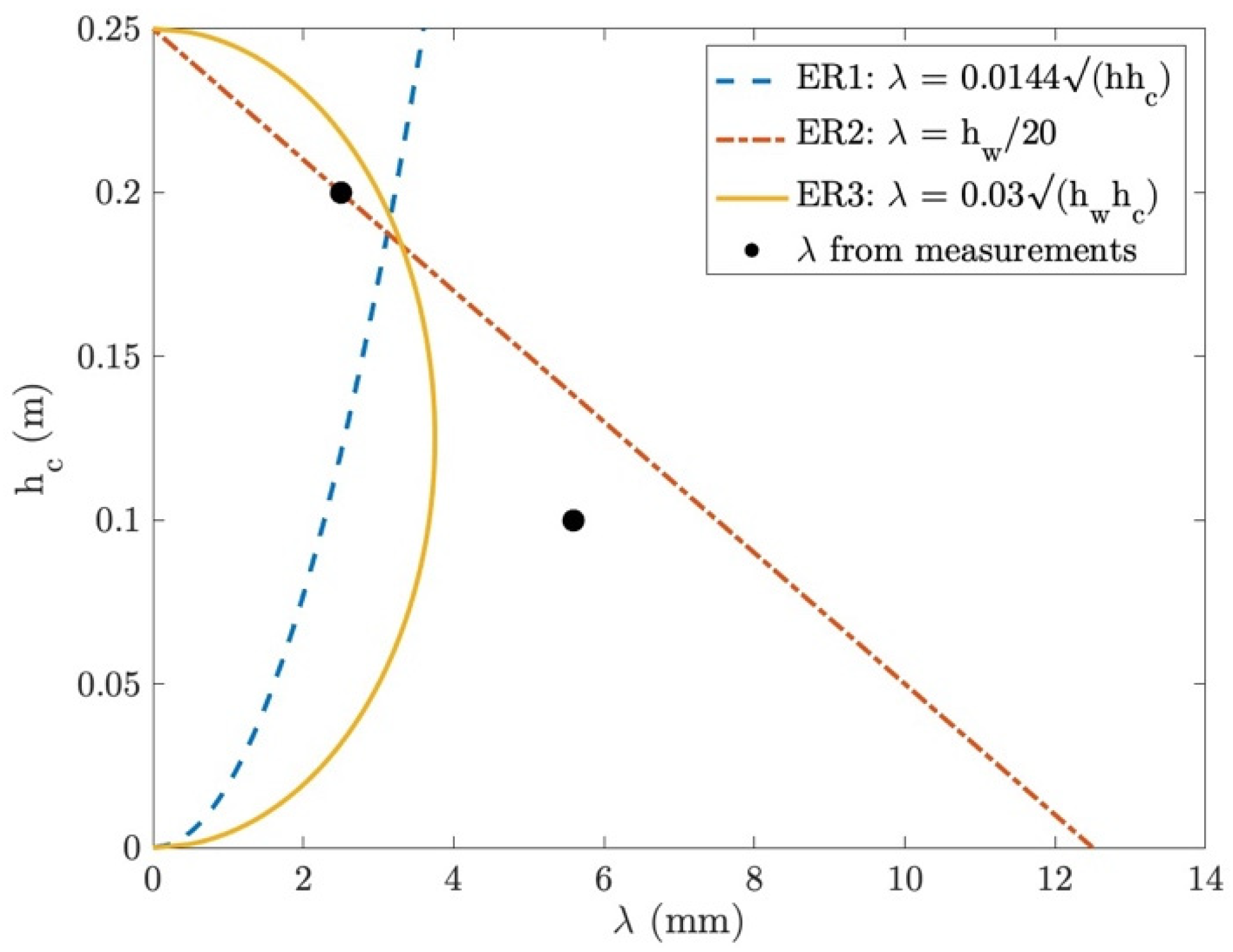
5.3. Applicability of the N-Zone Model into Submerged Vegetation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Green, E.P.; Short, F. World Atlas of Seagrasses; University of California Press: Berkeley, CA, USA, 2003; Volume 47. [Google Scholar] [CrossRef]
- Westlake, D.F. Aquatic macrophytes and the oxygen balance of running water. SIL Proc. 1922–2010 1961, 14, 499–504. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Lodge, D.M. Effects of submersed macrophytes on ecosystem processes. Aquat. Bot. 1986, 26, 341–370. [Google Scholar] [CrossRef]
- Moore, K.A. Influence of Seagrasses on Water Quality in Shallow Regions of the Lower Chesapeake Bay. J. Coast. Res. 2004, 10045, 162–178. [Google Scholar] [CrossRef]
- Kadlec, R.H.; Wallace, S.D. Treatment Wetlands; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Abdelrhman, M. Effect of eelgrass Zostera marina canopies on flow and transport. Mar. Ecol. Prog. Ser. 2003, 248, 67–83. [Google Scholar] [CrossRef]
- Chambers, P.; Prepas, E. Nutrient dynamics in riverbeds: The impact of sewage effluent and aquatic macrophytes. Water Res. 1994, 28, 453–464. [Google Scholar] [CrossRef]
- Schulz, M.; Kozerski, H.-P.; Pluntke, T.; Rinke, K. The influence of macrophytes on sedimentation and nutrient retention in the lower River Spree (Germany). Water Res. 2002, 37, 569–578. [Google Scholar] [CrossRef]
- Butcher, R.W. Studies on the Ecology of Rivers: I. On the Distribution of Macrophytic Vegetation in the Rivers of Britain. J. Ecol. 1933, 21, 58. [Google Scholar] [CrossRef]
- Harrod, J.J. The Distribution of Invertebrates on Submerged Aquatic Plants in a Chalk Stream. J. Anim. Ecol. 1964, 33, 335. [Google Scholar] [CrossRef]
- Gambi, M.; Nowell, A.; Jumars, P. Flume observations on flow density dynamics in Zosteramarina (eelgrass) beds. Mar. Ecol. Prog. Ser. 1990, 61, 159–169. [Google Scholar] [CrossRef]
- Koch, E.W.; Ackerman, J.D.; Verduin, J.; van Keulen, M. Fluid Dynamics in Seagrass Ecology—From Molecules to Ecosystems. In Seagrasses: Biology, Ecologyand Conservation; Springer: Dordrecht, The Netherlands, 2006; pp. 193–225. [Google Scholar] [CrossRef]
- Gregg, W.W.; Rose, F.L. The effects of aquatic macrophytes on the stream microenvironment. Aquat. Bot. 1982, 14, 309–324. [Google Scholar] [CrossRef]
- Sand-Jensen, K.; Mebus, J.R. Fine-Scale Patterns of Water Velocity within Macrophyte Patches in Streams. Oikos 1996, 76, 169. [Google Scholar] [CrossRef]
- López, F.; García, M.H. Mean Flow and Turbulence Structure of Open-Channel Flow through Non-Emergent Vegetation. J. Hydraul. Eng. 2001, 127, 392–402. [Google Scholar] [CrossRef]
- Winant, C.D.; Browand, F.K. Vortex pairing: The mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 1974, 63, 237–255. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. Oceans 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. Atmos. 2002, 107, 3-1–3-11. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and Transport in Regions with Aquatic Vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow Over and Through Biota. In Treatise on Estuarine and Coastal Science; Elsevier: Amsterdam, The Netherlands, 2011; Volume 2, pp. 267–288. [Google Scholar]
- von Kármán, T. Mechanical similitude and turbulence—Reprint from Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1930; National Advisory Committee on Aeronautics: Washington, DC, USA, 1931. [Google Scholar]
- Okamoto, T.-A.; Nezu, I. Spatial evolution of coherent motions in finite-length vegetation patch flow. Environ. Fluid Mech. 2013, 13, 417–434. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H. Mass Transport in Vegetated Shear Flows. Environ. Fluid Mech. 2005, 5, 527–551. [Google Scholar] [CrossRef]
- Ikeda, S.; Kanazawa, M. Three-Dimensional Organized Vortices above Flexible Water Plants. J. Hydraul. Eng. 1996, 122, 634–640. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Chapter 4: Shear Flow Dispersion. In Mixing in Inland and Coastal Waters; Academic Press Inc. (London) Ltd.: London, UK, 1979; pp. 81–102. [Google Scholar]
- Elder, J.W. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Kenworthy, W. Effects of current on photosynthesis and distribution of seagrasses. Aquat. Bot. 1987, 27, 59–78. [Google Scholar] [CrossRef]
- Murphy, E.; Ghisalberti, M.; Nepf, H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 2007, 43, W05438. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. The limited growth of vegetated shear layers. Water Resour. Res. 2004, 40, W07502. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M.; White, B.; Murphy, E. Retention time and dispersion associated with submerged aquatic canopies. Water Resour. Res. 2007, 43, W04422. [Google Scholar] [CrossRef]
- Fischer, H.B. The Mechanics of Dispersion in Natural Streams. J. Hydraul. Div. 1967, 93, 187–216. [Google Scholar] [CrossRef]
- Patil, S.; Li, X.; Li, C.; Tam, B.Y.F.; Song, C.Y.; Chen, Y.P.; Zhang, Q. Longitudinal dispersion in wave-current-vegetation flow. Phys. Oceanogr. 2009, 19, 45–61. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Chapter 2: Fickian Diffusion. In Mixing in Inland and Coastal Waters; Academic Press Inc (London) Ltd.: London, UK, 1979. [Google Scholar]
- Shucksmith, J.D.; Boxall, J.B.; Guymer, I. Effects of emergent and submerged natural vegetation on longitudinal mixing in open channel flow. Water Resour. Res. 2010, 46, W04504. [Google Scholar] [CrossRef]
- Shucksmith, J.D.; Boxall, J.B.; Guymer, I. Determining longitudinal dispersion coefficients for submerged vegetated flow. Water Resour. Res. 2011, 47, W10516. [Google Scholar] [CrossRef]
- Noori, R.; Ghiasi, B.; Sheikhian, H.; Adamowski, J.F. Estimation of the Dispersion Coefficient in Natural Rivers Using a Granular Computing Model. J. Hydraul. Eng. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Noori, R.; Mirchi, A.; Hooshyaripor, F.; Bhattarai, R.; Haghighi, A.T.; Kløve, B. Reliability of functional forms for calculation of longitudinal dispersion coefficient in rivers. Sci. Total. Environ. 2021, 791, 148394. [Google Scholar] [CrossRef]
- Lowe, R.J.; Koseff, J.R.; Monismith, S.G. Oscillatory flow through submerged canopies: 1. Velocity structure. J. Geophys. Res. Atmos. 2005, 110, C10016. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Thuy, N.B.; Tanimoto, K.; Tanaka, N.; Harada, K.; Iimura, K. Effect of open gap in coastal forest on tsunami run-up—Investigations by experiment and numerical simulation. Ocean Eng. 2009, 36, 1258–1269. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Chang, C.-W.; Mei, C.C.; Lomonaco, P.; Martin, F.L.; Maza, M. Periodic water waves through an aquatic forest. Coast. Eng. 2015, 96, 100–117. [Google Scholar] [CrossRef]
- Abdolahpour, M.; Ghisalberti, M.; Lavery, P.; McMahon, K. Vertical mixing in coastal canopies. Limnol. Oceanogr. 2017, 62, 26–42. [Google Scholar] [CrossRef]
- Abdolahpour, M.; Hambleton, M.; Ghisalberti, M. The wave-driven current in coastal canopies. J. Geophys. Res. Oceans 2017, 122, 3660–3674. [Google Scholar] [CrossRef]
- Luhar, M.; Coutu, S.; Infantes, E.; Fox, S.; Nepf, H. Wave-induced velocities inside a model seagrass bed. J. Geophys. Res. Atmos. 2010, 115, C12005. [Google Scholar] [CrossRef]
- Thomas, R.E.; Schindfessel, L.; McLelland, S.J.; Creëlle, S.; De Mulder, T. Bias in mean velocities and noise in variances and covariances measured using a multistatic acoustic profiler: The Nortek Vectrino Profiler. Meas. Sci. Technol. 2017, 28, 075302. [Google Scholar] [CrossRef]
- Chikwendu, S.C. Calculation of longitudinal shear dispersivity using an N-zone model as N → ∞. J. Fluid Mech. 1986, 167, 19–30. [Google Scholar] [CrossRef]
- Tang, X. A mixing-length-scale-based analytical model for predicting velocity profiles of open-channel flows with submerged rigid vegetation. Water Environ. J. 2019, 33, 610–619. [Google Scholar] [CrossRef]
- Prandtl, L. 7. Bericht über Untersuchungen zur ausgebildeten Turbulenz. ZAMM—Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik 1925, 5, 136–139. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Klopstra, D.; Barneveld, H.J.; van Noortwijk, J.M.; van Velzen, E.H. Analytical model for hydraulic roughness of submerged vegetation. In Proceedings of the Theme A, Managing Water: Coping with Scarcity and Abundance: The 27th Congress of the International Association for Hydraulic Research, San Francisco, CA, USA, 10–15 August 1997; pp. 775–780. [Google Scholar]
- Meijer, D.G.; Van Velzen, E.H. Prototype-scale flume experiments on hydraulic roughness of submerged vegetation. In Proceedings of the 28th IHAR World Congress, Graz, Austria, 22–27 August 1999. [Google Scholar]
- Baptist, M.J.; Babovic, V.; Uthurburu, J.R.; Keijzer, M.; Uittenbogaard, R.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Chikwendu, S.C.; Ojiakor, G.U. Slow-zone model for longitudinal dispersion in two-dimensional shear flows. J. Fluid Mech. 1985, 152, 15–38. [Google Scholar] [CrossRef]
- Boghi, A.; Di Venuta, I.; Gori, F. Passive scalar diffusion in the near field region of turbulent rectangular submerged free jets. Int. J. Heat Mass Transf. 2017, 112, 1017–1031. [Google Scholar] [CrossRef]
- Di Venuta, I.; Boghi, A.; Angelino, M.; Gori, F. Passive scalar diffusion in three-dimensional turbulent rectangular free jets with numerical evaluation of turbulent Prandtl/Schmidt number. Int. Commun. Heat Mass Transf. 2018, 95, 106–115. [Google Scholar] [CrossRef]
| (m) | Measured inside the Canopy | Measured above the Canopy | |||||
|---|---|---|---|---|---|---|---|
| 0.1 | 5 | - | 1.23 | 3.35 | 1.75 | 1.39 | 1.69 |
| 9 | 6.2 | 2.02 | 5.71 | 2.84 | 5.37 | 2.61 | |
| 13 | 5.2 | 2.69 | 7.10 | 3.79 | 5.45 | 4.41 | |
| 17 | 5.4 | 4.06 | 22.97 | 5.55 | 3.97 | 6.09 | |
| 21 | 5.5 | 5.20 | 24.69 | 7.10 | 9.96 | 7.09 | |
| 0.2 | 5 | - | 0.47 | 0.77 | 1.97 | 1.13 | 2.56 |
| 9 | 2.5 | 0.71 | 0.72 | 3.65 | 27.73 | 4.37 | |
| 13 | 2.6 | 0.80 | 2.87 | 5.06 | 5.61 | 5.80 | |
| 17 | 2.4 | 1.40 | 14.89 | 7.37 | 64.98 | 7.34 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nipuni Odara, M.G.; Pearson, J. Longitudinal Mixing in Flows with Submerged Rigid Aquatic Canopies. Water 2023, 15, 3021. https://doi.org/10.3390/w15173021
Nipuni Odara MG, Pearson J. Longitudinal Mixing in Flows with Submerged Rigid Aquatic Canopies. Water. 2023; 15(17):3021. https://doi.org/10.3390/w15173021
Chicago/Turabian StyleNipuni Odara, Merenchi Galappaththige, and Jonathan Pearson. 2023. "Longitudinal Mixing in Flows with Submerged Rigid Aquatic Canopies" Water 15, no. 17: 3021. https://doi.org/10.3390/w15173021






