1. Introduction
Sudden environmental risk refers to the leakage of environmental risk materials caused by accidents in industrial production and transportation processes [
1]. A sudden water pollution incident is defined as an occurrence wherein a substantial quantity of pollutants is rapidly released into a water body as a result of human activities, natural calamities, or other unforeseen emergencies [
2,
3,
4]. The pollutants involved in such incidents primarily encompass hazardous substances such as petroleum, heavy metals, and toxic organic compounds [
5,
6]. The emergence of sudden water pollution incidents presents an escalating and pressing menace to water ecology, environmental quality, and overall water security [
7,
8]. The unpredictability and uncertainty of sudden water pollution accidents are attributed to the challenges in determining the characteristics, quantity, leakage mode, and environmental impact capacity of pollutants during the incident, particularly in light of changes in hydrometeorological conditions [
9,
10]. It is noteworthy that the construction of bridges across tributaries in river network areas has experienced a substantial increase due to the rapid development of industrialization and the expansion of cities. Consequently, the proportion of cargo transport has consistently risen over the years. However, road transport remains a prevalent method for transporting dangerous goods [
11], leading to a higher frequency of accidents involving the transportation of hazardous materials [
12,
13,
14]. Consequently, these accidents contribute to the occurrence of frequent instances of sudden water pollution [
14,
15,
16]. Therefore, vehicles utilized for the transportation of dangerous goods can be regarded as mobile hazard sources [
17]. The occurrence of water pollution incidents resulting from traffic accidents and unforeseen circumstances presents a significant hazard to societal and economic progress, as well as human well-being [
4,
18]. Consequently, conducting a risk assessment of hazardous material transportation accidents leading to sudden water pollution is imperative in order to establish a foundation for appropriate emergency prevention and mitigation measures [
19,
20].
Research on the risk assessment of dangerous goods transportation started early and achieved many research advancements [
21,
22,
23]. The American Chemical Company proposed an evaluation index method for fire explosions in 1964 [
24]. Previous scholars initially focused on qualitative descriptions of the damage caused by sudden water pollution, but now, research emphasis has shifted to establishing an index system and assessment model to quantify the degree of risk [
18]. Hou et al. [
2] employed the Monte Carlo method to quantify the likelihood of water pollution. Additionally, they incorporated expert experience judgment and the risk matrix method to ascertain the level of risk associated with water pollution. Tang et al. [
25] utilized a Bayesian network model to assess the probability of water pollution risks. Furthermore, they proposed a comprehensive risk prediction model based on the integration of the Bayesian network and water quality models. Stojanovic et al. [
17] examined the underlying factors contributing to traffic accidents during the transportation of hazardous materials. Additionally, the authors conducted an analysis on the resultant environmental impact of such accidents and proposed measures to prevent them and mitigate their consequences. Ren et al. [
26] assessed the risk associated with managing environmental pollution accidents in water quality emergency monitoring through the development of a fuzzy Bayesian network risk assessment model. Liu et al. [
27] conducted a case study on the Weihe River, where they developed a water pollution risk assessment model using fuzzy theory. They subsequently assessed the risk of water pollution in the Weihe River. Li et al. [
28] focused on the Yixing river network area and proposed a comprehensive method for analyzing sudden water pollution risk. This method incorporated fuzzy logic, expert participation, and random simulation, thereby offering a valuable approach for integrating the numerous uncertainties present in complex river network systems. Zhang et al. [
29] utilized the Yongding River as a case study to partition the area into distinct units for the purpose of assessing sudden water pollution risks. They subsequently established a prioritization framework for managing water environment risks and employed the analytic hierarchy process and fuzzy comprehensive evaluation methods to evaluate the levels of risk. Guan et al. [
30] developed a cumulative risk assessment system specifically for the upstream rivers of Baiyangdian Lake; they then employed the grid environmental risk analysis method to evaluate the risk of sudden water pollution in these upstream rivers. In summary, there is a need for further enhancement in the precision and feasibility of identifying and assessing water pollution risks during the transportation of hazardous materials.
Presently, research on water pollution emergencies primarily concentrates on stationary sources of risk, with limited attention given to mobile sources, such as vehicles involved in the transportation of dangerous chemicals [
31]. Additionally, scholars have shown relatively less interest in investigating the risk assessment of abrupt water pollution incidents in non-marine regions [
18]. Bayesian networks, also known as belief networks, are the product of the combination of artificial intelligence, probability theory, graph theory, and decision-making analysis. They have been widely applied to describe uncertainty and probability, which can intuitively express the interaction between various factors and obtain an inference from incomplete or uncertain information [
32]. Bayesian networks have significant advantages for small sample events by using prior knowledge of probability calculations [
33]. The utilization of Bayesian network models for the identification and analysis of sudden water pollution risks remains infrequent within the realm of research methods. Moreover, the assessment of risk grades pertaining to sudden water pollution serves as a manifestation of the potential risks associated with such events [
29]. Despite improvements in risk assessment for sudden water pollution accidents, there is a lack of comprehensive consideration for the various types of risk sources in different regions. The evaluation method that disregards the holistic assessment of risk sources and instead isolates them may compromise the accuracy of the results. Consequently, it is imperative to thoroughly consider the different types and sources of risk within a specific region prior to the occurrence of sudden water pollution. Hence, this study employed the expert evaluation fuzzy language method to discern and categorize the risk sources associated with sudden water pollution events in Baiyangdian, considering various perspectives. Subsequently, a Bayesian network model was employed to assess the likelihood of occurrence for different types of risk factors; then, a one-dimensional water quality model was used to simulate the results of oil leakage in the Nanliuzhuang section.
Baiyangdian Lake is an important part of Xiongan New Area in China and plays a significant role in ecological and environmental protection [
34].With the improvement of urbanization and industrialization, the polluting enterprises are densely distributed around the lake and the surrounding tributaries, and many sewage treatment stations with dense drainage pipes are distributed in the area [
35]. Furthermore, there are many cross-tributary bridges between the nine rivers entering the lake and the roads, and the ships are transported frequently. Thus, the risk of sudden water pollution in Baiyangdian Lake is high due to rollover, leakage, and ship accidents. The frequent occurrence of water pollution accidents in the Baiyangdian Lake area poses serious threats to the safety and reliability of water supply [
30].Hence, it is imperative to conduct appropriate risk identification and assessment, simulate potential water pollution incidents in the future, and implement tailored emergency prevention and control measures to mitigate the adverse effects of such incidents. However, as of now, no risk assessment for the Baiyangdian Lake sudden water pollution accident has been reported. Therefore, this study chose Baiyangdian Lake as the focal point to investigate and assess the risk factors associated with abrupt water pollution incidents during the transportation of hazardous materials. It has simulated such incidents occurring at tributary bridges and subsequently proposed pertinent recommendations for the management of sudden water pollution risks in Baiyangdian Lake. These recommendations encompass preventive measures and emergency response strategies.
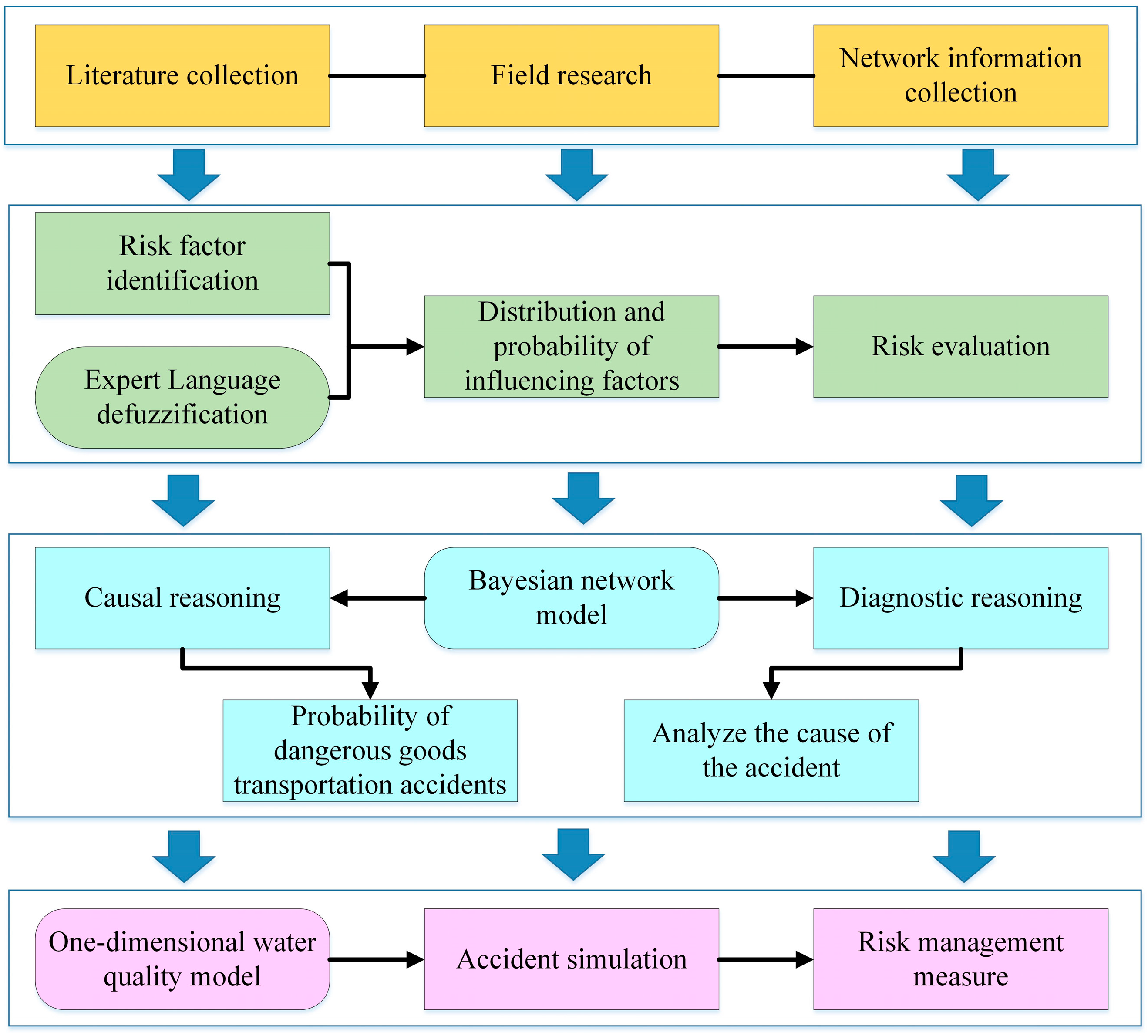
The study encompasses the following components: (1) introduction of the overall situation of Baiyangdian; (2) presentation of the structure and parameters of the Bayes network model, along with the specific details of causal reasoning and diagnostic reasoning; (3) explanation of the process involved in calculating the conditional probability of each node of the Bayes network using the expert evaluation fuzzy language method; (4) utilization of a one-dimensional water quality model to simulate the oil leakage in the Nanliuzhuang section; (5) proposal of emergency prevention and control countermeasures of the inter-regional water pollution accident in Baiyangdian.
Overall, the aim of this study was to: (i) identify and determine the risk factors of dangerous goods transportation accidents on cross-tributary bridges around Baiyangdian Lake by field investigation and the expert evaluation fuzzy language method; (ii) establish the Bayesian network, that is, the probability of a dangerous goods transportation accident is calculated by causal reasoning, and the cause of the accident is analyzed by diagnostic reasoning; (iii) simulate the sudden water pollution accidents on Baiyangdian Lake by using the one-dimensional water quality model, and the corresponding emergency prevention and control measures are put forward
Figure 1 to show the schematic diagram of this paper.
2. Study Area
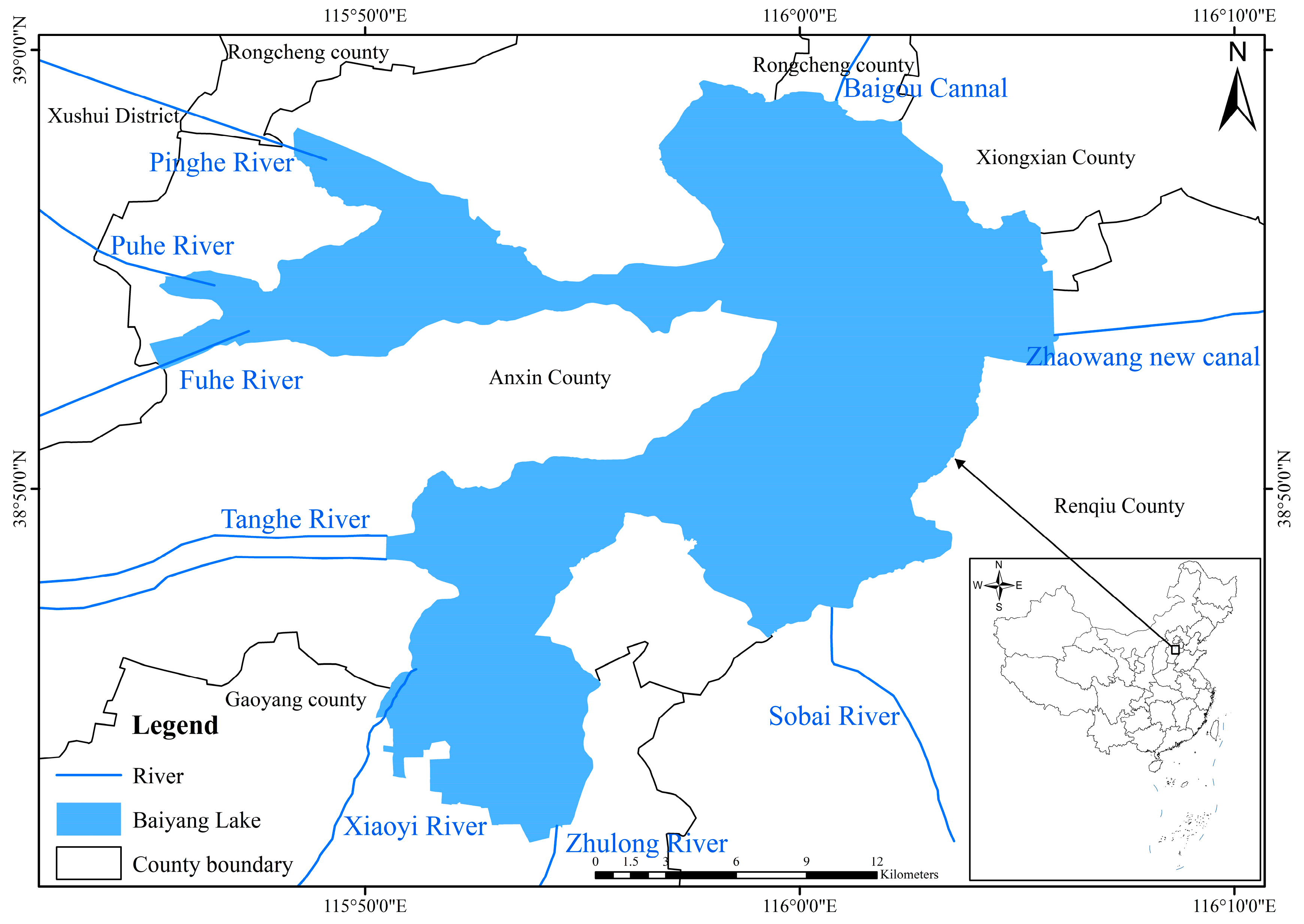
Baiyangdian Lake is the largest freshwater shallow lake in North China (113°400′~116°480′ E, 38°100~40°30′ N), as shown in
Figure 2. It plays an important role in flood mitigation, drought prevention, regional microclimate improvement, and biodiversity protection [
34]. In addition, it supports water resources for hundreds of thousands of people and enjoys the reputation of “Pearl of North China” and “the End of Nine Rivers” in China. The climate belongs to continental monsoon, with means annual precipitation of 554 mm and temperature of 7~12 °C. Additionally, over 60% of the rainfall is concentrated during shorter periods between June and August. Wetlands, arable cropland (e.g., paddy fields and dry lands), forestland, grassland, and residential and industrial land are the main land-use types in this basin. Baiyangdian Lake receives water from nine rivers, including Baigouyin River, Bao River, Cao River, Fu River, Zhulong River, Ping River, Qingshui River, Tang River, and Xiaoyi River. Moreover, the water body of the Baiyangdian Basin is partly maintained by the water diversion from the Yellow River and the South-to-North Water Diversion Project [
30], thereby increasing the water resources and improving the water quality. Baiyangdian Lake Basin rapidly developed, as it has been included in the Xiongan New Area of China since 2017. As a result, there exists numerous cross-tributary bridges due to dense river networks, abundant water compensation projects, and high-intensity human activities. Therefore, there is a high occurrence frequency of sudden water pollution accidents associated with dangerous goods transportation on the cross-tributary bridges of Baiyangdian Lake [
36,
37,
38].
5. Conclusions
This study explored the potential risk of sudden water pollution accidents associated with dangerous goods transportation on the cross-tributary bridges of Baiyangdian Lake. The conclusions are as follows:
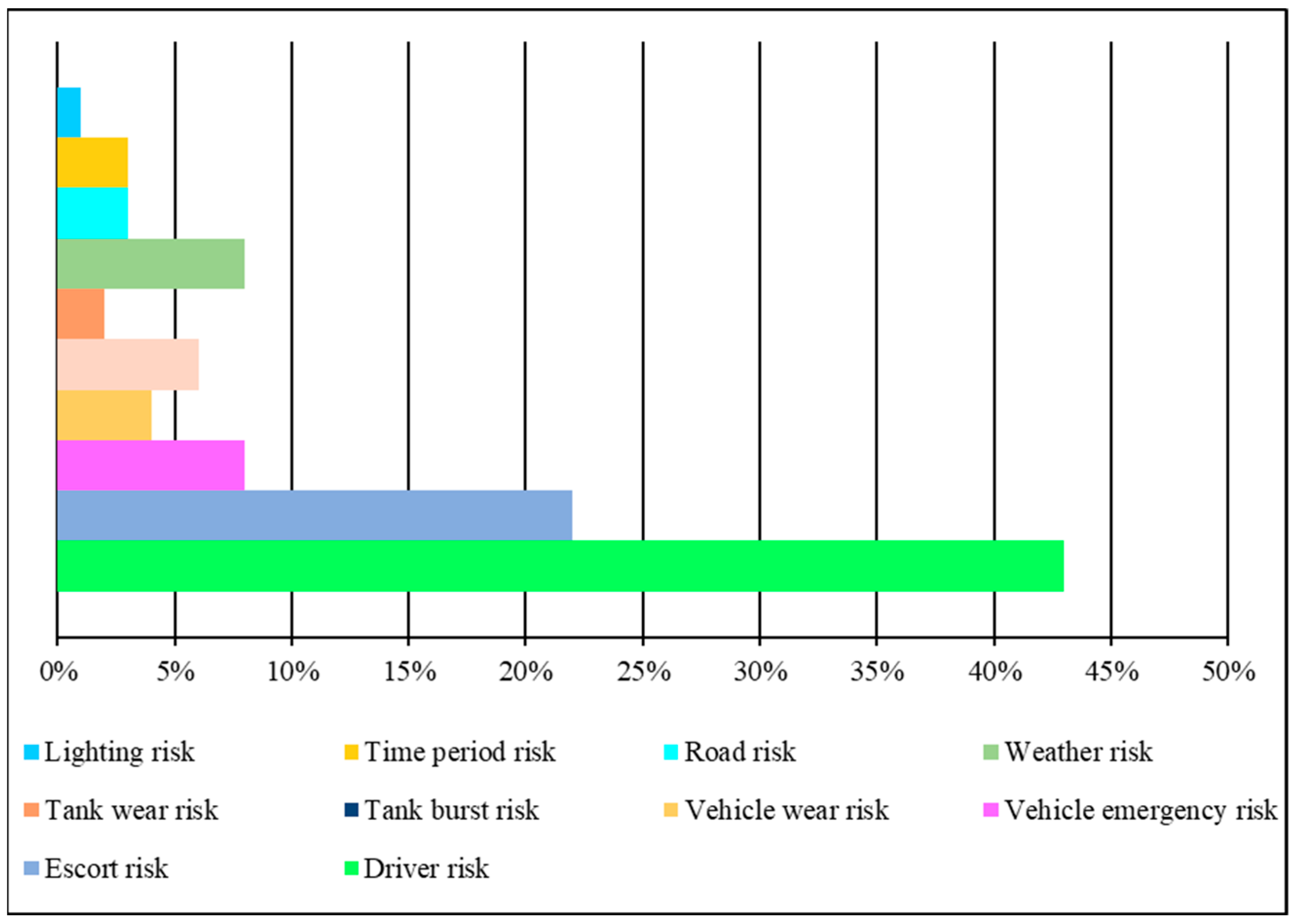
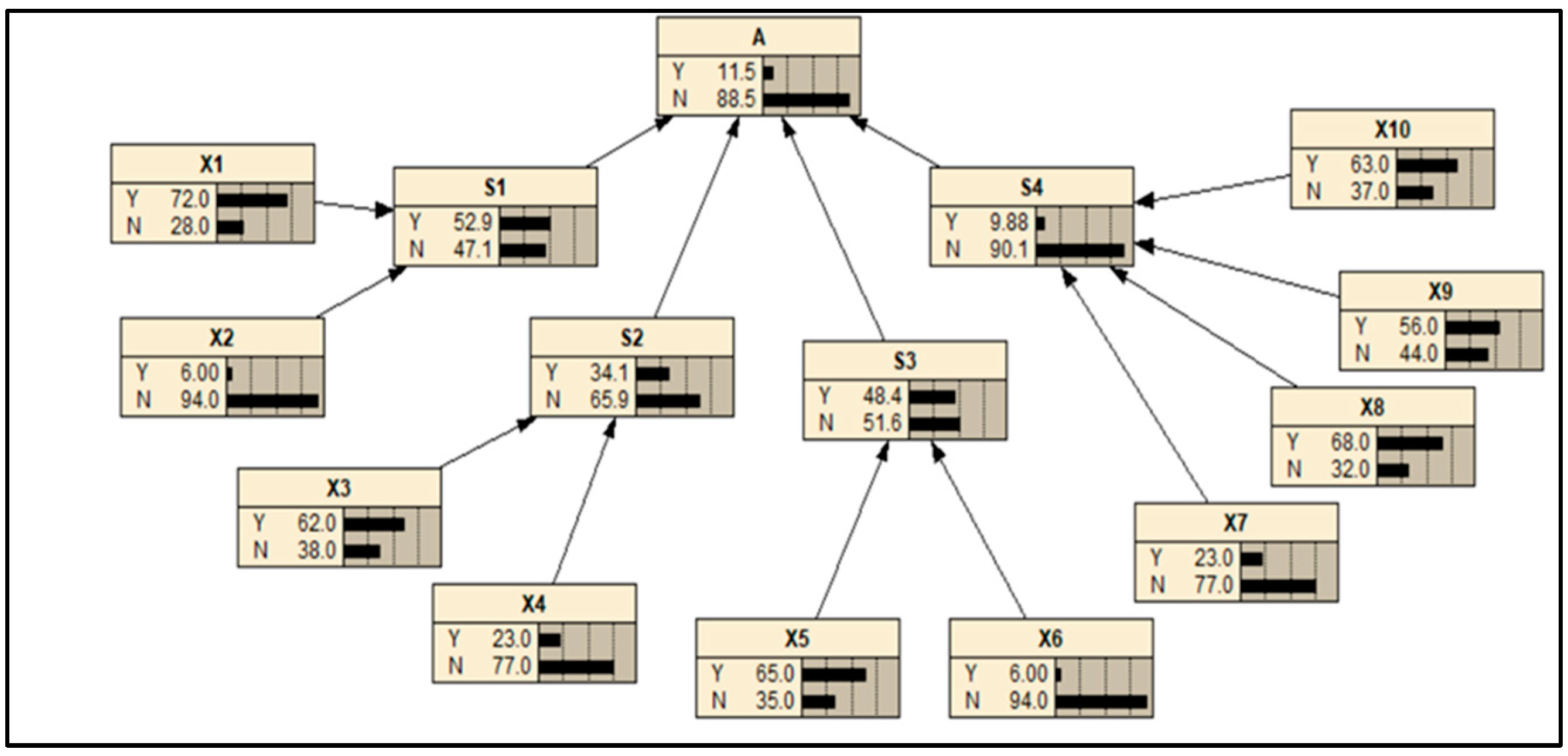
(1) This research divided the risk degree of dangerous goods transportation accidents into seven levels: very low (VL), low (L), flat low (FL), medium (M), flat high (FH), high (H), and very high (VH). (2) According to the results of the conditional probability calculation, the probability of the driver factor, vehicle emergency factor, tank emergency factor, road factor, and lighting situation occurring was high. (3) The dangerous goods transportation accidents on the cross-tributary bridges of Baiyangdian Lake were possible events, with a node A (PA) value of 0.115 and logarithmic probability P value of 4.061. The risk level was relatively high, indicating that accidents posed a potential threat to water environment and human health. (4) Vehicle emergent factors, vehicle wear factors, and weather factors had a greater impact on the occurrence of accidents, with the decreasing order of X4 > X3 > X7. (5) The combination of X1, X4, X6, and X7 contributed to an accident the most. This showed that the highest probability (0.142) of an accident occurred in the region where the driver was not in good condition, the vehicle and tank were worn, and the weather was bad. (6) When the vehicle and the tank were in good condition, the most likely combination of conditions leading to the accident was: X1, X7, X9, X10. This indicated that the probability of an accident was the highest (0.117) on the cross-tributary bridges with poor driver status, bad weather conditions, and no street lighting at night. (7) Emergency prevention and control measures proved to be effective approaches to mitigating the risk of sudden water pollution accidents.
The identification and assessment of sudden water pollution risk in Baiyangdian Lake are influenced by numerous uncertain variables. Further research is required in the following areas:
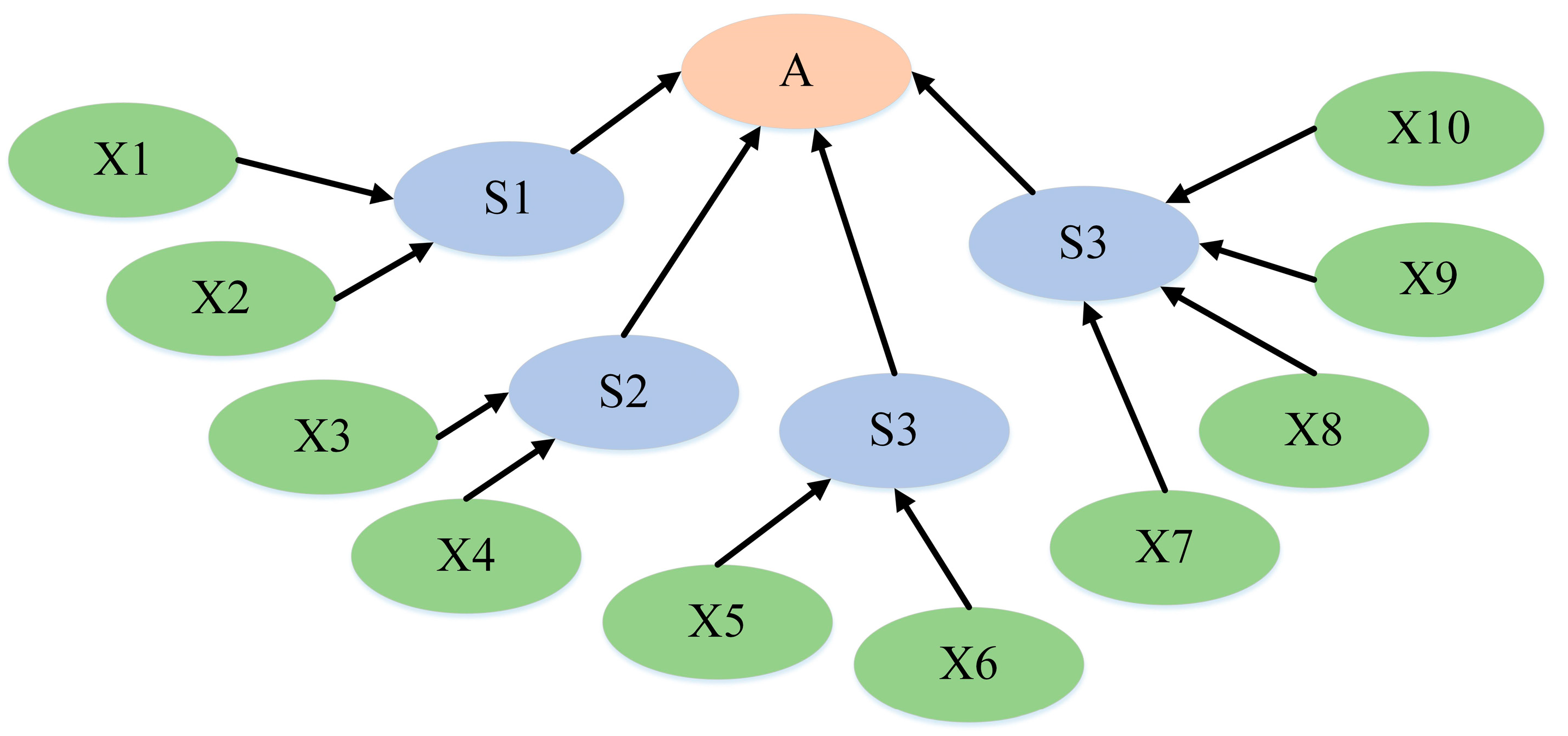
(1) To successfully build a flawless Bayesian network structure, the chosen factors for constructing the model must be refined further. Collaborative discussions among experts are necessary for the perfect determination of the Bayesian network structure. The quantitative analysis of accidents relies on accurately determining the probability of each factor in the network. This study utilized the expert consultation method to acquire the probability of each parameter. The constant revision and updating of the network should be performed by incorporating historical traffic accident data in future research.
(2) With the ongoing advancements in geographic information system technology, future studies can utilize a GIS visual operating system to establish an emergency plan GIS system for sudden water pollution incidents in Baiyangdian Lake. This system will offer spatial auxiliary decision support for the management of sudden water pollution in Baiyangdian Lake and the development of emergency measures for water pollution accidents.