The Seepage Evolution Characteristics in Undisturbed Loess under Dynamic Preferential Flow: New Insights from X-ray Computed Tomography
Abstract
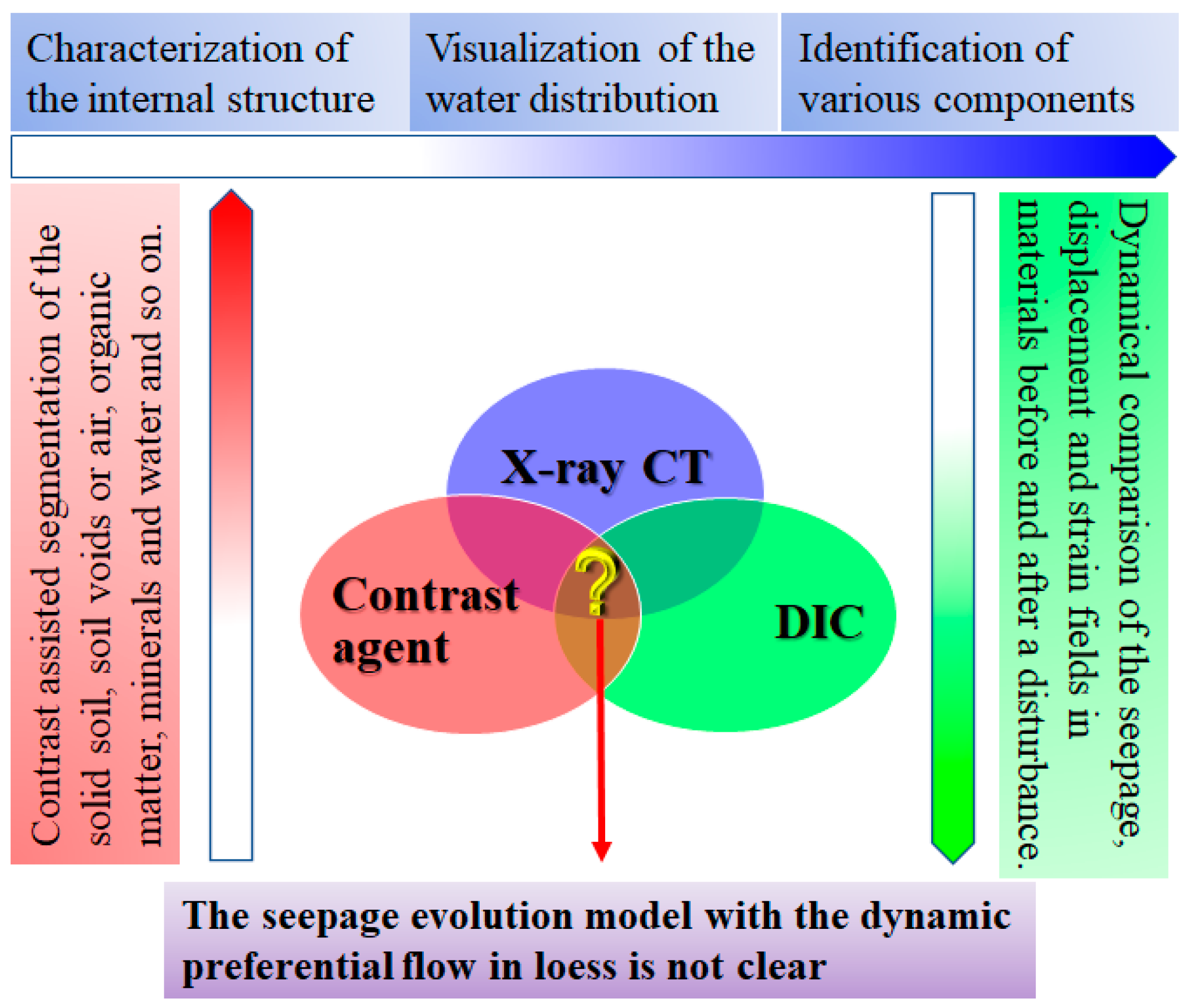
:1. Introduction
2. Materials and Methods
2.1. Study Site and Sample Preparation
2.2. Apparatus for the Preferential Infiltration Experiment
2.3. Preferential Infiltration Experiment
2.4. 3D Image Registration
2.5. Data Processing and Analysis
3. Results and Analyses
3.1. Infiltration Characteristics under Dynamic Seepage Conditions
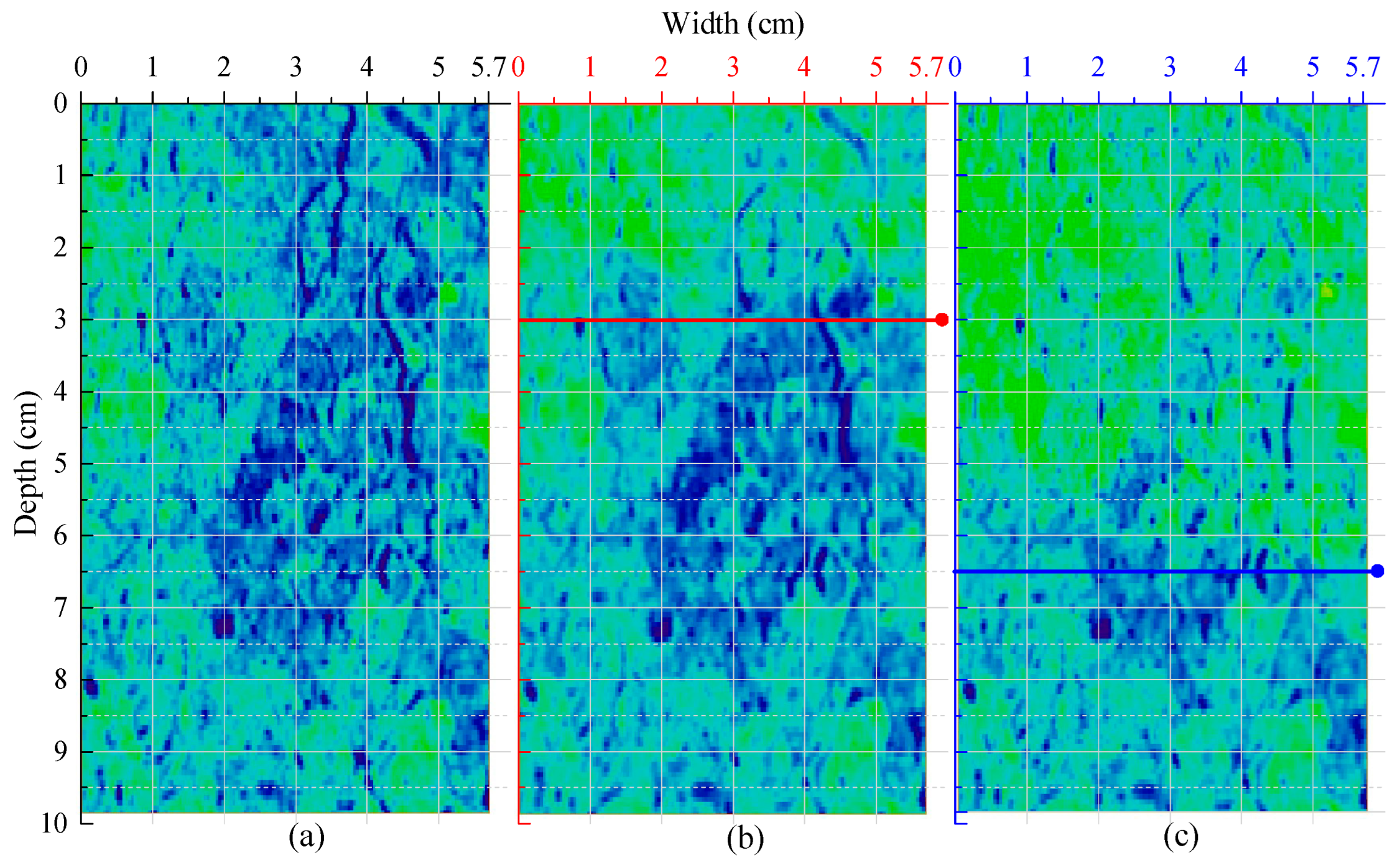
3.1.1. Two-Dimensional Preferential Flow Characteristics
3.1.2. Three-Dimensional Preferential Flow Characteristics
3.1.3. Characteristics of 3D Macropores
3.2. Quantitative Characteristics of Pore Structure Change in the Seepage Process
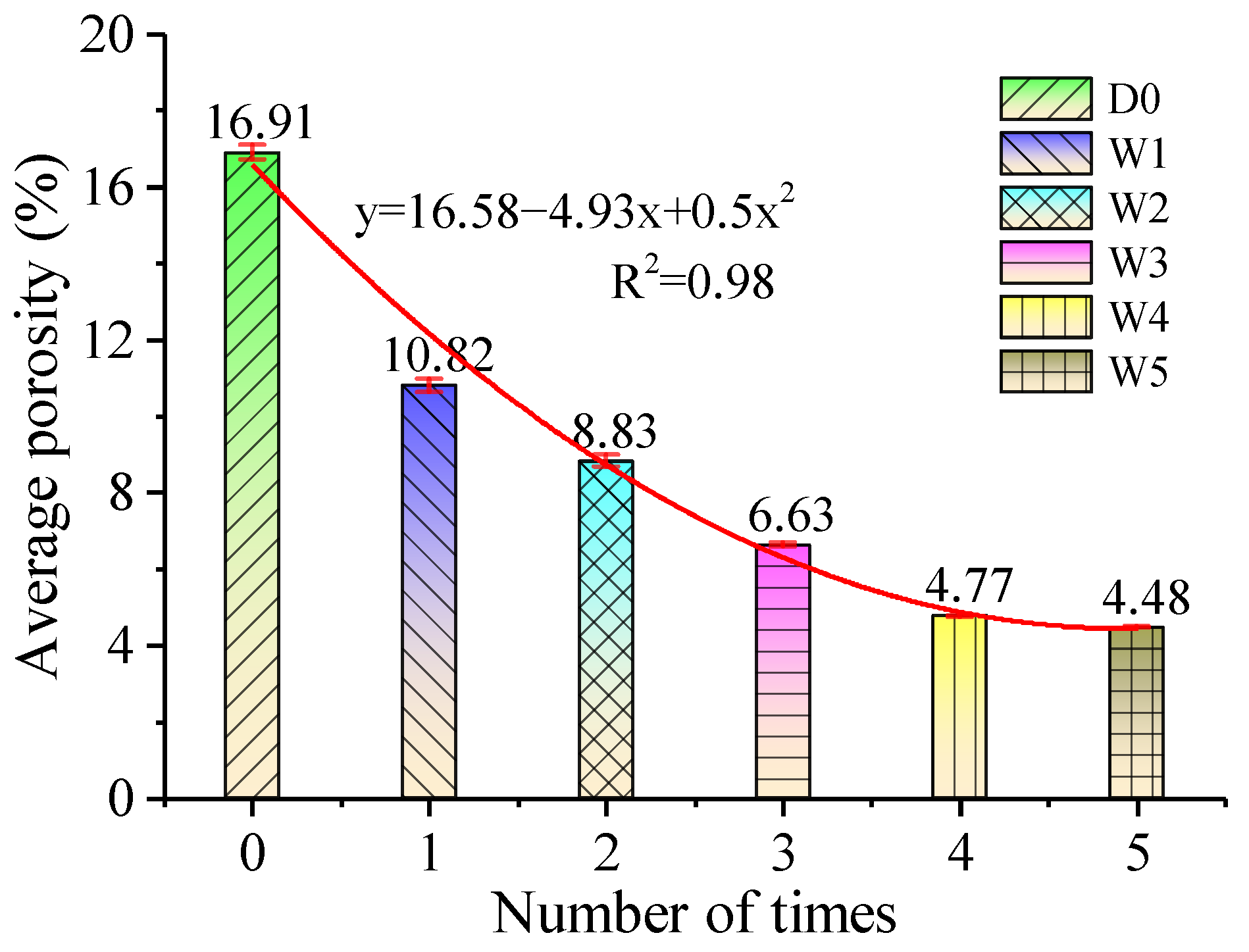
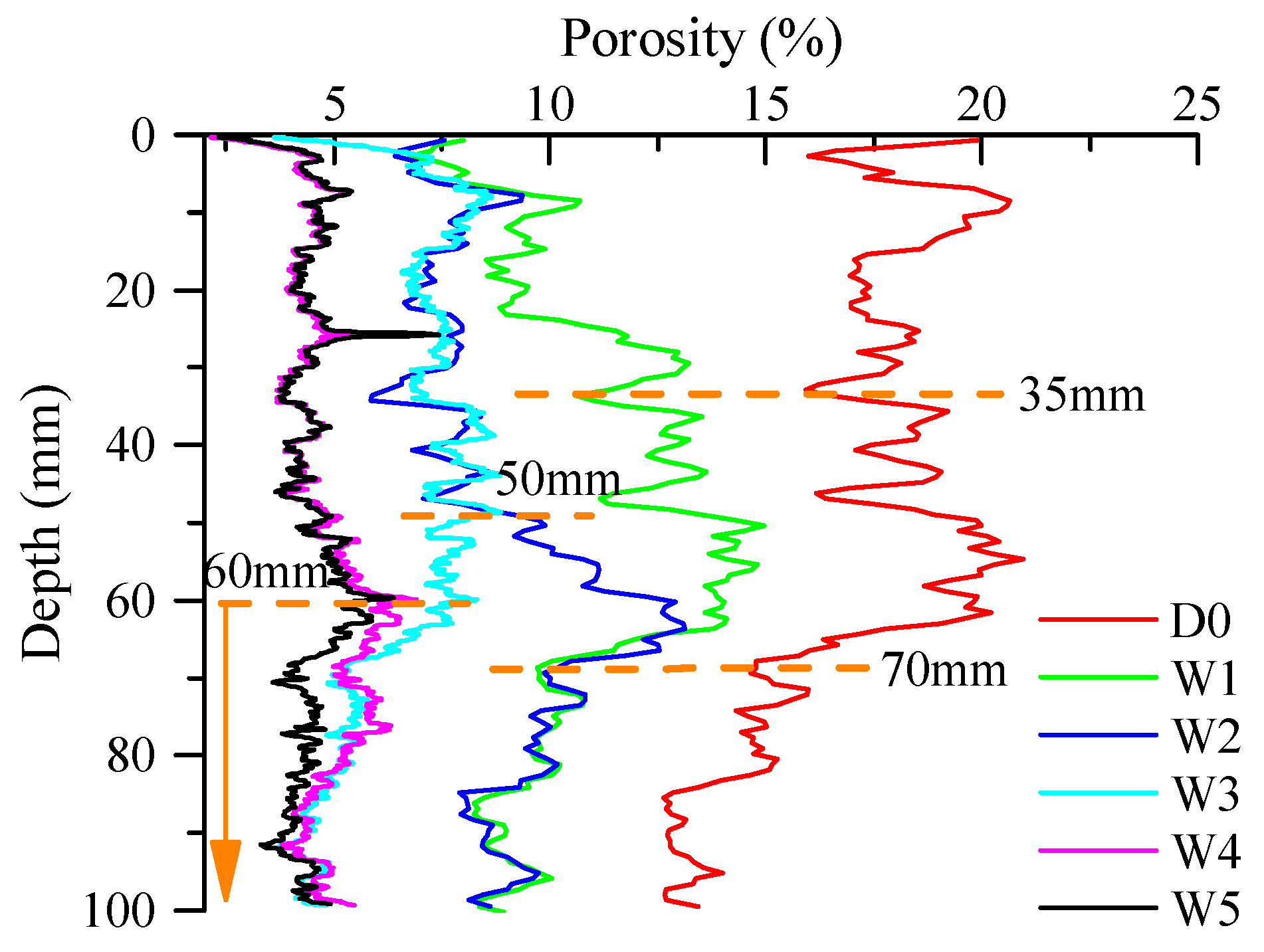
3.2.1. Porosity
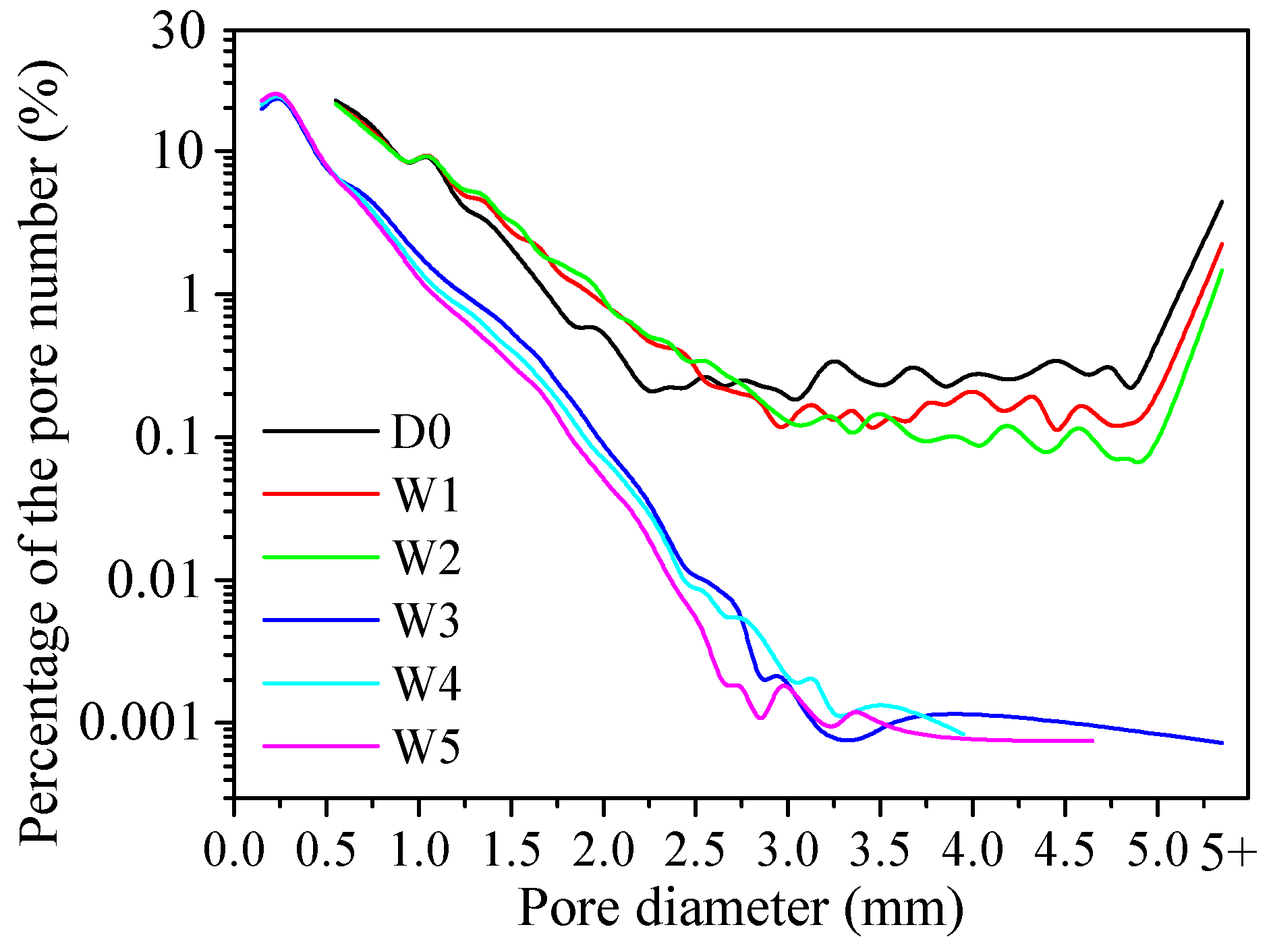
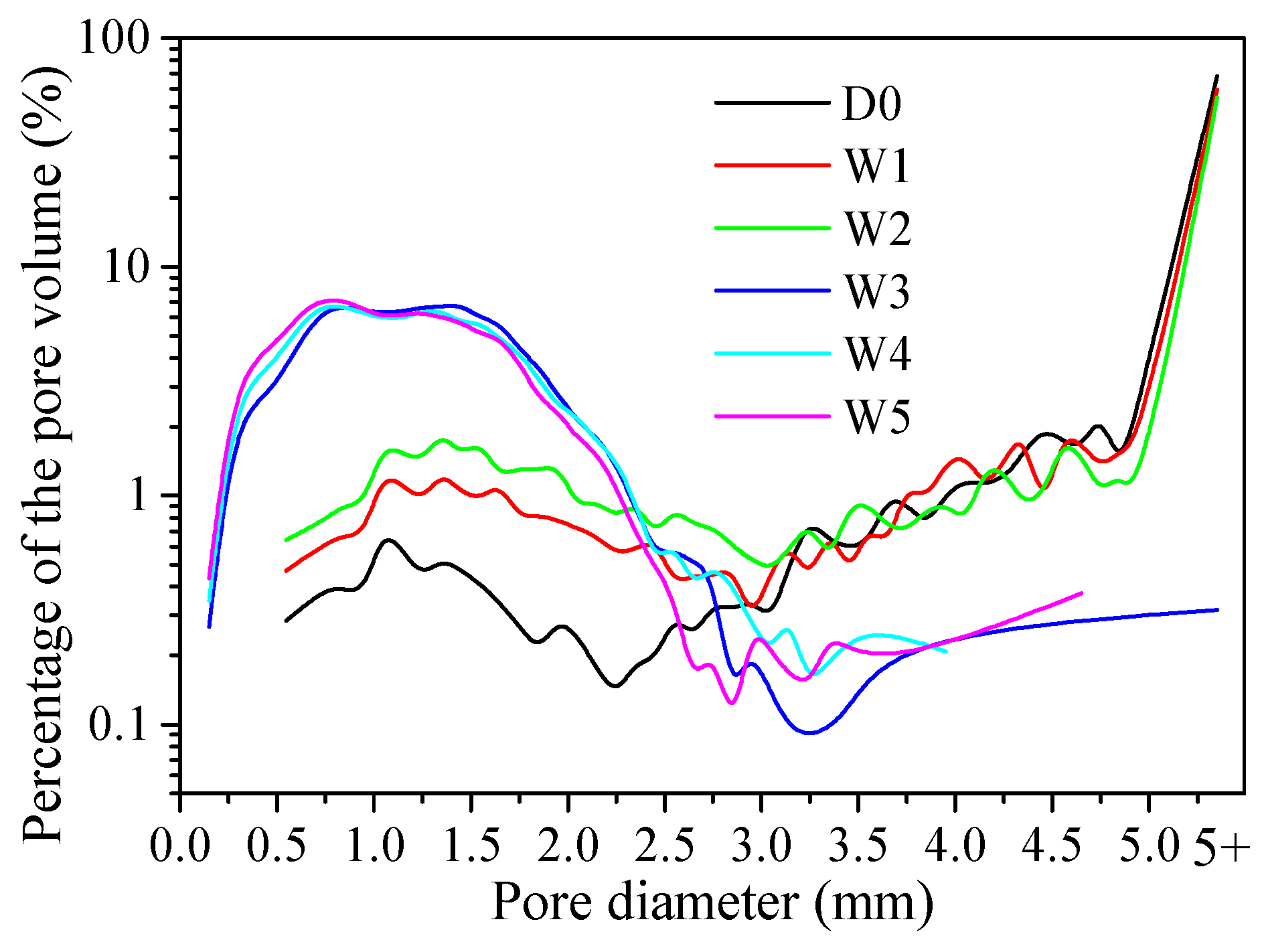
3.2.2. Pore Number and Volume
3.2.3. Dip Angle
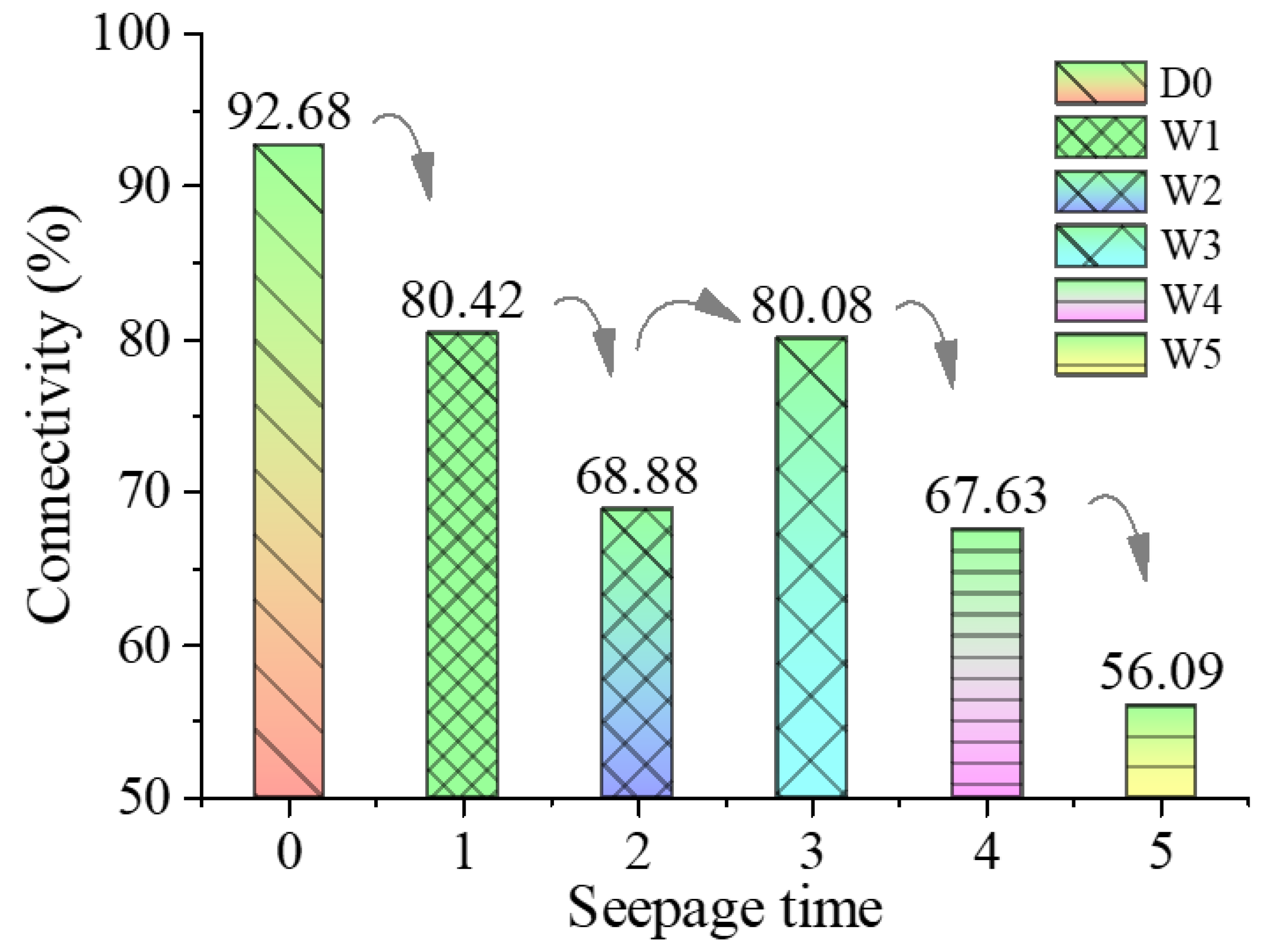
3.2.4. Connectivity
4. Discussions
4.1. The Formation Process of the Seepage Evolution Model
4.2. Evidence for the Seepage Evolution Model
4.3. The Inner Motivation of Percolation
4.4. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, T. The Mass Composition and Structure of Loess; Science Press: Beijing, China, 1966. (In Chinese) [Google Scholar]
- Sun, J.-Z. Loessology (Volume I); Hong Kong Archaeological Society: Hong Kong, 2005. (In Chinese) [Google Scholar]
- Wei, Y.-N.; Fan, W.; Yu, N.; Deng, L.-S.; Wei, T. Permeability of loess from the South Jingyang Plateau under different consolidation pressures in terms of the three-dimensional microstructure. Bull. Eng. Geol. Environ. 2020, 79, 4841–4857. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Y.; Li, X.; Lu, Y.; Pan, W. Microscopic structure changes of Malan loess after humidification in South Jingyang Plateau, China. Environ. Earth Sci. 2019, 78, 287. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, Q.; Qian, H.; Qu, W.; Li, M. Microstructure and permeability evolution of remolded loess with different dry densities under saturated seepage. Eng. Geol. 2020, 282, 105875. [Google Scholar] [CrossRef]
- Yu, B.; Fan, W.; Dijkstra, T.; Wei, Y.; Deng, L. Heterogeneous evolution of pore structure during loess collapse: Insights from X-ray micro-computed tomography. CATENA 2021, 201, 105206. [Google Scholar] [CrossRef]
- Wei, Y.; Fan, W.; Yu, B.; Deng, L.; Wei, T. Characterization and evolution of three-dimensional microstructure of Malan loess. CATENA 2020, 192, 104585. [Google Scholar] [CrossRef]
- Feng, L.; Lin, H.; Zhang, M.; Guo, L.; Jin, Z.; Liu, X. Development and evolution of Loess vertical joints on the Chinese Loess Plateau at different spatiotemporal scales. Eng. Geol. 2020, 265, 105372. [Google Scholar] [CrossRef]
- Li, P.; Qian, H.; Wu, J. Environment: Accelerate research on land creation. Nature 2014, 510, 29–31. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, J. Controlling factors of loess landslides in western China. Environ. Earth Sci. 2010, 59, 1671–1680. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: A case study in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Q.; Zhuang, J.; Leng, Y.; Fan, Z.; Wang, S. Dynamic formation mechanism of landslide disaster on the Loess Plateau. J. Geomech. 2020, 26, 714–730. (In Chinese) [Google Scholar]
- Dijkstra, T.A.; Rogers, C.D.F.; Smalley, I.J.; Derbyshire, E.; Li, Y.J.; Meng, X.M. The loess of north-central China: Geotechnical properties and their relation to slope stability. Eng. Geol. 1994, 36, 153–171. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Zhang, Y.; Xu, Q. Geometrical appearance and spatial arrangement of structural blocks of the Malan loess in NW China and the implications for the formation of loess columns. J. Asian Earth Sci. 2018, 158, 18–28. [Google Scholar] [CrossRef]
- Wei, T.; Fan, W.; Yu, N.; Wei, Y.-n. Three-dimensional microstructure characterization of loess based on a serial sectioning technique. Eng. Geol. 2019, 261, 105265. [Google Scholar] [CrossRef]
- Giménez, R.G.; Martín, J.A.G. Characterization of loess in central Spain: A microstructural study. Environ. Earth Sci. 2012, 65, 2125–2137. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Lu, Y.; Lu, Y.; Fan, W. A study on the collapse characteristics of loess based on energy spectrum superposition method. Heliyon 2023, 9, 18643. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, F.; Ma, F.; Wang, M.; Bai, X.; Zheng, Y.; Yin, H.; Zhang, G. Collapsibility, composition, and microstructure of loess in China. Can. Geotech. J. 2015, 53, 673–686. [Google Scholar] [CrossRef]
- Jotisankasa, A. Collapse Behaviour of a Compacted Silty Clay; University of London: London, UK, 2005. [Google Scholar]
- Zhang, M.S.; Hu, W.; Sun, P.P.; Wang, X.L. Advances and prospects of water sensitivity of loess and the induced loess landslides. J. Earth Environ. 2016, 7, 323–334. [Google Scholar] [CrossRef]
- Luo, H.; Wu, F.; Chang, J.; Xu, J. Microstructural constraints on geotechnical properties of Malan Loess: A case study from Zhaojiaan landslide in Shaanxi province, China. Eng. Geol. 2018, 236, 60–69. [Google Scholar] [CrossRef]
- Yan, G.; Bore, T.; Schlaeger, S.; Scheuermann, A.; Li, L. Investigating scale effects in soil water retention curve via spatial time domain reflectometry. J. Hydrol. 2022, 612, 128238. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Bore, T.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. A lattice Boltzmann exploration of two-phase displacement in 2D porous media under various pressure boundary conditions. J. Rock Mech. Geotech. Eng. 2022, 14, 1782–1798. [Google Scholar] [CrossRef]
- Li, X.; Lu, Y.; Zhang, X.; Fan, W.; Lu, Y.; Pan, W. Quantification of macropores of Malan loess and the hydraulic significance on slope stability by X-ray computed tomography. Environ. Earth Sci. 2019, 78, 522–540. [Google Scholar] [CrossRef]
- Fan, W.; Deng, L.; Yuan, W. Double parameter binary-medium model of fissured loess. Eng. Geol. 2018, 31, 1752–1756. [Google Scholar] [CrossRef]
- Li, Y.; He, S.; Deng, X.; Xu, Y. Characterization of macropore structure of Malan loess in China based on 3D pipe models constructed by using computed tomography technology. J. Asian Earth Sci. 2018, 154, 271–279. [Google Scholar] [CrossRef]
- Zhang, J.F.; Lin, X.C.; Wang, W.Y. Characteristics of macro-pore and macro-pore flow in loess soil. J. Soil Water Conserv. 2003, 17, 168–171. (In Chinese) [Google Scholar] [CrossRef]
- Lipiec, J.; Turski, M.; Hajnos, M.; Świeboda, R. Pore structure, stability and water repellency of earthworm casts and natural aggregates in loess soil. Geoderma 2015, 243–244, 124–129. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Niu, J.; Zheng, H. The preferential flow of soil: A widespread phenomenon in pedological perspectives. Eurasian Soil Sci. 2016, 49, 661–672. [Google Scholar] [CrossRef]
- Guo, Z.; Torra, O.; Hürlimann, M.; Abancó, C.; Medina, V. FSLAM: A QGIS plugin for fast regional susceptibility assessment of rainfall-induced landslides. Environ. Model. Softw. 2022, 150, 105354. [Google Scholar] [CrossRef]
- Pan, W.; Xu, Y.; Lu, Y.; Gao, L.a.; Yao, X. Quantitative determination of preferential flow characteristics of loess based on nonuniformity and fractional dimension. Trans. Chin. Soc. Agric. Eng. 2017, 33, 140–147. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Lu, Y.; Fan, W.; Pan, W.; Zhang, X.; Lu, Y. Current Status and Prospects of Research on Mechanism of Preferential Flow-induced Sliding in Loess Slope. Bull. Soil Water Conserv. 2019, 39, 294–301+324. (In Chinese) [Google Scholar] [CrossRef]
- Peng, J.; Lan, H.; Qian, H.; Wang, W.; Li, R.; Li, Z.; Zhuang, J.; Liu, X.; Liu, S. Scientific research framework of livable yellow river. J. Eng. Geol. 2020, 28, 189–201. (In Chinese) [Google Scholar]
- Li, Y.; Zhao, J. Loess and Loess Geohazards in China; CRC Press: London, UK, 2017. [Google Scholar] [CrossRef]
- Peng, J.B.; Lin, H.C.; Wang, Q.Y.; Zhuang, J.Q.; Cheng, Y.X.; Zhu, X.H. The critical issues and creative concepts in mitigation research of loess geological hazards. J. Eng. Geol. 2014, 22, 684–691. (In Chinese) [Google Scholar] [CrossRef]
- Heijs, A.W.J.; de Lange, J.; Schoute, J.F.T.; Bouma, J. Computed tomography as a tool for non-destructive analysis of flow patterns in macroporous clay soils. Geoderma 1995, 64, 183–196. [Google Scholar] [CrossRef]
- Carmignato, S.; Dewulf, W.; Leach, R. Industrial X-ray Computed Tomography; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Taina, I.A.; Heck, R.J.; Elliot, T.R. Application of x-ray computed tomography to soil science: A literature review. Can. J. Soil Sci. 2008, 88, 1–19. [Google Scholar] [CrossRef]
- Li, Z.; Tang, L. Using Synchrotron-Based X-Ray Microcomputed Tomography to Characterize Water Distribution in Compacted Soils. Adv. Mater. Sci. Eng. 2019, 2019, 7147283. [Google Scholar] [CrossRef]
- Tippkötter, R.; Eickhorst, T.; Taubner, H.; Gredner, B.; Rademaker, G. Detection of soil water in macropores of undisturbed soil using microfocus X-ray tube computerized tomography (μCT). Soil Tillage Res. 2009, 105, 12–20. [Google Scholar] [CrossRef]
- Cnudde, V.; Boone, M.N. High-resolution X-ray computed tomography in geosciences: A review of the current technology and applications. Earth Sci. Rev. 2013, 123, 1–17. [Google Scholar] [CrossRef]
- Loo, D.V.; Bouckaert, L.; Leroux, O.; Pauwels, E.; Dierick, M.; Hoorebeke, L.V.; Cnudde, V.; Neve, S.D.; Sleutel, S. Contrast agents for soil investigation with X-ray computed tomography. Geoderma 2014, 213, 485–491. [Google Scholar] [CrossRef]
- Mooney, S.J. Three-dimensional visualization and quantification of soil macroporosity and water flow patterns using computed tomography. Soil Use Manag. 2002, 18, 142–151. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Halleck, P. Quantifying Soil Structure and Preferential Flow in Intact Soil Using X-ray Computed Tomography. Soil Sci. Soc. Am. J. 2008, 72, 1058–1069. [Google Scholar] [CrossRef]
- Luo, L. Quantification of Soil Macropore Network and Its Relationship to Preferential Flow Using Combined X-ray Computed Tomography and Breakthrough Curve Analysis. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2009. [Google Scholar]
- Wildenschild, D.; Hopmans, J.W.; Rivers, M.; Kent, A. Quantitative analysis of flow processes in a sand using synchrotron-based X-ray microtomography. Vadose Zone J. 2005, 4, 112–126. [Google Scholar] [CrossRef]
- Willson, C.; Lu, N.; Likos, W. Quantification of Grain, Pore, and Fluid Microstructure of Unsaturated Sand from X-Ray Computed Tomography Images. Geotech. Test. J. 2012, 35, 911–923. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Li, S. Quantification of 3-D soil macropore networks in different soil types and land uses using computed tomography. J. Hydrol. 2010, 393, 53–64. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Y.; Liu, Z.; Zhao, P.; Liu, C. In-situ tracking of water transport in cement paste using X-ray computed tomography combined with CsCl enhancing. Mater. Lett. 2015, 160, 381–383. [Google Scholar] [CrossRef]
- Jianmei, W.; Zengchao, F.; Dong, Z.; Jing, Z. Microscopic Imaging of the Sandstone Under Hydrostatic Pressure and Its Preliminary Analysis Based on the Micro-CT and Medical Imaging Agents. J. Taiyuan Univ. Technol. 2015, 46, 405–409. (In Chinese) [Google Scholar] [CrossRef]
- Dai, X.; He, L.; Wu, W.; Chen, J. Visualization experiment technology based on transparent geotechnical materials and its engineering application. J. Vis. 2023, 26, 145–159. [Google Scholar] [CrossRef]
- Iskander, M.; Sadek, S.; Liu, J. Soil structure interaction in transparent synthetic soils using digital image correlation. In Proceedings of the TRB 2003 Session on Recent Advances in Modeling Techniques in Geomechanics, Washington, DC, USA, January 2003; p. 03-2360. Available online: https://www.researchgate.net/publication/258311199_Soil_structure_interaction_in_transparent_synthetic_soils_using_digital_image_correlation (accessed on 12 August 2023).
- Chen, Y.; Xu, J.; Peng, S.; Zhang, Q.; Chen, C. Strain localisation and seepage characteristics of rock under triaxial compression by 3D digital image correlation. Int. J. Rock Mech. Min. Sci. 2022, 152, 105064. [Google Scholar] [CrossRef]
- Pengjin, Y.; Shengjun, M.; Yuting, M.; Wenxuan, Y.; Xiangfan, S. Multi-dimensional non-uniform deformation and failure of siltstone determined using acoustic, 3D-digital image correlation, and computed tomography. Theor. Appl. Fract. Mech. 2023, 125, 103800. [Google Scholar] [CrossRef]
- Higo, Y.; Oka, F.; Sato, T.; Matsushima, Y.; Kimoto, S. Investigation of localized deformation in partially saturated sand under triaxial compression using microfocus X-ray CT with digital image correlation. Soils Found. 2013, 53, 181–198. [Google Scholar] [CrossRef]
- Nohara, S.; Mukunoki, T. Quantitative Evaluation of Soil Structure and Strain in Three Dimensions under Shear Using X-ray Computed Tomography Image Analysis. J. Imaging 2021, 7, 230. [Google Scholar] [CrossRef]
- Doreau-Malioche, J.; Galvis-Castro, A.; Tovar-Valencia, R.; Viggiani, G.; Combe, G.; Prezzi, M.; Salgado, R. Characterising processes at sand-pile interface using digital image analysis and X-ray CT. Geotech Lett. 2019, 9, 254–262. [Google Scholar] [CrossRef]
- Keyes, S.D.; Cooper, L.; Duncan, S.; Koebernick, N.; McKay Fletcher, D.M.; Scotson, C.P.; van Veelen, A.; Sinclair, I.; Roose, T. Measurement of micro-scale soil deformation around roots using four-dimensional synchrotron tomography and image correlation. J. R. Soc. Interface 2017, 14, 20170560. [Google Scholar] [CrossRef] [PubMed]
- Khatami, H.; Deng, A.; Jaksa, M. An experimental study of the active arching effect in soil using the digital image correlation technique. Comput. Geotech. 2019, 108, 183–196. [Google Scholar] [CrossRef]
- Tianhua, W.; Yu, Z.; Li, W.; Jinmei, S.; Huan, Z.; Zheng, S. Mesoscopic study of interaction mechanism between circular hole and fissures inrock under uniaxial compression. Rock Soil Mech. 2018, 39, 463–472. (In Chinese) [Google Scholar] [CrossRef]
- Wu, Y.; Li, X.; Zhang, L.; Zhou, J.; Mao, T.; Li, M. Analysis on Spatial Variability of SRM Based on Real-Time CT and the DIC Method Under Uniaxial Loading. Front. Phys. 2022, 10, 789068. [Google Scholar] [CrossRef]
- Keyes, S.D.; Gillard, F.; Soper, N.; Mavrogordato, M.N.; Sinclair, I.; Roose, T. Mapping soil deformation around plant roots using in vivo 4D X-ray Computed Tomography and Digital Volume Correlation. J. Biomech. 2016, 49, 1802–1811. [Google Scholar] [CrossRef]
- Xu, P.; Lin, T.; Qian, H.; Zhang, Q. Anisotropic microstructure of loess-paleosol sequence and its significance for engineering and paleoclimate: A case study from Xiushidu (XSD) profile, southern Chinese Loess Plateau. Eng. Geol. 2021, 286, 106092. [Google Scholar] [CrossRef]
- Hou, K. Pedogenic and Composition Characteristics of the Loess Soil and Its Paleo-environmental Significance in the Xiushidu Profile of Jingyang. Master’s Thesis, Chang’an University, Xi’an, China, 2018. (In Chinese). [Google Scholar]
- Gerke, K.M.; Karsanina, M.V. Pore-scale modelling of flow and transport phenomena in soils. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Yan, R.-X.; Peng, J.-B.; Huang, Q.-B.; Chen, L.-J.; Kang, C.-Y.; Shen, Y.-J. Triggering influence of seasonal agricultural irrigation on shallow loess landslides on the south Jingyang Plateau, China. Water 2019, 11, 1474. [Google Scholar] [CrossRef]
- Hong, B.; Du, S.; Li, X.a.; Wang, L.; Wang, S.; Zhang, H. Infiltration Characteristics and Disaster-forming Mechanism of Loess in South Jinghe Tableland. Bull. Soil Water Conserv. 2019, 39, 75–79. (In Chinese) [Google Scholar]
- Claes, N.; Paige, G.B.; Parsekian, A.D. Uniform and lateral preferential flows under flood irrigation at field scale. Hydrol. Process. 2019, 33, 2131–2147. [Google Scholar] [CrossRef]
- GBT50123-2019; Standard for Geotechnical Testing Method. China Planning Press: Beijing, China, 2019.
- Latham, S.; Varslot, T.; Sheppard, A. Image registration: Enhancing and Calibrating X-ray Micro-CT Imaging. In Proceedings of the International Symposium of the Society of Core Analysts, Austin, TX, USA, 19–22 September 2008; p. 12. [Google Scholar]
- Takano, D.; Lenoir, N.; Otani, J.; Hall, S.A. Localised deformation in a wide-grained sand under triaxial compression revealed by X-ray tomography and digital image correlation. Soils Found. 2015, 55, 906–915. [Google Scholar] [CrossRef]
- Ma, J.; Zeng, R.; Yao, Y.; Meng, X.; Meng, X.; Zhang, Z.; Wang, H.; Zhao, S. Characterization and quantitative evaluation of preferential infiltration in loess, based on a soil column field test. CATENA 2022, 213, 106164. [Google Scholar] [CrossRef]
- Nimmo, J.R. Preferential flow occurs in unsaturated conditions. Hydrol. Process. 2012, 26, 786–789. [Google Scholar] [CrossRef]
- Cristiano, E.; Bogaard, T.; Barontini, S. Effects of Anisotropy of Preferential flow on the Hydrology and Stability of Landslides. Procedia Earth Planet. Sci. 2016, 16, 204–214. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Hu, X.; Li, P.; Wang, Y. Discussion on preferential flow and piston flow in thick loess vadose zone. J. Eng. Geol. 2022, 30, 1842–1848. (In Chinese) [Google Scholar] [CrossRef]
- Liu, M.; Guo, L.; Yi, J.; Lin, H.; Lou, S.; Zhang, H.; Li, T. Characterising preferential flow and its interaction with the soil matrix using dye tracing in the Three Gorges Reservoir Area of China. Soil Res. 2018, 56, 588–600. [Google Scholar] [CrossRef]
- Li, X.; Lu, Y.; Zhang, X.; Lu, Y.; Yang, Y. Pore-fissure Identification and Characterization of Paleosol Based on X-ray Computed Tomography. Bull. Soil Water Conserv. 2018, 38, 224–230. (In Chinese) [Google Scholar] [CrossRef]
- Chen, Y.; Hu, R.; Zhou, C.; Li, D.; Rong, G.; Jiang, Q. A new classification of seepage control mechanisms in geotechnical engineering. J. Rock Mech. Geotech. Eng. 2010, 2, 209–222. [Google Scholar] [CrossRef]
- Chambers, J.E.; Gunn, D.A.; Wilkinson, P.B.; Meldrum, P.I.; Haslam, E.; Holyoake, S.; Kirkham, M.; Kuras, O.; Merritt, A.; Wragg, J. 4D electrical resistivity tomography monitoring of soil moisture dynamics in an operational railway embankment. Near Surf. Geophys. 2014, 12, 61–72. [Google Scholar] [CrossRef]
- Polemio, M.; Lollino, P. Failure of infrastructure embankments induced by flooding and seepage: A neglected source of hazard. Nat. Hazards Earth Syst. Sci. 2011, 11, 3383–3396. [Google Scholar] [CrossRef]
- Li, Q.; Wu, B.-Z.; Li, X.; Jia, S.; Zhen, F.-H.; Gao, S. The Relatively Stable Seepage Field: A New Concept to Determine Seepage Field in the Design of a Dry-Stack Tailings Pond. Appl. Sci. 2022, 12, 12123. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Gu, Y.; Wang, S. Experimental Investigation of the Seepage-Induced Failure Process in Granular Soils. Geofluids 2022, 2022, 5703151. [Google Scholar] [CrossRef]
- Zhang, D.-M.; Gao, C.-P.; Yin, Z.-Y. CFD-DEM modeling of seepage erosion around shield tunnels. Tunn. Undergr. Space Technol. 2019, 83, 60–72. [Google Scholar] [CrossRef]
- Li, X.; Chen, R.; Liu, L.; Zhou, C.; Bate, B. A non-Darcy flow CFD–DEM method for simulating ground collapse induced by leakage through underground pipeline defect. Comput. Geotech. 2023, 162, 105695. [Google Scholar] [CrossRef]
- Lu, Y.; Lu, Y.; Lu, T.; Wang, B.; Zeng, G.; Zhang, X. Computing of Permeability Tensor and Seepage Flow Model of Intact Malan Loess by X-ray Computed Tomography. Water 2023, 15, 2851. [Google Scholar] [CrossRef]
- Qin, Y.; Qiu, J.; Lai, J.; Liu, F.; Wang, L.; Luo, Y.; Liu, T. Seepage characteristics in loess strata subjected to single point water supply. J. Hydrol. 2022, 609, 127611. [Google Scholar] [CrossRef]
- Chen, G.; Meng, X.; Qiao, L.; Zhang, Y.; Wang, S. Response of a loess landslide to rainfall: Observations from a field artificial rainfall experiment in Bailong River Basin, China. Landslides 2018, 15, 895–911. [Google Scholar] [CrossRef]
- Soto-Gómez, D.; Vázquez Juíz, L.; Pérez-Rodríguez, P.; López-Periago, J.E.; Paradelo, M.; Koestel, J. Percolation theory applied to soil tomography. Geoderma 2020, 357, 113959. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; Genuchten, M.T.V.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Wilson, G.V.; Cullum, R.F.; Römkens, M.J.M. Ephemeral gully erosion by preferential flow through a discontinuous soil-pipe. CATENA 2008, 73, 98–106. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Gu, Y.; Wang, S. Fractal Characteristics of the Seepage Erosion Process in Porous Soil. Geofluids 2022, 2022, 3383773. [Google Scholar] [CrossRef]
- Nieber, J.L.; Sidle, R.C.; Beven, K.J. How do disconnected macropores in sloping soils facilitate preferential flow? Hydrol. Process. 2010, 24, 1582–1594. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, K.; Zhou, H.; Lin, H.; Li, D.; Peng, X. Linking saturated hydraulic conductivity and air permeability to the characteristics of biopores derived from X-ray computed tomography. J. Hydrol. 2019, 571, 1–10. [Google Scholar] [CrossRef]
- Wilkinson, D.J.; Willemsen, J.F. Invasion Percolation: A New Form of Percolation Theory. J. Phys. A Gen. Phys. 1999, 16, 3365. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G. Improving unsaturated hydraulic conductivity estimation in soils via percolation theory. Geoderma 2017, 303, 9–18. [Google Scholar] [CrossRef]
- Sedighi, M. An Investigation of Hydro-Geochemical Processes in Coupled Thermal, Hydraulic, Chemical and Mechanical Behaviour of Unsaturated Soils; Cardiff University (United Kingdom): Cardiff, UK, 2011. [Google Scholar]
- Xu, P.; Zhang, Q.; Qian, H.; Guo, M.; Yang, F. Exploring the saturated permeability of remolded loess under inorganic salt solution seepage. Eng. Geol. 2021, 294, 105927. [Google Scholar] [CrossRef]

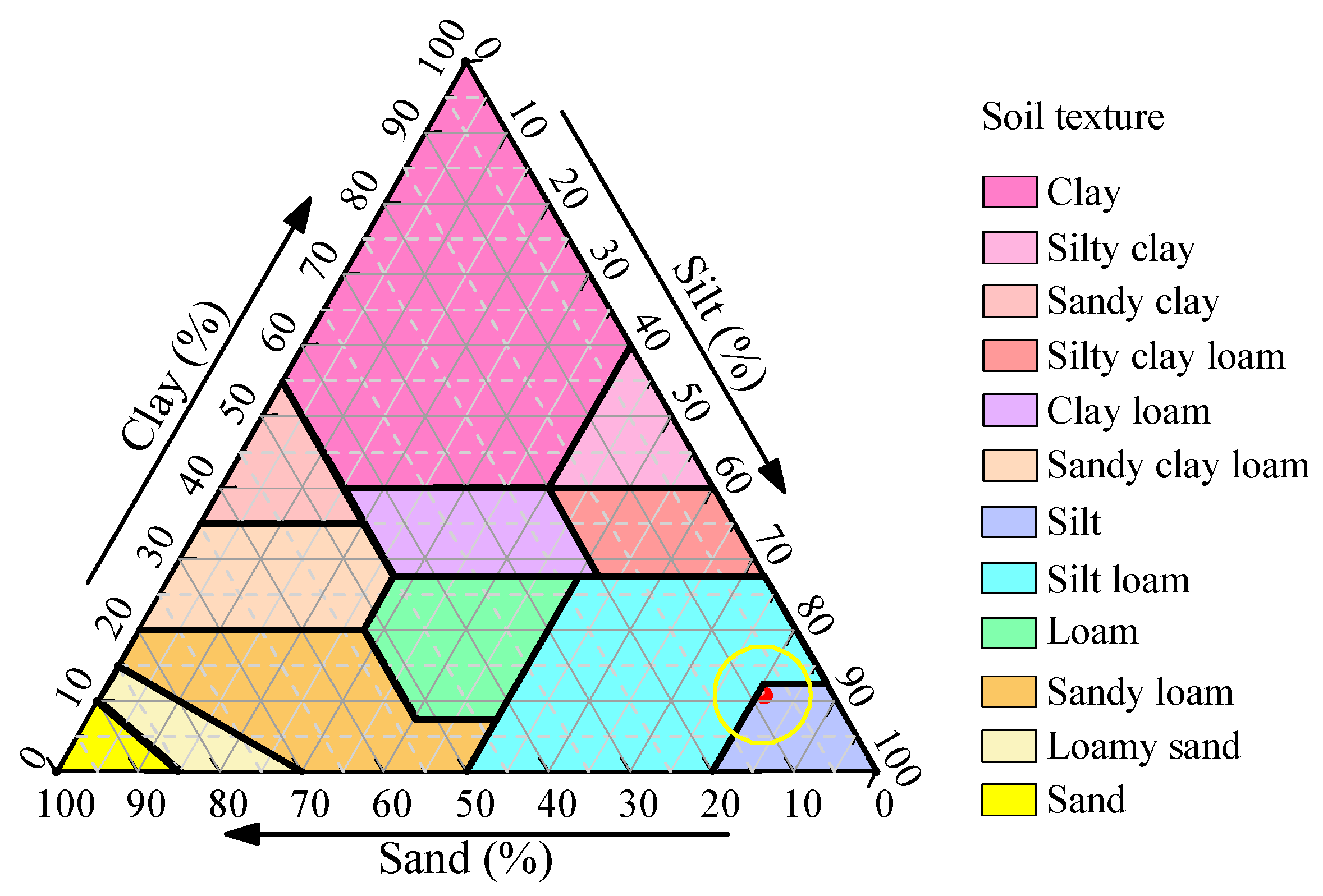
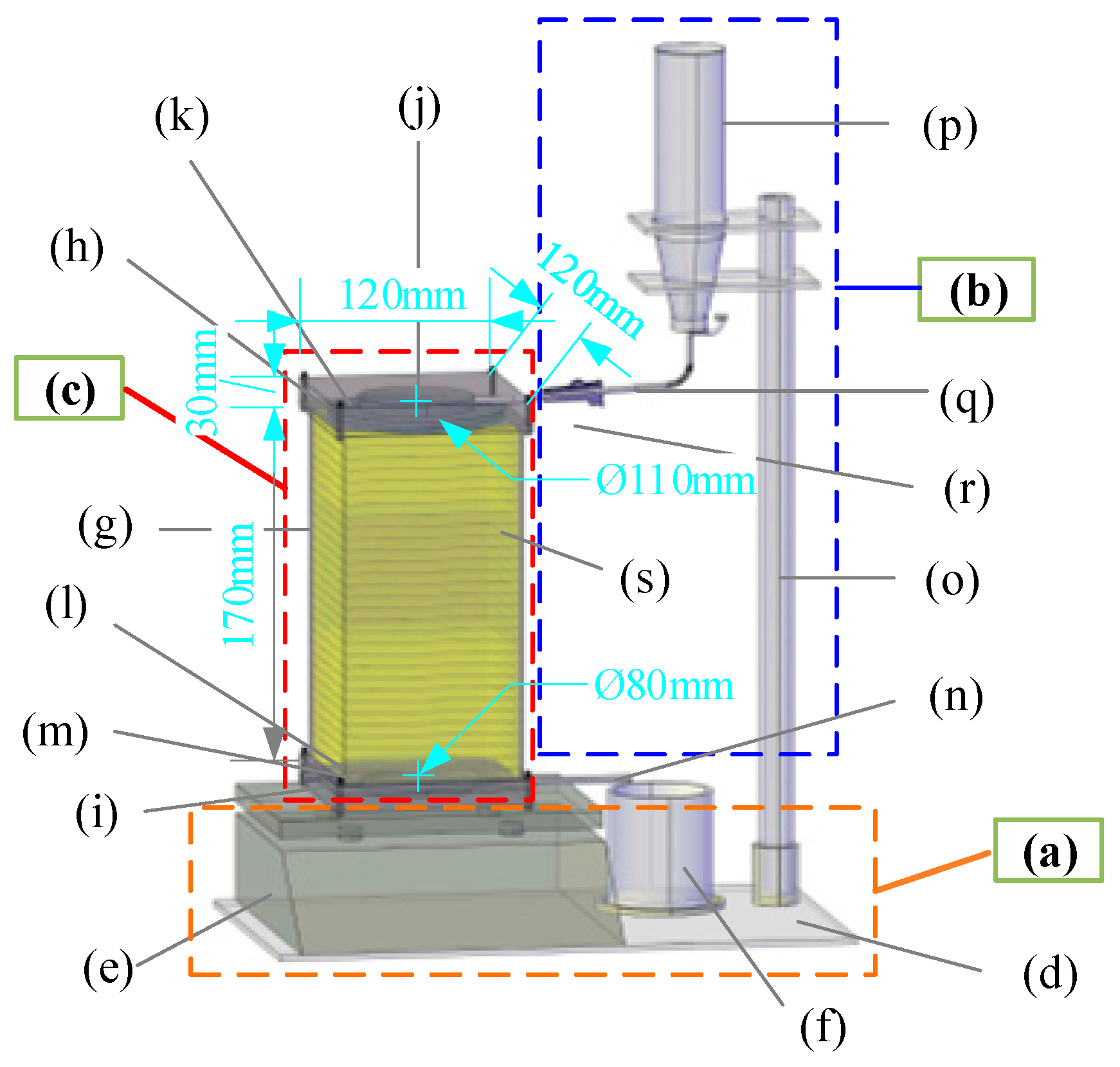






| Dry Density (g/cm3) | Specific Gravity | Porosity (%) | Void Ratio | Liquid Limit | Plastic Limit | Plastic Index | Clay (%) (d ≤ 2 μm) | Silt (%) (2 < d ≤ 50 μm) | Sand (%) (d > 50 μm) | Soil Type | Cu | Cc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.32 | 2.67 | 43.94 | 0.79 | 28.21 | 16.05 | 11.94 | 10.65 | 81.06 | 8.29 | Silt | 14.50 | 2.45 |
| State Mark | Average | Minimum | Maximum | Standard Error | Standard Deviation | Variance |
|---|---|---|---|---|---|---|
| D0 | 16.91% | 12.61% | 20.97% | ±0.20% | 2.38% | 5.66% |
| W1 | 10.82% | 6.75% | 14.95% | ±0.17% | 2.09% | 4.35% |
| W2 | 8.83% | 5.85% | 13.13% | ±0.14% | 1.69% | 2.87% |
| W3 | 6.63% | 3.62% | 8.88% | ±0.04% | 1.37% | 1.89% |
| W4 | 4.77% | 2.15% | 6.92% | ±0.02% | 0.71% | 0.50% |
| W5 | 4.48% | 2.35% | 7.45% | ±0.02% | 0.54% | 0.29% |
| Equal Diameter (mm) | Changing Percentage of the Pore Number (%) | ||||
|---|---|---|---|---|---|
| W1 | W2 | W3 | W4 | W5 | |
| <1 | –3.049 | –0.583 | +40.726 | +1.553 | +0.948 |
| 1~2 | +6.686 | +2.123 | –33.573 | –1.525 | –0.879 |
| 2~3 | +1.001 | +0.238 | –3.615 | –0.032 | –0.066 |
| 3~4 | –1.074 | –0.378 | –1.173 | +0.005 | –0.003 |
| 4~5 | –1.371 | –0.631 | –0.895 | 0.000 | 0.000 |
| >5 | –2.193 | –0.769 | –1.469 | 0.000 | 0.000 |
| Equal Diameter (mm) | Changing Percentage of the Pore Volume (%) | ||||
|---|---|---|---|---|---|
| W1 | W2 | W3 | W4 | W5 | |
| <1 | +0.989 | +0.824 | +32.042 | +3.610 | +4.134 |
| 1~2 | +5.895 | +4.804 | +40.320 | –4.370 | –1.797 |
| 2~3 | +2.765 | +2.481 | +0.955 | +0.363 | –2.347 |
| 3~4 | +0.414 | –0.115 | –6.971 | +0.714 | –0.364 |
| 4~5 | –1.681 | –3.142 | –11.745 | 0.000 | 0.000 |
| >5 | –8.382 | –4.853 | –54.600 | 0.000 | 0.000 |
| Dip Angle (°) | D0 | W1 | W2 | W3 | W4 | W5 | Δ |
|---|---|---|---|---|---|---|---|
| 0~10 | 7.47 | 7.23 | 7.42 | 18.56 | 20.92 | 21.83 | +14.37 |
| 10~20 | 6.47 | 6.89 | 6.75 | 17.70 | 18.22 | 18.86 | +12.39 |
| 20~30 | 8.53 | 7.82 | 8.18 | 15.67 | 15.52 | 15.68 | +7.15 |
| 30~40 | 9.95 | 9.31 | 9.31 | 14.17 | 13.01 | 12.62 | +2.67 |
| 40~50 | 12.85 | 12.95 | 12.27 | 11.69 | 10.58 | 10.00 | –2.86 |
| 50~60 | 16.09 | 15.80 | 15.56 | 9.07 | 8.66 | 8.03 | –8.06 |
| 60~70 | 18.31 | 18.72 | 16.63 | 6.88 | 6.76 | 6.63 | –11.68 |
| 70~80 | 14.39 | 14.94 | 16.22 | 4.62 | 4.65 | 4.54 | –9.85 |
| 80~90 | 5.94 | 6.35 | 7.66 | 1.64 | 1.67 | 1.81 | –4.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, Y.; Li, Q.; Zhang, X.; Shi, X.; Lu, Y.; Zhang, S.; Zhang, L. The Seepage Evolution Characteristics in Undisturbed Loess under Dynamic Preferential Flow: New Insights from X-ray Computed Tomography. Water 2023, 15, 2963. https://doi.org/10.3390/w15162963
Li X, Li Y, Li Q, Zhang X, Shi X, Lu Y, Zhang S, Zhang L. The Seepage Evolution Characteristics in Undisturbed Loess under Dynamic Preferential Flow: New Insights from X-ray Computed Tomography. Water. 2023; 15(16):2963. https://doi.org/10.3390/w15162963
Chicago/Turabian StyleLi, Xin, Yang Li, Qiang Li, Xiaozhou Zhang, Xuechen Shi, Yudong Lu, Shaoxiong Zhang, and Liting Zhang. 2023. "The Seepage Evolution Characteristics in Undisturbed Loess under Dynamic Preferential Flow: New Insights from X-ray Computed Tomography" Water 15, no. 16: 2963. https://doi.org/10.3390/w15162963





