Ice Phenology and Thickness Modelling for Lake Ice Climatology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Equations for Water Temperature
2.2. Ice–Water Model
3. Equilibrium
3.1. Temperature Equilibrium
3.2. Ice Equilibrium
4. Time Evolution
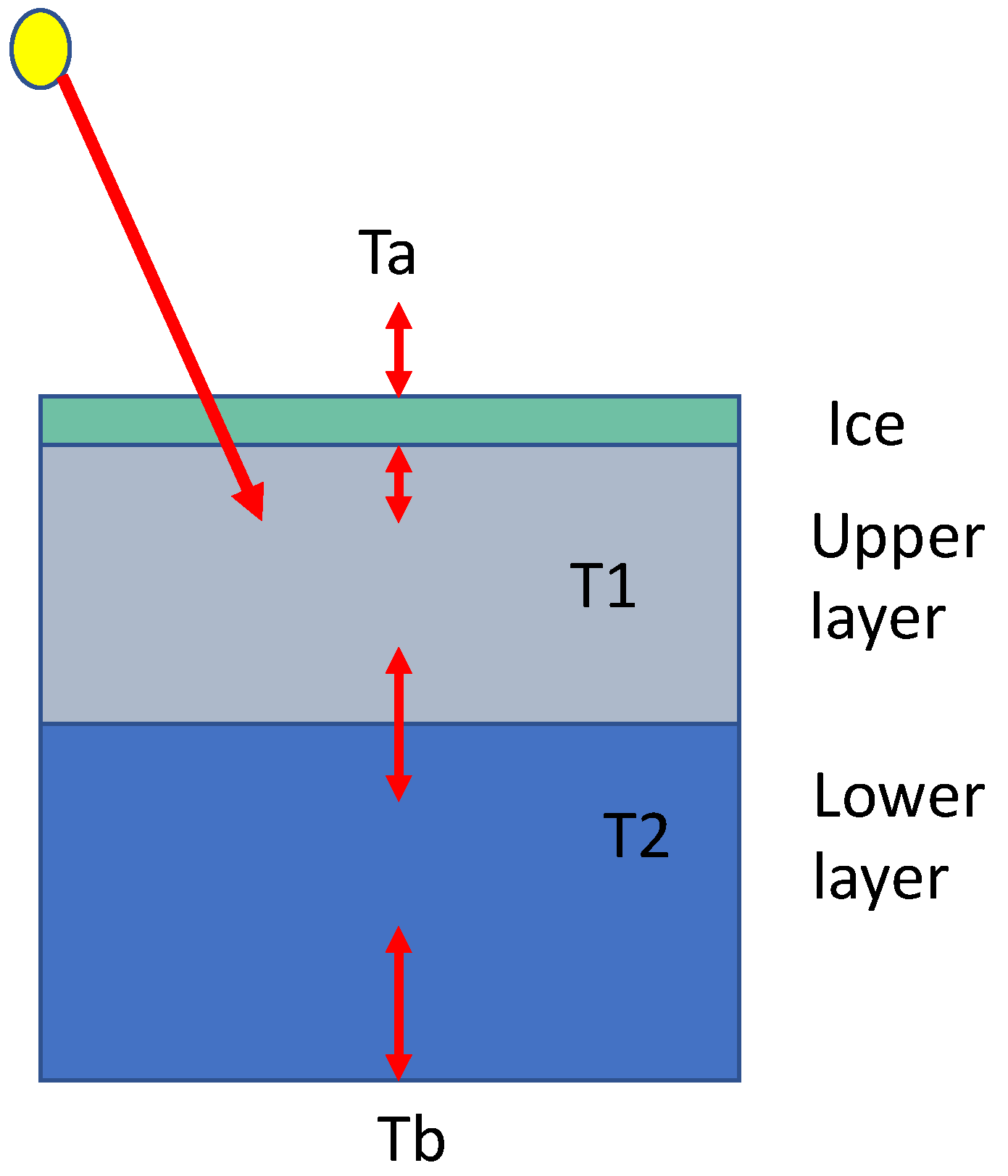
4.1. The Two-Layer System
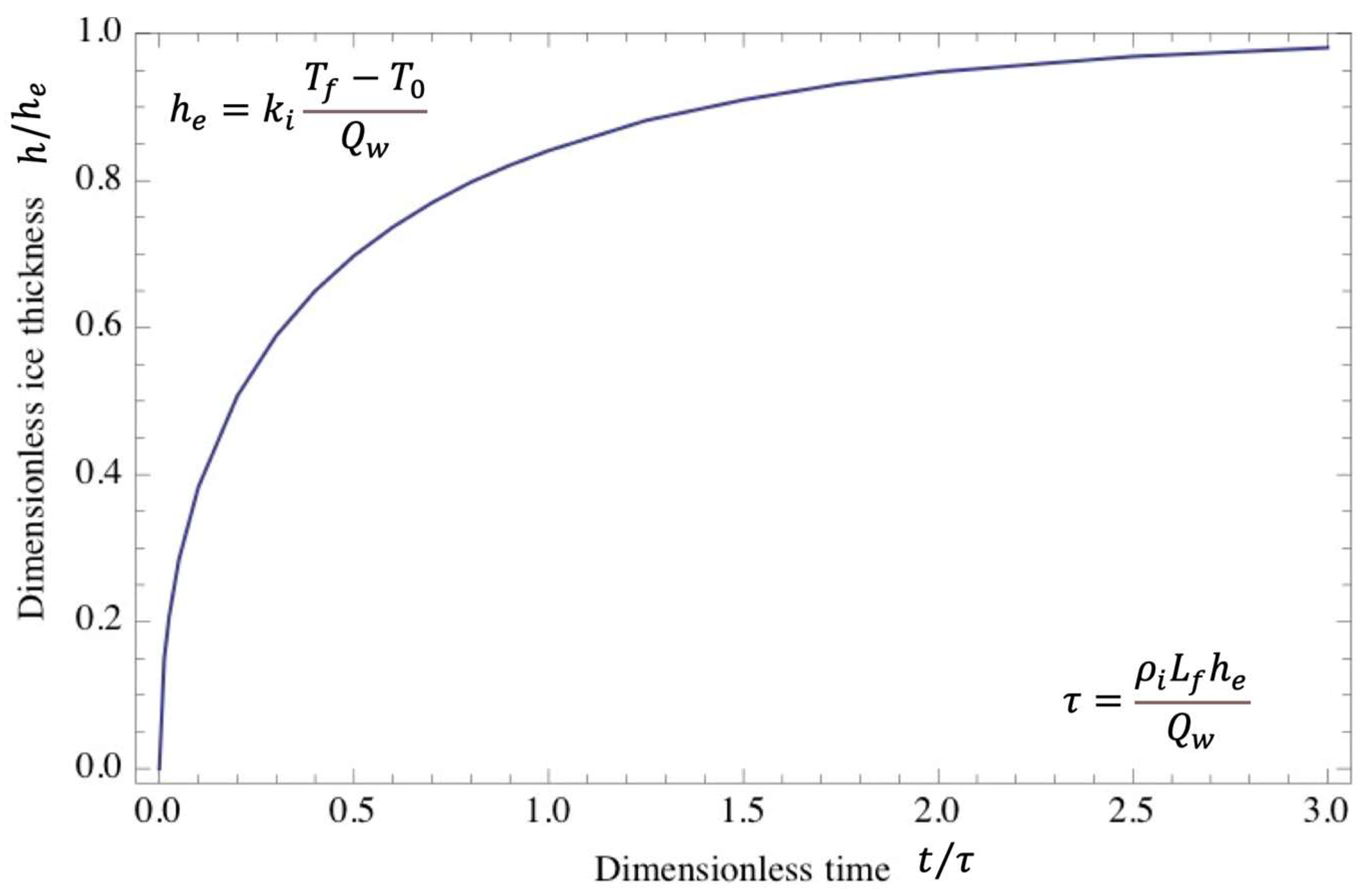
4.2. Ice-Cover Thickness
5. Discussion
6. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salonen, K.; Leppäranta, M.; Viljanen, M.; Gulati, R. Perspectives in winter limnology: Closing the annual cycle of freezing lakes. Aquat. Ecol. 2009, 43, 609–616. [Google Scholar] [CrossRef]
- George, G. (Ed.) Climate Change Impact on European Lakes; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Knoll, L.B.; Sharma, S.; Denfeld, B.A.; Flaim, G.; Hori, Y.; Magnuson, J.J.; Straile, D.; Weyhenmeyer, G. Consequences of lake and river ice loss on cultural ecosystem services. Limnol. Oceanogr. Lett. 2019, 4, 119–131. [Google Scholar] [CrossRef]
- Leppäranta, M. Freezing of Lakes and the Evolution of Their Ice Cover, 2nd ed.; Springer-Praxis: Heidelberg, Germany, 2023. [Google Scholar]
- Ashton, G. Freshwater ice growth, motion, and decay. In Dynamics of Snow and Ice Masses; Colbeck, S., Ed.; Academic Press: New York, NY, USA, 1980; pp. 261–304. [Google Scholar]
- Sharma, S.; Blagrave, K.; Magnuson, J.J.; O’Reilly, C.M.; Oliver, S.; Batt, R.D.; Magee, R.M.; Straile, D.; Weyhenmeyer, G.A.; Winslow, L.; et al. Widespread loss of lake ice around the Northern Hemisphere in a warming world. Nat. Clim. Chang. 2019, 9, 227–231. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Saari, M.; Pulkkanen, M.; Kløve, B. Six decades of thermal change in a pristine lake situated north of the Arctic Circle. Water Resour. Res. 2022, 58, e2021WR031543. [Google Scholar] [CrossRef]
- Noori, R.; Bateni, S.M.; Saari, M.; Almazroui, M.; Torabi Haghighi, A. Strong warming rates in the surface and bottom layers of a boreal lake: Results from approximately six decades of measurements (1964–2020). Earth Space Sci. 2022, 9, e2021EA001973. [Google Scholar] [CrossRef]
- Magnuson, J.J.; Robertson, D.M.; Benson, B.J.; Wynne, R.H.; Livingstone, D.M.; Arai, T.; Assel, R.A.; Barry, R.G.; Card, V.; Kuusisto, E.; et al. Historical trends in lake and river ice cover in the northern hemisphere. Science 2000, 289, 1743–1746, Erratum in Science 2001, 291, 254. [Google Scholar] [CrossRef] [PubMed]
- Korhonen, J. Long-term changes in lake ice cover in Finland. Nord. Hydrol. 2006, 37, 347–363. [Google Scholar] [CrossRef]
- Livingstone, D.; Adrian, R. Modeling the duration of intermittent ice cover on a lake for climate-change studies. Limnol. Oceanogr. 2009, 54, 1709–1722. [Google Scholar] [CrossRef]
- Bernhardt, J.; Engelhardt, C.; Kirillin, G.; Matschullat, J. Lake ice phenology in Berlin-Brandenburg from 1947–2007: Observations and model hindcasts. Clim. Chang. 2011, 112, 791–817. [Google Scholar] [CrossRef]
- Efremova, T.; Palshin, N. Ice phenomena terms on the water bodies of northwestern Russia. Meteorol. Hydrol. 2011, 36, 559–565. [Google Scholar] [CrossRef]
- Karetnikov, S.; Leppäranta, M.; Montonen, A. Time series over 100 years of the ice season in Lake Ladoga. J. Great Lakes Res. 2017, 43, 979–988. [Google Scholar] [CrossRef]
- Mironov, D.; Ritter, B.; Schulz, J.-P.; Buchhold, M.; Lange, M.; MacHulskaya, E. Parameterisation of sea and lake ice in numerical weather prediction models of the German Weather Service. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 17330. [Google Scholar] [CrossRef]
- Yang, Y.; Leppäranta, M.; Li, Z.; Cheng, B. An ice model for Lake Vanajavesi, Finland. Tellus A 2012, 64, 17202. [Google Scholar] [CrossRef]
- Leppäranta, M.; Wen, L. Ice phenology in Eurasian lakes over spatial location and altitude. Water 2022, 14, 1037. [Google Scholar] [CrossRef]
- Wang, J.; Bai, X.; Hu, H.; Clites, A.; Holton, M.; Lofgren, B. Temporal and spatial variability of Great Lakes ice cover, 1973–2010. J. Clim. 2012, 25, 1318–1329. [Google Scholar] [CrossRef]
- Murfitt, J.; Duguay, C.R. 50 years of lake ice research from active microwave remote sensing: Progress and prospects. Remote Sens. Environ. 2021, 264, 112616. [Google Scholar] [CrossRef]
- Wang, X.; Qiu, Y.; Zhang, Y.; Lemmetyinen, J.; Cheng, B.; Liang, E.; Leppäranta, M. A lake ice phenology dataset for the Northern Hemisphere based on passive microwave remote sensing. Big Earth Data 2021, 6, 401–419. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Repina, I.A.; Ganbat, G.; Davaa, G. Numerical simulation of ice cover in saline lakes. Izv. Atmos. Ocean. Phys. 2019, 55, 129–139. [Google Scholar] [CrossRef]
- Leppäranta, M. Interpretation of statistics of lake ice time series for climate variability. Hydrol. Res. 2014, 45, 673–684. [Google Scholar] [CrossRef]
- Kirillin, G.; Leppäranta, M.; Terzhevik, A.; Bernhardt, J.; Engelhardt, C.; Granin, N.; Golosov, S.; Efremova, T.; Palshin, N.; Sherstyankin, P.; et al. Physics of seasonally ice-covered lakes: Major drivers and temporal/spatial scales. Aquat. Ecol. 2012, 74, 659–682. [Google Scholar]
- Sahlberg, J. A hydrodynamical model for calculating the vertical temperature profile in lakes during cooling. Nord. Hydrol. 1983, 14, 239–254. [Google Scholar] [CrossRef]
- Thompson, R.; Price, D.; Cameron, N.; Jones, V.; Bigler, C.; Catalan, J.; Rosén, P.; Hall, R.I.; Weckström, J.; Korhola, A. Quantitative calibration of remote mountain lake sediments as climate recorders of ice-cover duration. Arct. Antarct. Alp. Res. 2005, 37, 626–635. [Google Scholar] [CrossRef]
- Cao, X.; Lu, P.; Leppäranta, M.; Arvola, L.; Huotari, J.; Shi, X.; Li, G.; Li, Z. Solar radiation transfer for an ice-covered lake in the central Asian arid climate zone. Inland Waters 2020, 11, 89–103. [Google Scholar] [CrossRef]
- Huang, W.F.; Li, Z.; Han, H.; Niu, F.; Lin, Z.; Leppäranta, M. Structural analysis of thermokarst lake ice in Beiluhe Basin, Qinghai–Tibet Plateau. Cold Reg. Sci. Technol. 2012, 72, 33–42. [Google Scholar] [CrossRef]
- Leppäranta, M.; Lindgren, E.; Arvola, L. Heat balance of supraglacial lakes in the western Dronning Maud Land. Ann. Glaciol. 2016, 57, 39–46. [Google Scholar] [CrossRef]
- Leppäranta, M.; Lindgren, E.; Wen, L.; Kirillin, G. Ice cover decay and heat balance in Lake Kilpisjärvi in Arctic tundra. J. Limnol. 2019, 78, 163–175. [Google Scholar] [CrossRef]
- Rodhe, B. On the relation between air temperature and ice formation in the Baltic. Geogr. Ann. 1952, 1–2, 176–202. [Google Scholar]
- Hodgson, D.A. Antarctic lakes. In Encyclopedia of Lakes and Reservoirs; Bengtsson, L., Herschy, R.W., Fairbridge, R.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 26–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leppäranta, M. Ice Phenology and Thickness Modelling for Lake Ice Climatology. Water 2023, 15, 2951. https://doi.org/10.3390/w15162951
Leppäranta M. Ice Phenology and Thickness Modelling for Lake Ice Climatology. Water. 2023; 15(16):2951. https://doi.org/10.3390/w15162951
Chicago/Turabian StyleLeppäranta, Matti. 2023. "Ice Phenology and Thickness Modelling for Lake Ice Climatology" Water 15, no. 16: 2951. https://doi.org/10.3390/w15162951





