Characteristics of the Sediment Transport Process in Vegetation Hillslopes under Different Flow Rates
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Apparatus and Treatments
2.2. Data Measurement and Analysis
3. Results and Discussion
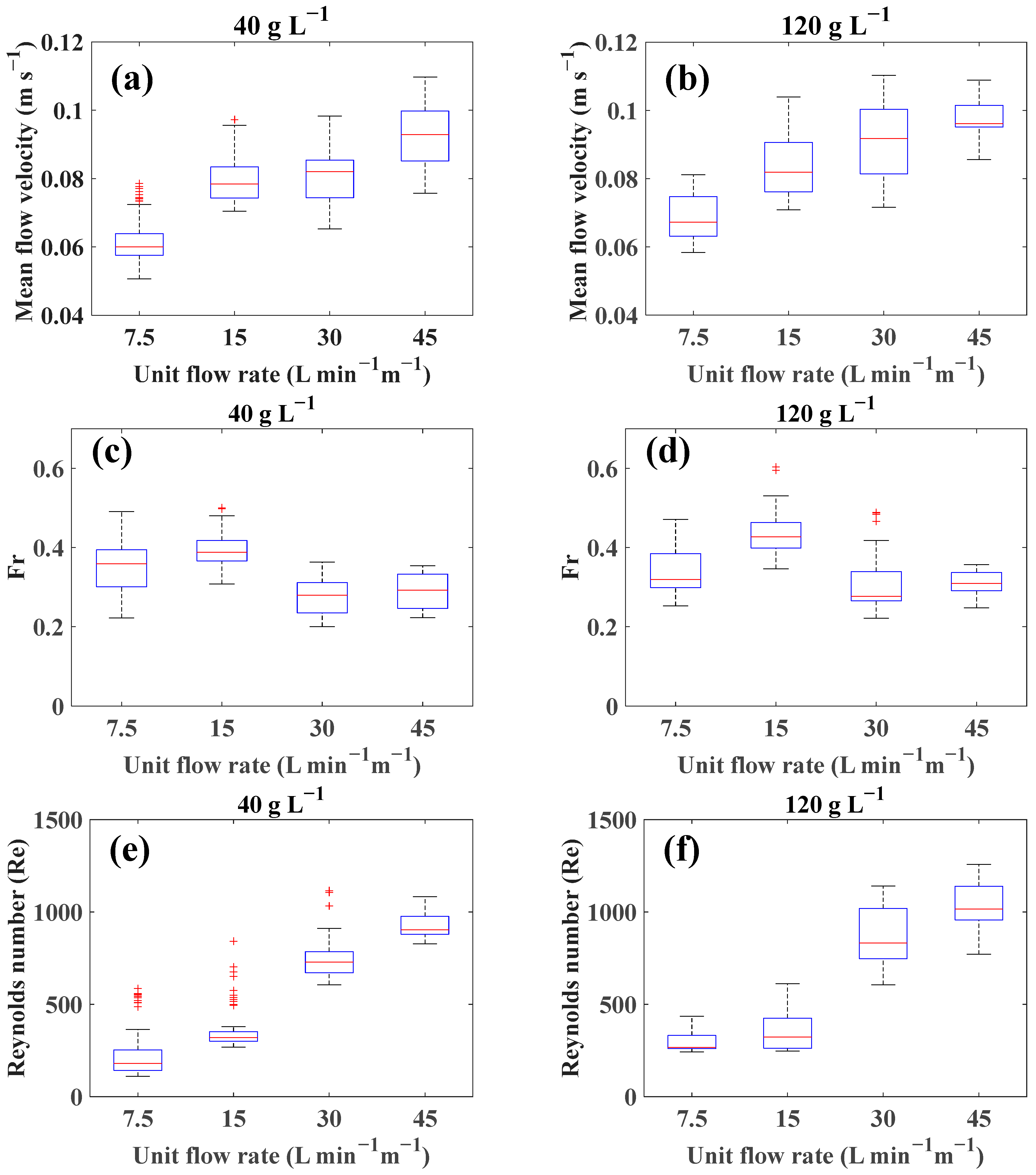
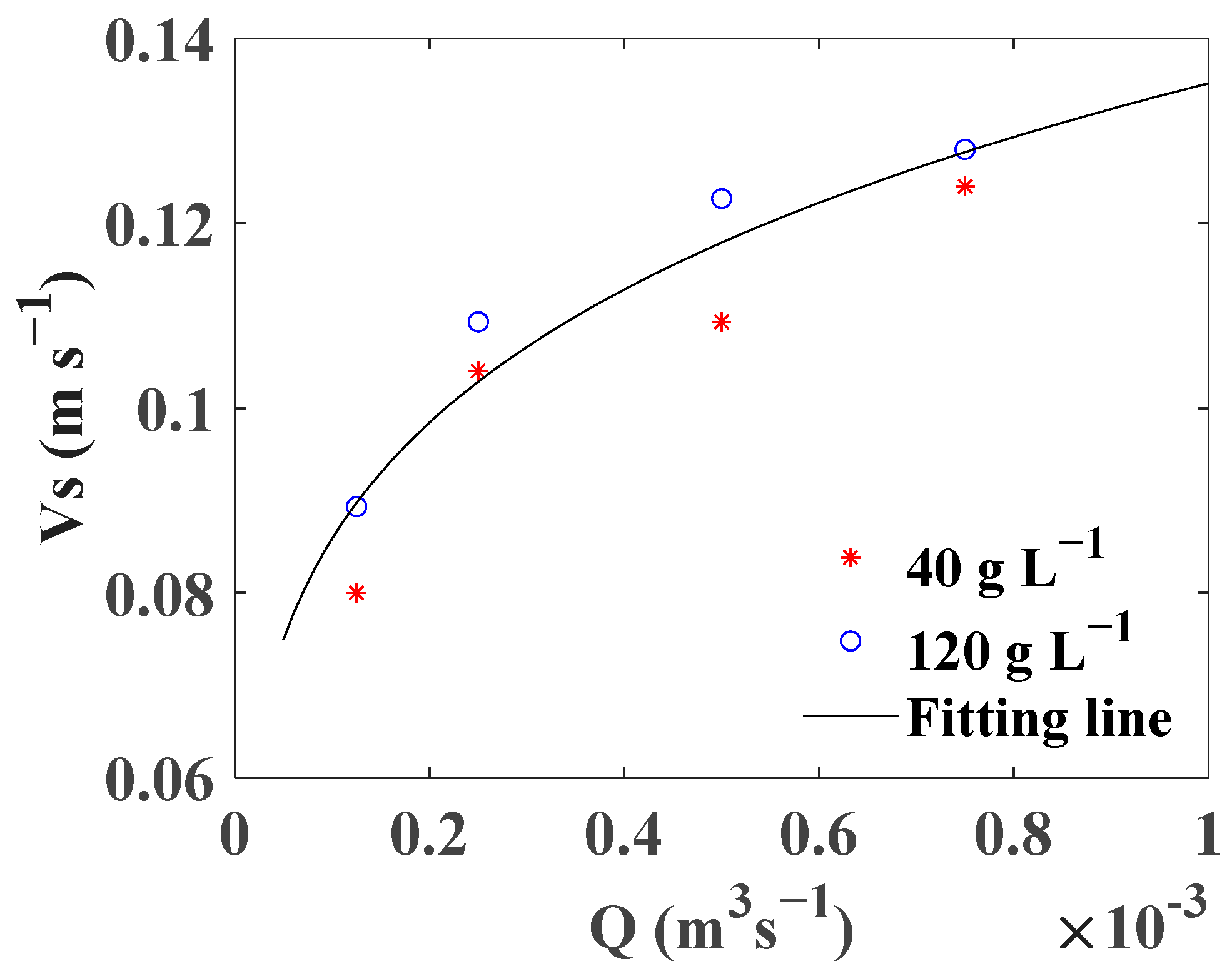
3.1. Overland Flow Pattern under Different Inflow Rates
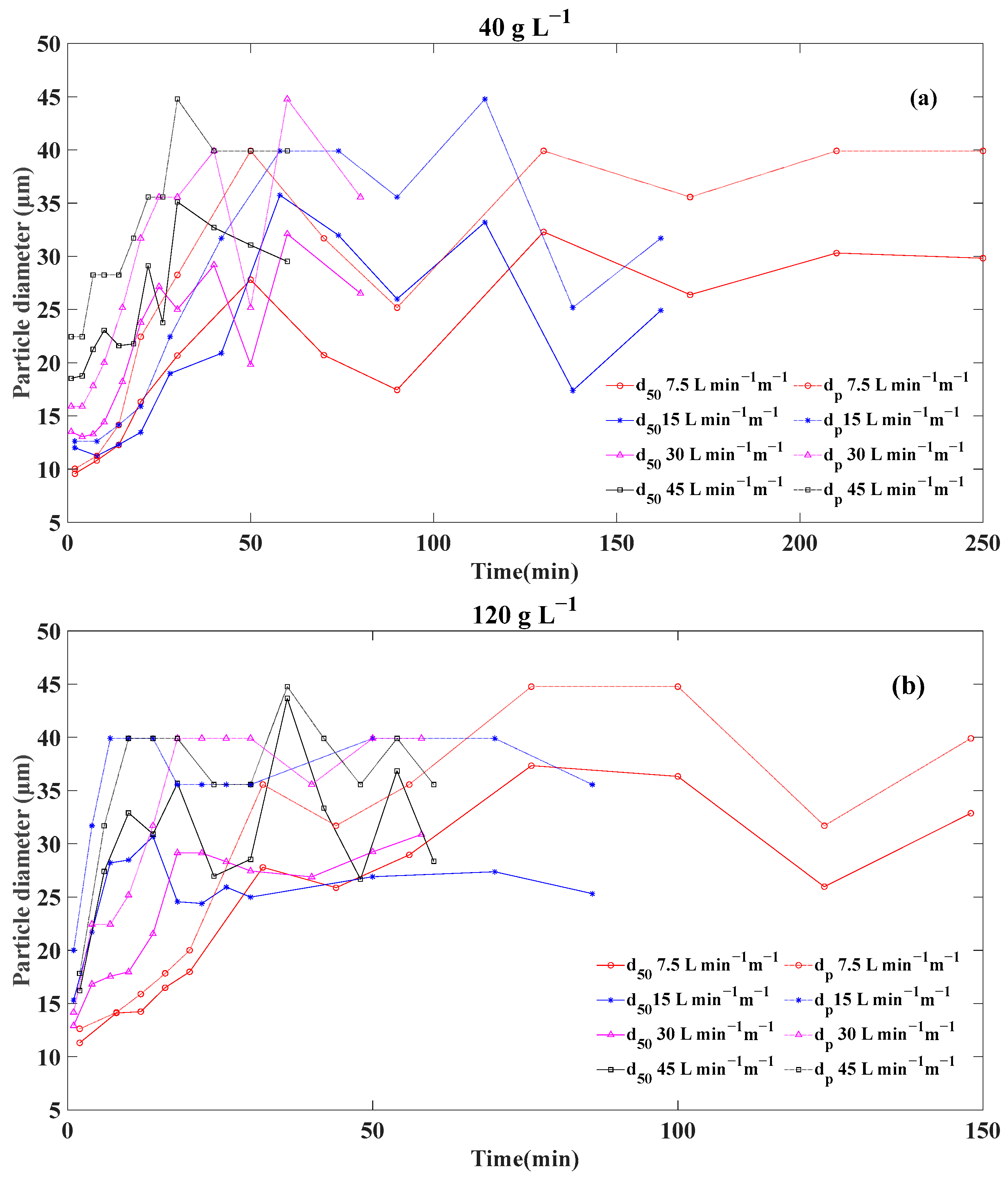
3.2. Relationship between Representative Particle Sizes and Sediment Delivery Rate
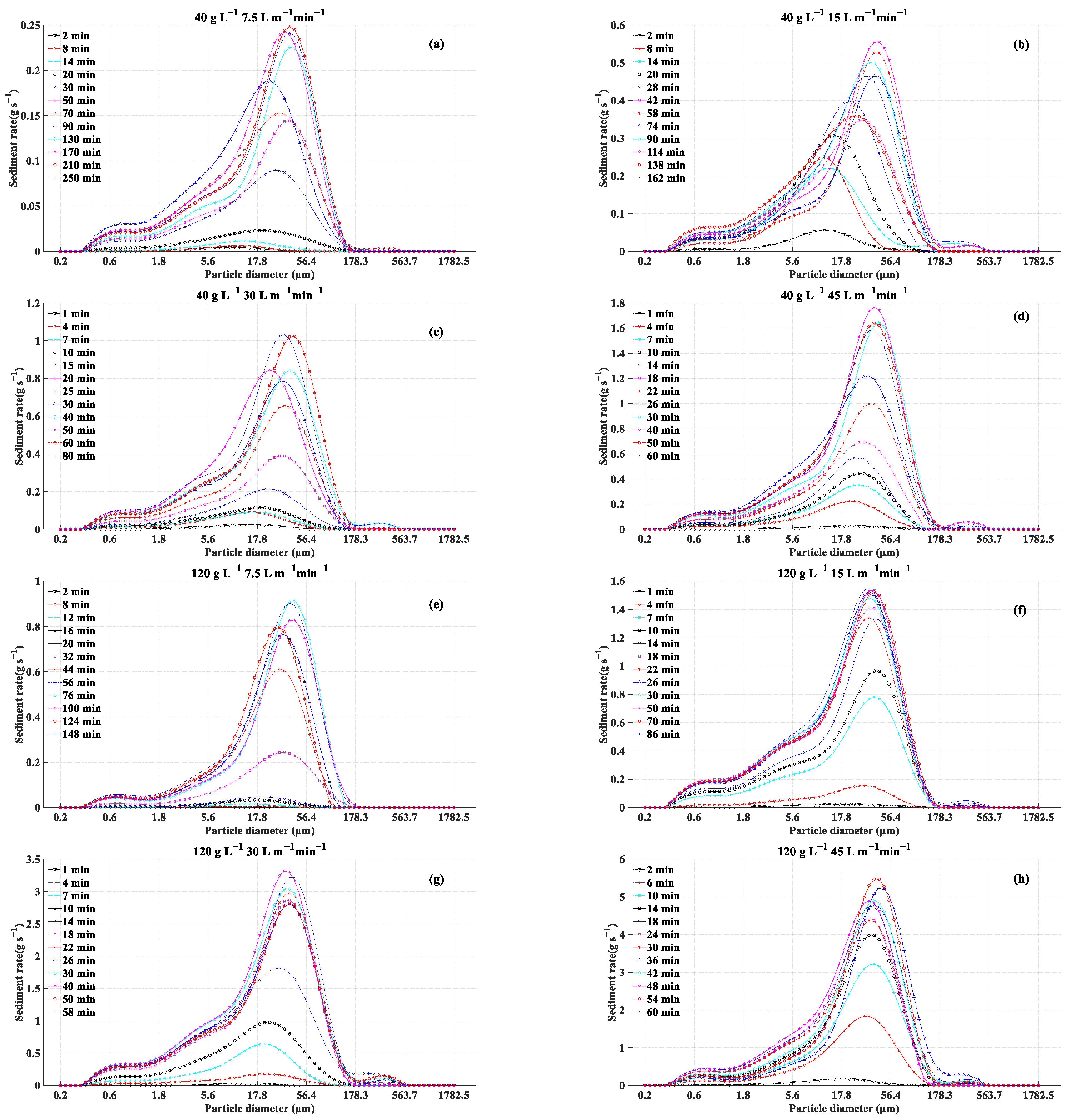
3.3. Particle Sorting of Sediment Transport by Overland Flow in VFSs
4. Conclusions
- (1)
- During the process of sediment trapping by VFSs, the differences in sediment concentration of overland flow do not affect the parameters in the power relationship between the discharge and flow velocity.
- (2)
- The calculation results showed that some measurement points were still laminar flow when Re was used to indicate the flow pattern of the shallow overland flow on the vegetation hillslope. Under the influence of dense vegetation on the slope, it is difficult to form laminar flow when the slope flow is disturbed. Therefore, using Re alone may not be effective in determining the flow pattern on vegetation-covered hillslopes.
- (3)
- When describing the relationship between sediment particle size and sediment delivery rate on vegetation hillslopes, the peak particle size was better than the median particle size and the linear function was more stable than the power function. Therefore, they can be considered for the construction of relevant erosion models.
- (4)
- During the sediment-trapping process by VFSs, the sediment-trapping capacity of VFSs gradually decreases and the increase in sediment discharge is accompanied by a greater proportion of coarse sediment particles. Under the same flow rate conditions, when the sediment concentration was greater, the amount and proportion of coarse sediment particles at the outlet increased faster. Using only a certain particle size threshold to distinguish suspended and bed load sediment may lead to inaccurate estimation of sediment-trapping performance by VFSs. The assumption that the coverage of sediment deposition changes the original underlying surface, resulting in a decrease in sediment-trapping efficiency, should be considered simultaneously.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmad, N.S.B.N.; Mustafa, F.B.; Didams, G. A systematic review of soil erosion control practices on the agricultural land in Asia. Int. Soil Water Conserv. Res. 2020, 8, 103–115. [Google Scholar] [CrossRef]
- Meena, D.C.; Rao, C.A.R.; Dhyani, B.L.; Dogra, P.; Samuel, J.; Dupdal, R.; Dubey, S.K.; Mishra, P.K. Socio-Economic and Environment Benefits of Soil and Water Conservation Technologies in India: A Critical Review. Int. J. Curr. Microbiol. Appl. Sci. 2020, 9, 2867–2881. [Google Scholar] [CrossRef]
- Sharifi, A.; Hosseingholizadeh, M. The Effect of Rapid Population Growth on Urban Expansion and Destruction of Green Space in Tehran from 1972 to 2017. J. Indian Soc. Remote. Sens. 2019, 47, 1063–1071. [Google Scholar] [CrossRef]
- Deng, L.; Shangguan, Z.-P.; Li, R. Effects of the grain-for-green program on soil erosion in China. Int. J. Sediment Res. 2012, 27, 120–127. [Google Scholar] [CrossRef]
- Sun, W.; Shao, Q.; Liu, J.; Zhai, J. Assessing the effects of land use and topography on soil erosion on the Loess Plateau in China. Catena 2014, 121, 151–163. [Google Scholar] [CrossRef]
- Mekonnen, M.; Keesstra, S.D.; Stroosnijder, L.; Baartman, J.E.M.; Maroulis, J. Soil Conservation Through Sediment Trapping: A Review. Land Degrad. Dev. 2015, 26, 544–556. [Google Scholar] [CrossRef]
- Baptist, M.J.; Babovic, V.; Uthurburu, J.R.; Keijzer, M.; Uittenbogaard, R.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Gumiere, S.J.; Le Bissonnais, Y.; Raclot, D.; Cheviron, B. Vegetated filter effects on sedimentological connectivity of agricultural catchments in erosion modelling: A review. Earth Surf. Process. Landforms 2011, 36, 3–19. [Google Scholar] [CrossRef]
- Flanagan, D.C.; Nearing, M.A. Sediment particle sorting on hillslope profiles in the WEPP model. Trans. ASAE 2000, 43, 573–583. [Google Scholar] [CrossRef]
- Ghadiri, H.; Rose, C.W.; Hogarth, W.L. The influence of grass and porous barrier strips on runoff hydrology and sediment transport. Trans. ASAE 2001, 44, 259–268. [Google Scholar] [CrossRef]
- Hairsine, P.B.; Beuselinck, L.; Sander, G.C. Sediment transport through an area of net deposition. Water Resour. Res. 2002, 38, 22-1–22-7. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Parsons, J.E.; Gilliam, J. Modeling hydrology and sediment transport in vegetative filter strips. J. Hydrol. 1999, 214, 111–129. [Google Scholar] [CrossRef]
- Luo, M.; Pan, C.; Liu, C. Modeling study on the time-varying process of sediment trapping in vegetative filter strips. Sci. Total Environ. 2020, 725, 138361. [Google Scholar] [CrossRef]
- Luo, M.; Pan, C.; Cui, Y.; Wu, Y.; Liu, C. Sediment particle selectivity and its response to overland flow hydraulics within grass strips. Hydrol. Process. 2020, 34, 5528–5542. [Google Scholar] [CrossRef]
- Saleh, I.; Kavian, A.; Roushan, M.H.; Jafarian, Z. The efficiency of vegetative buffer strips in runoff quality and quantity control. Int. J. Environ. Sci. Technol. 2018, 15, 811–820. [Google Scholar] [CrossRef]
- Zhou, Z.-C.; Gan, Z.-T.; Shangguan, Z.-P. Sediment Trapping from Hyperconcentrated Flow as Affected by Grass Filter Strips. Pedosphere 2013, 23, 372–375. [Google Scholar] [CrossRef]
- Jin, C.; Römkens, M.J.M. Experimental studies of factors in determining sediment trapping in vegetative filter strips. Trans. ASAE 2001, 44, 277–288. [Google Scholar] [CrossRef]
- Zhao, C.-H.; Gao, J.-E.; Zhang, M.-J.; Wang, F.; Zhang, T. Sediment deposition and overland flow hydraulics in simulated vegetative filter strips under varying vegetation covers. Hydrol. Process. 2016, 30, 163–175. [Google Scholar] [CrossRef]
- Ma, L.; Pan, C.; Teng, Y.; Shangguan, Z. The performance of grass filter strips in controlling high-concentration suspended sediment from overland flow under rainfall/non-rainfall conditions. Earth Surf. Process. Landforms 2013, 38, 1523–1534. [Google Scholar] [CrossRef]
- Wang, S.; Flanagan, D.C.; Engel, B.A. Estimating sediment transport capacity for overland flow. J. Hydrol. 2019, 578, 123985. [Google Scholar] [CrossRef]
- Pan, C.; Ma, L.; Shangguan, Z.; Ding, A. Determining the sediment trapping capacity of grass filter strips. J. Hydrol. 2011, 405, 209–216. [Google Scholar] [CrossRef]
- Farenhorst, A.; Bryan, R. Particle size distribution of sediment transported by shallow flow. Catena 1995, 25, 47–62. [Google Scholar] [CrossRef]
- Hayes, J.C.; Barfield, B.J.; Barnhisel, R.I. Performance of Grass Filters Under Laboratory and Field Conditions. Trans. ASAE 1984, 27, 1321–1331. [Google Scholar] [CrossRef]
- Deletic, A. Sediment transport in urban runoff over grassed areas. J. Hydrol. 2005, 301, 108–122. [Google Scholar] [CrossRef]
- Zhang, G.-H.; Wang, L.-L.; Tang, K.-M.; Luo, R.-T.; Zhang, X.C. Effects of sediment size on transport capacity of overland flow on steep slopes. Hydrol. Sci. J. 2011, 56, 1289–1299. [Google Scholar] [CrossRef]
- Wang, W.; Li, Z.; Su, H.; Xiao, J.; Han, F.; Li, Z. Spatial and seasonal variability, control factors and health risk of fluoride in natural water in the Loess Plateau of China. J. Hazard. Mater. 2022, 434, 128897. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Pan, C.; Li, C.; Luo, M.; Wang, X. A field investigation on ephemeral gully erosion processes under different upslope inflow and sediment conditions. J. Hydrol. 2019, 572, 517–527. [Google Scholar] [CrossRef]
- Martínez-Mena, M.; Castillo, V.; Albaladejo, J. Relations between interrill erosion processes and sediment particle size distribution in a semiarid Mediterranean area of SE of Spain. Geomorphology 2002, 45, 261–275. [Google Scholar] [CrossRef]
- Pan, C.; Ma, L.; Wainwright, J.; Shangguan, Z. Overland flow resistances on varying slope gradients and partitioning on grassed slopes under simulated rainfall. Water Resour. Res. 2016, 52, 2490–2512. [Google Scholar] [CrossRef] [Green Version]
- Luk, S.H.; Merz, W. Use of the salt tracing technique to determine the velocity of overland flow. Soil Technol. 1992, 5, 289–301. [Google Scholar] [CrossRef]
- Shang, H.; Zhang, K.; Wang, Z.; Yang, J.; He, M.; Pan, X.; Fang, C. Effect of varying wheatgrass density on resistance to overland flow. J. Hydrol. 2020, 591, 125594. [Google Scholar] [CrossRef]
- Mu, H.; Yu, X.; Fu, S.; Yu, B.; Liu, Y.; Zhang, G. Effect of stem basal cover on the sediment transport capacity of overland flows. Geoderma 2019, 337, 384–393. [Google Scholar] [CrossRef]
- Luo, M.; Pan, C.; Cui, Y.; Guo, Y.; Wu, Y. Effects of Different Aboveground Structural Parts of Grass Strips on the Sediment-Trapping Process. Sustainability 2021, 13, 7591. [Google Scholar] [CrossRef]
- Fu, X.T.; Zhang, L.P.; Wu, X.Y.; Wang, X.Y.; Zhang, H.S. Dynamic simulation on hydraulic characteristic values of overland flow. Water Resour. 2012, 39, 474–480. [Google Scholar] [CrossRef]
- Liu, G.; Xu, W.N.; Zhang, Q.; Xia, Z.Y. Interrill and Rill Erosion on Hillslope. Appl. Mech. Mater. 2012, 170, 1344–1347. [Google Scholar] [CrossRef]
- Beuselinck, L.; Govers, G.; Hairsine, P.; Sander, G.; Breynaert, M. The influence of rainfall on sediment transport by overland flow over areas of net deposition. J. Hydrol. 2002, 257, 145–163. [Google Scholar] [CrossRef]
- Pan, C.; Ma, L.; Wainwright, J. Particle selectivity of sediment deposited over grass barriers and the effect of rainfall. Water Resour. Res. 2016, 52, 7963–7979. [Google Scholar] [CrossRef] [Green Version]
- Lambrechts, T.; François, S.; Lutts, S.; Muñoz-Carpena, R.; Bielders, C.L. Impact of plant growth and morphology and of sediment concentration on sediment retention efficiency of vegetative filter strips: Flume experiments and VFSMOD modeling. J. Hydrol. 2014, 511, 800–810. [Google Scholar] [CrossRef]
- Pan, D.; Gao, X.; Dyck, M.; Song, Y.; Wu, P.; Zhao, X. Dynamics of runoff and sediment trapping performance of vegetative filter strips: Run-on experiments and modeling. Sci. Total. Environ. 2017, 593, 54–64. [Google Scholar] [CrossRef]


| Soil Type | Soil Texture | The Median Diameter (d50/μm) | ||||||
|---|---|---|---|---|---|---|---|---|
| Loessial soil | Sandy loam soil | 39.9 ± 2.7 | ||||||
| Particle size distribution (%)/μm | ||||||||
| >1000 | 1000−500 | 500−250 | 250−100 | 100−50 | 50−20 | 20−2 | 2−1 | <1 |
| 0 | 0.55 ± 0.34 | 1.14 ± 0.07 | 5.27 ± 1.48 | 29.15 ± 2.73 | 46.04 ± 1.43 | 15.32 ± 2.15 | 0.87 ± 0.11 | 1.66 ± 0.14 |
| Test Code * | Slope and Sediment Concentration | Designed Flow Rate Q (L min−1 m−1) | Duration t (min) |
|---|---|---|---|
| S15Q7.5SC40 | S = 15° SC = 40 g L−1 | 7.5 | 250 |
| S15Q15SC40 | 15 | 162 | |
| S15Q30SC40 | 30 | 88 | |
| S15Q45SC40 | 45 | 62 | |
| S15Q7.5SC120 | S = 15° SC = 120 g L−1 | 7.5 | 156 |
| S15Q15SC120 | 15 | 90 | |
| S15Q30SC120 | 30 | 58 | |
| S15Q45SC120 | 45 | 60 |
| Experimental Code | V (m/s) | Fr | Re |
|---|---|---|---|
| S15Q7.5SC40 | 0.051~0.079 | 0.22~0.49 | 110~585 |
| S15Q15SC40 | 0.070~0.097 | 0.31~0.50 | 268~842 |
| S15Q30SC40 | 0.065~0.098 | 0.20~0.36 | 606~1115 |
| S15Q45SC40 | 0.076~0.110 | 0.22~0.35 | 828~1083 |
| S15Q7.5SC120 | 0.058~0.081 | 0.25~0.47 | 243~436 |
| S15Q15SC120 | 0.071~0.104 | 0.35~0.60 | 247~612 |
| S15Q30SC120 | 0.072~0.110 | 0.22~0.49 | 606~1141 |
| S15Q45SC120 | 0.086~0.109 | 0.25~0.36 | 771~1257 |
| Test Code | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α | β | R2 | k | b | R2 | α | β | R2 | k | b | R2 | |
| S15Q7.5SC40 | 0.028 | 1.471 | 0.65 | 0.196 | −1.55 | 0.69 | 0.016 | 1.520 | 0.72 | 0.141 | −1.38 | 0.74 |
| S15Q15SC40 | 0.881 | 0.623 | 0.61 | 0.246 | 1.94 | 0.58 | 0.694 | 0.717 | 0.73 | 0.205 | 1.66 | 0.71 |
| S15Q30SC40 | 0.026 | 1.927 | 0.72 | 0.944 | −10.23 | 0.76 | 0.026 | 1.758 | 0.71 | 0.640 | −8.39 | 0.74 |
| S15Q45SC40 | 0.010 | 2.291 | 0.73 | 1.730 | −26.83 | 0.78 | 0.002 | 2.632 | 0.86 | 1.458 | −30.89 | 0.91 |
| S15Q7.5SC120 | 0.009 | 2.072 | 0.78 | 0.647 | −8.56 | 0.84 | 0.009 | 1.945 | 0.79 | 0.488 | −6.96 | 0.83 |
| S15Q15SC120 | 0.116 | 1.632 | 0.34 | 1.734 | −21.28 | 0.39 | 0.024 | 1.913 | 0.39 | 1.277 | −23.01 | 0.44 |
| S15Q30SC120 | 0.028 | 2.269 | 0.86 | 3.722 | −48.24 | 0.91 | 0.012 | 2.313 | 0.90 | 2.538 | −41.64 | 0.92 |
| S15Q45SC120 | 3.071 | 0.917 | 0.38 | 2.429 | −4.04 | 0.38 | 0.308 | 1.511 | 0.58 | 3.145 | −43.95 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, M.; Pan, C.; Peng, J.; Wang, L. Characteristics of the Sediment Transport Process in Vegetation Hillslopes under Different Flow Rates. Water 2023, 15, 2922. https://doi.org/10.3390/w15162922
Luo M, Pan C, Peng J, Wang L. Characteristics of the Sediment Transport Process in Vegetation Hillslopes under Different Flow Rates. Water. 2023; 15(16):2922. https://doi.org/10.3390/w15162922
Chicago/Turabian StyleLuo, Mingjie, Chengzhong Pan, Jun Peng, and Li Wang. 2023. "Characteristics of the Sediment Transport Process in Vegetation Hillslopes under Different Flow Rates" Water 15, no. 16: 2922. https://doi.org/10.3390/w15162922
APA StyleLuo, M., Pan, C., Peng, J., & Wang, L. (2023). Characteristics of the Sediment Transport Process in Vegetation Hillslopes under Different Flow Rates. Water, 15(16), 2922. https://doi.org/10.3390/w15162922






