Detecting Annual and Seasonal Hydrological Change Using Marginal Distributions of Daily Flows
Abstract
:1. Introduction
2. Study Area and Data
3. Methodology
3.1. Daily Flows as a Stochastic Process
3.2. Periodicity Analysis
3.3. Marginal Distributions
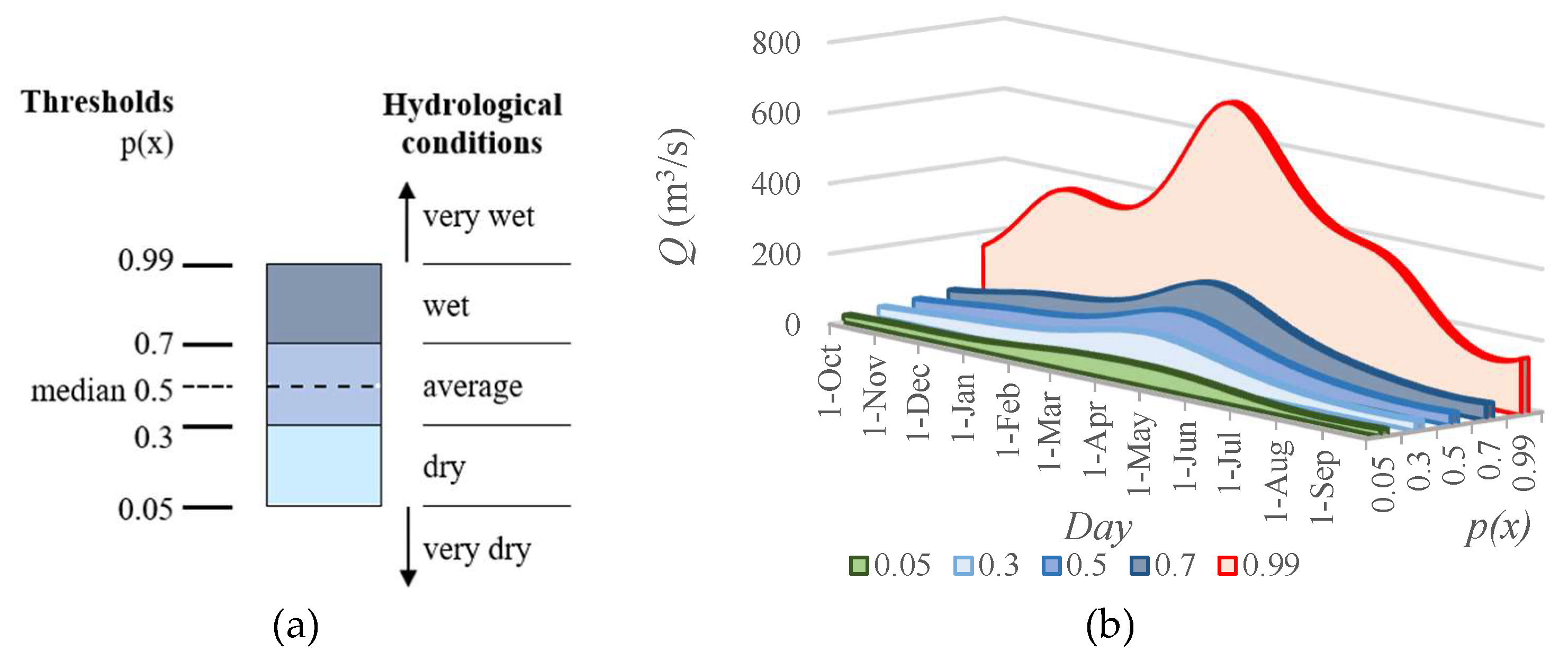
3.4. Hydrological Condition Zones
3.5. Estimating Change in Hydrological Regime
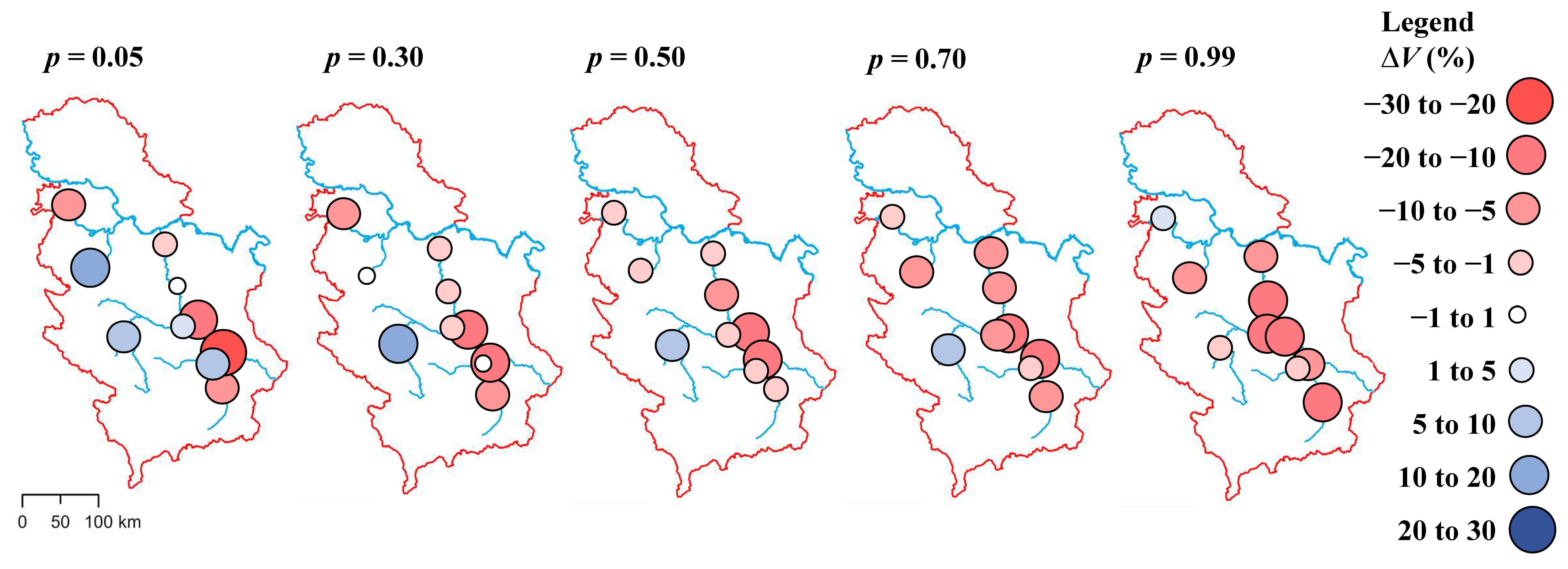
- Relative change in runoff volume, ∆Vp (%):where Vp is runoff volume below the p-th MDDF quantile representing the upper threshold of the zone for the given period.
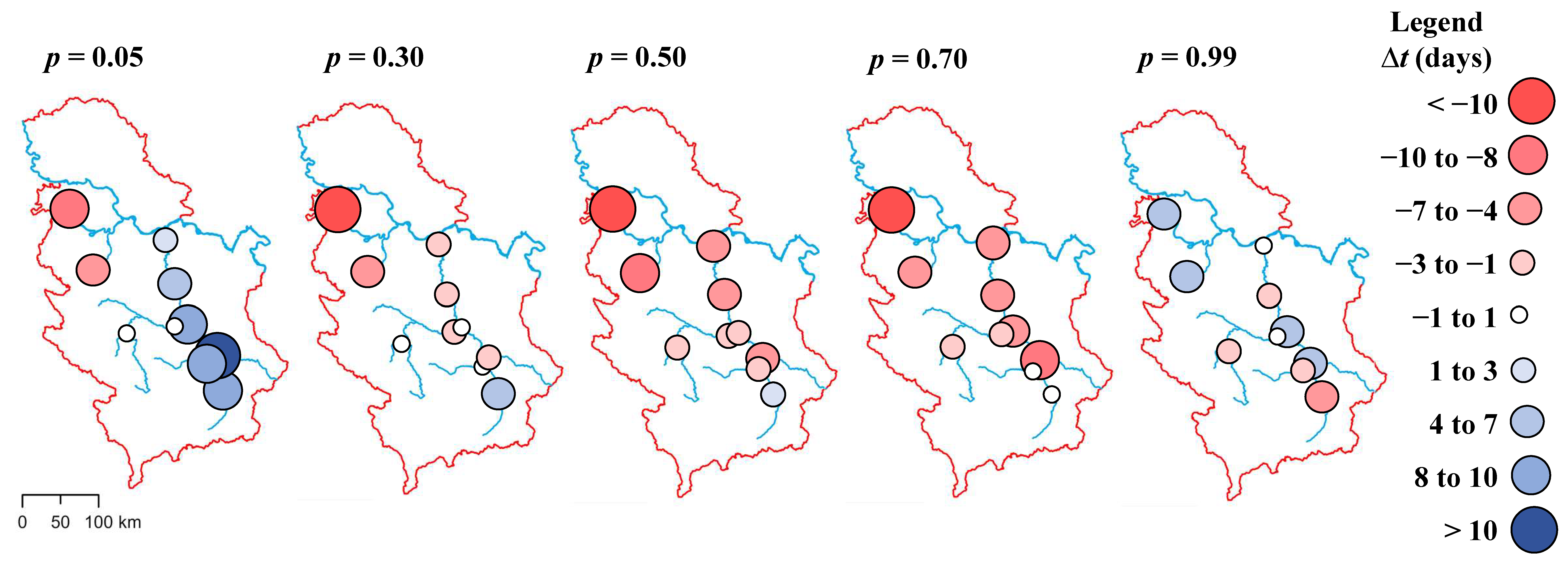
- Time shift of the centroid of the area below the MDDF quantile line, ∆t (in days):where Cp is the time coordinate (ordinal number of day within year) of the centroid of the area under the p-th MDDF quantile for the given period.
4. Results
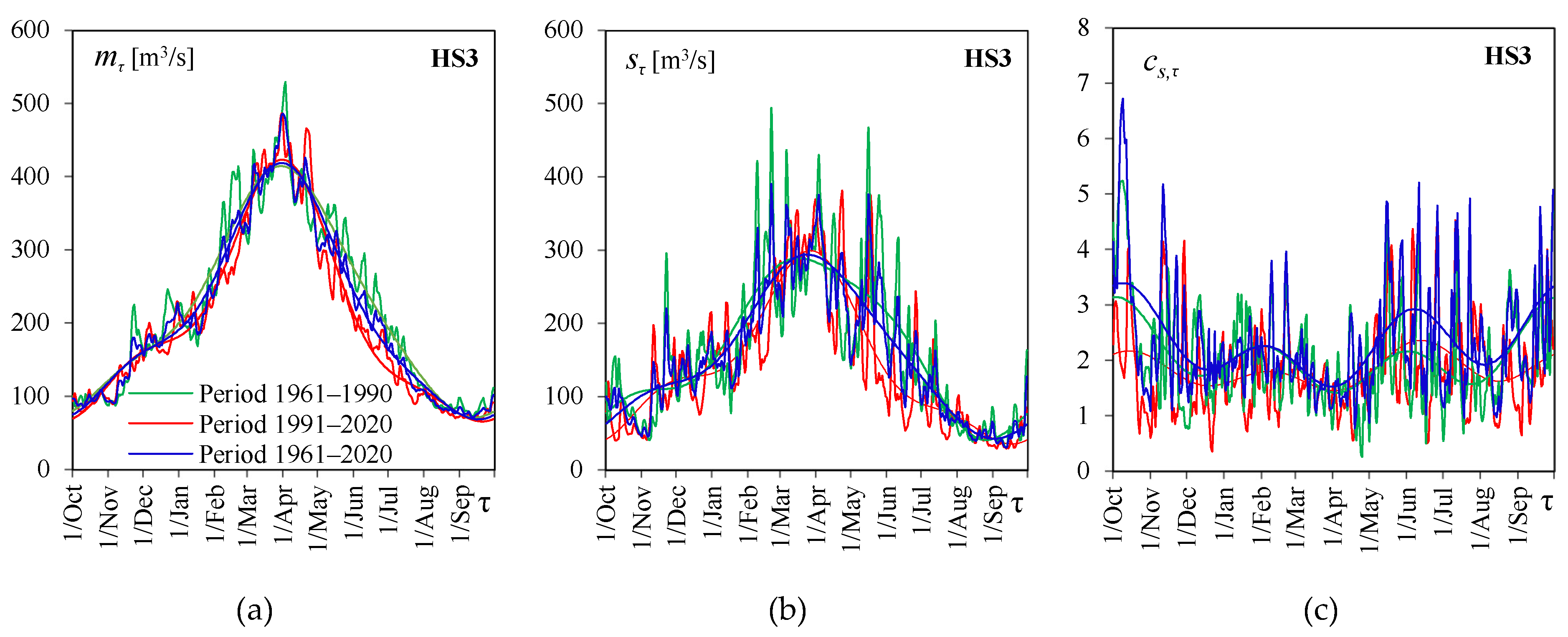
4.1. Daily Flow Statistics and Their Periodicity
4.2. Periodic Parameters of the Marginal LPT3 Distributions
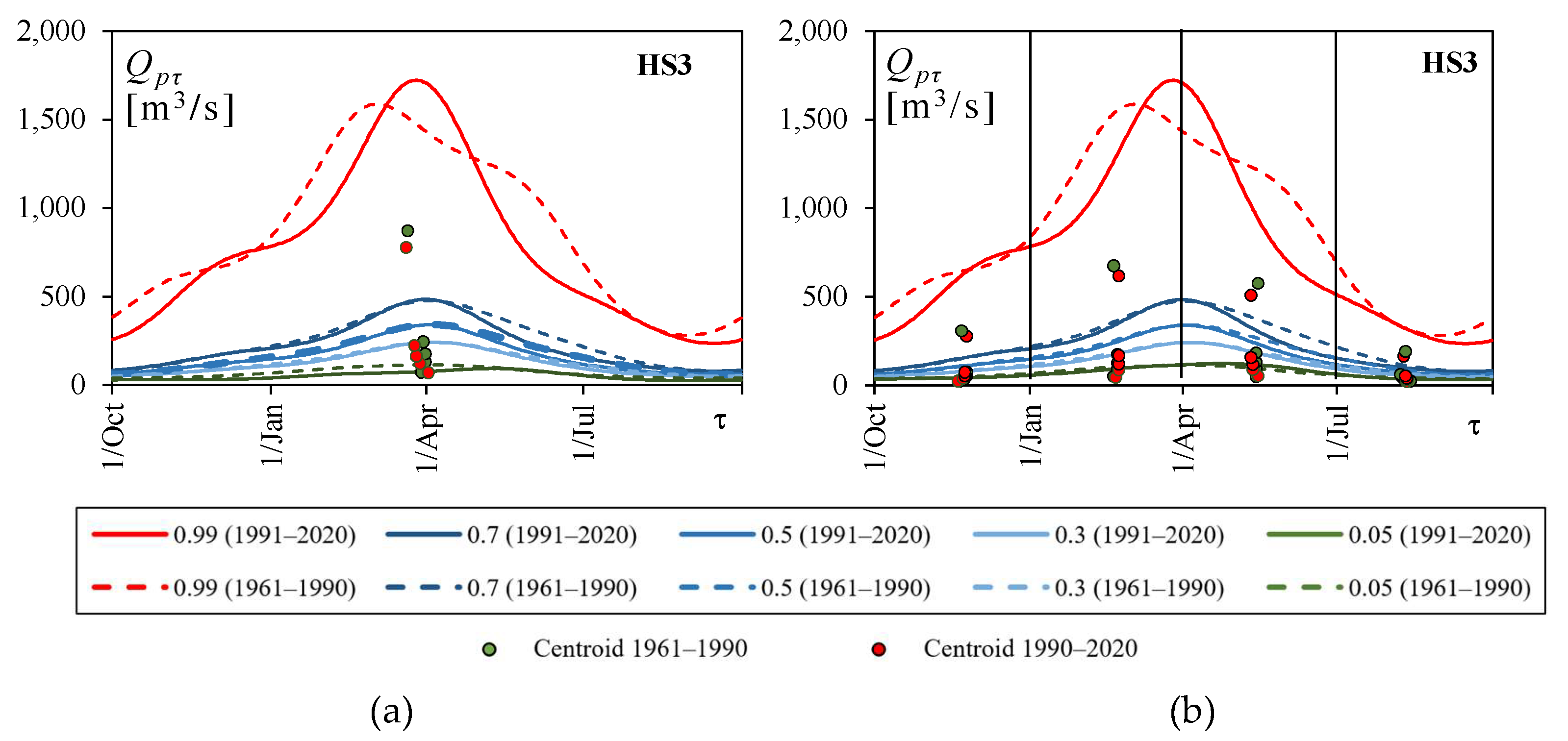
4.3. Marginal Distributions of Daily Flows
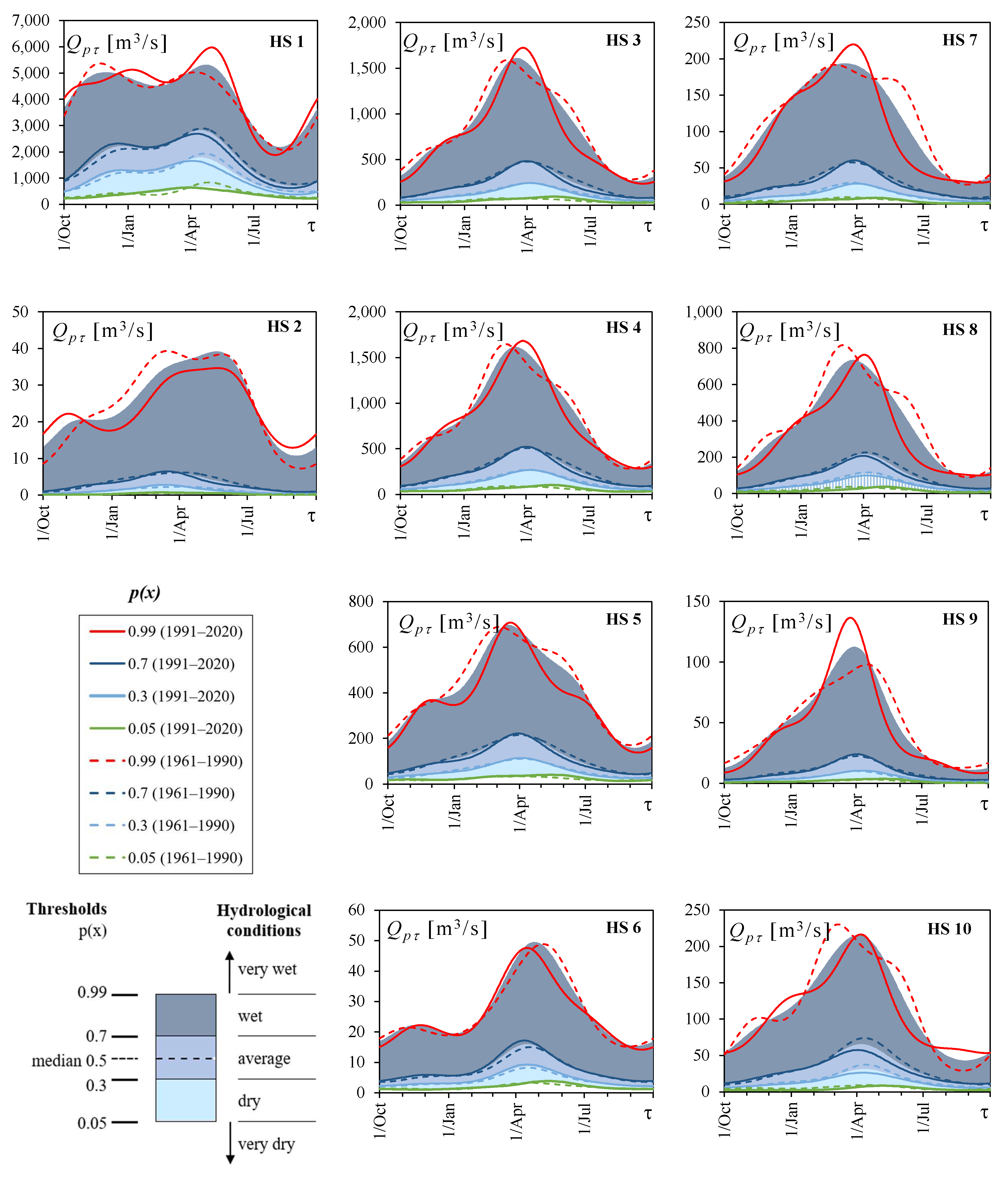
4.4. The Zones of Hydrological Conditions
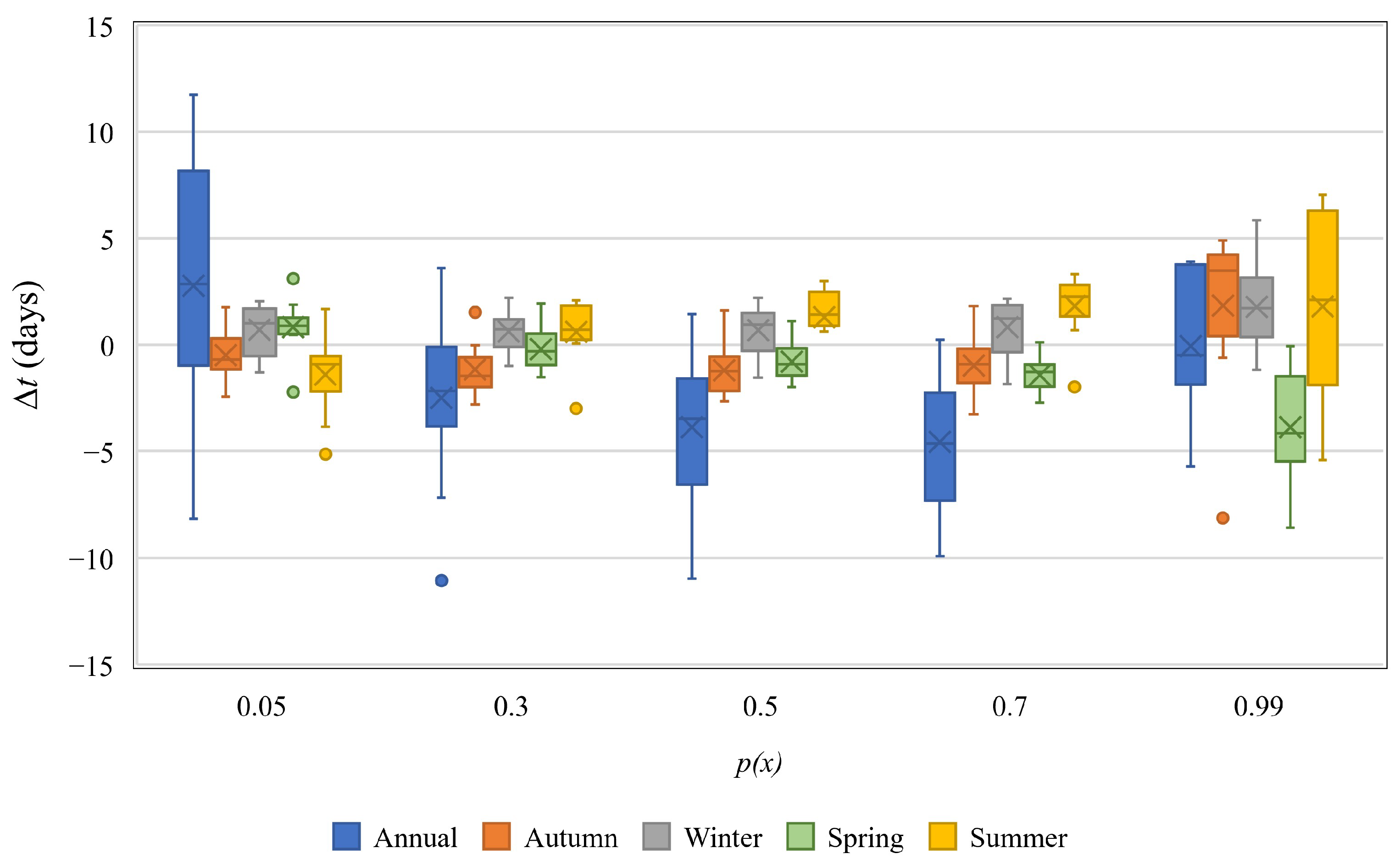
4.5. Annual and Seasonal Hydrologic Condition Changes
5. Discussion
5.1. Long-Term Changes in Hydrological Regime
5.2. Probabilistic Annual Runoff Cycle as an Indicator of Hydrological Conditions
6. Conclusions
- The seasonal runoff pattern changed from one period to another in terms of temporal shift and the occurrence of more extreme flows. However, the general pattern of seasonal runoff remained the same. The prevailing pattern is simple and unimodal, while the less present mixed regime is bimodal.
- In most of the catchments, runoff volume has decreased in the recent 1991–2020 period at both the annual and seasonal scales. The critical season is summer for dry and average conditions, with volume reduction in all catchments.
- The most pronounced shift in runoff timing is found on the annual scale. Dry and average conditions occur earlier at this scale. The change in runoff timing is found to be insignificant for all seasons and zones, except for wet conditions, which occur earlier in spring.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| HS# | Z 1 | F 2 | L 3 | M-W 4 | W-W 5 | M-K 6 |
|---|---|---|---|---|---|---|
| 1 | 0.792 | 0.888 | 0.946 | 0.792 | 0.520 | 0.444 |
| 2 | 0.507 | 0.469 | 0.732 | 0.584 | 0.367 | 0.329 |
| 3 | 0.150 | 0.430 | 0.563 | 0.092 | 0.899 | 0.211 |
| 4 | 0.402 | 0.344 | 0.442 | 0.382 | 0.700 | 0.506 |
| 5 | 0.206 | 0.809 | 0.420 | 0.152 | 0.896 | 0.367 |
| 6 | 0.374 | 0.673 | 0.619 | 0.393 | 0.053 | 0.415 |
| 7 | 0.358 | 0.089 | 0.215 | 0.184 | 0.520 | 0.255 |
| 8 | 0.111 | 0.729 | 0.793 | 0.084 | 0.367 | 0.154 |
| 9 | 0.254 | 0.968 | 0.588 | 0.262 | 0.520 | 0.293 |
| 10 | 0.601 | 0.654 | 0.390 | 0.516 | 0.700 | 0.354 |
References
- Bridgewater, P.; Guarino, E.; Thompson, R.M. Hydrology in the Anthropocene. In Encyclopedia of the Anthropocene; Elsevier: Amsterdam, The Netherlands, 2017; Volume 1–5, pp. 87–92. ISBN 9780128096659. [Google Scholar]
- WMO Hydrological Coordination Panel. Statement on the Term Hydrological Normal. Available online: https://community.wmo.int/en/activity-areas/hydrology-and-water-resources/hydrological-coordination-panel (accessed on 13 June 2023).
- Pekarova, P.; Gorbachova, L.; Mitkova, V.B.; Pekar, J.; Miklanek, P. Statistical Analysis of Hydrological Regime of the Danube River at Ceatal Izmail Station. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 012035. [Google Scholar] [CrossRef]
- Renner, M.; Bernhofer, C. Long Term Variability of the Annual Hydrological Regime and Sensitivity to Temperature Phase Shifts in Saxony/Germany. Hydrol. Earth Syst. Sci. 2011, 15, 1819–1833. [Google Scholar] [CrossRef] [Green Version]
- Plavšić, J.; Milutinović, R. O računskim nivoima vode za zaštitu od poplava na Dunavu kod Novog Sada. Vodoprivreda 2010, 42, 69–78. [Google Scholar]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes toward Earlier Streamflow Timing across Western North America. J. Clim. 2005, 18, 1136–1155. [Google Scholar] [CrossRef]
- Laaha, G.; Blöschl, G. Seasonality Indices for Regionalizing Low Flows. Hydrol. Process. 2006, 20, 3851–3878. [Google Scholar] [CrossRef] [Green Version]
- Eisner, S.; Flörke, M.; Chamorro, A.; Daggupati, P.; Donnelly, C.; Huang, J.; Hundecha, Y.; Koch, H.; Kalugin, A.; Krylenko, I.; et al. An Ensemble Analysis of Climate Change Impacts on Streamflow Seasonality across 11 Large River Basins. Clim. Chang. 2017, 141, 401–417. [Google Scholar] [CrossRef]
- Poschlod, B.; Willkofer, F.; Ludwig, R. Impact of Climate Change on the Hydrological Regimes in Bavaria. Water 2020, 12, 1599. [Google Scholar] [CrossRef]
- Yeste, P.; Rosa-Cánovas, J.J.; Romero-Jiménez, E.; García-Valdecasas Ojeda, M.; Gámiz-Fortis, S.R.; Castro-Díez, Y.; Esteban-Parra, M.J. Projected Hydrologic Changes over the North of the Iberian Peninsula Using a Euro-CORDEX Multi-Model Ensemble. Sci. Total Environ. 2021, 777, 146126. [Google Scholar] [CrossRef]
- Hobeichi, S.; Abramowitz, G.; Ukkola, A.M.; De Kauwe, M.; Pitman, A.; Evans, J.P.; Beck, H. Reconciling Historical Changes in the Hydrological Cycle over Land. NPJ Clim. Atmos. Sci. 2022, 5, 17. [Google Scholar] [CrossRef]
- Brunner, M.I.; Melsen, L.A.; Newman, A.J.; Wood, A.W.; Clark, M.P. Future Streamflow Regime Changes in the United States: Assessment Using Functional Classification. Hydrol. Earth Syst. Sci. 2020, 24, 3951–3966. [Google Scholar] [CrossRef]
- Stojković, M.; Plavšić, J.; Prohaska, S. Dugoročne promene godišnjih i sezonskih proticaja: Primer reke Save. Vodoprivreda 2014, 46, 39–48. [Google Scholar]
- Stojković, M.; Ilić, A.; Prohaska, S.; Plavšić, J. Multi-Temporal Analysis of Mean Annual and Seasonal Stream Flow Trends, Including Periodicity and Multiple Non-Linear Regression. Water Resour. Manag. 2014, 28, 4319–4335. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Robson, A. (Eds.) Detecting Trend and Other Changes in Hydrological Data; WMO/TD-No. 1013; World Meteorological Organization: Geneva, Switzerland, 2000.
- Hamed, K.H.; Ramachandra Rao, A. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. Appl. Stat. 1979, 28, 126. [Google Scholar] [CrossRef]
- Zhang, A.; Zheng, C.; Wang, S.; Yao, Y. Analysis of Streamflow Variations in the Heihe River Basin, Northwest China: Trends, Abrupt Changes, Driving Factors and Ecological Influences. J. Hydrol. Reg. Stud. 2015, 3, 106–124. [Google Scholar] [CrossRef] [Green Version]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable Nonstationarity: An Assessment of the Fitness for Purpose of Trend Tests in Hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Hannaford, J.; Buys, G.; Stahl, K.; Tallaksen, L.M. The Influence of Decadal-Scale Variability on Trends in Long European Streamflow Records. Hydrol. Earth Syst. Sci. 2013, 17, 2717–2733. [Google Scholar] [CrossRef] [Green Version]
- Stojković, M.; Prohaska, S.; Plavšić, J. Stochastic Structure of Annual Discharges of Large European Rivers. J. Hydrol. Hydromech. 2015, 63, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. (Eds.) Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-1-107-02818-0. [Google Scholar]
- Salinas-Rodríguez, S.A.; Sánchez-Navarro, R.; Barrios-Ordóñez, J.E. Frequency of Occurrence of Flow Regime Components: A Hydrology-Based Approach for Environmental Flow Assessments and Water Allocation for the Environment. Hydrol. Sci. J. 2021, 66, 193–213. [Google Scholar] [CrossRef]
- Zeiringer, B.; Seliger, C.; Greimel, F.; Schmutz, S. River Hydrology, Flow Alteration, and Environmental Flow. In Riverine Ecosystem Management; Springer International Publishing: Cham, Switzerland, 2018; pp. 67–89. [Google Scholar]
- Cammalleri, C.; Vogt, J.; Salamon, P. Development of an Operational Low-Flow Index for Hydrological Drought Monitoring over Europe. Hydrol. Sci. J. 2016, 62, 346–358. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, P.A.; Clark, M.P.; Mizukami, N.; Newman, A.J.; Barlage, M.; Gutmann, E.D.; Rasmussen, R.M.; Rajagopalan, B.; Brekke, L.D.; Arnold, J.R. Effects of Hydrologic Model Choice and Calibration on the Portrayal of Climate Change Impacts. J. Hydrometeorol. 2015, 16, 762–780. [Google Scholar] [CrossRef]
- Abdul Aziz, O.I.; Burn, D.H. Trends and Variability in the Hydrological Regime of the Mackenzie River Basin. J. Hydrol. 2006, 319, 282–294. [Google Scholar] [CrossRef]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A Global Evaluation of Streamflow Drought Characteristics. Hydrol. Earth Syst. Sci. 2006, 10, 535–552. [Google Scholar] [CrossRef] [Green Version]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate Computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef] [Green Version]
- Mihailović, V.; Blagojević, B. Izbor teorijske raspodele verovatnoća na osnovu L-momenata u proračunu pokazatelja meteorološke i hidrološke suše. Vodoprivreda 2015, 47, 273–278. [Google Scholar]
- Ozkaya, A.; Zerberg, Y. A 40-Year Analysis of the Hydrological Drought Index for the Tigris Basin, Turkey. Water 2019, 11, 657. [Google Scholar] [CrossRef] [Green Version]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Sutanto, S.J.; Van Lanen, H.A.J. Streamflow Drought: Implication of Drought Definitions and Its Application for Drought Forecasting. Hydrol. Earth Syst. Sci. 2021, 25, 3991–4023. [Google Scholar] [CrossRef]
- Yevjevich, V. Structure of Daily Hydrologic Series; Water Resources Publications: Littleton, CO, USA, 1984. [Google Scholar]
- Blum, A.G.; Archfield, S.A.; Vogel, R.M. On the Probability Distribution of Daily Streamflow in the United States. Hydrol. Earth Syst. Sci. 2017, 21, 3093–3103. [Google Scholar] [CrossRef] [Green Version]
- Yevjevich, V. Stochastic Processes in Hydrology; Water Resources Publications: Littleton, CO, USA, 1972. [Google Scholar]
- Radić, Z.; Mihailović, V. Marginalne raspodele dnevnih proticaja na reprezentativnim profilima u Srbiji. Vodoprivreda 2010, 42, 17–38. [Google Scholar]
- Mihailović, V. Složena Analiza Hidroloških Vremenskih Serija za Potrebe Modeliranja Ekstremnih Događaja (A Complex Analysis of Hydrological Time Series for Modelling Extreme Events). Doctoral Thesis, University of Belgrade—Faculty of Civil Engineering, Belgrade, Serbia, 2012. [Google Scholar]
- Hayes, D.S.; Brändle, J.M.; Seliger, C.; Zeiringer, B.; Ferreira, T.; Schmutz, S. Advancing towards Functional Environmental Flows for Temperate Floodplain Rivers. Sci. Total Environ. 2018, 633, 1089–1104. [Google Scholar] [CrossRef] [PubMed]
- Bogojević, A. Strukturna Analiza Serija Dnevnih Protoka u Profilima Hidroloških Stanica na Teritoriji Srbije (Structural Analysis of Daily Flow Series at Hydrological Stations in the Territory of Serbia). Bachelor’s Thesis, University of Niš, Faculty of Civil Engineering and Architecture, Niš, Serbia, 2022. [Google Scholar]
- Bobée, B.; Ashkar, F. The Gamma Family and Derived Distributions Applied in Hydrology; Water Resources Publications: Littleton, CO, USA, 1991; ISBN 978-0918334688. [Google Scholar]
- Elektroprivreda Srbije, HE Pirot. Available online: https://www.eps.rs/lat/djerdap/Stranice/he_pirot.aspx (accessed on 4 August 2023).
- Olsson, J.; Arheimer, B.; Borris, M.; Donnelly, C.; Foster, K.; Nikulin, G.; Persson, M.; Perttu, A.-M.; Uvo, C.; Viklander, M.; et al. Hydrological Climate Change Impact Assessment at Small and Large Scales: Key Messages from Recent Progress in Sweden. Climate 2016, 4, 39. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing Climate Both Increases and Decreases European River Floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Lobanova, A.; Liersch, S.; Nunes, J.P.; Didovets, I.; Stagl, J.; Huang, S.; Koch, H.; López, M.D.R.R.; Maule, C.F.; Hattermann, F.; et al. Hydrological Impacts of Moderate and High-End Climate Change across European River Basins. J. Hydrol. Reg. Stud. 2018, 18, 15–30. [Google Scholar] [CrossRef]
- Kovacevic-Majkic, J.; Urosev, M. Trends of Mean Annual and Seasonal Discharges of Rivers in Serbia. J. Geogr. Inst. Jovan Cvijic SASA 2014, 64, 143–160. [Google Scholar] [CrossRef]
- Leščešen, I.; Šraj, M.; Pantelić, M.; Dolinaj, D. Assessing the Impact of Climate on Annual and Seasonal Discharges at the Sremska Mitrovica Station on the Sava River, Serbia. Water Supply 2022, 22, 195–207. [Google Scholar] [CrossRef]
- The World Bank. Water and Climate Adaptation Plan for the Sava River Basin: Main Report; World Bank Group: Washington, DC, USA, 2015. Available online: https://www.savacommission.org/documents-and-publications/technical-and-project-reports/water-and-climate-adaptation-plan-for-the-sava-river-basin-watcap/245 (accessed on 13 June 2023).
- Pandžić, K.; Trninić, D.; Likso, T.; Bošnjak, T. Long-Term Variations in Water Balance Components for Croatia. Theor. Appl. Climatol. 2009, 95, 39–51. [Google Scholar] [CrossRef]
- Langsholt, E.; Lawrence, D.; Wong, W.K.; Andjelic, M.; Ivkovic, M.; Vujadinovic, M. Effects of Climate Change in The Kolubara and Toplica Catchments, Serbia; Haddeland, I., Ed.; Norwegian Water Resources and Energy Directorate: Oslo, Norway, 2013. [Google Scholar]
- Idrizovic, D.; Pocuca, V.; Vujadinovic Mandic, M.; Djurovic, N.; Matovic, G.; Gregoric, E. Impact of Climate Change on Water Resource Availability in a Mountainous Catchment: A Case Study of the Toplica River Catchment, Serbia. J. Hydrol. 2020, 587, 124992. [Google Scholar] [CrossRef]
- Tijdeman, E.; Stahl, K.; Tallaksen, L.M. Drought Characteristics Derived Based on the Standardized Streamflow Index: A Large Sample Comparison for Parametric and Nonparametric Methods. Water Resour. Res. 2020, 56, e2019WR026315. [Google Scholar] [CrossRef]
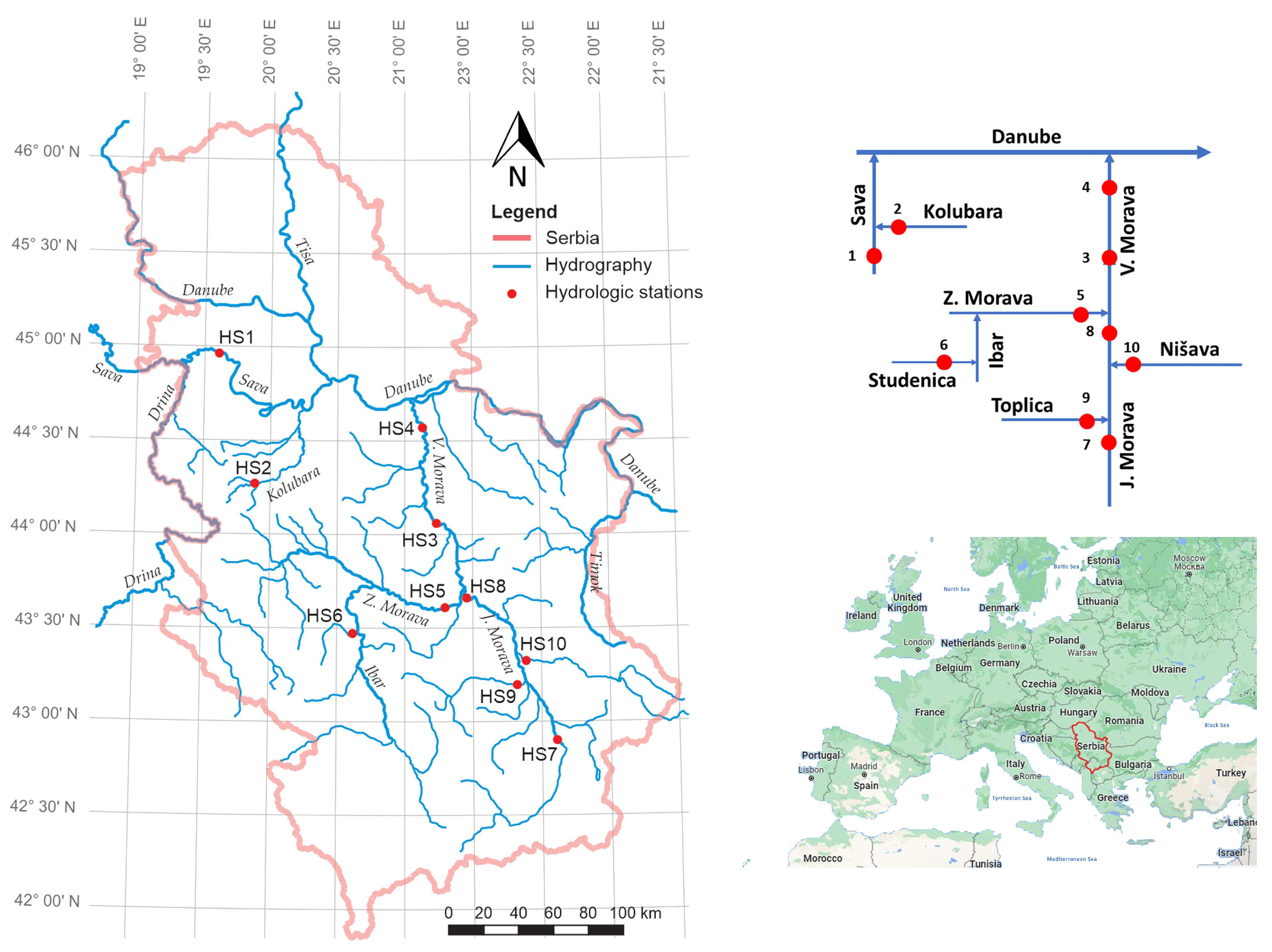





| HS# | Station Name | River | Catchment Area [km2] | Watershed |
|---|---|---|---|---|
| 1 | Sremska Mitrovica | Sava | 87,996 | Sava |
| 2 | Valjevo | Kolubara | 340 | Kolubara |
| 3 | Bagrdan | Velika Morava | 33,446 | Velika Morava |
| 4 | Ljubičevski most | Velika Morava | 37,320 | Velika Morava |
| 5 | Jasika | Zapadna Morava | 14,721 | Zapadna Morava |
| 6 | Ušće | Studenica | 540 | ZapadnaMorava |
| 7 | Grdelica | Južna Morava | 3782 | Južna Morava |
| 8 | Mojsinje | Južna Morava | 15,390 | Južna Morava |
| 9 | Doljevac | Toplica | 2052 | Južna Morava |
| 10 | Niš | Nišava | 3870 | Južna Morava |
| p(x) | Season | HS1 | HS2 | HS3 | HS4 | HS5 | HS6 | HS7 | HS8 | HS9 | HS10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | Ann. | −8 | 11 | −1 | −2 | 5 | 7 | −8 | −15 | 9 | −23 |
| Aut. | −3 | −9 | −10 | −3 | 7 | −2 | −24 | −25 | 0 | −37 | |
| Win. | 14 | 34 | −9 | −13 | −1 | 6 | −16 | −28 | 2 | −33 | |
| Spr. | −22 | 2 | 16 | 11 | 16 | 17 | 8 | 3 | 28 | −12 | |
| Sum. | −16 | −13 | −10 | −7 | −4 | −2 | 0 | −17 | −15 | −13 | |
| 0.3 | Ann. | −5 | −1 | −6 | −5 | −2 | 10 | −5 | −11 | 1 | −18 |
| Aut. | 12 | 4 | −2 | 3 | 5 | 8 | −7 | −3 | −5 | −8 | |
| Win. | 5 | 15 | −5 | −6 | −4 | 13 | −11 | −14 | −2 | −16 | |
| Spr. | −19 | −16 | −5 | −4 | −1 | 12 | 2 | −12 | 10 | −23 | |
| Sum. | −19 | −13 | −14 | −10 | −7 | 2 | 1 | −8 | −10 | −15 | |
| 0.5 | Ann. | −4 | −5 | −7 | −5 | −5 | 10 | −4 | −10 | −2 | −15 |
| Aut. | 15 | 9 | 0 | 4 | 3 | 11 | −2 | 3 | −8 | 4 | |
| Win. | 3 | 6 | −4 | −4 | −6 | 15 | −9 | −9 | −2 | −11 | |
| Spr. | −16 | −20 | −11 | −8 | −7 | 9 | −2 | −16 | 3 | −25 | |
| Sum. | −19 | −11 | −15 | −10 | −8 | 3 | −1 | −6 | −9 | −13 | |
| 0.7 | Ann. | −2 | −8 | −8 | −5 | −7 | 9 | −5 | −10 | −4 | −12 |
| Aut. | 15 | 11 | 1 | 5 | 1 | 12 | −1 | 6 | −11 | 12 | |
| Win. | 2 | −2 | −4 | −3 | −7 | 15 | −6 | −7 | −1 | −7 | |
| Spr. | −11 | −23 | −14 | −10 | −10 | 6 | −6 | −19 | −3 | −26 | |
| Sum. | −17 | −7 | −16 | −10 | −9 | 3 | −4 | −6 | −9 | −8 | |
| 0.99 | Ann. | 5 | −6 | −11 | −6 | −12 | −2 | −15 | −19 | −5 | −8 |
| Aut. | −3 | 12 | −11 | −2 | −8 | −1 | −21 | −20 | −19 | −4 | |
| Win. | 5 | −26 | −8 | −9 | −13 | 5 | 3 | −17 | 14 | −14 | |
| Spr. | 15 | −9 | −12 | −5 | −14 | −10 | −28 | −21 | −18 | −15 | |
| Sum. | 3 | 29 | −13 | −2 | −7 | 2 | −24 | −21 | −13 | 38 | |
| Legend: ΔV (%) |  | ||||||||||
| p(x) | Season | HS1 | HS2 | HS3 | HS4 | HS5 | HS6 | HS7 | HS8 | HS9 | HS10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | Ann. | −8 | −4 | 4 | 3 | 0 | 1 | 9 | 8 | 3 | 12 |
| Aut. | 0 | −1 | −1 | −1 | −2 | 1 | 2 | −1 | 0 | −1 | |
| Win. | 0 | 2 | 2 | 1 | 1 | −1 | −1 | 1 | 2 | 1 | |
| Spr. | 0 | −2 | 1 | 1 | 1 | 1 | 0 | 1 | 2 | 3 | |
| Sum. | 0 | 2 | −2 | −1 | −1 | −1 | −1 | −2 | −5 | −4 | |
| 0.3 | Ann. | −11 | −7 | −3 | −2 | −2 | −1 | 4 | −1 | 1 | −3 |
| Aut. | 0 | −2 | −1 | −1 | −3 | −1 | 2 | −1 | −2 | −2 | |
| Win. | −1 | 2 | 1 | 1 | 2 | 1 | 1 | 0 | 1 | −1 | |
| Spr. | 0 | −2 | −1 | −1 | −1 | 0 | 0 | 1 | 0 | 2 | |
| Sum. | 1 | 1 | 2 | 2 | 2 | 0 | −3 | 0 | 1 | 0 | |
| 0.5 | Ann. | −11 | −8 | −4 | −4 | −3 | −2 | 1 | −3 | 1 | −6 |
| Aut. | 0 | −2 | −1 | −1 | −3 | −1 | 2 | −1 | −2 | −2 | |
| Win. | −1 | 2 | 1 | 1 | 2 | 1 | 1 | 0 | 1 | −2 | |
| Spr. | −1 | −1 | −2 | −2 | −1 | −1 | 0 | 0 | −1 | 1 | |
| Sum. | 1 | 1 | 3 | 2 | 2 | 1 | −3 | 1 | 3 | 2 | |
| 0.7 | Ann. | −10 | −7 | −5 | −4 | −3 | −3 | −1 | −5 | 0 | −8 |
| Aut. | 0 | −3 | −1 | −1 | −2 | −1 | 2 | 0 | −2 | −2 | |
| Win. | −1 | 2 | 1 | 1 | 2 | 2 | 2 | 0 | 2 | −2 | |
| Spr. | −1 | −1 | −3 | −2 | −2 | −1 | −1 | −1 | −2 | 0 | |
| Sum. | 2 | 2 | 3 | 3 | 2 | 1 | −2 | 2 | 3 | 3 | |
| 0.99 | Ann. | 4 | 4 | −1 | 0 | 0 | −2 | −6 | −2 | −2 | 4 |
| Aut. | −1 | −8 | 4 | 3 | 1 | 2 | 4 | 5 | 4 | 4 | |
| Win. | −1 | 2 | 3 | 2 | 3 | 2 | 2 | 1 | 6 | −1 | |
| Spr. | −1 | 0 | −5 | −4 | −2 | −2 | −9 | −8 | −4 | −5 | |
| Sum. | 4 | 7 | −1 | 0 | −3 | −2 | 7 | 6 | −5 | 4 | |
| Legend: Δt (days) |  | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blagojević, B.; Mihailović, V.; Bogojević, A.; Plavšić, J. Detecting Annual and Seasonal Hydrological Change Using Marginal Distributions of Daily Flows. Water 2023, 15, 2919. https://doi.org/10.3390/w15162919
Blagojević B, Mihailović V, Bogojević A, Plavšić J. Detecting Annual and Seasonal Hydrological Change Using Marginal Distributions of Daily Flows. Water. 2023; 15(16):2919. https://doi.org/10.3390/w15162919
Chicago/Turabian StyleBlagojević, Borislava, Vladislava Mihailović, Aleksandar Bogojević, and Jasna Plavšić. 2023. "Detecting Annual and Seasonal Hydrological Change Using Marginal Distributions of Daily Flows" Water 15, no. 16: 2919. https://doi.org/10.3390/w15162919






